Single-Photon Counting with Semiconductor Resonant Tunneling Devices
Abstract
:1. Introduction
2. The Fundamentals of Resonant Tunneling Single-Photon Detection
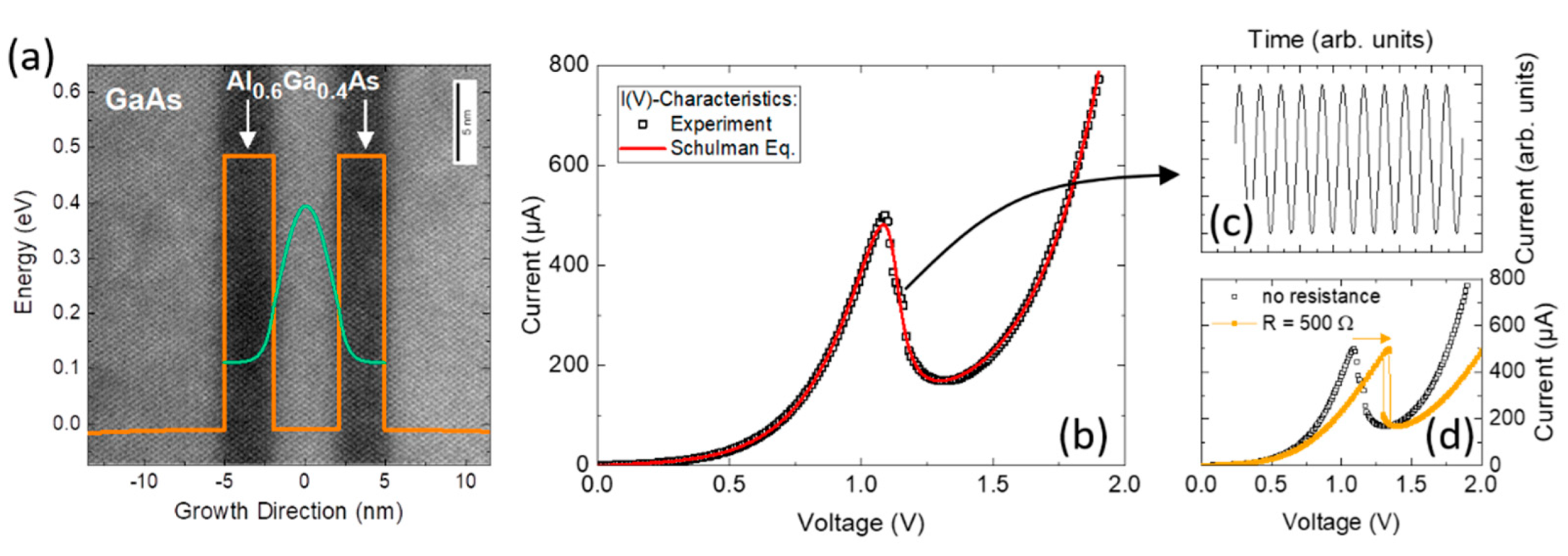
2.1. Resonant Tunneling Diodes
2.2. The Photodetection Mechanism and Operational Modes
2.2.1. Phototransistor Mode
2.2.2. Geiger Mode
2.2.3. Oscillator Mode
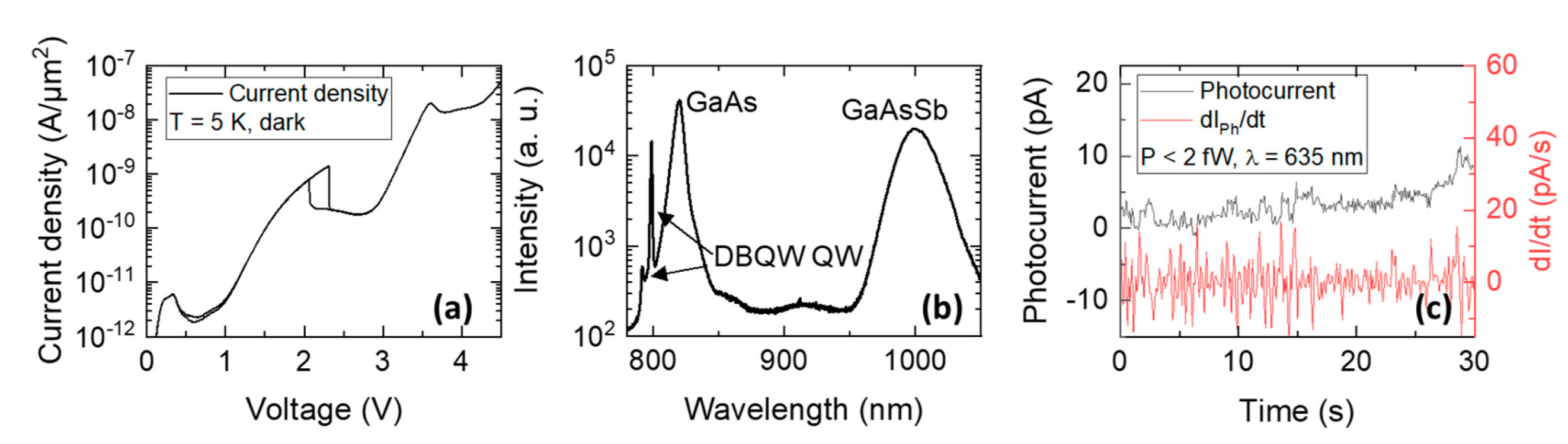
2.3. Single-Photon Detection with Resonant Tunneling Diodes
3. Practical Device Design Considerations
3.1. Quantum Dots Are Not a Necessity
3.2. Detector Architectures and Device Design
3.2.1. Ring Contact
3.2.2. Integrated Waveguide
3.2.3. Nano-Injector
3.2.4. Cross-Wire Structure
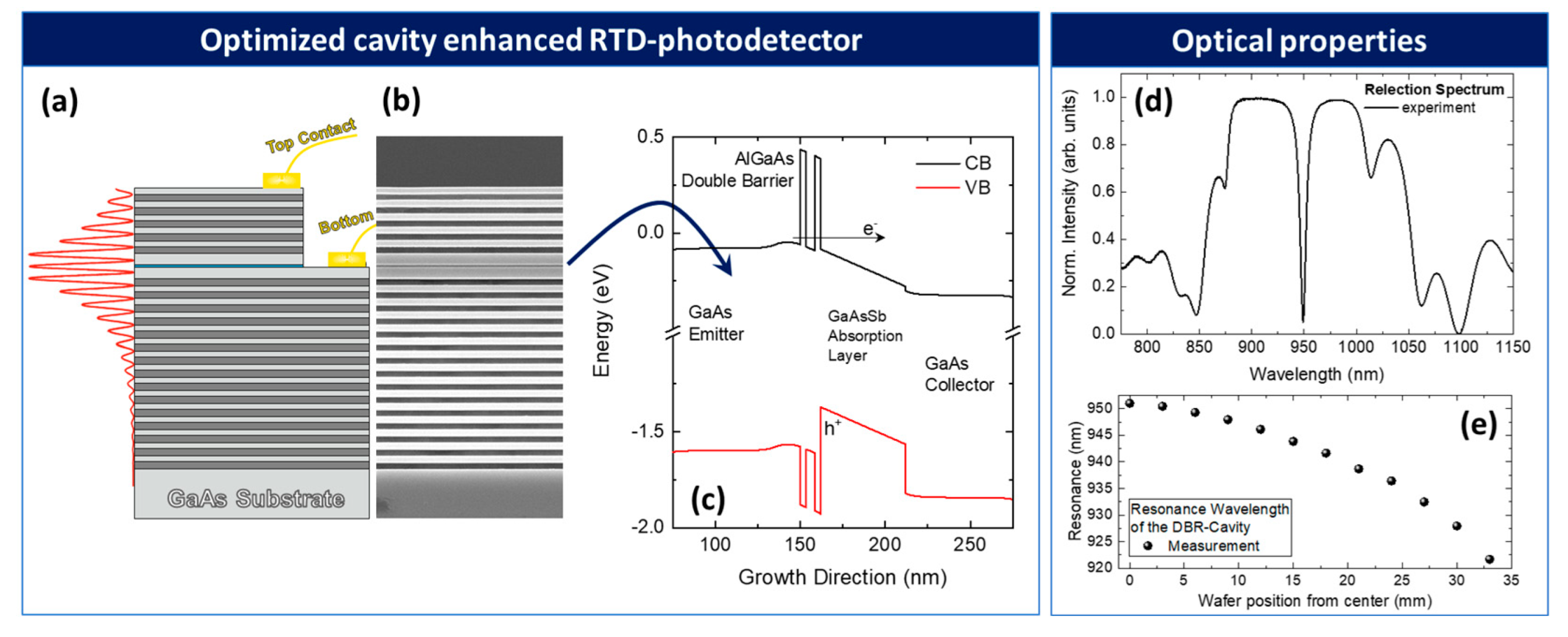
3.3. Strategies against the Quantum Efficiency Dilemma: Cavity-Enhanced Detectors
4. Quantifying the Device Performance of RTD-SPD
4.1. Spectral Range
4.2. Deadtime
4.3. Dark-Count Rate
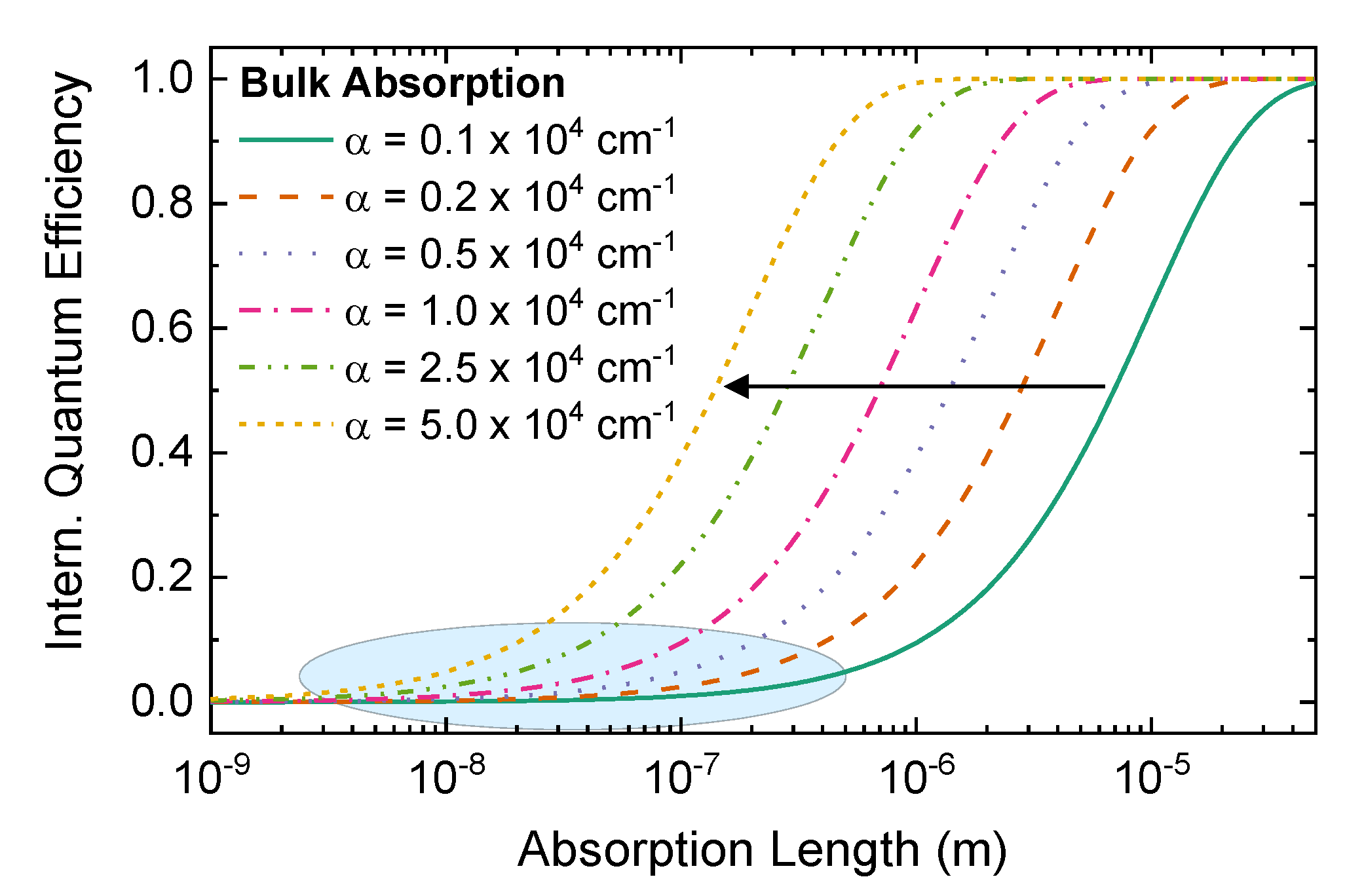
4.4. Detection Efficiency
4.5. Timing Jitter
4.6. Photon-Number Resolution
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Diamanti, E.; Lo, H.-K.; Qi, B.; Yuan, Z. Practical challenges in quantum key distribution. Pract. Chall. Quantum Key Distrib. NPJ Quantum Inf. 2016, 2, 16025. [Google Scholar] [CrossRef] [Green Version]
- Zhong, H.-S.; Wang, H.; Deng, Y.-H.; Chen, M.-C.; Peng, L.-C.; Luo, Y.-H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 1463, 1460–1463. [Google Scholar] [CrossRef] [PubMed]
- Varnava, M.; Browne, D.E.; Rudolph, T. How good must single photon sources and detectors Be for efficient linear optical quantum computation? Phys. Rev. Lett. 2008, 100, 060502. [Google Scholar] [CrossRef] [Green Version]
- Rudolph, T. Why i am optimistic about the silicon-photonic route to quantum computing. APL Photonics 2017, 2, 030901. [Google Scholar] [CrossRef] [Green Version]
- Tzitrin, I.; Bourassa, J.E.; Menicucci, N.C.; Sabapathy, K.K. Progress towards practical qubit computation using approximate Gottesman-Kitaev-Preskill codes. Phys. Rev. A 2020, 101, 032315. [Google Scholar] [CrossRef] [Green Version]
- Bourassa, J.E.; Alexander, R.N.; Vasmer, M.; Patil, A.; Tzitrin, I.; Matsuura, T.; Su, D.; Baragiola, B.Q.; Guha, S.; Dauphinais, G.; et al. Blueprint for a Scalable Photonic Fault-Tolerant Quantum Computer. Quantum 2021, 5, 392. [Google Scholar] [CrossRef]
- Arrazola, J.M.; Bergholm, V.; Brádler, K.; Bromley, T.R.; Collins, M.J.; Dhand, I.; Fumagalli, A.; Gerrits, T.; Goussev, A.; Helt, L.G.; et al. Quantum circuits with many photons on a programmable nanophotonic chip. Nature 2021, 591, 54–60. [Google Scholar] [CrossRef]
- Gol’tsman, G.N.; Okunev, O.; Chulkova, G.; Lipatov, A.; Semenov, A.; Smirnov, K.; Voronov, B.; Dzardanov, A.; Williams, C.; Sobolewski, R. Picosecond superconducting single-photon optical detector. Appl. Phys. Lett. 2001, 79, 705–707. [Google Scholar] [CrossRef]
- Natarajan, C.M.; Tanner, M.G.; Hadfield, R.H. Superconducting nanowire single-photon detectors: Physics and applications. Supercond. Sci. Technol. 2012, 25, 063001. [Google Scholar] [CrossRef]
- Blakesley, J.C.; See, P.; Shields, A.J.; Kardynałl, B.E.; Atkinson, P.; Farrer, I.; Ritchie, D.A. Efficient single photon detection by quantum dot resonant tunneling diodes. Phys. Rev. Lett. 2005, 94, 067401. [Google Scholar] [CrossRef]
- Tsu, R.; Esaki, L. Tunneling in a finite superlattice. Appl. Phys. Lett. 1973, 22, 562. [Google Scholar] [CrossRef]
- Chang, L.L.; Esaki, L.; Tsu, R. Resonant tunneling in semiconductor double barriers. Appl. Phys. Lett. 1974, 24, 593–595. [Google Scholar] [CrossRef]
- Sun, J.P.; Haddad, G.; Mazumder, P.; Schulman, J.N. Resonant tunneling diodes: Models and properties. Proc. IEEE 1998, 86, 641–660. [Google Scholar] [CrossRef] [Green Version]
- Asada, M.; Suzuki, S.; Kishimoto, N. Resonant Tunneling Diodes for Sub-Terahertz and Terahertz Oscillators. Jpn. J. Appl. Phys. 2008, 47, 4375–4384. [Google Scholar] [CrossRef]
- Feiginov, M. Frequency Limitations of Resonant-Tunnelling Diodes in Sub-THz and THz Oscillators and Detectors. J. Infrared Millim. Terahertz Waves 2019, 40, 365–394. [Google Scholar] [CrossRef] [Green Version]
- Romeira, B.; Avó, R.; Figueiredo, J.M.L.; Barland, S.; Javaloyes, J. Regenerative memory in time-delayed neuromorphic photonic resonators. Sci. Rep. 2016, 6, 19510. [Google Scholar] [CrossRef]
- Hejda, M.; Alanis, J.A.; Ortega-Piwonka, I.; Lourenço, J.; Figueiredo, J.; Javaloyes, J.; Romeira, B.; Hurtado, A. Resonant Tunneling Diode Nano-Optoelectronic Excitable Nodes for Neuromorphic Spike-Based Information Processing. Phys. Rev. Appl. 2022, 17, 024072. [Google Scholar] [CrossRef]
- Pfenning, A.; Hartmann, F.; Rebello Sousa Dias, M.; Langer, F.; Kamp, M.; Castelano, L.K.L.K.; Lopez-Richard, V.; Marques, G.E.G.E.; Höfling, S.; Worschech, L. Photocurrent-voltage relation of resonant tunneling diode photodetectors. Appl. Phys. Lett. 2015, 107, 081104. [Google Scholar] [CrossRef] [Green Version]
- Pfenning, A.; Hartmann, F.; Langer, F.; Kamp, M.; Höfling, S.; Worschech, L. Sensitivity of resonant tunneling diode photodetectors. Nanotechnology 2016, 27, 355202. [Google Scholar] [CrossRef]
- Weng, Q.; An, Z.; Zhang, B.; Chen, P.; Chen, X.; Zhu, Z.; Lu, W. Quantum dot single-photon switches of resonant tunneling current for discriminating-photon-number detection. Sci. Rep. 2015, 5, 9389. [Google Scholar] [CrossRef] [Green Version]
- Pfenning, A.; Jurkat, J.; Naranjo, A.; Köck, D.; Hartmann, F.; Höfling, S. Resonant tunneling diode photon number resolving single-photon detectors. In Infrared Remote Sensing and Instrumentation XXVII; Strojnik, M., Arnold, G.E., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 1112808, pp. 47–56. [Google Scholar] [CrossRef]
- Pfenning, A.; Hartmann, F.; Höfling, S. Photon counting with resonant tunneling diodes: Overview and recent developments. In Advanced Photon Counting Techniques XIV; Itzler, M.A., McIntosh, K.A., Bienfang, J.C., Eds.; SPIE: Bellingham, WA, USA, 2020; Volume 1138606, p. 5. [Google Scholar] [CrossRef]
- Schulman, J.; De Los Santos, H.J.; Chow, D.H. Physics-based RTD current-voltage equation. IEEE Electron. Device Lett. 1996, 17, 220–222. [Google Scholar] [CrossRef]
- Izumi, R.; Suzuki, S.; Asada, M. 1.98 THz resonant-tunneling-diode oscillator with reduced conduction loss by thick antenna electrode. In Proceedings of the 2017 42nd International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Cancun, Mexico, 27 August–1 September 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Asada, M.; Suzuki, S. Room-Temperature Oscillation of Resonant Tunneling Diodes close to 2 THz and Their Functions for Various Applications. J. Infrared Millim. Terahertz Waves 2016, 37, 1185–1198. [Google Scholar] [CrossRef]
- Berger, P.R.; Ramesh, A. Negative Differential Resistance Devices and Circuits. In Comprehensive Semiconductor Science and Technology; Elsevier: Amsterdam, The Netherlands, 2011; pp. 176–241. [Google Scholar] [CrossRef]
- England, P.; Golub, J.E.; Florez, L.T.; Harbison, J.P. Optical switching in a resonant tunneling structure. Appl. Phys. Lett. 1991, 58, 887. [Google Scholar] [CrossRef]
- Coêlho, I.J.S.; Martins-Filho, J.F.; Figueiredo, J.M.L.; Ironside, C.N. Modeling of light-sensitive resonant-tunneling-diode devices. J. Appl. Phys. 2004, 95, 8258. [Google Scholar] [CrossRef]
- Romeira, B.; Pessoa, L.; Salgado, H.; Ironside, C.; Figueiredo, J. Photo-Detectors Integrated with Resonant Tunneling Diodes. Sensors 2013, 13, 9464–9482. [Google Scholar] [CrossRef]
- Hartmann, F.; Gammaitoni, L.; Höfling, S.; Forchel, A.; Worschech, L. Light-induced stochastic resonance in a nanoscale resonant-tunneling diode. Appl. Phys. Lett. 2011, 98, 242109. [Google Scholar] [CrossRef]
- Moise, T.S.; Kao, Y.-C.; Garrett, L.D.; Campbell, J.C. Optically switched resonant tunneling diodes. Appl. Phys. Lett. 1995, 66, 1104. [Google Scholar] [CrossRef]
- Pfenning, A.; Hartmann, F.; Langer, F.; Höfling, S.; Kamp, M.; Worschech, L. Cavity-enhanced resonant tunneling photodetector at telecommunication wavelengths. Appl. Phys. Lett. 2014, 104, 101109. [Google Scholar] [CrossRef] [Green Version]
- Rothmayr, F.; Pfenning, A.; Kistner, C.; Koeth, J.; Knebl, G.; Schade, A.; Krueger, S.; Worschech, L.; Hartmann, F.; Höfling, S. Mid-infrared GaSb-based resonant tunneling diode photodetectors for gas sensing applications. Appl. Phys. Lett. 2018, 112, 161107. [Google Scholar] [CrossRef] [Green Version]
- Pfenning, A.; Hartmann, F.; Weih, R.; Emmerling, M.; Worschech, L.; Höfling, S. p-Type Doped AlAsSb/GaSb Resonant Tunneling Diode Photodetector for the Mid-Infrared Spectral Region. Adv. Opt. Mater. 2018, 6, 1800972. [Google Scholar] [CrossRef] [Green Version]
- Nie, B.; Huang, J.; Zhao, C.; Huang, W.; Zhang, Y.; Cao, Y.; Ma, W. InAs/GaSb superlattice resonant tunneling diode photodetector with InAs/AlSb double barrier structure. Appl. Phys. Lett. 2019, 114, 053509. [Google Scholar] [CrossRef]
- Growden, T.A.; Brown, E.R.; Zhang, W.; Droopad, R.; Berger, P.R. Experimental determination of quantum-well lifetime effect on large-signal resonant tunneling diode switching time. Appl. Phys. Lett. 2015, 107, 153506. [Google Scholar] [CrossRef]
- Hartmann, F.S. Elektrooptische Transporteigenschaften und Stochastisch Aktivierte Prozesse Resonanter Tunneldioden; Julius Maximilians Universität Würzburg: Würzburg, Germany, 2012. [Google Scholar]
- Ironside, C.; Romeira, B.; Figueiredo, J. Resonant Tunneling Diode Photonics Devices and Applications; Morgan & Claypool Publishers: San Rafael, CA, USA, 2019; ISBN 9781643277448. [Google Scholar]
- Zhang, W.; Watson, S.; Figueiredo, J.; Wang, J.; Cantú, H.I.; Tavares, J.; Pessoa, L.; Al-Khalidi, A.; Salgado, H.; Wasige, E.; et al. Optical direct intensity modulation of a 79 GHz resonant tunneling diode-photodetector oscillator. Opt. Express 2019, 27, 16791. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Al-Khalidi, A.; Figueiredo, J.; Al-Taai, Q.R.A.; Wasige, E.; Hadfield, R.H. Analysis of Excitability in Resonant Tunneling Diode-Photodetectors. Nanomaterials 2021, 11, 1590. [Google Scholar] [CrossRef]
- Iannaccone, G.; Lombardi, G.; Macucci, M.; Pellegrini, B. Enhanced Shot Noise in Resonant Tunneling: Theory and Experiment. Phys. Rev. Lett. 1998, 80, 1054–1057. [Google Scholar] [CrossRef] [Green Version]
- Blanter, Y.; Büttiker, M. Transition from sub-Poissonian to super-Poissonian shot noise in resonant quantum wells. Phys. Rev. B 1999, 59, 10217–10226. [Google Scholar] [CrossRef] [Green Version]
- Pfenning, A.; Hartmann, F.; Langer, F.; Kamp, M.; Höfling, S.; Worschech, L. Cavity-enhanced AlGaAs/GaAs resonant tunneling photodetectors for telecommunication wavelength light detection at 1.3 μm. In Infrared Remote Sensing and Instrumentation XXIII; Strojnik Scholl, M., Páez, G., Eds.; SPIE: Bellingham, WA, USA, 2015; Volume 9608, pp. 270–277. [Google Scholar]
- Figueiredo, J.M.L.; Stanley, C.R.; Boyd, A.R.; Ironside, C.N.; McMeekin, S.G.; Leite, A.M.P. Optical modulation in a resonant tunneling relaxation oscillator. Appl. Phys. Lett. 1999, 74, 1197–1199. [Google Scholar] [CrossRef]
- Figueiredo, J.M.L.; Boyd, A.R.; Stanley, C.R.; Ironside, C.N.; McMeekin, S.G.; Leite, A.M.P. Optical modulation at around 1550 nm in an InGaAlAs optical waveguide containing an InGaAs/AlAs resonant tunneling diode. Appl. Phys. Lett. 1999, 75, 3443–3445. [Google Scholar] [CrossRef]
- Figueiredo, J.M.L.; Ironside, C.N.; Stanley, C.R. Ultralow voltage resonant tunnelling diode electroabsorption modulator. J. Mod. Opt. 2002, 49, 939–945. [Google Scholar] [CrossRef]
- Romeira, B.; Figueiredo, J. Optical injection locking of a resonant tunnelling diode-optical waveguide photo-detector. In Proceedings of the EICO, Florence, Italy, 12–24 July 2010. [Google Scholar]
- Romeira, B.; Seunarine, K.; Ironside, C.N.; Kelly, A.E.; Figueiredo, J.M.L. A self-synchronized optoelectronic oscillator based on an RTD photodetector and a laser diode. IEEE Photonics Technol. Lett. 2011, 23, 1148–1150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohseni, H. Single-photon imaging inspired by human vision. In Human Vision and Electronic Imaging XIII; Rogowitz, B.E., Pappas, T.N., Eds.; SPIE: Bellingham, WA, USA, 2008; Volume 6806, pp. 34–39. [Google Scholar]
- Memis, O.G.; Katsnelson, A.; Kong, S.C.; Mohseni, H.; Yan, M.; Zhang, S.; Hossain, T.; Jin, N.; Adesida, I. A photon detector with very high gain at low bias and at room temperature. Appl. Phys. Lett. 2007, 91, 6–9. [Google Scholar] [CrossRef] [Green Version]
- Fathipour, V.; Bonakdar, A.; Mohseni, H. Advances on Sensitive Electron-Injection Based Cameras for Low-Flux, Short-Wave Infrared Applications. Front. Mater. 2016, 3, 33. [Google Scholar] [CrossRef] [Green Version]
- Fathipour, V.; Memis, O.G.; Jang, S.J.; Brown, R.L.; Nia, I.H.; Mohseni, H. Isolated Electron Injection Detectors With High Gain and Record Low Dark Current at Telecom Wavelength. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 65–70. [Google Scholar] [CrossRef]
- Fathipour, V.; Jang, S.J.; Nia, I.H.; Mohseni, H. Impact of three-dimensional geometry on the performance of isolated electron-injection infrared detectors. Appl. Phys. Lett. 2015, 106, 021116. [Google Scholar] [CrossRef]
- Movassaghi, Y.; Fathipour, V.; Fathipour, M.; Mohseni, H. Analytical modeling and numerical simulation of the short-wave infrared electron-injection detectors. Appl. Phys. Lett. 2016, 108, 121102. [Google Scholar] [CrossRef] [Green Version]
- Memis, O.G.; Kohoutek, J.; Dey, D.; Wu, W.; Mohseni, H. Resonant tunneling injection detectors and imagers. In Proceedings of the 2009 IEEE LEOS Annual Meeting Conference Proceedings, Antalya, Turkey, 4–8 October 2009; pp. 363–364. [Google Scholar]
- Bianconi, S.; Mohseni, H.; Rezaei, M. Tuning the gain-bandwidth product of electron Injector photodetectors. Quantum Sens. Nano Electron. Photonics XVI 2019, 97, 343–348. [Google Scholar] [CrossRef]
- Wang, J.; Beton, P.H.; Mori, N.; Buhmann, H.; Mansouri, L.; Eaves, L.; Main, P.C.; Foster, T.J.; Henini, M. Submicrometer resonant tunnelling diodes fabricated by photolithography and selective wet etching. Appl. Phys. Lett. 1994, 65, 1124. [Google Scholar] [CrossRef]
- Buhmann, H.; Mansouri, L.; Wang, J.; Beton, P.H.; Eaves, L.; Henini, M. High efficiency submicron light-emitting resonant tunneling diodes. Appl. Phys. Lett. 1994, 65, 3332. [Google Scholar] [CrossRef]
- Mansouri, L.; Buhmann, H.; Wang, J.; Beton, P.P.H.; Eaves, L.; Henini, M. Discrete electroluminescence lines in sub-micron pin resonant tunnelling diodes. Superlattices Microstruct. 1994, 16, 169. [Google Scholar] [CrossRef]
- Buhmann, H.; Wang, J.; Mansouri, L.; Beton, P.H.; Eaves, L.; Heath, M.; Henini, M. Photohole-induced resonant tunneling of electrons in selectively etched small area GaAs/AlAs double barrier diodes. Solid. State. Electron. 1994, 37, 973–976. [Google Scholar] [CrossRef]
- Hees, S.S.; Kardynal, B.E.; See, P.; Shields, A.J.; Farrer, I.; Ritchie, D.A. Effect of InAs dots on noise of quantum dot resonant tunneling single-photon detectors. Appl. Phys. Lett. 2006, 89, 153510. [Google Scholar] [CrossRef]
- Weng, Q.C.; An, Z.H.; Zhu, Z.Q.; Song, J.D.; Choi, W.J. Electronic-state-controlled reset operation in quantum dot resonant-tunneling single-photon detectors. Appl. Phys. Lett. 2014, 104, 051113. [Google Scholar] [CrossRef]
- Li, H.W.; Kardynał, B.E.; Ellis, D.J.P.; Shields, A.J.; Farrer, I.; Ritchie, D.A. Quantum dot resonant tunneling diode single photon detector with aluminum oxide aperture defined tunneling area. Appl. Phys. Lett. 2008, 93, 153503. [Google Scholar] [CrossRef] [Green Version]
- Li, H.W.; Kardynał, B.E.; See, P.; Shields, A.J.; Simmonds, P.; Beere, H.E.; Ritchie, D.A. Quantum dot resonant tunneling diode for telecommunication wavelength single photon detection. Appl. Phys. Lett. 2007, 91, 073516. [Google Scholar] [CrossRef]
- Weng, Q.C.; An, Z.H.; Xiong, D.Y.; Zhang, B.; Chen, P.P.; Li, T.X.; Zhu, Z.Q.; Lu, W. Photocurrent spectrum study of a quantum dot single-photon detector based on resonant tunneling effect with near-infrared response. Appl. Phys. Lett. 2014, 105, 031114. [Google Scholar] [CrossRef]
- Moise, T.S.; Kao, Y.-C.; Goldsmith, C.L.; Schow, C.L.; Campbell, J.C. High-speed resonant-tunneling photodetectors with low-switching energy. IEEE Photonics Technol. Lett. 1997, 9, 803–805. [Google Scholar] [CrossRef]
- Akhlaghi, M.K.; Schelew, E.; Young, J.F. Waveguide integrated superconducting single-photon detectors implemented as near-perfect absorbers of coherent radiation. Nat. Commun. 2015, 6, 8233. [Google Scholar] [CrossRef] [Green Version]
- Hadfield, R.H. Single-photon detectors for optical quantum information applications. Nat. Photonics 2009, 3, 696–705. [Google Scholar] [CrossRef]
- Cardozo De Oliveira, E.R.; Naranjo, A.; Pfenning, A.; Lopez-Richard, V.; Marques, G.E.; Worschech, L.; Hartmann, F.; Höfling, S.; Teodoro, M.D. Determination of Carrier Density and Dynamics via Magnetoelectroluminescence Spectroscopy in Resonant-Tunneling Diodes. Phys. Rev. Appl. 2021, 15, 014042. [Google Scholar] [CrossRef]
- Guarin Castro, E.D.; Pfenning, A.; Hartmann, F.; Knebl, G.; Daldin Teodoro, M.; Marques, G.E.; Höfling, S.; Bastard, G.; Lopez-Richard, V. Optical Mapping of Nonequilibrium Charge Carriers. J. Phys. Chem. C 2021, 125, 14741–14750. [Google Scholar] [CrossRef]
- Memis, O.G.; Katsnelson, A.; Mohseni, H.; Yan, M.; Zhang, S.; Hossain, T.; Jin, N.; Adesida, I. On the Source of Jitter in a Room-Temperature Nanoinjection Photon Detector at 1.55 um. IEEE Electron. Device Lett. 2008, 29, 867–869. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pfenning, A.; Krüger, S.; Jabeen, F.; Worschech, L.; Hartmann, F.; Höfling, S. Single-Photon Counting with Semiconductor Resonant Tunneling Devices. Nanomaterials 2022, 12, 2358. https://doi.org/10.3390/nano12142358
Pfenning A, Krüger S, Jabeen F, Worschech L, Hartmann F, Höfling S. Single-Photon Counting with Semiconductor Resonant Tunneling Devices. Nanomaterials. 2022; 12(14):2358. https://doi.org/10.3390/nano12142358
Chicago/Turabian StylePfenning, Andreas, Sebastian Krüger, Fauzia Jabeen, Lukas Worschech, Fabian Hartmann, and Sven Höfling. 2022. "Single-Photon Counting with Semiconductor Resonant Tunneling Devices" Nanomaterials 12, no. 14: 2358. https://doi.org/10.3390/nano12142358
APA StylePfenning, A., Krüger, S., Jabeen, F., Worschech, L., Hartmann, F., & Höfling, S. (2022). Single-Photon Counting with Semiconductor Resonant Tunneling Devices. Nanomaterials, 12(14), 2358. https://doi.org/10.3390/nano12142358




