Temperature Dependence of Thermal Conductivity of Giant-Scale Supported Monolayer Graphene
Abstract
:1. Introduction
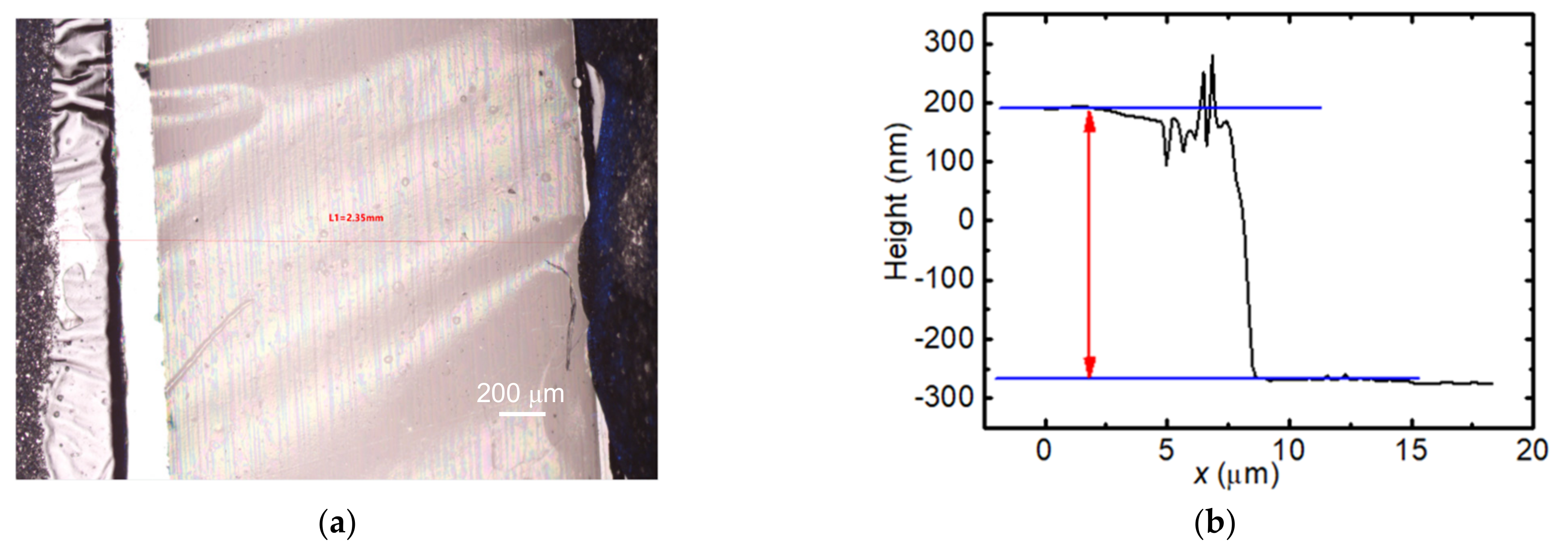
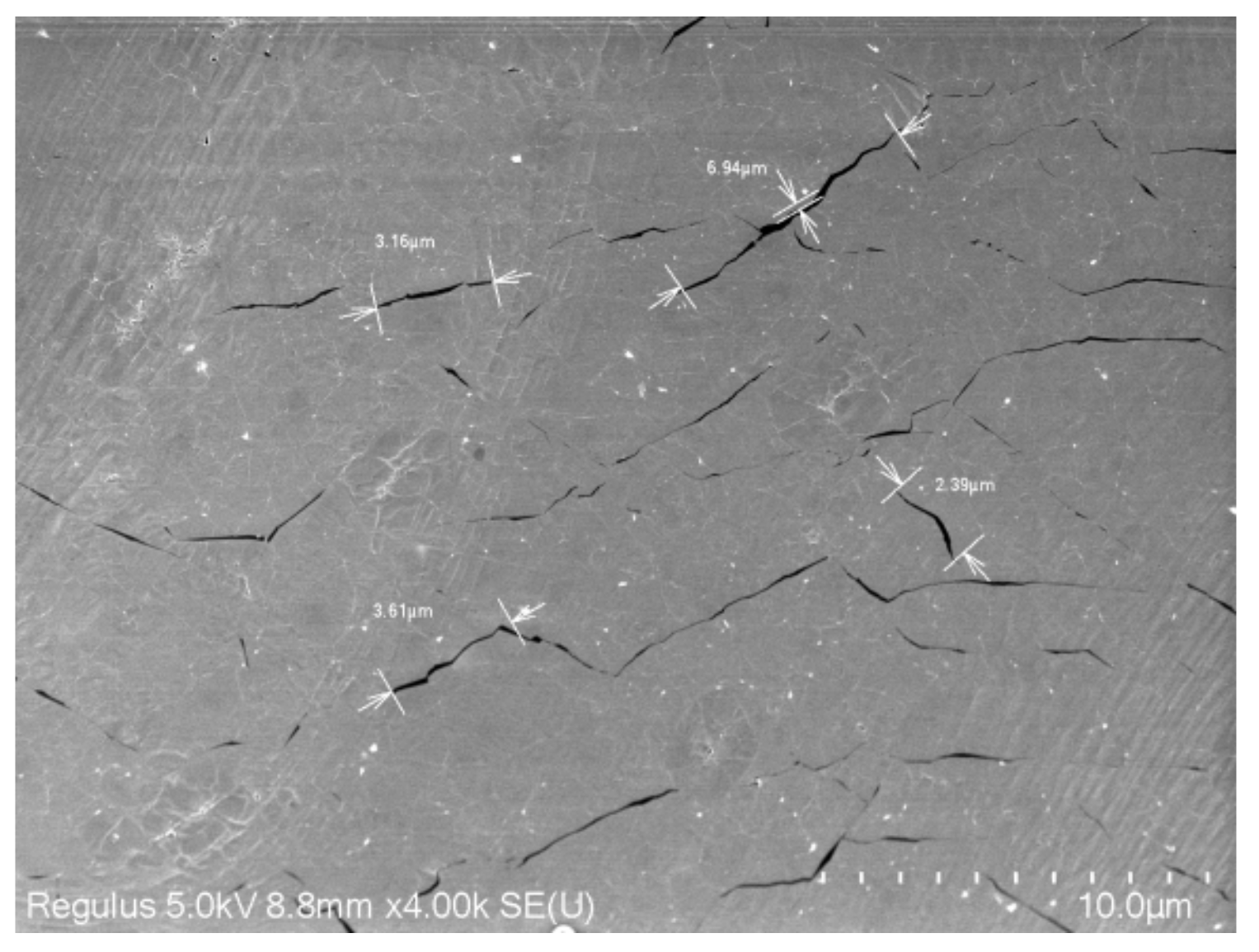
2. Sample Preparation and Characterization
2.1. Sample Preparation
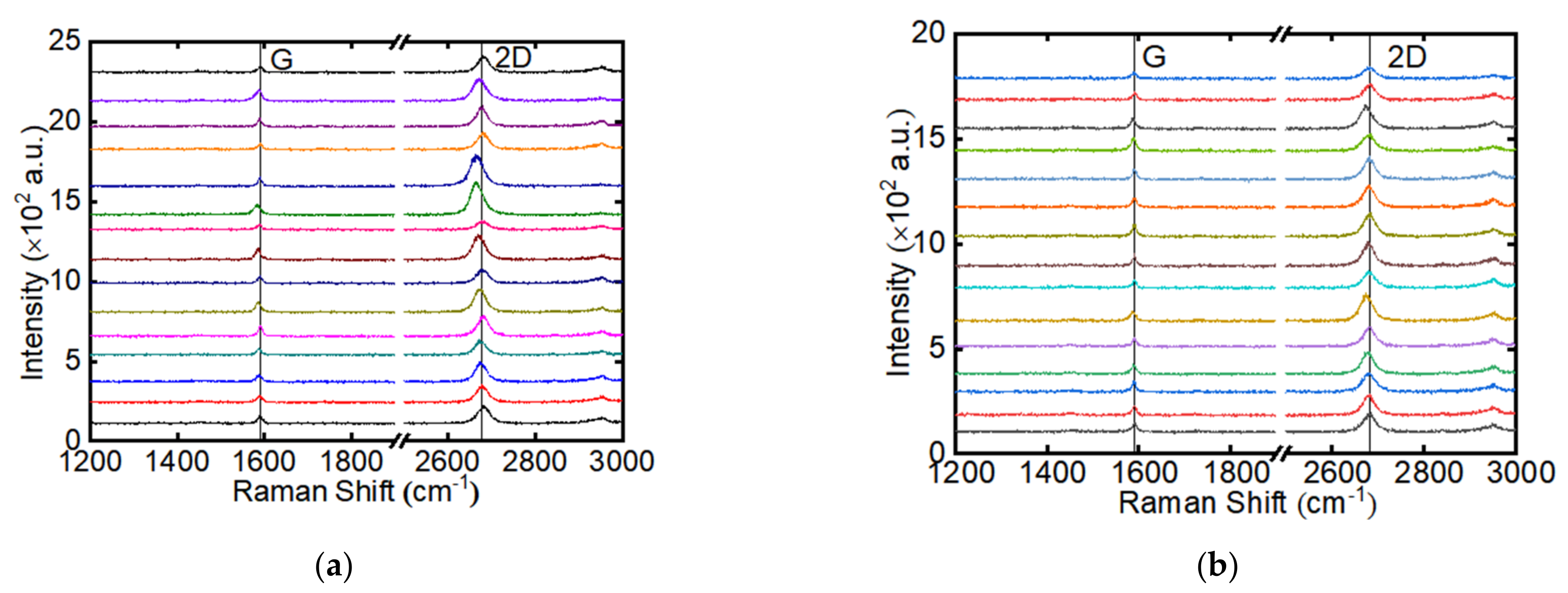
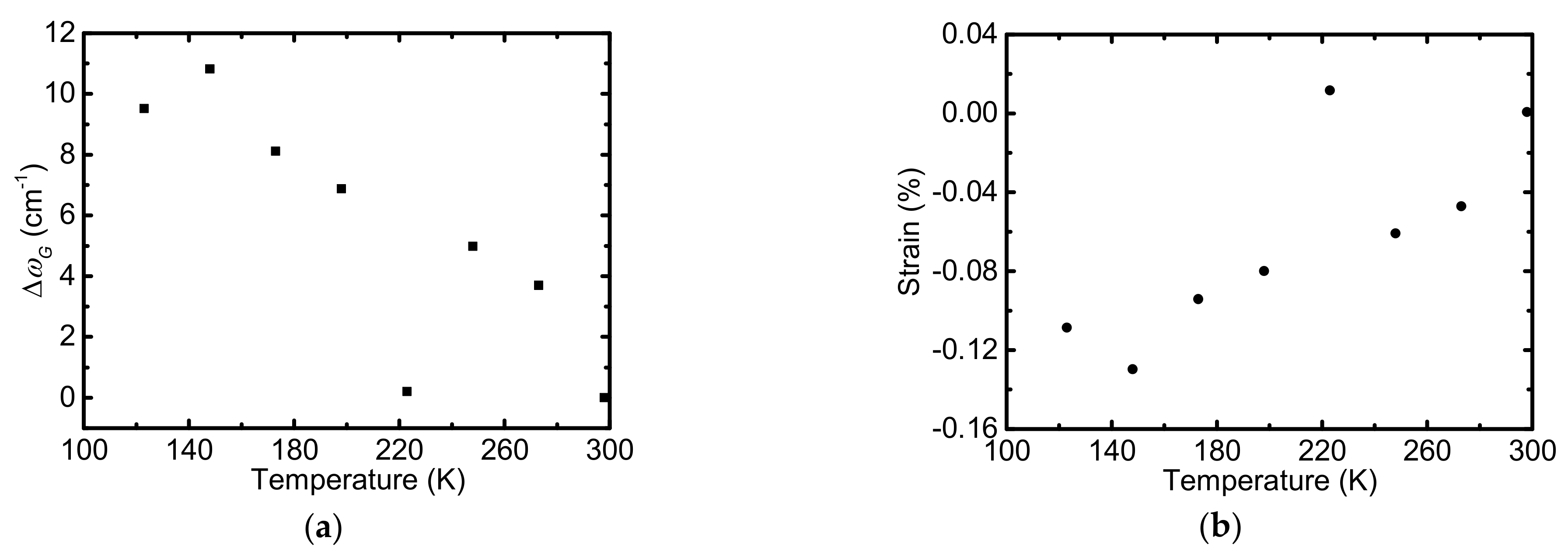
2.2. Structure Study Based on Raman Spectroscopy
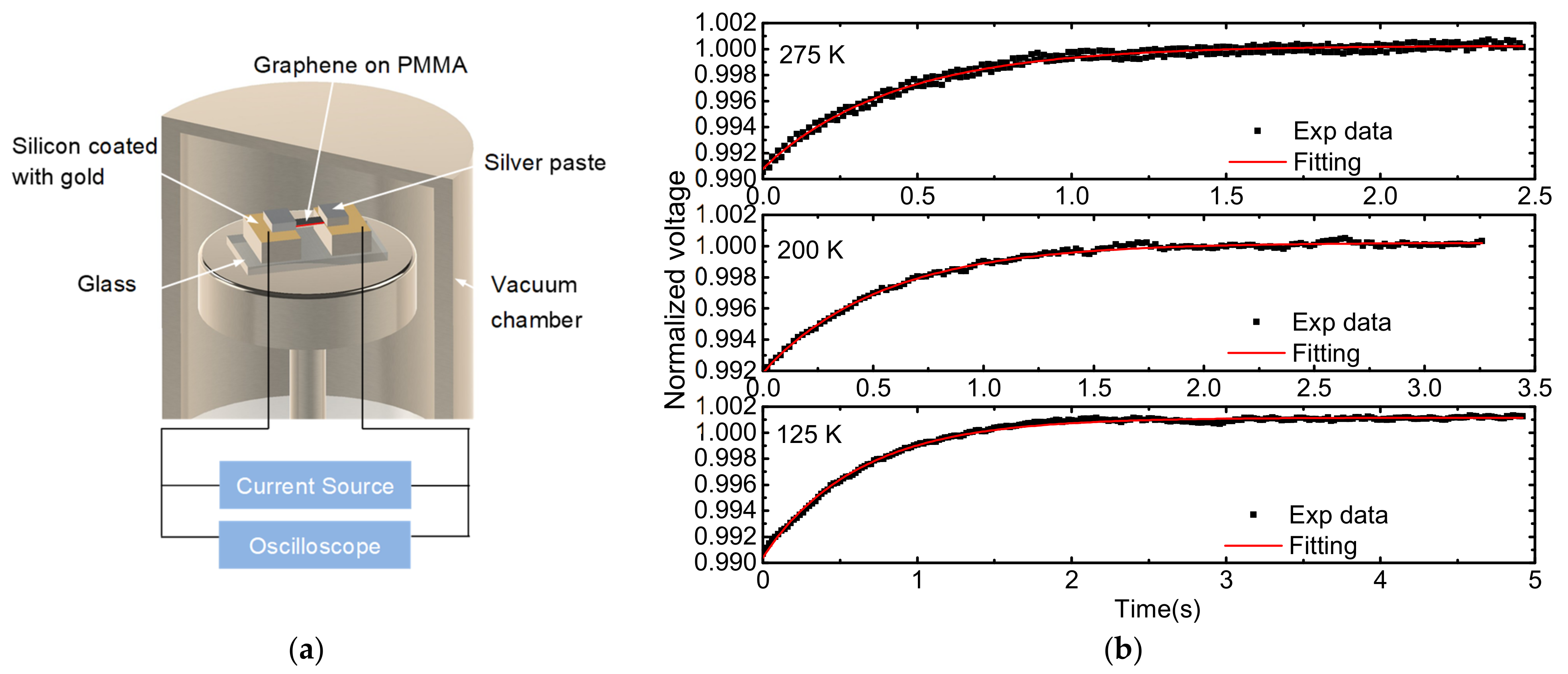
3. Thermal Transport Characterization of Giant-Scale Graphene Supported by PMMA
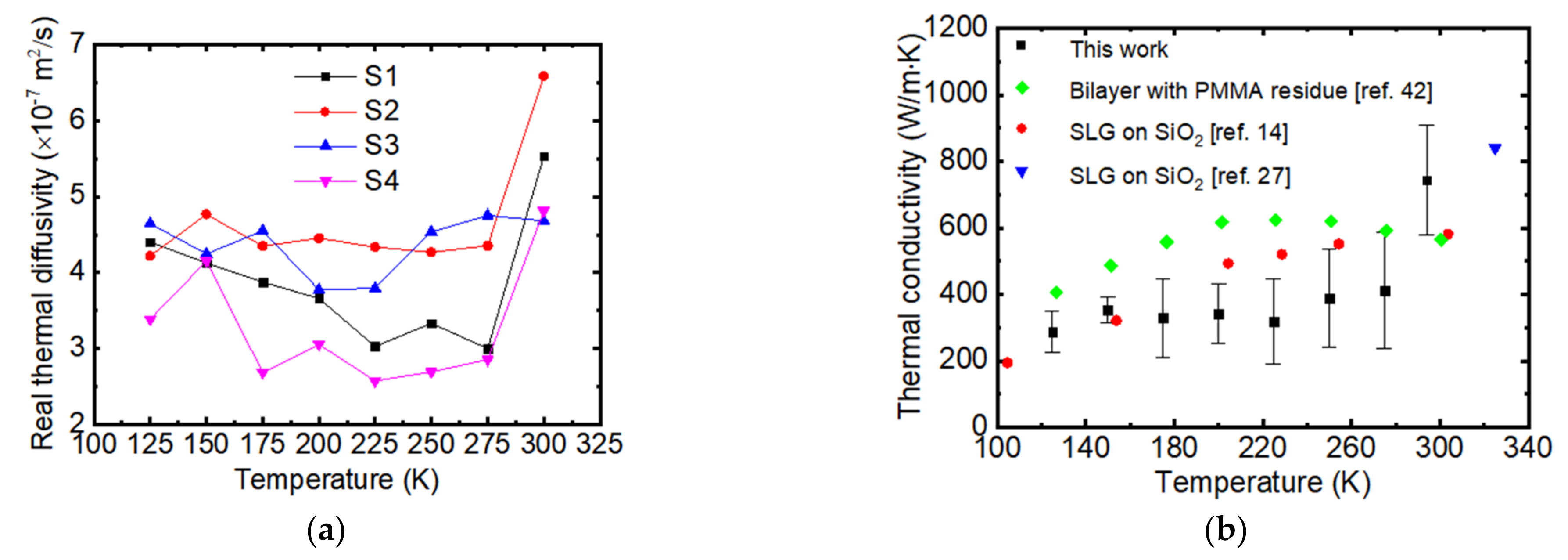
4. Results and Discussion
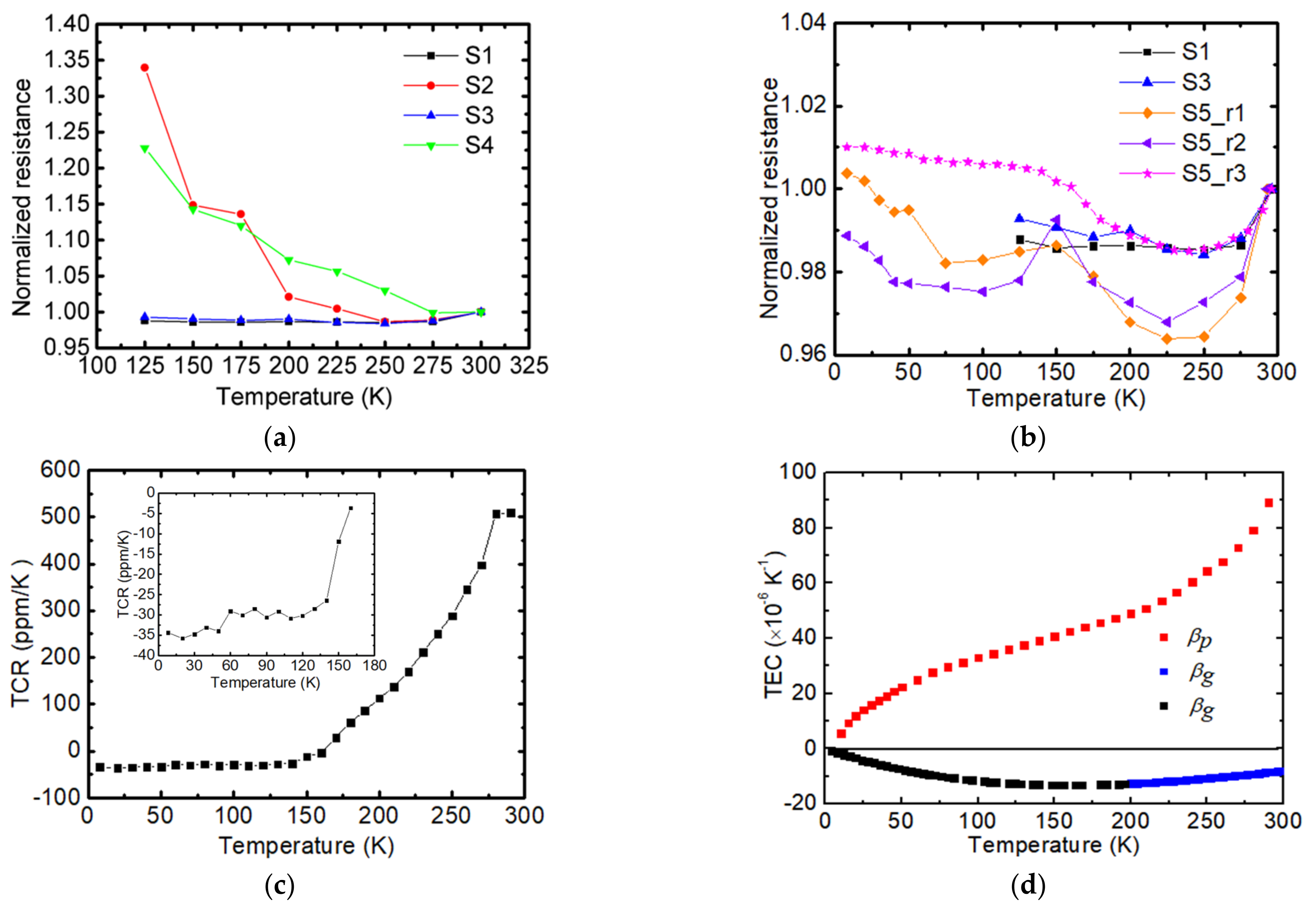
4.1. Abnormal Temperature Coefficient of Resistance for Graphene Supported by PMMA
4.2. Thermal Properties of SLG Supported by PMMA
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghosh, S.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 2008, 92, 151911. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Ni, G.X.; Yang, H.Z.; Ji, W.; Baeck, S.J.; Toh, C.T.; Ahn, J.H.; Pereira, V.M.; Ozyilmaz, B. Tuning Optical Conductivity of Large-Scale CVD Graphene by Strain Engineering. Adv. Mater. 2014, 26, 1081–1086. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Gu, X.K.; Wei, Y.J.; Yin, X.B.; Li, B.W.; Yang, R.G. Colloquium: Phononic thermal properties of two-dimensional materials. Rev. Mod. Phys. 2018, 90, 041002. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid. State. Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.D.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- You, R.; Liu, Y.Q.; Hao, Y.L.; Han, D.D.; Zhang, Y.L.; You, Z. Laser Fabrication of Graphene-Based Flexible Electronics. Adv. Mater. 2020, 32, 1901981. [Google Scholar] [CrossRef]
- Secor, E.B.; Lim, S.; Zhang, H.; Frisbie, C.D.; Francis, L.F.; Hersam, M.C. Gravure Printing of Graphene for Large-Area Flexible Electronics. Adv. Mater. 2014, 26, 1401052. [Google Scholar] [CrossRef] [PubMed]
- Freitag, M.; Low, T.; Avouris, P. Increased Responsivity of Suspended Graphene Photodetectors. Nano Lett. 2013, 13, 1644–1648. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.Y.; Lai, L.F.; Shen, Z.X.; Lin, J.Y. Graphene and graphene-based composites as Li-ion battery electrode materials and their application in full cells. J. Mater. Chem. A 2017, 5, 15423–15446. [Google Scholar] [CrossRef]
- Cai, C.L.; Wang, T.; Zhang, Y.X.; He, N.Y. Facile fabrication of ultra-large graphene film with high photothermal effect and thermal conductivity. Appl. Surf. Sci. 2021, 563, 150354. [Google Scholar] [CrossRef]
- Cai, W.W.; Moore, A.L.; Zhu, Y.W.; Li, X.S.; Chen, S.S.; Shi, L.; Ruoff, R.S. Thermal Transport in Suspended and Supported Monolayer Graphene Grown by Chemical Vapor Deposition. Nano Lett. 2010, 10, 1645–1651. [Google Scholar] [CrossRef]
- Seol, J.H.; Jo, I.; Moore, A.L.; Lindsay, L.; Aitken, Z.H.; Pettes, M.T.; Li, X.S.; Yao, Z.; Huang, R.; Broido, D.; et al. Two-Dimensional Phonon Transport in Supported Graphene. Science 2010, 328, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Ong, Z.Y.; Pop, E. Effect of substrate modes on thermal transport in supported graphene. Phys. Rev. B 2011, 84, 075471. [Google Scholar] [CrossRef]
- Wei, Z.Y.; Yang, J.K.; Bi, K.D.; Chen, Y.F. Mode dependent lattice thermal conductivity of single layer graphene. J. Appl. Phys. 2014, 116, 153503. [Google Scholar] [CrossRef]
- Xu, X.F.; Pereira, L.F.C.; Wang, Y.; Wu, J.; Zhang, K.W.; Zhao, X.M.; Bae, S.; Bui, C.T.; Xie, R.G.; Thong, J.T.L.; et al. Length-dependent thermal conductivity in suspended single-layer graphene. Nat. Commun. 2014, 5, 3689. [Google Scholar] [CrossRef] [PubMed]
- Malekpour, H.; Ramnani, P.; Srinivasan, S.; Balasubramanian, G.; Nika, D.L.; Mulchandani, A.; Lake, R.K.; Balandin, A.A. Thermal conductivity of graphene with defects induced by electron beam irradiation. Nanoscale 2016, 8, 14608–14616. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.Q.; Chen, J.; Yang, N.; Li, B.W. Thermal transport transport in graphene with defect and doping: Phonon modes analysis. Carbon 2017, 116, 139–144. [Google Scholar] [CrossRef]
- Li, M.Y.; Deng, T.Z.X.; Zheng, B.; Zhang, Y.; Liao, Y.G.; Zhou, H.M. Effect of Defects on the Mechanical and Thermal Properties of Graphene. Nanomaterials 2019, 9, 347. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, G.; Li, B.W. Substrate coupling suppresses size dependence of thermal conductivity in supported graphene. Nanoscale 2013, 5, 532–536. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Zhang, J.C.; Hu, X.J.; Yue, Y. Thermal transport across graphene/SiC interface: Effects of atomic bond and crystallinity of substrate. Appl. Phys. A 2015, 119, 415–424. [Google Scholar] [CrossRef]
- Liu, H.K.; Lin, Y.; Luo, S.N. Grain Boundary Energy and Grain Size Dependences of Thermal Conductivity of Polycrystalline Graphene. J. Phys. Chem. C 2014, 118, 24797–24802. [Google Scholar] [CrossRef]
- Limbu, T.B.; Hahn, K.R.; Mendoza, F.; Sahoo, S.; Razink, J.J.; Katiyar, R.S.; Weiner, B.R.; Morell, G. Grain size-dependent thermal conductivity of polycrystalline twisted bilayer graphene. Carbon 2017, 117, 367–375. [Google Scholar] [CrossRef]
- Lee, W.; Kihm, K.D.; Kim, H.G.; Shin, S.; Lee, C.; Park, J.S.; Cheon, S.; Kwon, O.M.; Lim, G.; Lee, W. In-Plane Thermal Conductivity of Polycrystalline Chemical Vapor Deposition Graphene with Controlled Grain Sizes. Nano Lett. 2017, 17, 2361–2366. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Li, Q.; Zhang, Q.; Qu, Y.; Ji, H.; Ruoff, R.S.; Cai, W. Thermal conductivity measurements of suspended graphene with and without wrinkles by microRaman mapping. Nanotechnology 2012, 23, 365701. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.Y.; Xia, K.L.; Zhang, J.; Zhang, Y.Y.; Li, Q.Y.; Takahashi, K.; Zhang, X. Measurement of specific heat and thermal conductivity of supported and suspended graphene by a comprehensive Raman optothermal method. Nanoscale 2017, 9, 10784–10793. [Google Scholar] [CrossRef]
- Wang, R.D.; Wang, T.Y.; Zobeiri, H.; Li, D.C.; Wang, X.W. Energy and Charge Transport in 2D Atomic Layer Materials: Raman-Based Characterization. Nanomaterials 2020, 10, 1807. [Google Scholar] [CrossRef]
- Li, Q.Y.; Katakami, K.; Ikuta, T.; Kohno, M.; Zhang, X.; Takahashi, K. Measurement of thermal contact resistance between individual carbon fibers using a laser-flash Raman mapping method. Carbon 2019, 141, 92–98. [Google Scholar] [CrossRef]
- Li, Q.Y.; Zhang, X.; Takahashi, K. Variable-spot-size laser-flash Raman method to measure in-plane and interfacial thermal properties of 2D van der Waals heterostructures. Int. J. Heat Mass Trans. 2018, 125, 1230–1239. [Google Scholar] [CrossRef]
- Vallabhaneni, A.K.; Singh, D.; Bao, H.; Murthy, J.; Ruan, X.L. Reliability of Raman measurements of thermal conductivity of single-layer graphene due to selective electron-phonon coupling: A first-principles study. Phys. Rev. B 2016, 93, 125432. [Google Scholar] [CrossRef]
- Wang, R.D.; Zobeiri, H.; Xie, Y.S.; Wang, X.W.; Zhang, X.; Yue, Y.N. Distinguishing Optical and Acoustic Phonon Temperatures and Their Energy Coupling Factor under Photon Excitation in nm 2D Materials. Adv. Sci. 2020, 7, 2000097. [Google Scholar] [CrossRef]
- Liu, J.; Li, P.; Zheng, H. Review on Techniques for Thermal Characterization of Graphene and Related 2D Materials. Nanomaterials 2021, 11, 2787. [Google Scholar] [CrossRef]
- Wang, L.; Hu, B.B.; Li, B.W. Logarithmic divergent thermal conductivity in two-dimensional nonlinear lattices. Phys. Rev. E 2012, 86, 040101. [Google Scholar] [CrossRef] [PubMed]
- Su, R.X.; Zhang, X. Size effect of thermal conductivity in monolayer graphene. Appl. Therm. Eng. 2018, 144, 488–494. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.L.; Cheng, Z.; Xu, S.; Wang, X.W. Thermal Conductivity of Ultrahigh Molecular Weight Polyethylene Crystal: Defect Effect Uncovered by 0 K Limit Phonon Diffusion. ACS Appl. Mater. Inter. 2015, 7, 27279–27288. [Google Scholar] [CrossRef]
- Graf, D.; Molitor, F.; Ensslin, K.; Stampfer, C.; Jungen, A.; Hierold, C.; Wirtz, L. Spatially resolved raman spectroscopy of single- and few-layer graphene. Nano Lett. 2007, 7, 238–242. [Google Scholar] [CrossRef] [PubMed]
- Putnam, S.A.; Cahill, D.G.; Ash, B.J.; Schadler, L.S. High-precision thermal conductivity measurements as a probe of polymer/nanoparticle interfaces. J. Appl. Phys. 2003, 94, 6785. [Google Scholar] [CrossRef]
- Esposito, M.; Buontempo, S.; Petriccione, A.; Zarrelli, M.; Breglio, G.; Saccomanno, A.; Szillasi, Z.; Makovec, A.; Cusano, A.; Chhiuchiolo, A.; et al. and Giordano, M. Fiber Bragg Grating sensors to measure the coefficient of thermal expansion of polymers at cryogenic temperatures. Sens. Actuators 2013, 189, 195–203. [Google Scholar] [CrossRef]
- D’Souza, R.; Mukherjee, S. First-principles study of the electrical and lattice thermal transport in monolayer and bilayer graphene. Phys. Rev. B 2017, 95, 085435. [Google Scholar] [CrossRef]
- Hinnefeld, J.H.; Gill, S.T.; Zhu, S.; Swanson, W.J.; Li, T.; Mason, N. Reversible Mechanical and Electrical Properties of Ripped Graphene. Phys. Rev. Appl. 2015, 3, 014010. [Google Scholar] [CrossRef]
- Pettes, M.T.; Jo, I.S.; Yao, Z.; Shi, L. Influence of Polymeric Residue on the Thermal Conductivity of Suspended Bilayer Graphene. Nano Lett. 2011, 11, 1195–1200. [Google Scholar] [CrossRef] [PubMed]
- Li, X.B.; Maute, K.; Dunn, M.L.; Yang, R.G. Strain effects on the thermal conductivity of nanostructures. Phys. Rev. B 2010, 81, 245318. [Google Scholar] [CrossRef]
- Guo, Z.X.; Zhang, D.; Gong, X.G. Thermal conductivity of graphene nanoribbons. Appl. Phys. Lett. 2009, 95, 163103. [Google Scholar] [CrossRef]
- Yoon, D.; Son, Y.W.; Cheong, H. Negative Thermal Expansion Coefficient of Graphene Measured by Raman Spectroscopy. Nano Lett. 2011, 11, 3227–3231. [Google Scholar] [CrossRef]
- Yoon, D.; Son, Y.W.; Cheong, H. Strain-Dependent Splitting of the Double-Resonance Raman Scattering Band in Graphene. Phys. Rev. Lett. 2011, 106, 155502. [Google Scholar] [CrossRef]
- Bonini, N.; Lazzeri, M.; Marzari, N.; Mauri, F. Phonon anharmonicities in graphite and graphene. Phys. Rev. Lett. 2007, 99, 176802. [Google Scholar] [CrossRef]
- Wei, N.; Xu, L.Q.; Wang, H.Q.; Zheng, J.C. Strain engineering of thermal conductivity in graphene sheets and nanoribbons: A demonstration of magic flexibility. Nanotechnology 2011, 22, 105705. [Google Scholar] [CrossRef]
| Sample | S1 | S2 | S3 | S4 | S5 |
|---|---|---|---|---|---|
| PMMA thickness(nm) | 457 | 457 | 457 | 457 | 457 |
| Graphene layer number | 1 | 1 | 1 | 1 | 1 |
| Length (mm) | 1.73 | 1.53 | 2.35 | 2.25 | 2.09 |
| Width (mm) | 1.92 | 1.85 | 3.20 | 2.80 | 0.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Li, P.; Xu, S.; Xie, Y.; Wang, Q.; Ma, L. Temperature Dependence of Thermal Conductivity of Giant-Scale Supported Monolayer Graphene. Nanomaterials 2022, 12, 2799. https://doi.org/10.3390/nano12162799
Liu J, Li P, Xu S, Xie Y, Wang Q, Ma L. Temperature Dependence of Thermal Conductivity of Giant-Scale Supported Monolayer Graphene. Nanomaterials. 2022; 12(16):2799. https://doi.org/10.3390/nano12162799
Chicago/Turabian StyleLiu, Jing, Pei Li, Shen Xu, Yangsu Xie, Qin Wang, and Lei Ma. 2022. "Temperature Dependence of Thermal Conductivity of Giant-Scale Supported Monolayer Graphene" Nanomaterials 12, no. 16: 2799. https://doi.org/10.3390/nano12162799
APA StyleLiu, J., Li, P., Xu, S., Xie, Y., Wang, Q., & Ma, L. (2022). Temperature Dependence of Thermal Conductivity of Giant-Scale Supported Monolayer Graphene. Nanomaterials, 12(16), 2799. https://doi.org/10.3390/nano12162799







