Mathematical Modeling of Drain Current Estimation in a CSDG MOSFET, Based on La2O3 Oxide Layer with Fabrication—A Nanomaterial Approach
Abstract
1. Introduction
2. Extensive Modeling of the CSDG MOSFET for Fabrication Perspective
2.1. Three-Dimensional Surface Potential Modeling
2.2. Mobility Modeling in the Cylindrical Structure
2.3. Drain Current Modeling for the Cylindrical Structure
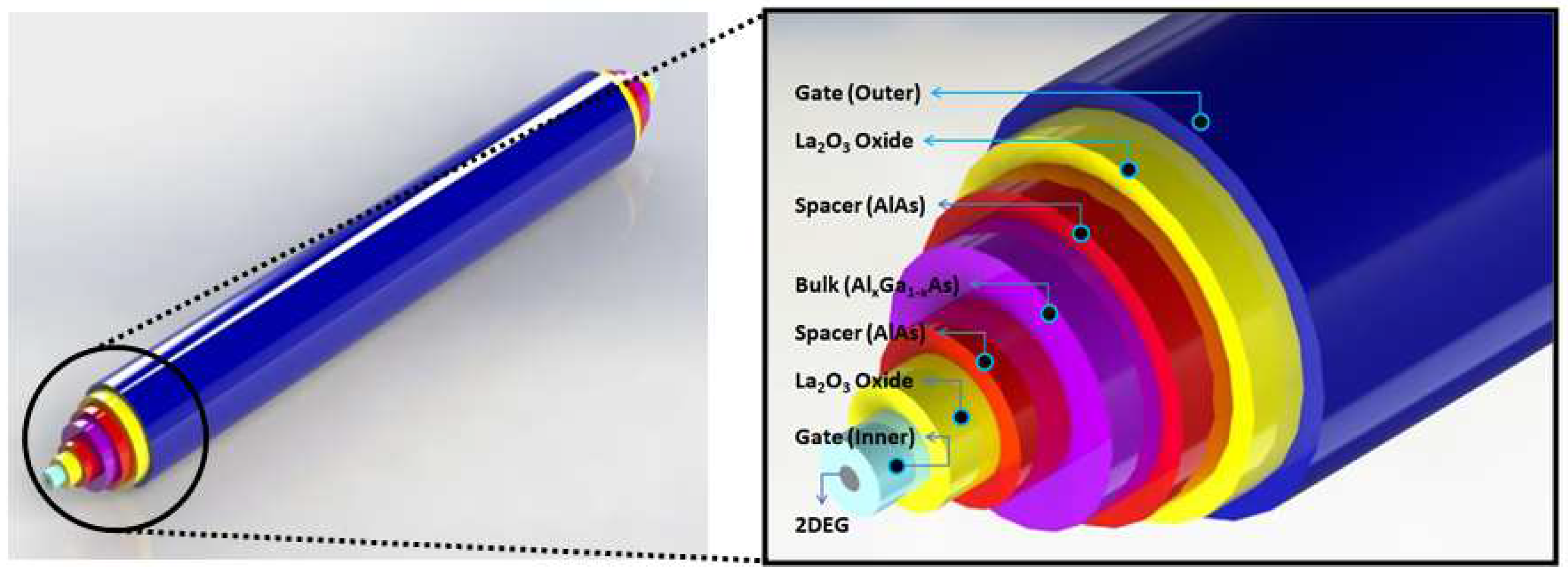
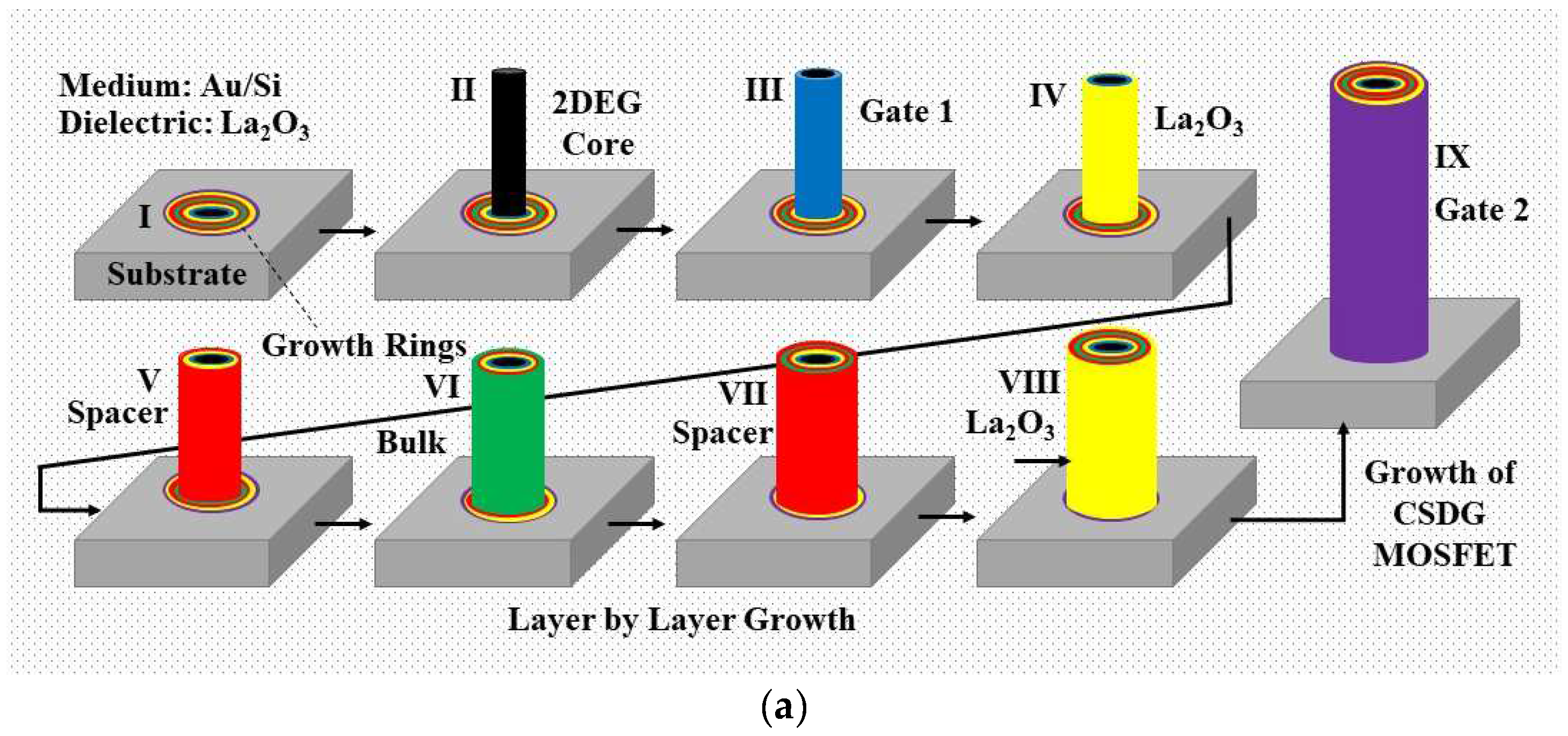
3. Fabrication Model of the CSDG MOSFET
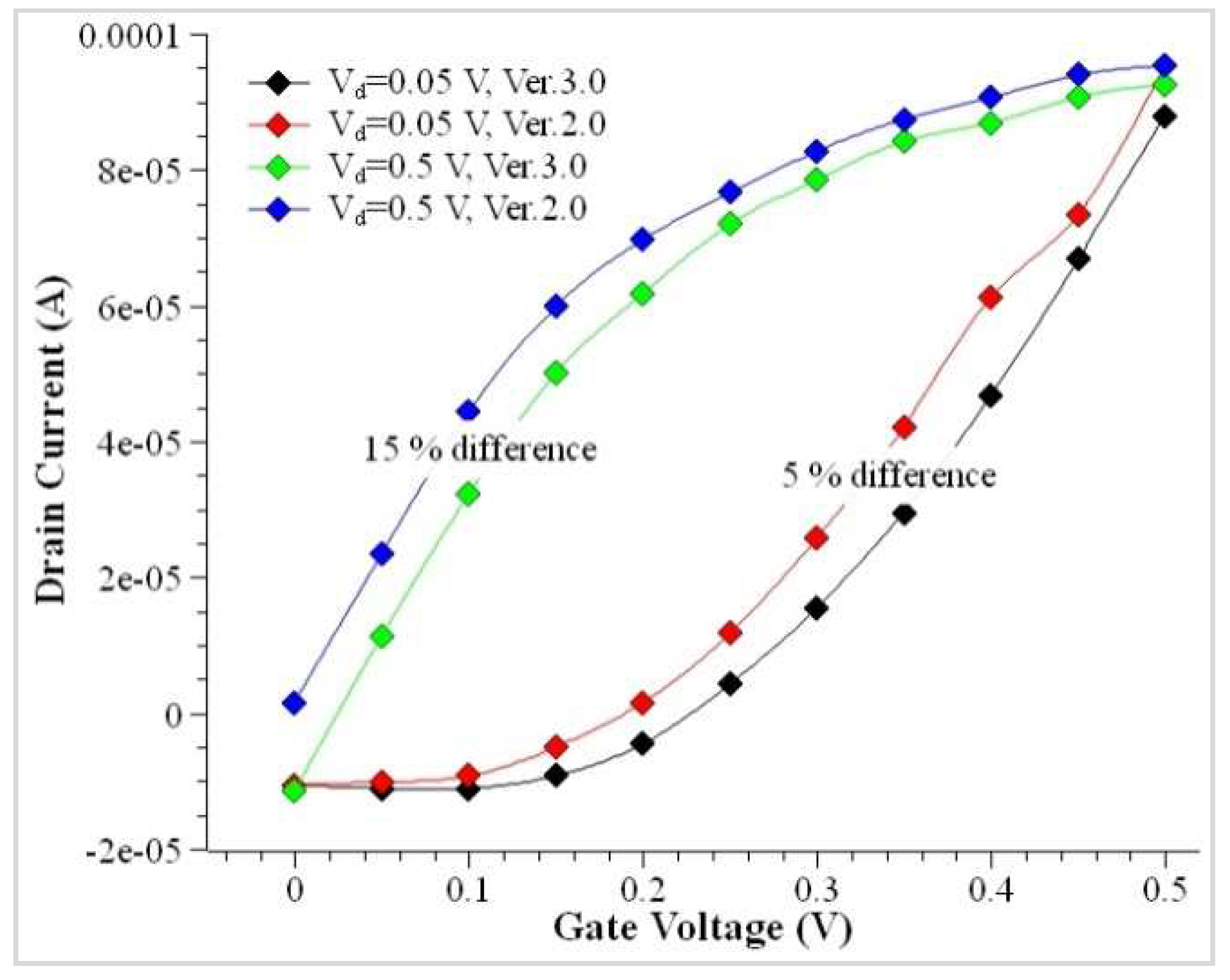
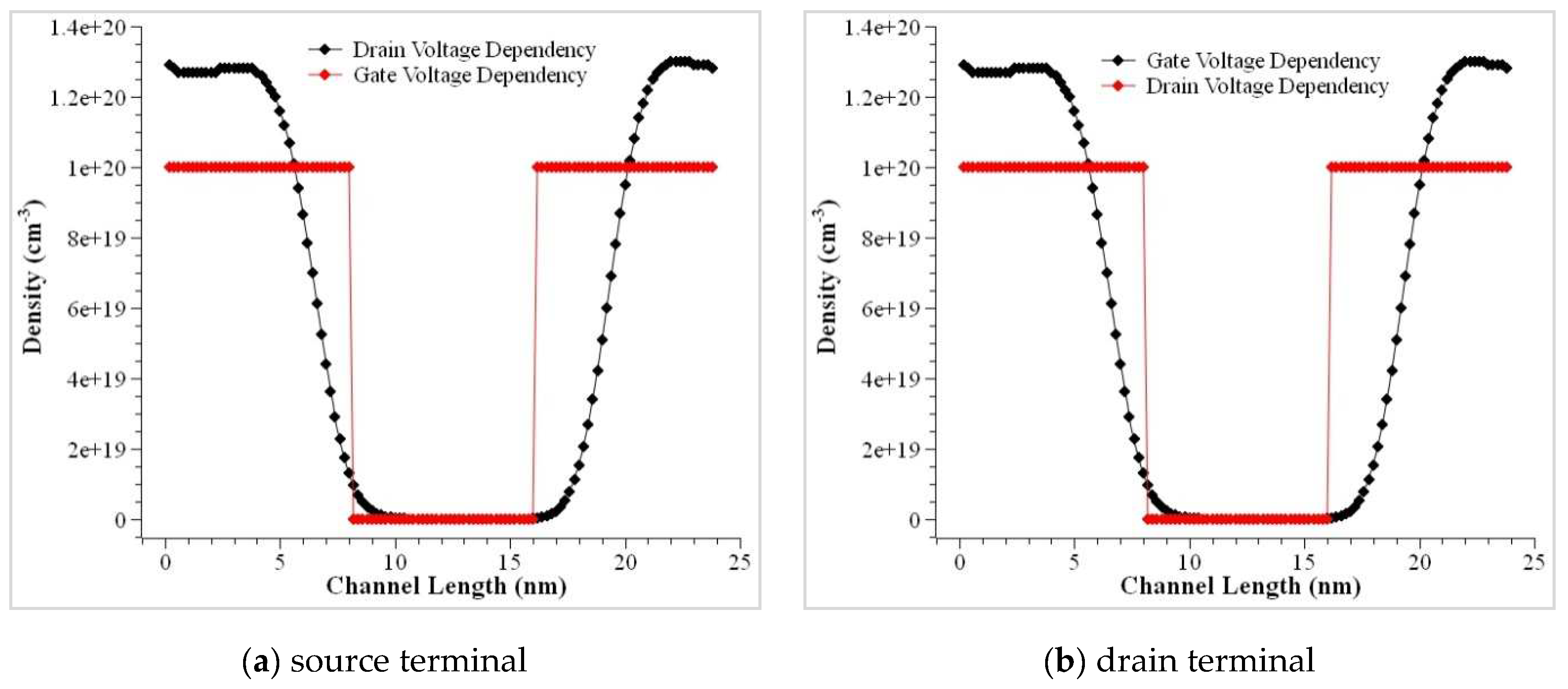
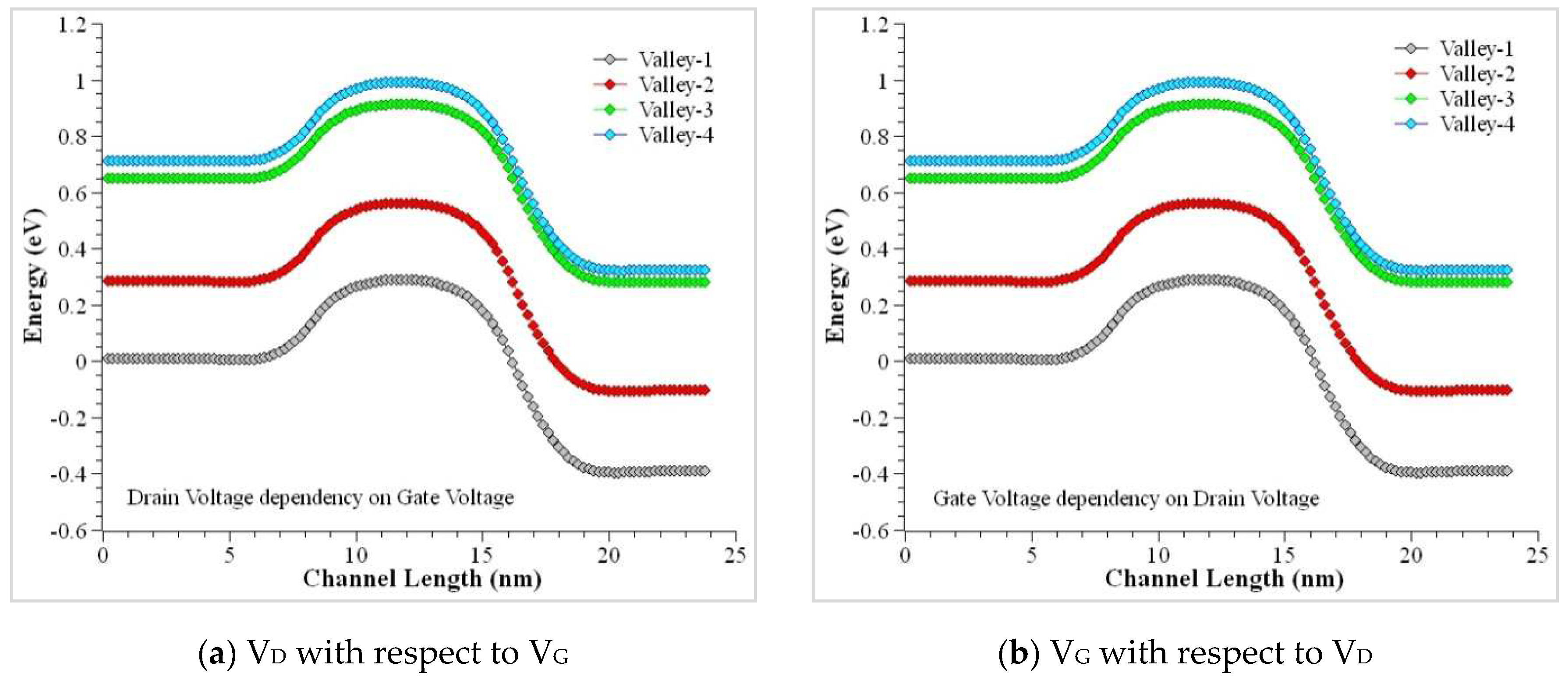
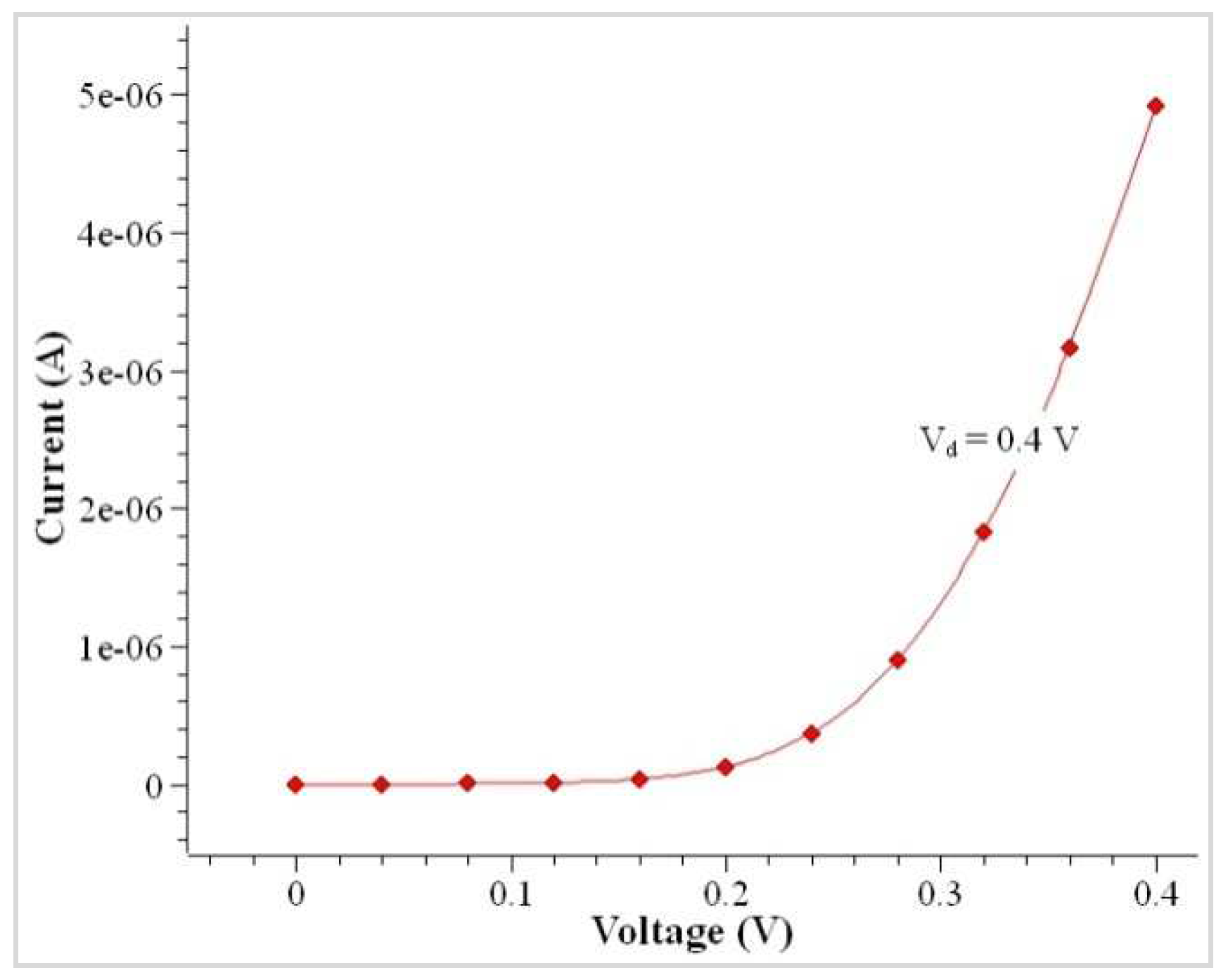
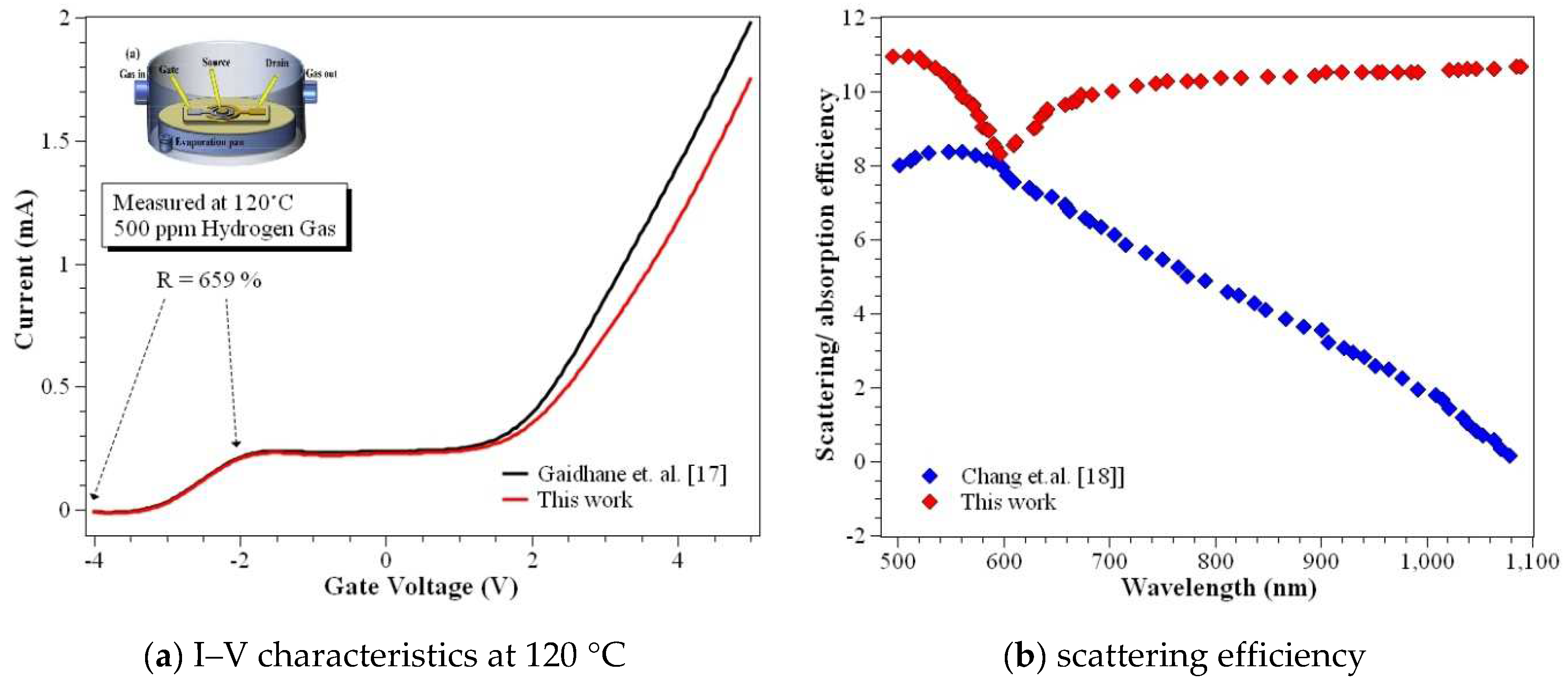
4. Results and Discussion
5. Conclusions and Future Considerations
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
Appendix A
| L, Leff | Channel Length, Effective Channel Length |
| tox, tsi | The thickness of the gate oxide, Thickness of Silicon Film |
| ηi | Carrier Concentration (Intrinsic Semiconductor) |
| εsi, εox | The permittivity of Silicon, Permittivity of oxide |
| φ(x,y,z) | Channel Potential |
| ϕfb | Fermi Potential of lightly p-doped body |
| ψ, ψs, ψ0 | Band Bending Potential |
| K, T | Boltzmann Constant, Temperature |
| q | Charge of an electron |
| Vt, VT, V | The voltage at kT/q, threshold voltage, Fermi level potential |
| VDS, VGS, VFB | Drain to source voltage, the gate to source voltage, flat band voltage |
| Na | Acceptor Doping Concentration |
| H | Electric Field |
| C0 | Oxide Capacitance |
| QI | Inversion Charge Density |
| μeff,μe,si | Effective Mobility, Mobility of electron in Silicon |
| Evertical, Ehorizontal | Vertical and horizontal Electric Field |
| ψS0, ψSL, ψ00, ψ0L | Surface Potential at source and drain, the center of the film |
References
- International Roadmap for Devices and Systems (IRDS™) 2021 Edition. Available online: https://irds.ieee.org (accessed on 9 April 2022).
- Dubey, S.; Kumar, P.; Tiwari, S. A two-dimensional model for the potential distribution and threshold voltage of short-channel double-gate metal-oxide-semiconductor field-effect transistors with a vertical Gaussian-like doping profile. J. Appl. Phys. 2010, 108, 34518. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, Z.; Hu, J. A novel tri-input Schottky barrier FET exhibiting three-input series switching function. In Proceedings of the IEEE 14th International Conference on ASIC (ASICON), Kunming, China, 26–29 October 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Meriga, C.; Ponnuri, R.T.; Krishna, B.V.; Saidulu, S.A.; Prakesh, M.D. Dual gate junctionless gate-all-around (JL-GAA) FETs using hybrid structured channels. In Proceedings of the International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Gupta, S.; Pandey, N.; Gupta, R.S. Investigation of Dual-Material Double Gate Junction Less Accumulation-Mode Cylindrical Gate All Around (DMDG-JLAM-CGAA) MOSFET with high-k gate stack for low power digital applications. In Proceedings of the IEEE 17th India Council International Conference (INDICON), New Delhi, India, 10–13 December 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Gowthaman, N.; Srivastava, V.M. Capacitive modeling of cylindrical surrounding double-gate MOSFETs for hybrid RF applications. IEEE Access 2021, 9, 89234–89242. [Google Scholar] [CrossRef]
- Dargar, A.; Srivastava, V.M. Capacitive model of CSDG MOSFET at pinch-off for switching characteristics. In Proceedings of the 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kanpur, India, 6–8 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Gowthaman, N.; Srivastava, V.M. Arbitrary alloy semiconductor material based DG MOSFET for high-frequency industrial and hybrid consumer applications. In Proceedings of the IEEE AFRICON, Arusha, Tanzania, 13–15 September 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, S.; Lu, L.; Ye, R.; Wu, H.; Chen, H.; Wu, W.; Sun, W.; Ma, S.; Liu, Y.; He, B.; et al. Hot-carrier-induced degradation and optimization for 700-V high-voltage lateral DMOS by the AC stress. IEEE Trans. Electron Devices 2020, 67, 1090–1097. [Google Scholar] [CrossRef]
- Paramasivam, P.; Gowthaman, N.; Srivastava, V.M. Design and analysis of InP/InAs/AlGaAs based Cylindrical Surrounding Double-Gate (CSDG) MOSFETs with La2O3 for 5-nm technology. IEEE Access 2021, 9, 159566–159576. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Ray, P.; Deyasi, A. Computing gate asymmetric effect on drain current of DG-MOSFET following Ortiz-Conde model. In Proceedings of the National Conference on Emerging Trends on Sustainable Technology and Engineering Applications (NCETSTEA), Durgapur, India, 7–8 February 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Deyasi, A.; Chowdhury, A.R.; Roy, K.; Sarkar, A. Effect of high-k dielectric on drain current of ID-DG MOSFET using Ortiz-Conde model. In Proceedings of the IEEE Electron Devices Kolkata Conference (EDKCON), Kolkata, India, 15 November 2018; pp. 176–181. [Google Scholar] [CrossRef]
- Knoll, J.S.; Son, G.; Dimarino, C.; Li, Q.; Stahr, H.; Morianz, M. A PCB-embedded 1.2 kV SiC MOSFET half-bridge package for a 22 kW AC-DC Converter. IEEE Trans. Power Electron. 2022, 37, 11927–11936. [Google Scholar] [CrossRef]
- Horii, K.; Morikawa, R.; Katada, R.; Hata, K.; Sakurai, T.; Hayashi, S.-I.; Wada, K.; Omura, I.; Takamiya, M. Equalization of DC and surge components of drain current of two parallel-connected SiC MOSFETs using single-input dual-output digital gate driver IC. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 1406–1412. [Google Scholar] [CrossRef]
- Gowthaman, N.; Srivastava, V.M. Parametric analysis of CSDG MOSFET with La2O3 gate oxide: Based on electrical field estimation. IEEE Access 2021, 9, 159421–159431. [Google Scholar] [CrossRef]
- Robertson, J. High dielectric constant oxides. Eur. Phys. J. Appl. Phys. 2004, 28, 265–291. [Google Scholar] [CrossRef]
- Gaidhane, A.D.; Pahwa, G.; Verma, A.; Chauhan, Y.S. Gate-induced drain leakage in negative capacitance FinFETs. IEEE Trans. Electron Devices 2020, 67, 802–809. [Google Scholar] [CrossRef]
- Chang, P.C.; Hsiao, C.J.; Lumbantoruan, F.J.; Wu, C.H.; Lin, Y.K.; Lin, Y.C.; Sze, S.M.; Chang, E.Y. InGaAs junctionless FinFETs with self-aligned Ni-InGaAs S/D. IEEE J. Electron Devices Soc. 2018, 6, 856–860. [Google Scholar] [CrossRef]
- Sze, S.M.; Li, Y.; Ng, K.K. Physics of Semiconductor Devices, 4th ed.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Gowthaman, N.; Srivastava, V.M. InP/AlGaAs based CSDG MOSFET with Au/Pt Gate materials for high frequency/hybrid applications. In Proceedings of the XXX International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 15–17 September 2021; pp. 1–5. [Google Scholar] [CrossRef]
- García, I.; Rey-Stolle, I.; Galiana, B.; Algora, C. Analysis of tellurium as the n-type dopant in GaInP: Doping, diffusion, memory effect, and surfactant properties. J. Cryst. Growth 2007, 298, 794–799. [Google Scholar] [CrossRef]
- Ansari, M.H.R.; Cho, S.; Lee, J.H.; Park, B.G. Core-shell dual-gate nanowire memory as a synaptic device for neuromorphic application. IEEE J. Electron Devices Soc. 2021, 9, 1282–1289. [Google Scholar] [CrossRef]
- Passlack, M. Development methodology for high-κ gate dielectrics on III–V semiconductors: GdxGa0.4-xO0.6/Ga2O3 dielectric stacks on GaAs. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2005, 23, 1773–1781. [Google Scholar] [CrossRef]
- Varadharajan, S.; Kaya, S. Study of dual-gate SOI MOSFETs as RF mixers. In Proceedings of the International Semiconductor Device Research Symposium (ISDRS), Bethesda, MD, USA, 7–9 December 2005; pp. 7–8. [Google Scholar] [CrossRef]
- Kumar, A.; Srinivas, P.S.T.N.; Tiwari, P.K. Compact drain current model of silicon-nanotube-based double gate-all-around (DGAA) MOSFETs incorporating short channel effects. In Proceedings of the 14th Nanotechnology Materials and Devices Conference (NMDC), Stockholm, Sweden, 27–30 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Srivastava, V.M.; Yadav, K.S.; Singh, G. Application of VEE Pro software for measurement of MOS device parameters using C-V curve. Int. J. Comput. Appl. 2010, 1, 43–46. [Google Scholar] [CrossRef]
- Mao, C.; Solis, D.J.; Reiss, B.D.; Kottmann, S.T.; Sweeney, R.Y.; Hayhurst, A.; Georgiou, G.; Iverson, B.; Belcher, A.M. Virus-based toolkit for the directed synthesis of magnetic and semiconducting nanowires. Science 2004, 303, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Antoniadis, D.A.; Del Alamo, J.A. Off-state leakage induced by band-to-band tunneling and floating-body bipolar effect in InGaAs quantum-well MOSFETs. IEEE Electron Device Lett. 2014, 35, 1203–1205. [Google Scholar] [CrossRef]
- Lin, J.; Antoniadis, D.A.; Del Alamo, J.A. Physics and mitigation of excess OFF-state current in InGaAs quantum-well MOSFETs. IEEE Trans. Electron Devices 2015, 62, 1448–1455. [Google Scholar] [CrossRef]
- Lim, S.K.; Crawford, S.; Haberfehlner, G.; Gradecak, S. Controlled modulation of diameter and composition along individual III–V nitride nanowires. Nano Lett. 2013, 13, 331–336. [Google Scholar] [CrossRef]
- Kim, S.; Kim, S.K.; Shin, S.; Han, J.H.; Geum, D.M.; Shim, J.P.; Lee, S.; Kim, H.; Ju, G.; Song, J.D.; et al. Highly stable self-aligned Ni-InGaAs and non-self-aligned Mo contact for monolithic 3-D integration of InGaAs MOSFETs. IEEE J. Electron Devices Soc. 2019, 7, 869–877. [Google Scholar] [CrossRef]
- Mo, J.; Lind, E.; Wernersson, L.E. Asymmetric InGaAs/InP MOSFETs with source/drain engineering. IEEE Electron Device Lett. 2014, 35, 515–517. [Google Scholar]
- Zhang, X.; Guo, H.; Lin, H.Y.; Ivana; Gong, X.; Zhou, Q.; Lin, Y.R.; Ko, C.H.; Wann, C.H.; Yeo, Y.C. Reduction of off-state leakage current in In0.7Ga0.3As channel n-MOSFETs with self-aligned Ni-InGaAs contact metallization. Electrochem. Solid-State Lett. 2011, 14, H212–H214. [Google Scholar] [CrossRef]
- Goto, S.; Matsunaga, T.; Chen, J.J.; Makishi, W.; Esashi, M.; Haga, Y. Fabrication techniques for multilayer metalization and patterning, and surface mounting of components on cylindrical substrates for tube-shaped micro-tools. In Proceedings of the International Conference on Microtechnologies in Medicine and Biology, Okinawa, Japan, 9–12 May 2006; pp. 217–220. [Google Scholar]
- Sallese, J.M.; Jazaeri, F.; Barbut, L.; Chevillon, N.; Lallement, C. A common core model for junctionless nanowires and symmetric double-gate FETs. IEEE Trans. Electron Devices 2013, 60, 4277–4280. [Google Scholar] [CrossRef]
- Holtij, T.; Graef, M.; Hain, F.M.; Kloes, A.; Iñíguez, B. Compact model for short-channel junctionless accumulation mode double-gate MOSFETs. IEEE Trans. Electron Devices 2014, 61, 288–299. [Google Scholar] [CrossRef]
- Duarte, J.P.; Choi, S.J.; Moon, D.I.; Choi, Y.K. A Non-piece-wise model for long-channel junctionless cylindrical nanowire FETs. IEEE Electron Device Lett. 2012, 33, 155–157. [Google Scholar] [CrossRef]
- Villa, J.; Ramiro, I.; Ripalda, J.M.; Tobías, I.; García-Linares, P.; Antolin, E.; Martí, A. Contribution to the study of sub-bandgap photon absorption in quantum dot InAs/AlGaAs intermediate band solar cells. IEEE J. Photovolt. 2021, 11, 420–428. [Google Scholar] [CrossRef]
- Shahrjerdi, D.; Rotter, T.; Balakrishnan, G.; Huffaker, D.; Tutuc, E.; Banerjee, S.K. Fabrication of self-aligned enhancement-mode In0.53Ga0.47As MOSFETs with TaN/HfO2/AlN gate stack. IEEE Electron Device Lett. 2008, 29, 557–560. [Google Scholar] [CrossRef]
- Taur, Y.; Ning, T.H. Fundamentals of Modern VLSI Devices, 3rd ed.; Cambridge University Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Dorow, C.; O’Brien, K.; Naylor, C.H.; Lee, S.; Penumatcha, A.; Hsiao, A.; Tronic, T.; Christenson, M.; Maxey, K.; Zhu, H.; et al. Advancing Monolayer 2D nMOS and pMOS transistor integration from growth to van der Waals interface engineering for ultimate CMOS scaling. IEEE Trans. Electron Devices 2021, 68, 6592–6598. [Google Scholar] [CrossRef]
- Fu, H.; Fu, K.; Chowdhury, S.; Palacios, T.; Zhao, Y. Vertical GaN power devices: Device principles and fabrication technologies—Part II. IEEE Trans. Electron Devices 2021, 68, 3212–3222. [Google Scholar] [CrossRef]
- Kim, S.; Kim, M.; Ryu, D.; Lee, K.; Kim, S.; Lee, J.; Lee, R.; Kim, S.; Lee, J.H.; Park, B.G. Investigation of electrical characteristic behavior induced by the channel-release process in stacked nanosheet gate-all-around MOSFETs. IEEE Trans. Electron Devices 2020, 67, 2648–2652. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Abbasi, H.N.; Chang, X.; Zhang, X.; Zhu, T.; Liu, Z.; Song, W.; Chen, G.; Wang, H. LiF/Al₂O₃ as Dielectrics for MOSFET on a single-crystal hydrogen-terminated diamond. IEEE Electron Device Lett. 2020, 41, 808–811. [Google Scholar] [CrossRef]
- Srivastava, V.M.; Yadav, K.S.; Singh, G. Drain current and noise model of cylindrical surrounding double-gate MOSFET for RF switch. Procedia Eng. 2012, 38, 517–521. [Google Scholar] [CrossRef]
- Gowthaman, N.; Srivastava, V.M. Design of Concentric Cylindrical Surrounding Double-Gate (CSDG) MOSFETs—A Fabrication Perspective in Nanoscale Regime; Springer: Berlin/Heidelberg, Germany, 2022; Under Review. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gowthaman, N.; Srivastava, V.M. Mathematical Modeling of Drain Current Estimation in a CSDG MOSFET, Based on La2O3 Oxide Layer with Fabrication—A Nanomaterial Approach. Nanomaterials 2022, 12, 3374. https://doi.org/10.3390/nano12193374
Gowthaman N, Srivastava VM. Mathematical Modeling of Drain Current Estimation in a CSDG MOSFET, Based on La2O3 Oxide Layer with Fabrication—A Nanomaterial Approach. Nanomaterials. 2022; 12(19):3374. https://doi.org/10.3390/nano12193374
Chicago/Turabian StyleGowthaman, Naveenbalaji, and Viranjay M. Srivastava. 2022. "Mathematical Modeling of Drain Current Estimation in a CSDG MOSFET, Based on La2O3 Oxide Layer with Fabrication—A Nanomaterial Approach" Nanomaterials 12, no. 19: 3374. https://doi.org/10.3390/nano12193374
APA StyleGowthaman, N., & Srivastava, V. M. (2022). Mathematical Modeling of Drain Current Estimation in a CSDG MOSFET, Based on La2O3 Oxide Layer with Fabrication—A Nanomaterial Approach. Nanomaterials, 12(19), 3374. https://doi.org/10.3390/nano12193374





