Torsional Properties of Bundles with Randomly Packed Carbon Nanotubes
Abstract
:1. Introduction
2. Methods
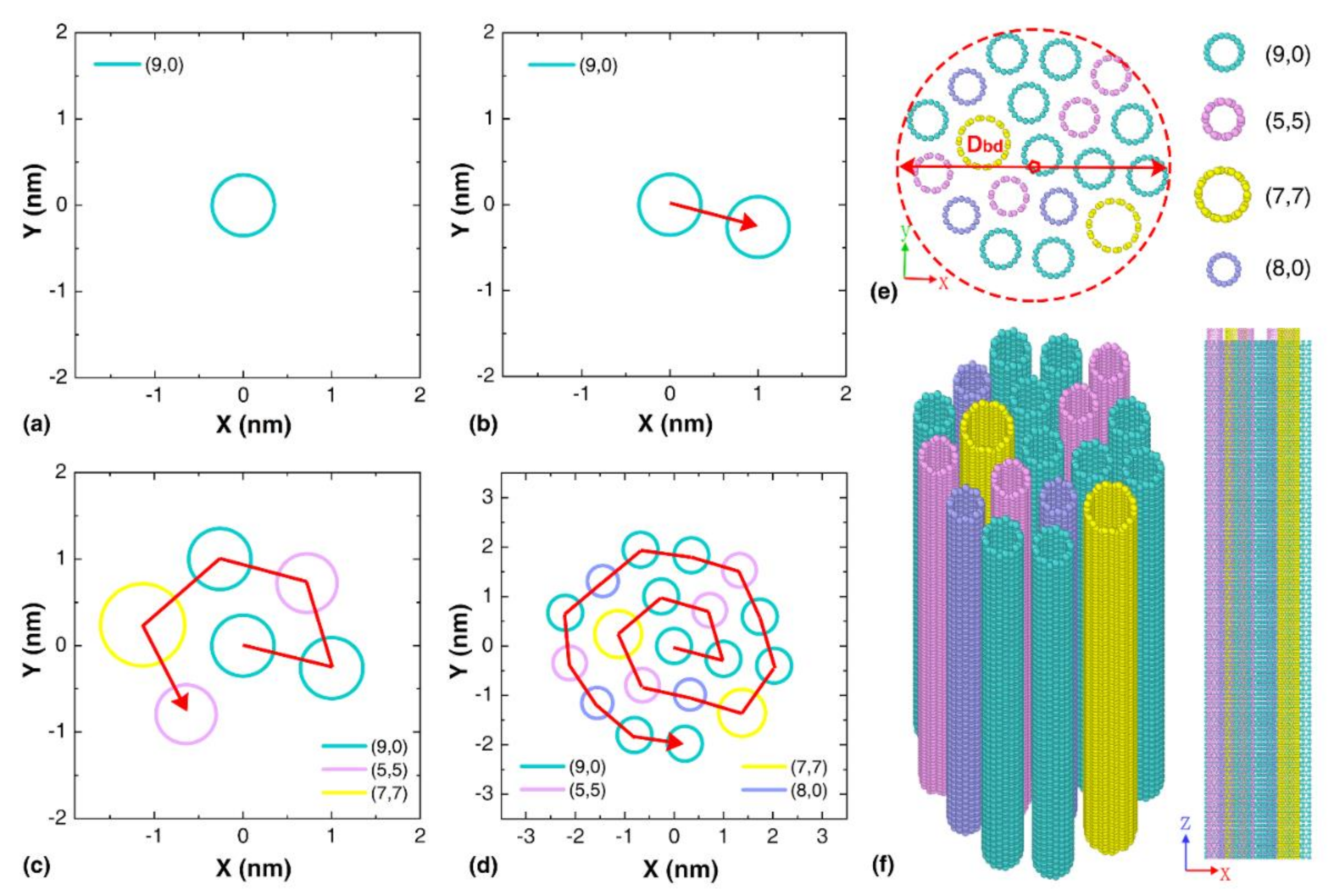
2.1. Bundle Packing Method
2.2. Simulation Details
3. Results and Discussions
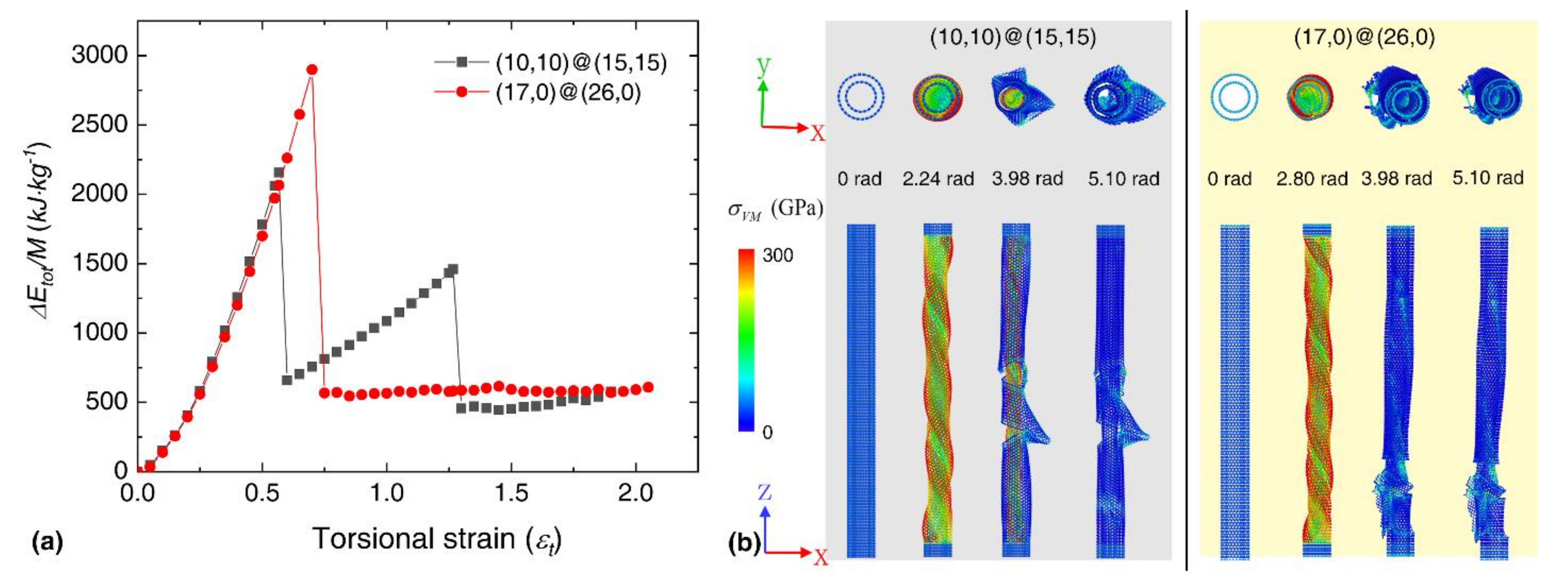
3.1. Torsional Properties of Individual SWNTs
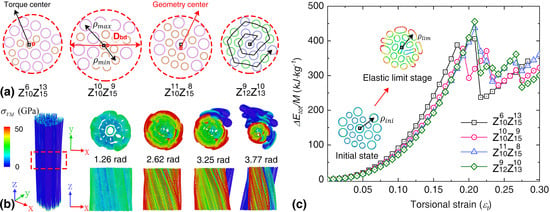
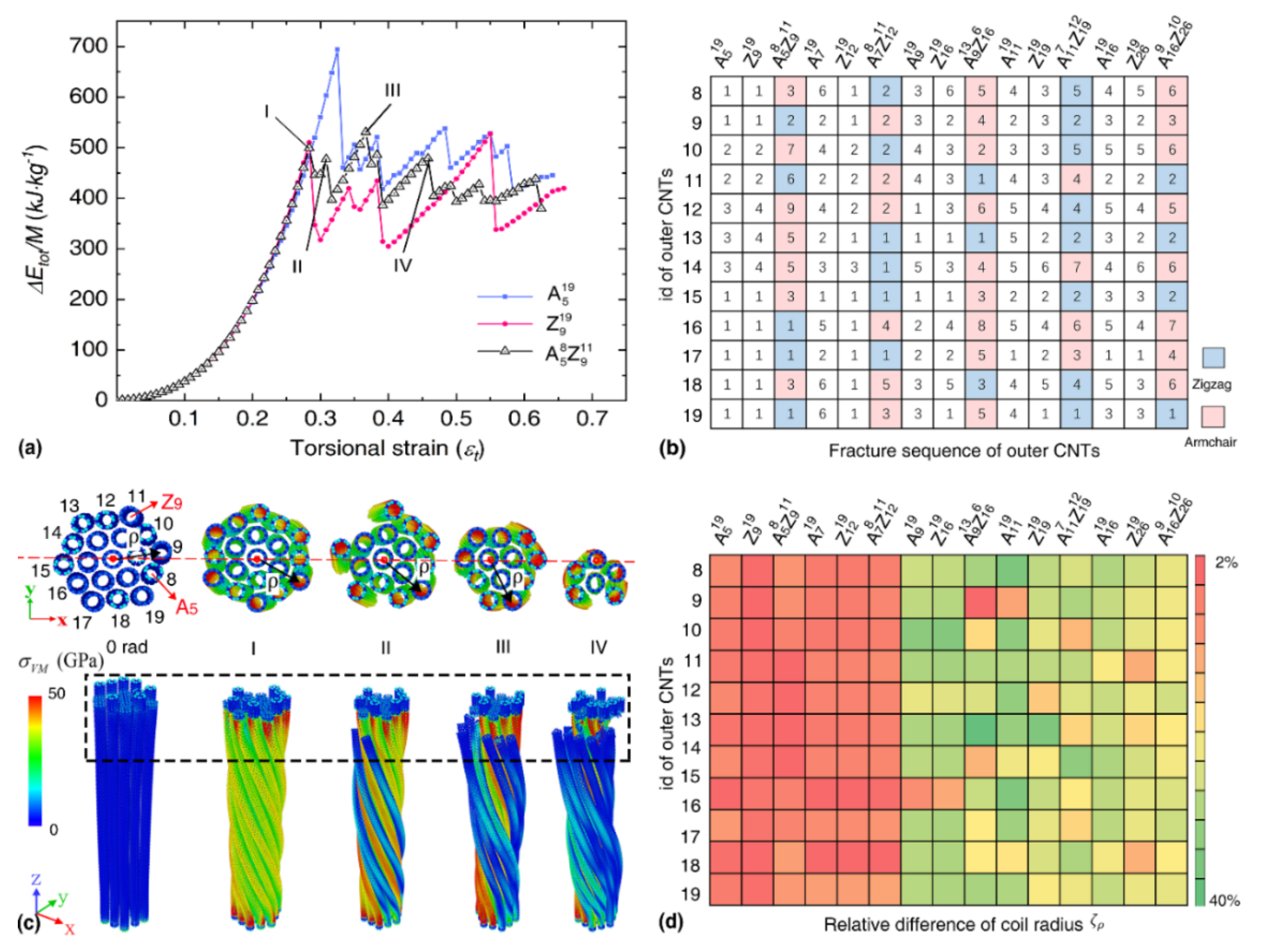
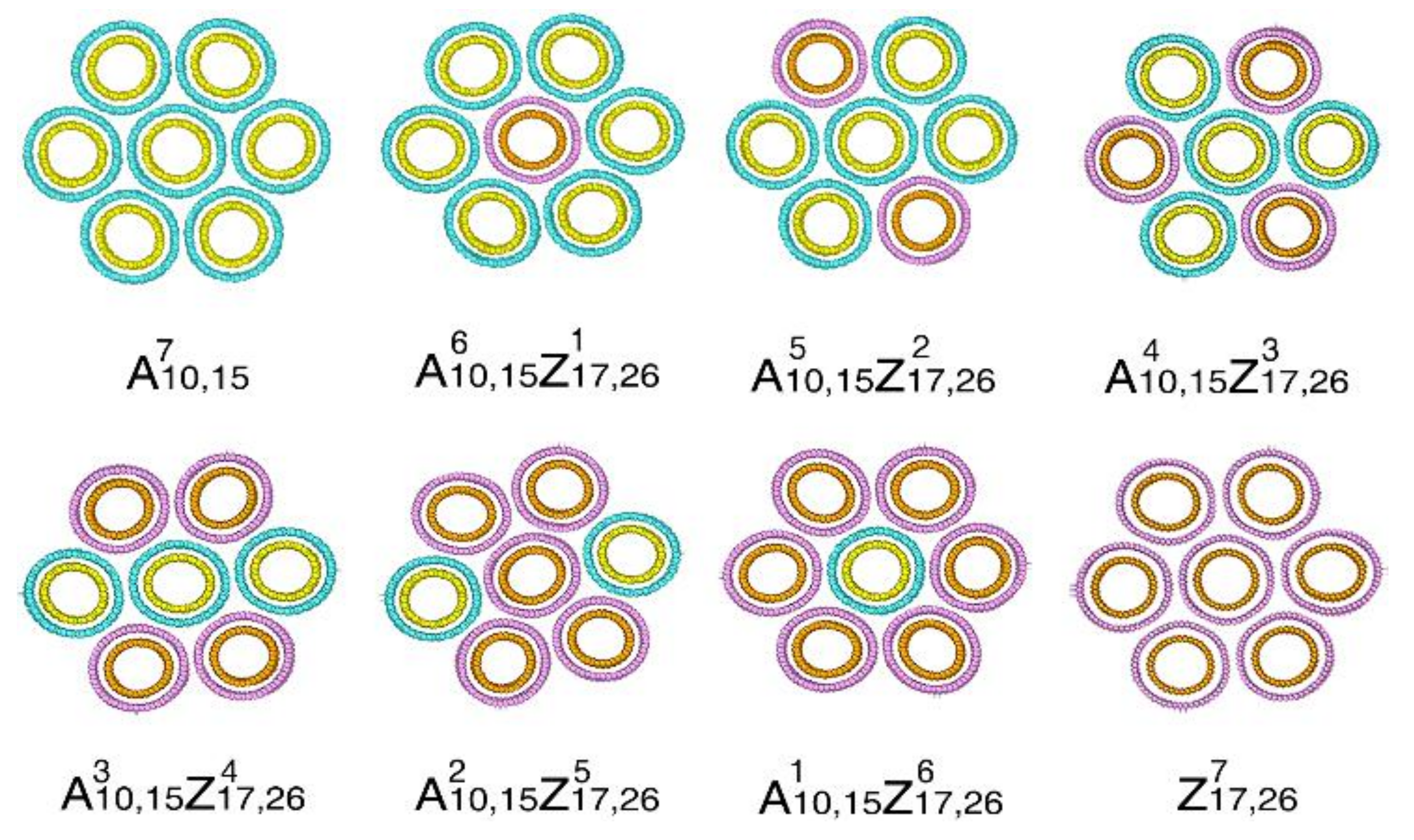
3.2. Bundle Structure Consists of SWNTs with Different Chirality
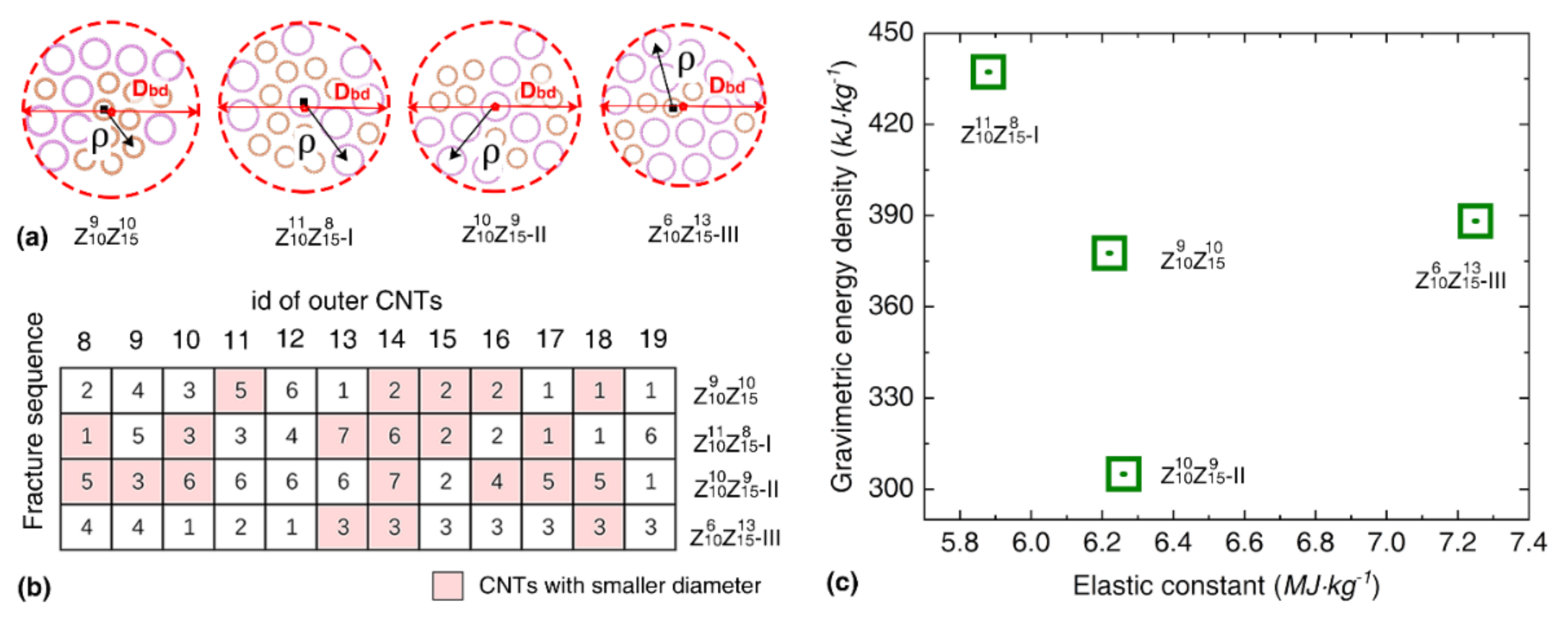
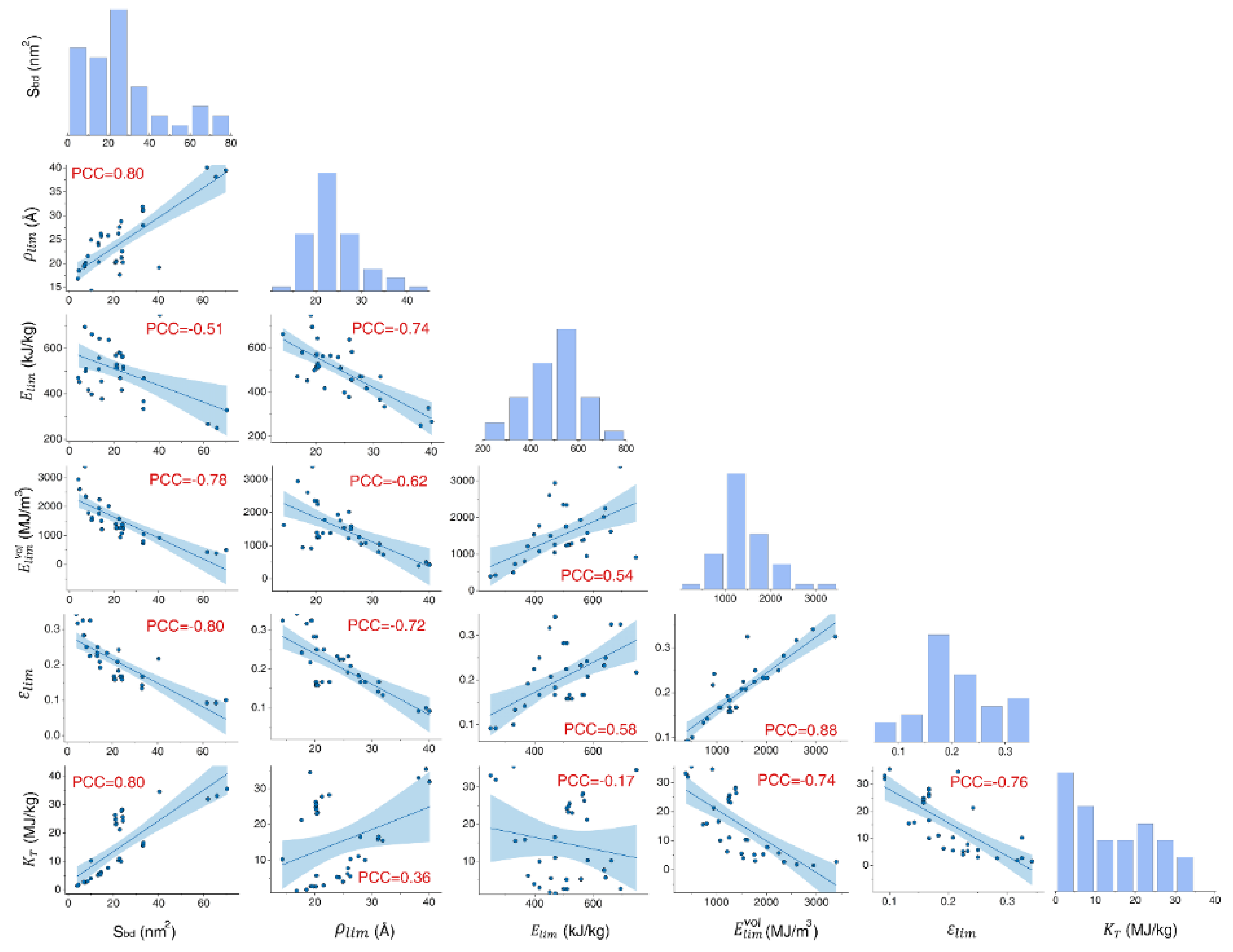
3.3. Bundle Structure Consists of SWNTs with Different Diameter Ratios
3.4. Bundle Structure Consists of SWNTs with Different Mass Density
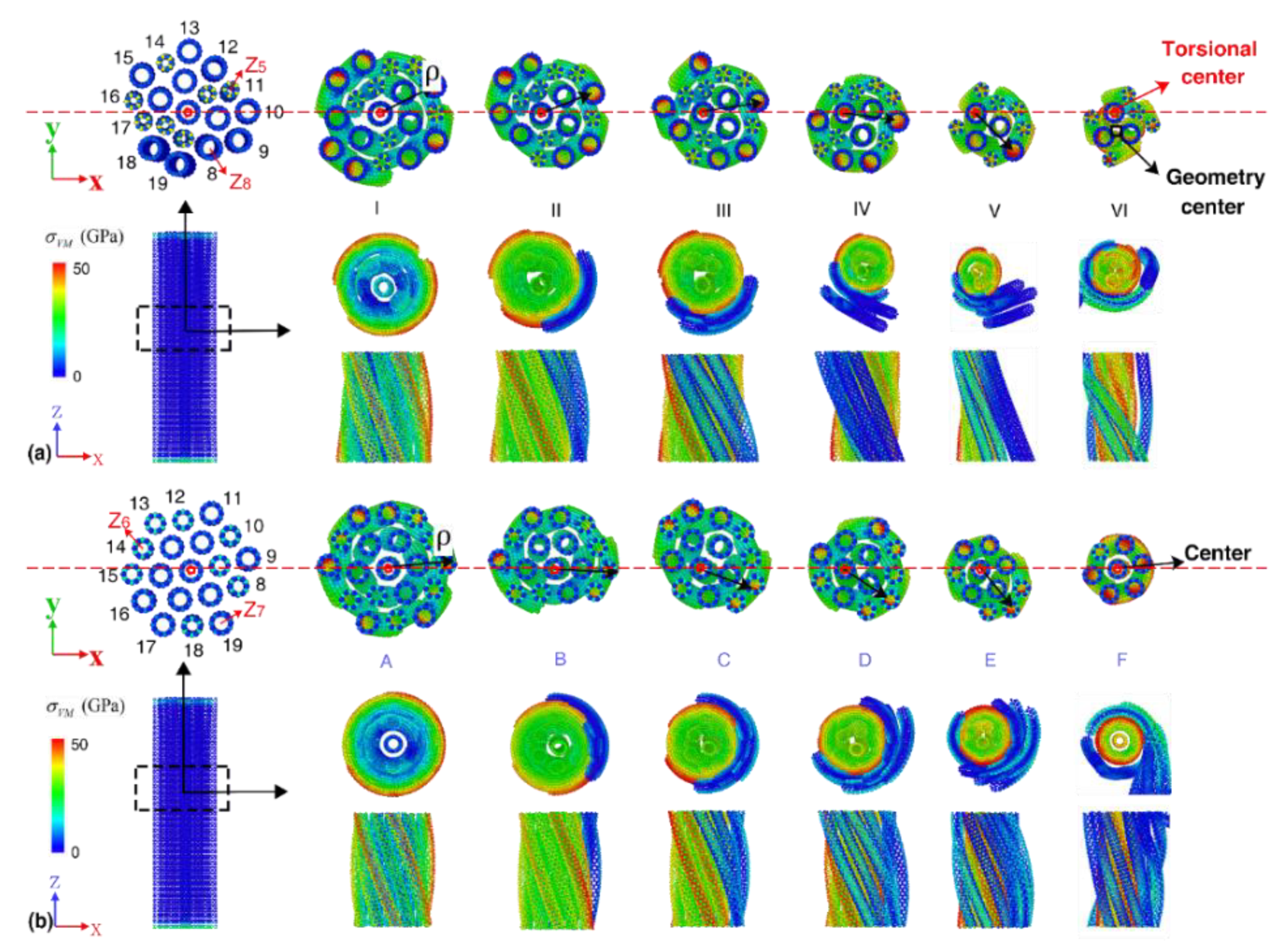
3.5. Bundle Structure Consists of Double-Walled CNTs with Similar Diameter
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hill, F.; Havel, T.; Livermore, C. Modeling Mechanical Energy Storage in Springs Based on Carbon Nanotubes. Nanotechnology 2009, 20, 255704. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.H.; Haines, C.S.; Li, N.; Kim, K.J.; Mun, T.J.; Choi, C. Harvesting Electrical Energy from Carbon Nanotube Yarn Twist. Science 2017, 357, 773–778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aziz, S.; Martinez, J.G.; Foroughi, J.; Spinks, G.M.; Jager, E.W. Artificial Muscles from Hybrid Carbon Nanotube-Polypyrrole-Coated Twisted and Coiled Yarns. Macromol. Mater. Eng. 2020, 305, 2000421. [Google Scholar] [CrossRef]
- Lima, M.; Li, N.; Andrade, M.J.D.; Fang, S.; Oh, J.; Spinks, G.M.; Kozlov, M.E.; Haines, C.S.; Suh, D.; Foroughi, J. Electrically, Chemically, and Photonically Powered Torsional and Tensile Actuation of Hybrid Carbon Nanotube Yarn Muscles. Science 2012, 338, 928–932. [Google Scholar] [CrossRef]
- Di, J.; Zhang, X.; Yong, Z.; Zhang, Y.; Li, D.; Li, R.; Li, Q. Carbon-Nanotube Fibers for Wearable Devices and Smart Textiles. Adv. Mater. 2016, 28, 10529–10538. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, X.; Xin, Y.; Lubineau, G. Strain Sensors: Coaxial Thermoplastic Elastomer-Wrapped Carbon Nanotube Fibers for Deformable and Wearable Strain Sensors. Adv. Funct. Mater. 2018, 28, 1870101. [Google Scholar] [CrossRef] [Green Version]
- Mukhopadhyay, K.; Koshio, A.; Sugai, T.; Tanaka, N.; Shinohara, H.; Konya, Z.; Nagy, J.B. Bulk Production of Quasi-Aligned Carbon Nanotube Bundles by the Catalytic Chemical Vapour Deposition (CCVD) Method. Chem. Phys. Lett. 1999, 303, 117–124. [Google Scholar] [CrossRef]
- Vigolo, B.; Penicaud, A.; Coulon, C.; Sauder, C.; Pailler, R.; Journet, C.; Bernier, P.; Poulin, P. Macroscopic Fibers and Ribbons of Oriented Carbon Nanotubes. Science 2000, 290, 1331–1334. [Google Scholar] [CrossRef]
- Vigolo, B.; Poulin, P.; Lucas, M.; Launois, P.; Bernier, P. Improved Structure and Properties of Single-Wall Carbon Nanotube Spun Fibers. Appl. Phys. Lett. 2002, 81, 1210–1212. [Google Scholar] [CrossRef]
- Liu, M.; Ye, X.; Bai, Y.; Zhang, R.; Wei, F.; Li, X. Multi-Scale Analysis of the Interaction in Ultra-Long Carbon Nanotubes and Bundles. J. Mech. Phys. Solids 2020, 142, 104032. [Google Scholar] [CrossRef]
- Chen, G.; Futaba, D.N.; Kimura, H.; Sakurai, S.; Yumura, M.; Hata, K. Absence of an Ideal Single-Walled Carbon Nanotube Forest Structure for Thermal and Electrical Conductivities. ACS Nano 2013, 7, 10218–10224. [Google Scholar] [CrossRef]
- Xu, M.; Futaba, D.N.; Yumura, M.; Hata, K. Alignment Control of Carbon Nanotube Forest from Random to Nearly Perfectly Aligned by Utilizing the Crowding Effect. ACS Nano 2012, 6, 5837–5844. [Google Scholar] [CrossRef]
- Mirzaeifar, R.; Qin, Z.; Buehler, M. Mesoscale Mechanics of Twisting Carbon Nanotube Yarns. Nanoscale 2015, 7, 5435–5445. [Google Scholar] [CrossRef]
- Vilatela, J.J.; Elliott, J.A.; Windle, A.H. A Model for the Strength of Yarn-Like Carbon Nanotube Fibers. ACS Nano 2011, 5, 1921–1927. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, K.; Feng, C.; Liu, P.; Zhang, L.; Kong, J.; Zhang, T.; Li, Q.; Fan, S. Spinning and Processing Continuous Yarns from 4-Inch Wafer Scale Super-Aligned Carbon Nanotube Arrays. Adv. Mater. 2006, 18, 1505–1510. [Google Scholar] [CrossRef]
- Ma, W.; Liu, L.; Yang, R.; Zhang, T.; Zhang, Z.; Song, L.; Ren, Y.; Shen, J.; Niu, Z.; Zhou, W. Monitoring a Micromechanical Process in Macroscale Carbon Nanotube Films and Fibers. Adv. Mater. 2009, 21, 603–608. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, R.; Ye, X.; Zhu, Z.; Xie, H.; Shen, B.; Cai, D.; Liu, B.; Zhang, C.; Jia, Z. Carbon Nanotube Bundles with Tensile Strength over 80 GPa. Nat. Nanotechnol. 2018, 13, 589–595. [Google Scholar] [CrossRef]
- Chen, J.; Xu, X.; Zhang, L.; Huang, S. Controlling the Diameter of Single-Walled Carbon Nanotubes by Improving the Dispersion of the Uniform Catalyst Nanoparticles on Substrate. Nanomicro Lett. 2015, 7, 353–359. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Luo, S.; Wu, Y.; He, X.; Zhao, F.; Wang, J.; Jiang, K.; Fan, S. Super-Aligned Carbon Nanotube Films as Current Collectors for Lightweight and Flexible Lithium Ion Batteries. Adv. Funct. Mater. 2013, 23, 846–853. [Google Scholar] [CrossRef]
- Lu, W.; Zu, M.; Byun, J.H.; Kim, B.S.; Chou, T.W. State of the Art of Carbon Nanotube Fibers: Opportunities and Challenges. Adv. Mater. 2012, 24, 1805–1833. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Q.; Holesinger, T.G.; Arendt, P.N.; Huang, J.; Kirven, P.D.; Clapp, T.G.; DePaula, R.F.; Liao, X.; Zhao, Y. Ultrastrong, Stiff, and Lightweight Carbon-Nanotube Fibers. Adv. Mater. 2007, 19, 4198–4201. [Google Scholar] [CrossRef]
- Nishimura, M.; Takahashi, N.; Takagi, Y. Relationship between Local Buckling and Atomic Elastic Stiffness in Multi-Walled Carbon Nanotubes under Compression and Bending Deformations. Comput. Mater. Sci. 2017, 130, 214–221. [Google Scholar] [CrossRef]
- Chang, T. Torsional Behavior of Chiral Single-Walled Carbon Nanotubes Is Loading Direction Dependent. Appl. Phys. Lett. 2007, 90, 201910. [Google Scholar] [CrossRef]
- Mirnezhad, M.; Ansari, R.; Falahatgar, S.; Aghdasi, P. Torsional Buckling Analysis of MWCNTs Considering Quantum Effects of Fine Scaling Based on Dft and Molecular Mechanics Method. J. Mol. Graph. Model. 2021, 104, 107843. [Google Scholar] [CrossRef]
- Jeong, B.-W.; Lim, J.-K.; Sinnott, S.B. Elastic Torsional Responses of Carbon Nanotube Systems. J. Appl. Phys. 2007, 101, 622. [Google Scholar] [CrossRef]
- Khademolhosseini, F.; Rajapakse, R.; Nojeh, A. Torsional Buckling of Carbon Nanotubes Based on Nonlocal Elasticity Shell Models. Comput. Mater. Sci. 2010, 48, 736–742. [Google Scholar] [CrossRef]
- Cheng, H.-C.; Liu, Y.-L.; Hsu, Y.-C.; Chen, W.-H. Atomistic-Continuum Modeling for Mechanical Properties of Single-Walled Carbon Nanotubes. Int. J. Solids Struct. 2009, 46, 1695–1704. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, A.R.; Wang, C.M.; Koh, S. Continuum Shell Model for Buckling of Armchair Carbon Nanotubes under Compression or Torsion. Int. J. Appl. Mech. 2014, 06, 1450006. [Google Scholar] [CrossRef]
- Cao, A.; Dickrell, P.; Sawyer, W.; Ghasemi-Nejhad, M.; Ajayan, P. Super-Compressible Foamlike Carbon Nanotube Films. Science 2005, 310, 1307–1310. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, W.; Xi, W.X.; Xianggui, N. Atomistic Simulation of the Torsion Deformation of Carbon Nanotubes. Model. Simul. Mat. Sci. Eng. 2004, 12, 1099. [Google Scholar] [CrossRef]
- Rahmani, R.; Antonov, M. Axial and Torsional Buckling Analysis of Single- and Multi-Walled Carbon Nanotubes: Finite Element Comparison between Armchair and Zigzag Types. SN Appl. Sci. 2019, 1, 1134. [Google Scholar] [CrossRef] [Green Version]
- Kalamkarov, A.L.; Georgiades, A.V.; Rokkam, S.K.; Veedu, V.P.; Ghasemi-Nejhad, M.N. Analytical and Numerical Techniques to Predict Carbon Nanotubes Properties. Int. J. Solids Struct. 2006, 43, 6832–6854. [Google Scholar] [CrossRef] [Green Version]
- Zhan, H.; Zhang, G.; Bell, J.M.; Tan, V.B.C.; Gu, Y. High Density Mechanical Energy Storage with Carbon Nanothread Bundle. Nat. Commun. 2020, 11, 1905. [Google Scholar] [CrossRef]
- Liu, X.; Lu, W.; Ayala, O.M.; Wang, L.-P.; Karlsson, A.M.; Yang, Q.; Chou, T.-W. Microstructural Evolution of Carbon Nanotube Fibers: Deformation and Strength Mechanism. Nanoscale 2013, 5, 2002–2008. [Google Scholar] [CrossRef]
- Zhang, Q.W.; Li, B. Torsional Behavior of Single-Walled Carbon Nanotubes. Carbon 2015, 94, 826–835. [Google Scholar] [CrossRef]
- Wang, W.; Haruehanroengra, S.; Shang, L.; Liu, M. Inductance of Mixed Carbon Nanotube Bundles. Micro Nano Lett. 2007, 2, 35–39. [Google Scholar] [CrossRef]
- Wei, H.; Zhan, H.; Wang, Y.; Gu, Y.; Li, M. Impacts from the Stacking Morphology on the Tensile Performance of Double-Walled Carbon Nanotube Bundles. Carbon 2021, 178, 345–354. [Google Scholar] [CrossRef]
- Hifi, M.; M’hallah, R. A Literature Review on Circle and Sphere Packing Problems: Models and Methodologies. Adv. Oper. Res. 2009, 2009, 150624. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, W.; Zhou, G.; Li, Q. Understanding the Mechanical and Conductive Properties of Carbon Nanotube Fibers for Smart Electronics. Adv. Mater. 2020, 32, 1902028. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, X.; Huang, Y.; Zou, J.; Liu, T.; Liang, N.; Yu, F.; Pan, Z.; Zhu, Y.; Miao, M. A Comparison of the Twisted and Untwisted Structures for One-Dimensional Carbon Nanotube Assemblies. Mater. Des. 2018, 146, 20–27. [Google Scholar] [CrossRef]
- Flores, J.J.; Martínez, J.; Calderon, F. Evolutionary Computation Solutions to the Circle Packing Problem. Soft Comput. 2016, 20, 1521–1535. [Google Scholar] [CrossRef]
- Gadagkar, V.; Maiti, P.K.; Lansac, Y.; Jagota, A.; Sood, A. Collapse of Double-Walled Carbon Nanotube Bundles under Hydrostatic Pressure. Phys. Rev. B 2006, 73, 085402. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A Reactive Potential for Hydrocarbons with Intermolecular Interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef] [Green Version]
- Liew, K.; Wong, C.; Tan, M. Tensile and Compressive Properties of Carbon Nanotube Bundles. Acta Mater. 2006, 54, 225–231. [Google Scholar] [CrossRef]
- Brenner, D.W. Empirical Potential for Hydrocarbons for Use in Simulating the Chemical Vapor Deposition of Diamond Films. Phys. Rev. B 1990, 42, 9458–9471. [Google Scholar] [CrossRef]
- Shenderova, O.; Brenner, D.; Omeltchenko, A.; Su, X.; Yang, L. Atomistic Modeling of the Fracture of Polycrystalline Diamond. Phys. Rev. B 2000, 61, 3877. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Guo, S.; Lei, J.; Sha, Z.; Liu, Z. The Effect of Stone-Thrower-Wales Defects on Mechanical Properties of Graphene Sheets–A Molecular Dynamics Study. Carbon 2014, 75, 124–132. [Google Scholar] [CrossRef]
- Zhan, H.; Zhang, G.; Bell, J.M.; Gu, Y. Thermal Conductivity of Configurable Two-Dimensional Carbon Nanotube Architecture and Strain Modulation. Appl. Phys. Lett. 2014, 105, 153105. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
- Diao, J.; Gall, K.; Dunn, M.L. Atomistic Simulation of the Structure and Elastic Properties of Gold Nanowires. J. Mech. Phys. Solids 2004, 52, 1935–1962. [Google Scholar] [CrossRef]
- Teich, D.; Fthenakis, Z.G.; Seifert, G.; Tomanek, D. Nanomechanical Energy Storage in Twisted Nanotube Ropes. Phys. Rev. Lett. 2012, 109, 255501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fthenakis, Z.G.; Zhen, Z.; Teich, D.; Seifert, G.; Tomanek, D. Limits of Mechanical Energy Storage and Structural Changes in Twisted Carbon Nanotube Ropes. Phys. Rev. B 2013, 88, 245402. [Google Scholar] [CrossRef] [Green Version]
- Teich, D.; Seifert, G.; Iijima, S.; Tománek, D. Helicity in Ropes of Chiral Nanotubes: Calculations and Observation. Phys. Rev. Lett. 2012, 108, 235501. [Google Scholar] [CrossRef] [Green Version]
- Gere, J.M.; Timoshenko, S.P. Mechanics of Materials, Third Si Edition; Cengage Learning: Boston, MA, USA, 1994. [Google Scholar]
- Wang, Q. Torsional Buckling of Double-Walled Carbon Nanotubes. Carbon 2008, 46, 1172–1174. [Google Scholar] [CrossRef]
- Silvestre, N. On the Accuracy of Shell Models for Torsional Buckling of Carbon Nanotubes. Eur. J. Mech. A Solids 2012, 32, 103–108. [Google Scholar] [CrossRef]
- Izadi, R.; Tuna, M.; Trovalusci, P.; Ghavanloo, E. Torsional Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulation. Nanomaterials 2021, 11, 453. [Google Scholar] [CrossRef]
- Zhao, W.; Devel, R.; Dulmet, R. Twisting Carbon Nanotubes: A Molecular Dynamics Study. Surf. Sci. 2010, 604, 496–499. [Google Scholar]
- Yin, H.; Qi, H.J.; Fan, F.; Zhu, T.; Wang, B.; Wei, Y. Griffith Criterion for Brittle Fracture in Graphene. Nano Lett. 2015, 15, 1918–1924. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Li, X.; Yakobson, B.I.; Ding, F. Interaction between Graphene Layers and the Mechanisms of Graphite’s Superlubricity and Self-Retraction. Nanoscale 2013, 5, 6736–6741. [Google Scholar] [CrossRef]
- Dienwiebel, M.; Verhoeven, G.S.; Pradeep, N.; Frenken, J.W.; Heimberg, J.A.; Zandbergen, H.W. Superlubricity of Graphite. Phys. Rev. Lett. 2004, 92, 126101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| Notation | (m,n) | N | (Å) | ||||
|---|---|---|---|---|---|---|---|
| A5 | (5,5) | 2030 | 247.96 | 6.78 | 2.83 | 1.40 | 3.07 |
| A7 | (7,7) | 2842 | 247.96 | 9.49 | 3.15 | 1.43 | 5.40 |
| A8 | (8,8) | 3248 | 247.96 | 10.85 | 3.03 | 1.43 | 6.70 |
| A9 | (9,9) | 3654 | 247.96 | 12.20 | 2.79 | 1.38 | 8.32 |
| A10 | (10,10) | 4060 | 247.96 | 13.56 | 2.64 | 1.32 | 10.16 |
| A11 | (11,11) | 4466 | 247.96 | 14.92 | 2.43 | 1.25 | 12.24 |
| A15 | (15,15) | 6090 | 247.96 | 20.34 | 2.16 | 1.04 | 13.28 |
| A16 | (16,16) | 6496 | 247.96 | 21.70 | 2.23 | 1.02 | 12.45 |
| A20 | (20,20) | 8120 | 247.96 | 27.12 | 2.50 | 0.97 | 9.31 |
| Z5 | (5,0) | 1145 | 242.38 | 3.91 | 3.93 | 1.87 | 1.47 |
| Z6 | (6,0) | 1374 | 242.38 | 4.70 | 1.99 | 1.12 | 1.87 |
| Z7 | (7,0) | 1603 | 242.38 | 5.48 | 2.83 | 1.34 | 2.26 |
| Z8 | (8,0) | 1832 | 242.38 | 6.26 | 2.92 | 1.37 | 2.65 |
| Z9 | (9,0) | 2061 | 242.38 | 7.05 | 2.94 | 1.36 | 3.12 |
| Z10 | (10,0) | 2290 | 242.38 | 7.83 | 2.63 | 1.24 | 3.62 |
| Z12 | (12,0) | 2748 | 242.38 | 9.39 | 2.96 | 1.33 | 4.86 |
| Z13 | (13,0) | 2977 | 242.38 | 10.18 | 3.03 | 1.38 | 5.69 |
| Z15 | (15,0) | 3435 | 242.38 | 11.74 | 2.84 | 1.34 | 7.49 |
| Z16 | (16,0) | 3664 | 242.38 | 12.53 | 2.80 | 1.33 | 8.44 |
| Z19 | (19,0) | 4351 | 242.38 | 14.87 | 2.68 | 1.27 | 11.94 |
| Z26 | (26,0) | 5954 | 242.38 | 20.36 | 2.24 | 1.02 | 13.36 |
| Group | Notation | (nm) | (Å) | (nm2) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 38,570 | 4.75 | 1 | 19.31 | 6.86 | 694.09 | 0.325 | 2.72 | |
| 39,159 | 4.88 | 1 | 20.16 | 7.42 | 510.46 | 0.283 | 2.66 | ||
| 38,911 | 4.82 | 1.04 | 19.76 | 7.18 | 499.18 | 0.283 | 2.67 | ||
| 2 | 53,998 | 6.11 | 1 | 20.29 | 13.44 | 642.94 | 0.250 | 5.72 | |
| 52,212 | 6.06 | 1 | 24.30 | 13.16 | 508.77 | 0.225 | 5.17 | ||
| 53,360 | 6.06 | 1.01 | 23.88 | 13.28 | 558.18 | 0.233 | 5.29 | ||
| 3 | 69,426 | 7.46 | 1 | 26.25 | 22.21 | 581.55 | 0.208 | 10.32 | |
| 69,616 | 7.62 | 1 | 28.79 | 23.43 | 416.64 | 0.167 | 10.03 | ||
| 69,486 | 7.54 | 1.03 | 27.64 | 22.59 | 469.85 | 0.183 | 11.07 | ||
| 4 | 84,854 | 8.82 | 1 | 27.99 | 33.22 | 469.25 | 0.167 | 16.57 | |
| 82,669 | 8.88 | 1 | 31.89 | 33.00 | 333.94 | 0.133 | 15.52 | ||
| 83,474 | 8.81 | 1.00 | 31.07 | 33.08 | 366.61 | 0.142 | 15.89 | ||
| 5 | 123,424 | 12.21 | 1 | 39.49 | 70.27 | 327.95 | 0.100 | 35.53 | |
| 113,126 | 11.54 | 1 | 40.09 | 61.86 | 266.80 | 0.092 | 31.98 | ||
| 118,004 | 11.87 | 1.07 | 38.16 | 65.84 | 249.15 | 0.092 | 33.10 |
| Group | Notation | (nm) | (nm2) | (Å) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 29,999 | 1.60 | 3.90 | 4.53 | 18.52 | 451.87 | 0.317 | 1.77 | |
| 28,625 | 1.17 | 3.90 | 3.98 | 16.79 | 470.21 | 0.342 | 1.47 | ||
| 2 | 44,197 | 1.71 | 5.08 | 9.96 | 24.95 | 398.07 | 0.225 | 3.99 | |
| 41,678 | 1.11 | 5.08 | 8.51 | 21.54 | 416.69 | 0.250 | 3.01 | ||
| 3 | 53,815 | 1.50 | 6.25 | 14.56 | 25.75 | 377.66 | 0.192 | 6.22 | |
| 54,502 | 1.08 | 6.25 | 14.37 | 26.21 | 455.50 | 0.208 | 5.51 |
| Group | Notation | (nm) | (Å) | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 38,570 | 4.75 | 19.46 | 694.09 | 3396 | 0.325 | 2.72 | |
| 28,420 | 4.75 | 14.28 | 662.15 | 1620 | 0.325 | 10.25 | ||
| 2 | 61,712 | 6.78 | 25.82 | 637.04 | 2016 | 0.233 | 7.74 | |
| 42,630 | 6.78 | 17.66 | 579.06 | 944 | 0.242 | 21.22 | ||
| 3 | 84,854 | 8.82 | 31.18 | 469.25 | 1043 | 0.167 | 16.57 | |
| 56,840 | 8.82 | 19.16 | 748.19 | 915 | 0.217 | 34.58 |
| Notation | |||||||
|---|---|---|---|---|---|---|---|
| 71,400 | 23.87 | 22.55 | 565.08 | 1380 | 0.167 | 28.28 | |
| 71,348 | 23.58 | 21.22 | 562.92 | 1378 | 0.167 | 27.85 | |
| 71,296 | 20.77 | 20.17 | 569.74 | 1395 | 0.167 | 26.35 | |
| 71,244 | 24.10 | 20.23 | 519.18 | 1262 | 0.167 | 25.64 | |
| 71,192 | 20.91 | 20.20 | 515.97 | 1254 | 0.158 | 24.85 | |
| 71,140 | 24.21 | 20.26 | 509.85 | 1240 | 0.158 | 24.30 | |
| 71,088 | 21.22 | 20.52 | 514.58 | 1254 | 0.158 | 23.34 | |
| 71,036 | 21.06 | 20.35 | 528.33 | 1288 | 0.158 | 23.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H.; Ting, H.Z.J.; Gong, Y.; Lü, C.; Glukhova, O.E.; Zhan, H. Torsional Properties of Bundles with Randomly Packed Carbon Nanotubes. Nanomaterials 2022, 12, 760. https://doi.org/10.3390/nano12050760
Wei H, Ting HZJ, Gong Y, Lü C, Glukhova OE, Zhan H. Torsional Properties of Bundles with Randomly Packed Carbon Nanotubes. Nanomaterials. 2022; 12(5):760. https://doi.org/10.3390/nano12050760
Chicago/Turabian StyleWei, Hanqing, Heidi Zhi Jin Ting, Yongji Gong, Chaofeng Lü, Olga E. Glukhova, and Haifei Zhan. 2022. "Torsional Properties of Bundles with Randomly Packed Carbon Nanotubes" Nanomaterials 12, no. 5: 760. https://doi.org/10.3390/nano12050760
APA StyleWei, H., Ting, H. Z. J., Gong, Y., Lü, C., Glukhova, O. E., & Zhan, H. (2022). Torsional Properties of Bundles with Randomly Packed Carbon Nanotubes. Nanomaterials, 12(5), 760. https://doi.org/10.3390/nano12050760