Near-Infrared Perfect Absorption and Refractive Index Sensing Enabled by Split Ring Nanostructures
Abstract
:1. Introduction
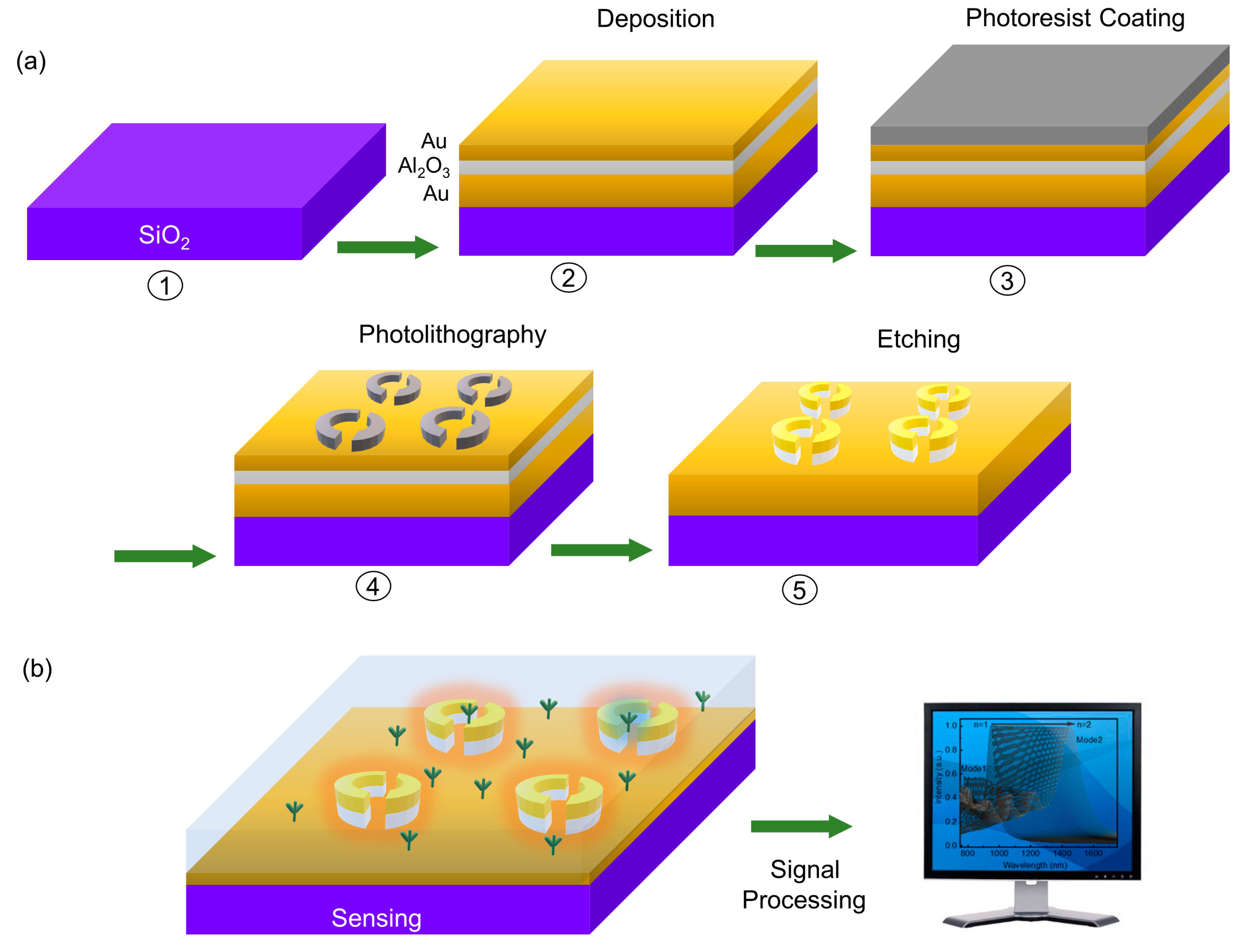
2. Methods
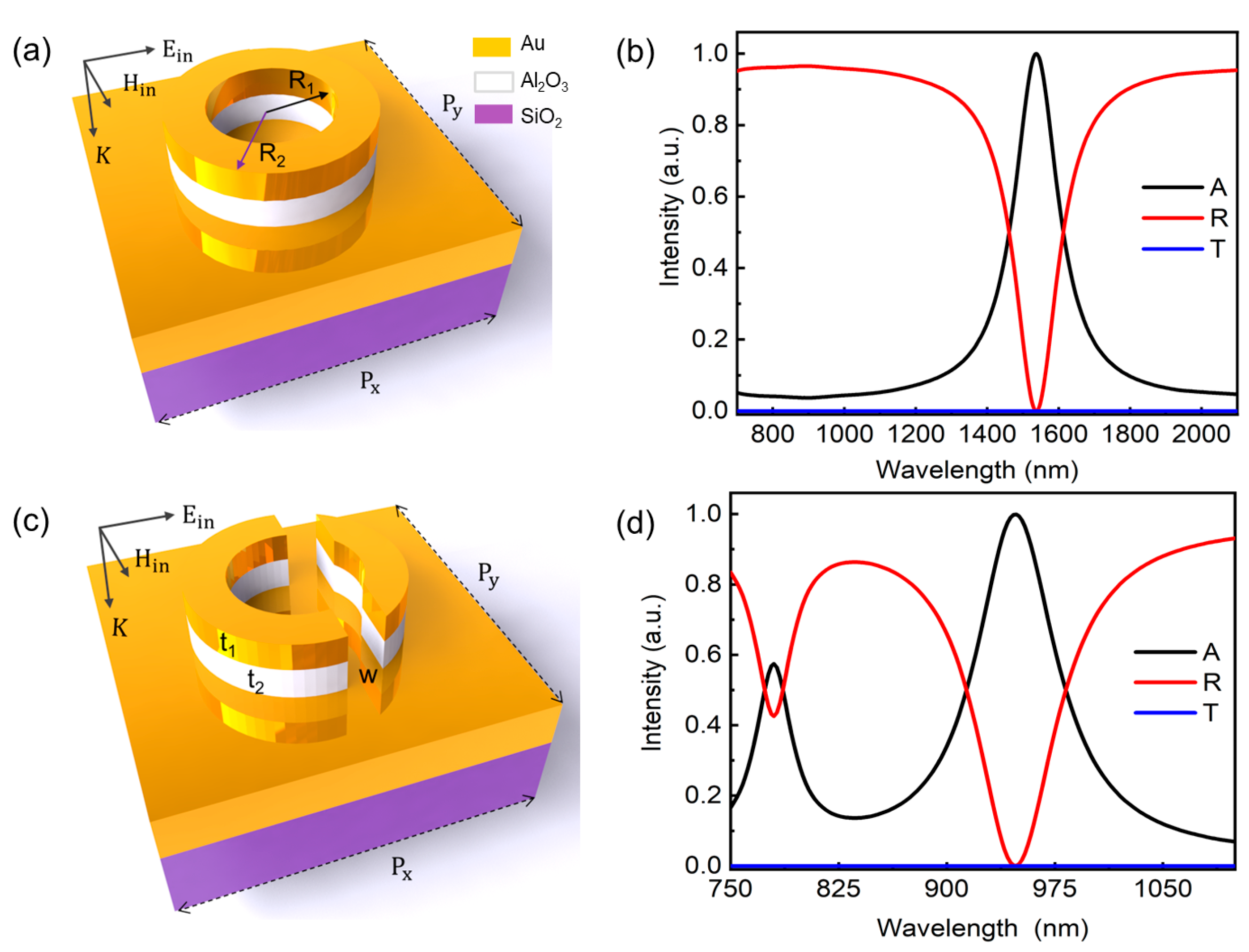
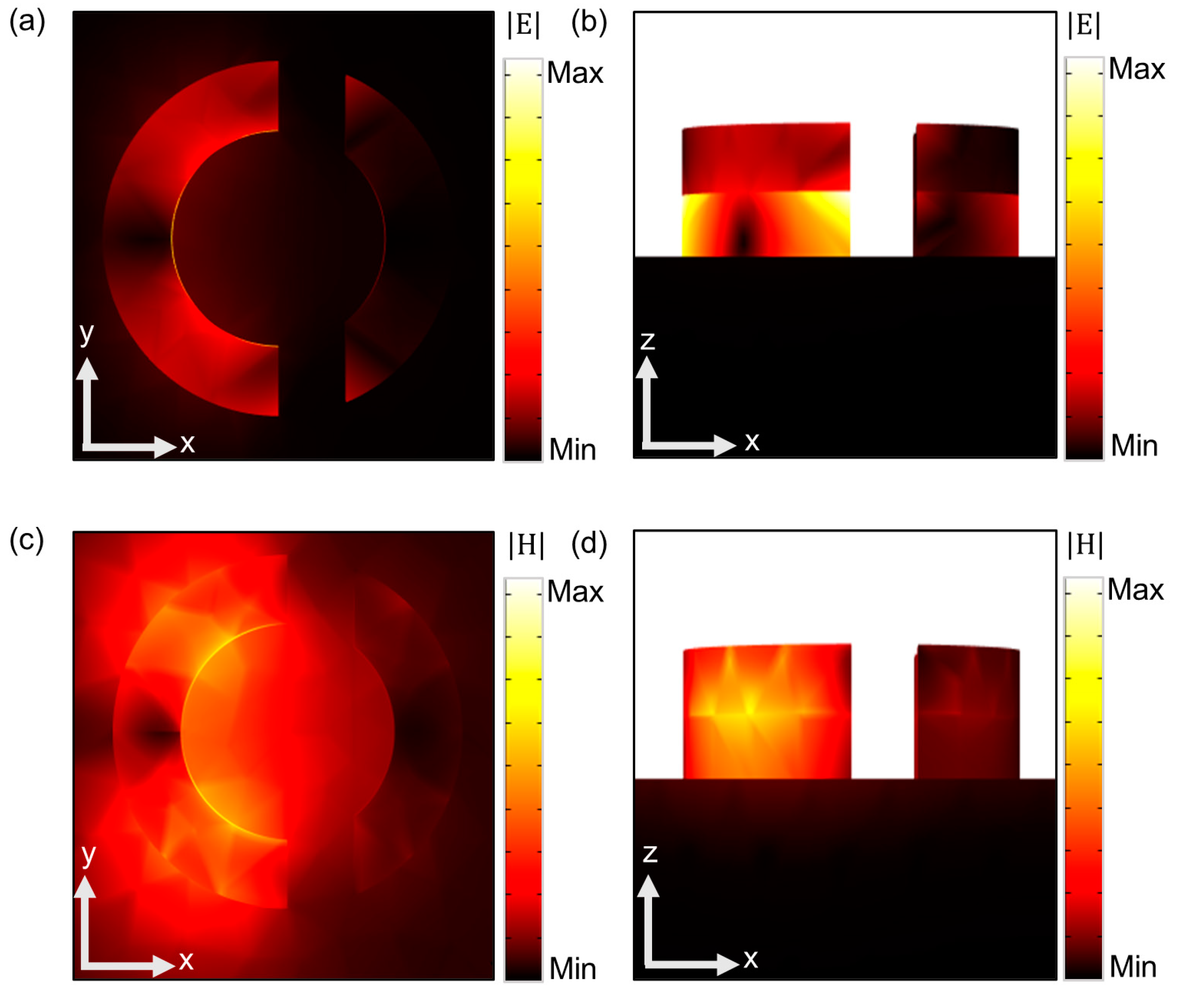
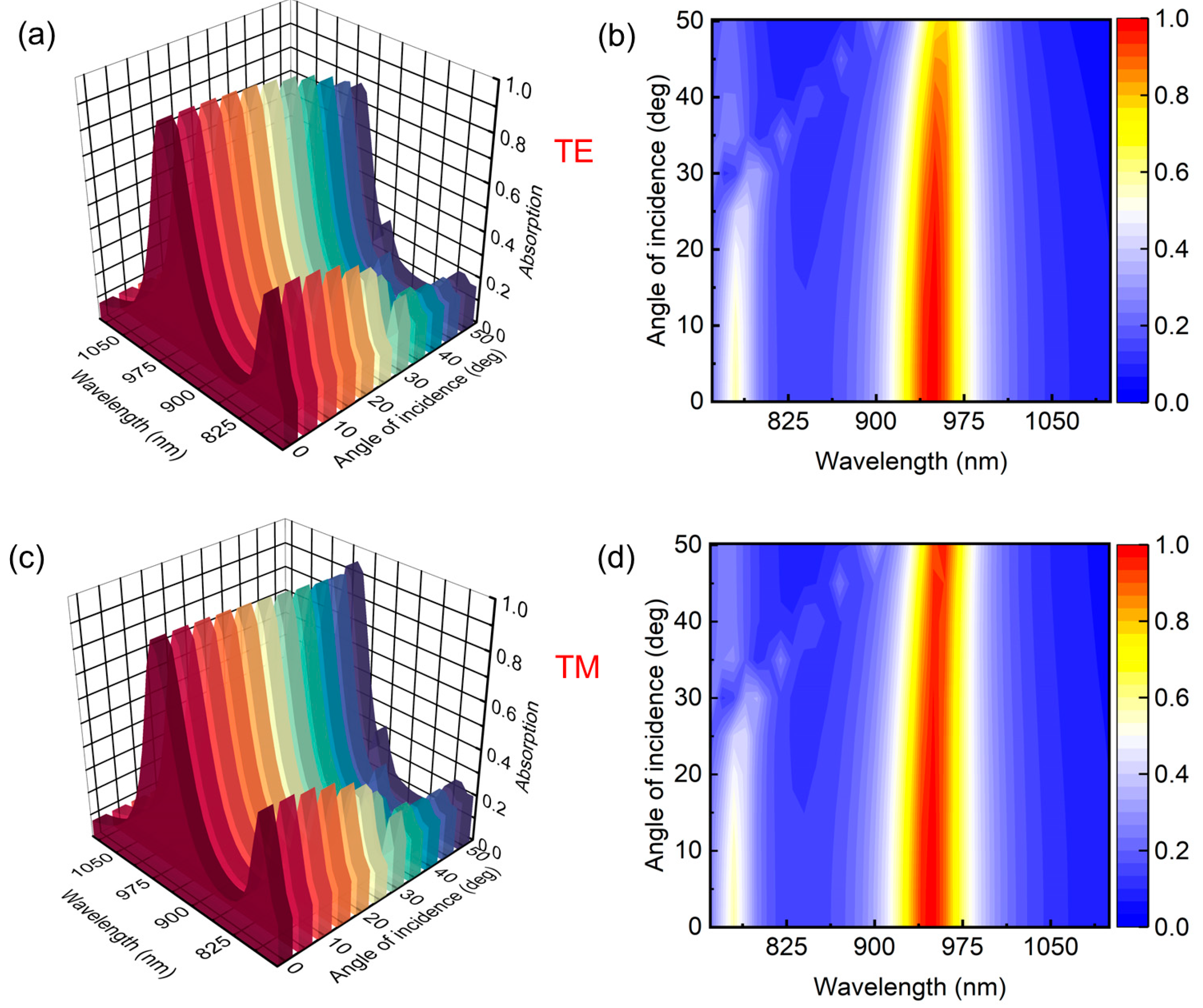
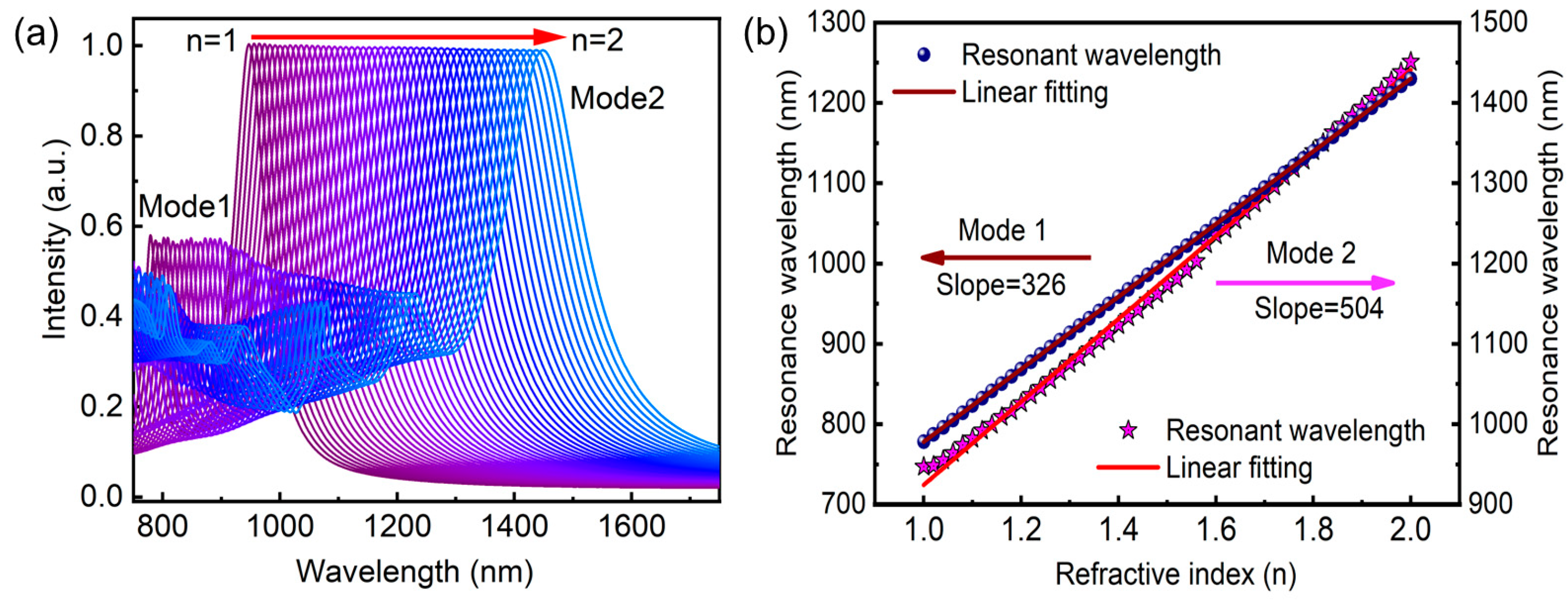
3. Result and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, X.; Tsai, D.; Gu, M.; Hong, M. Extraordinary optical fields in nanostructures: From sub-diffraction-limited optics to sensing and energy conversion. Chem. Soc. Rev. 2019, 48, 2458–2494. [Google Scholar] [CrossRef]
- Maier, S.A.; Atwater, H.A. Plasmonics: Localization and guiding of electromagnetic energy in metal/dielectric structures. J. Appl. Phys. 2005, 98, 011101. [Google Scholar] [CrossRef]
- Aioub, M.; Kang, B.; Mackey, M.A.; El-Sayed, M.A. Biological targeting of plasmonic nanoparticles improves cellular imaging via the enhanced scattering in the aggregates formed. J. Phys. Chem. 2014, 5, 2555–2561. [Google Scholar] [CrossRef]
- Guo, X.; Li, N.; Wu, C.; Dai, X.; Qi, R.; Qiao, T.; Su, T.; Lei, D.; Liu, N.; Du, J. Studying plasmon dispersion of MXene for enhanced electromagnetic absorption. Adv. Mater. 2022, 34, 2201120. [Google Scholar] [CrossRef]
- Kim, S.H.; Rho, Y.; Cho, E.; Myung, J.S.; Lee, S.-J. Surface plasmonic resonance tunable nanocomposite thin films applicable to color filters, heat mirrors, semi-transparent electrodes, and electromagnetic-shields. Nanoscale 2021, 13, 12260–12270. [Google Scholar] [CrossRef]
- Chen, H.; Su, L.; Jiang, M.; Fang, X. Highly desirable photodetectors derived from versatile plasmonic nanostructures. Adv. Funct. Mater. 2017, 27, 1704181. [Google Scholar] [CrossRef]
- Oyarzún, M.P.; Tapia-Arellano, A.; Cabrera, P.; Jara-Guajardo, P.; Kogan, M.J. Plasmonic nanoparticles as optical sensing probes for the detection of alzheimer’s disease. Sensors 2021, 21, 2067. [Google Scholar] [CrossRef]
- Damasceno, G.H.B.; Carvalho, W.O.F.; Mejía-Salazar, J.R. Design of Plasmonic Yagi–Uda Nanoantennas for Chip-Scale Optical Wireless Communications. Sensors 2022, 22, 7336. [Google Scholar] [CrossRef]
- Ali, A.; Mitra, A.; Aïssa, B. Metamaterials and metasurfaces: A review from the perspectives of materials, mechanisms and advanced metadevices. Nanomaterials 2022, 12, 1027. [Google Scholar] [CrossRef]
- Strobbia, P.; Languirand, E.; Cullum, B.M. Recent advances in plasmonic nanostructures for sensing: A review. Opt. Eng. 2015, 54, 100902. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Z.; Kotsifaki, D.G. Plasmonic and metamaterial biosensors: A game-changer for virus detection. Sens. Diagn. 2023, 2, 600–619. [Google Scholar] [CrossRef]
- Jin, G.; Zhou, T.; Tang, B. Ultra-Narrowband Anisotropic Perfect Absorber Based on α-MoO3 Metamaterials in the Visible Light Region. Nanomaterials 2022, 12, 1375. [Google Scholar] [CrossRef] [PubMed]
- Chao, C.-T.C.; Kooh, M.R.; Lim, C.M.; Thotagamuge, R.; Mahadi, A.H.; Chau, Y.-F.C. Visible-Range Multiple-Channel Metal-Shell Rod-Shaped Narrowband Plasmonic Metamaterial Absorber for Refractive Index and Temperature Sensing. Micromachines 2023, 1, 340. [Google Scholar] [CrossRef] [PubMed]
- Kang, P.; Kim, K.-H.; Park, H.-G.; Nam, S. Mechanically reconfigurable architectured graphene for tunable plasmonic resonances. Light Sci. Appl. 2018, 7, 17. [Google Scholar] [CrossRef]
- Fang, Z.; Zhu, X. Plasmonics in nanostructures. Adv. Mater. 2013, 25, 3840–3856. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Rose, M.; Prosvirnin, S.L.; Papasimakis, N.; Zheludev, N.I. Sharp trapped-mode resonances in planar metamaterials with a broken structural symmetry. Phys. Rev. Lett. 2007, 99, 147401. [Google Scholar] [CrossRef]
- Shi, Y.; Chen, X.; Lou, F.; Chen, Y.; Yan, M.; Wosinski, L.; Qiu, M. All-optical switching of silicon disk resonator based on photothermal effect in metal–insulator–metal absorber. Opt. Lett. 2014, 39, 4431–4434. [Google Scholar] [CrossRef]
- Bonin, G.O.; Barrow, S.J.; Connell, T.U.; Roberts, A.; Chesman, A.S.R.; Gómez, D.E. Self-Assembly of Plasmonic Near-Perfect Absorbers of Light: The Effect of Particle Size. J. Phys. Chem. 2020, 11, 8378–8385. [Google Scholar] [CrossRef]
- Kocer, H.; Butun, S.; Li, Z.; Aydin, K. Reduced near-infrared absorption using ultra-thin lossy metals in Fabry-Perot cavities. Sci. Rep. 2015, 5, 8157. [Google Scholar] [CrossRef]
- Park, C.S.; Lee, S.S. Narrowband and flexible perfect absorber based on a thin-film nano-resonator incorporating a dielectric overlay. Sci. Rep. 2020, 10, 17727. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, H.; Sun, L.; Li, J.; Yu, C. Double-band perfect absorber based on the dielectric grating and Fabry–Perot cavity. Appl. Phys. A 2019, 125, 792. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Z.; Liu, J.; Cheng, J.; Zhou, Y.; Xiao, L.; Chen, K. Ultra-narrow band mid-infrared perfect absorber based on hybrid dielectric metasurface. Nanomaterials 2019, 9, 1350. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Wang, Y.; Yi, Z.; Huang, Z.; Xu, Z.; Jiang, P. A near-infrared multi-band perfect absorber based on 1D gold grating Fabry-Perot structure. IEEE Access 2020, 8, 72742–72748. [Google Scholar] [CrossRef]
- Zhang, H.; Ling, F.; Zhang, B. Broadband tunable terahertz metamaterial absorber based on vanadium dioxide and Fabry-Perot cavity. Opt. Mater. 2021, 112, 110803. [Google Scholar] [CrossRef]
- Ouyang, L.; Wang, W.; Rosenmann, D.; Czaplewski, D.A.; Gao, J.; Yang, X. Near-infrared chiral plasmonic metasurface absorbers. Opt. Express 2018, 26, 31484–31489. [Google Scholar] [CrossRef]
- Mahmud, M.S.; Rosenmann, D.; Czaplewski, D.A.; Gao, J.; Yang, X. Chiral plasmonic metasurface absorbers in the mid-infrared wavelength range. Opt. Lett. 2020, 45, 5372–5375. [Google Scholar] [CrossRef]
- Tang, H.; Rosenmann, D.; Czaplewski, D.A.; Yang, X.; Gao, J. Dual-band selective circular dichroism in mid-infrared chiral metasurfaces. Opt. Express 2022, 30, 20063–20075. [Google Scholar] [CrossRef]
- Zeng, X.; Rosenmann, D.; Czaplewski, D.A.; Gao, J.; Yang, X. Mid-infrared chiral metasurface absorbers with split-ellipse structures. Opt. Commun. 2022, 525, 128854. [Google Scholar] [CrossRef]
- Zeng, X.; Rosenmann, D.; Czaplewski, D.A.; Gao, J.; Yang, X. Chiral metasurfaces of wavy rectangle resonators with tunable circular dichroism. Optik 2023, 286, 171024. [Google Scholar] [CrossRef]
- Tang, H.; Stan, L.; Czaplewski, D.A.; Yang, X.; Gao, J. Wavelength-tunable infrared chiral metasurfaces with phase-change materials. Opt. Express 2023, 31, 21118–21127. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, Y.; Li, Y.; Ren, L.; Chen, F.; Cheng, S.; Yang, W.; Ma, C.; Wang, Z.; Zhou, X. Triple-band perfect absorber based on the gold-Al2O3-grating structure in visible and near-infrared wavelength range. Opt. Quantum Electron. 2022, 54, 43. [Google Scholar] [CrossRef]
- Zhong, M. Design and measurement of a narrow band metamaterial absorber in terahertz range. Opt. Mater. 2020, 100, 109712. [Google Scholar] [CrossRef]
- Karthikeyan, M.; Jayabala, P.; Ramachandran, S.; Dhanabalan, S.S.; Sivanesan, T.; Ponnusamy, M. Tunable optimal dual band metamaterial absorber for high sensitivity THz refractive index sensing. Nanomaterials 2022, 12, 2693. [Google Scholar] [CrossRef] [PubMed]
- Johnson, P.B.; Christy, R.-W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Ali, W.; Iqbal, S.; Ullah, M.; Wang, X.J.P. An ultrahigh narrowband absorber close to the information communication window. Plasmonics 2022, 17, 709–715. [Google Scholar] [CrossRef]
- Yao, J.; Ou, J.-Y.; Savinov, V.; Chen, M.K.; Kuo, H.Y.; Zheludev, N.I.; Tsai, D.P. Plasmonic anapole metamaterial for refractive index sensing. PhotoniX 2022, 3, 23. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, W.; Liu, W.; Liu, Y.; Li, Z. Near-Infrared Perfect Absorption and Refractive Index Sensing Enabled by Split Ring Nanostructures. Nanomaterials 2023, 13, 2668. https://doi.org/10.3390/nano13192668
Ali W, Liu W, Liu Y, Li Z. Near-Infrared Perfect Absorption and Refractive Index Sensing Enabled by Split Ring Nanostructures. Nanomaterials. 2023; 13(19):2668. https://doi.org/10.3390/nano13192668
Chicago/Turabian StyleAli, Wajid, Weitao Liu, Ye Liu, and Ziwei Li. 2023. "Near-Infrared Perfect Absorption and Refractive Index Sensing Enabled by Split Ring Nanostructures" Nanomaterials 13, no. 19: 2668. https://doi.org/10.3390/nano13192668
APA StyleAli, W., Liu, W., Liu, Y., & Li, Z. (2023). Near-Infrared Perfect Absorption and Refractive Index Sensing Enabled by Split Ring Nanostructures. Nanomaterials, 13(19), 2668. https://doi.org/10.3390/nano13192668






