Supercurrent in Bi4Te3 Topological Material-Based Three-Terminal Junctions
Abstract
:1. Introduction
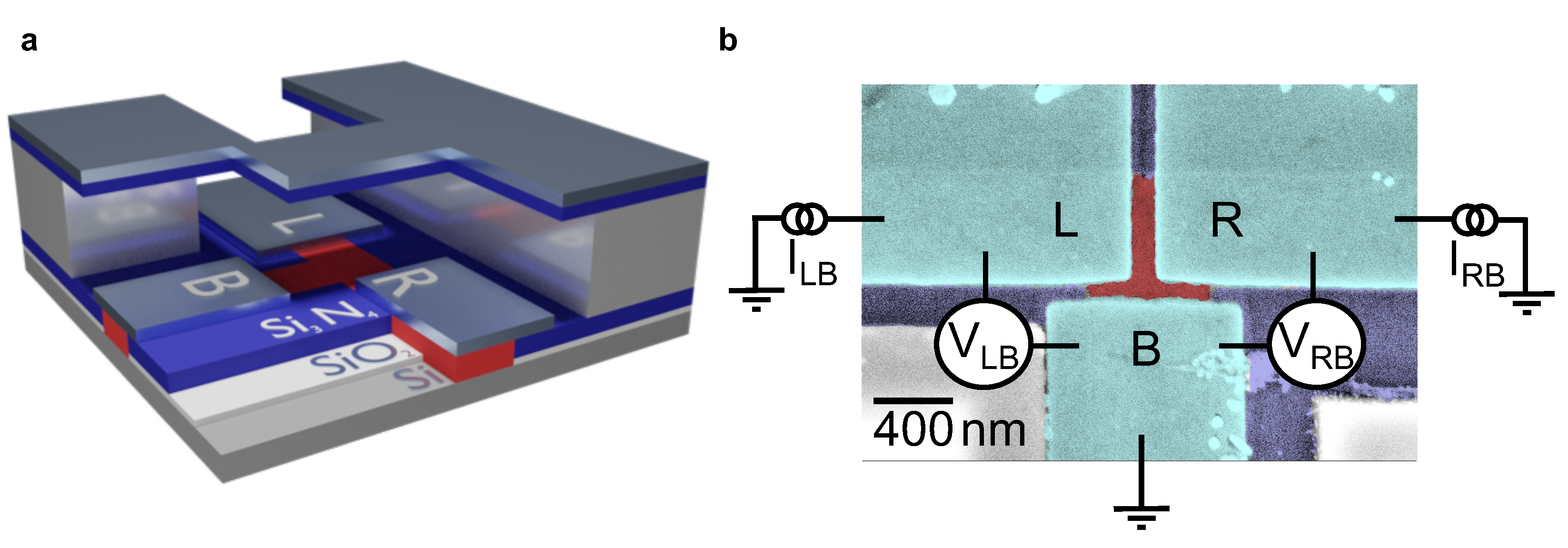
2. Materials and Methods
3. Results and Discussion
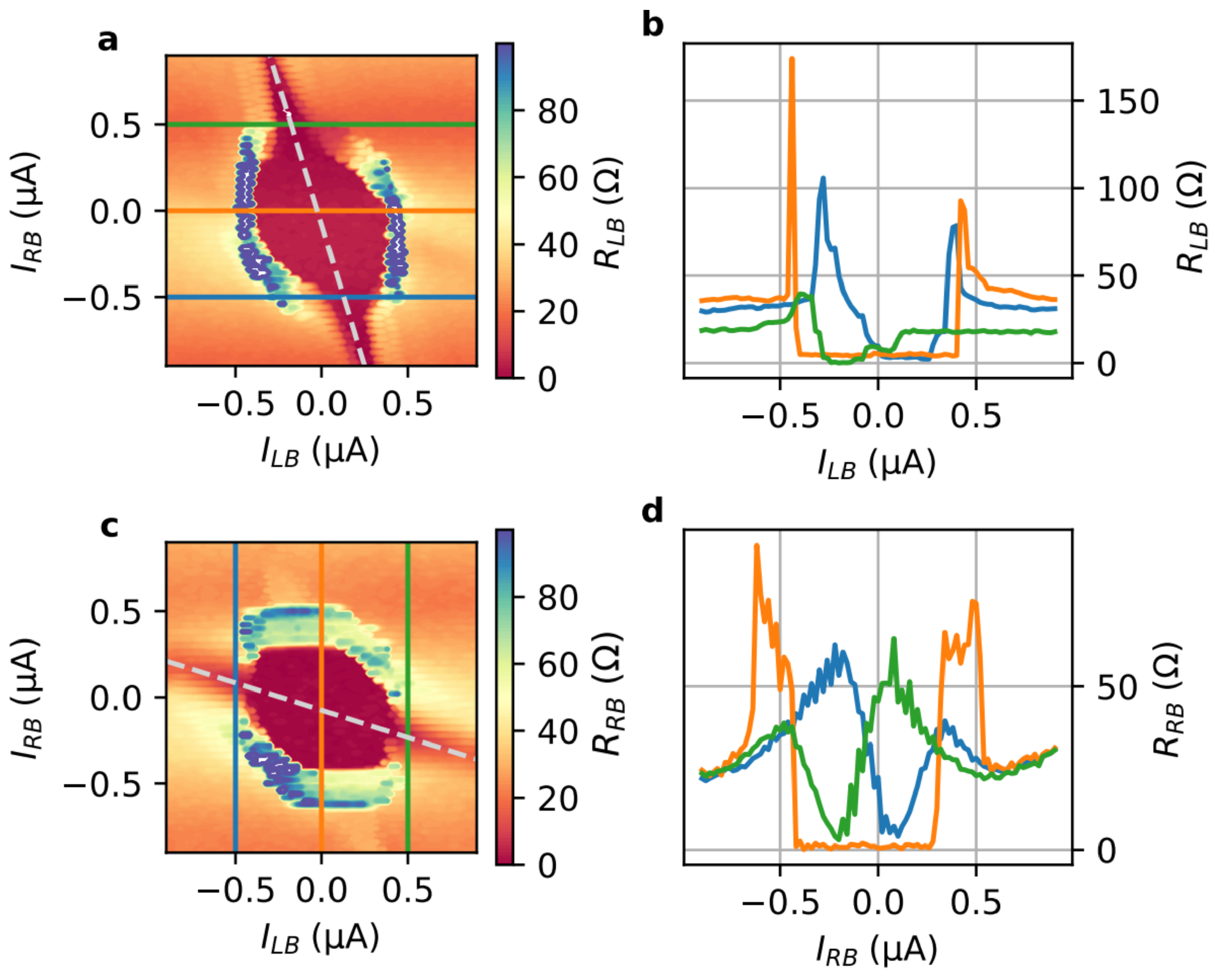
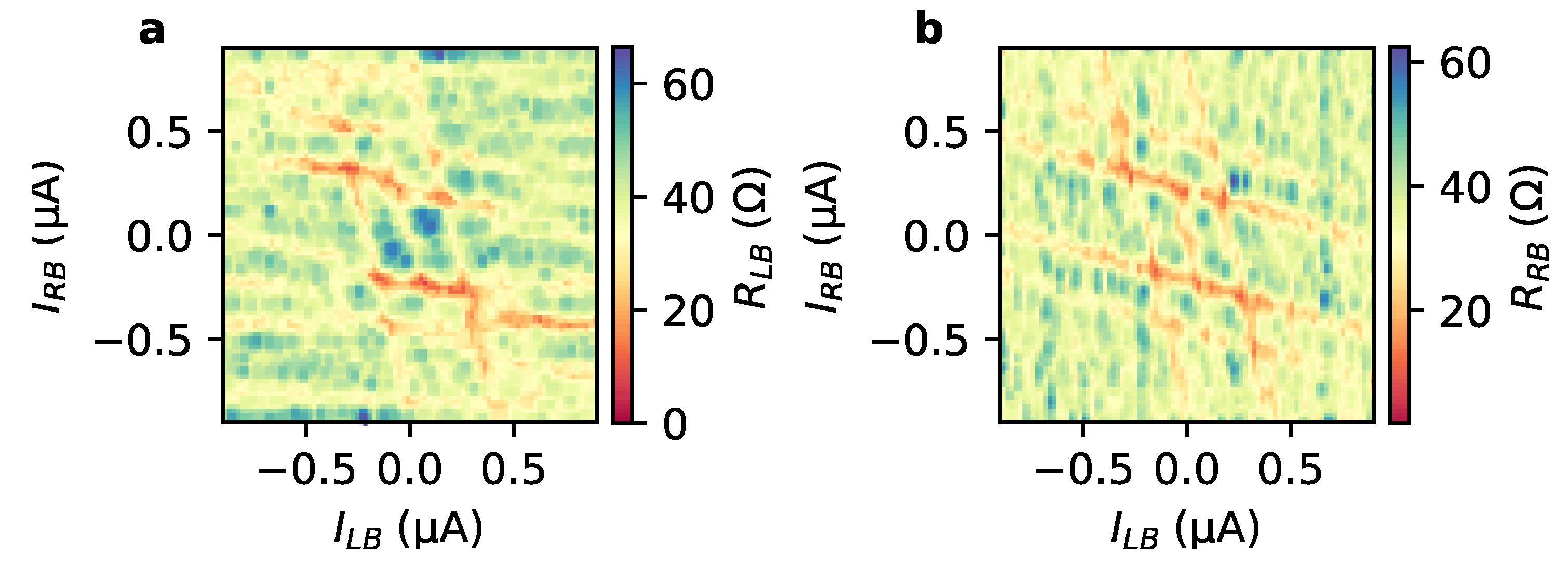
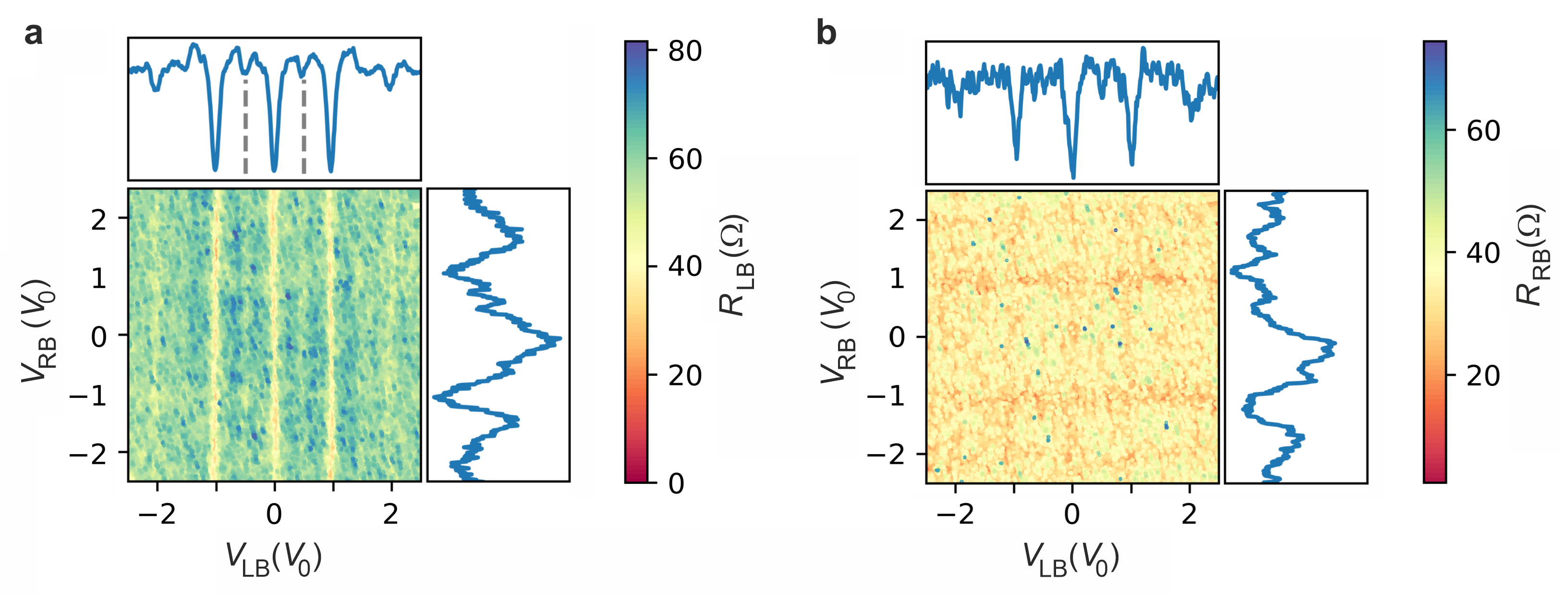
3.1. DC Characteristics
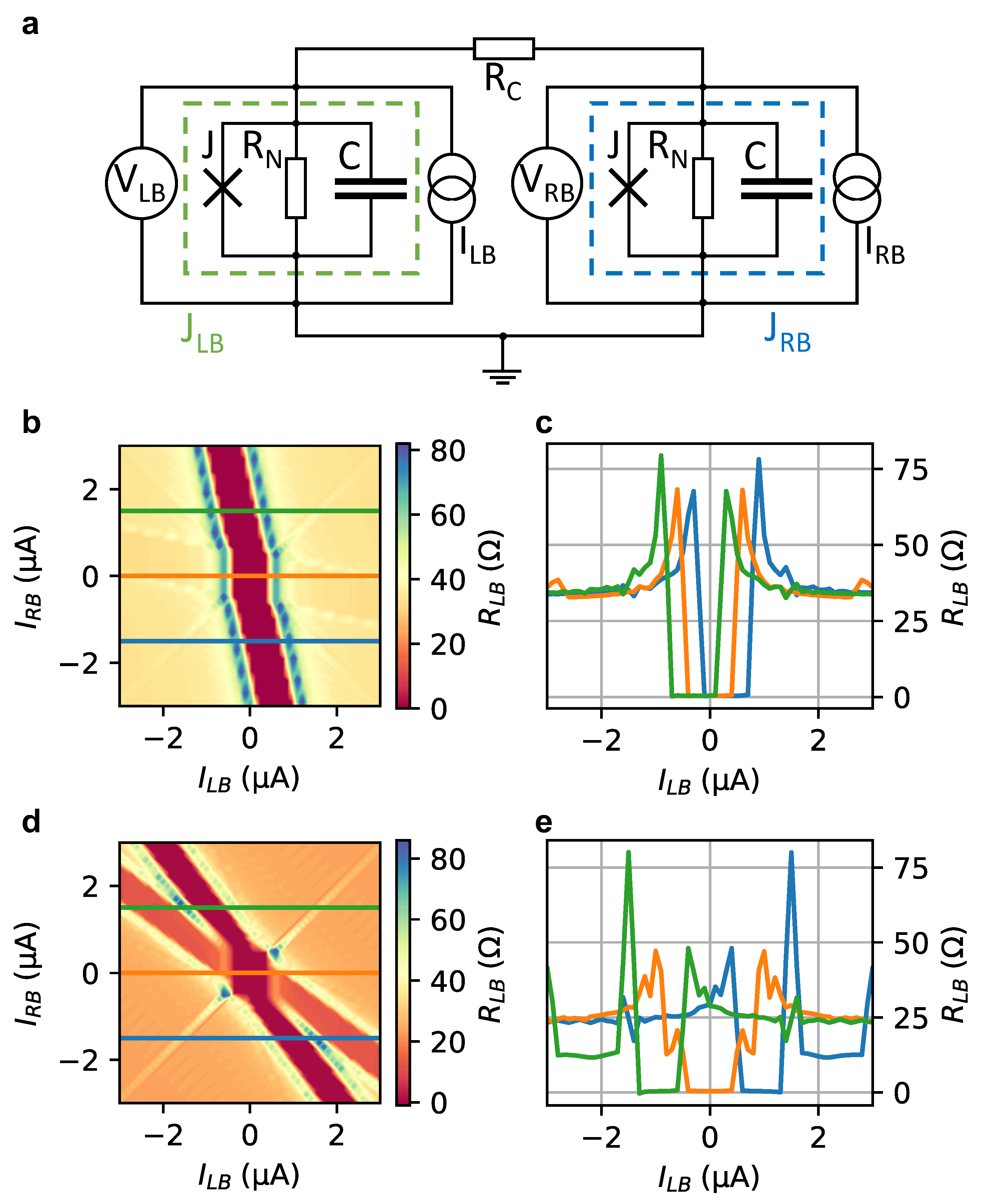
3.2. Simulations
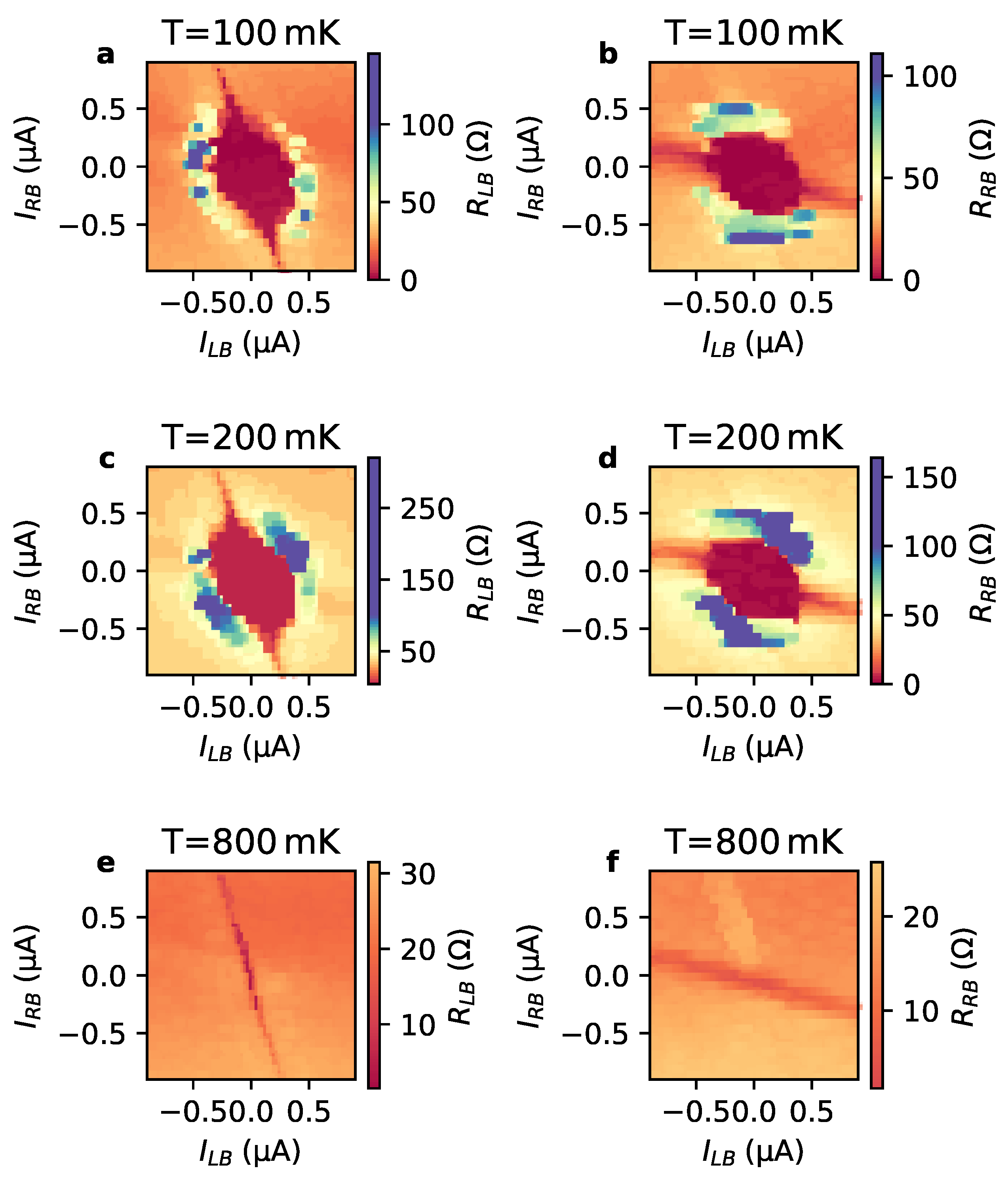
3.3. Temperature Dependence
3.4. rf Characteristics
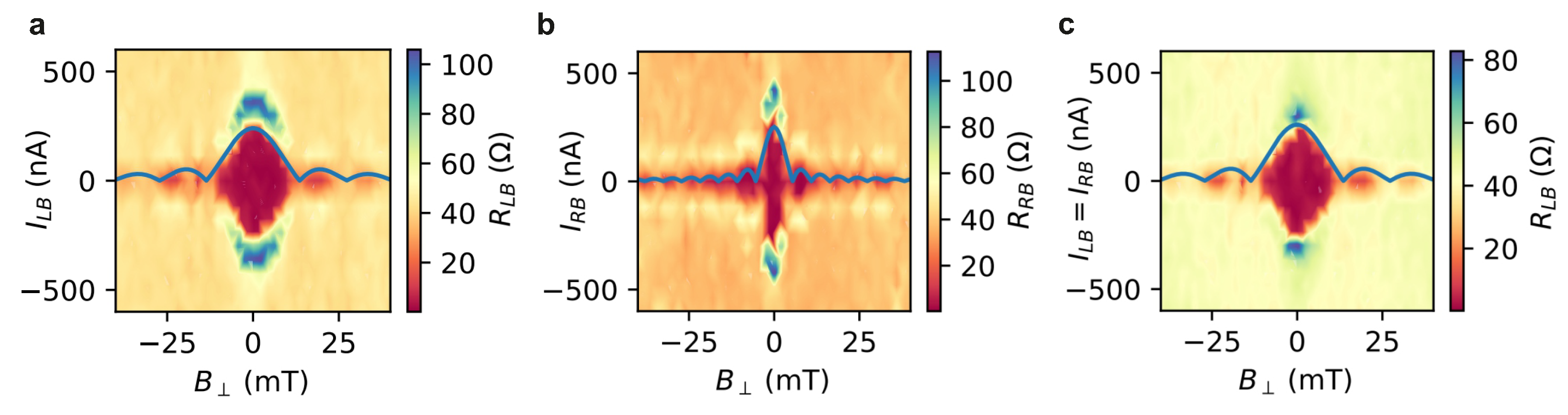
3.5. Magnetic Field Response
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RCSJ | resistively and capacitively shunted junction |
References
- Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 2003, 303, 2–30. [Google Scholar] [CrossRef] [Green Version]
- Hyart, T.; van Heck, B.; Fulga, I.C.; Burrello, M.; Akhmerov, A.R.; Beenakker, C.W.J. Flux-controlled quantum computation with Majorana fermions. Phys. Rev. B 2013, 88, 035121. [Google Scholar] [CrossRef] [Green Version]
- Aasen, D.; Hell, M.; Mishmash, R.V.; Higginbotham, A.; Danon, J.; Leijnse, M.; Jespersen, T.S.; Folk, J.A.; Marcus, C.M.; Flensberg, K.; et al. Milestones Toward Majorana-Based Quantum Computing. Phys. Rev. X 2016, 6, 031016. [Google Scholar] [CrossRef] [Green Version]
- Manousakis, J.; Altland, A.; Bagrets, D.; Egger, R.; Ando, Y. Majorana qubits in a topological insulator nanoribbon architecture. Phys. Rev. B 2017, 95, 165424. [Google Scholar] [CrossRef] [Green Version]
- Cook, A.; Franz, M. Majorana fermions in a topological-insulator nanowire proximity-coupled to an s-wave superconductor. Phys. Rev. B 2011, 84, 201105. [Google Scholar] [CrossRef] [Green Version]
- Cook, A.M.; Vazifeh, M.M.; Franz, M. Stability of Majorana fermions in proximity-coupled topological insulator nanowires. Phys. Rev. B 2012, 86, 155431. [Google Scholar] [CrossRef] [Green Version]
- Legg, H.F.; Loss, D.; Klinovaja, J. Majorana bound states in topological insulators without a vortex. Phys. Rev. B 2021, 104, 165405. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [Green Version]
- Stenger, J.P.T.; Hatridge, M.; Frolov, S.M.; Pekker, D. Braiding quantum circuit based on the 4π Josephson effect. Phys. Rev. B 2019, 99, 035307. [Google Scholar] [CrossRef] [Green Version]
- Yokoyama, T.; Nazarov, Y.V. Singularities in the Andreev spectrum of a multiterminal Josephson junction. Phys. Rev. B 2015, 92, 155437. [Google Scholar] [CrossRef]
- Eriksson, E.; Riwar, R.P.; Houzet, M.; Meyer, J.S.; Nazarov, Y.V. Topological transconductance quantization in a four-terminal Josephson junction. Phys. Rev. B 2017, 95, 075417. [Google Scholar] [CrossRef] [Green Version]
- Xie, H.Y.; Vavilov, M.G.; Levchenko, A. Weyl nodes in Andreev spectra of multiterminal Josephson junctions: Chern numbers, conductances and supercurrents. Phys. Rev. B 2018, 97, 035443. [Google Scholar] [CrossRef] [Green Version]
- Riwar, R.P.; Houzet, M.; Meyer, J.S.; Nazarov, Y.V. Multi-terminal Josephson junctions as topological matter. Nat. Commun. 2016, 7, 11167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Houzet, M.; Samuelsson, P. Multiple Andreev reflections in hybrid multiterminal junctions. Phys. Rev. B 2010, 82, 060517. [Google Scholar] [CrossRef] [Green Version]
- Freyn, A.; Douçot, B.; Feinberg, D.; Mélin, R. Production of Nonlocal Quartets and Phase-Sensitive Entanglement in a Superconducting Beam Splitter. Phys. Rev. Lett. 2011, 106, 257005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nowak, M.P.; Wimmer, M.; Akhmerov, A.R. Supercurrent carried by nonequilibrium quasiparticles in a multiterminal Josephson junction. Phys. Rev. B 2019, 99, 075416. [Google Scholar] [CrossRef] [Green Version]
- Melo, A.; Fatemi, V.; Akhmerov, A.R. Multiplet supercurrent in Josephson tunneling circuits. SciPost Phys. 2022, 12, 17. [Google Scholar] [CrossRef]
- Huang, K.F.; Ronen, Y.; Mélin, R.; Feinberg, D.; Watanabe, K.; Taniguchi, T.; Kim, P. Evidence for 4e charge of Cooper quartets in a biased multi-terminal graphene-based Josephson junction. Nat. Commun. 2022, 13, 3032. [Google Scholar] [CrossRef]
- Pfeffer, A.H.; Duvauchelle, J.E.; Courtois, H.; Mélin, R.; Feinberg, D.; Lefloch, F. Subgap structure in the conductance of a three-terminal Josephson junction. Phys. Rev. B 2014, 90, 075401. [Google Scholar] [CrossRef] [Green Version]
- Cohen, Y.; Ronen, Y.; Kang, J.H.; Heiblum, M.; Feinberg, D.; Mélin, R.; Shtrikman, H. Nonlocal supercurrent of quartets in a three-terminal Josephson junction. Proc. Natl. Acad. Sci. USA 2018, 115, 6991–6994. [Google Scholar] [CrossRef]
- Duvauchelle, J.E.; Pfeffer, A.H.; Courtois, H.; Lefloch, F. Quantum Coherence of the Quartet Scheme Observed by Shapiro Resonance Under Radio-Frequency Irradiation in Three Terminal Josephson Junctions. IEEE Trans. Appl. Supercond. 2016, 26, 1–4. [Google Scholar] [CrossRef]
- Draelos, A.W.; Wei, M.T.; Seredinski, A.; Li, H.; Mehta, Y.; Watanabe, K.; Taniguchi, T.; Borzenets, I.V.; Amet, F.; Finkelstein, G. Supercurrent Flow in Multiterminal Graphene Josephson Junctions. Nano Lett. 2019, 19, 1039–1043. [Google Scholar] [CrossRef] [Green Version]
- Arnault, E.G.; Larson, T.F.Q.; Seredinski, A.; Zhao, L.; Idris, S.; McConnell, A.; Watanabe, K.; Taniguchi, T.; Borzenets, I.; Amet, F.; et al. Multiterminal Inverse AC Josephson Effect. Nano Lett. 2021, 21, 9668–9674. [Google Scholar] [CrossRef]
- Graziano, G.V.; Lee, J.S.; Pendharkar, M.; Palmstrøm, C.J.; Pribiag, V.S. Transport studies in a gate-tunable three-terminal Josephson junction. Phys. Rev. B 2020, 101, 054510. [Google Scholar] [CrossRef] [Green Version]
- Pankratova, N.; Lee, H.; Kuzmin, R.; Wickramasinghe, K.; Mayer, W.; Yuan, J.; Vavilov, M.G.; Shabani, J.; Manucharyan, V.E. Multiterminal Josephson Effect. Phys. Rev. X 2020, 10, 031051. [Google Scholar] [CrossRef]
- Graziano, G.V.; Gupta, M.; Pendharkar, M.; Dong, J.T.; Dempsey, C.P.; Palmstrøm, C.; Pribiag, V.S. Selective Control of Conductance Modes in Multi-terminal Josephson Junctions. arXiv 2022, arXiv:2201.01373. [Google Scholar]
- Kurter, C.; Finck, A.; Hor, Y.S.; Van Harlingen, D.J. Evidence for an anomalous current–phase relation in topological insulator Josephson junctions. Nat. Commun. 2015, 6, 7130. [Google Scholar] [CrossRef] [Green Version]
- Yang, G.; Lyu, Z.; Wang, J.; Ying, J.; Zhang, X.; Shen, J.; Liu, G.; Fan, J.; Ji, Z.; Jing, X.; et al. Protected gap closing in Josephson trijunctions constructed on Bi2Te3. Phys. Rev. B 2019, 100, 180501. [Google Scholar] [CrossRef] [Green Version]
- Schüffelgen, P.; Rosenbach, D.; Li, C.; Schmitt, T.W.; Schleenvoigt, M.; Jalil, A.R.; Schmitt, S.; Kölzer, J.; Wang, M.; Bennemann, B.; et al. Selective area growth and stencil lithography for in situ fabricated quantum devices. Nat. Nanotechnol. 2019, 14, 825–831. [Google Scholar] [CrossRef]
- Saito, Y.; Fons, P.; Makino, K.; Mitrofanov, K.V.; Uesugi, F.; Takeguchi, M.; Kolobov, A.V.; Tominaga, J. Compositional tuning in sputter-grown highly oriented Bi–Te films and their optical and electronic structures. Nanoscale 2017, 9, 15115–15121. [Google Scholar] [CrossRef] [PubMed]
- Chagas, T.; Ribeiro, G.A.S.; Gonçalves, P.H.R.; Calil, L.; Silva, W.S.; Malachias, Â.; Mazzoni, M.S.C.; Magalhães-Paniago, R. Bi2:Bi2Te3 stacking influence on the surface electronic response of the topological insulator Bi4Te3. Electron. Struct. 2020, 2, 015002. [Google Scholar] [CrossRef]
- Chagas, T.; Ashour, O.A.; Ribeiro, G.A.S.; Silva, W.S.; Li, Z.; Louie, S.G.; Magalhães Paniago, R.; Petroff, Y. Multiple strong topological gaps and hexagonal warping in Bi4Te3. Phys. Rev. B 2022, 105, L081409. [Google Scholar] [CrossRef]
- Nabok, D.; Tas, M.; Kusaka, S.; Durgun, E.; Friedrich, C.; Bihlmayer, G.; Blügel, S.; Hirahara, T.; Aguilera, I. Bulk and surface electronic structure of Bi4Te3 from GW calculations and photoemission experiments. Phys. Rev. Mater. 2022, 6, 034204. [Google Scholar] [CrossRef]
- Michiardi, M.; Aguilera, I.; Bianchi, M.; de Carvalho, V.E.; Ladeira, L.O.; Teixeira, N.G.; Soares, E.A.; Friedrich, C.; Blügel, S.; Hofmann, P. Bulk band structure of Bi2Te3. Phys. Rev. B 2014, 90, 075105. [Google Scholar] [CrossRef] [Green Version]
- Jalil, A.R. Engineering Topological Superlattices and Their Epitaxial Integration in Selectively Grown Hybrid Nanostructures via MBE. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2022. [Google Scholar] [CrossRef]
- Yang, B.J.; Nagaosa, N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 2014, 5, 4898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rauch, T.c.v.; Flieger, M.; Henk, J.; Mertig, I.; Ernst, A. Dual Topological Character of Chalcogenides: Theory for Bi2Te3. Phys. Rev. Lett. 2014, 112, 016802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosenbach, D.; Schmitt, T.W.; Schüffelgen, P.; Stehno, M.P.; Li, C.; Schleenvoigt, M.; Jalil, A.R.; Mussler, G.; Neumann, E.; Trellenkamp, S.; et al. Reappearance of first Shapiro step in narrow topological Josephson junctions. Sci. Adv. 2021, 7, eabf1854. [Google Scholar] [CrossRef]
- Schmitt, T.W.; Connolly, M.R.; Schleenvoigt, M.; Liu, C.; Kennedy, O.; Chávez-Garcia, J.M.; Jalil, A.R.; Bennemann, B.; Trellenkamp, S.; Lentz, F.; et al. Integration of topological insulator Josephson junctions in superconducting qubit circuits. Nano Lett. 2022, 22, 2595–2602. [Google Scholar] [CrossRef]
- Kölzer, J.; Moors, K.; Jalil, A.R.; Zimmermann, E.; Rosenbach, D.; Kibkalo, L.; Schüffelgen, P.; Mussler, G.; Grützmacher, D.; Schmidt, T.L.; et al. In-plane magnetic field-driven symmetry breaking in topological insulator-based three-terminal junctions. Commun. Mater. 2021, 2, 116. [Google Scholar] [CrossRef]
- Snyder, R.A.; Trimble, C.J.; Rong, C.C.; Folkes, P.A.; Taylor, P.J.; Williams, J.R. Weak-link Josephson Junctions made from topological crystalline insulators. Phys. Rev. Lett. 2018, 121, 097701. [Google Scholar] [CrossRef]
- Panghotra, R.; Raes, B.; de Souza Silva, C.C.; Cools, I.; Keijers, W.; Scheerder, J.E.; Moshchalkov, V.V.; Van de Vondel, J. Giant fractional Shapiro steps in anisotropic Josephson junction arrays. Commun. Phys. 2020, 3, 53. [Google Scholar] [CrossRef] [Green Version]
- Raes, B.; Tubsrinuan, N.; Sreedhar, R.; Guala, D.S.; Panghotra, R.; Dausy, H.; de Souza Silva, C.C.; Van de Vondel, J. Fractional Shapiro steps in resistively shunted Josephson junctions as a fingerprint of a skewed current–phase relationship. Phys. Rev. B 2020, 102, 054507. [Google Scholar] [CrossRef]
- Rosenbach, D. Quantum Transport and Induced Superconductivity in Selectively Deposited Topological Insulator Devices. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2021. [Google Scholar] [CrossRef]
- Domínguez, F.; Kashuba, O.; Bocquillon, E.; Wiedenmann, J.; Deacon, R.S.; Klapwijk, T.M.; Platero, G.; Molenkamp, L.W.; Trauzettel, B.; Hankiewicz, E.M. Josephson junction dynamics in the presence of 2π- and 4π-periodic supercurrents. Phys. Rev. B 2017, 95, 195430. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kölzer, J.; Jalil, A.R.; Rosenbach, D.; Arndt, L.; Mussler, G.; Schüffelgen, P.; Grützmacher, D.; Lüth, H.; Schäpers, T. Supercurrent in Bi4Te3 Topological Material-Based Three-Terminal Junctions. Nanomaterials 2023, 13, 293. https://doi.org/10.3390/nano13020293
Kölzer J, Jalil AR, Rosenbach D, Arndt L, Mussler G, Schüffelgen P, Grützmacher D, Lüth H, Schäpers T. Supercurrent in Bi4Te3 Topological Material-Based Three-Terminal Junctions. Nanomaterials. 2023; 13(2):293. https://doi.org/10.3390/nano13020293
Chicago/Turabian StyleKölzer, Jonas, Abdur Rehman Jalil, Daniel Rosenbach, Lisa Arndt, Gregor Mussler, Peter Schüffelgen, Detlev Grützmacher, Hans Lüth, and Thomas Schäpers. 2023. "Supercurrent in Bi4Te3 Topological Material-Based Three-Terminal Junctions" Nanomaterials 13, no. 2: 293. https://doi.org/10.3390/nano13020293
APA StyleKölzer, J., Jalil, A. R., Rosenbach, D., Arndt, L., Mussler, G., Schüffelgen, P., Grützmacher, D., Lüth, H., & Schäpers, T. (2023). Supercurrent in Bi4Te3 Topological Material-Based Three-Terminal Junctions. Nanomaterials, 13(2), 293. https://doi.org/10.3390/nano13020293







