Enhanced Magnetism and Anomalous Hall Transport through Two-Dimensional Tungsten Disulfide Interfaces
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Material’s Characterization
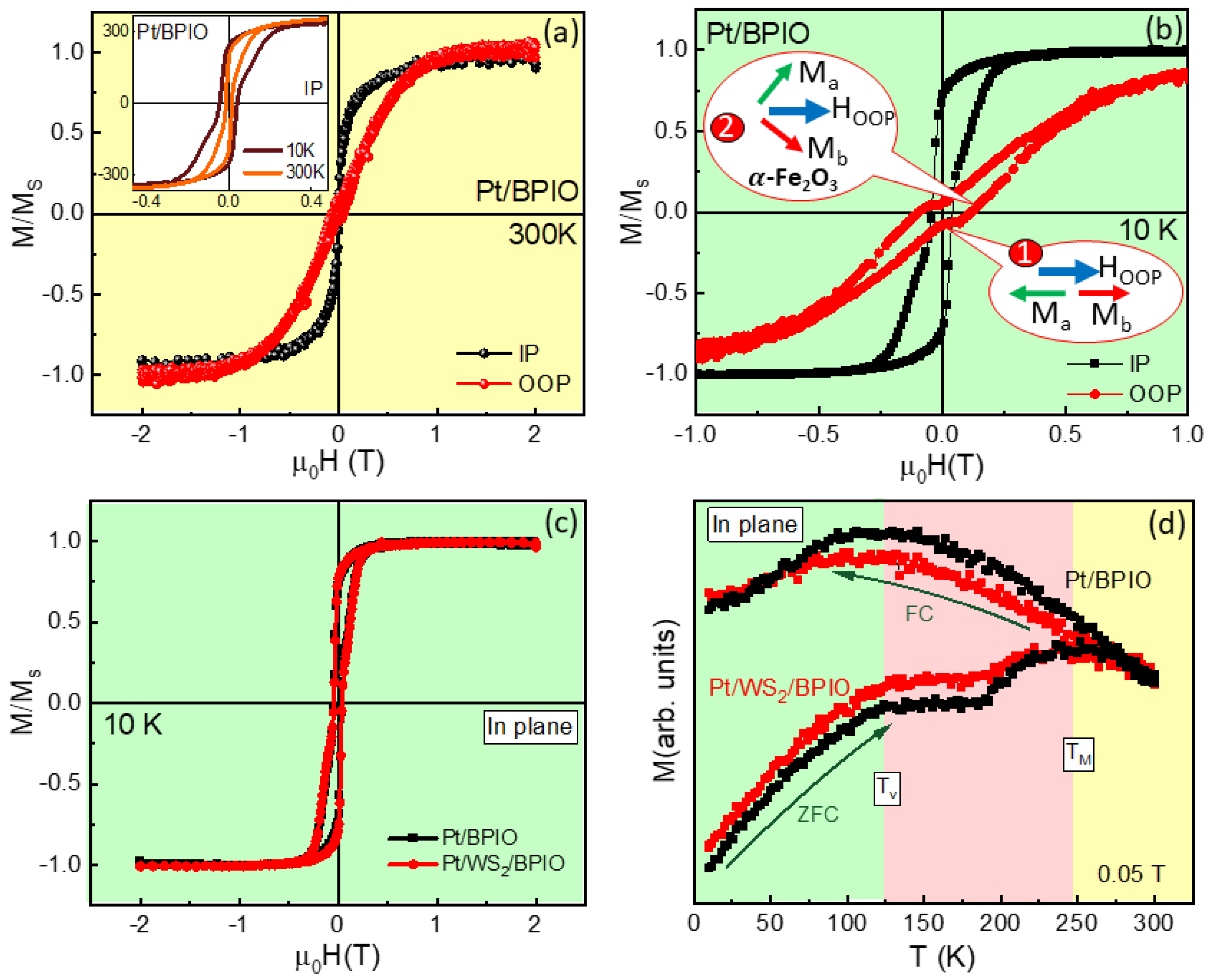
3.2. Magnetic Properties
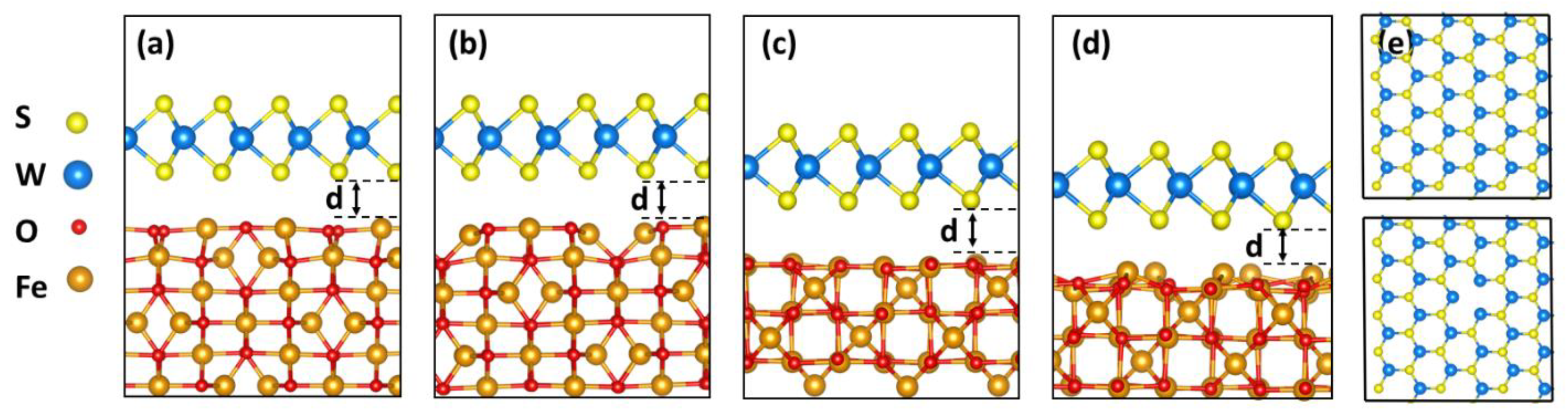
3.3. First Principles Calculations
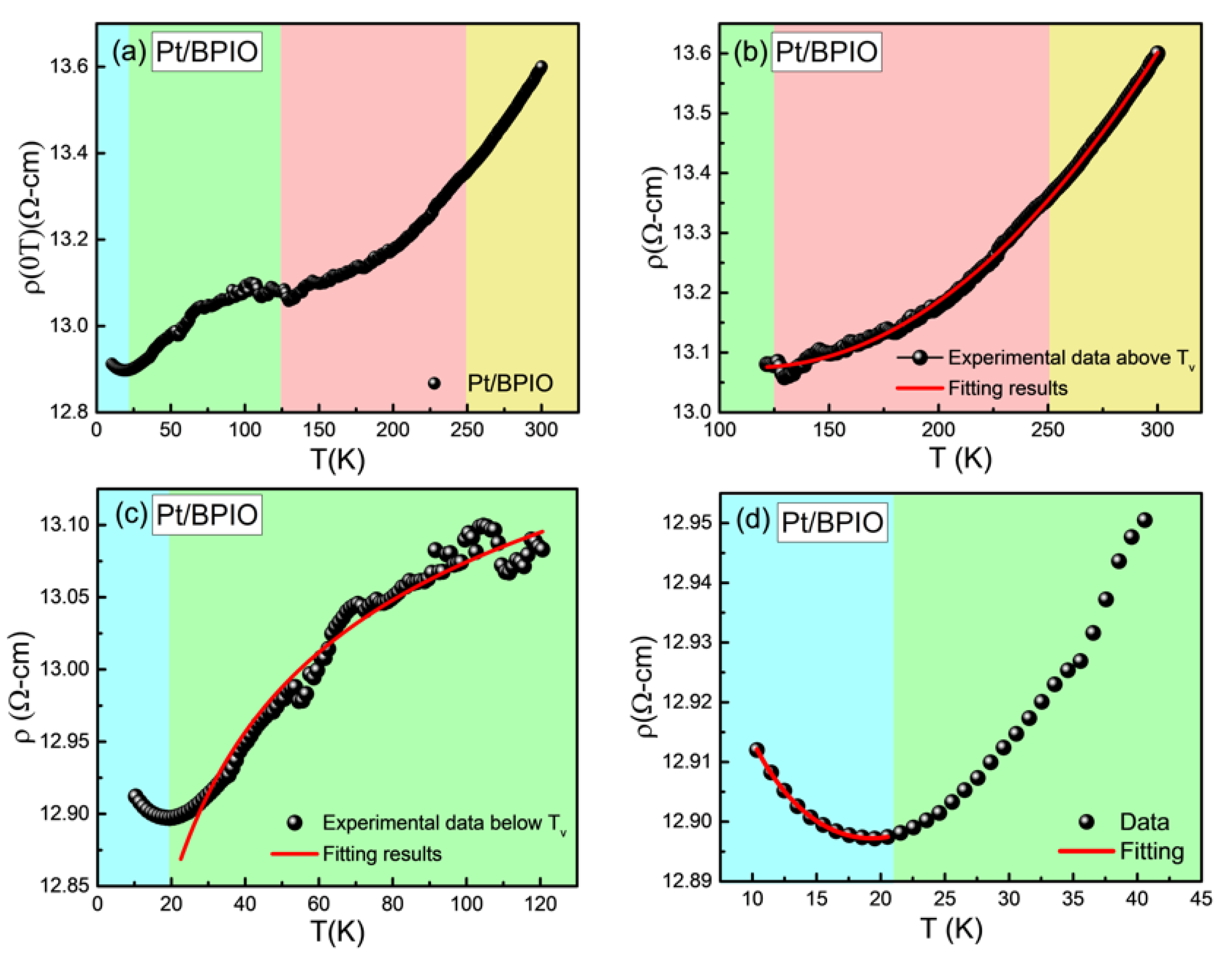
3.4. Four-Probe Measurement
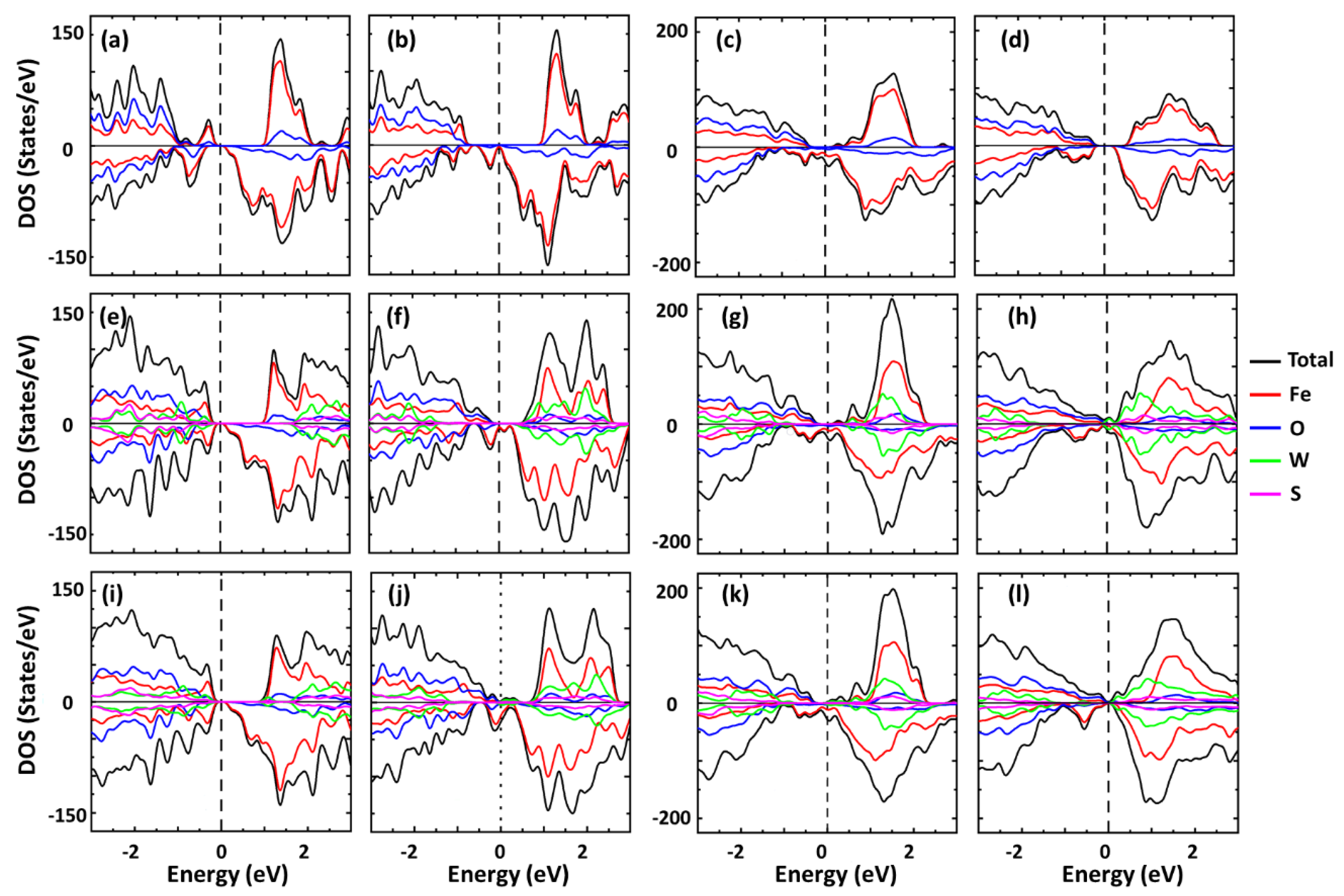
3.5. Atomically Resolved Spin Polarized Density of State
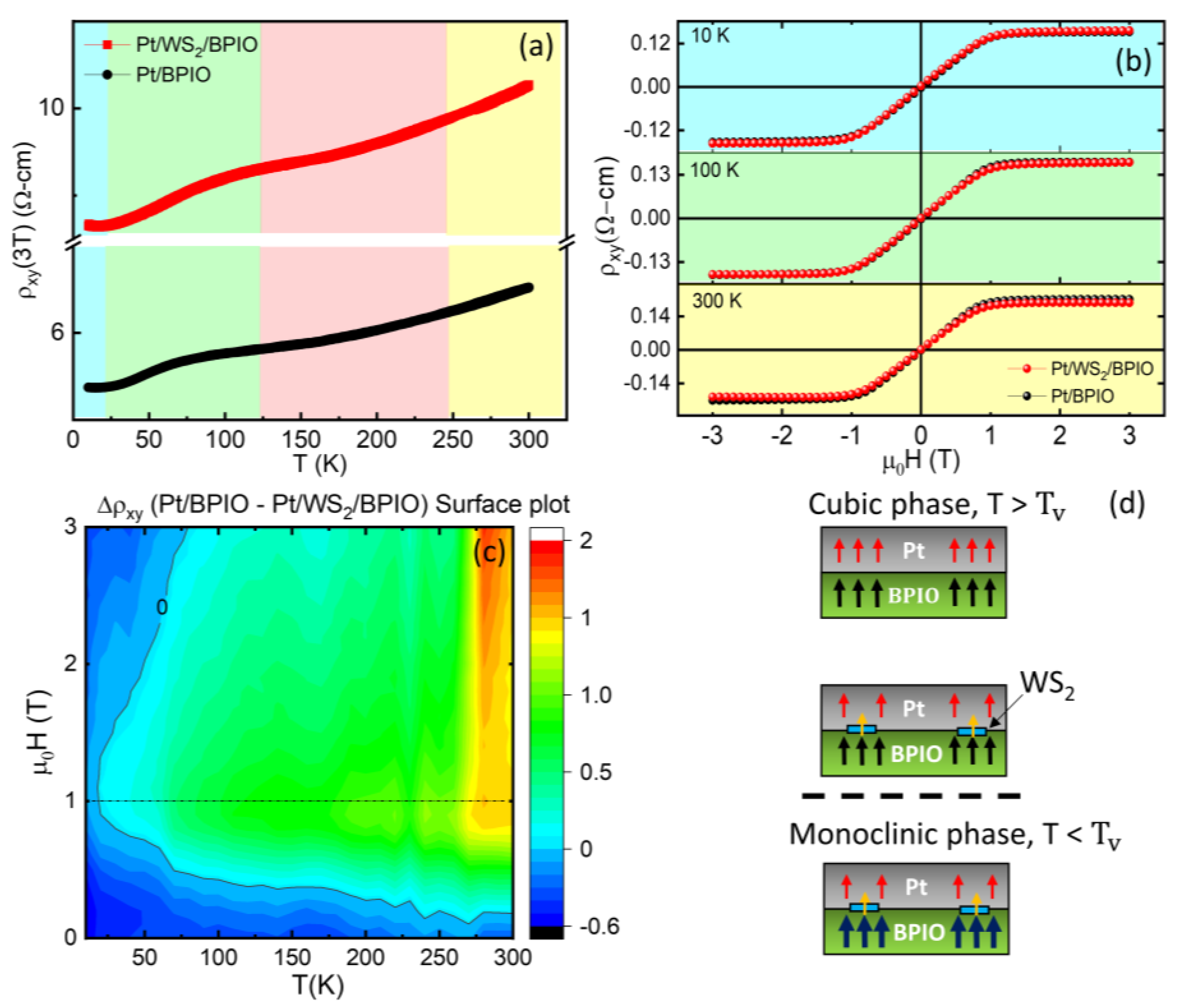
3.6. Anomalous Hall Effect Measurement
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Gao, Y.; Zhang, S.; He, J.; Yu, J.; Liu, Z. Valleytronics in Transition Metal Dichalcogenides Materials. Nano Res. 2019, 12, 2695–2711. [Google Scholar] [CrossRef]
- Liang, S.; Shi, S.; Hsu, C.H.; Cai, K.; Wang, Y.; He, P.; Wu, Y.; Pereira, V.M.; Yang, H. Spin-Orbit Torque Magnetization Switching in MoTe2/Permalloy Heterostructures. Adv. Mater. 2020, 32, 2002799. [Google Scholar] [CrossRef]
- Lee, W.Y.; Kang, M.S.; Kim, G.S.; Park, N.W.; Choi, K.Y.; Le, C.T.; Rashid, M.U.; Saitoh, E.; Kim, Y.S.; Lee, S.K. Role of Ferromagnetic Monolayer WSe2Flakes in the Pt/Y3Fe5O12Bilayer Structure in the Longitudinal Spin Seebeck Effect. ACS Appl. Mater. Interfaces 2021, 13, 15783–15790. [Google Scholar] [CrossRef] [PubMed]
- Phan, M.H.; Trinh, M.T.; Eggers, T.; Kalappattil, V.; Uchida, K.I.; Woods, L.M.; Terrones, M. A Perspective on Two-Dimensional van Der Waals Opto-Spin-Caloritronics. Appl. Phys. Lett. 2021, 119, 250501. [Google Scholar] [CrossRef]
- Tsai, S.P.; Yang, C.Y.; Lee, C.J.; Lu, L.S.; Liang, H.L.; Lin, J.X.; Yu, Y.H.; Chen, C.C.; Chung, T.K.; Kaun, C.C.; et al. Room-Temperature Ferromagnetism of Single-Layer MoS2 Induced by Antiferromagnetic Proximity of Yttrium Iron Garnet. Adv. Quantum Technol. 2021, 4, 2000104. [Google Scholar] [CrossRef]
- Lin, W.H.; Tseng, W.S.; Went, C.M.; Teague, M.L.; Rossman, G.R.; Atwater, H.A.; Yeh, N.C. Nearly 90% Circularly Polarized Emission in Monolayer WS2 Single Crystals by Chemical Vapor Deposition. ACS Nano 2020, 14, 1350–1359. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhao, X.; Deng, L.; Shi, Z.; Liu, S.; Wei, Q.; Zhang, L.; Cheng, Y.; Zhang, L.; Lu, H.; et al. Enhanced Valley Zeeman Splitting in Fe-Doped Monolayer MoS2. ACS Nano 2020, 14, 4636–4645. [Google Scholar] [CrossRef]
- Lin, W.-H.; Wu, P.C.; Akbari, H.; Rossman, G.R.; Yeh, N.-C.; Atwater, H.A.; Lin, W.-H.; Akbari, H.; Atwater, H.A.; Wu, P.C.; et al. Electrically Tunable and Dramatically Enhanced Valley-Polarized Emission of Monolayer WS2 at Room Temperature with Plasmonic Archimedes Spiral Nanostructures. Adv. Mater. 2022, 34, 2104863. [Google Scholar] [CrossRef]
- Zhang, Y.; Shinokita, K.; Watanabe, K.; Taniguchi, T.; Goto, M.; Kan, D.; Shimakawa, Y.; Moritomo, Y.; Nishihara, T.; Miyauchi, Y.; et al. Controllable Magnetic Proximity Effect and Charge Transfer in 2D Semiconductor and Double-Layered Perovskite Manganese Oxide van Der Waals Heterostructure. Adv. Mater. 2020, 32, 2003501. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Wong, P.K.J.; Yuan, J.; Vinai, G.; Torelli, P.; van der Laan, G.; Feng, Y.P.; Wee, A.T.S. Magnetic Transition in Monolayer VSe2 via Interface Hybridization. ACS Nano 2019, 13, 8997–9004. [Google Scholar] [CrossRef]
- Messaoudi, O.; Ibañez-Azpiroz, J.; Bouzar, H.; Lounis, S. Nondegenerate Valleys in the Half-Metallic Ferromagnet Fe/WS2. Phys. Rev. B 2018, 97, 035404. [Google Scholar] [CrossRef]
- Zhang, F.; Mi, W.; Wang, X. Tunable Valley and Spin Splitting in 2 H -VSe2/BiFeO3(111) Triferroic Heterostructures. Nanoscale 2019, 11, 10329–10338. [Google Scholar] [CrossRef] [PubMed]
- Rossi, E.; Triola, C. Van Der Waals Heterostructures with Spin-Orbit Coupling. Ann. Der Phys. 2020, 532. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, Y.; Zhu, H. Deciphering Asymmetric Charge Transfer at Transition Metal Dichalcogenide-Graphene Interface by Helicity-Resolved Ultrafast Spectroscopy. Sci. Adv. 2021, 7, eabg2999. [Google Scholar] [CrossRef] [PubMed]
- Manna, P.K.; Yusuf, S.M. Two Interface Effects: Exchange Bias and Magnetic Proximity. Phys. Rep. 2014, 535, 61–99. [Google Scholar] [CrossRef]
- Peng, B.; Li, Q.; Liang, X.; Song, P.; Li, J.; He, K.; Fu, D.; Li, Y.; Shen, C.; Wang, H.; et al. Valley Polarization of Trions and Magnetoresistance in Heterostructures of MoS2 and Yttrium Iron Garnet. ACS Nano 2017, 11, 12257–12265. [Google Scholar] [CrossRef]
- Hellman, F.; Hoffmann, A.; Tserkovnyak, Y.; Beach, G.S.D.; Fullerton, E.E.; Leighton, C.; Macdonald, A.H.; Ralph, D.C.; Arena, D.A.; Dürr, H.A.; et al. Interface-Induced Phenomena in Magnetism. Rev. Mod. Phys. 2017, 89, 025006. [Google Scholar] [CrossRef] [PubMed]
- Mendes, J.B.S.; Alves Santos, O.; Meireles, L.M.; Lacerda, R.G.; Vilela-Leão, L.H.; Machado, F.L.A.; Rodríguez-Suárez, R.L.; Azevedo, A.; Rezende, S.M. Spin-Current to Charge-Current Conversion and Magnetoresistance in a Hybrid Structure of Graphene and Yttrium Iron Garnet. Phys. Rev. Lett. 2015, 115, 226601. [Google Scholar] [CrossRef]
- Jie, W.; Yang, Z.; Zhang, F.; Bai, G.; Leung, C.W.; Hao, J. Observation of Room-Temperature Magnetoresistance in Monolayer MoS2 by Ferromagnetic Gating. ACS Nano 2017, 11, 6950–6958. [Google Scholar] [CrossRef]
- Lee, S.K.; Lee, W.Y.; Kikkawa, T.; Le, C.T.; Kang, M.S.; Kim, G.S.; Nguyen, A.D.; Kim, Y.S.; Park, N.W.; Saitoh, E. Enhanced Spin Seebeck Effect in Monolayer Tungsten Diselenide Due to Strong Spin Current Injection at Interface. Adv. Funct. Mater. 2020, 30, 2003192. [Google Scholar] [CrossRef]
- Thi-Xuan Dang, D.; Barik, R.K.; Phan, M.-H.; Woods, L.M. Enhanced Magnetism in Heterostructures with Transition-Metal Dichalcogenide Monolayers. J. Phys. Chem. Lett. 2022, 13, 8879–8887. [Google Scholar] [CrossRef]
- Norden, T.; Zhao, C.; Zhang, P.; Sabirianov, R.; Petrou, A.; Zeng, H. Giant Valley Splitting in Monolayer WS2 by Magnetic Proximity Effect. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.Q.; Wang, X.W.; Cao, T.F. Large Band Offset in Monolayer MoS 2 on Oppositely Polarized BiFeO 3 (0001) Polar Surfaces. J. Phys. Chem. C 2019, 123, 3039–3047. [Google Scholar] [CrossRef]
- Chanda, A.; DeTellem, D.; Hai Pham, Y.T.; Shoup, J.E.; Duong, A.T.; Das, R.; Cho, S.; Voronine, D.V.; Trinh, M.T.; Arena, D.A.; et al. Spin Seebeck Effect in Iron Oxide Thin Films: Effects of Phase Transition, Phase Coexistence, And Surface Magnetism. ACS Appl. Mater. Interfaces 2022, 14, 13468–13479. [Google Scholar] [CrossRef]
- Kukreja, R.; Hua, N.; Ruby, J.; Barbour, A.; Hu, W.; Mazzoli, C.; Wilkins, S.; Fullerton, E.E.; Shpyrko, O.G. Orbital Domain Dynamics in Magnetite below the Verwey Transition. Phys. Rev. Lett. 2018, 121, 177601. [Google Scholar] [CrossRef]
- Lenge, N.; Kronmuller, H.; Walz, F. The Relation between Electrical Conductivity Mechanisms and Magnetic After-Effects in Single Crystal Magnetite. J. Phys. Soc. Jpn. 1984, 53, 1406–1414. [Google Scholar] [CrossRef]
- Yasui, S.; Honda, S.; Okabayashi, J.; Yanase, T.; Shimada, T.; Nagahama, T. Large Inverse Tunnel Magnetoresistance in Magnetic Tunnel Junctions with an Fe3 O4 Electrode. Phys. Rev. Appl. 2021, 15, 034042. [Google Scholar] [CrossRef]
- Wu, H.C.; Coileáin, C.; Abid, M.; Mauit, O.; Syrlybekov, A.; Khalid, A.; Xu, H.; Gatensby, R.; Jing Wang, J.; Liu, H.; et al. Spin-Dependent Transport Properties of Fe3O4/MoS2/Fe3O4 Junctions. Sci. Rep. 2015, 5, 15984. [Google Scholar] [CrossRef] [PubMed]
- Hirohata, A.; Yamada, K.; Nakatani, Y.; Prejbeanu, L.; Diény, B.; Pirro, P.; Hillebrands, B. Review on Spintronics: Principles and Device Applications. J. Magn. Magn. Mater. 2020, 509, 166711. [Google Scholar] [CrossRef]
- Fernández-Pacheco, A.; de Teresa, J.M.; Orna, J.; Morellon, L.; Algarabel, P.A.; Pardo, J.A.; Ibarra, M.R.; Magen, C.; Snoeck, E. Giant Planar Hall Effect in Epitaxial Fe3O4 Thin Films and Its Temperature Dependence. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 78, 212402. [Google Scholar] [CrossRef]
- Fernández-Pacheco, A.; de Teresa, J.M.; Orna, J.; Morellon, L.; Algarabel, P.A.; Pardo, J.A.; Ibarra, M.R. Universal Scaling of the Anomalous Hall Effect in Fe3O4 Epitaxial Thin Films. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 77, 100403. [Google Scholar] [CrossRef]
- Gridin, V.V.; Hearne, G.R.; Honig, J.M. Magnetoresistance Extremum at the First-Order Verwey Transition in Magnetite Fe3O4. Phys. Rev. B 1996, 53, 15518. [Google Scholar] [CrossRef] [PubMed]
- Genuzio, F.; Sala, A.; Schmidt, T.; Menzel, D.; Freund, H.J. Interconversion of α-Fe2O3 and Fe3O4 Thin Films: Mechanisms, Morphology, and Evidence for Unexpected Substrate Participation. J. Phys. Chem. C 2014, 118, 29068–29076. [Google Scholar] [CrossRef]
- Attanayake, S.B.; Chanda, A.; Das, R.; Phan, M.H.; Srikanth, H. Emergent Magnetic Properties of Biphase Iron Oxide Nanorods. AIP Adv. 2022, 12, 035136. [Google Scholar] [CrossRef]
- Cao, D.; Li, H.; Pan, L.; Li, J.; Wang, X.; Jing, P.; Cheng, X.; Wang, W.; Wang, J.; Liu, Q. High Saturation Magnetization of γ-Fe2O3 Nano-Particles by a Facile One-Step Synthesis Approach. Sci. Rep. 2016, 6, 1–9. [Google Scholar] [CrossRef]
- Tuček, J.; Zbořil, R.; Namai, A.; Ohkoshi, S.I. ε-Fe2O3: An Advanced Nanomaterial Exhibiting Giant Coercive Field, Millimeter-Wave Ferromagnetic Resonance, and Magnetoelectric Coupling. Chem. Mater. 2010, 22, 6483–6505. [Google Scholar] [CrossRef]
- Zhang, P.; Chou, C.-T.; Yun, H.; Mcgoldrick, B.C.; Hou, J.T.; Mkhoyan, K.A.; Liu, L. Control of Néel Vector with Spin-Orbit Torques in an Antiferromagnetic Insulator with Tilted Easy Plane. Phys. Rev. Lett. 2022, 129, 017203. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Chanda, A.; Hung, C.M.; Duong, A.T.; Cho, S.; Srikanth, H.; Phan, M.H. Magnetism and Spin-Dependent Transport Phenomena across Verwey and Morin Transitions in Iron Oxide/Pt Bilayers. J. Magn. Magn. Mater. 2023, 568, 170370. [Google Scholar] [CrossRef]
- Grimme, S. Density Functional Theory with London Dispersion Corrections. Ltd. WIREs Comput Mol Sci 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Jeng, H.T.; Guo, G.Y.; Huang, D.J. Charge-Orbital Ordering in Low-Temperature Structures of Magnetite: GGA + U Investigations. Phys. Rev. B-Condens. Matter Mater. Phys. 2006, 74, 195115. [Google Scholar] [CrossRef]
- Yu, X.; Huo, C.F.; Li, Y.W.; Wang, J.; Jiao, H. Fe3O4 Surface Electronic Structures and Stability from GGA + U. Surf. Sci. 2012, 606, 872–879. [Google Scholar] [CrossRef]
- Li, Y.L.; Yao, K.L.; Liu, Z.L. First-Principle Studies on the Electronic Structure of Fe3O4(110) Surface. Front. Phys. China 2007, 2, 76–80. [Google Scholar] [CrossRef]
- Ingham, B.; Toney, M.F. X-Ray Diffraction for Characterizing Metallic Films. In Metallic Films for Electronic, Optical and Magnetic Applications; Woodhead Publishing: Sawston, UK, 2014; pp. 3–38. [Google Scholar] [CrossRef]
- Lee, C.; Jeong, B.G.; Yun, S.J.; Lee, Y.H.; Lee, S.M.; Jeong, M.S. Unveiling Defect-Related Raman Mode of Monolayer WS2 via Tip-Enhanced Resonance Raman Scattering. ACS Nano 2018, 12, 9982–9990. [Google Scholar] [CrossRef]
- Pollard, T.D.; Thomas, D.; Earnshaw, W.C.; Lippincott-Schwartz, J.; Johnson, G.T. Cell Biology, 3rd ed.; Elsevier: Philadelphia, PA, USA, 2017. [Google Scholar]
- Liu, X.H.; Rata, A.D.; Chang, C.F.; Komarek, A.C.; Tjeng, L.H. Verwey Transition in Fe3O4 Thin Films: Influence of Oxygen Stoichiometry and Substrate-Induced Microstructure. Phys. Rev. B 2014, 90, 125142. [Google Scholar] [CrossRef]
- Lin, T.T.; Young, S.L.; Kung, C.Y.; Chen, H.Z.; Kao, M.C.; Chang, M.C.; Ou, C.R. Variable-Range Hopping and Thermal Activation Conduction of y-Doped ZnO Nanocrystalline Films. IEEE Trans. Nanotechnol. 2014, 13, 425–430. [Google Scholar] [CrossRef]
- Ramos, R.; Arora, S.K.; Shvets, I. Anomalous Anisotropic Magnetoresistance in Epitaxial Fe3O4 Thin Films on MgO(001). Phys. Rev. B 2008, 78, 214402. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Shklovskii, B.I.; Efros, A.L. Electronic Properties of Doped Semiconductors; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 45. [Google Scholar]
- De, K.; Das, S. Low-temperature localization in the transport properties of self-doped La0.9Mn0.98Zn0.02O3. Bull. Mater. Sci. 2010, 39, 293–298. [Google Scholar] [CrossRef]
- Cirillo, C.; Barone, C.; Bradshaw, H.; Urban, F.; di Bernardo, A.; Mauro, C.; Robinson, J.W.A.; Pagano, S.; Attanasio, C. Magnetotransport and Magnetic Properties of Amorphous NdNi 5 Thin Films. Sci. Rep. 2020, 10, 13693. [Google Scholar] [CrossRef]
- Shiomi, Y.; Ohtani, T.; Iguchi, S.; Sasaki, T.; Qiu, Z.; Nakayama, H.; Uchida, K.; Saitoh, E. Interface-Dependent Magnetotransport Properties for Thin Pt Films on Ferrimagnetic Y3Fe5O12. Appl. Phys. Lett. 2014, 104, 242406. [Google Scholar] [CrossRef]
- Lee, P.A.; Ramakrishnan, T.V. Disordered Electronic Systems. Rev. Mod. Phys. 1985, 57, 287. [Google Scholar] [CrossRef]
- Pollak, A.L.E.M. Electron-Electron Interactions in Disordered Systems, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 10. [Google Scholar]
- Kondo, J. Resistance Minimum in Dilute Magnetic Alloys. Prog. Theor. Phys. 1964, 32, 37–49. [Google Scholar] [CrossRef]
- Venkat, G.; Cox, C.D.W.; Voneshen, D.; Caruana, A.J.; Piovano, A.; Cropper, M.D.; Morrison, K. Magnon Diffusion Lengths in Bulk and Thin Film Fe3O4 for Spin Seebeck Applications. arXiv 2020, arXiv:2001.03738. [Google Scholar] [CrossRef]
- Chen, Y.-T.; Takahashi, S.; Nakayama, H.; Althammer, M.; Goennenwein, S.T.B.; Saitoh, E.; Bauer, G.E.W. Theory of Spin Hall Magnetoresistance. Phys. Rev. B 2013, 87, 144411. [Google Scholar] [CrossRef]
- Shao, Q.; Grutter, A.; Liu, Y.; Yu, G.; Yang, C.Y.; Gilbert, D.A.; Arenholz, E.; Shafer, P.; Che, X.; Tang, C.; et al. Exploring Interfacial Exchange Coupling and Sublattice Effect in Heavy Metal/Ferrimagnetic Insulator Heterostructures Using Hall Measurements, X-ray Magnetic Circular Dichroism, and Neutron Reflectometry. Phys. Rev. B 2019, 99, 104401. [Google Scholar] [CrossRef]
- Toyosaki, H.; Fukumura, T.; Yamada, Y.; Nakajima, K.; Chikyow, T.; Hasegawa, T.; Koinuma, H.; Kawasaki, M. Anomalous Hall Effect Governed by Electron Doping in a Room-Temperature Transparent Ferromagnetic Semiconductor. Nat. Mater. 2004, 3, 221–224. [Google Scholar] [CrossRef] [PubMed]
- Pham, Y.T.H.; Liu, M.; Jimenez, V.O.; Yu, Z.; Kalappattil, V.; Zhang, F.; Wang, K.; Williams, T.; Terrones, M.; Phan, M.H. Tunable Ferromagnetism and Thermally Induced Spin Flip in Vanadium-Doped Tungsten Diselenide Monolayers at Room Temperature. Adv. Mater. 2020, 32, 2003607. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zheng, B.; Sebastian, A.; Olson, D.H.; Liu, M.; Fujisawa, K.; Thi Hai Pham, Y.; Ortiz Jimenez, V.; Kalappattil, V.; Miao, L.; et al. COMMUNICATION Monolayer Vanadium-Doped Tungsten Disulfide: A Room-Temperature Dilute Magnetic Semiconductor. Adv. Sci. 2020, 7, 2001174. [Google Scholar] [CrossRef] [PubMed]
- Ortiz Jimenez, V.; Pham, Y.T.H.; Liu, M.; Zhang, F.; Yu, Z.; Kalappattil, V.; Muchharla, B.; Eggers, T.; Duong, D.L.; Terrones, M.; et al. Light-Controlled Room Temperature Ferromagnetism in Vanadium-Doped Tungsten Disulfide Semiconducting Monolayers. Adv. Electron. Mater. 2021, 7, 2100030. [Google Scholar] [CrossRef]

Distance d (Å) | |||||||
|---|---|---|---|---|---|---|---|
| Cubic-B | - | - | −3.865 | 3.983 | 0.118 | - | 0.667 |
| Cubic-B/WS2 | 2.521 | −21.967 | −3.862 | 3.988 | 0.114 | 0.003 | 0.667 |
| Cubic-B/WS2 (VS-S) | 2.505 | −22.981 | −3.862 | 3.986 | 0.115 | 0.003 | 0.667 |
| Cubic-AB | - | - | −3.875 | 3.983 | 0.118 | - | 0.667 |
| Cubic-AB/WS2 | 2.642 | −34.880 | −3.871 | 3.994 | 0.112 | 0.006 | 0.667 |
| Cubic-AB/WS2 (VS-S) | 2.537 | −35.288 | −3.869 | 4.000 | 0.113 | 0.003 | 0.666 |
| Monoclinic-B | - | - | −3.907 | 4.007 | 0.139 | - | 0.667 |
| Monoclinic-B/WS2 | 2.822 | −20.322 | −3.886 | 3.992 | 0.134 | 0.003 | 0.667 |
| Monoclinic-B/WS2 (VS-S) | 2.780 | −17.715 | −3.887 | 3.997 | 0.136 | 0.002 | 0.668 |
| Monoclinic-A | - | - | −3.887 | 3.971 | 0.129 | - | 0.667 |
| Monoclinic-A/WS2 | 2.207 | −30.058 | −3.874 | 3.977 | 0.132 | 0.00006 | 0.672 |
| Monoclinic-A/WS2 (VS-S) | 1.958 | −27.378 | −3.867 | 3.986 | 0.127 | −0.001 | 0.671 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, C.-M.; Dang, D.T.-X.; Chanda, A.; Detellem, D.; Alzahrani, N.; Kapuruge, N.; Pham, Y.T.H.; Liu, M.; Zhou, D.; Gutierrez, H.R.; et al. Enhanced Magnetism and Anomalous Hall Transport through Two-Dimensional Tungsten Disulfide Interfaces. Nanomaterials 2023, 13, 771. https://doi.org/10.3390/nano13040771
Hung C-M, Dang DT-X, Chanda A, Detellem D, Alzahrani N, Kapuruge N, Pham YTH, Liu M, Zhou D, Gutierrez HR, et al. Enhanced Magnetism and Anomalous Hall Transport through Two-Dimensional Tungsten Disulfide Interfaces. Nanomaterials. 2023; 13(4):771. https://doi.org/10.3390/nano13040771
Chicago/Turabian StyleHung, Chang-Ming, Diem Thi-Xuan Dang, Amit Chanda, Derick Detellem, Noha Alzahrani, Nalaka Kapuruge, Yen T. H. Pham, Mingzu Liu, Da Zhou, Humberto R. Gutierrez, and et al. 2023. "Enhanced Magnetism and Anomalous Hall Transport through Two-Dimensional Tungsten Disulfide Interfaces" Nanomaterials 13, no. 4: 771. https://doi.org/10.3390/nano13040771
APA StyleHung, C.-M., Dang, D. T.-X., Chanda, A., Detellem, D., Alzahrani, N., Kapuruge, N., Pham, Y. T. H., Liu, M., Zhou, D., Gutierrez, H. R., Arena, D. A., Terrones, M., Witanachchi, S., Woods, L. M., Srikanth, H., & Phan, M.-H. (2023). Enhanced Magnetism and Anomalous Hall Transport through Two-Dimensional Tungsten Disulfide Interfaces. Nanomaterials, 13(4), 771. https://doi.org/10.3390/nano13040771









