Mechanism of Skyrmion Attraction in Chiral Magnets near the Ordering Temperatures
Abstract
:1. Introduction
2. Phenomenological Theory
3. Solutions for High-Temperature Isolated Skyrmions
3.1. Equations
3.2. Asymptotic Behaviour of Skyrmion Solutions
3.3. The Internal Structure of Confined Isolated Skyrmions
4. The Properties of Confined Isolated Skyrmions
4.1. Collapse of Skyrmions at High Fields
4.2. Inter-Skyrmion Attraction
4.3. Phenomenon of Skyrmion Confinement
5. Three-Dimensional Attracting Skyrmions within the Conical Phase of Cubic Helimagnets
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bogdanov, A.N.; Yablonsky, D.A. Thermodynamically stable vortices in magnetically ordered crystals. Mixed state of magnetics. Zh. Eksp. Teor. Fiz. 1989, 95, 178–182. [Google Scholar]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Finocchio, G.; Panagopoulos, C. (Eds.) Magnetic Skyrmions and Their Applications; Woodhead Publishing: Cambridge, UK, 2020. [Google Scholar]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef] [Green Version]
- Wilhelm, H.; Leonov, A.O.; Rößler, U.K.; Burger, P.; Hardy, F.; Meingast, C.; Gruner, M.E.; Schnelle, W.; Schmidt, M.; Baenitz, M. Scaling Study and Thermodynamic Properties of the cubic Helimagnet FeGe. Phys. Rev. B 2016, 94, 144424. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Bauer, A.; Pfleiderer, C. Topological Structures in Ferroic Materials; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 1–28. [Google Scholar]
- Bannenberg, L.J.; Wilhelm, H.; Cubitt, R.; Labh, A.; Schmidt, M.P.; Lelièvre-Berna, E.; Pappas, C.; Mostovoy, M.; Leonov, A.O. Multiple low-temperature skyrmionic states in a bulk chiral magnet. NPJ Quantum Mater. 2019, 4, 11. [Google Scholar] [CrossRef] [Green Version]
- Okubo, T.; Chung, S.; Kawamura, H. Multiple-q States and the Skyrmion Lattice of the Triangular-Lattice Heisenberg Antiferromagnet under Magnetic Fields. Phys. Rev. Lett. 2012, 108, 017206. [Google Scholar] [CrossRef] [Green Version]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef] [Green Version]
- Leonov, A.O.; Mostovoy, M. Edge states and skyrmion dynamics in nanostripes of frustrated magnets. Nat. Commun. 2017, 8, 14394. [Google Scholar] [CrossRef] [Green Version]
- Kurumaji, T.; Nakajima, T.; Hirschberger, M.; Kikkawa, A.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Taguchi, Y.; Arima, T.H.; Tokura, Y. Skyrmion lattice with a giant topological Hall effect in a frustrated triangular-lattice magnet. Science 2019, 365, 914–918. [Google Scholar] [CrossRef] [Green Version]
- Tomasello, R.; Martinez, E.; Zivieri, R.; Torres, L.; Carpentieri, M.; Finocchio, G. A strategy for the design of skyrmion racetrack memories. Sci. Rep. 2014, 4, 6784. [Google Scholar] [CrossRef] [Green Version]
- Müller, J. Magnetic skyrmions on a two-lane racetrack. New J. Phys. 2017, 19, 025002. [Google Scholar] [CrossRef]
- Kang, W.; Huang, Y.; Zheng, C.; Lv, W.; Lei, N.; Zhang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Voltage Controlled Magnetic Skyrmion Motion for Racetrack Memory. Sci. Rep. 2016, 6, 23164. [Google Scholar] [CrossRef] [Green Version]
- Dzyaloshinskii, I.E. Theory of helicoidal structures in antiferromagnets. I. Nonmetals. Sov. Phys. JETP-USSR 1964, 19, 960–971. [Google Scholar]
- Dzyaloshinskii, I.E. The theory of helicoidal structures in antiferromagnets. II. Metals. Sov. Phys. JETP-USSR 1965, 20, 223–231. [Google Scholar]
- Dzyaloshinskii, I.E. Theory of helicoidal structures in antiferromagnets. III. Sov. Phys. JETP-USSR 1965, 20, 665–668. [Google Scholar]
- Moriya, T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics. Course of Theoretical Physics; Pergamon Press: Oxford, UK, 1997; Volume V. [Google Scholar]
- Leonov, A.O.; Togawa, Y.; Monchesky, T.L.; Bogdanov, A.N.; Kishine, J.; Kousaka, Y.; Miyagawa, M.; Koyama, T.; Akimitsu, J.; Koyama, T.; et al. Chiral Surface Twists and Skyrmion Stability in Nanolayers of Cubic Helimagnets. Phys. Rev. Lett. 2016, 117, 087202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, S.L.; Van Der Laan, G.; Wang, W.W.; Haghighirad, A.A.; Hesjedal, T. Direct Observation of Twisted Surface skyrmions in Bulk Crystals. Phys. Rev. Lett. 2018, 120, 227202. [Google Scholar] [CrossRef] [PubMed]
- McGrouther, D.; Lamb, R.J.; Krajnak, M.; McFadzean, S.; McVitie, S.; Stamps, R.L.; Leonov, A.O.; Bogdanov, A.N.; Togawa, Y. Internal structure of hexagonal skyrmion lattices in cubic helimagnets. New J. Phys. 2016, 18, 095004. [Google Scholar] [CrossRef] [Green Version]
- Loudon, J.C.; Leonov, A.O.; Bogdanov, A.N.; Hatnean, M.C. Direct observation of attractive skyrmions and skyrmion clusters in the cubic helimagnet Cu2OSeO3. Phys. Rev. B 2018, 97, 134403. [Google Scholar] [CrossRef] [Green Version]
- Leonov, A.O.; Pappas, C.; Smalyukh, I. Field-driven metamorphoses of isolated skyrmions within the conical state of cubic helimagnets. Phys. Rev. B 2021, 104, 064432. [Google Scholar] [CrossRef]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Bogdanov, A.; Hubert, A. The stability of vortex-like structures in uniaxial ferromagnets. J. Magn. Magn. Mater. 1999, 195, 182–192. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef] [Green Version]
- Babaev, E.; Carlström, J.; Garaud, J.; Silaev, M.; Speight, J.M. Type-1.5 superconductivity in multiband systems: Magnetic response, broken symmetries and microscopic theory. A brief overview. Phys. C Supercond. 2012, 479, 2–14. [Google Scholar] [CrossRef] [Green Version]
- Rößler, U.K.; Leonov, A.; Bogdanov, A.N. Chiral skyrmionic matter in non-centrosymmetric magnets. J. Phys. Conf. Ser. 2011, 303, 012105. [Google Scholar] [CrossRef] [Green Version]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [Green Version]
- Janson, O.; Rousochatzakis, I.; Tsirlin, A.A.; Belesi, M.; Leonov, A.A.; Rößler, U.K.; Van Den Brink, J.; Rosner, H. The quantum nature of skyrmions and half-skyrmions in Cu2OSeO3. Nat. Commun. 2014, 5, 5376. [Google Scholar] [CrossRef] [Green Version]
- Lebech, B.; Bernhard, J.; Freltoft, T. Magnetic structures of cubic FeGe studied by small-angle neutron scattering. J. Phys. Condens. Matter 1989, 1, 6105–6122. [Google Scholar] [CrossRef]
- Wilhelm, H.; Baenitz, M.; Schmidt, M.; Rößler, U.K.; Leonov, A.A.; Bogdanov, A.N. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 2011, 107, 127203. [Google Scholar] [CrossRef]
- Pappas, C.; Lelievre-Berna, E.; Falus, P.; Bentley, P.M.; Moskvin, E.; Grigoriev, S.; Fouquet, P.; Farago, B. Chiral paramagnetic skyrmion-like phase in MnSi. Phys. Rev. Lett. 2009, 102, 197202. [Google Scholar] [CrossRef] [Green Version]
- Bak, P.; Jensen, M.H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C Solid State Phys. 1980, 13, L881. [Google Scholar] [CrossRef]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.M.; White, J.S.; Rønnow, H.M.; Dewhurst, C.D.; Mochizuki, M.; Yanai, K.; et al. Neel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schaub, B.; Mukamel, D. Phase diagrams of systems exhibiting incommensurate structures. Phys. Rev. B 1985, 32, 6385–6393. [Google Scholar] [CrossRef]
- Yamashita, M. First Order Phase Transition Accompanying Soliton Lattices near a Tricritical Point–Chiral Smectic C Liquid Crystal in an Electric Field. J. Phys. Soc. Jap. 1987, 56, 1414–1422. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Muckel, F.; von Malottki, S.; Holl, C.; Pestka, B.; Pratzer, M.; Bessarab, P.F.; Heinze, S.; Morgenstern, M. Experimental identification of two distinct skyrmion collapse mechanisms. Nat. Phys. 2021, 17, 395–402. [Google Scholar] [CrossRef]
- Ackerman, P.J.; Smalyukh, I.I. Diversity of Knot Solitons in Liquid Crystals Manifested by Linking of Preimages in Torons and Hopfions. Phys. Rev. X 2017, 7, 011006. [Google Scholar] [CrossRef] [Green Version]
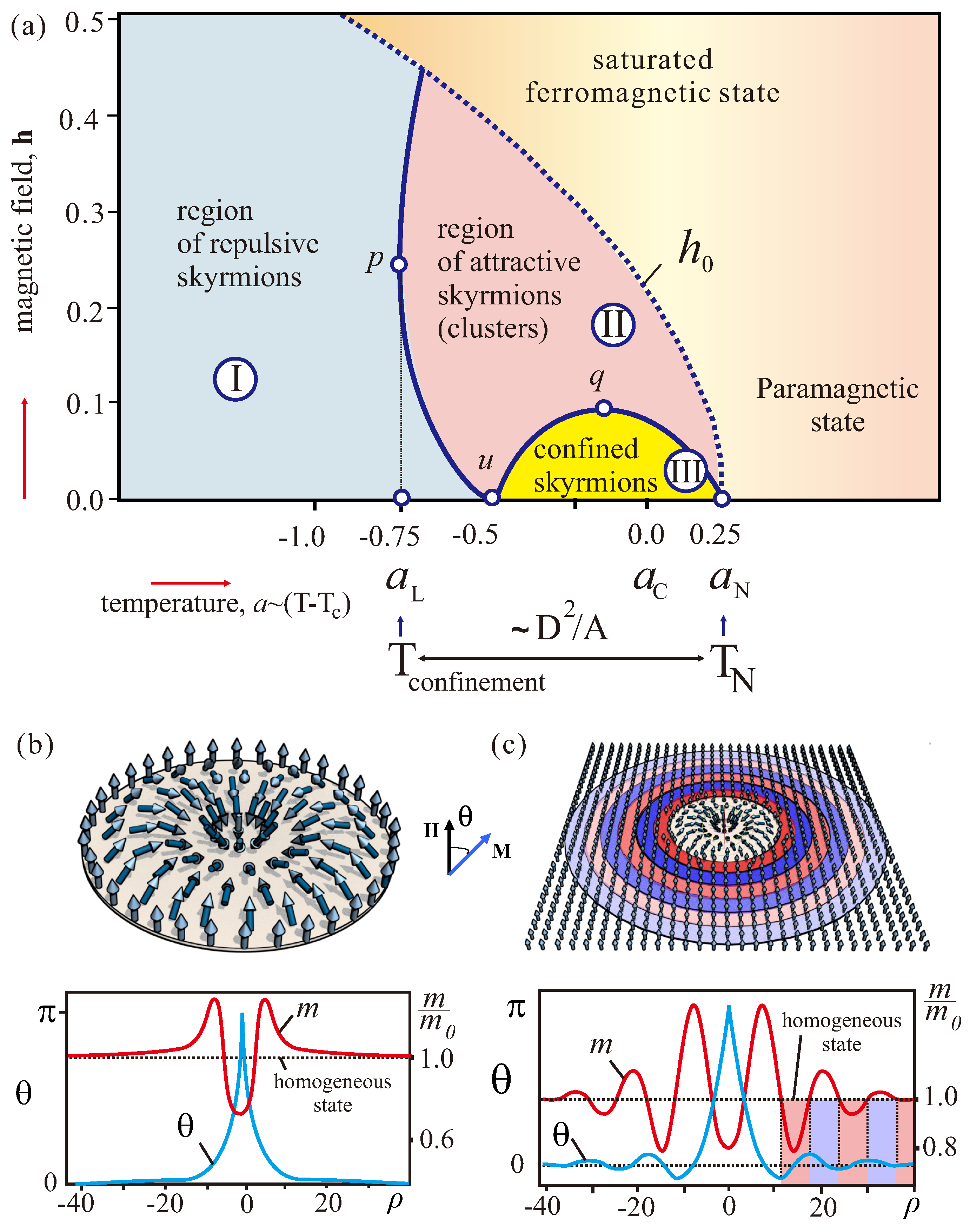

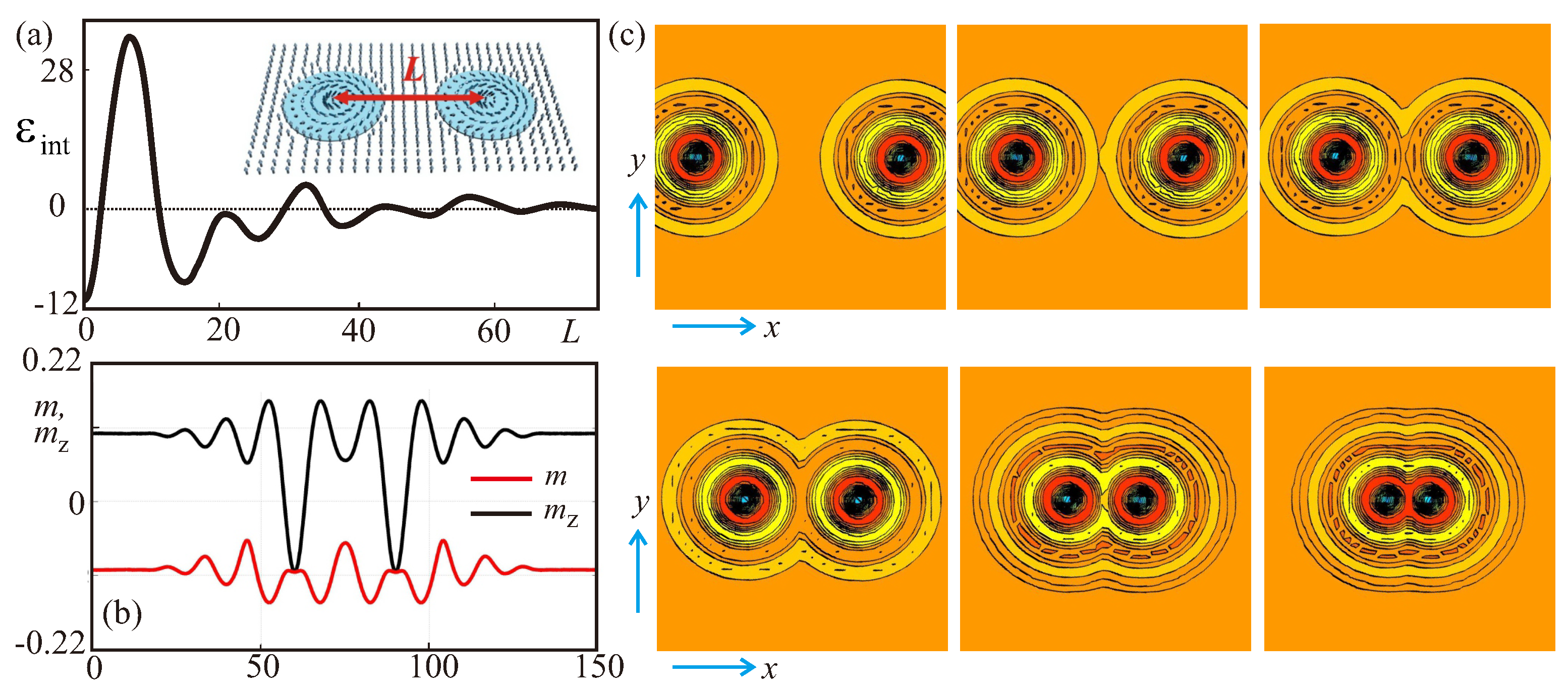
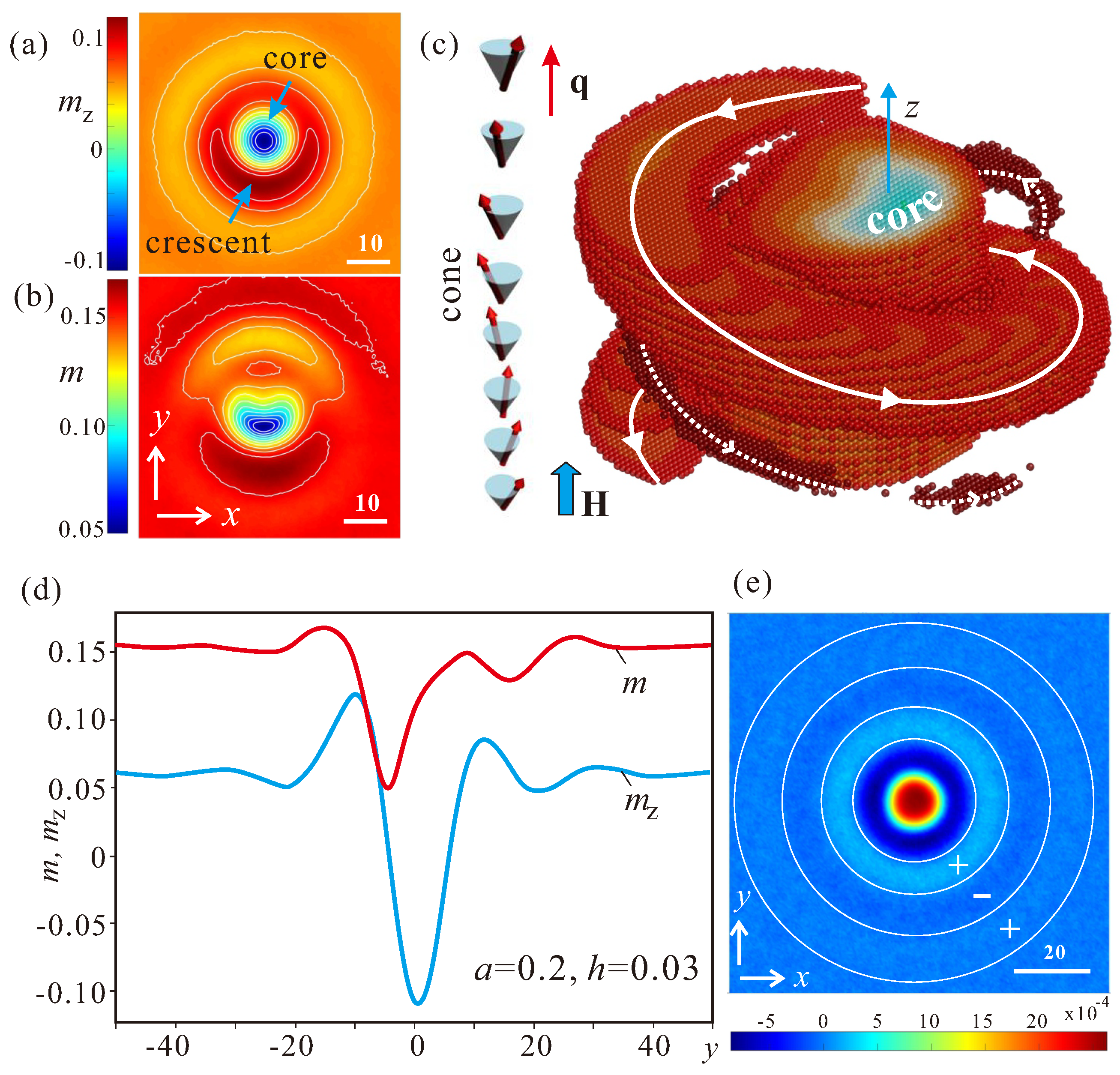
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leonov, A.O.; Rößler, U.K. Mechanism of Skyrmion Attraction in Chiral Magnets near the Ordering Temperatures. Nanomaterials 2023, 13, 891. https://doi.org/10.3390/nano13050891
Leonov AO, Rößler UK. Mechanism of Skyrmion Attraction in Chiral Magnets near the Ordering Temperatures. Nanomaterials. 2023; 13(5):891. https://doi.org/10.3390/nano13050891
Chicago/Turabian StyleLeonov, Andrey O., and Ulrich K. Rößler. 2023. "Mechanism of Skyrmion Attraction in Chiral Magnets near the Ordering Temperatures" Nanomaterials 13, no. 5: 891. https://doi.org/10.3390/nano13050891
APA StyleLeonov, A. O., & Rößler, U. K. (2023). Mechanism of Skyrmion Attraction in Chiral Magnets near the Ordering Temperatures. Nanomaterials, 13(5), 891. https://doi.org/10.3390/nano13050891





