Optical Properties of Conical Quantum Dot: Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence
Abstract
:1. Introduction
2. Materials and Methods
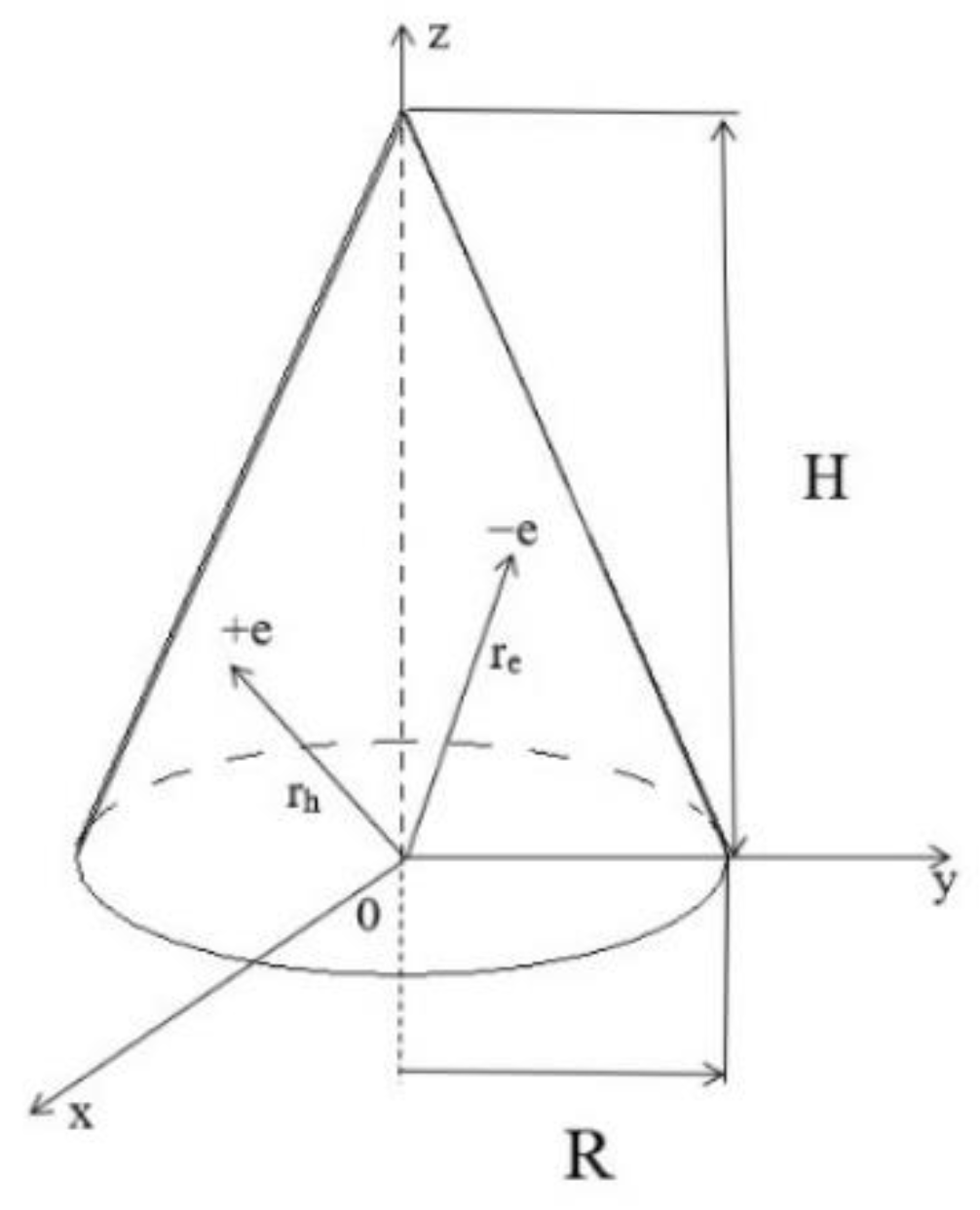
2.1. Exciton States in Conical Quantum Dots
2.2. Optical Properties
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Karabulut, İ.; Baskoutas, S. Linear and nonlinear optical absorption coefficients and refractive index changes in spherical quantum dots: Effects of impurities, electric field, size, and optical intensity. J. Appl. Phys. 2008, 103, 073512. [Google Scholar] [CrossRef]
- Shi, J.J.; Goldys, E.M. Intersubband optical absorption in strained double barrier quantum well infrared photodetectors. IEEE Trans. Electron Devices 1999, 46, 83–88. [Google Scholar] [CrossRef]
- Karabulut, I.; Atav, Ü.; Şafak, H.; Tomak, M.E.H.M.E.T. Linear and nonlinear intersubband optical absorptions in an asymmetric rectangular quantum well. Eur. Phys. J. B 2007, 55, 283–288. [Google Scholar] [CrossRef]
- Kan, Y.; Nagai, H.; Yamanishi, M.; Suemune, I. Field effects on the refractive index and absorption coefficient in AlGaAs quantum well structures and their feasibility for electrooptic device applications. IEEE J. Quantum Electron. 1987, 23, 2167–2180. [Google Scholar] [CrossRef]
- Rodríguez-Magdaleno, K.A.; Pérez-Álvarez, R.; Martínez-Orozco, J.C. Intra-miniband absorption coefficient in GaAs/AlxGa1−xAs core/shell spherical quantum dot. J. Alloys Compd. 2018, 736, 211–215. [Google Scholar] [CrossRef]
- Yuen, S.Y. Fast relaxing absorptive nonlinear refraction in superlattices. Appl. Phys. Lett. 1983, 43, 813–815. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Guo, K.X.; Chen, B.; Wang, R.Z.; Kang, M.W.; Shao, S. Theoretical studies on the optical absorption coefficients and refractive index changes in parabolic quantum dots in the presence of electric and magnetic fields. Superlattices Microstruct. 2010, 47, 325–334. [Google Scholar] [CrossRef]
- Bondarenko, V.; Zhao, Y. Resonant photoionization absorption spectra of spherical quantum dots. J. Phys. Condens. Matter 2003, 15, 1377. [Google Scholar] [CrossRef]
- Baskoutas, S.; Paspalakis, E.; Terzis, A.F. Electronic structure and nonlinear optical rectification in a quantum dot: Effects of impurities and external electric field. J. Phys. Condens. Matter 2007, 19, 395024. [Google Scholar] [CrossRef]
- Wang, G.; Guo, K. Interband optical absorptions in a parabolic quantum dot. Phys. E Low-Dimens. Syst. Nanostructures 2005, 28, 14–21. [Google Scholar] [CrossRef]
- Kırak, M.; Yılmaz, S.; Şahin, M.; Gençaslan, M. The electric field effects on the binding energies and the nonlinear optical properties of a donor impurity in a spherical quantum dot. J. Appl. Phys. 2011, 109, 094309. [Google Scholar] [CrossRef]
- Sargsian, T.A.; Mkrtchyan, M.A.; Sarkisyan, H.A.; Hayrapetyan, D.B. Effects of external electric and magnetic fields on the linear and nonlinear optical properties of InAs cylindrical quantum dot with modified Pöschl-Teller and Morse confinement potentials. Phys. E Low-Dimens. Syst. Nanostructures 2021, 126, 114440. [Google Scholar] [CrossRef]
- Xie, W. Absorption spectra of a donor impurity in a quantum ring. Phys. Status Solidi B 2009, 246, 1313–1317. [Google Scholar] [CrossRef]
- Bleyan, Y.Y.; Mantashyan, P.A.; Kazaryan, E.M.; Sarkisyan, H.A.; Accorsi, G.; Baskoutas, S.; Hayrapetyan, D.B. Non-Linear Optical Properties of Biexciton in Ellipsoidal Quantum Dot. Nanomaterials 2022, 12, 1412. [Google Scholar] [CrossRef]
- Xie, W. Optical anisotropy of a donor in ellipsoidal quantum dots. Phys. B Condens. Matter 2012, 407, 4588–4591. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B.; Kazaryan, E.M.; Sarkisyan, H.A. Magneto-absorption in conical quantum dot ensemble: Possible applications for QD LED. Opt. Commun. 2016, 371, 138–143. [Google Scholar] [CrossRef]
- Khachatryan, K.S.; Mkrtchyan, M.A.; Hayrapetyan, D.B.; Kazaryan, E.M.; Sarkisyan, H.A. Adiabatic description of the electroabsorption in strongly prolate and oblate conical quantum dots. Phys. E Low-Dimens. Syst. Nanostructures 2021, 134, 114887. [Google Scholar] [CrossRef]
- Hayrapetyan, D.B. Hydrogen-like donor impurity states in strongly prolate ellipsoidal quantum dot. Phys. E Low-Dimens. Syst. Nanostructures 2023, 145, 115493. [Google Scholar] [CrossRef]
- Strelow, C.; Rehberg, H.; Schultz, C.M.; Welsch, H.; Heyn, C.; Heitmann, D.; Kipp, T. Optical microcavities formed by semiconductor microtubes using a bottlelike geometry. Phys. Rev. Lett. 2008, 101, 127403. [Google Scholar] [CrossRef]
- Baghdasaryan, D.A.; Hayrapetyan, D.B.; Kazaryan, E.M. Prolate spheroidal quantum dot: Electronic states, direct interband light absorption and electron dipole moment. Phys. B Condens. Matter 2015, 479, 85–89. [Google Scholar] [CrossRef]
- Tshantshapanyan, A.A.; Dvoyan, K.G.; Kazaryan, E.M. Light absorption in coated ellipsoidal quantum lenses. J. Mater. Sci. Mater. Electron. 2009, 20, 491–498. [Google Scholar] [CrossRef]
- Ferreyra, J.M.; Proetto, C.R. Strong-confinement approach for impurities in quantum dots. Phys. Rev. B 1995, 52, R2309. [Google Scholar] [CrossRef] [PubMed]
- Ferreyra, J.M.; Bosshard, P.; Proetto, C.R. Strong-confinement approach for impurities in parabolic quantum dots. Phys. Rev. B 1997, 55, 13682. [Google Scholar] [CrossRef]
- Moreels, I.; Kockaert, P.; Van Deun, R.; Driesen, K.; Loicq, J.; Van Thourhout, D.; Hens, Z. The non-linear refractive index of colloidal PbSe nanocrystals: Spectroscopy and saturation behaviour. J. Lumin. 2006, 121, 369–374. [Google Scholar] [CrossRef]
- Porras-Montenegro, N.; Pe, S.T. Hydrogenic impurities in GaAs-(Ga, Al) as quantum dots. Phys. Rev. B 1992, 46, 9780. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Chatterjee, A. The ground and the first excited states of an electron in a multidimensional polar semiconductor quantum dot: An all-coupling variational approach. J. Phys. Condens. Matter 1999, 11, 2071. [Google Scholar] [CrossRef]
- Pollock, E.L.; Koch, S.W. Path-integral study of excitons and biexcitons in semiconductor quantum dots. J. Chem. Phys. 1991, 94, 6776–6781. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Time-fractional Schrödinger equation from path integral and its implications in quantum dots and semiconductors. Eur. Phys. J. Plus 2018, 133, 394. [Google Scholar] [CrossRef]
- El Haouari, M.; Talbi, A.; Feddi, E.; El Ghazi, H.; Oukerroum, A.; Dujardin, F. Linear and nonlinear optical properties of a single dopant in strained AlAs/GaAs spherical core/shell quantum dots. Opt. Commun. 2017, 383, 231–237. [Google Scholar] [CrossRef]
- Gil-Corrales, A.; Morales, A.L.; Restrepo, R.L.; Mora-Ramos, M.E.; Duque, C.A. Donor-impurity-related optical response and electron Raman scattering in GaAs cone-like quantum dots. Phys. B Condens. Matter 2017, 507, 76–83. [Google Scholar] [CrossRef]
- Xie, W. Impurity effects on optical property of a spherical quantum dot in the presence of an electric field. Phys. B Condens. Matter 2010, 405, 3436–3440. [Google Scholar] [CrossRef]
- Bose, C.; Sarkar, C.K. Perturbation calculation of donor states in a spherical quantum dot. Solid-State Electron. 1998, 42, 1661–1663. [Google Scholar] [CrossRef]
- Mantashian, G.A.; Mantashyan, P.A.; Hayrapetyan, D.B. Modeling of Quantum Dots with the Finite Element Method. Computation 2023, 11, 5. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite element method. Wiley Encycl. Comput. Sci. Eng. 2007, 1–12. [Google Scholar] [CrossRef]
- Dhatt, G.; Lefrançois, E.; Touzot, G. Finite Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Satori, H.; Sali, A. The finite element simulation for the shallow impurity in quantum dots. Phys. E Low-Dimens. Syst. Nanostructures 2013, 48, 171–175. [Google Scholar] [CrossRef]
- Takagahara, T.; Takeda, K. Theory of the quantum confinement effect on excitons in quantum dots of indirect-gap materials. Phys. Rev. B 1992, 46, 15578. [Google Scholar] [CrossRef]
- Peterson, M.D.; Cass, L.C.; Harris, R.D.; Edme, K.; Sung, K.; Weiss, E.A. The role of ligands in determining the exciton relaxation dynamics in semiconductor quantum dots. Annu. Rev. Phys. Chem. 2014, 65, 317–339. [Google Scholar] [CrossRef]
- Stievater, T.H.; Li, X.; Steel, D.G.; Gammon, D.; Katzer, D.S.; Park, D.; Piermarocchi, C.; Sham, L.J. Rabi oscillations of excitons in single quantum dots. Phys. Rev. Lett. 2001, 87, 133603. [Google Scholar] [CrossRef]
- Empedocles, S.A.; Norris, D.J.; Bawendi, M.G. Photoluminescence spectroscopy of single CdSe nanocrystallite quantum dots. Phys. Rev. Lett. 1996, 77, 3873. [Google Scholar] [CrossRef]
- Hoy, J.; Morrison, P.J.; Steinberg, L.K.; Buhro, W.E.; Loomis, R.A. Excitation energy dependence of the photoluminescence quantum yields of core and core/shell quantum dots. J. Phys. Chem. Lett. 2013, 4, 2053–2060. [Google Scholar] [CrossRef]
- Valenta, J.; Juhasz, R.; Linnros, J. Photoluminescence spectroscopy of single silicon quantum dots. Appl. Phys. Lett. 2002, 80, 1070–1072. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron–phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Kozyrev, N.V.; Akhmadullin, R.R.; Namozov, B.R.; Kusrayev, Y.G.; Sedova, I.V.; Sorokin, S.V.; Ivanov, S.V. Multiple spin-flip Raman scattering in CdSe/ZnMnSe quantum dots. Phys. Rev. B 2019, 99, 035301. [Google Scholar] [CrossRef]
- Xie, W. Raman scattering of an exciton in a quantum dot. Phys. B Condens. Matter 2013, 413, 96–99. [Google Scholar] [CrossRef]
- Mantashian, G.A.; Mantashyan, P.A.; Sarkisyan, H.A.; Kazaryan, E.M.; Bester, G.; Baskoutas, S.; Hayrapetyan, D.B. Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence in Colloidal CdSe/CdS Core/Shell Quantum Dots Ensemble. Nanomaterial 2021, 11, 1274. [Google Scholar] [CrossRef]
- Berkinsky, D.B.; Proppe, A.H.; Utzat, H.; Krajewska, C.J.; Sun, W.; Sverko, T.; Yoo, J.J.; Chung, H.; Won, Y.H.; Kim, T.; et al. Narrow Intrinsic Line Widths and Electron–Phonon Coupling of InP Colloidal Quantum Dots. ACS Nano 2023, 17, 3598–3609. [Google Scholar] [CrossRef]
- Jin, X.; Xie, K.; Zhang, T.; Lian, H.; Zhang, Z.; Xu, B.; Li, D.; Li, Q. Cation exchange assisted synthesis of ZnCdSe/ZnSe quantum dots with narrow emission line widths and near-unity photoluminescence quantum yields. Chem. Commun. 2020, 56, 6130–6133. [Google Scholar] [CrossRef]
- Yang, H.; Li, R.; Zhang, Y.; Yu, M.; Wang, Z.; Liu, X.; You, W.; Tu, D.; Sun, Z.; Zhang, R.; et al. Colloidal alloyed quantum dots with enhanced photoluminescence quantum yield in the NIR-II window. J. Am. Chem. Soc. 2021, 143, 2601–2607. [Google Scholar] [CrossRef]
- Yi, Z.; Li, X.; Zhang, H.; Ji, X.; Sun, W.; Yu, Y.; Liu, Y.; Huang, J.; Sarshar, Z.; Sain, M. High quantum yield photoluminescent N-doped carbon dots for switch sensing and imaging. Talanta 2021, 222, 121663. [Google Scholar] [CrossRef]
- Park, Y.S.; Roh, J.; Diroll, B.T.; Schaller, R.D.; Klimov, V.I. Colloidal quantum dot lasers. Nat. Rev. Mater. 2021, 6, 382–401. [Google Scholar] [CrossRef]
- Shu, Y.; Lin, X.; Qin, H.; Hu, Z.; Jin, Y.; Peng, X. Quantum dots for display applications. Angew. Chem. 2020, 132, 22496–22507. [Google Scholar] [CrossRef]
- Molaei, M.J. Principles, mechanisms, and application of carbon quantum dots in sensors: A review. Anal. Methods 2020, 12, 1266–1287. [Google Scholar] [CrossRef]
- Lesiak, A.; Drzozga, K.; Cabaj, J.; Bański, M.; Malecha, K.; Podhorodecki, A. Optical sensors based on II–VI quantum dots. Nanomaterials 2019, 9, 192. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Jin, W.; Zhang, Y.; Yang, T.; Reiss, P.; Zhong, Q.; Bach, U.; Li, Q.; Wang, Y.; Zhang, H.; et al. High efficiency mesoscopic solar cells using CsPbI3 perovskite quantum dots enabled by chemical interface engineering. J. Am. Chem. Soc. 2020, 142, 3775–3783. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Lin, Y.; Zhang, Z.; Rao, H.; Wang, W.; Fang, Y.; Pan, Z.; Zhong, X. Improving the efficiency of quantum dot sensitized solar cells beyond 15% via secondary deposition. J. Am. Chem. Soc. 2021, 143, 4790–4800. [Google Scholar] [CrossRef] [PubMed]
- Sahu, A.; Garg, A.; Dixit, A. A review on quantum dot sensitized solar cells: Past, present and future towards carrier multiplication with a possibility for higher efficiency. Sol. Energy 2020, 203, 210–239. [Google Scholar] [CrossRef]
- Fonoberov, V.A.; Balandin, A.A. Origin of ultraviolet photoluminescence in ZnO quantum dots: Confined excitons versus surface-bound impurity exciton complexes. Appl. Phys. Lett. 2004, 85, 5971–5973. [Google Scholar] [CrossRef]
- Efros, A.L.; Efros, A.L. Interband absorption of light in a semiconductor sphere. Semiconductors 1982, 16, 772–775. [Google Scholar]
- Ramaniah, L.M.; Nair, S.V. Optical absorption in semiconductor quantum dots: A Tight-Bind. Approach. Phys. Rev. B 1993, 47, 7132–7139. [Google Scholar] [CrossRef]
- Van Roosbroeck, W.; Shockley, W. Photon-Radiative Recombination of Electrons and Holes in Germanium. Phys. Rev. 1954, 94, 1558–1560. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Pal, B.; Bansal, B. On conversion of luminescence into absorption and the van Roosbroeck-Shockley relation. Appl. Phys. Lett. 2012, 100, 222103. [Google Scholar] [CrossRef]
- Chamberlain, M.P.; Trallero-Giner, C.; Cardona, M. Theory of one-phonon Raman scattering in semiconductor microcrys-tallites. Phys. Rev. B 1995, 51, 1680. [Google Scholar] [CrossRef] [PubMed]
- Trallero-Giner, C.; Debernardi, A.; Cardona, M.; Menendez-Proupin, E.; Ekimov, A.I. Optical vibrons in CdSe dots and dis-persion relation of the bulk material. Phys. Rev. B 1998, 57, 4664. [Google Scholar] [CrossRef]
- Trallero-Giner, C.; Cardona, M. Vibrational Resonant Raman Scattering in Spherical Quantum Dots: Exciton Effects. Phys. Status Solidi B 1997, 199, 81–94. [Google Scholar] [CrossRef]
- Sipahi, G.M.; Enderlein, R.; Scolfaro, L.M.R.; Leite, J.R.; Da Silva, E.C.F.; Levine, A. Theory of luminescence spectra from δ-doping structures: Application to GaAs. Phys. Rev. B 1998, 57, 9168. [Google Scholar] [CrossRef]
- Fu, Y.; Fu, Y. Optical properties of semiconductors. Phys. Model. Semicond. Quantum Devices 2014, 111–183. [Google Scholar] [CrossRef]






| 8 | 12 | 0.98 |
| 14 | 1.09 | |
| 16 | 1.18 | |
| 10 | 12 | 1.32 |
| 14 | 1.49 | |
| 16 | 1.651 | |
| 12 | 12 | 1.656 |
| 14 | 1.91 | |
| 16 | 2.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavalajyan, S.P.; Mantashian, G.A.; Kharatyan, G.T.; Sarkisyan, H.A.; Mantashyan, P.A.; Baskoutas, S.; Hayrapetyan, D.B. Optical Properties of Conical Quantum Dot: Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence. Nanomaterials 2023, 13, 1393. https://doi.org/10.3390/nano13081393
Gavalajyan SP, Mantashian GA, Kharatyan GT, Sarkisyan HA, Mantashyan PA, Baskoutas S, Hayrapetyan DB. Optical Properties of Conical Quantum Dot: Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence. Nanomaterials. 2023; 13(8):1393. https://doi.org/10.3390/nano13081393
Chicago/Turabian StyleGavalajyan, Sargis P., Grigor A. Mantashian, Gor Ts. Kharatyan, Hayk A. Sarkisyan, Paytsar A. Mantashyan, Sotirios Baskoutas, and David B. Hayrapetyan. 2023. "Optical Properties of Conical Quantum Dot: Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence" Nanomaterials 13, no. 8: 1393. https://doi.org/10.3390/nano13081393
APA StyleGavalajyan, S. P., Mantashian, G. A., Kharatyan, G. T., Sarkisyan, H. A., Mantashyan, P. A., Baskoutas, S., & Hayrapetyan, D. B. (2023). Optical Properties of Conical Quantum Dot: Exciton-Related Raman Scattering, Interband Absorption and Photoluminescence. Nanomaterials, 13(8), 1393. https://doi.org/10.3390/nano13081393









