Lattice Thermal Conductivity of Monolayer InSe Calculated by Machine Learning Potential
Abstract
1. Introduction
2. Methodology
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, M.Y.; Su, S.K.; Wong, H.S.P.; Li, L.J. How 2D semiconductors could extend Moore’s law. Nature 2019, 567, 169–170. [Google Scholar] [CrossRef] [PubMed]
- Fiori, G.; Bonaccorso, F.; Iannaccone, G.; Palacios, T.; Neumaier, D.; Seabaugh, A.; Banerjee, S.K.; Colombo, L. Electronics based on two-dimensional materials. Nat. Nanotechnol. 2014, 9, 768–779. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Zhang, S.; Lai, K.; Lei, L.; Zheng, Z.; Kang, D.; Zhao, Z.; Dai, J. Strongly anisotropic ultrafast dynamic behavior of GaTe dominated by the tilted and flat bands. Nanotechnology 2023, 34, 285703. [Google Scholar] [CrossRef] [PubMed]
- Lai, K.; Ju, S.; Zhu, H.; Wang, H.; Wu, H.; Yang, B.; Zhang, E.; Yang, M.; Li, F.; Cui, S.; et al. Strong bulk-surface interaction dominated in-plane anisotropy of electronic structure in GaTe. Commun. Phys. 2022, 5, 143. [Google Scholar] [CrossRef]
- Lai, K.; Dai, J. Stacking effect on the electronic structures of hexagonal GaTe. J. Phys. D Appl. Phys. 2023, 56, 275301. [Google Scholar] [CrossRef]
- Song, C.; Fan, F.; Xuan, N.; Huang, S.; Zhang, G.; Wang, C.; Sun, Z.; Wu, H.; Yan, H. Largely Tunable Band Structures of Few-Layer InSe by Uniaxial Strain. ACS Appl. Mater. Interfaces 2018, 10, 3994–4000. [Google Scholar] [CrossRef] [PubMed]
- Segura, A.; Pomer, F.; Cantarero, A.; Krause, W.; Chevy, A. Electron scattering mechanisms in n-type indium selenide. Phys. Rev. B 1984, 29, 5708–5717. [Google Scholar] [CrossRef]
- Poncé, S.; Li, W.; Reichardt, S.; Giustino, F. First-principles calculations of charge carrier mobility and conductivity in bulk semiconductors and two-dimensional materials. Rep. Prog. Phys. 2020, 83, 036501. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Tyurnina, A.V.; Yu, G.L.; Mishchenko, A.; Zólyomi, V.; Morozov, S.V.; Kumar, R.K.; Gorbachev, R.V.; Kudrynskyi, Z.R.; Pezzini, S.; et al. High electron mobility, quantum Hall effect and anomalous optical response in atomically thin InSe. Nat. Nanotechnol. 2017, 12, 223–227. [Google Scholar] [CrossRef]
- Ho, C.H.; Chu, Y.J. Bending Photoluminescence and Surface Photovoltaic Effect on Multilayer InSe 2D Microplate Crystals. Adv. Opt. Mater. 2015, 3, 1750–1758. [Google Scholar] [CrossRef]
- Lei, S.; Ge, L.; Najmaei, S.; George, A.; Kappera, R.; Lou, J.; Chhowalla, M.; Yamaguchi, H.; Gupta, G.; Vajtai, R.; et al. Evolution of the Electronic Band Structure and Efficient Photo-Detection in Atomic Layers of InSe. ACS Nano 2014, 8, 1263–1272. [Google Scholar] [CrossRef]
- Tamalampudi, S.R.; Lu, Y.Y.; U., R.K.; Sankar, R.; Liao, C.D.; B., K.M.; Cheng, C.H.; Chou, F.C.; Chen, Y.T. High Performance and Bendable Few-Layered InSe Photodetectors with Broad Spectral Response. Nano Lett. 2014, 14, 2800–2806. [Google Scholar] [CrossRef] [PubMed]
- Mudd, G.W.; Svatek, S.A.; Ren, T.; Patanè, A.; Makarovsky, O.; Eaves, L.; Beton, P.H.; Kovalyuk, Z.D.; Lashkarev, G.V.; Kudrynskyi, Z.R.; et al. Tuning the Bandgap of Exfoliated InSe Nanosheets by Quantum Confinement. Adv. Mater. 2013, 25, 5714–5718. [Google Scholar] [CrossRef]
- Rai, A.; Sangwan, V.K.; Gish, J.T.; Hersam, M.C.; Cahill, D.G. Anisotropic thermal conductivity of layered indium selenide. Appl. Phys. Lett. 2021, 118, 073101. [Google Scholar] [CrossRef]
- Li, K.; Hong, Y.; Li, Z.; Liu, X. Thermal property engineering of InSe layer by a thin Al2O3 stress liner. Appl. Phys. Lett. 2018, 113, 021903. [Google Scholar] [CrossRef]
- Buckley, D.; Kudrynskyi, Z.R.; Balakrishnan, N.; Vincent, T.; Mazumder, D.; Castanon, E.; Kovalyuk, Z.D.; Kolosov, O.; Kazakova, O.; Tzalenchuk, A.; et al. Anomalous Low Thermal Conductivity of Atomically Thin InSe Probed by Scanning Thermal Microscopy. Adv. Funct. Mater. 2021, 31, 2008967. [Google Scholar] [CrossRef]
- Pandey, T.; Parker, D.S.; Lindsay, L. Ab initio phonon thermal transport in monolayer InSe, GaSe, GaS, and alloys. Nanotechnology 2017, 28, 455706. [Google Scholar] [CrossRef] [PubMed]
- Nissimagoudar, A.S.; Rashid, Z.; Ma, J.; Li, W. Lattice Thermal Transport in Monolayer Group 13 Monochalcogenides MX (M = Ga, In; X = S, Se, Te): Interplay of Atomic Mass, Harmonicity, and Lone-Pair-Induced Anharmonicity. Inorg. Chem. 2020, 59, 14899–14909. [Google Scholar] [CrossRef] [PubMed]
- Nissimagoudar, A.S.; Ma, J.; Chen, Y.; Li, W. Thermal transport in monolayer InSe. J. Phys. Condens. Matter 2017, 29, 335702. [Google Scholar] [CrossRef]
- Majumdar, A.; Chowdhury, S.; Ahuja, R. Drastic reduction of thermal conductivity in hexagonal AX (A = Ga, In & Tl, X = S, Se & Te) monolayers due to alternative atomic configuration. Nano Energy 2021, 88, 106248. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, S.; Tadano, T.; Chen, Y. Anharmonic lattice dynamics and thermal transport of monolayer InSe under equibiaxial tensile strains. J. Phys. Condens. Matter 2020, 32, 475702. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.; Yuan, K.; Sun, Z.; Zhang, X.; Gao, Y.; Qin, G.; Tang, D. Ultralow lattice thermal conductivity and dramatically enhanced thermoelectric properties of monolayer InSe induced by an external electric field. Phys. Chem. Chem. Phys. 2021, 23, 13633–13646. [Google Scholar] [CrossRef]
- Lindsay, L.; Broido, D.A.; Reinecke, T.L. First-Principles Determination of Ultrahigh Thermal Conductivity of Boron Arsenide: A Competitor for Diamond? Phys. Rev. Lett. 2013, 111, 025901. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.S.; Li, M.; Wu, H.; Nguyen, H.; Hu, Y. Experimental observation of high thermal conductivity in boron arsenide. Science 2018, 361, 575–578. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zheng, Q.; Lv, Y.; Liu, X.; Wang, X.; Huang, P.Y.; Cahill, D.G.; Lv, B. High thermal conductivity in cubic boron arsenide crystals. Science 2018, 361, 579–581. [Google Scholar] [CrossRef]
- Tian, F.; Song, B.; Chen, X.; Ravichandran, N.K.; Lv, Y.; Chen, K.; Sullivan, S.; Kim, J.; Zhou, Y.; Liu, T.H.; et al. Unusual high thermal conductivity in boron arsenide bulk crystals. Science 2018, 361, 582–585. [Google Scholar] [CrossRef]
- Feng, T.; Ruan, X. Four-phonon scattering reduces intrinsic thermal conductivity of graphene and the contributions from flexural phonons. Phys. Rev. B 2018, 97, 045202. [Google Scholar] [CrossRef]
- Zhou, W.; Dai, Y.; Zhang, J.; Song, B.; Liu, T.H.; Yang, R. Effect of four-phonon interaction on phonon thermal conductivity and mean-free-path spectrum of high-temperature phase SnSe. Appl. Phys. Lett. 2022, 121, 112202. [Google Scholar] [CrossRef]
- Zhang, E.; Yao, Y.; Gao, T.; Kang, D.; Wu, J.; Dai, J. The effect of external temperature gradients on thermal conductivity in non-equilibrium molecular dynamics simulations: From nanowires to bulk Si. J. Chem. Phys. 2019, 151, 064116. [Google Scholar] [CrossRef]
- Qiu, R.; Yu, X.; Wang, D.; Zhang, S.; Kang, D.; Dai, J. Nanoscale Topological Morphology Transition and Controllable Thermal Conductivity of Wrinkled Hexagonal Boron Nitride: Implications for Thermal Manipulation and Management. ACS Appl. Nano Mater. 2021, 4, 10665–10673. [Google Scholar] [CrossRef]
- Pham, V.T.; Fang, T.H. Effects of temperature and intrinsic structural defects on mechanical properties and thermal conductivities of InSe monolayers. Sci. Rep. 2020, 10, 15082. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Zhang, L.; Car, R.; E, W. Deep Potential: A General Representation of a Many-Body Potential Energy Surface. Commun. Comput. Phys. 2018, 23, 629–639. [Google Scholar] [CrossRef]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; E, W. Deep Potential Molecular Dynamics: A Scalable Model with the Accuracy of Quantum Mechanics. Phys. Rev. Lett. 2018, 120, 143001. [Google Scholar] [CrossRef] [PubMed]
- Novikov, I.S.; Gubaev, K.; Podryabinkin, E.V.; Shapeev, A.V. The MLIP package: Moment tensor potentials with MPI and active learning. Mach. Learn. Sci. Technol. 2020, 2, 025002. [Google Scholar] [CrossRef]
- Zeng, Q.; Chen, B.; Yu, X.; Zhang, S.; Kang, D.; Wang, H.; Dai, J. Towards large-scale and spatiotemporally resolved diagnosis of electronic density of states by deep learning. Phys. Rev. B 2022, 105, 174109. [Google Scholar] [CrossRef]
- Li, R.; Lee, E.; Luo, T. A unified deep neural network potential capable of predicting thermal conductivity of silicon in different phases. Mater. Today Phys. 2020, 12, 100181. [Google Scholar] [CrossRef]
- Zeng, Q.; Yu, X.; Yao, Y.; Gao, T.; Chen, B.; Zhang, S.; Kang, D.; Wang, H.; Dai, J. Ab initio validation on the connection between atomistic and hydrodynamic description to unravel the ion dynamics of warm dense matter. Phys. Rev. Res. 2021, 3, 033116. [Google Scholar] [CrossRef]
- Mortazavi, B.; Podryabinkin, E.V.; Novikov, I.S.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. Accelerating first-principles estimation of thermal conductivity by machine-learning interatomic potentials: A MTP/ShengBTE solution. Comput. Phys. Commun. 2021, 258, 107583. [Google Scholar] [CrossRef]
- Mortazavi, B.; Novikov, I.S.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Shapeev, A.V.; Zhuang, X. Exploring phononic properties of two-dimensional materials using machine learning interatomic potentials. Appl. Mater. Today 2020, 20, 100685. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, X.; Zhang, B.; Li, W. High Thermal Conductivity of Wurtzite Boron Arsenide Predicted by Including Four-Phonon Scattering with Machine Learning Potential. ACS Appl. Mater. Interfaces 2021, 13, 53409–53415. [Google Scholar] [CrossRef]
- Yang, F.; Zeng, Q.; Chen, B.; Kang, D.; Zhang, S.; Wu, J.; Yu, X.; Dai, J. Lattice Thermal Conductivity of MgSiO3 Perovskite and Post-Perovskite under Lower Mantle Conditions Calculated by Deep Potential Molecular Dynamics. Chin. Phys. Lett. 2022, 39, 116301. [Google Scholar] [CrossRef]
- Hu, T.; Zhou, J.; Dong, J. Strain induced new phase and indirect–direct band gap transition of monolayer InSe. Phys. Chem. Chem. Phys. 2017, 19, 21722–21728. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Xiang, H.; Xu, B.; Xia, Y.; Yin, J.; Liu, Z. Ab initio study of carrier mobility of few-layer InSe. Appl. Phys. Express 2016, 9, 035203. [Google Scholar] [CrossRef]
- Wan, W.; Zhao, S.; Ge, Y.; Liu, Y. Phonon and electron transport in Janus monolayers based on InSe. J. Phys. Condens. Matter 2019, 31, 435501. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Han, J.; Weinan, E. DeePMD-kit: A deep learning package for many-body potential energy representation and molecular dynamics. Comput. Phys. Commun. 2018, 228, 178–184. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Zhang, L.; Lin, D.Y.; Wang, H.; Car, R.; Weinan, E. Active learning of uniformly accurate interatomic potentials for materials simulation. Phys. Rev. Mater. 2019, 3, 023804. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Holzwarth, N.; Tackett, A.; Matthews, G. A Projector Augmented Wave (PAW) code for electronic structure calculations, Part I: Atompaw for generating atom-centered functions. Comput. Phys. Commun. 2001, 135, 329–347. [Google Scholar] [CrossRef]
- Green, M. Markoff random processes and the statistical mechanics of time-dependent phenomena. J. Chem. Phys. 1952, 20, 1281–1295. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Colonna, N.; Carnimeo, I.; Dal Corso, A.; de Gironcoli, S.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Sohier, T.; Calandra, M.; Mauri, F. Density functional perturbation theory for gated two-dimensional heterostructures: Theoretical developments and application to flexural phonons in graphene. Phys. Rev. B 2017, 96, 075448. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Li, W.; Carrete, J.; Katcho, N.A.; Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 2014, 185, 1747–1758. [Google Scholar] [CrossRef]
- Wang, H.; Qin, G.; Yang, J.; Qin, Z.; Yao, Y.; Wang, Q.; Hu, M. First-principles study of electronic, optical and thermal transport properties of group III-VI monolayer MX (M = Ga, In; X = S, Se). J. Appl. Phys. 2019, 125, 245104. [Google Scholar] [CrossRef]
- Han, Z.; Yang, X.; Li, W.; Feng, T.; Ruan, X. FourPhonon: An extension module to ShengBTE for computing four-phonon scattering rates and thermal conductivity. Comput. Phys. Commun. 2022, 270, 108179. [Google Scholar] [CrossRef]
- Feng, T.; Ruan, X. Quantum mechanical prediction of four-phonon scattering rates and reduced thermal conductivity of solids. Phys. Rev. B 2016, 93, 045202. [Google Scholar] [CrossRef]
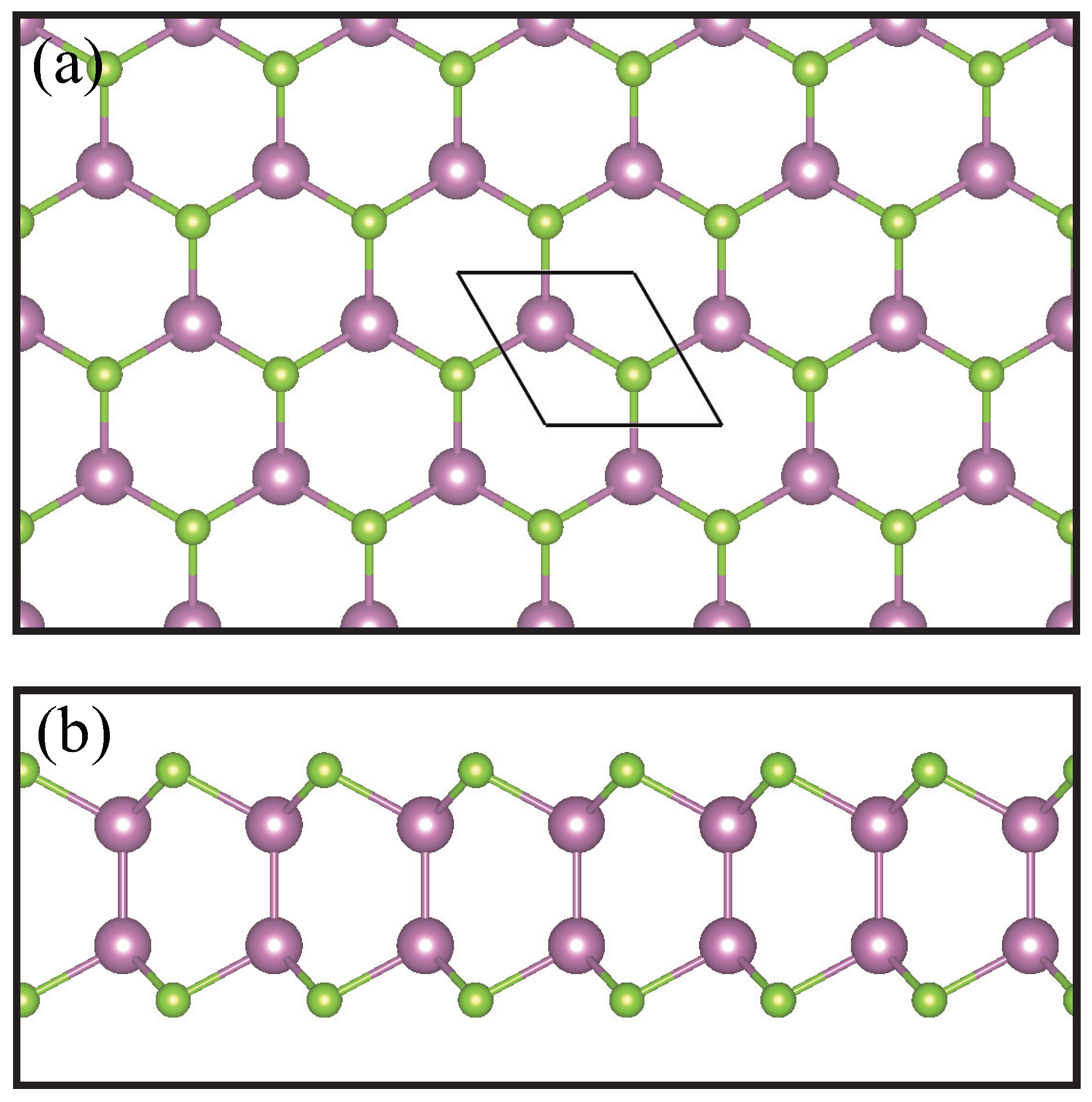
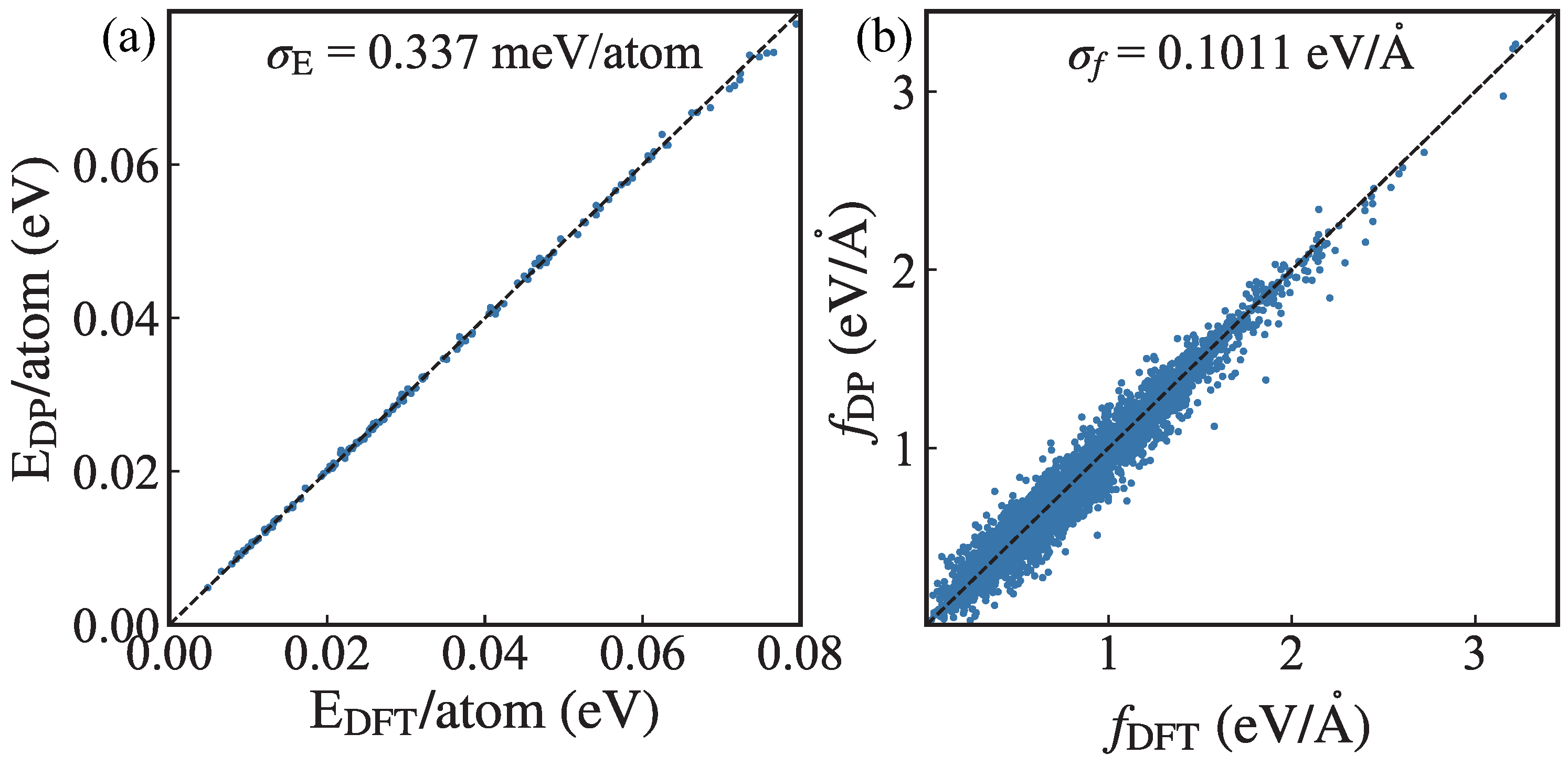
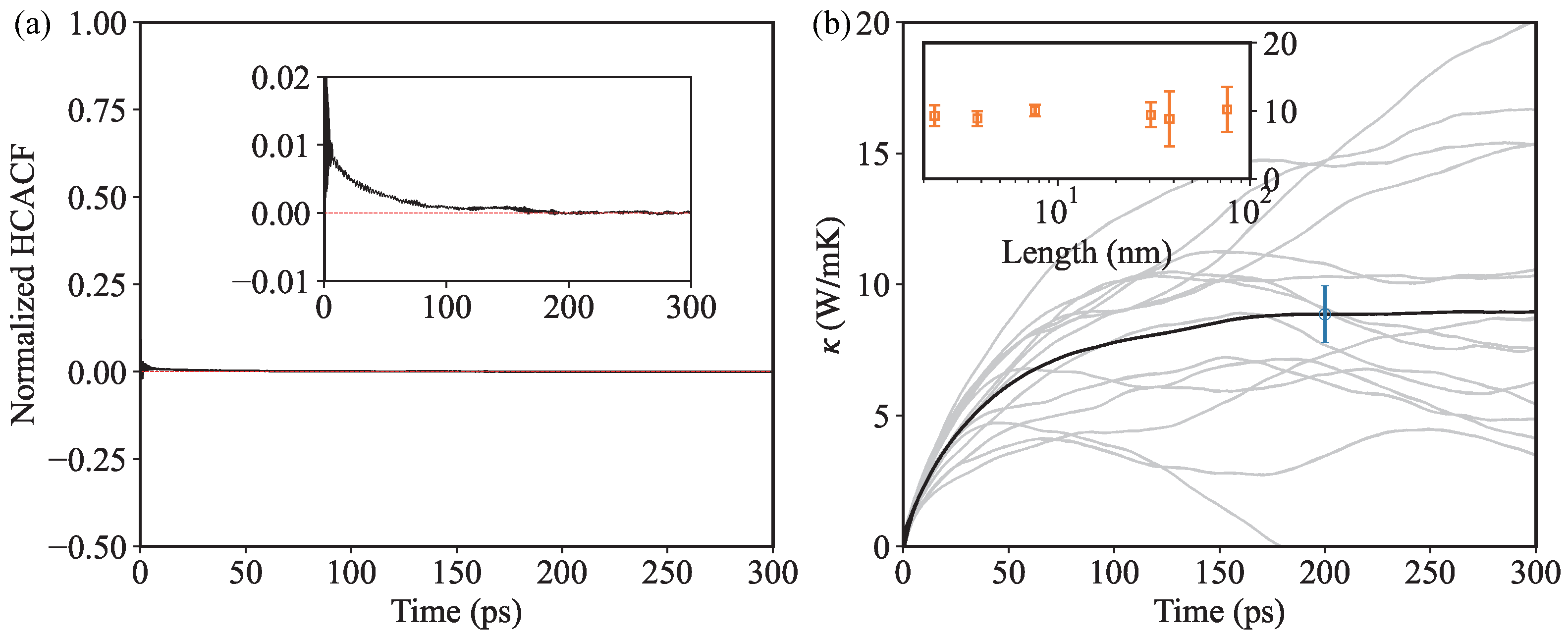

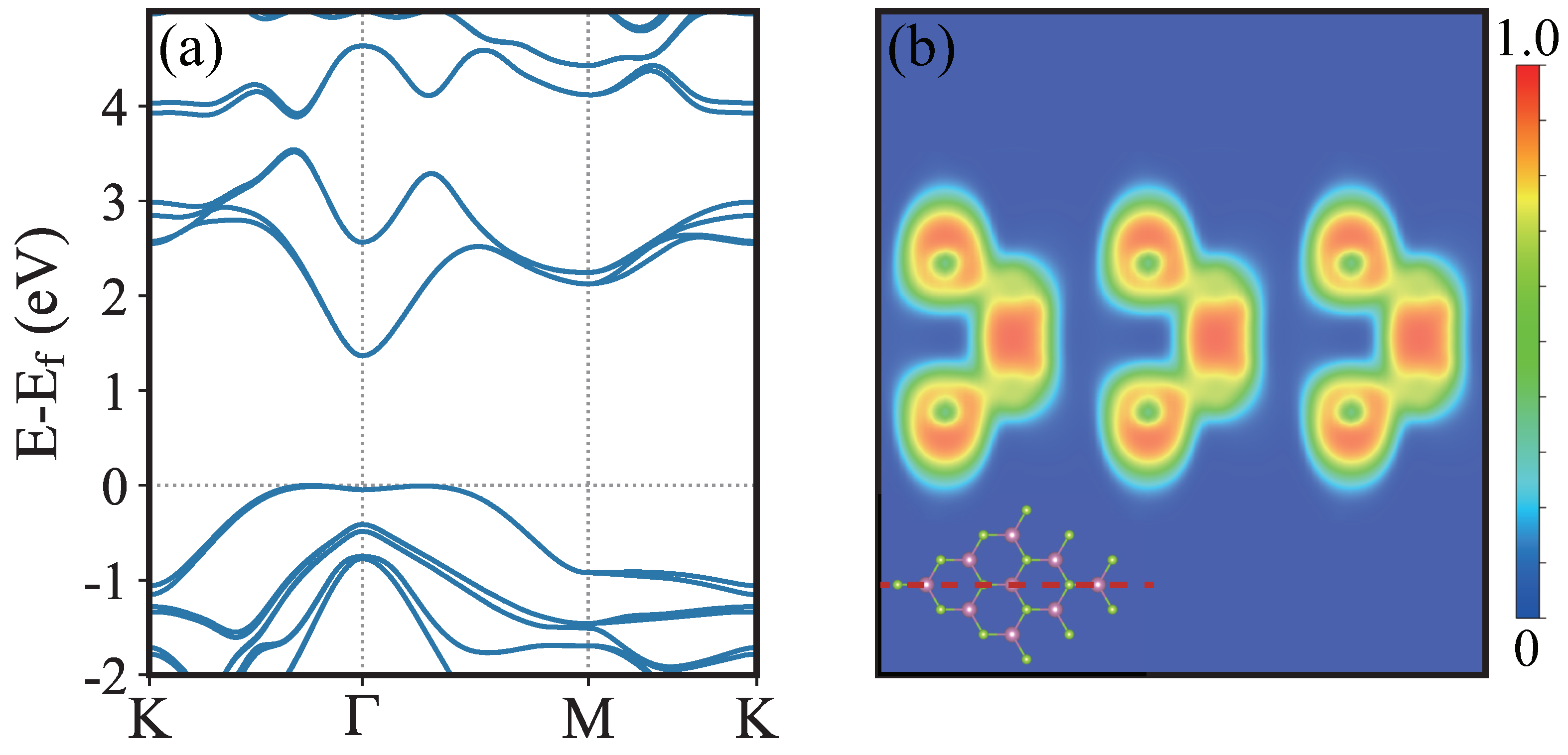
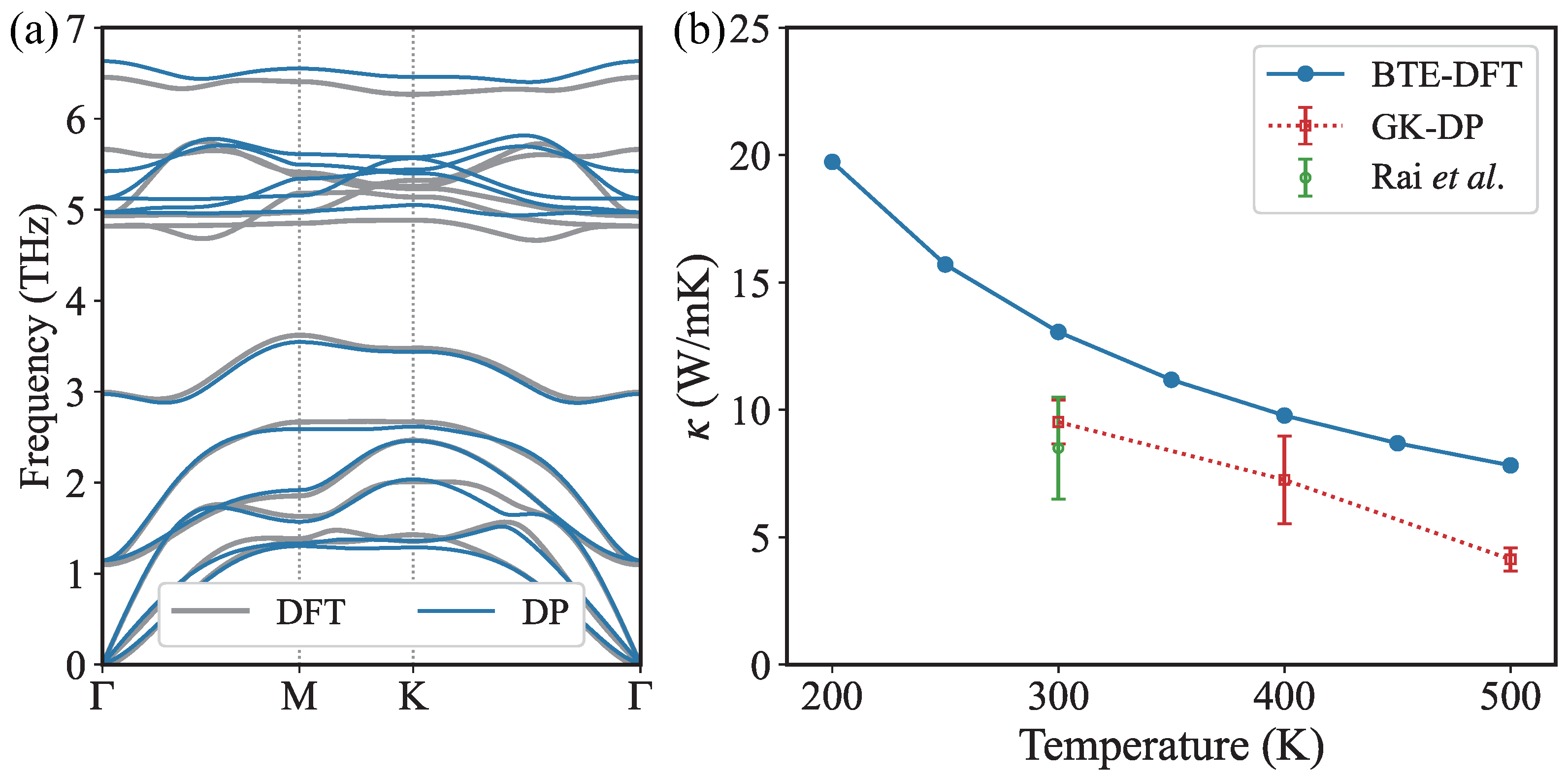

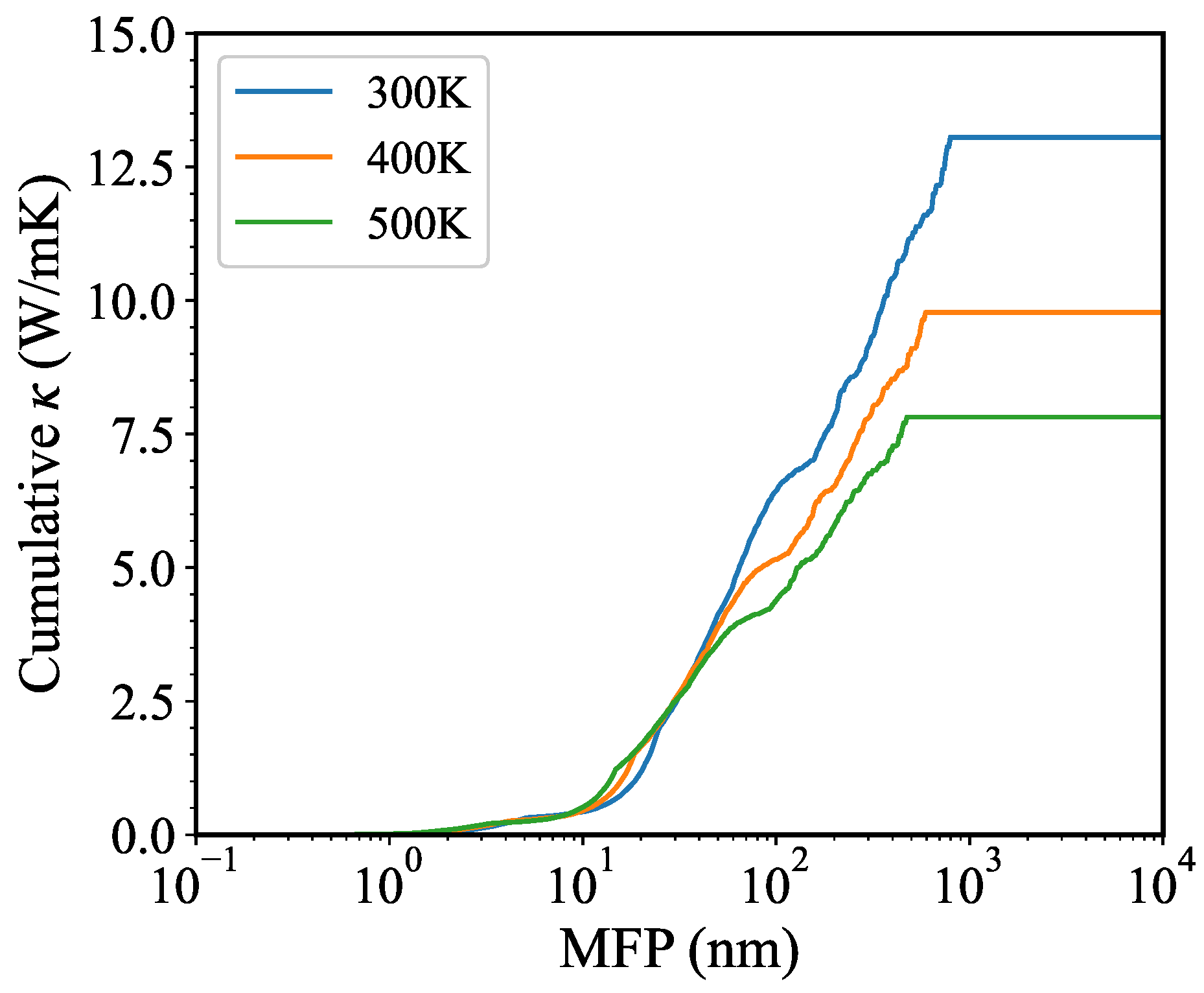
| Method | (W/mK) | Thickness (Å) | Recalculated (W/mK) | Thickness (Å) | Ref. |
|---|---|---|---|---|---|
| Exp. | 8.5 | - | - | - | Ref. [14] |
| DP-GK | 9.52 | 8.57 | - | - | This work |
| SW-GK | ∼46 | 5.385 | 28.9 | 8.57 | Ref. [31] |
| BTE | 13.08 | 8.57 | - | - | This work |
| BTE | 28.20 | 5.380 | 17.7 | 8.57 | Ref. [20] |
| BTE | 27.60 | 8.32 | 26.8 | 8.57 | Ref. [19] |
| BTE | 41.46 | 5.381 | 26.0 | 8.57 | Ref. [17] |
| BTE | 44.30 | 5.386 | 27.8 | 8.57 | Ref. [18] |
| BTE | 41.60 | 5.386 | 26.1 | 8.57 | Ref. [65] |
| BTE | 63.73 | 5.381 | 40.0 | 8.57 | Ref. [21] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Zeng, Q.; Chen, K.; Yu, X.; Dai, J. Lattice Thermal Conductivity of Monolayer InSe Calculated by Machine Learning Potential. Nanomaterials 2023, 13, 1576. https://doi.org/10.3390/nano13091576
Han J, Zeng Q, Chen K, Yu X, Dai J. Lattice Thermal Conductivity of Monolayer InSe Calculated by Machine Learning Potential. Nanomaterials. 2023; 13(9):1576. https://doi.org/10.3390/nano13091576
Chicago/Turabian StyleHan, Jinsen, Qiyu Zeng, Ke Chen, Xiaoxiang Yu, and Jiayu Dai. 2023. "Lattice Thermal Conductivity of Monolayer InSe Calculated by Machine Learning Potential" Nanomaterials 13, no. 9: 1576. https://doi.org/10.3390/nano13091576
APA StyleHan, J., Zeng, Q., Chen, K., Yu, X., & Dai, J. (2023). Lattice Thermal Conductivity of Monolayer InSe Calculated by Machine Learning Potential. Nanomaterials, 13(9), 1576. https://doi.org/10.3390/nano13091576






