Ultrahigh-Q Polarization-Independent Terahertz Metamaterial Absorber Using Pattern-Free Graphene for Sensing Applications
Abstract
1. Introduction
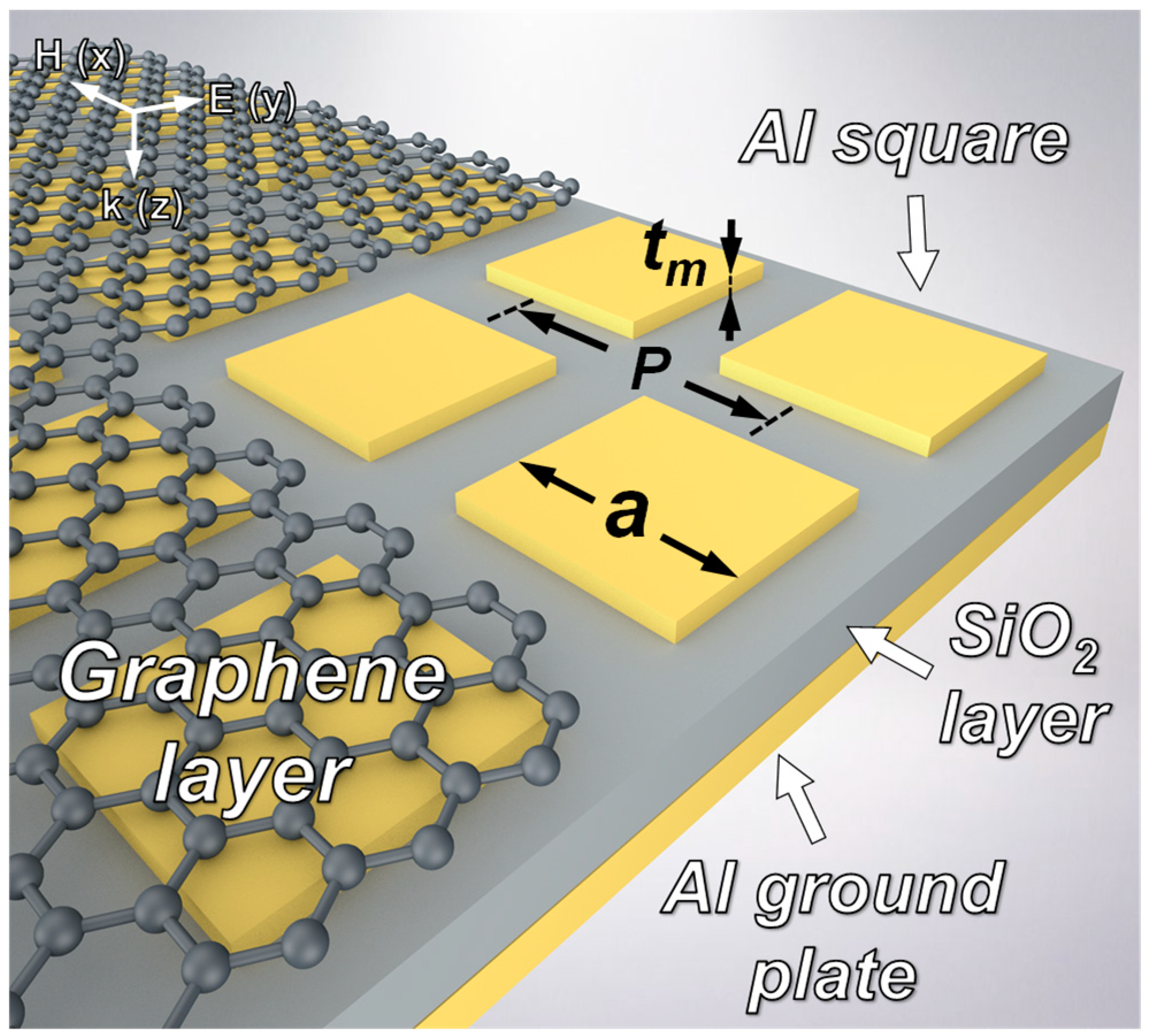
2. Design of the TMMA
3. Results and Discussions
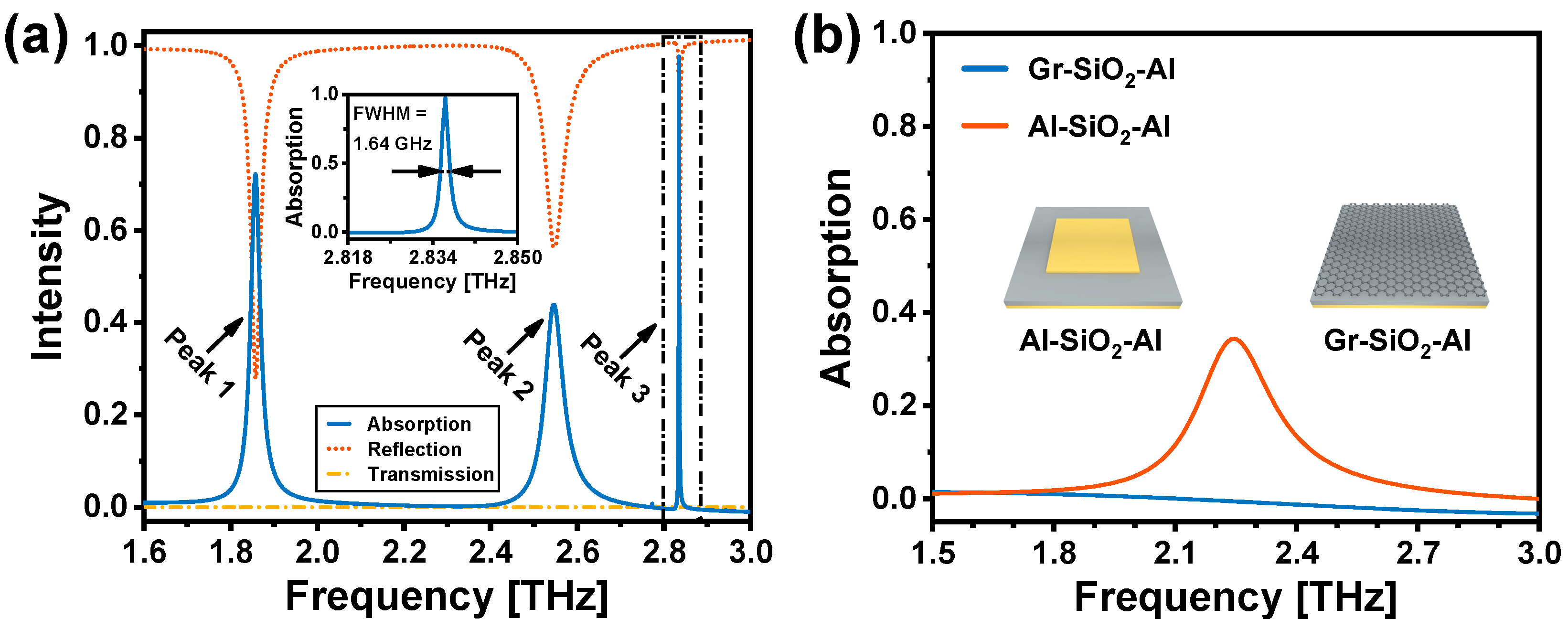
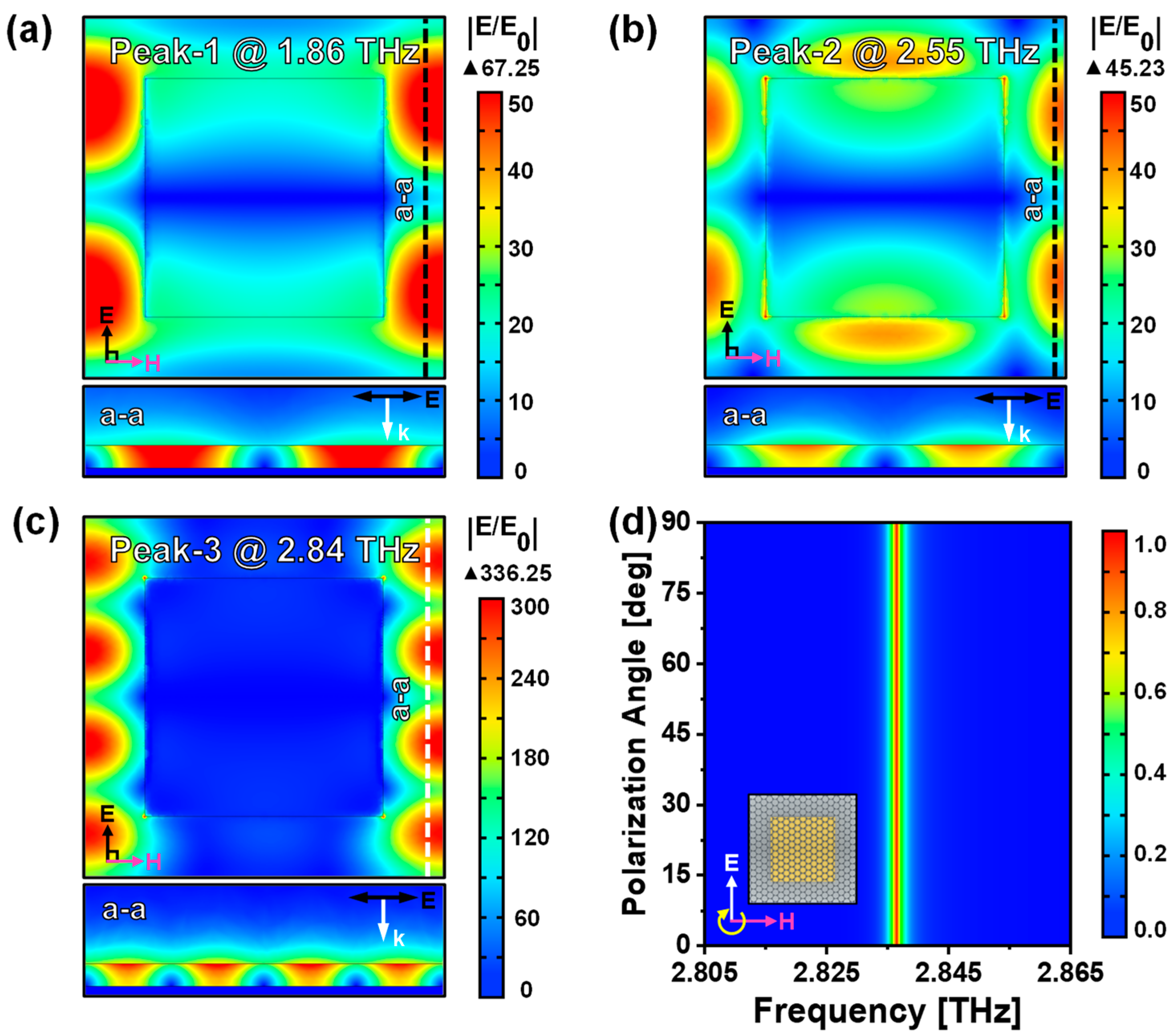
3.1. Analyses of Resonance Modes
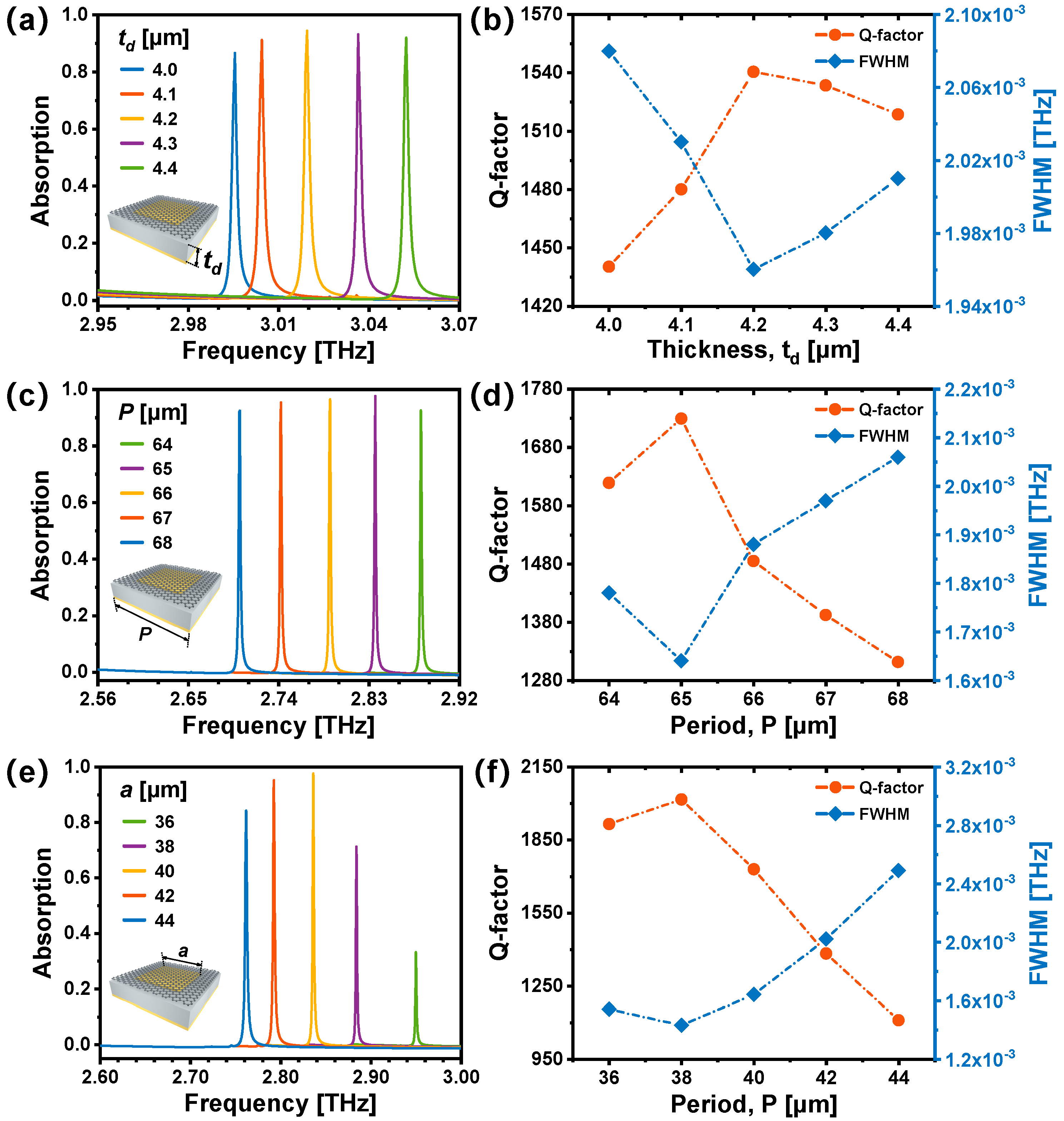
3.2. Tunability of the Graphene-Based TMMA
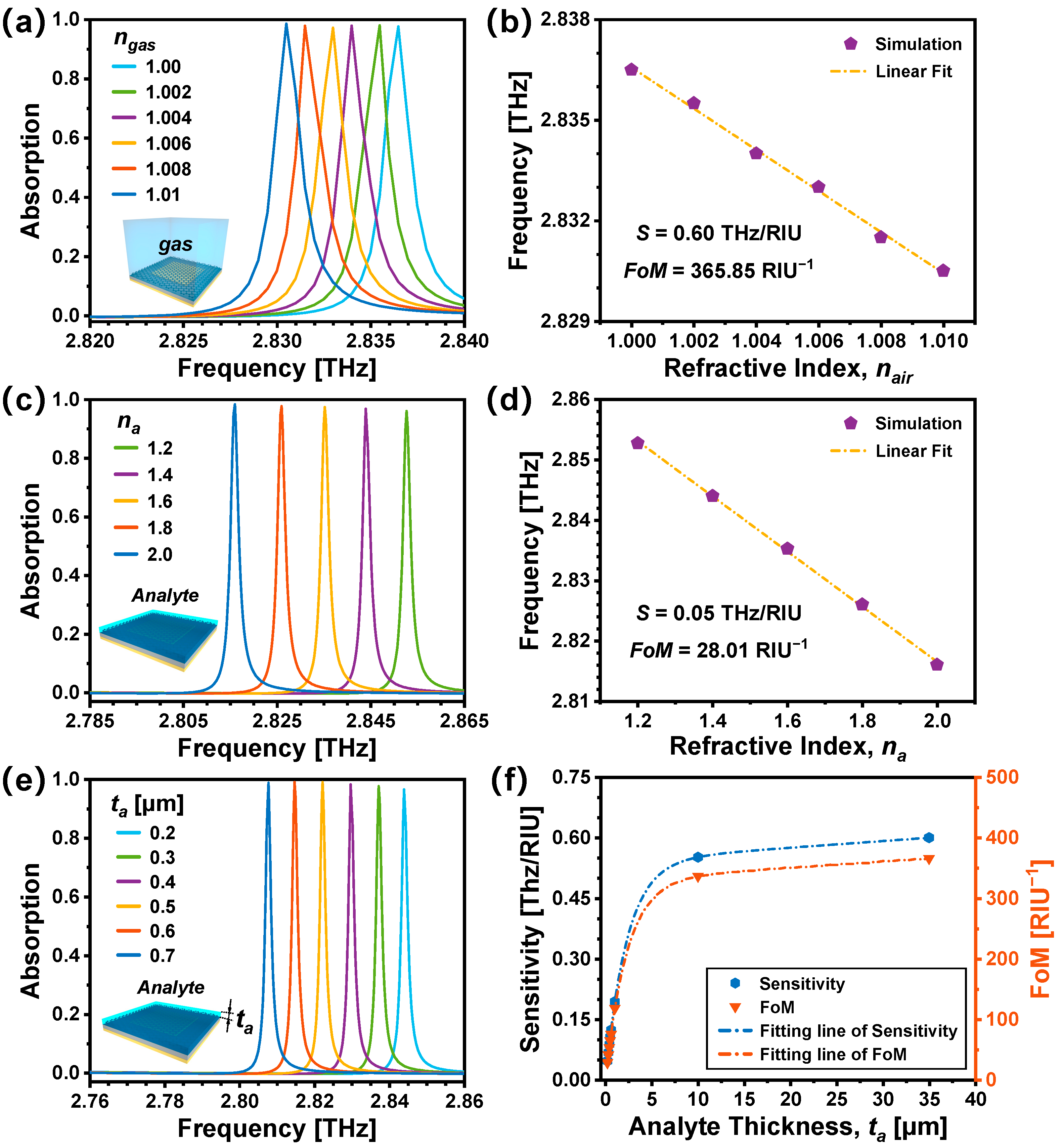
3.3. Sensing Capabilities of the Graphene-Based TMMA
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef]
- Pendry, J. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef]
- Schurig, D.; Mock, J.J.; Justice, B.J.; Cummer, S.A.; Pendry, J.B.; Starr, A.F.; Smith, D.R. Metamaterial electromagnetic cloak at microwave frequencies. Science 2006, 314, 977–980. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Roy Chowdhury, R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef]
- Pendry, J.; Schurig, D.; Smith, D. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Abdulkarim, Y.I.; Mohanty, A.; Acharya, O.P.; Appasani, B.; Khan, M.S.; Mohapatra, S.K.; Muhammadsharif, F.F.; Dong, J. A review on metamaterial absorbers: Microwave to optical. Front. Phys. 2020, 10, 893791. [Google Scholar]
- Chen, C.; Chai, M.; Jin, M.; He, T. Terahertz metamaterial absorbers. Adv. Mater. Technol. 2022, 7, 2101171. [Google Scholar] [CrossRef]
- Carranza, I.E.; Grant, J.P.; Gough, J.; Cumming, D. Terahertz metamaterial absorbers implemented in CMOS technology for imaging applications: Scaling to large format focal plane arrays. IEEE J. Sel. Top. Quant. 2017, 23, 4700508. [Google Scholar]
- Wang, B.; Huang, W.; Wang, L. Ultra-narrow terahertz perfect light absorber based on surface lattice resonance of a sandwich resonator for sensing applications. RSC Adv. 2017, 7, 42956–42963. [Google Scholar] [CrossRef]
- Kazanskiy, N.; Khonina, S.; Butt, M. Recent Development in Metasurfaces: A Focus on Sensing Applications. Nanomaterials 2023, 13, 118. [Google Scholar] [CrossRef]
- Rastgordani, A.; Kashani, Z. Robust design method for metasurface high-sensitivity sensors and absorbers. J. Opt. Soc. Am. B 2020, 37, 2006–2011. [Google Scholar] [CrossRef]
- Wang, J.; Hu, C.; Tian, Q.; Yu, W.; Tian, H.; Li, L.; Liu, J.; Zhou, Z. Ultrahigh-Q and polarization-independent terahertz metamaterial perfect absorber. Plasmonics 2020, 15, 1943–1947. [Google Scholar] [CrossRef]
- Reiten, M.T.; Roy Chowdhury, D.; Zhou, J.; Taylor, A.J.; O’Hara, J.F.; Azad, A.K. Resonance tuning behavior in closely spaced inhomogeneous bilayer metamaterials. Appl. Phys. Lett. 2011, 98, 131105. [Google Scholar] [CrossRef]
- Xie, Q.; Dong, G.; Wang, B.; Huang, W. High-Q Fano resonance in terahertz frequency based on an asymmetric metamaterial resonator. Nanoscale Res. Lett. 2018, 13, 294. [Google Scholar] [CrossRef]
- Mikhailov, S.A.; Ziegler, K. New electromagnetic mode in graphene. Phys. Rev. Lett. 2007, 99, 016803. [Google Scholar] [CrossRef]
- Bonaccorso, F.; Sun, Z.; Hasan, T.; Ferrari, A.C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4, 611–622. [Google Scholar] [CrossRef]
- Sang, M.; Shin, J.; Kim, K.; Yu, K.J. Electronic and thermal properties of graphene and recent advances in graphene based electronics applications. Nanomaterials 2019, 9, 374. [Google Scholar] [CrossRef]
- Oh, J.; Kim, K.; Yeom, G. Graphene doping methods and device applications. J. Nanosci. Nanotechnol. 2014, 14, 1120–1133. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhao, H.; Li, C. Broadband tunable terahertz metasurface absorber based on complementary-wheel-shaped graphene. Opt. Mater. 2020, 109, 110369. [Google Scholar] [CrossRef]
- Chen, F.; Cheng, Y.; Luo, H. A broadband tunable terahertz metamaterial absorber based on single-layer complementary gammadion-shaped graphene. Materials 2020, 13, 860. [Google Scholar] [CrossRef]
- Nagandla, P.; Pokkunuri, P.; Madhav, B. Graphene metasurface based broad band absorber for terahertz sensing applications. Meas. Sens. 2023, 30, 100927. [Google Scholar] [CrossRef]
- Alexandrou, K.; Petrone, N.; Hone, J.; Kymissis, I. Encapsulated graphene fieldeffect transistors for air stable operation. Appl. Phys. Lett. 2015, 106, 113104. [Google Scholar] [CrossRef]
- Li, K.; Ma, X.; Zhang, Z.; Song, J.; Xu, Y.; Song, G. Sensitive refractive index sensing with tunable sensing range and good operation angle-polarization-tolerance using graphene concentric ring arrays. J. Phys. D Appl. Phys. 2014, 47, 405101. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, T.; Wei, J.; Zhang, W.; Wu, K.; Wang, Q. Graphene-enhanced polarization-independent high-Q terahertz metamaterial absorber with tunability for sensing applications. Opt. Commun. 2024, 557, 130311. [Google Scholar] [CrossRef]
- Low, T.; Avouris, P. Graphene plasmonics for terahertz to mid-infrared applications. ACS Nano 2014, 8, 1086–1101. [Google Scholar] [CrossRef]
- Landy, N.I.; Bingham, C.M.; Tyler, T.; Jokerst, N.; Smith, D.R.; Padilla, W.J. Design, theory, and measurement of a polarization-insensitive absorber for terahertz imaging. Phys. Rev. B 2009, 79, 125104. [Google Scholar] [CrossRef]
- Barzegar-Parizi, S.; Ebrahimi, A. Ultrathin, polarization-insensitive multi-band absorbers based on graphene metasurface with THz sensing application. J. Opt. Soc. Amer. B 2020, 37, 2372–2381. [Google Scholar] [CrossRef]
- Rezagholizadeh, Q.; Biabanifard, M.; Borzooei, S. Analytical design of tunable THz refractive index sensor for TE and TM modes using graphene disks. J. Phys. D Appl. Phys. 2020, 53, 295107. [Google Scholar] [CrossRef]
- Ma, S.; Wen, S.; Mi, X.; Zhao, H.; Zhao, J. Bifunctional terahertz sensor based on tunable graphene metamaterial absorber. Opt. Commun. 2023, 532, 129254. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, P.; Mi, X.; Zhao, H. Highly sensitive terahertz sensor based on graphene metamaterial absorber. Opt. Commun. 2023, 528, 129021. [Google Scholar] [CrossRef]
- Jia, Y.; Yin, H.; Yao, H.; Wang, J.; Fan, C. Realization of multi-band perfect absorber in graphene based metal-insulator-metal metamaterials. Results Phys. 2021, 25, 104301. [Google Scholar] [CrossRef]
- Alves, F.; Kearney, B.; Grbovic, D.; Lavrik, N.V.; Karunasiri, G. Strong terahertz absorption using SiO2/Al based metamaterial structures. Appl. Phys. Lett. 2012, 100, 111104. [Google Scholar] [CrossRef]
- Yoon, M.; Kim, C.; Kim, J.; Lee, H.; Kim, K. Surface properties of CVD-grown graphene transferred by wet and dry transfer processes. Sensors 2022, 22, 3944. [Google Scholar] [CrossRef]
- Ye, Z.; Wu, P.; Wang, H.; Jiang, S.; Huang, M.; Lei, D.; Wu, F. Multimode tunable terahertz absorber based on a quarter graphene disk structure. Results Phys. 2023, 48, 106420. [Google Scholar] [CrossRef]
- Chen, M.; Xiao, Z. Metal-graphene hybrid terahertz metamaterial based on dynamically switchable electromagnetically induced transparency effect and its sensing performance. Diam. Relat. Mater. 2022, 124, 108935. [Google Scholar] [CrossRef]
- Xu, K.; Li, J.; Zhang, A.; Chen, Q. Tunable multi-band terahertz absorber using a single-layer square graphene ring structure with T-shaped graphene strips. Opt. Express 2020, 28, 11482–11492. [Google Scholar] [CrossRef]
- Han Lyn, F.; Nur Hanani, Z. Graphene-based polymer nanocomposites in food packaging and factors afecting the behaviour of graphene-based materials: A review. J. Nanopart. Res. 2022, 24, 179. [Google Scholar] [CrossRef]
- Banerjee, S.; Nath, U.; Dutta, P.; Jha, A.V.; Appasani, B.; Bizon, N. A theoretical terahertz metamaterial absorber structure with a high quality factor using two circular ring resonators for biomedical sensing. Inventions 2021, 6, 78. [Google Scholar] [CrossRef]
- Wang, D.; Xu, K.; Luo, S.; Cui, Y.; Zhang, L.; Cui, J. A high Q-factor dual-band terahertz metamaterial absorber and its sensing characteristics. Nanoscale 2023, 15, 3398–3407. [Google Scholar] [CrossRef]
- Chen, T.; Zhao, R.; Wang, B. Theoretical investigation of a simple design of triple-band terahertz metamaterial absorber for high-Q sensing. Appl. Sci. 2019, 9, 1410. [Google Scholar] [CrossRef]
- Qin, F.; Chen, Z.; Chen, X.; Yi, Z.; Yao, W.; Duan, T.; Wu, P.; Yang, H.; Li, G.; Yi, Y. A tunable triple-band near-infrared metamaterial absorber based on Au nano-cuboids array. Nanomaterials 2020, 10, 207. [Google Scholar] [CrossRef]
- Zou, H.; Cheng, Y. Design of a six-band terahertz metamaterial absorber for temperature sensing application. Opt. Mater. 2019, 88, 674–679. [Google Scholar] [CrossRef]
- Xu, Y.; Qiu, P.; Mao, J.; Jile, H.; Jiang, P. Dual-band narrow-band absorber with perfect absorption peaks in mid-infrared and near-infrared based on surface plasmon resonance. Diam. Relat. Mater. 2023, 132, 109624. [Google Scholar] [CrossRef]
- Zhou, F.; Qin, F.; Yi, Z.; Yao, W.; Liu, Z.; Wu, X.; Wu, P. Ultra-wideband and wide-angle perfect solar energy absorber based on Ti nanorings surface plasmon resonance. Phys. Chem. Chem. Phys. 2021, 23, 17041–17048. [Google Scholar] [CrossRef]
- Guo, X.; Hu, H.; Zhu, X.; Yang, X.; Dai, Q. Higher order Fano graphene metamaterials for nanoscale optical sensing. Nanoscale 2017, 9, 14998–15004. [Google Scholar] [CrossRef]
- Appasani, B.; Srinivasulu, A.; Ravariu, C. A high Q terahertz metamaterial absorber using concentric elliptical ring resonators for harmful gas sensing applications. Def. Technol. 2023, 22, 69–73. [Google Scholar] [CrossRef]
- Shruti; Pahadsingh, S.; Appasani, B.; Srinivasulu, A.; Bizon, N.; Thounthong, P. A reconfigurable terahertz metamaterial absorber for gas sensing applications. Crystals 2023, 13, 158. [Google Scholar] [CrossRef]
- Yahiaoui, R.; Strikwerda, A.C.; Jepsen, P.U. Terahertz plasmonic structure with enhanced sensing capabilities. IEEE Sens. J. 2016, 16, 2484–2488. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, K. Dynamically switchable terahertz absorber based on a hybrid metamaterial with vanadium dioxide and graphene. J. Opt. Soc. Amer. B 2021, 38, 3425–3434. [Google Scholar] [CrossRef]
- Sadafi, M.M.; Karami, H.; Hosseini, M. A tunable hybrid graphene-metal metamaterial absorber for sensing in the THz regime. Curr. Appl. Phys. 2021, 31, 132–140. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T.; Zeng, B.; Zhang, H.; Lv, H.; Huang, X.; Zhang, W.; Azad, A.K. A graphene based tunable terahertz sensor with double Fano resonances. Nanoscale 2015, 7, 12682–12688. [Google Scholar] [CrossRef]

| Structure | Year | Frequency (THz) | FoM (RIU−1) | Q Factor | Ref. |
|---|---|---|---|---|---|
| Monolayer graphene ring | 2021 | 5.55 | 8.75 | 27.75 | [51] |
| Graphene and Au SRR | 2021 | 2.5 | 9.48 | 49.2 | [52] |
| Graphene disks | 2020 | 5.9 | 5.3 | 50 | [29] |
| Circular graphene disks | 2015 | 9.01 | 6.57 | 59 | [53] |
| Graphene disks | 2020 | 6 | 24.5 | 80 | [30] |
| Graphene and InSb cylinder | 2023 | 8.53 | 9.65 | 59.53 | [31] |
| Graphene layer with circular holes | 2023 | 2.372 | 64.62 | 179.95 | [32] |
| Al resonators with unpatterned graphene | 2.84 | 365.85 | 1730 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Sun, G.; Wei, J.; Miao, Y.; Zhang, W.; Wu, K.; Wang, Q. Ultrahigh-Q Polarization-Independent Terahertz Metamaterial Absorber Using Pattern-Free Graphene for Sensing Applications. Nanomaterials 2024, 14, 605. https://doi.org/10.3390/nano14070605
Chen Y, Sun G, Wei J, Miao Y, Zhang W, Wu K, Wang Q. Ultrahigh-Q Polarization-Independent Terahertz Metamaterial Absorber Using Pattern-Free Graphene for Sensing Applications. Nanomaterials. 2024; 14(7):605. https://doi.org/10.3390/nano14070605
Chicago/Turabian StyleChen, Youxin, Guotao Sun, Jiang Wei, Yan Miao, Wenqian Zhang, Kaiyu Wu, and Qingkang Wang. 2024. "Ultrahigh-Q Polarization-Independent Terahertz Metamaterial Absorber Using Pattern-Free Graphene for Sensing Applications" Nanomaterials 14, no. 7: 605. https://doi.org/10.3390/nano14070605
APA StyleChen, Y., Sun, G., Wei, J., Miao, Y., Zhang, W., Wu, K., & Wang, Q. (2024). Ultrahigh-Q Polarization-Independent Terahertz Metamaterial Absorber Using Pattern-Free Graphene for Sensing Applications. Nanomaterials, 14(7), 605. https://doi.org/10.3390/nano14070605





