First-Principles Prediction of High and Low Resistance States in Ta/h-BN/Ta Atomristor
Abstract
:1. Introduction
2. Computational Methods
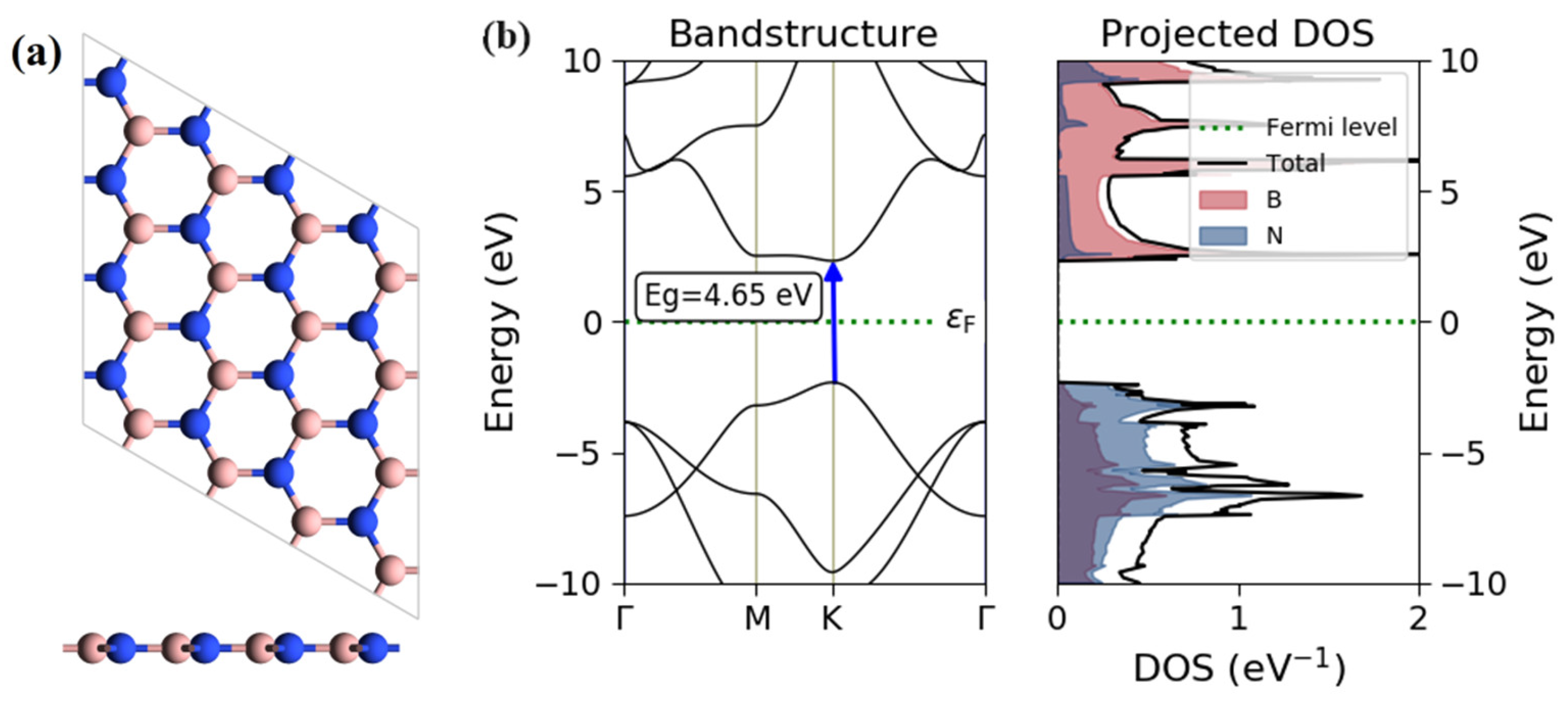
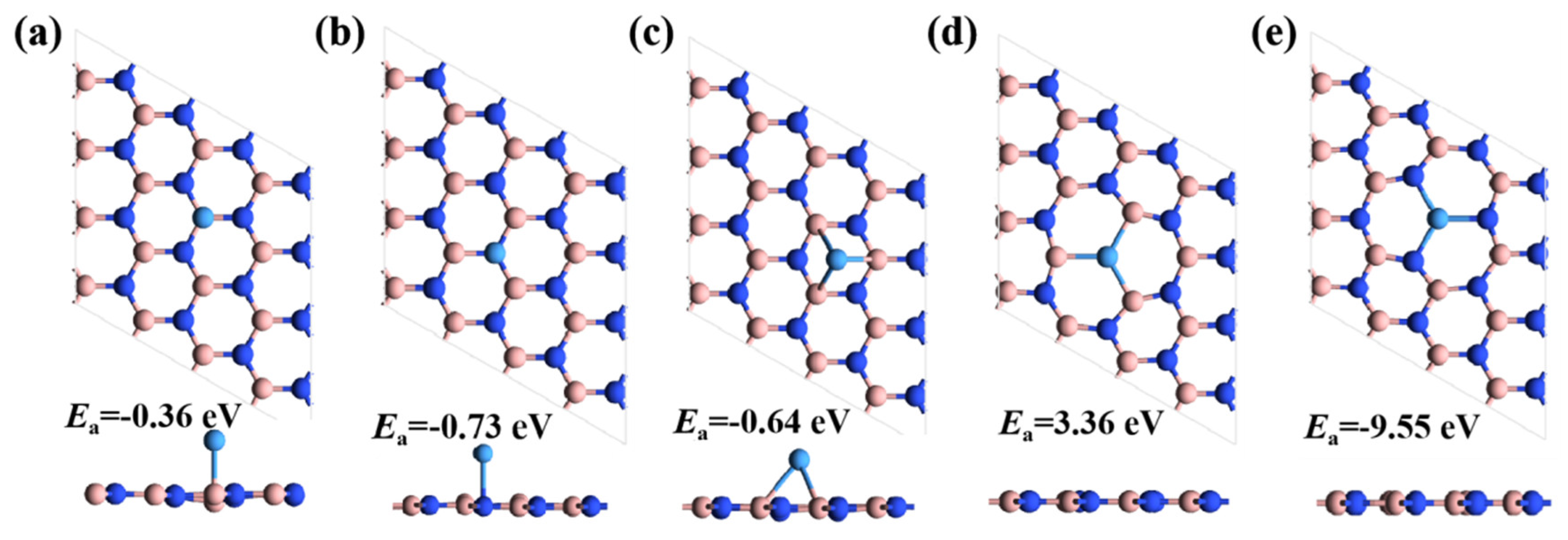
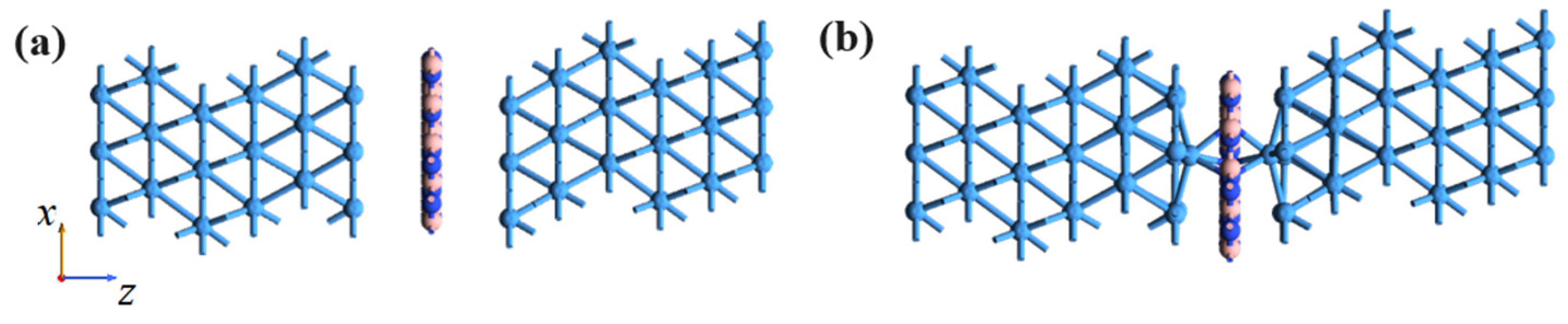
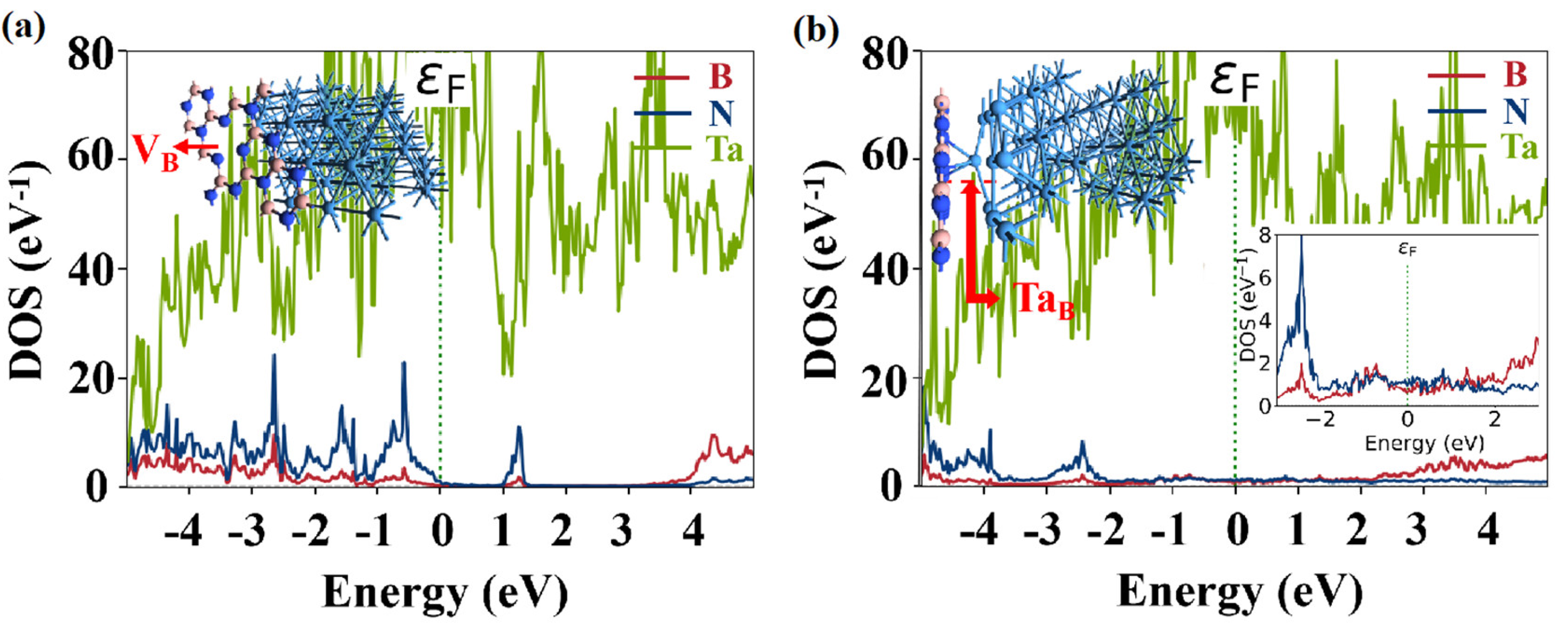
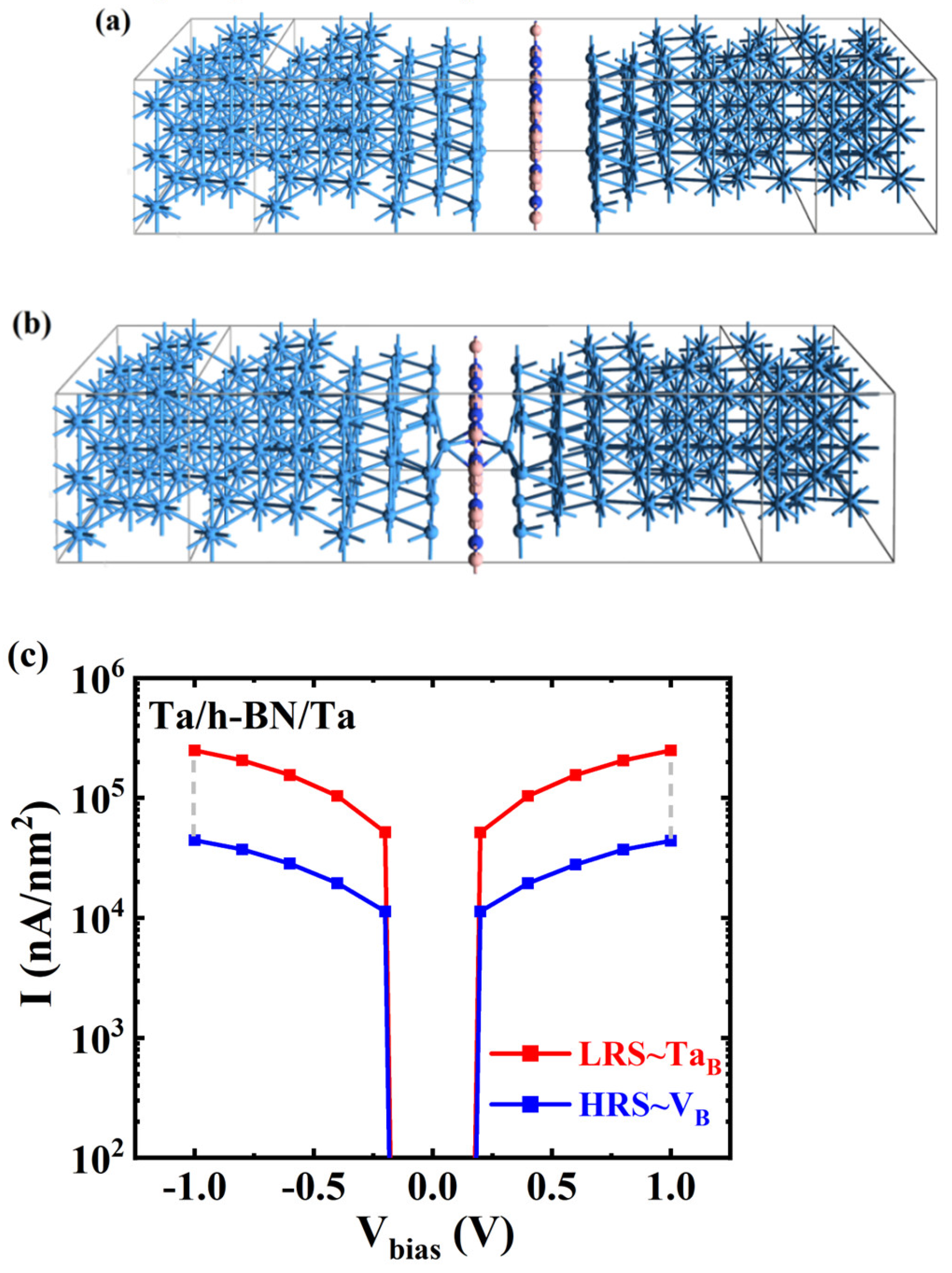
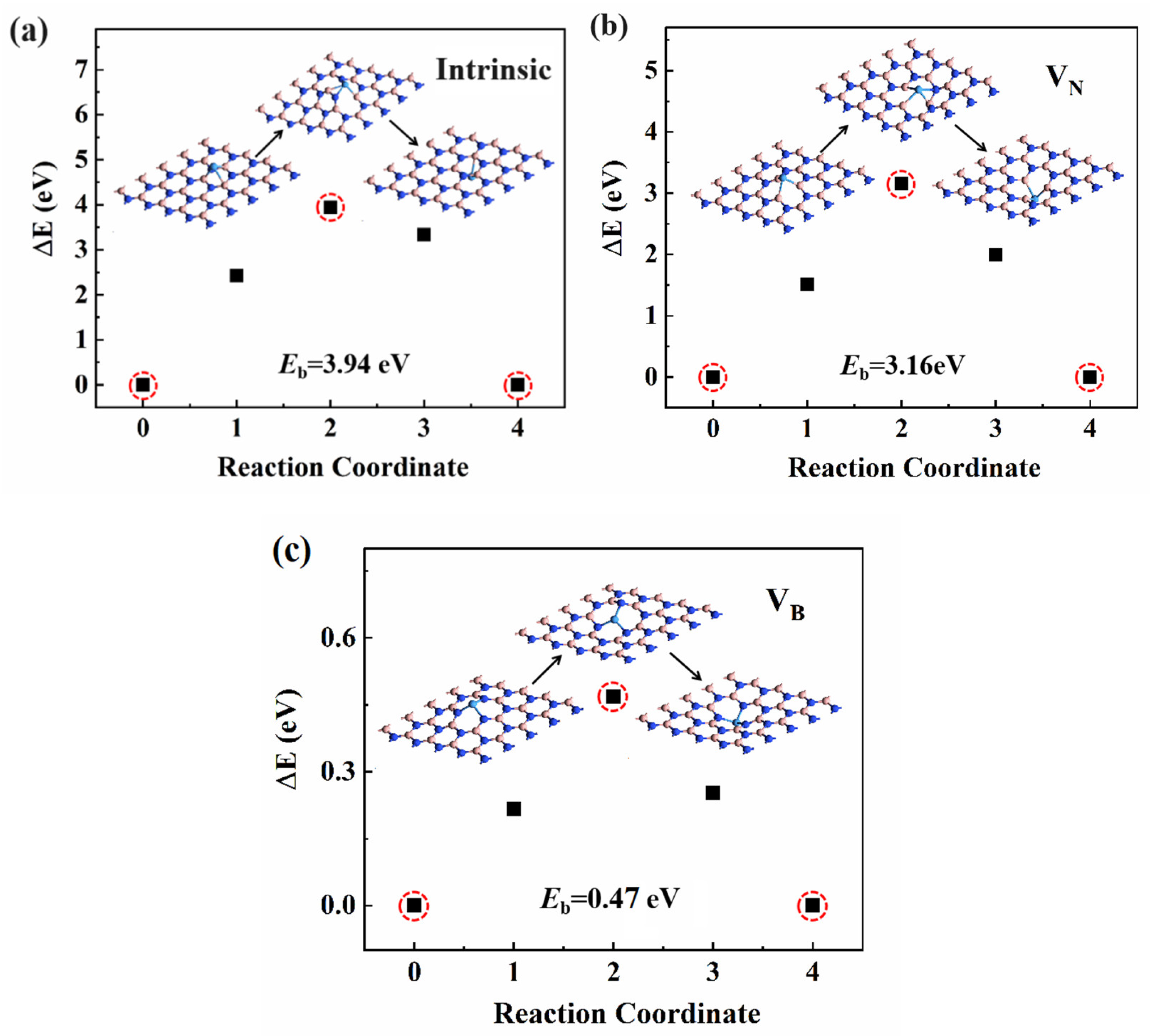
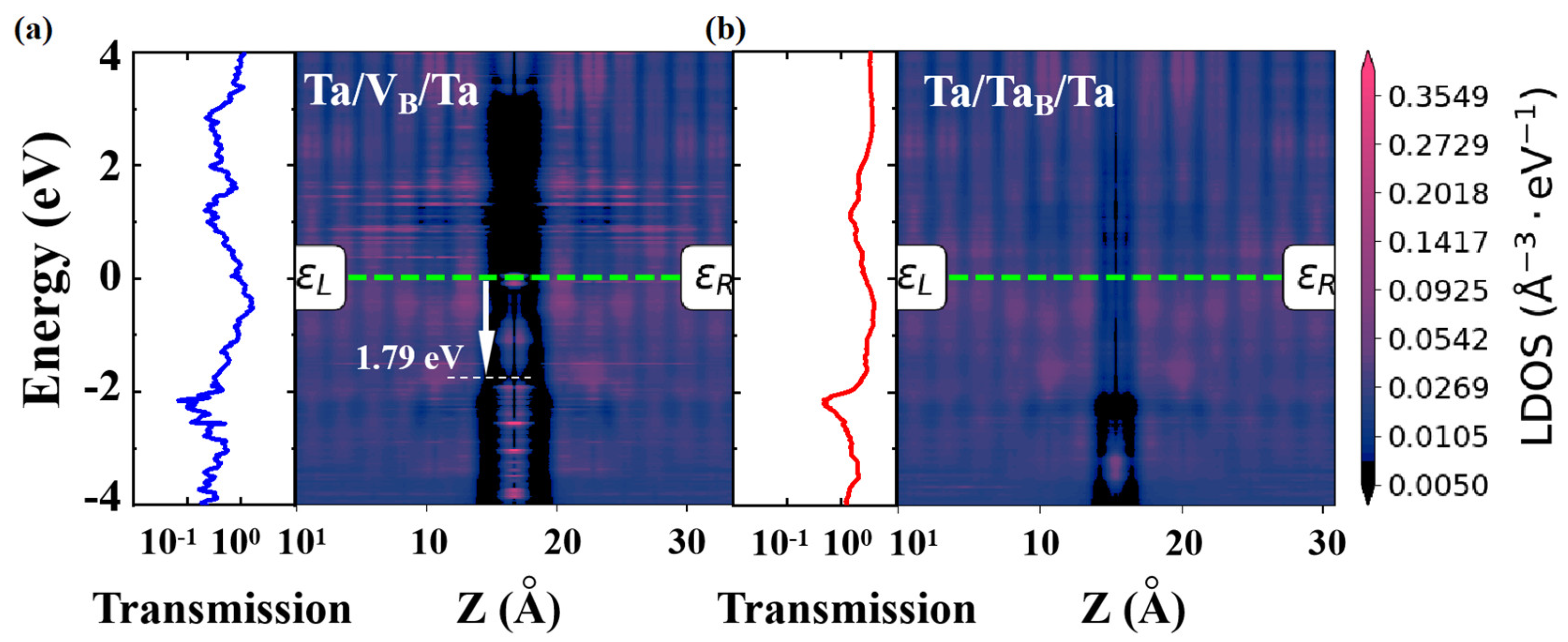
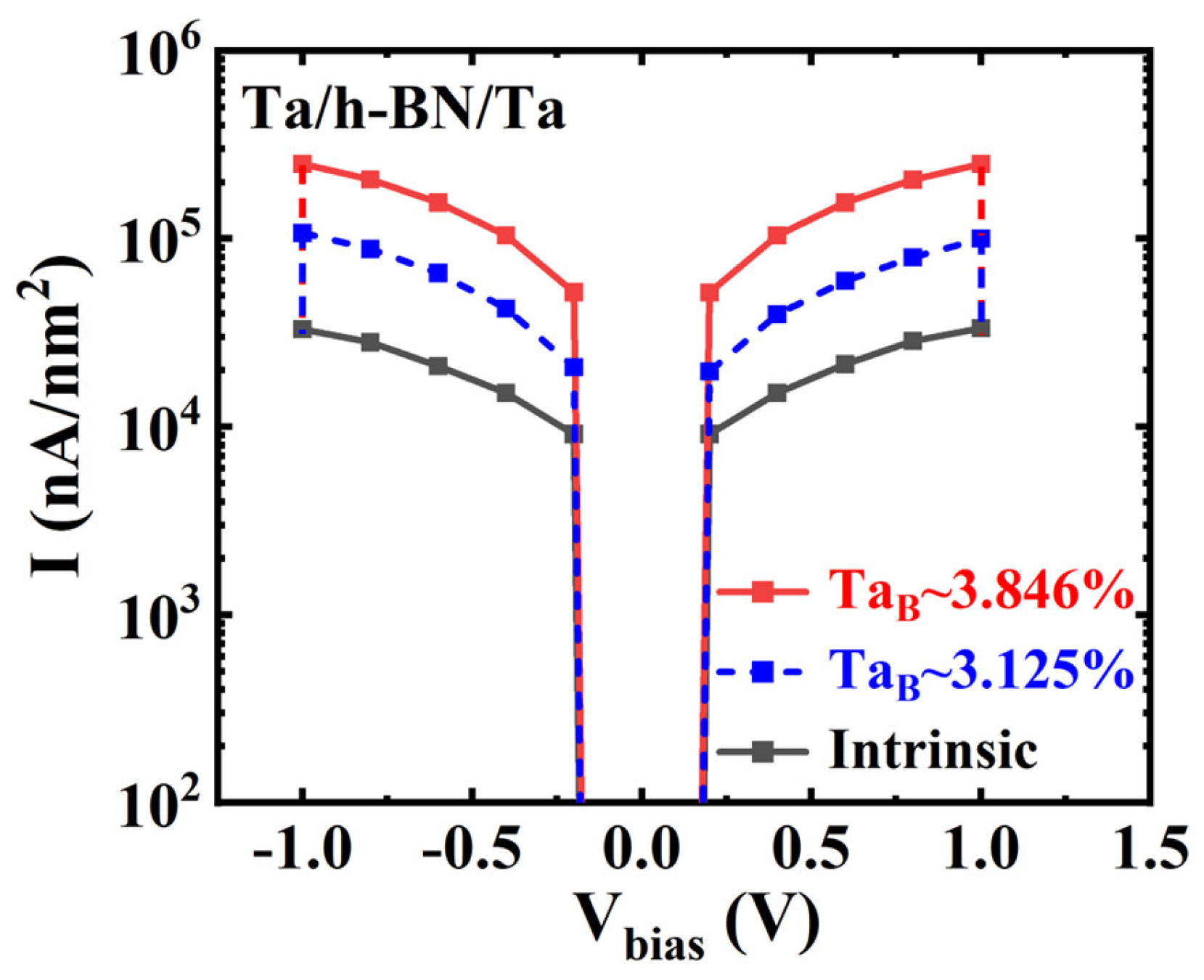
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wong, H.S.P.; Salahuddin, S. Memory leads the way to better computing. Nat. Nanotechnol. 2015, 10, 191–194. [Google Scholar] [CrossRef]
- Akinwande, D.; Huyghebaert, C.; Wang, C.H.; Serna, M.I.; Goossens, S.; Li, L.J.; Wong, H.S.P.; Koppens, F.H.L. Graphene and two-dimensional materials for silicon technology. Nature 2019, 573, 507–518. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Cai, S.; Pan, C.; Wang, C.; Lian, X.; Zhuo, Y.; Xu, K.; Cao, T.; Pan, X.; Wang, B.; et al. Robust memristors based on layered two-dimensional materials. Nat. Electron. 2018, 1, 130–136. [Google Scholar] [CrossRef]
- Xu, R.; Jang, H.; Lee, M.-H.; Amanov, D.; Cho, Y.; Kim, H.; Park, S.; Shin, H.-J.; Ham, D. Vertical MoS2 double-layer memristor with electrochemical metallization as an atomic-scale synapse with switching thresholds approaching 100 mV. Nano Lett. 2019, 19, 2411–2417. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, H.; Krylyuk, S.; Milligan, C.A.; Zhu, Y.; Zemlyanov, D.Y.; Bendersky, L.A.; Burton, B.P.; Davydov, A.V.; Appenzeller, J. Electric-field induced structural transition in vertical MoTe2-and Mo1-xWxTe2-based resistive memories. Nat. Mater. 2019, 18, 55–61. [Google Scholar] [CrossRef]
- Sangwan, V.K.; Hersam, M.C. Neuromorphic nanoelectronic materials. Nat. Nanotechnol. 2020, 15, 517–528. [Google Scholar] [CrossRef]
- Chand, U.; Huang, K.-C.; Huang, C.-Y.; Ho, C.-H.; Lin, C.-H.; Tseng, T.-Y. Investigation of thermal stability and reliability of HfO2 based resistive random access memory devices with cross-bar structure. J. Appl. Phys. 2015, 117, 184105. [Google Scholar] [CrossRef]
- Li, C.; Gao, B.; Yao, Y.; Guan, X.X.; Shen, X.; Wang, Y.G.; Huang, P.; Liu, L.F.; Liu, X.Y.; Li, J.J.; et al. Direct Observations of nanofilament evolution in switching processes in HfO2-based resistive random access memory by in situ TEM studies. Adv. Mater. 2017, 29, 1602976. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.Y.; Kamiya, K.; Magyari-Köpe, B.; Niwa, M.; Nishi, Y.; Shiraishi, K. Charge-dependent oxygen vacancy diffusion in Al2O3-based resistive random access memories. Appl. Phys. Lett. 2013, 103, 093504. [Google Scholar] [CrossRef]
- Jeong, H.Y.; Lee, J.Y.; Choi, S.Y. Interface-engineered amorphous TiO2-based resistive memory devices. Adv. Funct. Mater. 2010, 20, 3912–3917. [Google Scholar] [CrossRef]
- Kamiya, K.; Yang, M.Y.; Nagata, T.; Park, S.-G.; Magyari-Köpe, B.; Chikyow, T.; Yamada, K.; Niwa, M.; Nishi, Y.; Shiraishi, K. Generalized mechanism of the resistance switching in binary-oxide-based resistive random-access memories. Phys. Rev. B 2013, 87, 155201. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Lee, H.Y.; Yu, S.; Chen, Y.S.; Wu, Y.; Chen, P.S.; Lee, B.; Chen, F.T.; Tsai, M.J. Metal-oxide RRAM. Proc. IEEE 2012, 100, 1951–1970. [Google Scholar] [CrossRef]
- Zhou, F.; Chang, Y.F.; Byun, K.; Fowler, B.; Lee, J.C. Characterization of external resistance effect and performance optimization in unipolar-type SiOx-based resistive switching memory. Appl. Phys. Lett. 2014, 105, 133501. [Google Scholar] [CrossRef]
- Chen, Y.C.; Hu, S.T.; Lin, C.Y.; Fowler, B.; Huang, H.C.; Lin, C.C.; Kim, S.; Chang, Y.F.; Lee, J.C. Graphite-based selectorless RRAM: Improvable intrinsic nonlinearity for array applications. Nanoscale 2018, 10, 15608–15614. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lin, C.C.; Hu, S.T.; Lin, C.Y.; Fowler, B.; Lee, J. A novel resistive switching identification method through relaxation characteristics for sneak-path-constrained selectorless RRAM application. Sci. Rep. 2019, 9, 12420. [Google Scholar] [CrossRef]
- Bessonov, A.A.; Kirikova, M.N.; Petukhov, D.I.; Allen, M.; Ryhänen, T.; Bailey, M.J.A. Layered memristive and memcapacitive switches for printable electronics. Nat. Mater. 2015, 14, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Ge, R.; Wu, X.; Liang, L.; Hus, S.; Gu, Y.; Okogbue, E.; Chou, H.; Shi, J.; Zhang, Y.; Banerjee, S.K.; et al. A library of atomically thin 2D materials featuring the conductive-point resistive switching phenomenon. Adv. Mater. 2020, 33, 2007792. [Google Scholar] [CrossRef] [PubMed]
- Ge, R.; Wu, X.; Kim, M.; Shi, J.; Sonde, S.; Tao, L.; Zhang, Y.; Lee, J.C.; Akinwande, D. Atomristor: Nonvolatile resistance switching in atomic sheets of transition metal dichalcogenides. Nano Lett. 2018, 18, 434–441. [Google Scholar] [CrossRef]
- Son, D.; Chae, S.I.; Kim, M.; Choi, M.K.; Yang, J.; Park, K.; Kale, V.S.; Koo, J.H.; Choi, C.; Lee, M.; et al. Colloidal synthesis of uniform-sized molybdenum disulfide nanosheets for wafer-scale flexible nonvolatile memory. Adv. Mater. 2016, 28, 9326–9332. [Google Scholar] [CrossRef]
- Kim, M.; Ge, R.; Wu, X.; Lan, X.; Tice, J.; Lee, J.C.; Akinwande, D. Zero-static power radio-frequency switches based on MoS2 atomristors. Nat. Commun. 2018, 9, 2524. [Google Scholar] [CrossRef]
- Hus, S.M.; Ge, R.; Chen, P.A.; Liang, L.; Donnelly, G.E.; Ko, W.; Huang, F.; Chiang, M.-H.; Li, A.-P.; Akinwande, D. Observation of single-defect memristor in an MoS2 atomic sheet. Nat. Nanotechnol. 2021, 16, 58–62. [Google Scholar] [CrossRef]
- Pan, C.; Ji, Y.; Xiao, N.; Hui, F.; Tang, K.; Guo, Y.; Xie, X.; Puglisi, F.M.; Larcher, L.; Miranda, E.; et al. Coexistence of grain-boundaries-assisted bipolar and threshold resistive switching in multilayer hexagonal boron nitride. Adv. Funct. Mater. 2017, 27, 1604811. [Google Scholar] [CrossRef]
- Wu, X.; Ge, R.; Chen, P.-A.; Chou, H.; Zhang, Z.; Zhang, Y.; Banerjee, S.; Chiang, M.H.; Lee, J.C.; Akinwande, D. Thinnest nonvolatile memory based on monolayer h-BN. Adv. Mater. 2019, 31, 1806790. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Cui, Z.J.; He, Y.W.; Tian, H.; Yang, T.C.; Shou, C.Y.; Liu, J.L. Resistive switching properties of monolayer h-BN atomristors with different electrodes. Appl. Phys. Lett. 2022, 120, 173104. [Google Scholar] [CrossRef]
- Li, X.D.; Chen, N.K.; Wang, B.Q.; Li, X.B. Conductive mechanism in memristor at the thinnest limit: The case based on monolayer boron nitride. Appl. Phys. Lett. 2022, 121, 073505. [Google Scholar] [CrossRef]
- Ranjan, A.; Raghavan, N.; O’Shea, S.J.; Mei, S.; Bosman, M.; Shubhakar, K.; Pey, K.L. Conductive atomic force microscope study of bipolar and threshold resistive switching in 2D hexagonal boron nitride films. Sci. Rep. 2018, 8, 2854. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Cheng, S.; Qin, L.; Zhang, X.; Xie, B.; Zhang, Y.; Jie, W. Low-power memristor based on two-dimensional materials. J. Phys. Chem. Lett. 2022, 13, 7130–7138. [Google Scholar] [CrossRef]
- Lu, X.F.; Zhang, Y.; Wang, N.; Luo, S.; Peng, K.; Wang, L.; Chen, H.; Gao, W.; Chen, X.H.; Bao, Y.; et al. Exploring low power and ultrafast memristor on p-type van der waals SnS. Nano Lett. 2021, 21, 8800–8807. [Google Scholar] [CrossRef] [PubMed]
- Karpov, V.G.; Niraula, D. Resistive switching in nano-structures. Sci. Rep. 2018, 8, 12212. [Google Scholar] [CrossRef]
- Song, L.; Ci, L.; Lu, H.; Sorokin, P.B.; Jin, C.H.; Ni, J.; Kvashnin, A.G.; Kvashnin, D.G.; Lou, J.; Yakobson, B.I.; et al. Large scale growth and characterization of atomic hexagonal boron nitride layers. Nano Lett. 2010, 10, 3209–3215. [Google Scholar] [CrossRef]
- Wang, L.; Xu, X.Z.; Zhang, L.N.; Qiao, R.X.; Wu, M.H.; Wang, Z.C.; Zhang, S.; Liang, J.; Zhang, Z.H.; Zhang, Z.B.; et al. Epitaxial growth of a 100-square-centimetre singlecrystal hexagonal boron nitride monolayer on copper. Nature 2019, 570, 91–95. [Google Scholar] [CrossRef] [PubMed]
- He, Y.W.; Tian, H.; Das, P.; Cui, Z.J.; Pena, P.; Chiang, I.; Shi, W.H.; Xu, L.; Li, Y.; Yang, T.C.; et al. Growth of high-quality hexagonal boron nitride single-layer filmson carburized Ni substrates for metal-insulator-metal tunneling devices. Appl. Mater. Interfaces 2020, 12, 35318–35327. [Google Scholar] [CrossRef]
- Yang, S.J.; Dahan, M.M.; Levit, O.; Makal, F.; Peterson, P.; Alikpala, J.; Teja Nibhanupudi, S.S.; Luth, J.C.; Banerjee, S.K.; Kim, M.; et al. Reconfigurable low-voltage hexagonal boron nitride nonvolatile switches for millimeter-wave wireless communications. Nano Lett. 2023, 23, 1152–1158. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstiche, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Mat. 2020, 32, 015901. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space GTassian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641. [Google Scholar] [CrossRef]
- Huang, B.; Lee, H. Defect and impurity properties of hexagonal boron nitride: A first-principles calculation. Phys. Rev. B 2012, 86, 245406. [Google Scholar] [CrossRef]
- Kim, K.K.; Hsu, A.; Jia, X.; Jia, X.T.; Kim, S.M.; Shi, Y.M.; Hofmann, M.; Nezich, D.; Joaquin, F.; Nieva, R.; et al. Synthesis of monolayer hexagonal boron nitride on Cu foil using chemical vapor deposition. Nano Lett. 2012, 12, 161–166. [Google Scholar] [CrossRef]
- Guo, Y.Z.; Liu, D.; Robertson, J. 3D behavior of Schottky barriers of 2D transition-metal dichalcogenides. ACS Appl. Mater. Interfaces 2015, 7, 25709–25715. [Google Scholar] [CrossRef]
- Szczęśniak, D.; Hoehn, R.D.; Kais, S. Canonical Schottky barrier heights of transition metal dichalcogenide monolayers in contact with a metal. Phys. Rev. B 2018, 97, 195315. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Liu, S.Q.; Li, Q.H.; Quhe, R.G.; Yang, C.; Guo, Y.; Zhang, X.Y.; Pan, Y.Y.; Li, J.Z.; Zhang, H.; et al. Schottky barrier heights in two-dimensional field-effect transistors: From theory to experiment. Rep. Prog. Phys. 2021, 84, 056501. [Google Scholar] [CrossRef] [PubMed]
- Szczęśniak, D.; Ennaoui, A.; Ahzi, S. Complex band structures of transition metal. J. Phys. Condens. Mater. 2016, 28, 355301. [Google Scholar] [CrossRef] [PubMed]
- Reuter, M.G. A unified perspective of complex band structure: Interpretations, formulations, and applications. J. Phys. Condens. Mater. 2017, 29, 053001. [Google Scholar] [CrossRef]
- Huang, J.L.; Sung, Y.E.; Lieber, C.M. Field-induced surface modifcation on the atomic scale by scanning tunneling microscopy. Appl. Phys. Lett. 1992, 61, 1528–1530. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Lang, S.; Zhang, W.; Song, S.; Lyu, J.; Gong, J. First-Principles Prediction of High and Low Resistance States in Ta/h-BN/Ta Atomristor. Nanomaterials 2024, 14, 612. https://doi.org/10.3390/nano14070612
He L, Lang S, Zhang W, Song S, Lyu J, Gong J. First-Principles Prediction of High and Low Resistance States in Ta/h-BN/Ta Atomristor. Nanomaterials. 2024; 14(7):612. https://doi.org/10.3390/nano14070612
Chicago/Turabian StyleHe, Lan, Shuai Lang, Wei Zhang, Shun Song, Juan Lyu, and Jian Gong. 2024. "First-Principles Prediction of High and Low Resistance States in Ta/h-BN/Ta Atomristor" Nanomaterials 14, no. 7: 612. https://doi.org/10.3390/nano14070612
APA StyleHe, L., Lang, S., Zhang, W., Song, S., Lyu, J., & Gong, J. (2024). First-Principles Prediction of High and Low Resistance States in Ta/h-BN/Ta Atomristor. Nanomaterials, 14(7), 612. https://doi.org/10.3390/nano14070612




