Enhanced Imaging in Scanning Transmission X-Ray Microscopy Assisted by Ptychography
Abstract
1. Introduction
2. Principle and Methodology
2.1. Fundamentals of Deconvolution
2.2. Image Enhancement Strategy
2.2.1. Accurate Reconstruction Strategy for Illumination Spot Based on Ptychography
2.2.2. Setup of Deconvolution Parameter
- 1.
- Intensity compression of reconstructed focal spot
- 2.
- Noise-to-signal ratio (NSR)
- 3.
- Evaluation of image quality
- 4.
- Pixel matching
3. Results
3.1. Accurate Reconstruction of Focal Spot and STXM Image Enhancement with the Recovered Spot
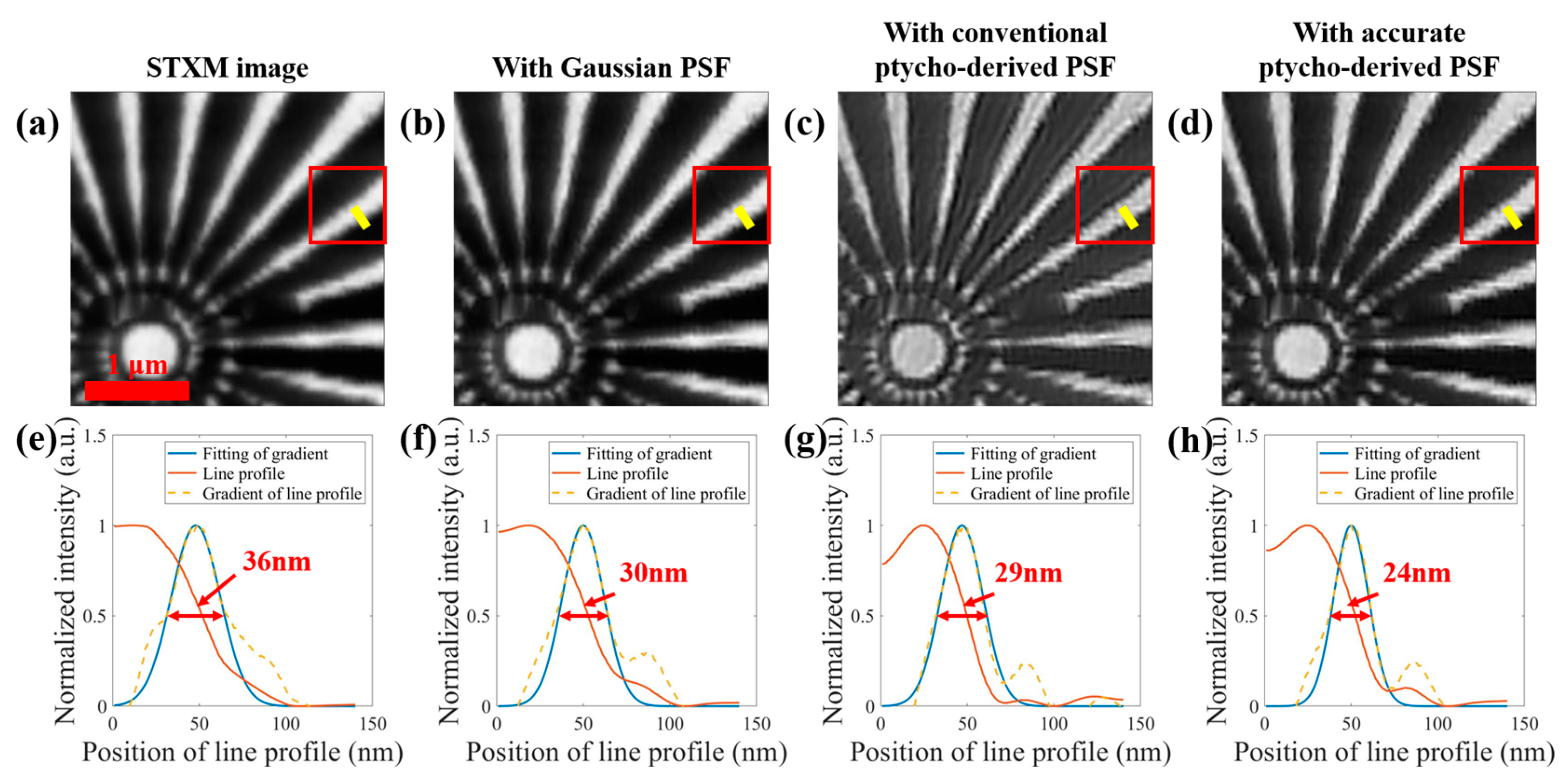
3.2. STXM Image Enhancement with Different Inverse Filters Based on Accurately-Recovered Focal Spot
3.3. Enhancing STXM Images with Different Scan Step Sizes
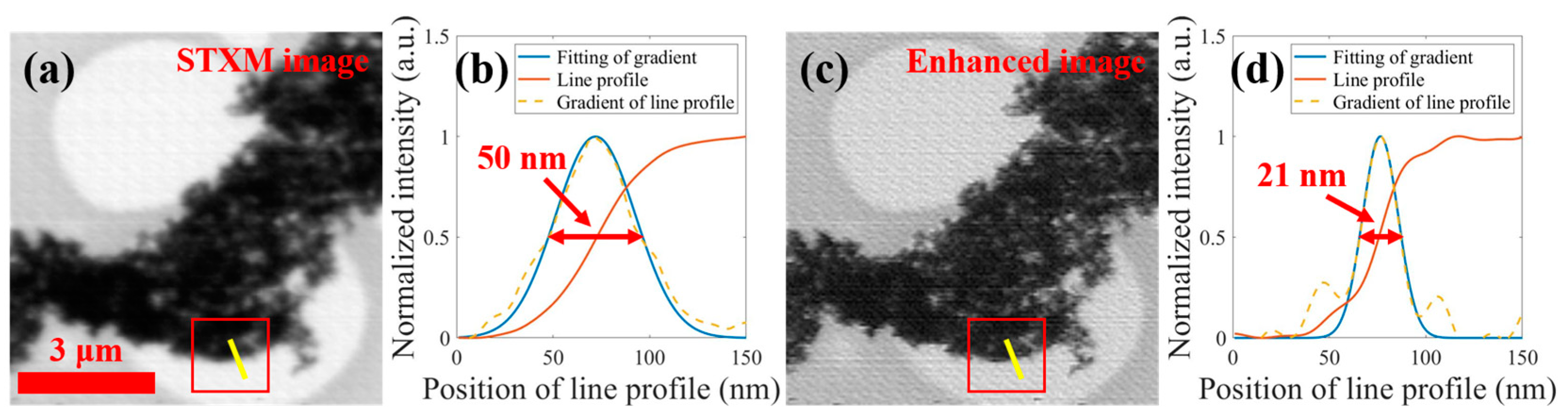
3.4. Enhancing STXM Images at Different Energies (Stack Data)
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Groot, F.M.F.; De Smit, E.; Van Schooneveld, M.M.; Aramburo, L.R.; Weckhuysen, B.M. In-situ Scanning Transmission X-Ray Microscopy of Catalytic Solids and Related Nanomaterials. ChemPhysChem 2010, 11, 951–962. [Google Scholar] [CrossRef]
- Hitchcock, A.P.; Dynes, J.J.; Lawrence, J.R.; Obst, M.; Swerhone, G.D.W.; Korber, D.R.; Leppard, G.G. Soft X-ray Spectromicroscopy of Nickel Sorption in a Natural River Biofilm. Geobiology 2009, 7, 432–453. [Google Scholar] [CrossRef] [PubMed]
- Kilcoyne, A.L.D.; Tyliszczak, T.; Steele, W.F.; Fakra, S.; Hitchcock, P.; Franck, K.; Anderson, E.; Harteneck, B.; Rightor, E.G.; Mitchell, G.E.; et al. Interferometer-Controlled Scanning Transmission X-Ray Microscopes at the Advanced Light Source. J. Synchrotron Radiat. 2003, 10, 125–136. [Google Scholar] [CrossRef]
- Ade, H.; Smith, A.P.; Zhang, H.; Zhuang, G.R.; Kirz, J.; Rightor, E.; Hitchcock, A. X-Ray Spectromicroscopy of Polymers and Tribological Surfaces at Beamline X1A at the NSLS. J. Electron Spectrosc. Relat. Phenom. 1997, 84, 53–72. [Google Scholar] [CrossRef]
- Ohigashi, T.; Nagasaka, M.; Horigome, T.; Kosugi, N.; Rosendahl, S.M.; Hitchcock, A.P. Development of In-Situ Sample Cells for Scanning Transmission X-Ray Microscopy. AIP Conf. Proc. 2016, 1741, 050002. [Google Scholar] [CrossRef]
- Warwick, T.; Franck, K.; Kortright, J.B.; Meigs, G.; Moronne, M.; Myneni, S.; Rotenberg, E.; Seal, S.; Steele, W.F.; Ade, H.; et al. A Scanning Transmission X-Ray Microscope for Materials Science Spectromicroscopy at the Advanced Light Source. Rev. Sci. Instrum. 1998, 69, 2964–2973. [Google Scholar] [CrossRef]
- Horowitz, P.; Howell, J.A. A Scanning X-Ray Microscope Using Synchrotron Radiation. Science 1972, 178, 608–611. [Google Scholar] [CrossRef]
- Johansson, G.A.; Tyliszczak, T.; Mitchell, G.E.; Keefe, M.H.; Hitchcock, A.P. Three-Dimensional Chemical Mapping by Scanning Transmission X-Ray Spectromicroscopy. J. Synchrotron Radiat. 2007, 14, 395–402. [Google Scholar] [CrossRef] [PubMed]
- Rösner, B.; Finizio, S.; Koch, F.; Döring, F.; Guzenko, V.A.; Langer, M.; Kirk, E.; Watts, B.; Meyer, M.; Loroña Ornelas, J.; et al. Soft X-Ray Microscopy with 7 nm Resolution. Optica 2020, 7, 1602. [Google Scholar] [CrossRef]
- Gianoncelli, A.; Bonanni, V.; Gariani, G.; Guzzi, F.; Pascolo, L.; Borghes, R.; Billè, F.; Kourousias, G. Soft X-Ray Microscopy Techniques for Medical and Biological Imaging at TwinMic—Elettra. Appl. Sci. 2021, 11, 7216. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, J.; Cutler, J.; Hu, E.; Yang, X.-Q. Imaging the Surface Morphology, Chemistry and Conductivity of LiNi1/3Fe1/3Mn4/3O4 Crystalline Facets Using Scanning Transmission X-Ray Microscopy. Phys. Chem. Chem. Phys. 2016, 18, 22789–22793. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the Methodology of X-Ray Crystallography to Allow Imaging of Micrometre-Sized Non-Crystalline Specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Miao, J.; Ishikawa, T.; Johnson, B.; Anderson, E.H.; Lai, B.; Hodgson, K.O. High Resolution 3D X-Ray Diffraction Microscopy. Phys. Rev. Lett. 2002, 89, 088303. [Google Scholar] [CrossRef]
- Faulkner, H.M.L.; Rodenburg, J.M. Movable Aperture Lensless Transmission Microscopy: A Novel Phase Retrieval Algorithm. Phys. Rev. Lett. 2004, 93, 023903. [Google Scholar] [CrossRef] [PubMed]
- Rodenburg, J.M.; Faulkner, H.M.L. A Phase Retrieval Algorithm for Shifting Illumination. Appl. Phys. Lett. 2004, 85, 4795–4797. [Google Scholar] [CrossRef]
- Pfeiffer, F. X-Ray Ptychography. Nat. Photonics 2018, 12, 9–17. [Google Scholar] [CrossRef]
- Edo, T.B.; Batey, D.J.; Maiden, A.M.; Rau, C.; Wagner, U.; Pešić, Z.D.; Waigh, T.A.; Rodenburg, J.M. Sampling in X-Ray Ptychography. Phys. Rev. A 2013, 87, 053850. [Google Scholar] [CrossRef]
- Shapiro, D.A.; Yu, Y.-S.; Tyliszczak, T.; Cabana, J.; Celestre, R.; Chao, W.; Kaznatcheev, K.; Kilcoyne, A.L.D.; Maia, F.; Marchesini, S.; et al. Chemical Composition Mapping with Nanometre Resolution by Soft X-Ray Microscopy. Nat. Photonics 2014, 8, 765–769. [Google Scholar] [CrossRef]
- Shapiro, D.A.; Babin, S.; Celestre, R.S.; Chao, W.; Conley, R.P.; Denes, P.; Enders, B.; Enfedaque, P.; James, S.; Joseph, J.M.; et al. An Ultrahigh-Resolution Soft x-Ray Microscope for Quantitative Analysis of Chemically Heterogeneous Nanomaterials. Sci. Adv. 2020, 6, eabc4904. [Google Scholar] [CrossRef]
- Kharitonov, K.; Mehrjoo, M.; Ruiz-Lopez, M.; Keitel, B.; Kreis, S.; Gang, S.; Pan, R.; Marras, A.; Correa, J.; Wunderer, C.B.; et al. Single-Shot Ptychography at a Soft X-Ray Free-Electron Laser. Sci. Rep. 2022, 12, 14430. [Google Scholar] [CrossRef]
- Ding, Z.; Gao, S.; Fang, W.; Huang, C.; Zhou, L.; Pei, X.; Liu, X.; Pan, X.; Fan, C.; Kirkland, A.I.; et al. Three-Dimensional Electron Ptychography of Organic–Inorganic Hybrid Nanostructures. Nat. Commun. 2022, 13, 4787. [Google Scholar] [CrossRef] [PubMed]
- Ishiguro, N.; Takahashi, Y. Method for Restoration of X-Ray Absorption Fine Structure in Sparse Spectroscopic Ptychography. J. Appl. Crystallogr. 2022, 55, 929–943. [Google Scholar] [CrossRef]
- Brooks, N.J.; Wang, B.; Binnie, I.; Tanksalvala, M.; Esashi, Y.; Knobloch, J.L.; Nguyen, Q.L.D.; McBennett, B.; Jenkins, N.W.; Gui, G.; et al. Temporal and Spectral Multiplexing for EUV Multibeam Ptychography with a High Harmonic Light Source. Opt. Express 2022, 30, 30331. [Google Scholar] [CrossRef] [PubMed]
- Sandberg, R.L.; Paul, A.; Raymondson, D.A.; Hädrich, S.; Gaudiosi, D.M.; Holtsnider, J.; Tobey, R.I.; Cohen, O.; Murnane, M.M.; Kapteyn, H.C.; et al. Lensless Diffractive Imaging Using Tabletop Coherent High-Harmonic Soft-X-Ray Beams. Phys. Rev. Lett. 2007, 99, 098103. [Google Scholar] [CrossRef] [PubMed]
- Wise, A.M.; Weker, J.N.; Kalirai, S.; Farmand, M.; Shapiro, D.A.; Meirer, F.; Weckhuysen, B.M. Nanoscale Chemical Imaging of an Individual Catalyst Particle with Soft X-Ray Ptychography. ACS Catal. 2016, 6, 2178–2181. [Google Scholar] [CrossRef]
- Grote, L.; Seyrich, M.; Döhrmann, R.; Harouna-Mayer, S.Y.; Mancini, F.; Kaziukenas, E.; Fernandez-Cuesta, I.; Zito, C.A.; Vasylieva, O.; Wittwer, F.; et al. Imaging Cu2O Nanocube Hollowing in Solution by Quantitative in Situ X-Ray Ptychography. Nat. Commun. 2022, 13, 4971. [Google Scholar] [CrossRef]
- Jacobsen, C.; Williams, S.; Anderson, E.; Browne, M.T.; Buckley, C.J.; Kern, D.; Kirz, J.; Rivers, M.; Zhang, X. Diffraction-Limited Imaging in a Scanning Transmission X-Ray Microscope. Opt. Commun. 1991, 86, 351–364. [Google Scholar] [CrossRef]
- Zhang, X.; Jacobsen, C.J.; Williams, S.P. Image Enhancement through Deconvolution. In Soft X-Ray Microscopy; SPIE: San Diego, CA, USA, 1993; Volume 1741, pp. 251–259. [Google Scholar] [CrossRef]
- Ornelas, J.L.; Rosner, B.; Spath, A.; Fink, R.H. STXMdeconv—A MATLAB Script for the Deconvolution of STXM Images. Microsc. Microanal. 2018, 24, 122–123. [Google Scholar] [CrossRef]
- Deng, J.; Vine, D.J.; Chen, S.; Jin, Q.; Nashed, Y.S.G.; Peterka, T.; Vogt, S.; Jacobsen, C. X-Ray Ptychographic and Fluorescence Microscopy of Frozen-Hydrated Cells Using Continuous Scanning. Sci. Rep. 2017, 7, 445. [Google Scholar] [CrossRef]
- Vine, D.J.; Pelliccia, D.; Holzner, C.; Baines, S.B.; Berry, A.; McNulty, I.; Vogt, S.; Peele, A.G.; Nugent, K.A. Simultaneous X-Ray Fluorescence and Ptychographic Microscopy of Cyclotella Meneghiniana. Opt. Express 2012, 20, 18287. [Google Scholar] [CrossRef]
- Nagy, J.G.; Strakos, Z. Enforcing Nonnegativity in Image Reconstruction Algorithms. In International Symposium on Optical Science and Technology; Wilson, D.C., Tagare, H.D., Bookstein, F.L., Preteux, F.J., Dougherty, E.R., Eds.; SPIE: San Diego, CA, USA, 2000; pp. 182–190. [Google Scholar] [CrossRef]
- Walden, A.T. Robust Deconvolution by Modified Wiener Filtering. Geophysics 1988, 53, 186–191. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Prentice-Hall Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Abe, M.; Ishiguro, N.; Uematsu, H.; Takazawa, S.; Kaneko, F.; Takahashi, Y. X-Ray Ptychographic and Fluorescence Microscopy Using Virtual Single-Pixel Imaging Based Deconvolution with Accurate Probe Images. Opt. Express 2023, 31, 26027. [Google Scholar] [CrossRef] [PubMed]
- Barrett, R.; Berry, M.; Chan, T.F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; Van Der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar]
- Paige, C.C.; Saunders, M.A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Biggs, D.S.C.; Andrews, M. Acceleration of Iterative Image Restoration Algorithms. Appl. Opt. 1997, 36, 1766. [Google Scholar] [CrossRef]
- Hanisch, R.J.; White, R.L.; Gilliland, R.L. Deconvolution of Hubbles Space Telescope Images and Spectra. In Deconvolution of Images and Spectra, 2nd ed.; Academic Press, Inc.: Cambridge, MA, USA, 1996; pp. 310–360. [Google Scholar]
- Maiden, A.M.; Rodenburg, J.M. An Improved Ptychographical Phase Retrieval Algorithm for Diffractive Imaging. Ultramicroscopy 2009, 109, 1256–1262. [Google Scholar] [CrossRef]
- Thibault, P.; Menzel, A. Reconstructing State Mixtures from Diffraction Measurements. Nature 2013, 494, 68–71. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Zhang, X.; Chen, B.; Wang, Y.; Tai, R. Position-Guided Ptychography for Vibration Suppression with the Aid of a Laser Interferometer. Opt. Lasers Eng. 2023, 160, 107297. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Xing, Z.; Zhang, X.; Li, R.; Qin, Z.; Wang, Y.; Tai, R. Periodic Artifacts Generation and Suppression in X-Ray Ptychography. Photonics 2023, 10, 532. [Google Scholar] [CrossRef]
- Stockmar, M.; Cloetens, P.; Zanette, I.; Enders, B.; Dierolf, M.; Pfeiffer, F.; Thibault, P. Near-Field Ptychography: Phase Retrieval for Inline Holography Using a Structured Illumination. Sci. Rep. 2013, 3, 1927. [Google Scholar] [CrossRef]
- Zhang, L.-J.; Xu, Z.-J.; Zhang, X.-Z.; Yu, H.-N.; Zou, Y.; Guo, Z.; Zhen, X.-J.; Cao, J.-F.; Meng, X.-Y.; Li, J.-Q.; et al. Latest Advances in Soft X-Ray Spectromicroscopy at SSRF. Nucl. Sci. Tech. 2015, 26, 040101. [Google Scholar]
- Sun, T.; Zhang, X.; Xu, Z.; Wang, Y.; Guo, Z.; Wang, J.; Tai, R. A Bidirectional Scanning Method for Scanning Transmission X-Ray Microscopy. J. Synchrotron Radiat. 2021, 28, 512–517. [Google Scholar] [CrossRef] [PubMed]
- Lewis, J.P. Fast Normalized Cross-Correlation. In Vision interface; World Scientific Publishing Company: Singapore, 1995; Volume 10, pp. 120–123. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Attwood, D. Soft X-Rays and Extreme Ultraviolet Radiation: Principles and Applications; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
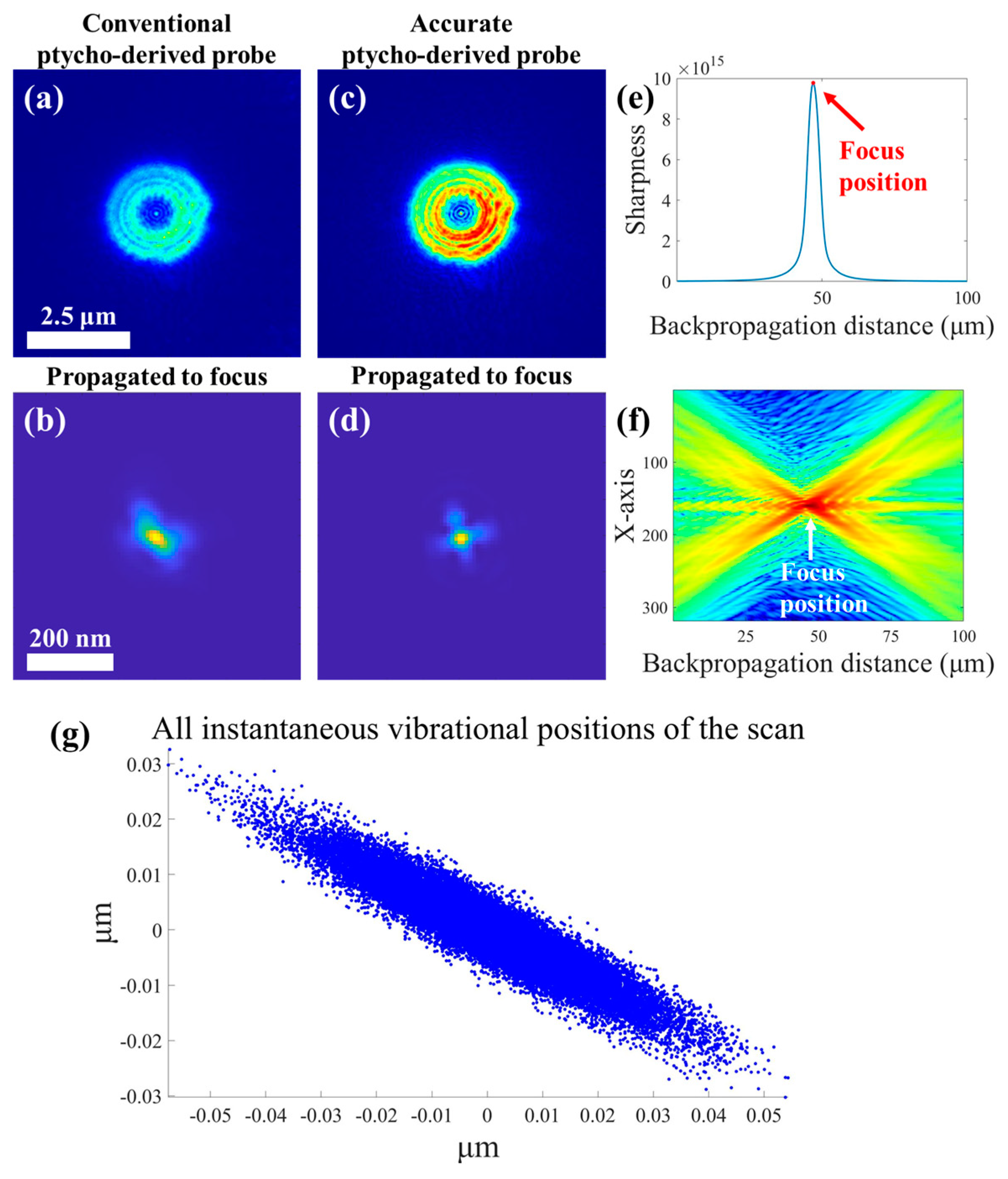

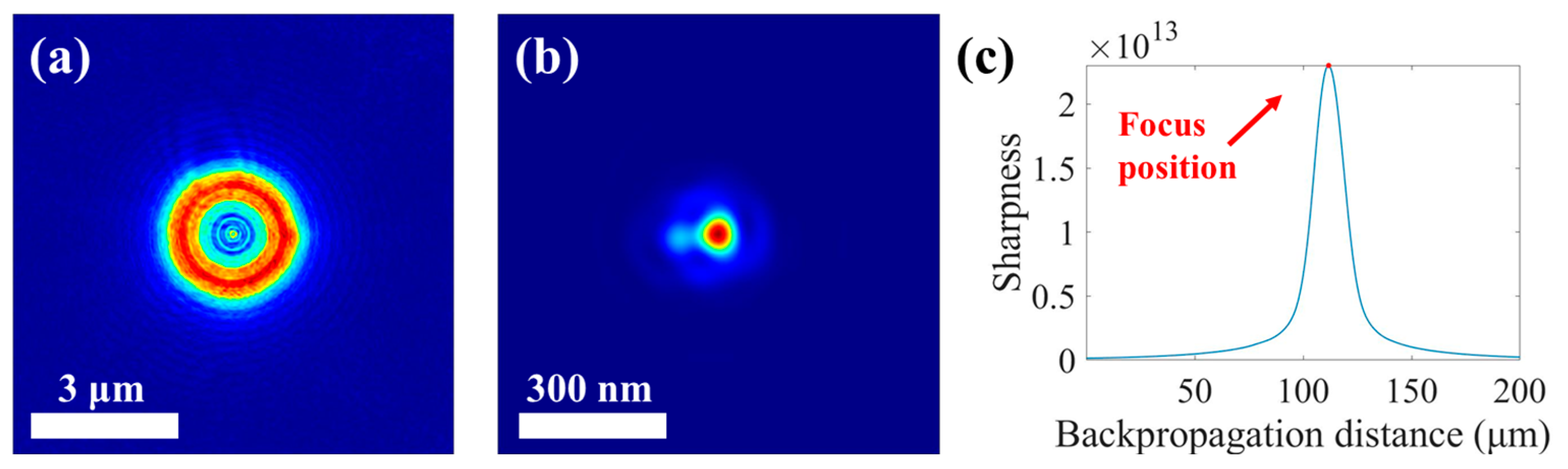




| Focal Spots Comparison | SSIM | NCC |
|---|---|---|
| 0.9621 | 0.9594 | |
| 0.9820 | 0.9975 | |
| 0.9697 | 0.9626 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Xu, Z.; Li, R.; Chen, S.; Zhang, Y.; Zhang, X.; Chen, Z.; Tai, R. Enhanced Imaging in Scanning Transmission X-Ray Microscopy Assisted by Ptychography. Nanomaterials 2025, 15, 496. https://doi.org/10.3390/nano15070496
Wu S, Xu Z, Li R, Chen S, Zhang Y, Zhang X, Chen Z, Tai R. Enhanced Imaging in Scanning Transmission X-Ray Microscopy Assisted by Ptychography. Nanomaterials. 2025; 15(7):496. https://doi.org/10.3390/nano15070496
Chicago/Turabian StyleWu, Shuhan, Zijian Xu, Ruoru Li, Sheng Chen, Yingling Zhang, Xiangzhi Zhang, Zhenhua Chen, and Renzhong Tai. 2025. "Enhanced Imaging in Scanning Transmission X-Ray Microscopy Assisted by Ptychography" Nanomaterials 15, no. 7: 496. https://doi.org/10.3390/nano15070496
APA StyleWu, S., Xu, Z., Li, R., Chen, S., Zhang, Y., Zhang, X., Chen, Z., & Tai, R. (2025). Enhanced Imaging in Scanning Transmission X-Ray Microscopy Assisted by Ptychography. Nanomaterials, 15(7), 496. https://doi.org/10.3390/nano15070496






