A Differentiable Dynamic Model for Musculoskeletal Simulation and Exoskeleton Control
Abstract
:1. Introduction
2. Materials and Methods
2.1. Myoelectric Processor
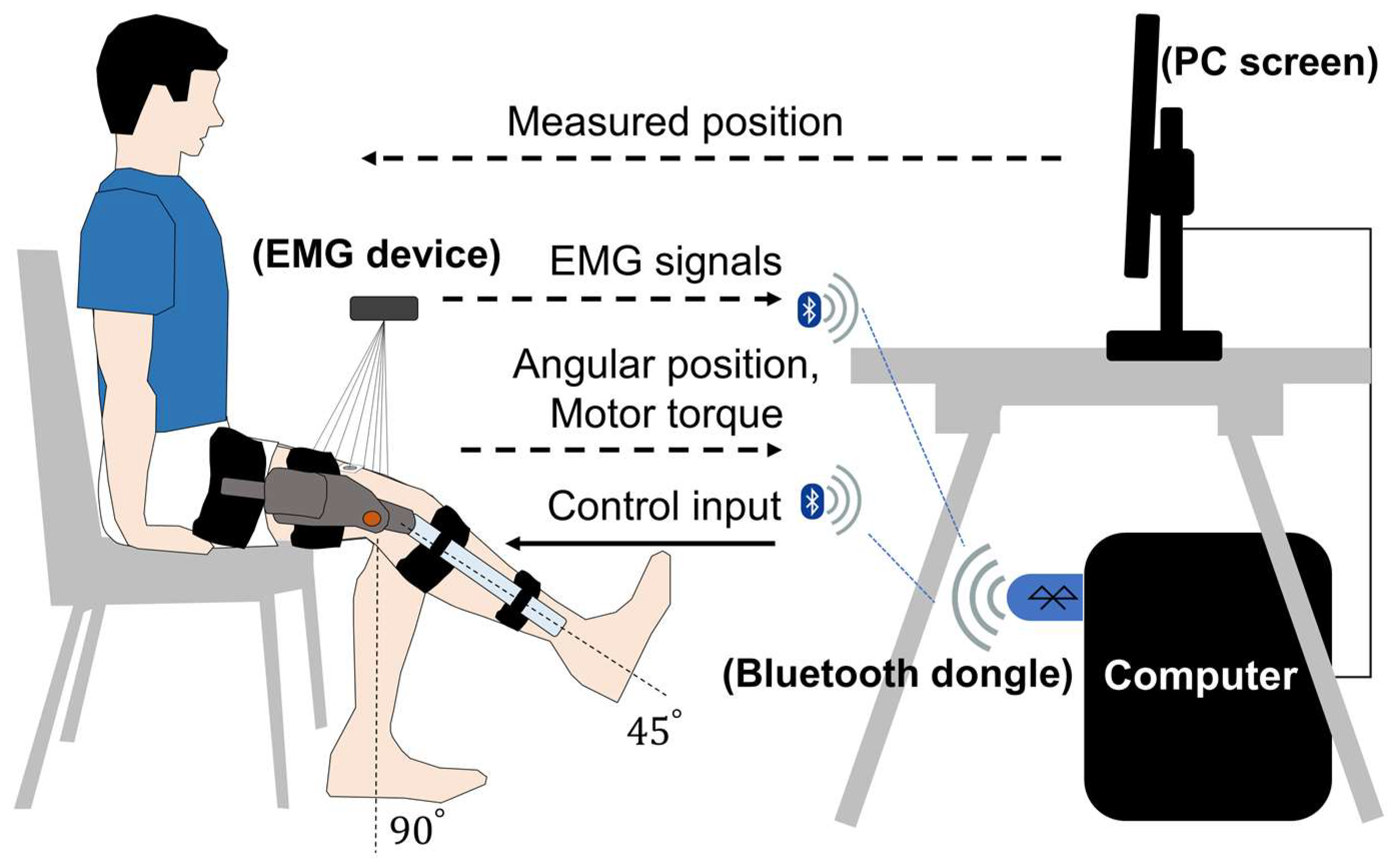
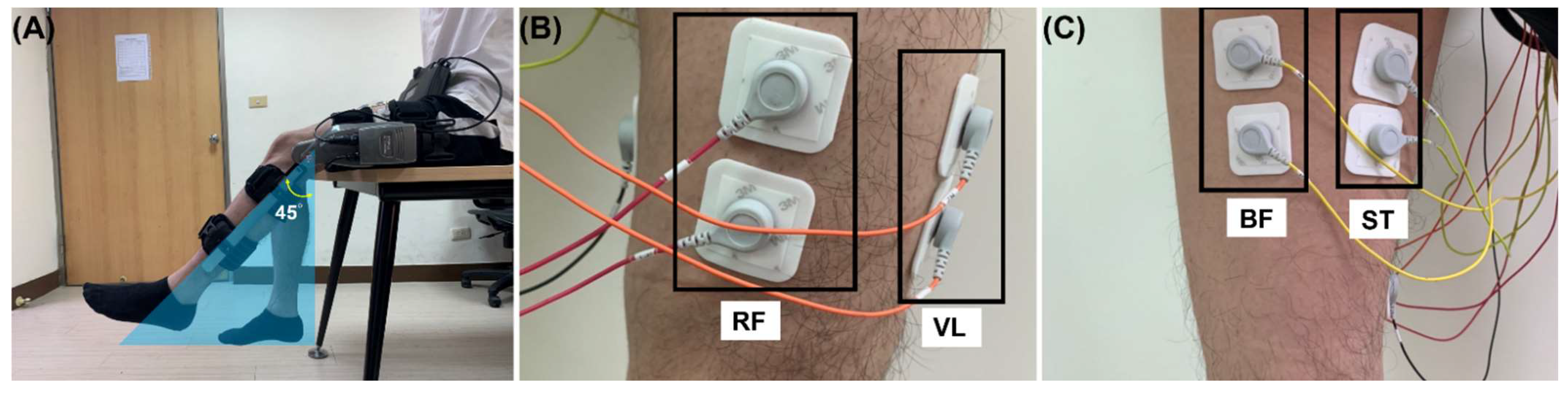
2.2. Experimental Setup
2.3. Preprocessing
2.4. Wearable Exoskeleton Modeling
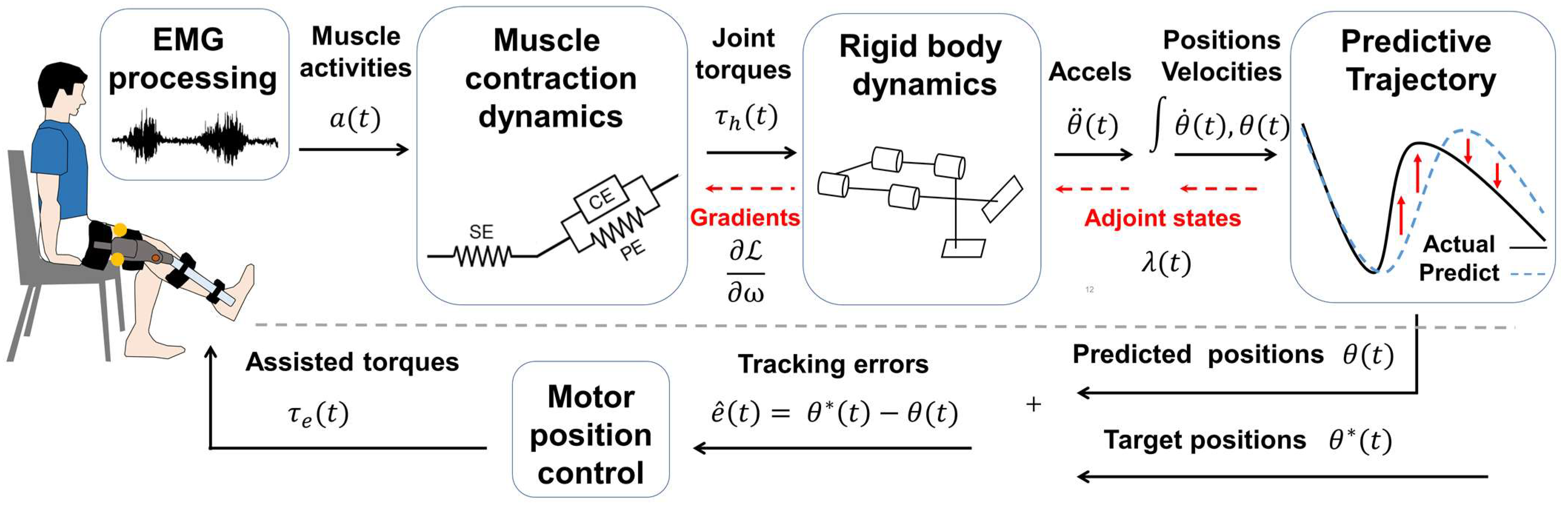
2.5. Differentiable Musculoskeletal Parameters Estimation
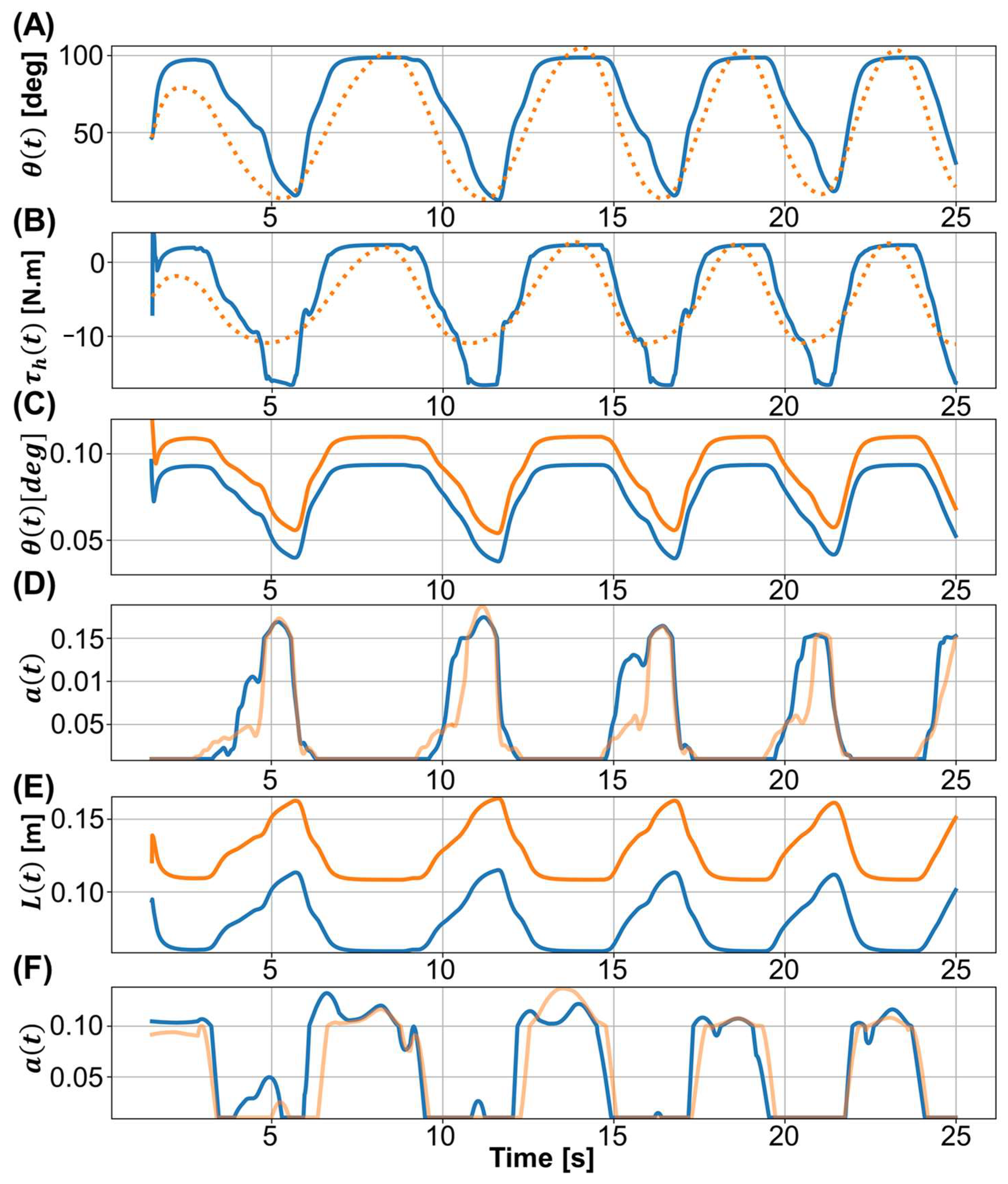
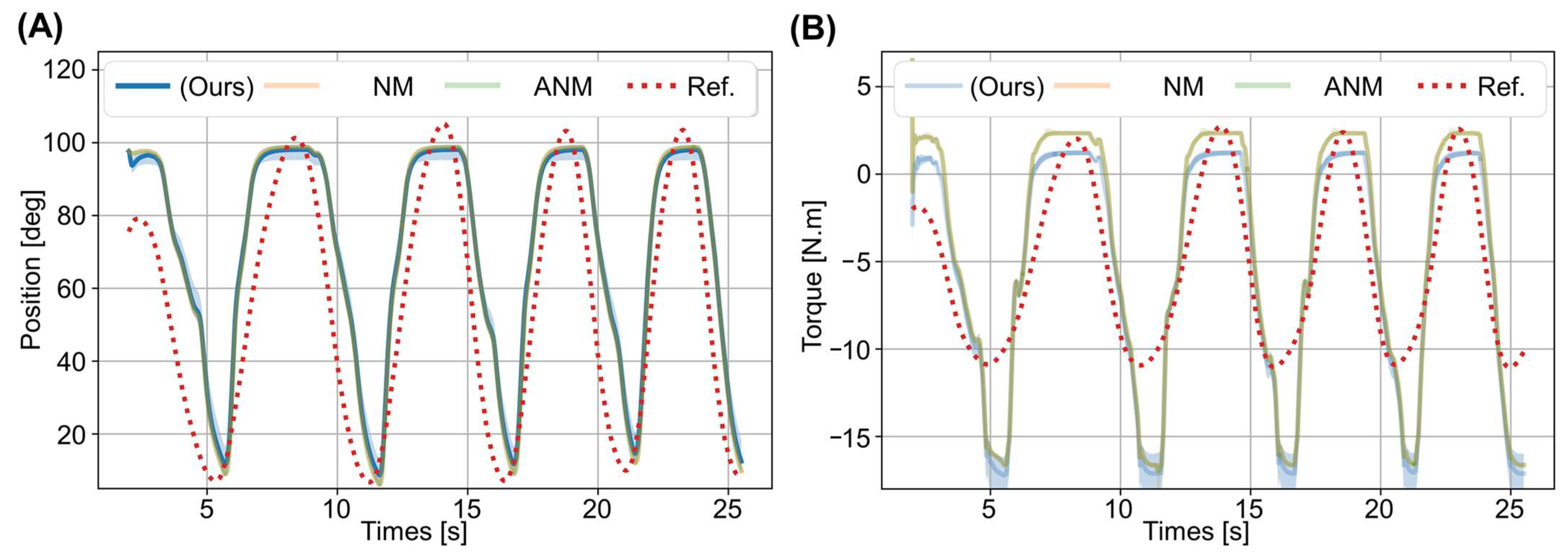
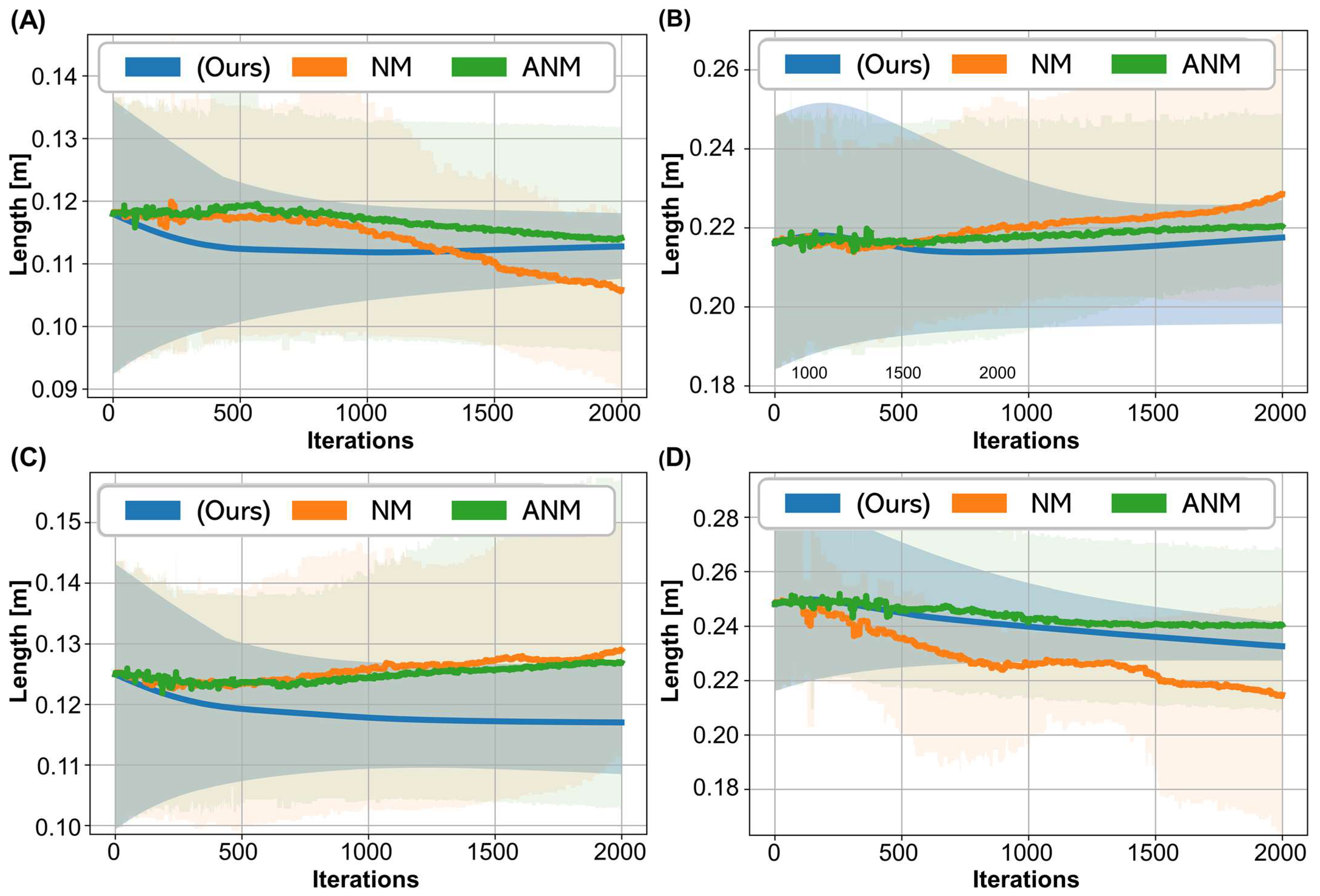
3. Results
3.1. Parameters Estimated in the Motion Equation
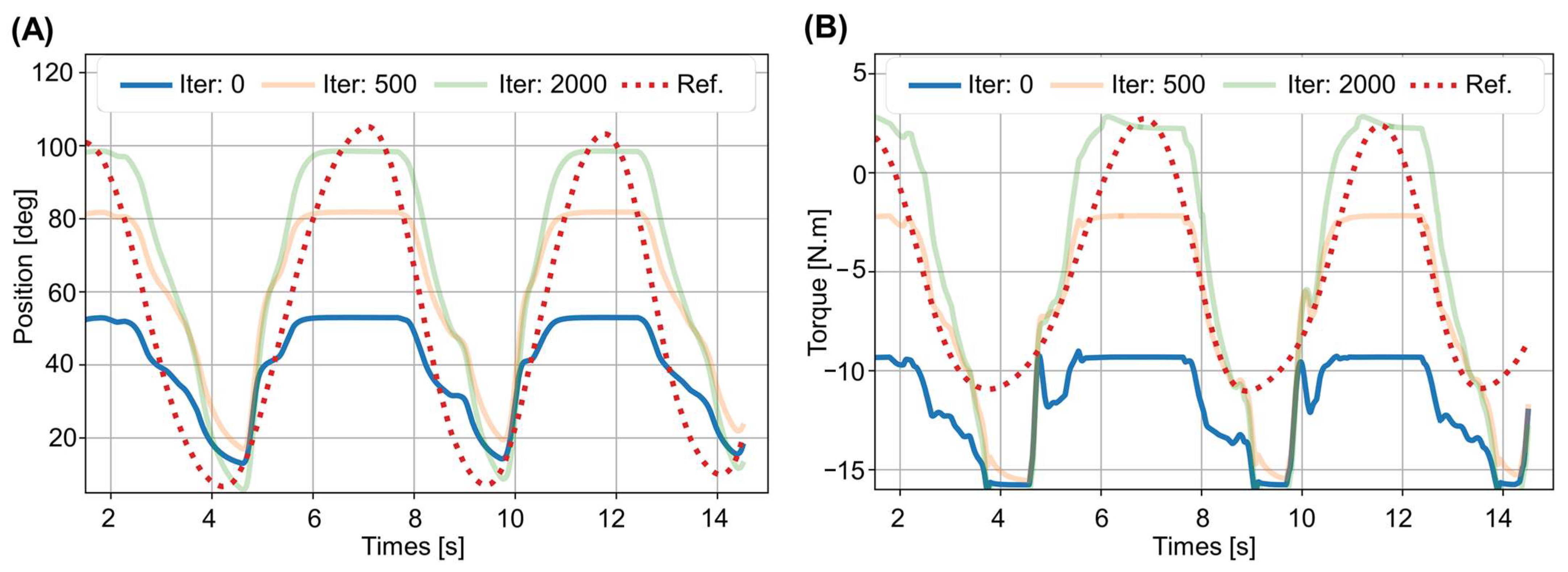
3.2. Prediction Results
3.3. Performance Analysis: Convergence and Execution Time
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zoss, A.B.; Kazerooni, H.; Chu, A. Biomechanical design of the berkeley lower extremity exoskeleton (bleex). IEEE/ASME Trans. Mechatron. 2006, 11, 128–138. [Google Scholar] [CrossRef]
- Maciejasz, P.; Eschweiler, J.; Gerlach-Hahn, K.; Jansen-Troy, A.; Leonhardt, S. A survey on robotic devices for upper limb rehabilitation. J. NeuroEngineering Rehabil. 2014, 11, 3. [Google Scholar] [CrossRef] [Green Version]
- Pazzaglia, M.; Molinari, M. The embodiment of assistive devices—from wheelchair to exoskeleton. Phys. Life Rev. 2016, 16, 163–175. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.H.; Blakely, T.M.; Wander, J.D.; Sarma, D.; Wu, J.; Casimo, K.; Weaver, K.E.; Ojemann, J.G. Context-dependent relationship in high-resolution micro-ecog studies during finger movements. J. Neurosurg. 2019, 132, 1358–1366. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.H.; Casimo, K.; Wu, J.; Collins, K.; Rice, P.; Chen, B.W.; Yang, S.H.; Lo, Y.C.; Novotny, E.J.; Weaver, K.E.; et al. Electrocorticography to investigate age-related brain lateralization on pediatric motor inhibition. Front. Neurol. 2022, 13, 747053. [Google Scholar] [CrossRef]
- McRuer, D.T.; Magdaleno, R.E.; Moore, G.P. A neuromuscular actuation system model. IEEE Trans. Man-Mach. Syst. 1968, 9, 61–71. [Google Scholar] [CrossRef]
- Mulder, M.; Pool, D.M.; Abbink, D.A.; Boer, E.R.; Zaal, P.M.T.; Drop, F.M.; van der El, K.; van Paassen, M.M. Manual control cybernetics: State-of-the-art and current trends. IEEE Trans. Hum.-Mach. Syst. 2018, 48, 468–485. [Google Scholar] [CrossRef]
- Choi, H.; Seo, K.; Hyung, S.; Shim, Y.; Lim, S.C. Compact hip-force sensor for a gait-assistance exoskeleton system. Sensors 2018, 18, 566. [Google Scholar] [CrossRef] [Green Version]
- Lyu, M.; Chen, W.-H.; Ding, X.; Wang, J.; Pei, Z.; Zhang, B. Development of an emg-controlled knee exoskeleton to assist home rehabilitation in a game context. Front. Neurorobotics 2019, 13, 67. [Google Scholar] [CrossRef] [Green Version]
- Pfurtscheller, G.; Guger, C.; Müller, G.; Krausz, G.; Neuper, C. Brain oscillations control hand orthosis in a tetraplegic. Neurosci. Lett. 2000, 292, 211–214. [Google Scholar] [CrossRef]
- Fleischer, C.; Hommel, G. A human—exoskeleton interface utilizing electromyography. IEEE Trans. Robot. 2008, 24, 872–882. [Google Scholar] [CrossRef]
- Elnady, A.M.; Zhang, X.; Xiao, Z.G.; Yong, X.; Randhawa, B.K.; Boyd, L.; Menon, C. A single-session preliminary evaluation of an affordable bci-controlled arm exoskeleton and motor-proprioception platform. Front. Hum. Neurosci. 2015, 9, 168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Yuan, Y.; Luo, L.; Su, W.; Zhao, K.; Xu, C.; Huang, J.; Pi, M. Hybrid brain/muscle signals powered wearable walking exoskeleton enhancing motor ability in climbing stairs activity. IEEE Trans. Med. Robot. Bionics 2019, 1, 218–227. [Google Scholar] [CrossRef]
- Tiboni, M.; Borboni, A.; Vérité, F.; Bregoli, C.; Amici, C. Sensors and actuation technologies in exoskeletons: A review. Sensors 2022, 22, 884. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, X.; Cheng, Y.; Xi, N. Surface emg based continuous estimation of human lower limb joint angles by using deep belief networks. Biomed. Signal Processing Control. 2018, 40, 335–342. [Google Scholar] [CrossRef]
- Hahn, M.E. Feasibility of estimating isokinetic knee torque using a neural network model. J. Biomech. 2007, 40, 1107–1114. [Google Scholar] [CrossRef]
- Jali, M.H.; Izzuddin, T.A.; Bohari, Z.H.; Sulaima, M.F.; Sarkawi, H. Predicting emg based elbow joint torque model using multiple input ann neurons for arm rehabilitation. In Proceedings of the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, 26–28 March 2014; pp. 189–194. [Google Scholar]
- Liu, Y.; Shih, S.M.; Tian, S.L.; Zhong, Y.J.; Li, L. Lower extremity joint torque predicted by using artificial neural network during vertical jump. J. Biomech. 2009, 42, 906–911. [Google Scholar] [CrossRef]
- Zajac, F.E. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 1989, 17, 359–411. [Google Scholar]
- Haeufle, D.F.B.; Günther, M.; Bayer, A.; Schmitt, S. Hill-type muscle model with serial damping and eccentric force–velocity relation. J. Biomech. 2014, 47, 1531–1536. [Google Scholar] [CrossRef]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. London. Ser. B-Biol. Sci. 1938, 126, 136–195. [Google Scholar]
- Rajagopal, A.; Dembia, C.L.; DeMers, M.S.; Delp, D.D.; Hicks, J.L.; Delp, S.L. Full-body musculoskeletal model for muscle-driven simulation of human gait. IEEE Trans. Biomed. Eng. 2016, 63, 2068–2079. [Google Scholar] [CrossRef] [PubMed]
- Ao, D.; Song, R.; Gao, J. Movement performance of human-robot cooperation control based on emg-driven hill-type and proportional models for an ankle power-assist exoskeleton robot. IEEE Trans. Neural. Syst. Rehabil. Eng. 2017, 25, 1125–1134. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, Z.; Hu, Y.; Smith, C.; Farewik, E.M.G.; Wang, R. Ankle joint torque estimation using an emg-driven neuromusculoskeletal model and an artificial neural network model. IEEE Trans. Autom. Sci. Eng. 2021, 18, 564–573. [Google Scholar] [CrossRef]
- Yao, S.; Zhuang, Y.; Li, Z.; Song, R. Adaptive admittance control for an ankle exoskeleton using an emg-driven musculoskeletal model. Front. Neurorobot. 2018, 12, 16. [Google Scholar] [CrossRef] [PubMed]
- Rockenfeller, R.; Herold, J.L.; Götz, T. Parameter estimation and experimental design for hill-type muscles: Impulses from optimization-based modeling. Math. Biosci. 2020, 327, 108432. [Google Scholar] [CrossRef]
- Zee, M.d.; Heinen, F.; Sørensen, S.N.; King, M.A.; Lewis, M.G.C.; Rasmussen, J. Parameter Estimations of the Hill Model in Subject-Specific Musculoskeletal Models: How Many Measurements Do We Need? In Proceedings of the XVI International Symposium on Computer Simulation in Biomechanics, Gold Coast, QLD, Australia, 20–22 July 2017. [Google Scholar]
- Ohlsson, M.L.; Gulliksson, M.E. Least Squares Approach to Inverse Problems in Musculoskeletal Biomechanics; Technical Report; Mid Sweden University: Ostersund, Sweden, 2009; ISSN 1650-5387. [Google Scholar]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Development of a minimal-intervention-based admittance control strategy for upper extremity rehabilitation exoskeleton. IEEE Trans. Syst. Man Cybern.Syst. 2018, 48, 1005–1016. [Google Scholar] [CrossRef]
- Cavallaro, E.E.; Rosen, J.; Perry, J.C.; Burns, S. Real-time myoprocessors for a neural controlled powered exoskeleton arm. IEEE Trans. Biomed. Eng. 2006, 53, 2387–2396. [Google Scholar] [CrossRef]
- Buongiorno, D.; Barsotti, M.; Barone, F.; Bevilacqua, V.; Frisoli, A. A linear approach to optimize an emg-driven neuromusculoskeletal model for movement intention detection in myo-control: A case study on shoulder and elbow joints. Front. Neurorobot 2018, 12, 74. [Google Scholar] [CrossRef]
- Degrave, J.; Hermans, M.; Dambre, J.; Wyffels, F. A differentiable physics engine for deep learning in robotics. Front. Neurorobot. 2019, 13, 6. [Google Scholar] [CrossRef] [Green Version]
- Erez, T.; Tassa, Y.; Todorov, E. Simulation tools for model-based robotics: Comparison of bullet, havok, mujoco, ode and physx. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4397–4404. [Google Scholar]
- Qiao, Y.-L.; Liang, J.; Koltun, V.; Lin, M.C. Efficient differentiable simulation of articulated bodies. In Proceedings of the 38th International Conference on Machine Learning, Virtual Event, 18–24 July 2021. [Google Scholar]
- Chuang, C.H.; Lu, S.W.; Chao, Y.P.; Peng, P.H.; Hsu, H.C.; Hung, C.C.; Chang, C.L.; Jung, T.P. Near-zero phase-lag hyperscanning in a novel wireless eeg system. J. Neural. Eng. 2021, 18, 066010. [Google Scholar] [CrossRef]
- Lloyd, D.G.; Besier, T.F. An emg-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Buchanan, T.S.; Lloyd, D.G.; Manal, K.; Besier, T.F. Neuromusculoskeletal modeling: Estimation of muscle forces and joint moments and movements from measurements of neural command. J. Appl. Biomech. 2004, 20, 367–395. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swevers, J.; Ganseman, C.; Tukel, D.B.; Schutter, J.d.; Brussel, H.V. Optimal robot excitation and identification. IEEE Trans. Robot. Autom. 1997, 13, 730–740. [Google Scholar] [CrossRef] [Green Version]
- Rifai, H.; Hassani, W.; Mohammed, S.; Amirat, Y. Bounded control of an actuated lower limb orthosis. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011. [Google Scholar]
- Hassani, W.; Mohammed, S.; Rifaï, H.; Amirat, Y. Powered orthosis for lower limb movements assistance and rehabilitation. Control. Eng. Pract. 2014, 26, 245–253. [Google Scholar] [CrossRef]
- Thelen, D.G. Adjustment of muscle mechanics model parameters to simulate dynamic contractions in older adults. J. Biomech. Eng. 2003, 125, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Audu, M.L.; Davy, D.T. The influence of muscle model complexity in musculoskeletal motion modeling. J. Biomech. Eng. 1985, 107, 147–157. [Google Scholar] [CrossRef]
- Magnusson, S.P.; Simonsen, E.B.; Aagaard, P.; Kjaer, M. Biomechanical responses to repeated stretches in human hamstring muscle in vivo. Am. J. Sports Med. 1996, 24, 622–628. [Google Scholar] [CrossRef]
- Gordon, A.M.; Huxley, A.F.; Julian, F.J. The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J. Physiol. 1966, 184, 170–192. [Google Scholar] [CrossRef]
- Epstein, M.; Herzog, W. Theoretical Models of Skeletal Muscle: Biological and Mathematical Considerations; Wiley: Chichester, NY, USA, 1998. [Google Scholar]
- Arnold, E.M.; Ward, S.R.; Lieber, R.L.; Delp, S.L. A model of the lower limb for analysis of human movement. Ann. Biomed. Eng. 2010, 38, 269–279. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, J.; Dvornek, N.; Li, X.; Tatikonda, S.; Papademetris, X.; Duncan, J. Adaptive checkpoint adjoint method for gradient estimation in neural ode. In Proceedings of the 37th International Conference on Machine Learning, ICML 2020, Virtual Event, 13–18 July 2020. [Google Scholar]
- Marlin, T.E. Process Control: Designing Processes and Control Systems for Dynamic Performance, 2nd ed.; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 2000; pp. 267–301. ISBN 978-0-07-040492-2. [Google Scholar]
- Kingma, D.P.; Adam, B.J. A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Gao, F.; Han, L. Implementing the nelder-mead simplex algorithm with adaptive parameters. Comput. Optim. Appl. 2012, 51, 259–277. [Google Scholar] [CrossRef]
- Conjugate Gradient Methods. In Numerical Optimization; Nocedal, J.; Wright, S.J. (Eds.) Springer New York: New York, NY, USA, 2006; pp. 101–134. [Google Scholar]
- Nash, S.G. Newton-type minimization via the lanczos method. SIAM J. Numer. Anal. 1984, 21, 770–788. [Google Scholar] [CrossRef]
- Kraft, D. A Software Package for Sequential Quadratic Programming; Technical Report DFVLR-FB 88-28; Institut für Dynamik der Flugsysteme: Oberpfaffenhofen, Germany, 1988. [Google Scholar]
- Moin, P. Fundamentals of Engineering Numerical Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-51-178143-8. [Google Scholar]
- Ward, S.R.; Eng, C.M.; Smallwood, L.H.; Lieber, R.L. Are current measurements of lower extremity muscle architecture accurate? Clin. Orthop. Relat. Res. 2009, 467, 1074–1082. [Google Scholar] [CrossRef] [Green Version]
| Symbol | Description | Equation Number |
|---|---|---|
| Filtered EMG signal d time steps earlier | (1) | |
| Neural activation one time step earlier | (1) | |
| Muscle activation of j-th muscle at time t | (6) | |
| Muscle length of j-th muscle at time t | (6) | |
| Muscle–tendon force of j-th muscle at time t | (6) | |
| Gravitational torque at the i-th sample of time t | (3), (4) | |
| Exoskeleton torque at the i-th sample of time t | (3), (4) | |
| Human (or muscle) torque at the i-th sample of time t | (3), (4), (20) | |
| Angular position, velocity, and acceleration, respectively, at the i-th sample of time t | (3), (4), (20) | |
| Predicted angular acceleration at the i-th sample of time t | (20) | |
| Predicted angular velocity at the i-th sample of time t | (20) |
| 1.5 | 1.27 | 5.5 | 0.16 |
| Groups | Muscles | Comparison | |||
|---|---|---|---|---|---|
| RF | Rectous femoris | _ | 9.8 | 32.8 | 850 |
| Prev | 7.6 | 34.6 | 848 | ||
| VM | Vastus lateralis | _ | 2260 | ||
| Prev | 2255 | ||||
| Vastus medialis | _ | 1445 | |||
| Prev | 1443 | ||||
| Vastus intermedius | _ | 1025 | |||
| Prev | 1024 | ||||
| ST | Semimembranosus | _ | 1092 | ||
| Prev | 1162 | ||||
| Semitendinosus | _ | 315 | |||
| Prev | 301 | ||||
| BF | Biceps long head | _ | 31.9 | 701 | |
| Prev | 705 | ||||
| Biceps short head | _ | 327 | |||
| Prev | 10.4 | 315 |
| NM | ANM | SLSQP | TNC | CG | (Ours) | |
|---|---|---|---|---|---|---|
| Gradient | free | free | approx. | approx. | approx. | analytic |
| #Eval/iter | 1.3 | 1.4 | 29.4 | 125 | 533 | 2 |
| Sec/iter | 0.08 | 0.09 | 0.56 | 2.51 | 4.72 | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuo, C.-H.; Chen, J.-W.; Yang, Y.; Lan, Y.-H.; Lu, S.-W.; Wang, C.-F.; Lo, Y.-C.; Lin, C.-L.; Lin, S.-H.; Chen, P.-C.; et al. A Differentiable Dynamic Model for Musculoskeletal Simulation and Exoskeleton Control. Biosensors 2022, 12, 312. https://doi.org/10.3390/bios12050312
Kuo C-H, Chen J-W, Yang Y, Lan Y-H, Lu S-W, Wang C-F, Lo Y-C, Lin C-L, Lin S-H, Chen P-C, et al. A Differentiable Dynamic Model for Musculoskeletal Simulation and Exoskeleton Control. Biosensors. 2022; 12(5):312. https://doi.org/10.3390/bios12050312
Chicago/Turabian StyleKuo, Chao-Hung, Jia-Wei Chen, Yi Yang, Yu-Hao Lan, Shao-Wei Lu, Ching-Fu Wang, Yu-Chun Lo, Chien-Lin Lin, Sheng-Huang Lin, Po-Chuan Chen, and et al. 2022. "A Differentiable Dynamic Model for Musculoskeletal Simulation and Exoskeleton Control" Biosensors 12, no. 5: 312. https://doi.org/10.3390/bios12050312
APA StyleKuo, C.-H., Chen, J.-W., Yang, Y., Lan, Y.-H., Lu, S.-W., Wang, C.-F., Lo, Y.-C., Lin, C.-L., Lin, S.-H., Chen, P.-C., & Chen, Y.-Y. (2022). A Differentiable Dynamic Model for Musculoskeletal Simulation and Exoskeleton Control. Biosensors, 12(5), 312. https://doi.org/10.3390/bios12050312






