Signal-Based Methods in Dielectrophoresis for Cell and Particle Separation
Abstract
:1. Introduction
2. Theoretical Background
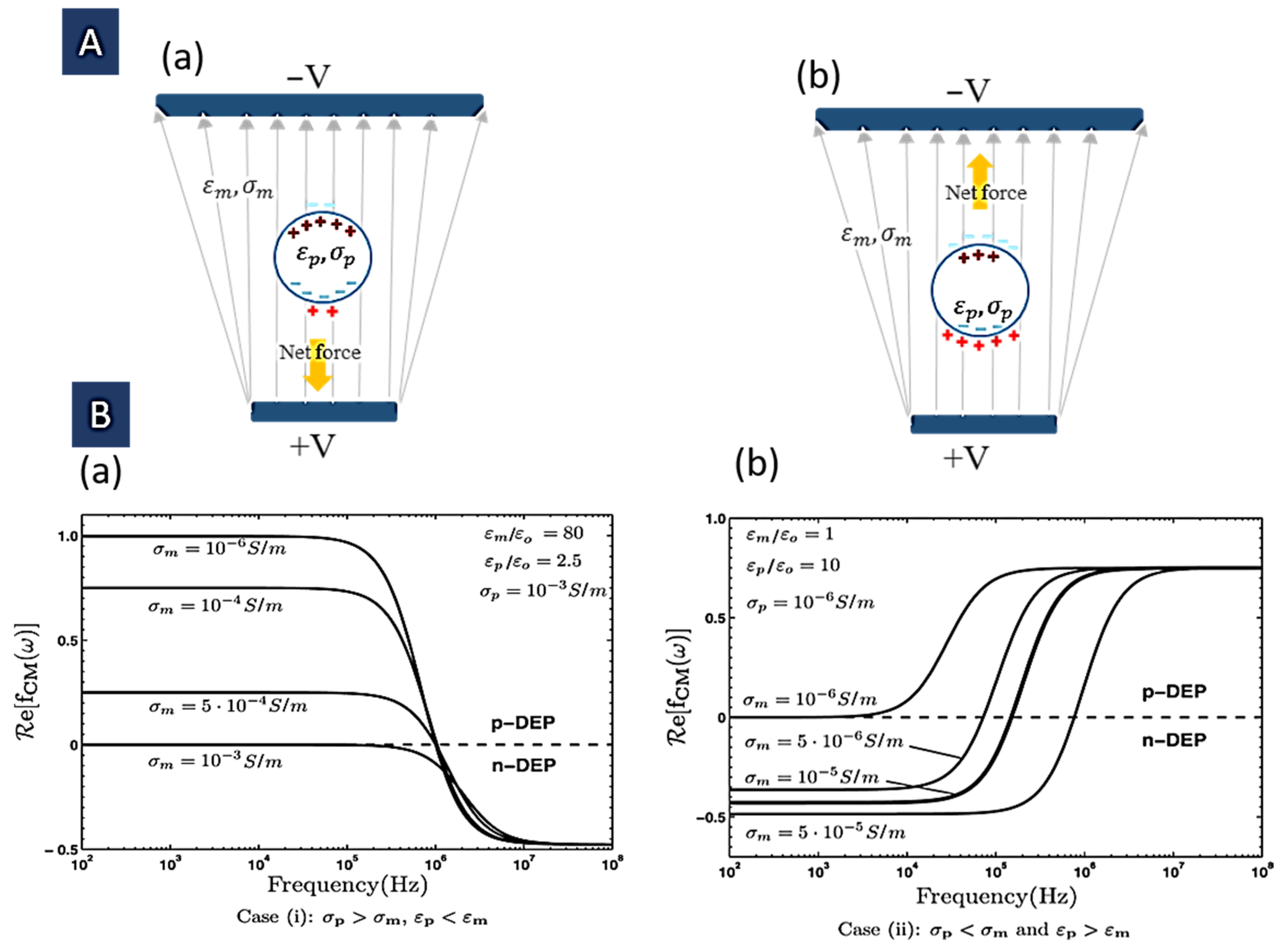
2.1. Clausius–Mossotti (CM) Factor
2.2. Cell Characteristics
3. Design Considerations
3.1. Integration of Microelectrodes
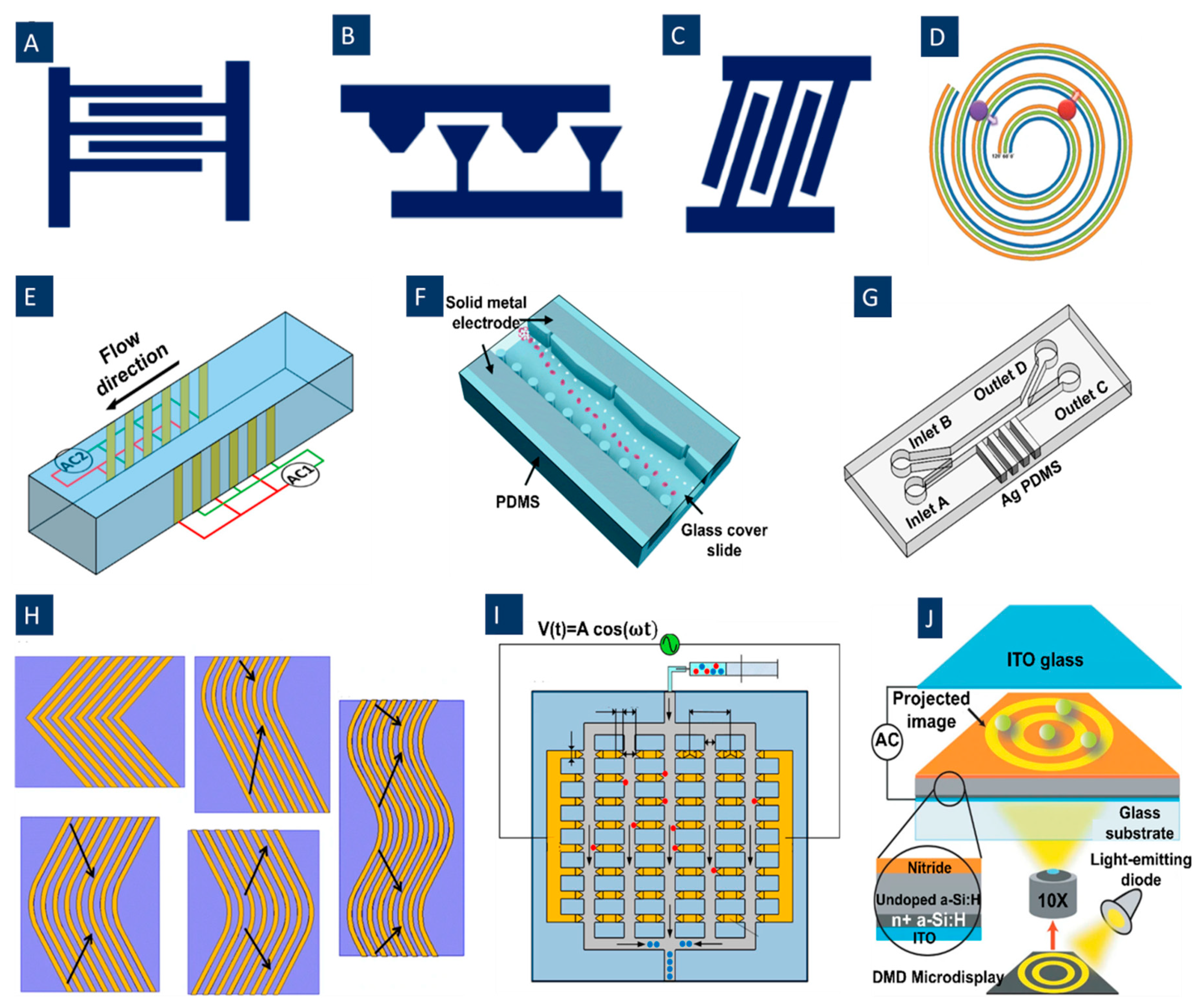
3.2. Minimizing the DEP Effects on the Live Cells
4. Signal-Based Methods
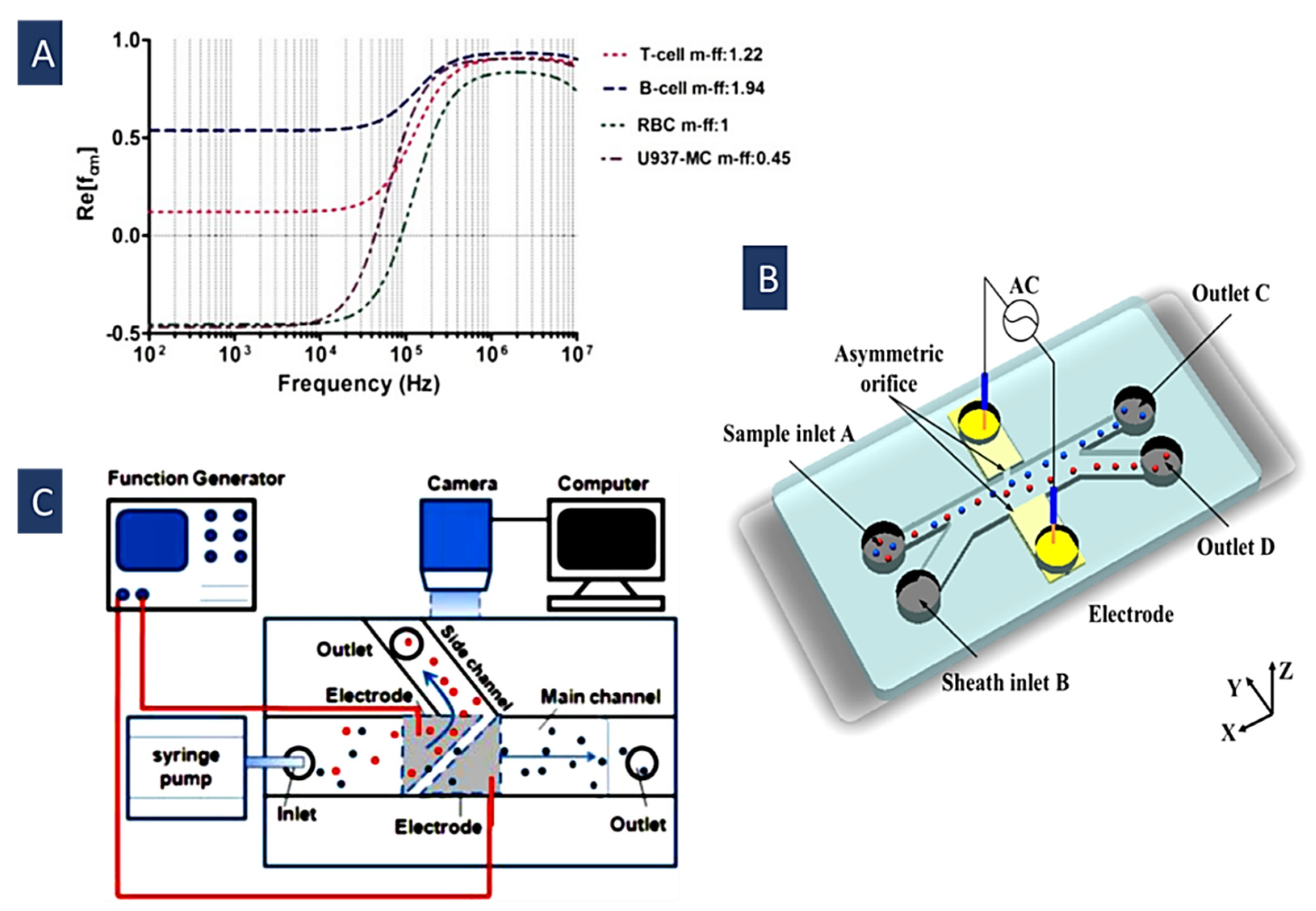
4.1. Separation Based on Crossover Frequency
4.1.1. Simple Single-Frequency Methods
4.1.2. Multiple Frequency Dielectrophoresis (MFDEP)

4.1.3. Ultra-High-Frequency Dielectrophoresis (UHF-DEP)
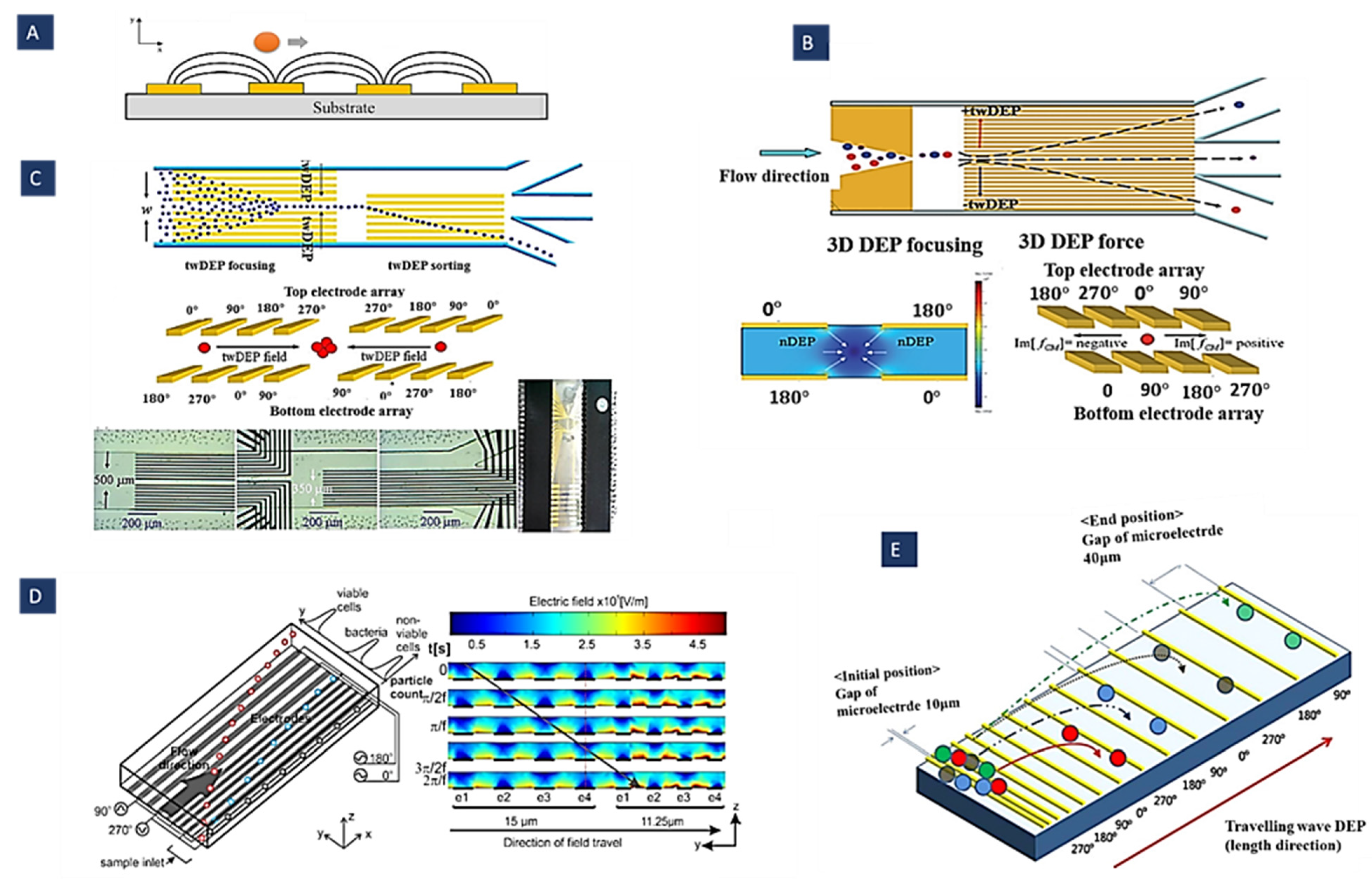
4.2. Travelling Wave Dielectrophoresis (twDEP)
4.3. Time Varying Dielectrophoresis
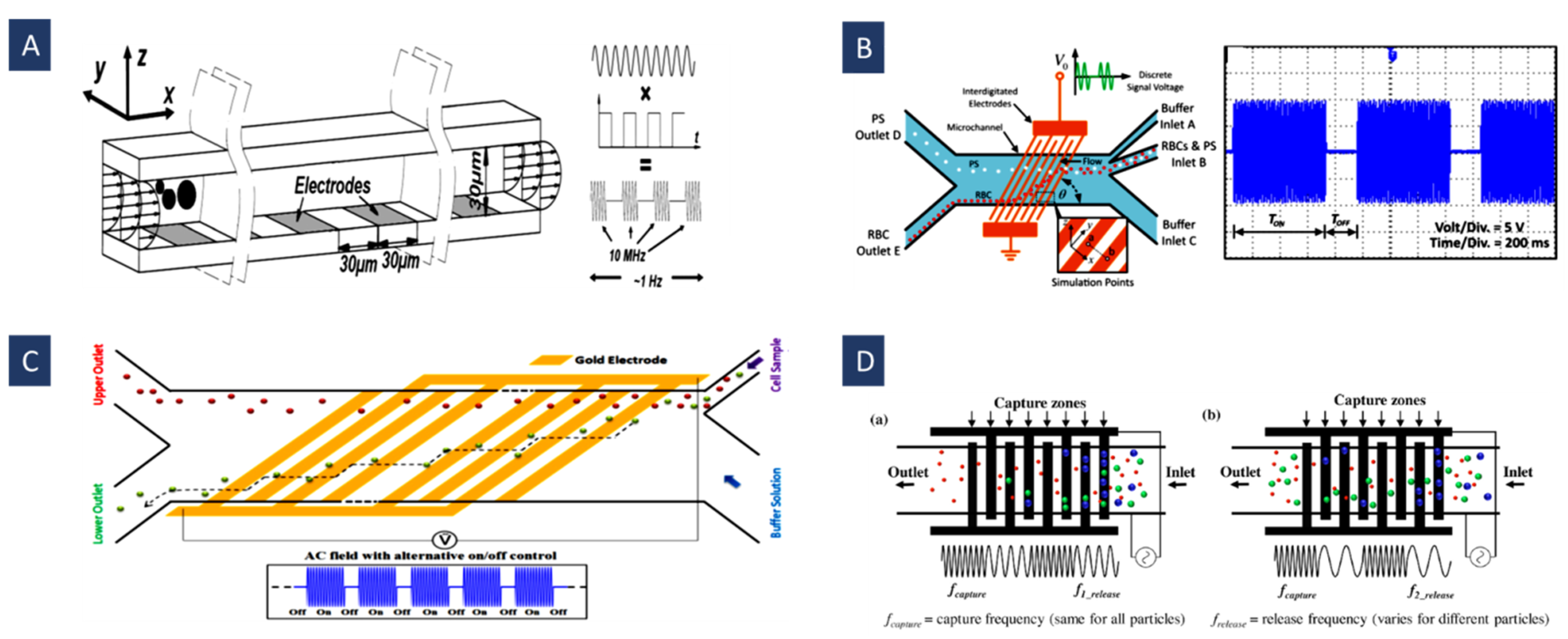
4.4. Moving Dielectrophoresis (mDEP)


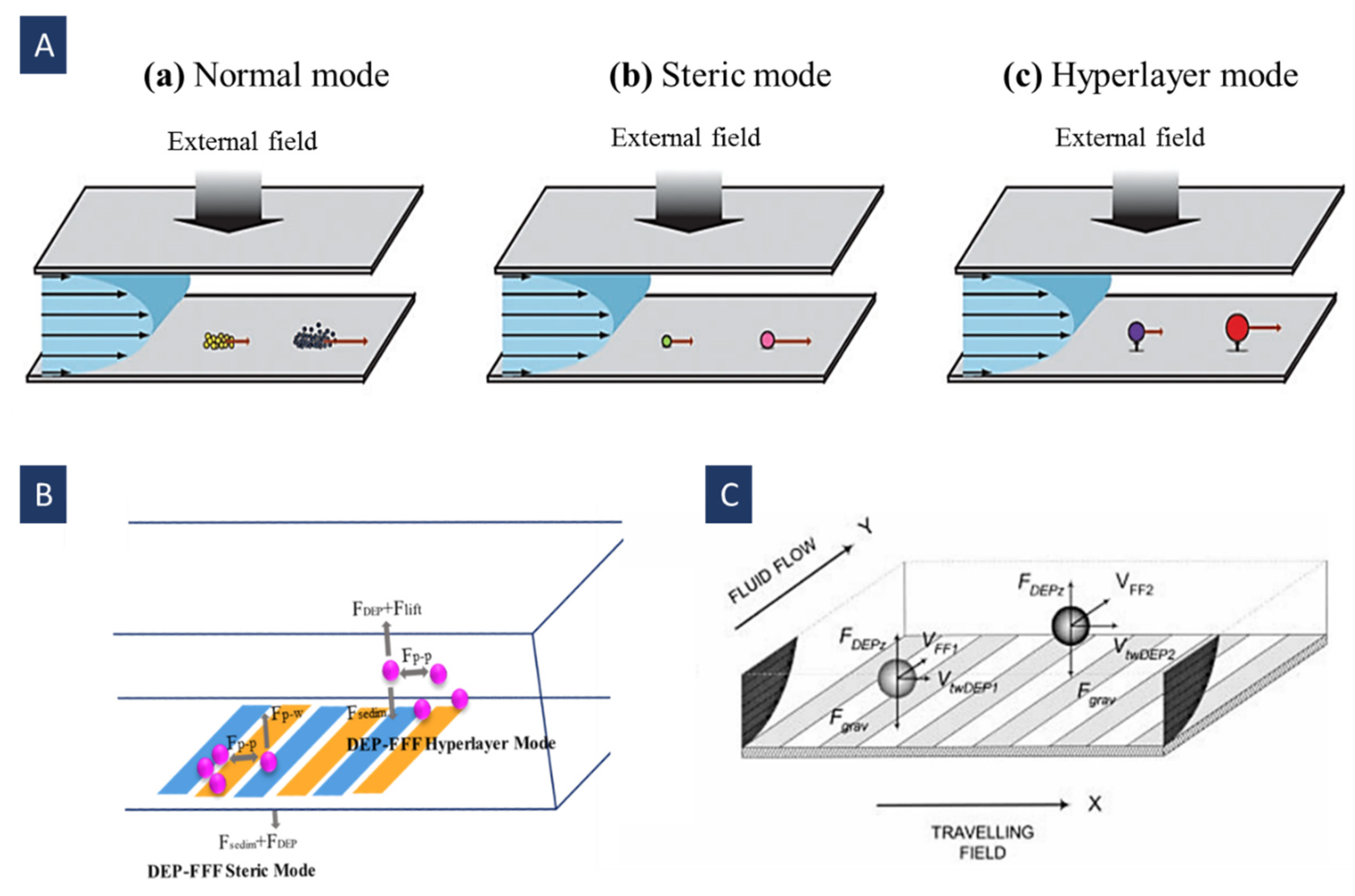
4.5. Field Flow Fractionation Dielectrophoresis (FFF-DEP)
| Refs (Method) | Target Particles | Frequency (Hz) | Medium Conductivity (s/m) | Particle Diameter (μm) | Flow Rate (μL/min) | Voltage (Vp–p) |
|---|---|---|---|---|---|---|
| [92] (Single frequency) | Live yeast cells- Dead yeast cells | 10 M | 7.5 | 0.225 | 6 | |
| [64] (Single frequency) | MCF7—HCT116 | 3.2 M | 0.3 | 0.1 | 9 | |
| [66] (Multiple frequency DEP) | Viable yeast cells- Nonviable yeast cells | F1 = 5 K F2 = 5 M | 0.0028 | 7(nonviable)-8(viable) | 5.7 | |
| [65] (Multiple frequency DEP) | PS particles-Yeast cells | 50 K and 60 K (focusing) 5 M (separation) | 0.126 | 2-4-5 (PS particles) | 10.4 | |
| [119] (Multiple frequency DEP) | Viable yeast cells- Non-viable yeast cells | 60–90 K (focusing) 5 M (separation) | 0.060 | 7(nonviable)-8(viable) | ~0 | 3.39 and 4.38 (focusing) 4.45 (separation) |
| [97] (UHF-DEP) | Different types of Mesenchymal Stem Cells (MSCs) | 90 M | 0.0224 |
| Refs (Method) | Target Particles | Frequency (Hz) | Medium Conductivity (s/m) | Particle Diameter (μm) | Flow Rate | Voltage (Vp–p) |
|---|---|---|---|---|---|---|
| [103] (twDEP-flow) | RBC-Liposome | 100–3 M | 0.1 m | 5.8 (RBC) 1.5–4.6 (liposome) | 1.67 (±0.83)–42 (±10) μm/s | 2–16 |
| [76] (Gradient twDEP) | S. cerevisiae bacteria- L. casei bacteria | 180 K | 10 m | 5–10 (S. cerevisiae) 2–4 (L. casei) | 3 μm/s | 3.5 |
| [106] (Gradient twDEP) | Latex microparticles | 200 K | 10 m | 3, 6, 10, 20 | 8 | |
| [120] (Spiral twDEP) | Trypanosomes- Mice RBCs- Human RBCs | 10–140 M | 10 μL/min | 2–4 | ||
| [67] (twDEP-EWOD) | Ground pine spores- AS latex beads Glass beads | 800 K 100 K 1 K | 120 m | 8 (Ground pine spore) 5 (latex beads) 8 (glass beads) | 10 μL/min | 15 (800 KHz) 10 (100 K) 120 (1 K) |
| [121] (twDEP-EWOD) | Viable yeast cells- Non-viable yeast cells | 70 K | 150 m | 8 (viable) 7 (non-viable) | 4 | |
| [101] (Gradient twDEP) | S. cerevisiae bacteria- yeast cells | 450 K | 5–10 (S. cerevisiae) 8 (yeast) | 4 | ||
| [122] (DEP-twDEP-ROT) | Viable Daudi cells- Non-viable Daudi cells Viable NCI-H929 cells- Non-Viable NCI-H929 cells | 78 m, 94 m | 12 (viable Daudi) 18 (non-viable Daudi) 14 (viable NCI-H929) 20 (non-viable NCI-H929) | 850 μm/s | ||
| [69] (twDEP) | Leukocyte | 500 K | 30 m | 7 | 10 | |
| [102] (Gradient twDEP) | E. coli bacteria-yeast cell | 100–350 K | 3 m, 10 m | 0.5 (E. coli) 8 (yeast) | 3.5–5 |
| Refs (Method) | Target Particles | Frequency (Hz) FS: Sine Signal Freq FP: Pulse Signal Freq DT: Duty Cycle | Medium Conductivity (s/m) | Particle Diameter (μm) | Flow Rate (μL/min) | Voltage (Vp-p) |
|---|---|---|---|---|---|---|
| [107] (puDEP) | PS beads | FS = 10 M Fp = 2 (10-μm beads) Fp = 1.05 (5-μm beads) Fp = 0.3 (3-μm beads) | 3, 5, 10 | 0.83 | 12 (10 μm) 20 (5 μm) 20 (3 μm) | |
| [12] (puDEP) | RBCs—PS beads | FS = 5 M FP = 1.25 DT = 0.75 | 0.025 | 7.9 ± 0.5 (RBC) 10 (PS) | 2.4 | 12 |
| [71] (puDEP) | Stem cells— their differentiation progeny. | FS = 3 M | 0.02 | 1.8–5.4 | 15.4 | |
| [72] (Frequency hopping) | PS beads RBC-MCF7 | 1*. Fcapture = 1 M, Frelease = 85 K, fshift = 1 2*. Fcapture = 1 M, Frelease = 20 K, fshift = 1 3*. Fcapture = 1 M, Frelease = 150 K, fshift = 1 | 0.028 | 3–5-10 (PS) 9.14 (RBC)-24.34 (MCF7) | 0.66 (PS beads) 0.83 (RBC-MCF7) | 20 |
| [73] (Moving DEP) | Viable-Nonviable Saccharomyces cerevisiae yeast cells | 2 M | 0.0305 | 8 (viable cells) 7 (nonviable cells) | 9.3 | |
| [74] (Moving puDEP) | PS beads | FS: 50 K (pDEP)—2 M (nDEP) 1.5 < Fp/FS < 5 | 0.0002 | 10 |
5. Technical and Biological Challenges of DEP Approaches
6. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| r | Radius | Electrode spatial frequency | |
| CM | Clausius–Mossotti | W | Width |
| fCM | Clausius–Mossotti factor | PDAC | Pancreatic ductal Adenocarcinoma |
| E | Electric field | MOSE | Mouse ovarian surface epithelial |
| FHD | Hydrodynamic drag force | HSP | Heat shock proteins |
| ɛ | Permittivity | RBC | Red blood cell |
| u | Velocity | MWO | Maxwell–Wagner–O’Konski |
| σ | Conductivity | DEP | Dielectrophoresis |
| Relaxation time | pDEP | Positive Dielectrophoresis | |
| ρ | Density | nDEP | Negative Dielectrophoresis |
| µ | Dynamic viscosity | MFDEP | Multiple frequency Dielectrophoresis |
| f | Frequency | twDEP | Traveling wave Dielectrophoresis |
| Angular Frequency | PuDEP | Pulsed Dielectrophoresis | |
| Electric Potential | UHF-DEP | Ultra-high frequency dielectrophoresis | |
| k | Boltzmann’s constant | tvDEP | Time-varying Dielectrophoresis |
| q | Electrical charge | mDEP | Moving Dielectrophoresis |
| K | Surface conductance | FFF-DEP | Field flow fractionation Dielectrophoresis |
| Re | Real | puDEP | Pulsed DEP |
| Im | Imaginary | LOC | Lab-on-Chip |
| DL | Double layer | ROT | Electrorotation |
| v | Flow rate | OSCC | Oral squamous cell carcinoma |
| m | Mass | SEM | Scanning electron microscopy |
| C | Concentration | NCAM | Neural cell adhesion molecule |
| T | Time | PSA | Polysialic acid |
| L | Characteristic length | cDEP | Contactless dielectrophoresis |
| DT | Duty cycle | oDEP | Optical dielectrophoresis |
| V | Electric voltage | iDEP | Insulating dielectrophoresis |
| C | Capacitance |
References
- Salafi, T.; Zhang, Y.; Zhang, Y. A Review on Deterministic Lateral Displacement for Particle Separation and Detection. Nano-Micro Lett. 2019, 11, 77. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tajik, P.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.T. Simple, Cost-Effective, and Continuous 3D Dielectrophoretic Microchip for Concentration and Separation of Bioparticles. Ind. Eng. Chem. Res. 2020, 59, 3772–3783. [Google Scholar] [CrossRef]
- Mehran, A.; Rostami, P.; Saidi, M.S.; Firoozabadi, B.; Kashaninejad, N. High-Throughput, Label-Free Isolation of White Blood Cells from Whole Blood Using Parallel Spiral Microchannels with U-Shaped Cross-Section. Biosensors 2021, 11, 406. [Google Scholar] [CrossRef]
- Folch, A. Introduction to BioMEMS; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9781466509382. [Google Scholar]
- Sajeesh, P.; Sen, A.K. Particle separation and sorting in microfluidic devices: A review. Microfluid. Nanofluidics 2013, 17, 1–52. [Google Scholar] [CrossRef]
- Lenshof, A.; Laurell, T. Continuous separation of cells and particles in microfluidic systems. Chem. Soc. Rev. 2010, 39, 1203–1217. [Google Scholar] [CrossRef]
- Pamme, N. Continuous flow separations in microfluidic devices Lab-on-a-chip platform for detection of early metastasis biomarkers View project Continuous flow separations in microfluidic devices. Lab Chip 2008, 7, 1644–1659. [Google Scholar] [CrossRef]
- Chen, X.; Cui, D.; Liu, C.; Li, H.; Chen, J. Continuous flow microfluidic device for cell separation, cell lysis and DNA purification. Anal. Chim. Acta 2007, 584, 237–243. [Google Scholar] [CrossRef]
- Ashkin, A. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA 1997, 94, 4853–4860. [Google Scholar] [CrossRef] [Green Version]
- Lenshof, A.; Magnusson, C.; Laurell, T. Acoustofluidics 8: Applications of acoustophoresis in continuous flow microsystems. Lab Chip 2012, 12, 1210–1223. [Google Scholar] [CrossRef]
- Pesch, G.R.; Du, F. A review of dielectrophoretic separation and classification of non-biological particles. Electrophoresis 2021, 42, 134–152. [Google Scholar] [CrossRef]
- Techaumnat, B.; Panklang, N.; Wisitsoraat, A.; Suzuki, Y. Study on the discrete dielectrophoresis for particle-cell separation. Electrophoresis 2020, 41, 991–1001. [Google Scholar] [CrossRef] [PubMed]
- Pohl, H.A. Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields; Cambridge University Press: Cambridge, UK, 1978; p. 579. [Google Scholar]
- Çetin, B.; Li, D. Dielectrophoresis in microfluidics technology. Electrophoresis 2011, 32, 2410–2427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pethig, R. Dielectrophoresis: Status of the theory, technology, and applications. Biomicrofluidics 2010, 4, 022811. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mohd Maidin, N.N.; Buyong, M.R.; Rahim, R.A.; Mohamed, M.A. Dielectrophoresis applications in biomedical field and future perspectives in biomedical technology. Electrophoresis 2021, 42, 2033–2059. [Google Scholar] [CrossRef]
- Abd Rahman, N.; Ibrahim, F.; Yafouz, B.; Rahman, N.A.; Ibrahim, F.; Yafouz, B.; Abd Rahman, N.; Ibrahim, F.; Yafouz, B. Dielectrophoresis for Biomedical Sciences Applications: A Review. Sensors 2017, 17, 449. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Yuan, Y.J. A review of polystyrene bead manipulation by dielectrophoresis. RSC Adv. 2019, 9, 4963–4981. [Google Scholar] [CrossRef] [Green Version]
- Chan, J.Y.; Ahmad Kayani, A.B.; Md Ali, M.A.; Kok, C.K.; Yeop Majlis, B.; Hoe, S.L.L.; Marzuki, M.; Khoo, A.S.B.; Ostrikov, K.; Ataur Rahman, M.; et al. Dielectrophoresis-based microfluidic platforms for cancer diagnostics. Biomicrofluidics 2018, 12, 011503. [Google Scholar] [CrossRef]
- Gascoyne, P.R.C.; Shim, S. Isolation of Circulating Tumor Cells by Dielectrophoresis. Cancers 2014, 6, 545–579. [Google Scholar] [CrossRef] [Green Version]
- Köehler, M. Isotropic Etching. In Encyclopedia of Microfluidics and Nanofluidics; Springer: Boston, MA, USA, 2014; pp. 1–11. [Google Scholar] [CrossRef]
- West, J.; Becker, M.; Tombrink, S.; Manz, A. Micro Total Analysis Systems: Latest Achievements. Anal. Chem. 2008, 80, 4403–4419. [Google Scholar] [CrossRef]
- Craighead, H. Future lab-on-a-chip technologies for interrogating individual molecules. Nanosci. Technol. A Collect. Rev. Nat. J. 2009, 442, 330–336. [Google Scholar] [CrossRef]
- El-Ali, J.; Sorger, P.K.; Jensen, K.F. Cells on chips. Nature 2006, 442, 403–411. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Chang, H.; Neuzil, P. DEP-on-a-chip: Dielectrophoresis applied to microfluidic platforms. Micromachines 2019, 10, 423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Yan, S.; Li, W.; Alici, G.; Nguyen, N.T. High throughput extraction of plasma using a secondary flow-aided inertial microfluidic device. RSC Adv. 2014, 4, 33149–33159. [Google Scholar] [CrossRef] [Green Version]
- Fallahi, H.; Zhang, J.; Phan, H.P.; Nguyen, N.T. Flexible Microfluidics: Fundamentals, Recent Developments, and Applications. Micromachines 2019, 10, 830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berthier, J. Introduction to Liquid Dielectrophoresis. In Micro-Drops and Digital Microfluidics; William Andrew: Norwich, NY, USA, 2013; pp. 303–324. [Google Scholar] [CrossRef]
- Pethig, R. The Clausius–Mossotti Factor. In Dielectrophoresis: Theory, Methodology and Biological Applications; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2017; pp. 119–144. [Google Scholar] [CrossRef]
- Gascoyne, P.R.C.; Vykoukal, J. Particle separation by dielectrophoresis. Electrophoresis 2002, 23, 1973. [Google Scholar] [CrossRef]
- Omori, R. Observation of a single-beam gradient-force optical trap for dielectric particles in air. Opt. Lett. 1997, 22, 816–818. [Google Scholar] [CrossRef]
- Prodromakis, T.; Papavassiliou, C. Engineering the Maxwell–Wagner polarization effect. Appl. Surf. Sci. 2009, 255, 6989–6994. [Google Scholar] [CrossRef]
- Mortadi, A.; El Melouky, A.; Chahid, E.G.; El Moznine, R.; Cherkaoui, O. Studies of the clausius–Mossotti factor. J. Phys. Stud. 2016, 20, 4001. [Google Scholar] [CrossRef]
- Wang, X.B.; Huang, Y.; Gascoyne, P.R.C.; Becker, F.F.; Hölzel, R.; Pethig, R. Changes in Friend murine erythroleukaemia cell membranes during induced differentiation determined by electrorotation. Biochim. Et Biophys. Acta 1994, 1193, 330–344. [Google Scholar] [CrossRef]
- Cheung, K.C.; Berardino, M.D.; Schade-Kampmann, G.; Hebeisen, M.; Pierzchalski, A.; Bocsi, J.; Mittag, A.; Tárnok, A. Microfluidic impedance-based flow cytometry. Cytom. Part A 2010, 77, 648–666. [Google Scholar] [CrossRef]
- Serhan, M.; Sprowls, M.; Jackemeyer, D.; Long, M.; Perez, I.D.; Maret, W.; Tao, N.; Forzani, E. Total iron measurement in human serum with a smartphone. AIChE Annu. Meet. Conf. Proc. 2020, 8, 2800309. [Google Scholar] [CrossRef]
- Gascoyne, P.R.C.; Pethig, R.; Burt, J.P.H.; Becker, F.F. Membrane changes accompanying the induced differentiation of Friend murine erythroleukemia cells studied by dielectrophoresis. Biochim. Et Biophys. Acta (BBA)-Biomembr. 1993, 1149, 119–126. [Google Scholar] [CrossRef]
- Moritani, S.; Ichihara, S.; Hasegawa, M.; Endo, T.; Oiwa, M.; Shiraiwa, M.; Nishida, C.; Morita, T.; Sato, Y.; Hayashi, T.; et al. Topographical, morphological and immunohistochemical characteristics of carcinoma in situ of the breast involving sclerosing adenosis. Two distinct topographical patterns and histological types of carcinoma in situ. Histopathology 2011, 58, 835–846. [Google Scholar] [CrossRef]
- Scarpelli, M.; Bartels, P.H.; Montironi, R.; Galluzzi, C.M.; Thompson, D. Morphometrically assisted grading of astrocytomas. Anal. Quant. Cytol. Histol. 1994, 16, 351–356. [Google Scholar]
- Duesberg, P.; Li, R.; Fabarius, A.; Hehlmann, R. The chromosomal basis of cancer. Anal. Cell. Pathol. 2005, 27, 293–318. [Google Scholar] [CrossRef] [PubMed]
- McGrath, J.S.; Honrado, C.; Moore, J.H.; Adair, S.J.; Varhue, W.B.; Salahi, A.; Farmehini, V.; Goudreau, B.J.; Nagdas, S.; Blais, E.M.; et al. Electrophysiology-based stratification of pancreatic tumorigenicity by label-free single-cell impedance cytometry. Anal. Chim. Acta 2020, 1101, 90–98. [Google Scholar] [CrossRef]
- Trainitoid, C.I.; Sweeneyid, D.C.; Čemažar, J.; Schmelz, E.M.; Franç Ais, O.; Le Pioufle, B.; Davalos, R. V Characterization of sequentially-staged cancer cells using electrorotation. PLoS ONE 2019, 14, e0222289. [Google Scholar] [CrossRef]
- Al Ahmad, M.; Al Natour, Z.; Mustafa, F.; Rizvi, T.A. Electrical Characterization of Normal and Cancer Cells. IEEE Access 2018, 6, 25979–25986. [Google Scholar] [CrossRef]
- Habaza, M.; Kirschbaum, M.; Guernth-Marschner, C.; Dardikman, G.; Barnea, I.; Korenstein, R.; Duschl, C.; Shaked, N.T.; Habaza, M.; Dardikman, G.; et al. Rapid 3D Refractive-Index Imaging of Live Cells in Suspension without Labeling Using Dielectrophoretic Cell Rotation. Adv. Sci. 2016, 4, 1600205. [Google Scholar] [CrossRef]
- Hu, X.; Arnold, W.M.; Zimmermann, U. Alterations in the electrical propertes of T and B lymphocyte membranes induced by mitogenic stimulation. Activation monitored by electro-rotation of single cells. Biochim. Biophys. Acta 1990, 1021, 191–200. [Google Scholar] [CrossRef]
- Pethig, R.; Noshari, J.; Becker, F.F. Use of Dielectrophoretic Collection Spectra for Characterizing Differences between Normal and Cancerous Cells. IEEE Trans. Ind. Appl. 1994, 30, 829–834. [Google Scholar] [CrossRef]
- Becker, F.F.; Wang, X.B.; Huang, Y.; Pethig, R.; Vykoukal, J.; Gascoyne, P.R. Separation of human breast cancer cells from blood by differential dielectric affinity. Proc. Natl. Acad. Sci. USA 1995, 92, 860–864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arnold, W.M.; Zimmermann, U. Electro-rotation: Development of a technique for dielectric measurements on individual cells and particles. J. Electrostat. 1988, 21, 151–191. [Google Scholar] [CrossRef]
- Huang, Y.; Joo, S.; Duhon, M.; Heller, M.; Wallace, B.; Xu, X. Dielectrophoretic cell separation and gene expression profiling on microelectronic chip arrays. Anal. Chem. 2002, 74, 3362–3371. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Duarte, R. Microfabrication technologies in dielectrophoresis applications—A review. Electrophoresis 2012, 33, 3110–3132. [Google Scholar] [CrossRef]
- Cummings, E.B.; Singh, A.K. Dielectrophoresis in Microchips Containing Arrays of Insulating Posts: Theoretical and Experimental Results. Anal. Chem. 2003, 75, 4724–4731. [Google Scholar] [CrossRef]
- Lapizco-Encinas, B.H. On the recent developments of insulator-based dielectrophoresis: A review. Electrophoresis 2019, 40, 358–375. [Google Scholar] [CrossRef]
- Huang, X.H.; Torres-Castro, K.; Varhue, W.; Salahi, A.; Rasin, A.; Honrado, C.; Brown, A.; Guler, J.; Swami, N.S. Self-aligned sequential lateral field non-uniformities over channel depth for high throughput dielectrophoretic cell deflection. Lab Chip 2021, 21, 835–843. [Google Scholar] [CrossRef]
- Choi, S.; Park, J.-K. Microfluidic system for dielectrophoretic separation based on a trapezoidal electrode array. Lab Chip 2005, 5, 1161–1167. [Google Scholar] [CrossRef]
- Kralj, J.G.; Lis, M.T.; Schmidt, M.A.; Jensen, K.F. Continuous Dielectrophoretic Size-Based Particle Sorting. Anal. Chem. 2006, 78, 5019–5025. [Google Scholar] [CrossRef]
- Wang, L.; Lu, J.; Marchenko, S.A.; Monuki, E.S.; Flanagan, L.A.; Lee, A.P. Dual frequency dielectrophoresis with interdigitated sidewall electrodes for microfluidic flow-through separation of beads and cells. Electrophoresis 2009, 30, 782–791. [Google Scholar] [CrossRef] [PubMed]
- Fiedler, S.; Shirley, S.G.; Schnelle, T.; Fuhr, G. Dielectrophoretic Sorting of Particles and Cells in a Microsystem. Anal. Chem. 1998, 70, 1909–1915. [Google Scholar] [CrossRef] [PubMed]
- Alnaimat, F.; Mathew, B.; Hilal-Alnaqbi, A. Modeling a Dielectrophoretic Microfluidic Device with Vertical Interdigitated Transducer Electrodes for Separation of Microparticles Based on Size. Micromachines 2020, 11, 563. [Google Scholar] [CrossRef] [PubMed]
- Beech, J.P.; Keim, K.; Dang Ho, B.; Guiducci, C.; Tegenfeldt, J.O. Active Posts in Deterministic Lateral Displacement Devices. Adv. Mater. Technol. 2019, 4, 1900339. [Google Scholar] [CrossRef] [Green Version]
- Siegel, A.C.; Tang, S.K.Y.; Nijhuis, C.A.; Hashimoto, M.; Phillips, S.T.; Dickey, M.D.; Whitesides, G.M. Cofabrication: A Strategy for Building Multicomponent Microsystems. Acc. Chem. Res. 2010, 43, 518–528. [Google Scholar] [CrossRef] [Green Version]
- So, J.H.; Dickey, M.D. Inherently aligned microfluidic electrodes composed of liquid metal. Lab Chip 2011, 11, 905–911. [Google Scholar] [CrossRef]
- Lewpiriyawong, N.; Yang, C.; Lam, Y.C. Continuous sorting and separation of microparticles by size using AC dielectrophoresis in a PDMS microfluidic device with 3-D conducting PDMS composite electrodes. Electrophoresis 2010, 31, 2622–2631. [Google Scholar] [CrossRef]
- Vahey, M.D.; Voldman, J. High-Throughput Cell and Particle Characterization Using Isodielectric Separation. Anal. Chem. 2009, 81, 2446–2455. [Google Scholar] [CrossRef] [Green Version]
- Alshareef, M.; Metrakos, N.; Juarez Perez, E.; Azer, F.; Yang, F.; Yang, X.; Wang, G. Separation of tumor cells with dielectrophoresis-based microfluidic chip. Biomicrofluidics 2013, 7, 011803. [Google Scholar] [CrossRef] [Green Version]
- Demierre, N.; Braschler, T.; Muller, R.; Renaud, P. Focusing and continuous separation of cells in a microfluidic device using lateral dielectrophoresis. Sens. Actuators B Chem. 2008, 132, 388–396. [Google Scholar] [CrossRef]
- Urdaneta, M.; Smela, E. Multiple frequency dielectrophoresis. Electrophoresis 2007, 28, 3145–3155. [Google Scholar] [CrossRef] [PubMed]
- Cheng, I.-F.; Froude, V.E.; Zhu, Y.; Chang, H.-C.; Chang, H.-C. A continuous high-throughput bioparticle sorter based on 3D traveling-wave dielectrophoresis. Lab Chip 2009, 9, 3193–3201. [Google Scholar] [CrossRef] [PubMed]
- Cheng, I.-F.; Chung, C.-C.; Chang, H.-C. High-throughput electrokinetic bioparticle focusing based on a travelling-wave dielectrophoretic field. Microfluid. Nanofluidics 2010, 10, 649–660. [Google Scholar] [CrossRef]
- Van Den Driesche, S.; Zirath, H.; Puchberger-Enengl, D.; Iuliano, F.; Wiesinger-Mayr, H.; Vellekoop, M.J. Separation of biological cells and bacteria by gradient electrodes. Procedia Eng. 2011, 25, 705–708. [Google Scholar] [CrossRef] [Green Version]
- Menachery, A.; Kremer, C.; Wong, P.E.; Carlsson, A.; Neale, S.L.; Barrett, M.P.; Cooper, J.M. Counterflow Dielectrophoresis for Trypanosome Enrichment and Detection in Blood. Sci. Rep. 2012, 2, 775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, H.; Rosano, J.M.; Wang, Y.; Garson, C.J.; Prabhakarpandian, B.; Pant, K.; Klarmann, G.J.; Perantoni, A.; Alvarez, L.M.; Lai, E. Continuous-flow sorting of stem cells and differentiation products based on dielectrophoresis. Lab Chip 2015, 15, 1320–1328. [Google Scholar] [CrossRef] [PubMed]
- Modarres, P.; Tabrizian, M. Frequency hopping dielectrophoresis as a new approach for microscale particle and cell enrichment. Sens. Actuators B Chem. 2019, 286, 493–500. [Google Scholar] [CrossRef]
- Kua, C.H.; Lam, Y.C.; Rodriguez, I.; Yang, C.; Youcef-Toumi, K. Dynamic Cell Fractionation and Transportation Using Moving Dielectrophoresis. Anal. Chem. 2007, 79, 6975–6987. [Google Scholar] [CrossRef]
- Honegger, T.; Peyrade, D. Moving pulsed dielectrophoresis. Lab Chip 2013, 13, 1538–1545. [Google Scholar] [CrossRef]
- De Gasperis, G.; Yang, J.; Becker, F.F.; Gascoyne, P.R.C.; Wang, X.-B. Microfluidic Cell Separation by 2-dimensional Dielectrophoresis. Biomed. Microdevices 1999, 2, 41–49. [Google Scholar] [CrossRef]
- Fathy, J.; Pourmand, A.; Ghavifekr, H.B. Design and simulation of a MEMS based cell separator utilizing 3D travelling-wave dielectrophoresis. Microsyst. Technol. 2015, 23, 1351–1360. [Google Scholar] [CrossRef]
- Jiang, T.; Ren, Y.; Liu, W.; Tang, D.; Tao, Y.; Xue, R.; Jiang, H. Dielectrophoretic separation with a floating-electrode array embedded in microfabricated fluidic networks. Phys. Fluids 2018, 30, 112003. [Google Scholar] [CrossRef]
- Zhang, C.; Khoshmanesh, K.; Mitchell, A.; Kalantar-Zadeh, K. Dielectrophoresis for manipulation of micro/nano particles in microfluidic systems. Anal. Bioanal. Chem. 2009, 396, 401–420. [Google Scholar] [CrossRef] [PubMed]
- Chiou, P.Y.; Ohta, A.T.; Wu, M.C. Massively parallel manipulation of single cells and microparticles using optical images. Nature 2005, 436, 370–372. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Liu, C.; Loo, J.; Stakenborg, T.; Lagae, L. Single cell viability observation in cell dielectrophoretic trapping on a microchip. Appl. Phys. Lett. 2014, 104, 3–8. [Google Scholar] [CrossRef]
- Archer, S.; Li, T.T.; Evans, A.T.; Britland, S.T.; Morgan, H. Cell reactions to dielectrophoretic manipulation. Biochem. Biophys. Res. Commun. 1999, 257, 687–698. [Google Scholar] [CrossRef]
- Wang, X.; Yang, J.; Gascoyne, P.R.C. Role of peroxide in AC electrical field exposure effects on Friend murine erythroleukemia cells during dielectrophoretic manipulations. Biochim. Biophys. Acta 1999, 1426, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Farasat, M.; Chavoshi, S.M.; Bakhshi, A.; Valipour, A.; Badieirostami, M. A dielectrophoresis-based microfluidic chip for trapping circulating tumor cells using a porous membrane. J. Micromech. Microeng. 2022, 32, 015008. [Google Scholar] [CrossRef]
- Dastani, K.; Moghimi Zand, M.; Kavand, H.; Javidi, R.; Hadi, A.; Valadkhani, Z.; Renaud, P. Effect of input voltage frequency on the distribution of electrical stresses on the cell surface based on single-cell dielectrophoresis analysis. Sci. Rep. 2020, 10, 68. [Google Scholar] [CrossRef]
- Nerguizian, V.; Stiharu, I.; Al-Azzam, N.; Yassine-Diab, B.; Alazzam, A. The effect of dielectrophoresis on living cells: Crossover frequencies and deregulation in gene expression. Analyst 2019, 144, 3853–3860. [Google Scholar] [CrossRef]
- Wong, T.-K.K.; Neumann, E. Electric field mediated gene transfer. Biochem. Biophys. Res. Commun. 1982, 107, 584–587. [Google Scholar] [CrossRef] [Green Version]
- Salipante, P.F.; Knorr, R.L.; Dimova, R.; Vlahovska, P.M. Electrodeformation method for measuring the capacitance of bilayer membranes. Soft Matter 2012, 8, 3810–3816. [Google Scholar] [CrossRef]
- Zhang, X.; Shen, L.; Bao, H.; Din, X.; Wang, R.; Liu, Y.; Gao, N.; Huang, Y. The effect of some medical treatments of thalassemia on the red blood cells. Hyperfine Interact. 1992, 71, 1251–1254. [Google Scholar] [CrossRef]
- Mueller, T.; Fuhr, G.; Glasser, H.; Miiller, T.; Schnelle, T. Cell manipulation and cultivation under a.c. electric field influence in highly conductive culture media AC-electrokinetic characterization and manipulation of cells and media View project Microrotation Imaging View project Biochi~ic~a et Biophysica A~ta. Artic. Biochim. Biophys. Acta 1995, 1201, 353–360. [Google Scholar] [CrossRef]
- Markx, G.H.; Pethig, R. Dielectrophoretic separation of cells: Continuous separation. Biotechnol. Bioeng. 1995, 45, 337–343. [Google Scholar] [CrossRef]
- Shkolnikov, V.; Xin, D.; Chen, C.-H. Continuous dielectrophoretic particle separation via isomotive dielectrophoresis with bifurcating stagnation flow. Electrophoresis 2019, 40, 2988–2995. [Google Scholar] [CrossRef]
- Zhao, K.; Larasati; Duncker, B.P.; Li, D. Continuous Cell Characterization and Separation by Microfluidic Alternating Current Dielectrophoresis. Anal. Chem. 2019, 91, 6304–6314. [Google Scholar] [CrossRef]
- Erdem, N.; Yildizhan, Y.; Elitas, M. A Numerical Approach for Dielectrophoretic Characterization and Separation of Human Hematopoietic Cells. Int. J. Eng. Res. 2017, 6, 1079–1082. [Google Scholar] [CrossRef]
- Gascoyne, P.R.C.; Wang, X.B.; Huang, Y.; Becker, R.F. Dielectrophoretic separation of cancer cells from blood. IEEE Trans. Ind. Appl. 1997, 33, 670–678. [Google Scholar] [CrossRef] [Green Version]
- Gimsa, J.; Marszalek, P.; Loewe, U.; Tsong, T.Y. Dielectrophoresis and electrorotation of neurospora slime and murine myeloma cells. Biophys. J. 1991, 60, 749–760. [Google Scholar] [CrossRef] [Green Version]
- Valero, A.; Braschler, T.; Rauch, A.; Demierre, N.; Barral, Y.; Renaud, P. Tracking and synchronization of the yeast cell cycle using dielectrophoretic opacity. Lab Chip 2011, 11, 1754–1760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Provent, T.; Manczak, R.; Saada, S.; Dalmay, C.; Bessette, B.; Begaud, G.; Battu, S.; Blondy, P.; Jauberteau, M.O.; Lalloue, F.; et al. Ultra-High Frequencies continuous biological cell sorting based on repulsive and low dielectrophoresis forces. In Proceedings of the 2019 IEEE MTT-S International Microwave Symposium (IMS), Boston, MA, USA, 2–7 June 2019; pp. 224–227. [Google Scholar] [CrossRef]
- Manczak, R.; Saada, S.; Provent, T.; Dalmay, C.; Bessette, B.; Bégaud, G.; Battu, S.; Blondy, P.; Jauberteau, M.O.; Baristiran Kaynak, C.; et al. UHF-Dielectrophoresis Crossover Frequency as a New Marker for Discrimination of Glioblastoma Undifferentiated Cells. IEEE J. Electromagn. RF Microwaves Med. Biol. 2019, 3, 191–198. [Google Scholar] [CrossRef]
- Chung, C.; Pethig, R.; Smith, S.; Waterfall, M. Intracellular potassium under osmotic stress determines the dielectrophoresis cross-over frequency of murine myeloma cells in the MHz range. Electrophoresis 2018, 39, 989–997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, S.K.; Huang, P.W.; Wang, T.T.; Peng, Y.H. Cross-scale electric manipulations of cells and droplets by frequency-modulated dielectrophoresis and electrowetting. Lab Chip 2008, 8, 1325–1331. [Google Scholar] [CrossRef]
- Turcan, I.; Olariu, M.A. Dielectrophoretic Manipulation of Cancer Cells and Their Electrical Characterization. ACS Comb. Sci. 2020, 22, 554–578. [Google Scholar] [CrossRef]
- Zhao, Y.; Yi, U.C.; Cho, S.K. Microparticle concentration and separation by traveling-wave dielectrophoresis (twDEP) for digital microfluidics. J. Microelectromechanical Syst. 2007, 16, 1472–1481. [Google Scholar] [CrossRef]
- Choi, E.; Kim, B.; Park, J. High-throughput microparticle separation using gradient traveling wave dielectrophoresis. J. Micromech. Microeng. 2009, 19, 125014. [Google Scholar] [CrossRef]
- Fair, R.B. Digital microfluidics: Is a true lab-on-a-chip possible? Microfluid. Nanofluidics 2007, 3, 245–281. [Google Scholar] [CrossRef]
- Fathy, J.; Pourmand, A.; Badri Ghavifekr, H. Utilizing electric field to separate cells with travelling-wave dielectrophoresis force in a droplet. In Proceedings of the 2017 Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 2–4 May 2017; pp. 435–439. [Google Scholar] [CrossRef]
- Cen, E.G.; Dalton, C.; Li, Y.; Adamia, S.; Pilarski, L.M.; Kaler, K.V.I.S. A combined dielectrophoresis, traveling wave dielectrophoresis and electrorotation microchip for the manipulation and characterization of human malignant cells. J. Microbiol. Methods 2004, 58, 387–401. [Google Scholar] [CrossRef]
- Cui, H.-H.; Voldman, J.; He, X.-F.; Lim, K.-M. Separation of particles by pulsed dielectrophoresis. Lab Chip 2009, 9, 2306–2312. [Google Scholar] [CrossRef]
- Modarres, P.; Tabrizian, M. Modeling and analysis of a novel approach for particle separation using time-varying amplitude dielectrophoresis. In Proceedings of the 2016 IEEE EMBS International Student Conference (ISC), Ottawa, ON, Canada, 29–31 May 2016. [Google Scholar] [CrossRef]
- Kua, C.H. Particle Manipulation Using Moving Dielectrophoresis. Ph.D. Thesis, Nanyang Technological University, Singapore, 2007. [Google Scholar] [CrossRef] [Green Version]
- Giddings, J.C. The conceptual basis of field-flow fractionation. J. Chem. Educ. 1973, 50, 667–669. [Google Scholar] [CrossRef]
- Giddings, J. Field-flow fractionation: Analysis of macromolecular, colloidal, and particulate materials. Science 1993, 260, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Gascoyne, P.R.C.; Noshari, J.; Anderson, T.J.; Becker, F.F. Isolation of rare cells from cell mixtures by dielectrophoresis. Electrophoresis 2009, 30, 1388–1398. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reschiglian, P.; Zattoni, A.; Roda, B.; Michelini, E.; Roda, A. Field-flow fractionation and biotechnology. Trends Biotechnol. 2005, 23, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Waheed, W.; Sharaf, O.Z.; Alazzam, A.; Abu-Nada, E. Dielectrophoresis-field flow fractionation for separation of particles: A critical review. J. Chromatogr. A 2021, 1637, 461799. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, K.D.; Cheng, Z.-Q.; Hradecky, P.; Giddings, J.C. Separation of human and animal cells by steric field-flow fractionation. Cell Biophys. 1984, 6, 233–251. [Google Scholar] [CrossRef]
- Giddings, J.C. Hyperlayer Field-Flow Fractionation. Sep. Sci. Technol. 2006, 18, 765–773. [Google Scholar] [CrossRef]
- Williams, P.S.; Koch, T.; Giddings, J.C. Characterization of near-wall hydrodynamic lift forces using sedimentation field-flow fractionation. Chem. Eng. Commun. 2007, 111, 121–147. [Google Scholar] [CrossRef]
- Tong, C.; Caldwell, K.D. Separation and characterization of red blood cells with different membrane deformability using steric field-flow fractionation. J. Chromatogr. B Biomed. Appl. 1995, 674, 39–47. [Google Scholar] [CrossRef]
- Braschler, T.; Demierre, N.; Nascimento, E.; Silva, T.; Oliva, A.G.; Renaud, P. Continuous separation of cells by balanced dielectrophoretic forces at multiple frequencies. Lab Chip 2008, 8, 280–286. [Google Scholar] [CrossRef]
- Flores-Mena, J.E.; García-Sánchez, P.; Ramos, A. micromachines Dipolophoresis and Travelling-Wave Dipolophoresis of Metal Microparticles. Micromachines 2020, 11, 259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morgan, H.; Green, G.; Hughes, M.P.; Monaghan, W.; Tan, T.C. Large-area travelling-wave dielectrophoresis particle separator. J. Micromech. Microeng 1997, 7, 65–70. [Google Scholar] [CrossRef]
- van den Driesche, S.; Bunge, F.; Tepner, S.; Kotitschke, M.; Vellekoop, M.J. Travelling-wave dielectrophoresis allowing flexible microchannel design for suspended cell handling. In Proceedings of the Bio-MEMS and Medical Microdevices III, Barcelona, Spain, 8–10 May 2017; Volume 10247, pp. 109–115. [Google Scholar] [CrossRef]
- Pethig, R. Review—Where Is Dielectrophoresis (DEP) Going? J. Electrochem. Soc. 2017, 164, B3049–B3055. [Google Scholar] [CrossRef]
- Wang, C.H.; Lee, Y.H.; Kuo, H.T.; Liang, W.F.; Li, W.J.; Lee, G. Bin Dielectrophoretically-assisted electroporation using light-activated virtual microelectrodes for multiple DNA transfection. Lab Chip 2013, 14, 592–601. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lee, H.F.; Zaro, J.L.; Shen, W.C. Effects of Receptor Binding on Plasma Half-Life of Bifunctional Transferrin Fusion Proteins. Mol. Pharm. 2011, 8, 457–465. [Google Scholar] [CrossRef] [Green Version]
- Patel, V.K.; Seyed-Yagoobi, J. Combined Electrohydrodynamic Conduction Pumping and Dielectrophoresis for Enhancement of Liquid Film Flow Boiling. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2016. [Google Scholar] [CrossRef]
- Henslee, E.A.; Sano, M.B.; Rojas, A.D.; Schmelz, E.M.; Davalos, R.V. Selective concentration of human cancer cells using contactless dielectrophoresis. Electrophoresis 2011, 32, 2523–2529. [Google Scholar] [CrossRef] [PubMed]
- Mahmudunnabi, R.G.; Farhana, F.Z.; Kashaninejad, N.; Firoz, S.H.; Shim, Y.B.; Shiddiky, M.J.A. Nanozyme-based electrochemical biosensors for disease biomarker detection. Analyst 2020, 145, 4398–4420. [Google Scholar] [CrossRef]
- Sarno, B.; Heineck, D.; Heller, M.J.; Ibsen, S.D. Dielectrophoresis: Developments and applications from 2010 to 2020. Electrophoresis 2021, 42, 539–564. [Google Scholar] [CrossRef]
- Kashaninejad, N.; Munaz, A.; Moghadas, H.; Yadav, S.; Umer, M.; Nguyen, N.T. Microneedle Arrays for Sampling and Sensing Skin Interstitial Fluid. Chemosens 2021, 9, 83. [Google Scholar] [CrossRef]
- Chen, Y.; Li, P.; Huang, P.-H.; Xie, Y.; Mai, J.D.; Wang, L.; Nguyen, N.-T.; Huang, T.J. Rare cell isolation and analysis in microfluidics. Lab Chip 2014, 14, 626. [Google Scholar] [CrossRef] [Green Version]
- Shields, C.W.; Ohiri, K.A.; Szott, L.M.; López, G.P. Translating microfluidics: Cell separation technologies and their barriers to commercialization. Cytom. Part B Clin. Cytom. 2017, 92, 115–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Becker, F.F.; Gascoyne, P.R. Membrane dielectric changes indicate induced apoptosis in HL-60 cells more sensitively than surface phosphatidylserine expression or DNA fragmentation. Biochim. Biophys. Acta-Biomembr. 2002, 1564, 412–420. [Google Scholar] [CrossRef] [Green Version]

| Refs | Electrode Types | Material | Methods |
|---|---|---|---|
| [64] | planar electrode (2 electrodes) | ITO | Crossover-based separation |
| [65] | Planar electrode | Ti/Pt | Crossover-based separation |
| [66] | Planar electrode (3 electrodes) | Au/Cr | Crossover-based separation |
| [67,68] | Top-bottom electrode array | Au/Cr | twDEP |
| [69] | Gradient electrodes | twDEP | |
| [70] | Spiral electrodes | Au/Cr | twDEP |
| [12] | Slanted interdigitated electrodes | Al/Cr | Time varying DEP |
| [71] | Slanted interdigitated electrodes | Au | Time varying DEP |
| [72] | Simple interdigitated electrodes | Au | Time varying DEP |
| [73] | Top-bottom electrode array | ITO-Au/Cr | Moving DEP |
| [74] | Top-bottom electrode array | ITO | Moving-pulsed DEP |
| [75] | Simple interdigitated electrodes | Au | FFF-DEP |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farasat, M.; Aalaei, E.; Kheirati Ronizi, S.; Bakhshi, A.; Mirhosseini, S.; Zhang, J.; Nguyen, N.-T.; Kashaninejad, N. Signal-Based Methods in Dielectrophoresis for Cell and Particle Separation. Biosensors 2022, 12, 510. https://doi.org/10.3390/bios12070510
Farasat M, Aalaei E, Kheirati Ronizi S, Bakhshi A, Mirhosseini S, Zhang J, Nguyen N-T, Kashaninejad N. Signal-Based Methods in Dielectrophoresis for Cell and Particle Separation. Biosensors. 2022; 12(7):510. https://doi.org/10.3390/bios12070510
Chicago/Turabian StyleFarasat, Malihe, Ehsan Aalaei, Saeed Kheirati Ronizi, Atin Bakhshi, Shaghayegh Mirhosseini, Jun Zhang, Nam-Trung Nguyen, and Navid Kashaninejad. 2022. "Signal-Based Methods in Dielectrophoresis for Cell and Particle Separation" Biosensors 12, no. 7: 510. https://doi.org/10.3390/bios12070510
APA StyleFarasat, M., Aalaei, E., Kheirati Ronizi, S., Bakhshi, A., Mirhosseini, S., Zhang, J., Nguyen, N.-T., & Kashaninejad, N. (2022). Signal-Based Methods in Dielectrophoresis for Cell and Particle Separation. Biosensors, 12(7), 510. https://doi.org/10.3390/bios12070510












