The Optimization of a T-Cell Resonator: Towards Highly Sensitive Photoacoustic Spectroscopy for Noninvasive Blood Glucose Detection
Abstract
1. Introduction
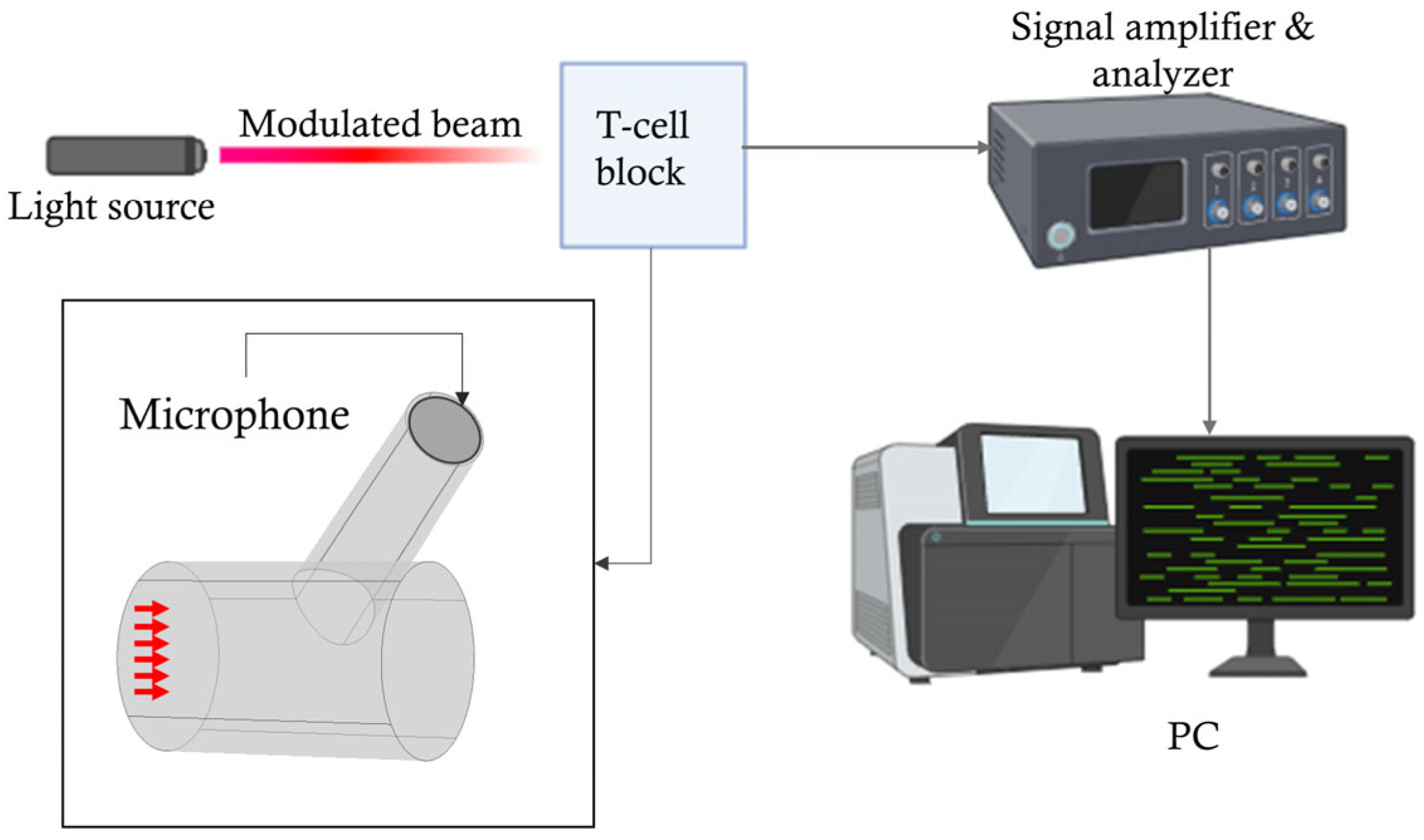
2. General Principle of Using PARs for Signal Amplification and Simulation Method
2.1. Principle of PAS
Photoacoustic Resonator Model
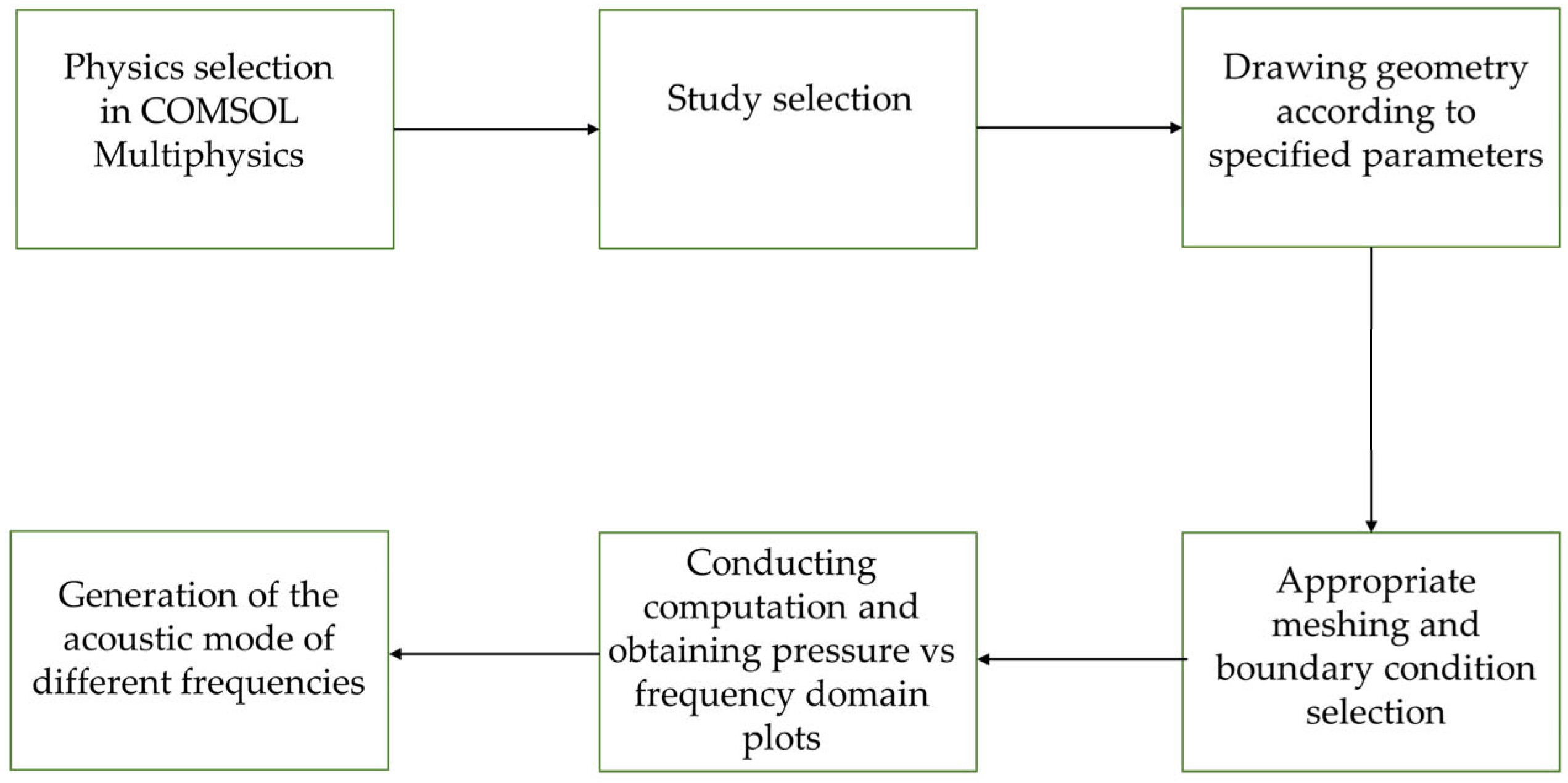
2.2. Simulation Procedure
- The frequency domain solver addressed problems subjected to harmonic excitation at specified excitation frequencies. It provided a numerically exact solution for each frequency, ensuring that the results were reliable, provided that the model converged and the meshing accurately resolved all relevant length scales in the physics.
- The Asymptotic Waveform Evaluation (AWE) did not compute the exact solution for every frequency. Instead, it performed a Taylor expansion of the solution around a few exact solutions, using lower-order approximations (such as Padé or Taylor) to estimate the solution across the desired frequency range.
- Additionally, the Frequency Domain Modal first determined a set of system eigenfrequencies and their corresponding eigenmodes, either by searching within a user-defined range or for a predetermined number of frequencies.
2.2.1. Related Modeling Equations and Variables
2.2.2. COMSOL Terminal and Meshed View
2.2.3. Quality () Factor and Amplification Factor () Determination
3. Results and Discussion
3.1. Results Obtained Using Initial Parameters of Reference Cell
3.2. Effect of Changing Different Geometrical Parameters
3.2.1. Effect of Changing Resonance Cylinder Parameters
3.2.2. Effect of Changing Cavity Cylinder Parameters
3.2.3. The Effect of Changing the Resonance Cylinder Position
3.2.4. The Effect of Changing Both the Resonance and Cavity Cylinder Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, T.; Yang, M.; Yang, F.; Zhao, L.; Jiang, Y.; Li, C. A three-dimensional modeling method for quantitative photoacoustic breast imaging with handheld probe. Photoacoustics 2020, 21, 100222. [Google Scholar] [CrossRef] [PubMed]
- Zeninari, V.; Ibrahim, C.M.; Vallon, R.; Parvitte, B. Simulation of the Non-Linearity of Photoacoustic Signals for the Detection of Molecules of Atmospheric Interest. 2020. Available online: https://api.semanticscholar.org/CorpusID:225733094 (accessed on 13 April 2025).
- Bauer, A.; Hertzberg, O.; Küderle, A.; Strobel, D.; Pleitez, M.A.; Mäntele, W. IR-spectroscopy of skin in vivo: Optimal skin sites and properties for non-invasive glucose measurement by photoacoustic and photothermal spectroscopy. J. Biophotonics 2018, 11, e201600261. [Google Scholar] [CrossRef] [PubMed]
- Pai, P.P.; Sanki, P.K.; Sarangi, S.; Banerjee, S. Modelling, verification, and calibration of a photoacoustics based continuous non-invasive blood glucose monitoring system. Rev. Sci. Instrum. 2015, 86, 064901. [Google Scholar] [CrossRef] [PubMed]
- Sadiek, I.; Mikkonen, T.; Vainio, M.; Toivonen, J.; Foltynowicz, A. Optical frequency comb photoacoustic spectroscopy. Phys. Chem. Chem. Phys. 2018, 20, 27849–27855. [Google Scholar] [CrossRef]
- de Cumis, M.S.; Viciani, S.; Borri, S.; Patimisco, P.; Sampaolo, A.; Scamarcio, G.; De Natale, P.; D’amato, F.; Spagnolo, V. Widely-tunable mid-infrared fiber-coupled quartz-enhanced photoacoustic sensor for environmental monitoring. Opt. Express 2014, 22, 28222–28231. [Google Scholar] [CrossRef]
- Hussain, A.; Petersen, W.; Staley, J.; Hondebrink, E.; Steenbergen, W. Quantitative blood oxygen saturation imaging using combined photoacoustics and acousto-optics. Opt. Lett. 2016, 41, 1720–1723. [Google Scholar] [CrossRef]
- Fu, L.; Lu, P.; Pan, Y.; Zhong, Y.; Sima, C.; Wu, Q.; Zhang, J.; Cui, L.; Liu, D. All-optical non-resonant photoacoustic spectroscopy for multicomponent gas detection based on aseismic photoacoustic cell. Photoacoustics 2023, 34, 100571. [Google Scholar] [CrossRef]
- Yadav, J.; Rani, A.; Singh, V.; Murari, B.M. Prospects and limitations of non-invasive blood glucose monitoring using near-infrared spectroscopy. Biomed. Signal Process. Control 2015, 18, 214–227. [Google Scholar] [CrossRef]
- Burmeister, J.J.; Arnold, M.A. Evaluation of Measurement Sites for Noninvasive Blood Glucose Sensing with Near-Infrared Transmission Spectroscopy. Clin. Chem. 1999, 45, 1621–1627. [Google Scholar] [CrossRef]
- Kottmann, J.; Rey, J.M.; Luginbühl, J.; Reichmann, E.; Sigrist, M.W. Glucose sensing in human epidermis using mid-infrared photoacoustic detection. Biomed. Opt. Express 2012, 3, 667–680. [Google Scholar] [CrossRef]
- Kottmann, J.; Grob, U.; Rey, J.M.; Sigrist, M.W. Mid-Infrared Fiber-Coupled Photoacoustic Sensor for Biomedical Applications. Sensors 2013, 13, 535–549. [Google Scholar] [CrossRef] [PubMed]
- Tachibana, K.; Okada, K.; Kobayashi, R.; Ishihara, Y. Development of a high-sensitivity and portable cell using Helmholtz resonance for noninvasive blood glucose-level measurement based on photoacoustic spectroscopy. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 6477–6480. [Google Scholar] [CrossRef]
- Tang, Z.; Ni, W.; Li, Z.; Hou, J.; Chen, S.; Shum, P.P.; Yang, C. Performance Enhancement of Opened Resonance Photoacoustic Cells Based on Three Dimensional Topology Optimization. Photonics 2021, 8, 380. [Google Scholar] [CrossRef]
- Manohar, S.; Razansky, D. Photoacoustics: A historical review. Adv. Opt. Photonics 2016, 8, 586–617. [Google Scholar] [CrossRef]
- Kapitanov, V.; Zeninari, V.; Parvitte, B.; Courtois, D.; Ponomarev, Y. Optimisation of photoacoustic resonant cells with commercial microphones for diode laser gas detection. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2002, 58, 2397–2404. [Google Scholar] [CrossRef]
- Pleitez, M.A.; Lieblein, T.; Bauer, A.; Hertzberg, O.; von Lilienfeld-Toal, H.; Mäntele, W. In Vivo Noninvasive Monitoring of Glucose Concentration in Human Epidermis by Mid-Infrared Pulsed Photoacoustic Spectroscopy. Anal. Chem. 2012, 85, 1013–1020. [Google Scholar] [CrossRef]
- Pleitez, M.A.; Lieblein, T.; Bauer, A.; Hertzberg, O.; Von Lilienfeld-Toal, H.; Mäntele, W. Windowless ultrasound photoacoustic cell forin vivomid-IR spectroscopy of human epidermis: Low interference by changes of air pressure, temperature, and humidity caused by skin contact opens the possibility for a non-invasive monitoring of glucose in the interstitial fluid. Rev. Sci. Instrum. 2013, 84, 084901. [Google Scholar] [CrossRef]
- Sim, J.Y.; Ahn, C.-G.; Jeong, E.; Kim, B.K. Photoacoustic spectroscopy that uses a resonant characteristic of a microphone for in vitro measurements of glucose concentration. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 4861–4864. [Google Scholar]
- Sim, J.Y.; Ahn, C.-G.; Huh, C.; Chung, K.H.; Jeong, E.-J.; Kim, B.K. Synergetic Resonance Matching of a Microphone and a Photoacoustic Cell. Sensors 2017, 17, 804. [Google Scholar] [CrossRef]
- El-Busaidy, S.A.S.; Baumann, B.; Wolff, M.; Duggen, L. Modelling of open photoacoustic resonators. Photoacoustics 2020, 18, 100161. [Google Scholar] [CrossRef]
- Sim, J.Y.; Ahn, C.-G.; Jeong, E.-J.; Kim, B.K. In vivo Microscopic Photoacoustic Spectroscopy for Non-Invasive Glucose Monitoring Invulnerable to Skin Secretion Products. Sci. Rep. 2018, 8, 1059. [Google Scholar] [CrossRef]
- Kost, B.; Baumann, B.; Wolff, M.; Groninga, H. Towards the optimization of photoacoustic sensors. In Computer Aided Optimum Design in Engineering X. In WIT Transactions on The Built Environment; WIT Press: Southampton, UK, 2007; Volume 91, pp. 97–106. [Google Scholar] [CrossRef]
- Wolff, M.; Kost, B.; Baumann, B. Shape-Optimized Photoacoustic Cell: Numerical Consolidation and Experimental Confirmation. Int. J. Thermophys. 2012, 33, 1953–1959. [Google Scholar] [CrossRef]
- Yin, X.; Dong, L.; Wu, H.; Zheng, H.; Ma, W.; Zhang, L.; Yin, W.; Jia, S.; Tittel, F.K. Sub-ppb nitrogen dioxide detection with a large linear dynamic range by use of a differential photoacoustic cell and a 3.5 W blue multimode diode laser. Sens. Actuators B Chem. 2017, 247, 329–335. [Google Scholar] [CrossRef]
- Gong, Z.; Chen, K.; Chen, Y.; Mei, L.; Yu, Q. Integration of T-type half-open photoacoustic cell and fiber-optic acoustic sensor for trace gas detection. Opt. Express 2019, 27, 18222–18231. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Gao, T.; Mei, L.; Chen, K.; Chen, Y.; Zhang, B.; Peng, W.; Yu, Q. Ppb-level detection of methane based on an optimized T-type photoacoustic cell and a NIR diode laser. Photoacoustics 2021, 21, 100216. [Google Scholar] [CrossRef] [PubMed]
- Kaysir, R.; Zaman, T.M.; Rassel, S.; Wang, J.; Ban, D. Photoacoustic Resonators for Non-Invasive Blood Glucose Detection Through Photoacoustic Spectroscopy: A Systematic Review. Sensors 2024, 24, 6963. [Google Scholar] [CrossRef]
- El-Busaidy, S.; Baumann, B.; Wolff, M.; Duggen, L.; Bruhns, H. Experimental and Numerical Investigation of a Photoacoustic Resonator for Solid Samples: Towards a Non-Invasive Glucose Sensor. Sensors 2019, 19, 2889. [Google Scholar] [CrossRef]
- Aloraynan, A.; Rassel, S.; Kaysir, R.; Ban, D. Dual quantum cascade lasers for noninvasive glucose detection using photoacoustic spectroscopy. Sci. Rep. 2023, 13, 7927. [Google Scholar] [CrossRef]
- Aloraynan, A.; Rassel, S.; Xu, C.; Ban, D. A Single Wavelength Mid-Infrared Photoacoustic Spectroscopy for Noninvasive Glucose Detection Using Machine Learning. Biosensors 2022, 12, 166. [Google Scholar] [CrossRef]
- Sound Hard Boundary (Wall). Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.aco/aco_ug_pressure.05.067.html (accessed on 11 April 2025).
- Helmholtz Resonator Analyzed with Different Frequency Domain Solvers. Available online: https://www.comsol.com/model/helmholtz-resonator-analyzed-with-different-frequency-domain-solvers-20263 (accessed on 25 December 2024).
- The Pressure Acoustics, Frequency Domain Interface. Available online: https://doc.comsol.com/5.5/doc/com.comsol.help.aco/aco_ug_pressure.05.002.html (accessed on 25 December 2024).
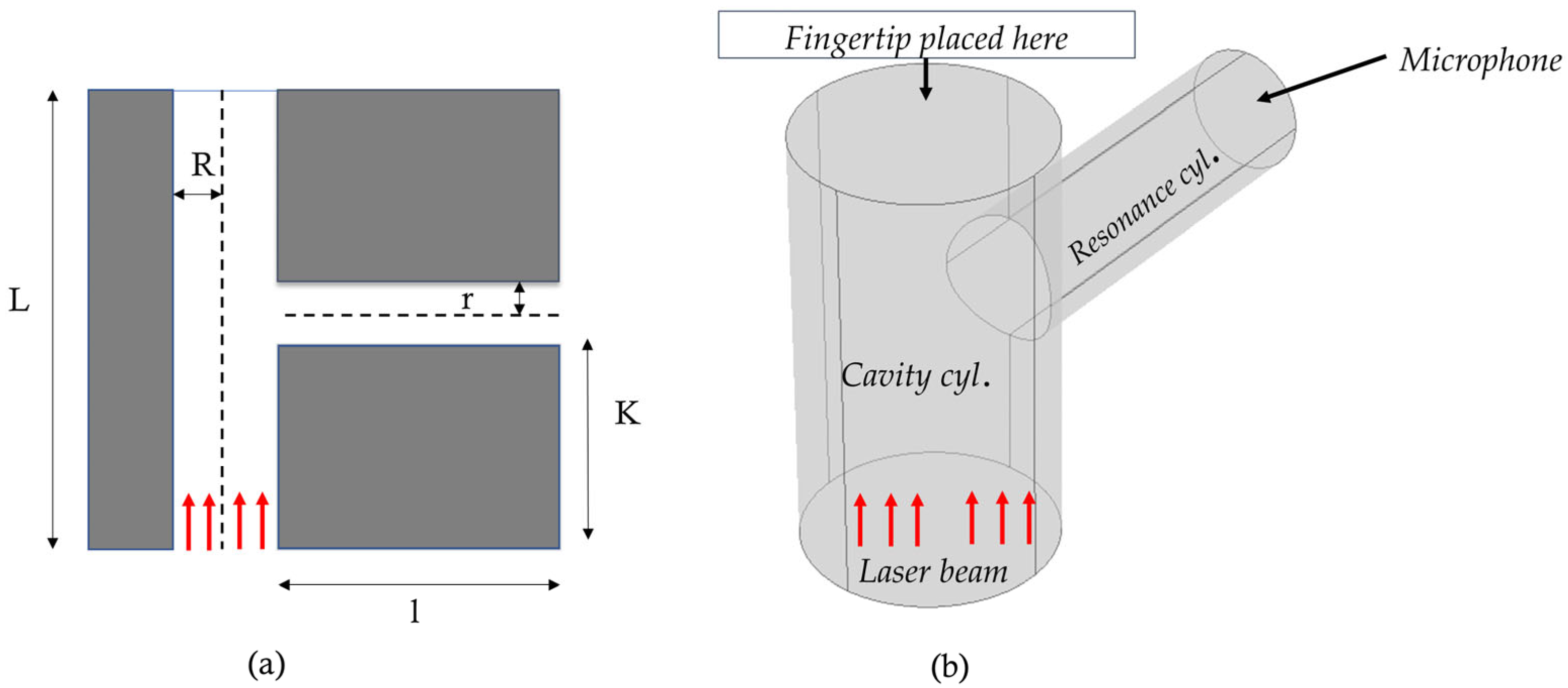
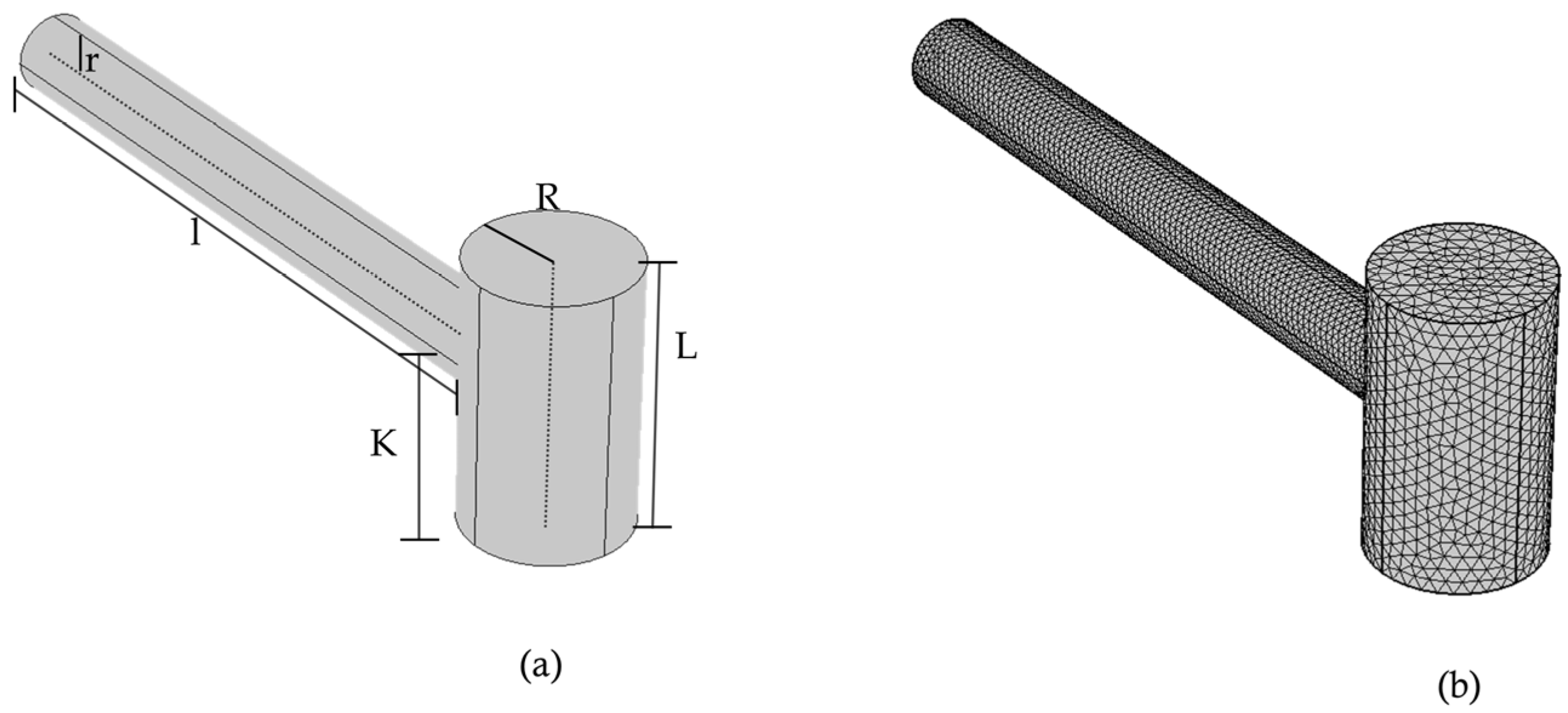

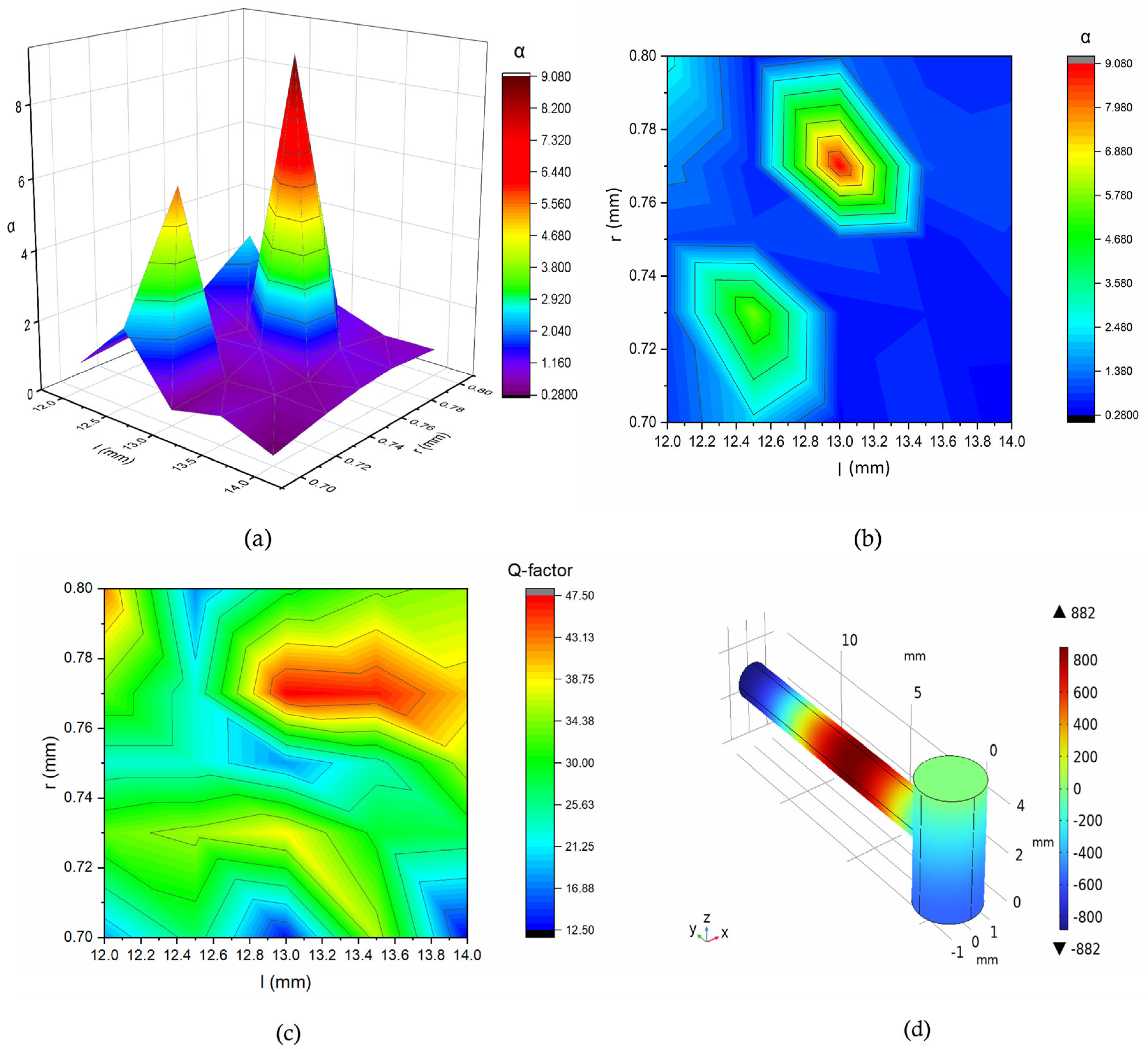

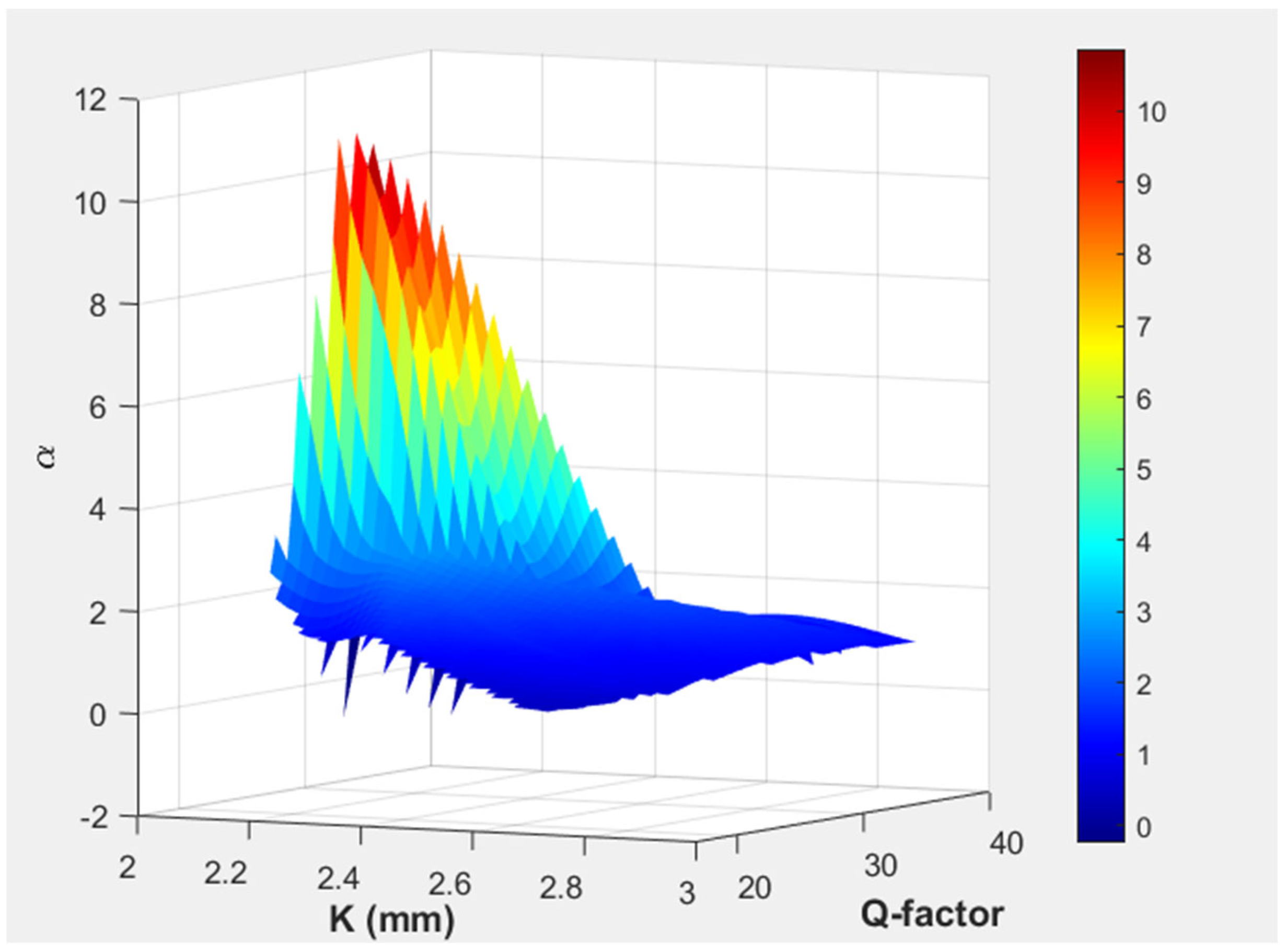

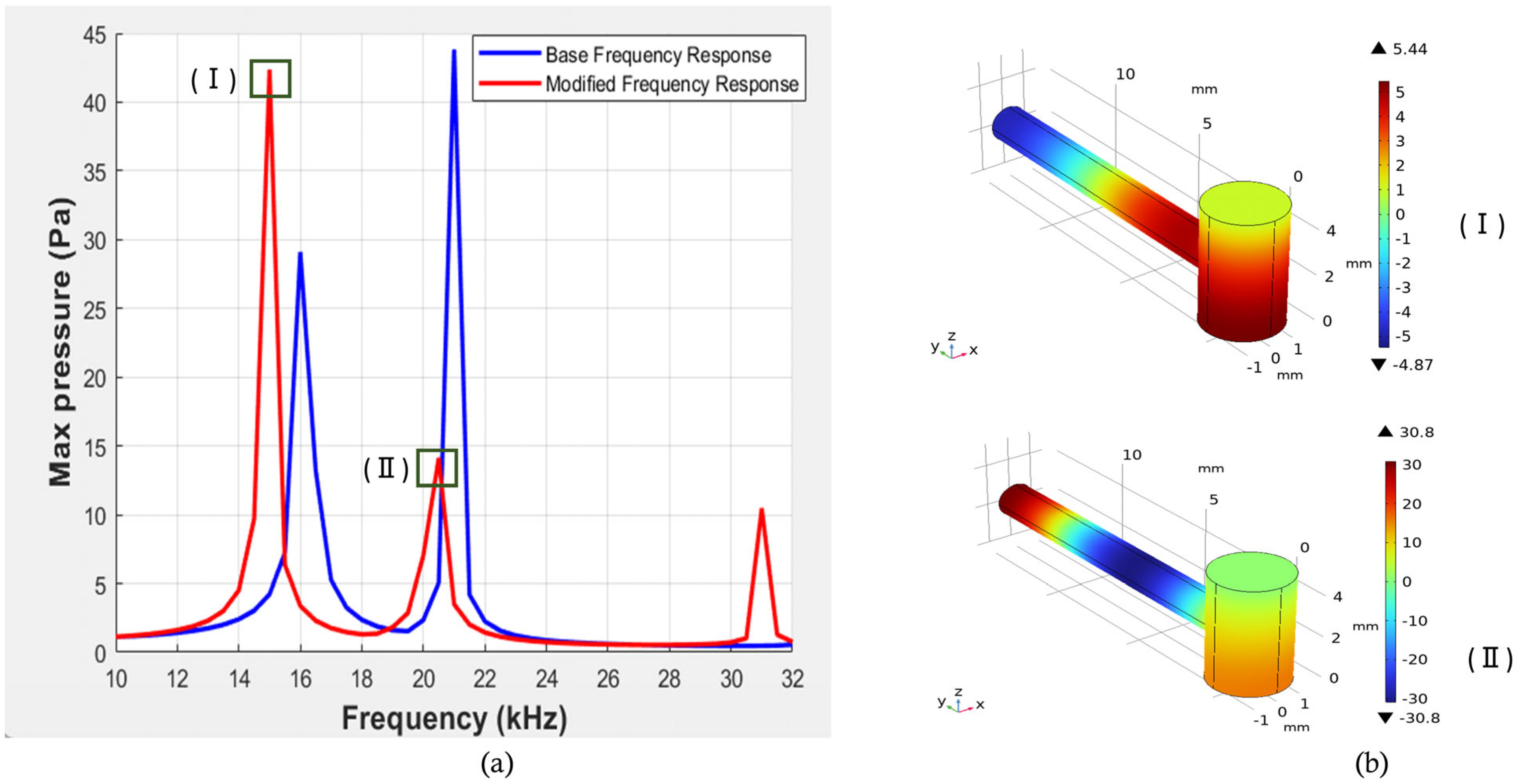
| Structural Parameter | Symbol | Values (mm) |
|---|---|---|
| Position of the Resonance Cylinder | K | 2.5 |
| Radius of the Cavity Cylinder | R | 1.5 |
| Length of the Cavity Cylinder | L | 5 |
| Radius of the Resonance Cylinder | r | 0.75 |
| Length of the Resonance Cylinder | l | 13 |
| Parameters | Amplification Ratio (α) | Q-Factor | |||||
|---|---|---|---|---|---|---|---|
| Combination | R (mm) | L (mm) | R (mm) | L (mm) | K (mm) | ||
| a | 1.5 | 5.0 | 0.77 | 13 | 2.5 | 9.07 | 47.5 |
| b | 1.55 | 5.1 | 0.75 | 13 | 2.5 | 12.76 | 47.5 |
| c | 1.55 | 5.1 | 0.77 | 13 | 2.5 | 2.7 | 42 |
| d | 1.5 | 5.0 | 0.75 | 13 | 2.09 | 11.6 | 29.42 |
| e | 1.55 | 5.1 | 0.77 | 13 | 2.09 | 0.93 | 42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaman, T.M.; Kaysir, M.R.; Rassel, S.; Ban, D. The Optimization of a T-Cell Resonator: Towards Highly Sensitive Photoacoustic Spectroscopy for Noninvasive Blood Glucose Detection. Biosensors 2025, 15, 254. https://doi.org/10.3390/bios15040254
Zaman TM, Kaysir MR, Rassel S, Ban D. The Optimization of a T-Cell Resonator: Towards Highly Sensitive Photoacoustic Spectroscopy for Noninvasive Blood Glucose Detection. Biosensors. 2025; 15(4):254. https://doi.org/10.3390/bios15040254
Chicago/Turabian StyleZaman, Thasin Mohammad, Md Rejvi Kaysir, Shazzad Rassel, and Dayan Ban. 2025. "The Optimization of a T-Cell Resonator: Towards Highly Sensitive Photoacoustic Spectroscopy for Noninvasive Blood Glucose Detection" Biosensors 15, no. 4: 254. https://doi.org/10.3390/bios15040254
APA StyleZaman, T. M., Kaysir, M. R., Rassel, S., & Ban, D. (2025). The Optimization of a T-Cell Resonator: Towards Highly Sensitive Photoacoustic Spectroscopy for Noninvasive Blood Glucose Detection. Biosensors, 15(4), 254. https://doi.org/10.3390/bios15040254





