On Magnetohydrodynamic Flow of Viscoelastic Nanofluids with Homogeneous–Heterogeneous Reactions
Abstract
:1. Introduction
2. Problem Formulation
3. Solution Methodology
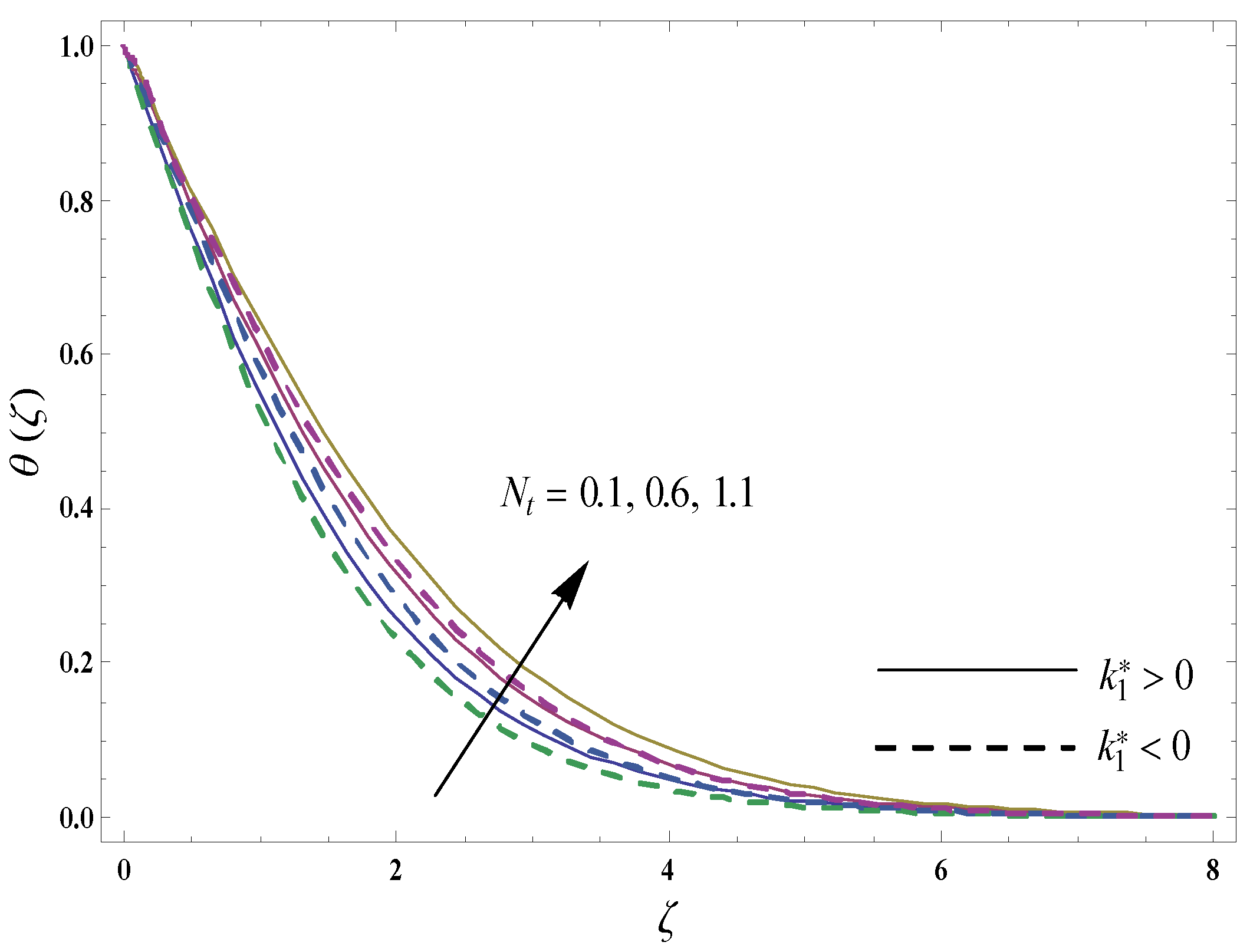
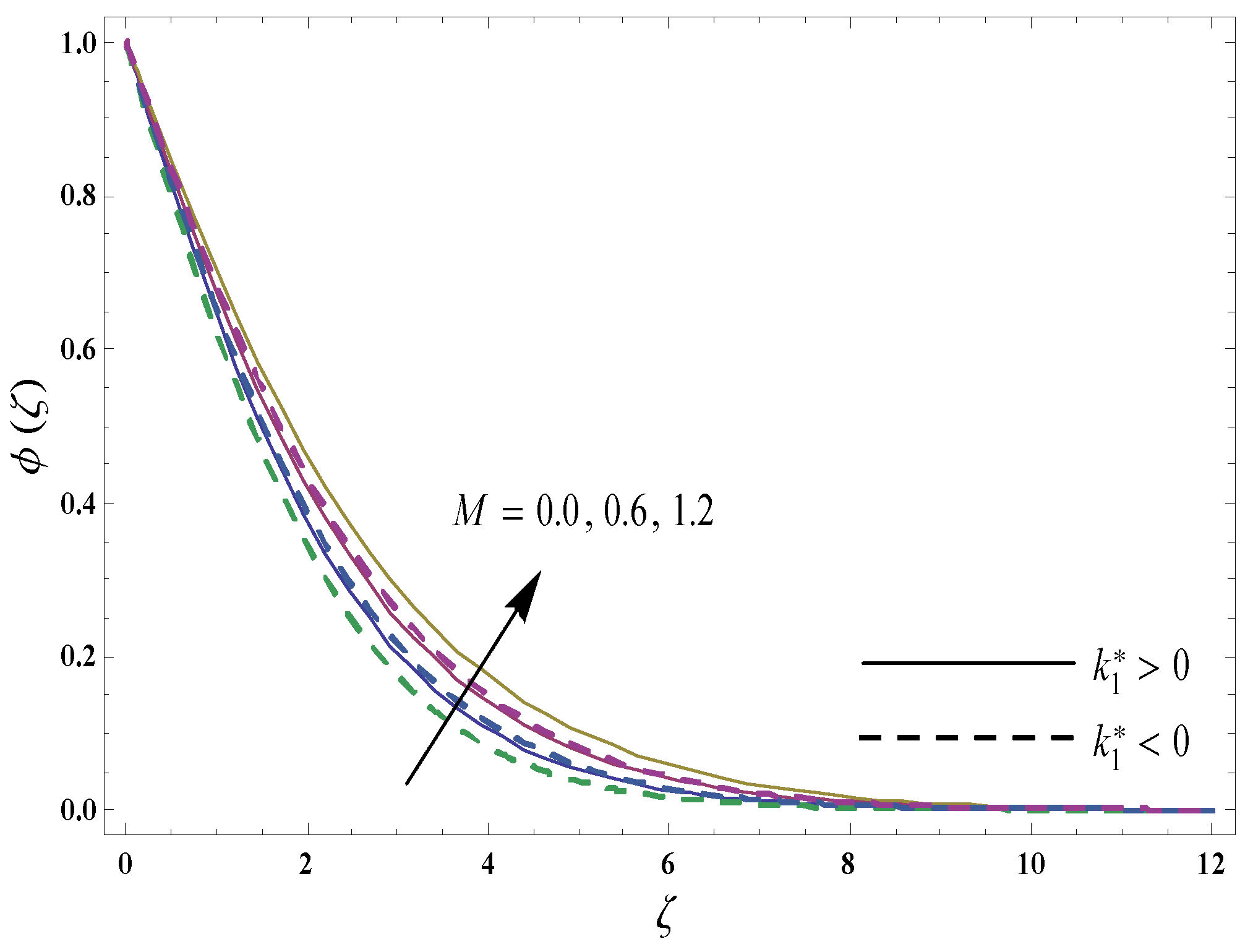
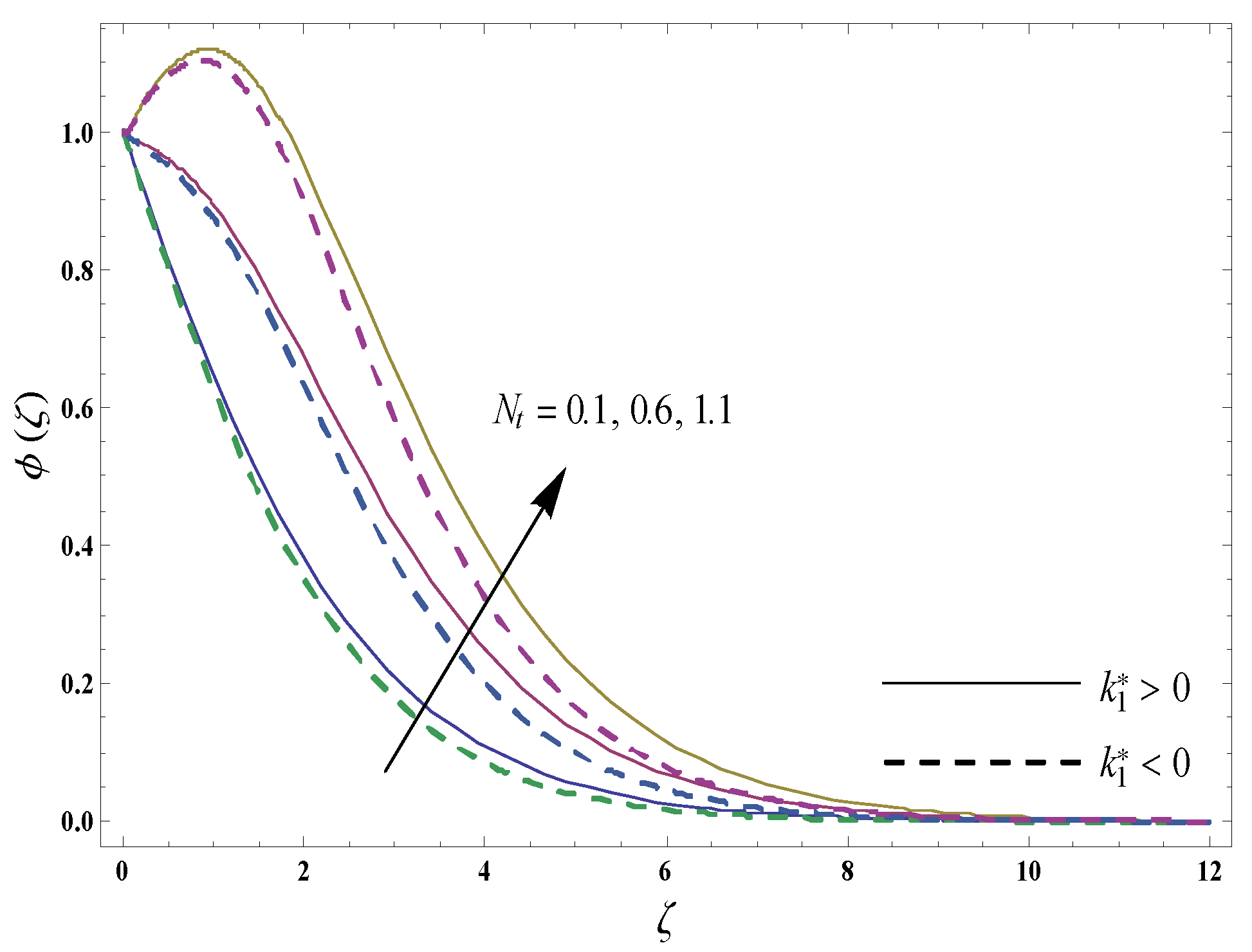
4. Graphical Results and Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| v | velocity components | y | coordinate axes |
| B | chemical species | rate constants | |
| dynamic viscosity | density of base fluid | ||
| b | concentrations of chemical species | elastic parameter | |
| kinematic viscosity | electrical conductivity | ||
| velocity distribution | magnetic field strength | ||
| Cauchy stress tensor | body force | ||
| material constants | material derivative | ||
| p | pressure | first and second Rivlin-Ericksen tensors | |
| * | matrix transpose | mass diffusion coefficients | |
| T | temperature | C | concentration |
| ambient fluid temperature | ambient fluid concentration | ||
| surface temperature | surface concentration | ||
| effective heat capacity of nanoparticles | heat capacity of fluid | ||
| thermal diffusivity | k | thermal conductivity | |
| surface velocity | c | positive constant | |
| Brownian diffusion coefficient | thermophoretic diffusion coefficient | ||
| similarity variable | dimensionless velocity | ||
| dimensionless temperature | dimensionless concentration | ||
| r | dimensionless concentration rate | viscoelastic parameter | |
| Schmidt number | M | magnetic parameter | |
| K | homogeneous-reaction strength | Pr | Prandtl number |
| Brownian motion parameter | thermophoresis parameter | ||
| heterogeneous-reaction strength | Schmidt number | ||
| skin friction coefficient | local Reynolds number | ||
| local Nusselt number | local Sherwood number |
References
- Ariel, P.D. On the flow of an elastico-viscous fluid near a rotating disk. J. Comput. Appl. Math. 2003, 154, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Tan, W.C.; Masuoka, T. Stokes’ first problem for a second grade fluid in a porous half-space with heated boundary. Int. J. Non Linear Mech. 2005, 40, 515–522. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Kimiaeifar, A. Application of homotopy perturbation method to find an analytical solution for magnetohydrodynamic flows of viscoelastic fluids in converging/diverging channels. J. Mech. Eng. Sci. 2011, 225, 347–353. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Z.; Farooq, M.; Alsaedi, A. Effects of homogeneous and heterogeneous reactions and melting heat in the viscoelastic fluid flow. J. Mol. Liq. 2016, 215, 749–755. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A.; Mustafa, M. A comparative study for flow of viscoelastic fluids with Cattaneo-Christov heat flux. PLoS ONE 2016, 11, e0155185. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Model and comparative study for flow of viscoelastic nanofluids with Cattaneo-Christov double diffusion. PLoS ONE 2017, 12, e0168824. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Haider, F.; Muhammad, T.; Alsaedi, A. On Darcy-Forchheimer flow of viscoelastic nanofluids: A comparative study. J. Mol. Liq. 2017, 233, 278–287. [Google Scholar] [CrossRef]
- Sheremet, M.; Pop, I. Natural convection combined with thermal radiation in a square cavity filled with a viscoelastic fluid. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 624–640. [Google Scholar] [CrossRef]
- Esmaeilzadeh, H.; Su, J.; Charmchi, M.; Sun, H. Effect of hydrophobicity on the water flow in carbon nanotube-A molecular dynamic study. Theor. Appl. Mech. Lett. 2018, 8, 284–290. [Google Scholar] [CrossRef]
- Chen, J.; Han, J. Comparative performance of carbon nanotubes and nanoclays as flame retardants for epoxy composites. Results Phys. 2019, 14, 102481. [Google Scholar] [CrossRef]
- Hayat, T.; Haider, F.; Muhammad, T.; Ahmad, B. Darcy-Forchheimer flow of carbon nanotubes due to a convectively heated rotating disk with homogeneous–heterogeneous reactions. J. Therm. Anal. Calorimet. 2019, 137, 1939–1949. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanfluids. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentatics in a two aided lid-driven differentially heated square cavity utilizing nanofluid. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Panday, A.K.; Kumar, M. Boundary layer flow and heat transfer analysis on Cu-water nanofluid flow over a stretching cylinder with slip. Alex. Eng. J. 2017, 56, 671–677. [Google Scholar] [CrossRef]
- Khan, S.U.; Shahzad, S.A.; Rauf, A.; Ali, N. Mixed convection flow of couple stress nanofluid over oscillatory stretching sheet with heat absorption/generation effects. Results Phys. 2018, 8, 1223–1231. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Free and circular jets cooled by single phase nanofluids. Eur. J. Mech. B/Fluid 2019, 76, 1–6. [Google Scholar] [CrossRef]
- Mahian, O.; Mahmud, S.; Heris, S.Z. Analysis of entropy generation between co-rotating cylinders using nanofluids. Energy 2012, 44, 438–446. [Google Scholar] [CrossRef]
- Goodarzi, M.; Safaei, M.R.; Vafai, K.; Ahmadi, G.; Dahari, M.; Kazi, S.N.; Jomhari, N. Investigation of nanofluid mixed convection in a shallow cavity using a twophase mixture model. Int. J. Therm. Sci. 2014, 75, 204–220. [Google Scholar] [CrossRef]
- Hsiao, K.L. Nanofluid flow with multimedia physical features for conjugate mixed convection and radiation. Comput. Fluids 2014, 104, 1–8. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. A note on the correspondence between certain nanofluid flows and standard fluid flows. ASME J. Heat Transf. 2015, 137, 024501. [Google Scholar] [CrossRef]
- Malvandi, A.; Safaei, M.R.; Kaffash, M.H.; Ganji, D.D. MHD mixed convection in a vertical annulus filled with Al2O3–water nanofluid considering nanoparticle migration. J. Magn. Magn. Mater. 2015, 382, 296–306. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A.; Alhuthali, M.S. Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. J. Magn. Magn. Mater. 2015, 385, 222–229. [Google Scholar] [CrossRef]
- Togun, H.; Ahmadi, G.; Abdulrazzaq, T.; Shkarah, A.J.; Kazi, S.N.; Badarudin, A.; Safaei, M.R. Thermal performance of nanofluid in ducts with double forward-facing steps. J. Taiwan Inst. Chem. Eng. 2015, 47, 28–42. [Google Scholar] [CrossRef]
- Nikkhah, Z.; Karimipour, A.; Safaei, M.R.; Tehrani, P.F.; Goodarzi, M.; Dahari, M.; Wongwises, S. Forced convective heat transfer of water/functionalized multi-walled carbon nanotube nanofluids in a microchannel with oscillating heat flux and slip boundary condition. Int. Commun. Heat Mass Transf. 2015, 68, 69–77. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Roşca, N.C. Magnetic field effect on the unsteady natural convection in a wavy-walled cavity filled with a nanofluid: Buongiorno’s mathematical model. J. Taiwan Inst. Chem. Eng. 2016, 61, 211–222. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. On magnetohydrodynamic three-dimensional flow of nanofluid over a convectively heated nonlinear stretching surface. Int. J. Heat Mass Transf. 2016, 100, 566–572. [Google Scholar] [CrossRef]
- Karimipour, A.; Taghipour, A.; Malvandi, A. Developing the laminar MHD forced convection flow of water/FMWNT carbon nanotubes in a microchannel imposed the uniform heat flux. J. Magn. Magn. Mater. 2016, 419, 420–428. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Z.; Muhammad, T.; Alsaedi, A. Effects of homogeneous and heterogeneous reactions in flow of nanofluids over a nonlinear stretching surface with variable surface thickness. J. Mol. Liq. 2016, 221, 1121–1127. [Google Scholar] [CrossRef]
- Hsiao, K.L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–861. [Google Scholar] [CrossRef]
- Hsiao, K.L. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl. Therm. Eng. 2017, 112, 1281–1288. [Google Scholar] [CrossRef]
- Muhammad, T.; Alsaedi, A.; Shehzad, S.A.; Hayat, T. A revised model for Darcy-Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chin. Phys. 2017, 55, 963–976. [Google Scholar] [CrossRef]
- Hayat, T.; Sajjad, R.; Muhammad, T.; Alsaedi, A.; Ellahi, R. On MHD nonlinear stretching flow of Powell-Eyring nanomaterial. Results Phys. 2017, 7, 535–543. [Google Scholar] [CrossRef]
- Muhammad, T.; Alsaedi, A.; Hayat, T.; Shehzad, S.A. A revised model for Darcy-Forchheimer three-dimensional flow of nanofluid subject to convective boundary condition. Results Phys. 2017, 7, 2791–2797. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. An analytical solution for magnetohydrodynamic Oldroyd-B nanofluid flow induced by a stretching sheet with heat generation/absorption. Int. J. Therm. Sci. 2017, 111, 274–288. [Google Scholar] [CrossRef]
- Rana, P.; Dhanai, R.; Kumar, L. MHD slip flow and heat transfer of Al2O3-water nanofluid over a horizontal shrinking cylinder using Buongiorno’s model: Effect of nanolayer and nanoparticle diameter. Adv. Powder Technol. 2017, 28, 1727–1738. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: A numerical study. Comp. Methods Appl. Mech. Eng. 2017, 315, 467–477. [Google Scholar] [CrossRef]
- Mahdy, A. Impacts of homogeneous–heterogeneous chemical reactions and inclined magnetic field on unsteady nanofluids flow. AIP Adv. 2018, 8, 115109. [Google Scholar] [CrossRef] [Green Version]
- Muhammad, T.; Lu, D.C.; Mahanthesh, B.; Eid, M.R.; Ramzan, M.; Dar, A. Significance of Darcy-Forchheimer porous medium in nanofluid through carbon nanotubes. Commun. Theor. Phys. 2018, 70, 361. [Google Scholar] [CrossRef]
- Tian, X.; Li, B.; Hu, Z. Convective stagnation point flow of a MHD non-Newtonian nanofluid towards a stretching plate. Int. J. Heat Mass Transf. 2018, 127, 768–780. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.A.M.; Muhammad, T.; Mallawi, F.; Wong, B.R. Numerical study for magnetohydrodynamic flow of nanofluid due to a rotating disk with binary chemical reaction and Arrhenius activation energy. Symmetry 2019, 11, 1282. [Google Scholar] [CrossRef] [Green Version]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.; Kasaeian, A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Therm. Anal. Calorim. 2019, 135, 1655–1666. [Google Scholar] [CrossRef]
- Saif, R.S.; Hayat, T.; Ellahi, R.; Muhammad, T.; Alsaedi, A. Darcy-Forchheimer flow of nanofluid due to a curved stretching surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2–20. [Google Scholar] [CrossRef]
- Riaz, A.; Alolaiyan, H.; Razaq, A. Convective heat transfer and magnetohydrodynamics across a peristaltic channel coated with nonlinear nanofluid. Coatings 2019, 9, 816. [Google Scholar] [CrossRef] [Green Version]
- Mahanthesh, B.; Gireesha, B.J.; Animasaun, I.L.; Muhammad, T.; Shashikumar, N.S. MHD flow of SWCNT and MWCNT nanoliquids past a rotating stretchable disk with thermal and exponential space dependent heat source. Phys. Scr. 2019, 94, 085214. [Google Scholar] [CrossRef]
- Eid, M.R.; Mahny, K.L.; Dar, A.; Muhammad, T. Numerical study for Carreau nanofluid flow over a convectively heated nonlinear stretching surface with chemically reactive species. Phys. A Stat. Mech. Appl. 2020, 540, 123063. [Google Scholar] [CrossRef]









| M | ||
|---|---|---|
| Numerical | HAM [5] | |
|---|---|---|
| - | |||
| - | |||
| - | |||
| - |
| - | |||
| - | |||
| - | |||
| - |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, M. On Magnetohydrodynamic Flow of Viscoelastic Nanofluids with Homogeneous–Heterogeneous Reactions. Coatings 2020, 10, 55. https://doi.org/10.3390/coatings10010055
Alghamdi M. On Magnetohydrodynamic Flow of Viscoelastic Nanofluids with Homogeneous–Heterogeneous Reactions. Coatings. 2020; 10(1):55. https://doi.org/10.3390/coatings10010055
Chicago/Turabian StyleAlghamdi, Metib. 2020. "On Magnetohydrodynamic Flow of Viscoelastic Nanofluids with Homogeneous–Heterogeneous Reactions" Coatings 10, no. 1: 55. https://doi.org/10.3390/coatings10010055
APA StyleAlghamdi, M. (2020). On Magnetohydrodynamic Flow of Viscoelastic Nanofluids with Homogeneous–Heterogeneous Reactions. Coatings, 10(1), 55. https://doi.org/10.3390/coatings10010055




