Temperature Sensing Utilizing Stimulate Brillouin Scattering Fast Light in Liquid-Filled Photonic Crystal Fibers
Abstract
:1. Introduction
2. Theoretical Analysis
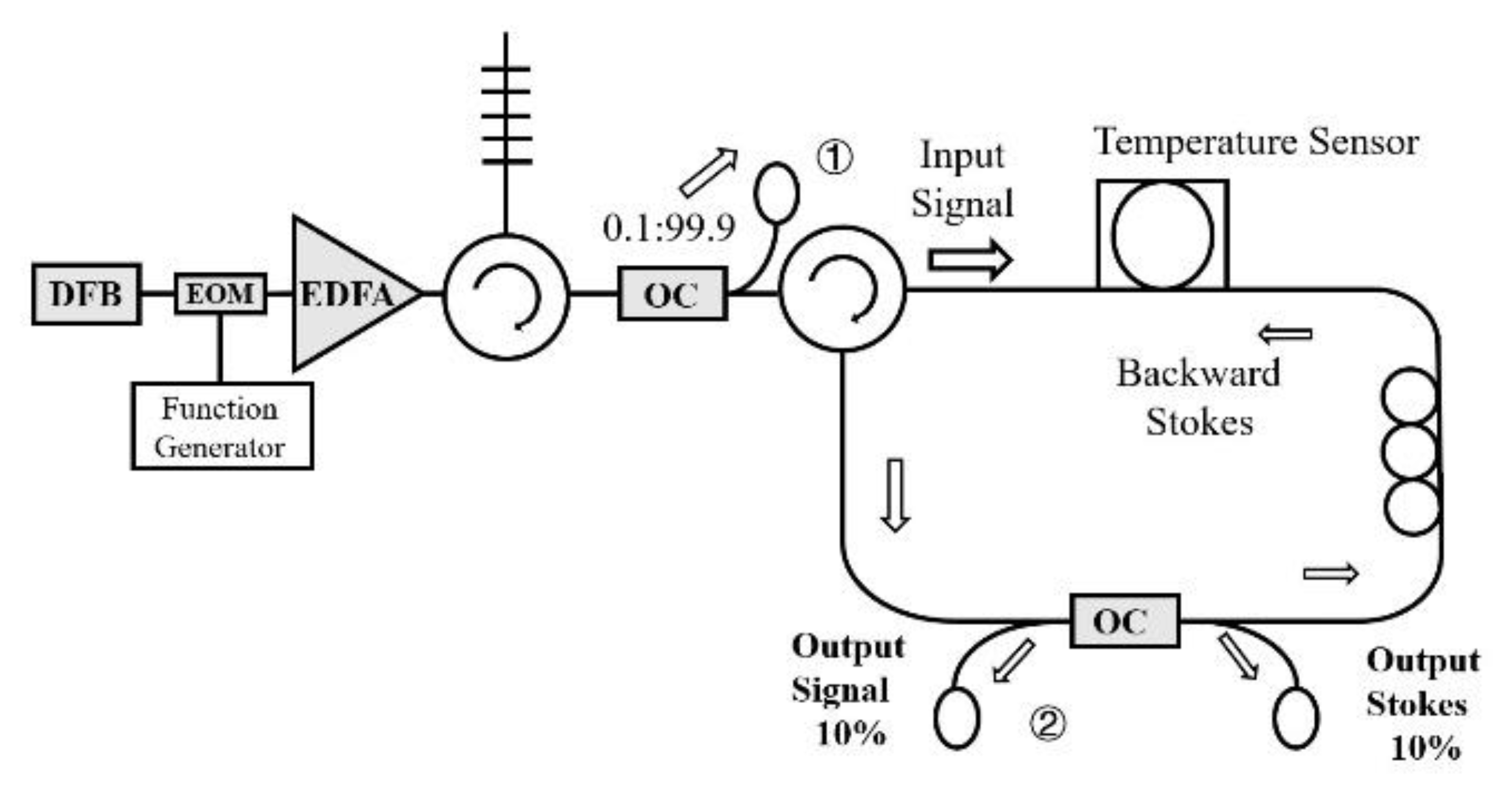
3. Proposed Experimental Setup
4. Numerical Simulation Results
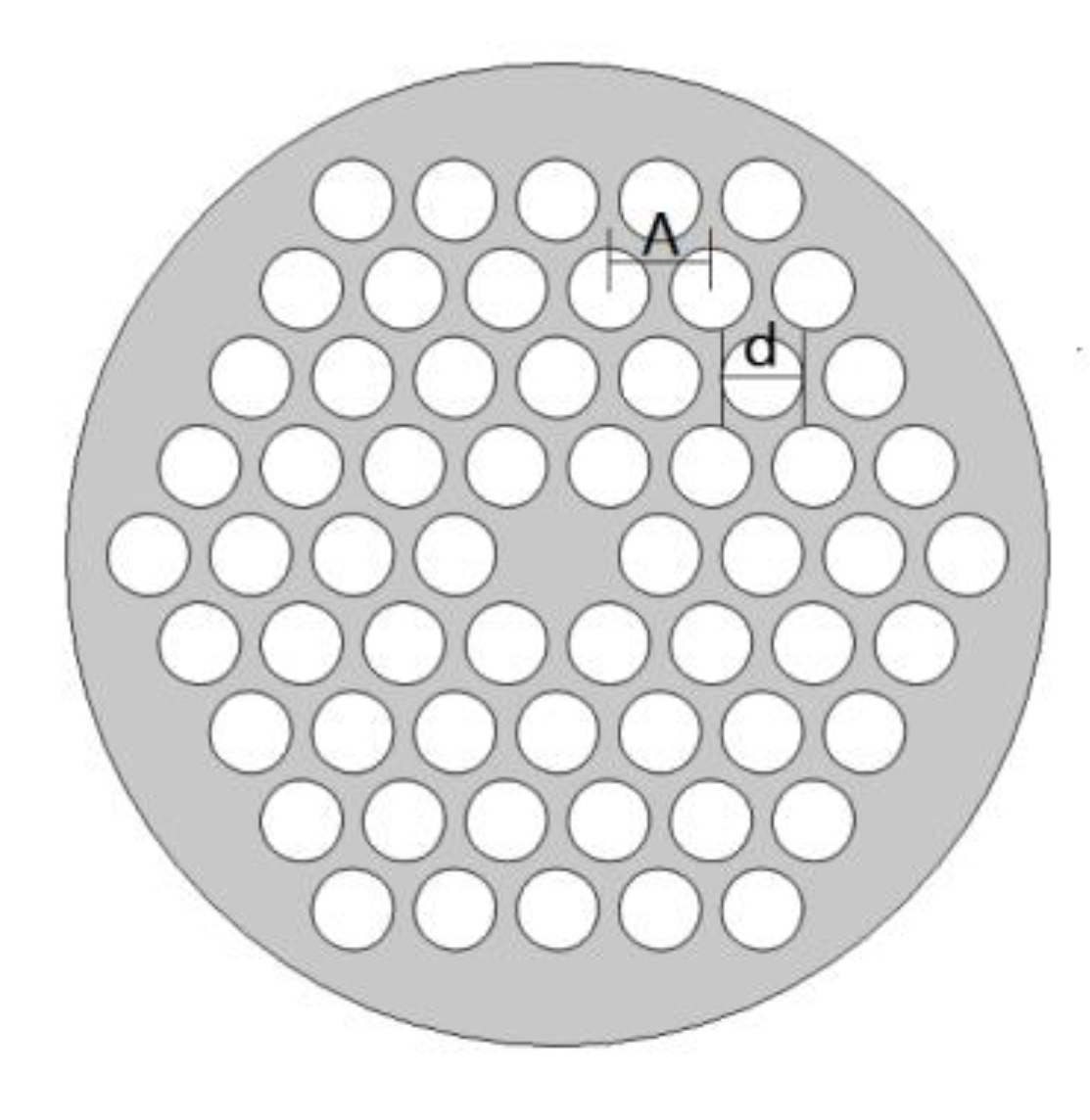
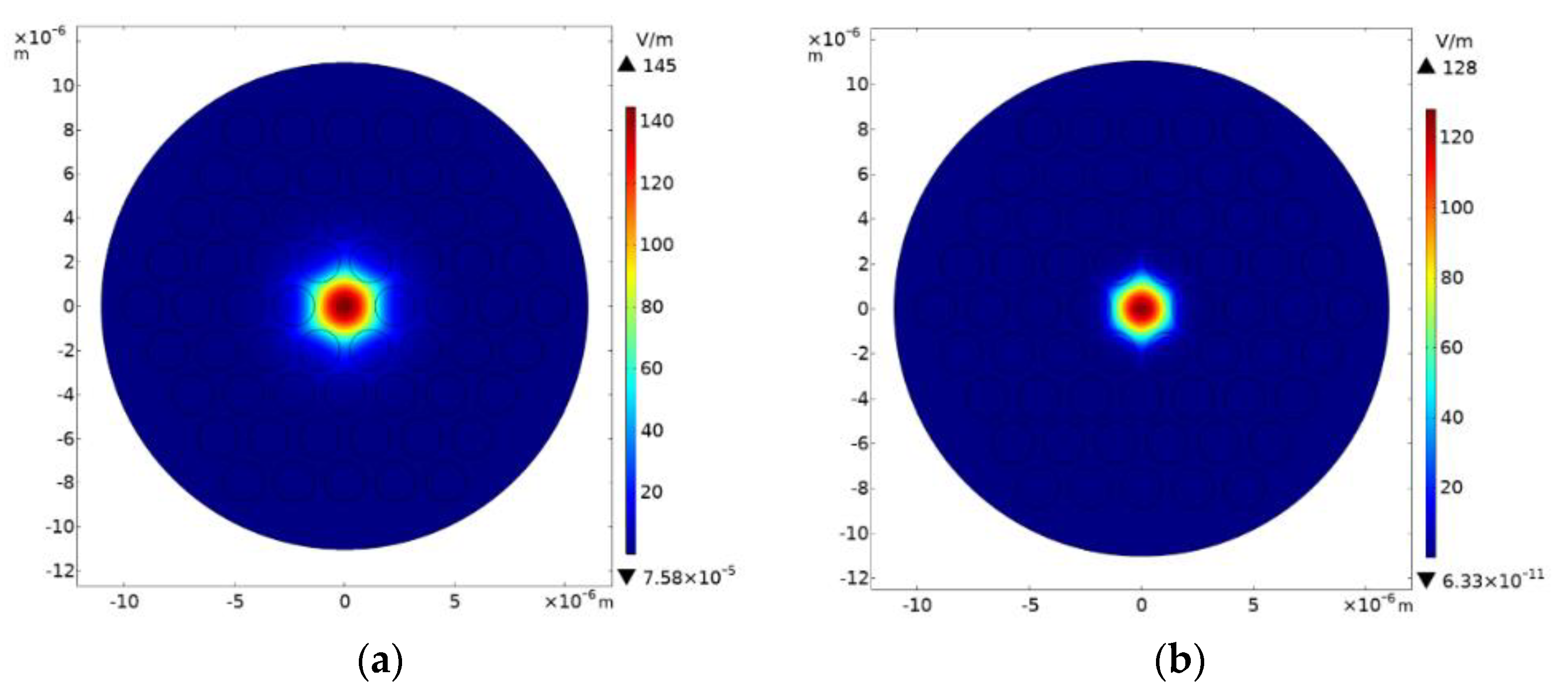
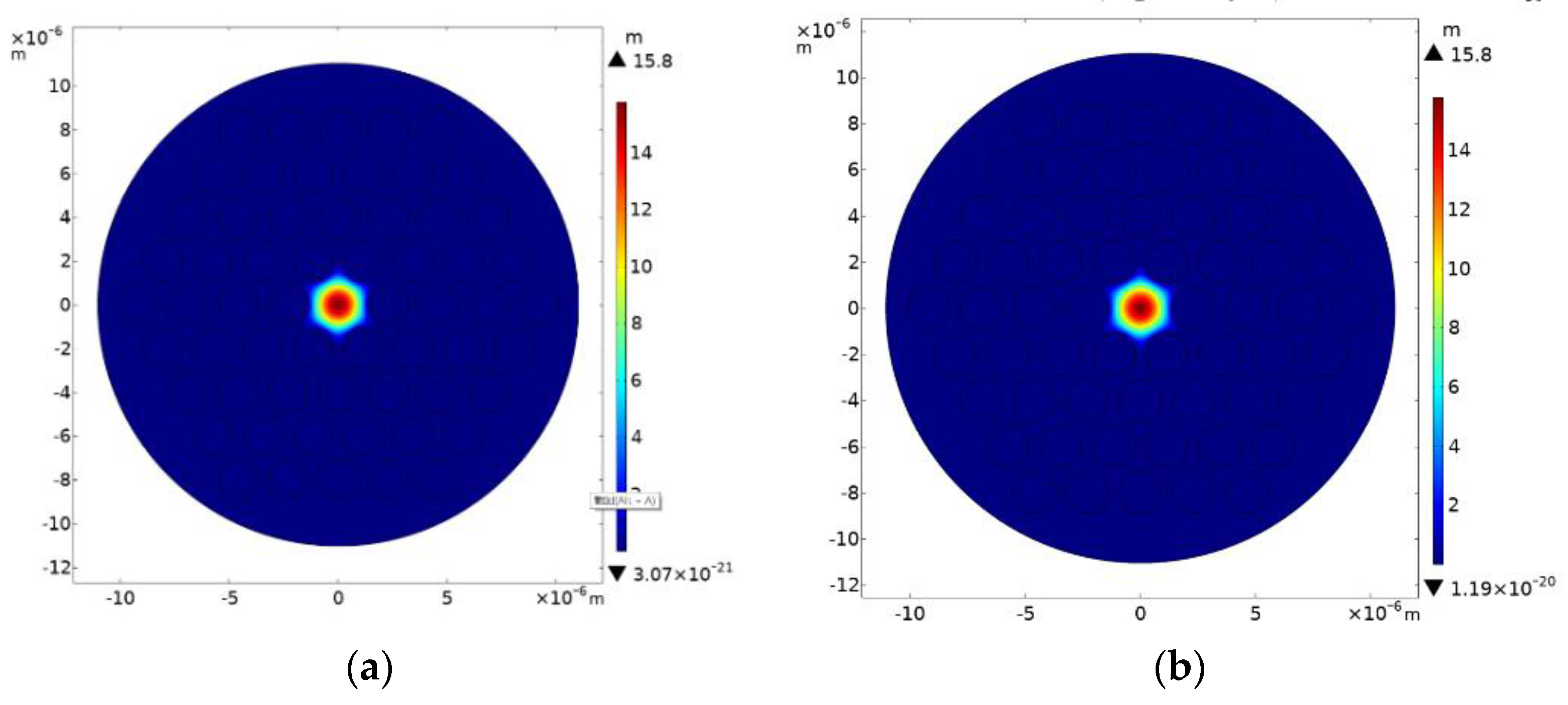
4.1. The Mode Field Distribution
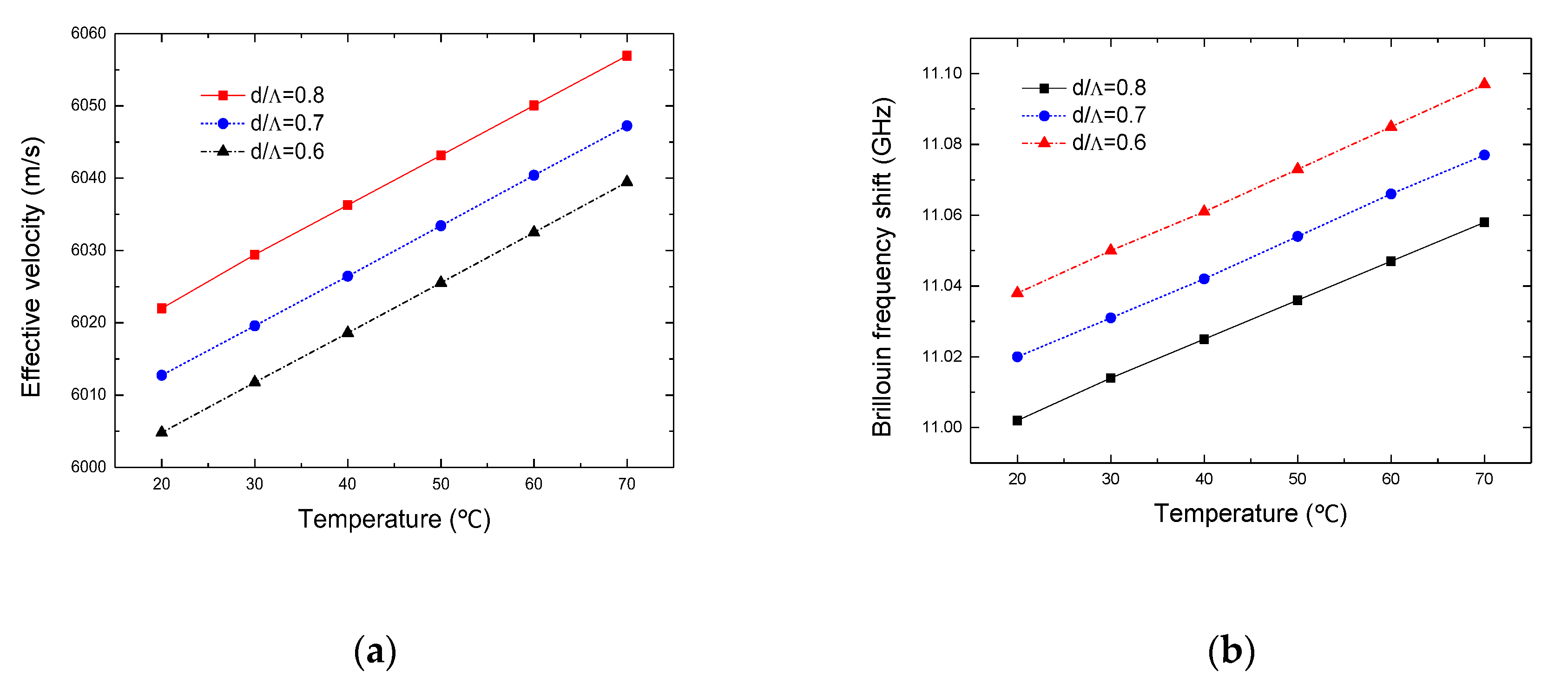
4.2. The Brillouin Frequency Shift
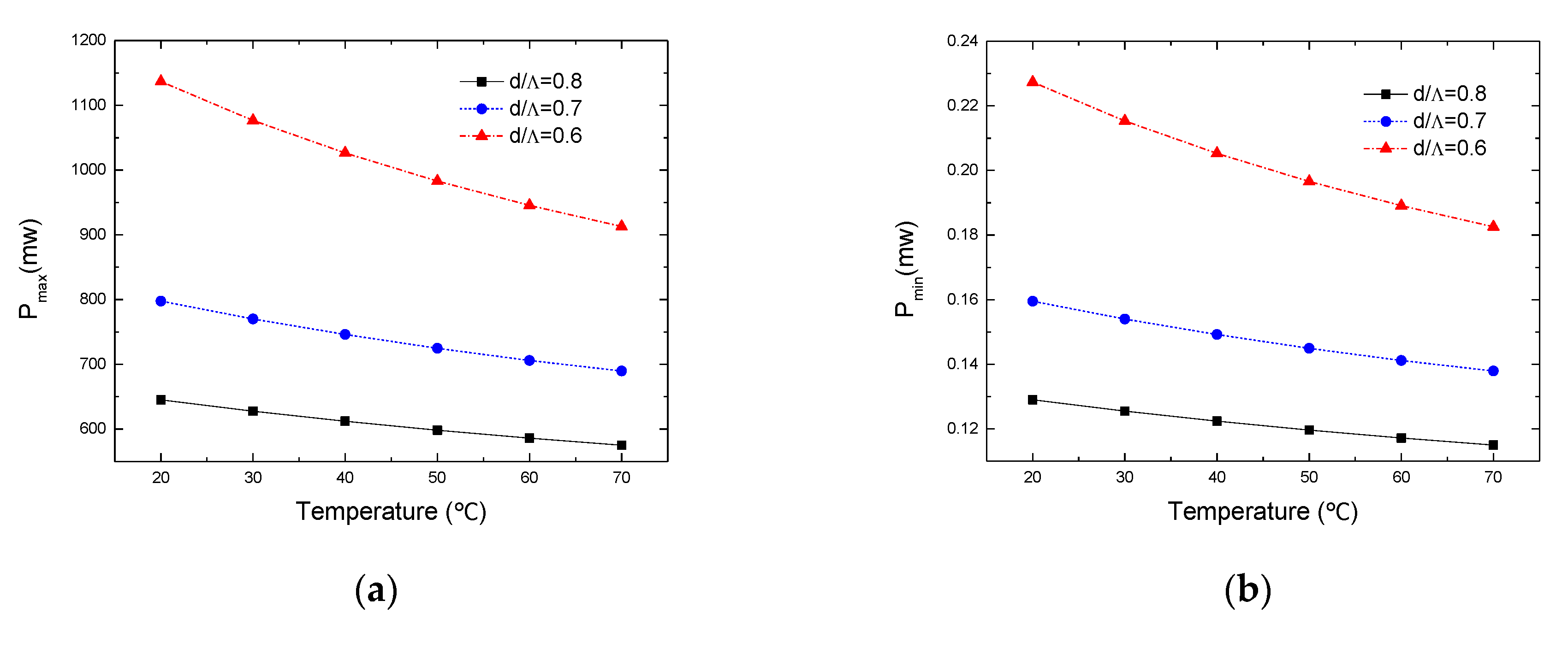
4.3. The Brillouin Threshold
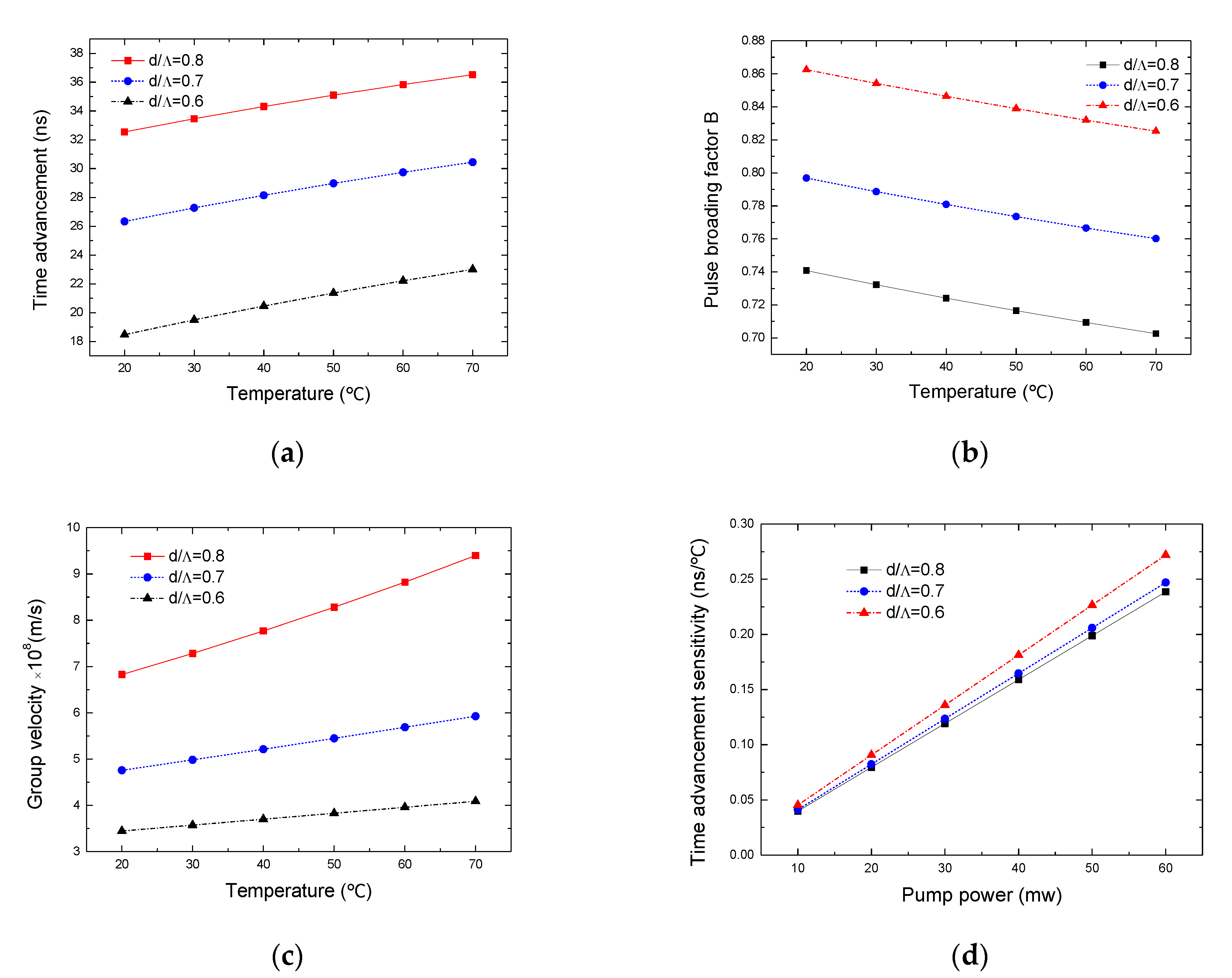
4.4. The Temperature Response of the Fast Light
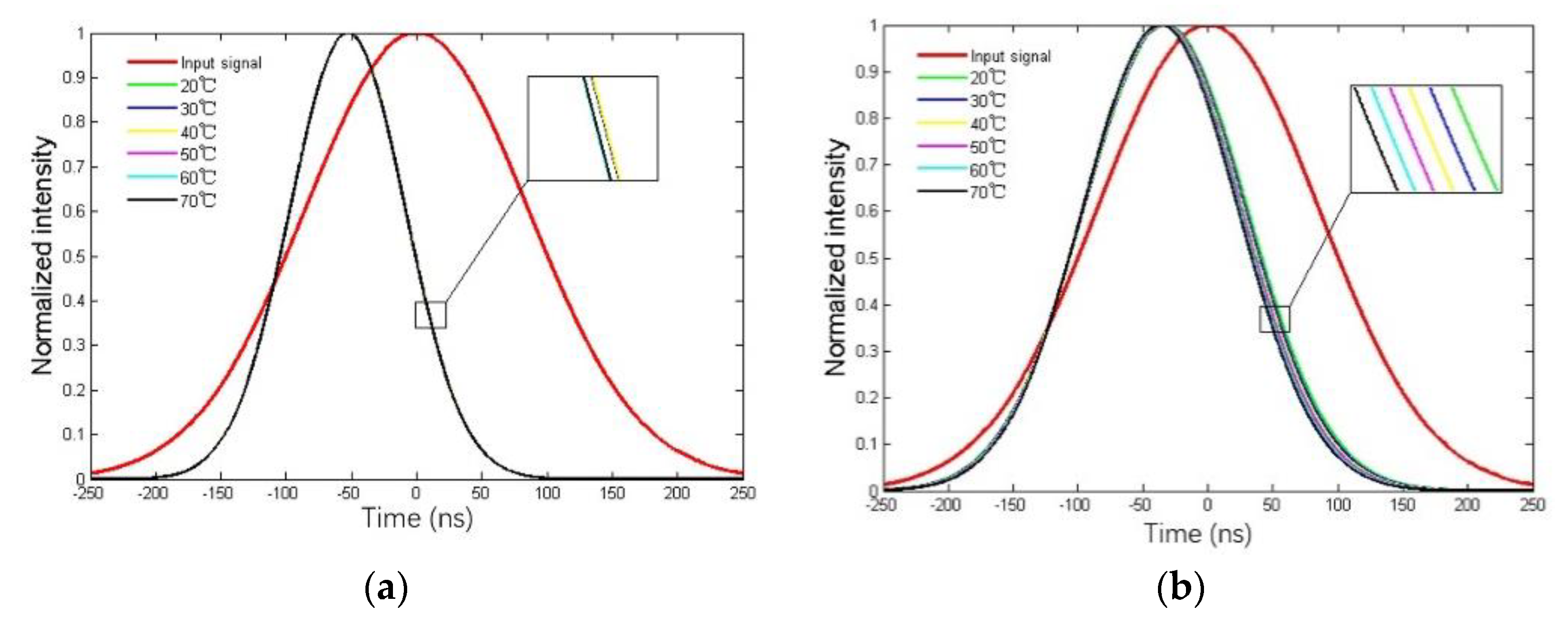
4.5. The Shape of the Output Signal Pulse
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hau, L.V.; Harris, S.E.; Dutton, Z.; Behroozi, C.H. Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature 1999, 397, 594–598. [Google Scholar] [CrossRef]
- Kash, M.M.; Sautenkov, V.A.; Zibrov, A.S.; Hollberg, L.; Welch, G.R.; Lukin, M.D.; Rostovtsev, Y.; Fry, E.S.; Scully, M.O. Ultraslow group velocity and enhanced nonlinear optical effects in a coherently driven hot atomic gas. Phys. Rev. Lett. 1999, 82, 5229–5232. [Google Scholar] [CrossRef] [Green Version]
- Chu, S.; Wong, S. Linear pulse propagation in an absorbing medium. Phys. Rev. Lett. 1982, 48, 738–741. [Google Scholar] [CrossRef]
- Stenner, M.D.; Gauthier, D.J.; Neifeld, M.A. The speed of information in a ‘fast-light’optical medium. Nature 2003, 425, 695–698. [Google Scholar] [CrossRef]
- Sharping, J.E.; Okawachi, Y.; Gaeta, A.L. Wide bandwidth slow light using a Raman fiber amplifier. Opt. Express 2005, 13, 6092–6098. [Google Scholar] [CrossRef] [PubMed]
- Okawachi, Y.; Bigelow, M.S.; Sharping, J.E.; Zhu, Z.; Schweinsberg, A.; Gauthier, D.J.; Boyd, R.W.; Gaeta, A.L. Tunable All-Optical Delays via Brillouin Slow Light in an Optical Fiber. Phys. Rev. Lett. 2005, 94, 153902. [Google Scholar] [CrossRef]
- Dahan, D.; Eisenstein, G. Tunable all optical delay via slow and fast light propagation in a Raman assisted fiber optical parametric amplifier: A route to all optical buffering. Opt. Express 2005, 13, 6234–6249. [Google Scholar] [CrossRef] [Green Version]
- Sinha, R.K.; Kumar, A.; Saini, T.S. Analysis and Design of Single-Mode As2Se3-Chalcogenide Photonic Crystal Fiber for Generation of Slow Light with Tunable Features. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 287–292. [Google Scholar] [CrossRef]
- Hassani, A.; Dupuis, A.; Skorobogatiy, M. Low loss porous terahertz fibers containing multiple subwavelength holes. Appl. Phys. Lett. 2008, 92, 071101. [Google Scholar] [CrossRef]
- Pisco, M.; Ricciardi, A.; Campopiano, S.; Caucheteur, C.; Mégret, P.; Cutolo, A.; Cusano, A. Fast and slow light in optical fibers through tilted fiber Bragg gratings. Opt. Express 2009, 17, 23502–23510. [Google Scholar] [CrossRef]
- Steinvurzel, P.; Eggleton, B.; De Sterke, C.M.; Steel, M.J. Continuously tunable bandpass filtering using high-index inclusion microstructured optical fibre. Electron. Lett. 2005, 41, 463. [Google Scholar] [CrossRef]
- Han, T.; Liu, Y.; Wang, Z.; Zou, B.; Tai, B.; Liu, B. Avoided-crossing-based ultrasensitive photonic crystal fiber refractive index sensor. Opt. Lett. 2010, 35, 2061–2063. [Google Scholar] [CrossRef]
- Geng, Y.; Li, X.; Tan, X.; Deng, Y.-L.; Hong, X. Compact and Ultrasensitive Temperature Sensor with a Fully Liquid-Filled Photonic Crystal Fiber Mach–Zehnder Interferometer. IEEE Sens. J. 2013, 14, 167–170. [Google Scholar] [CrossRef]
- Monfared, Y.E.; Ponomarenko, S.A. Slow light generation via stimulated Brillouin scattering in liquid-filled photonic crystal fibers. Optik 2016, 127, 5800–5805. [Google Scholar] [CrossRef]
- Song, S.; Jung, A.; Oh, K. High-Temperature Sensitivity in Stimulated Brillouin Scattering of 1060 nm Single-Mode Fibers. Sensors 2019, 19, 4731. [Google Scholar] [CrossRef] [Green Version]
- Kalosha, V.P.; Chen, L.; Bao, X. Slow and fast light via SBS in optical fibers for short pulses and broadband pump. Opt. Express 2006, 14, 12693–12703. [Google Scholar] [CrossRef]
- Kalosha, V.P.; Chen, L.; Bao, X. Slow light of subnanosecond pulses via stimulated Brillouin scattering in nonuniform fibers. Phys. Rev. A 2007, 75, 021802. [Google Scholar] [CrossRef]
- Qin, G.; Sotobayashi, H.; Tsuchiya, M.; Mori, A.; Suzuki, T.; Ohishi, Y. Stimulated Brillouin Scattering in a Single-Mode Tellurite Fiber for Amplification, Lasing, and Slow Light Generation. J. Lightwave Technol. 2008, 26, 492–498. [Google Scholar] [CrossRef]
- Cheng, T.; Liao, M.; Gao, W.; Duan, Z.; Suzuki, T.; Ohishi, Y. Suppression of stimulated Brillouin scattering in all-solid chalcogenide-tellurite photonic bandgap fiber. Opt. Express 2012, 20, 28846–28854. [Google Scholar] [CrossRef]
- Dasgupta, S.; Poletti, F.; Liu, S.; Petropoulos, P.; Richardson, D.J.; Grüner-Nielsen, L.; Herstrøm, S. Modeling Brillouin Gain Spectrum of Solid and Microstructured Optical Fibers Using a Finite Element Method. J. Light. Technol. 2010, 29, 22–30. [Google Scholar] [CrossRef]
- Hou, S.; Wen, B.; Li, H.; Liu, Y.; Wang, D.; Li, X.; Lei, J. Effects of SBS slow light on super-Gaussian pulses in fibers. Opt. Commun. 2014, 323, 13–18. [Google Scholar] [CrossRef]
- Huang, M.; Huang, J. Temperature Dependence of Brillouin Scattering Spectrum for High Nonlinear Photonic Crystal Fiber. Opto Electron. Eng. 2011, 38, 6–10. [Google Scholar]
- Jain, V.; Sharma, S.; Saini, T.S.; Kumar, A.; Sinha, R.K. Design and analysis of single-mode tellurite photonic crystal fibers for stimulated Brillouin scattering based slow-light generation. Appl. Opt. 2016, 55, 6791. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L. Influence of environment temperature wide-range variation on Brillouin shift in optical fiber. Acta Phys. Sin. 2010, 59, 6219–6223. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, J.; Niu, S.; Hou, S.; Wang, D.; Li, X. Temperature Sensing Utilizing Stimulate Brillouin Scattering Fast Light in Liquid-Filled Photonic Crystal Fibers. Coatings 2020, 10, 1123. https://doi.org/10.3390/coatings10111123
Lei J, Niu S, Hou S, Wang D, Li X. Temperature Sensing Utilizing Stimulate Brillouin Scattering Fast Light in Liquid-Filled Photonic Crystal Fibers. Coatings. 2020; 10(11):1123. https://doi.org/10.3390/coatings10111123
Chicago/Turabian StyleLei, Jingli, Shuaibin Niu, Shanglin Hou, Daobin Wang, and Xiaoxiao Li. 2020. "Temperature Sensing Utilizing Stimulate Brillouin Scattering Fast Light in Liquid-Filled Photonic Crystal Fibers" Coatings 10, no. 11: 1123. https://doi.org/10.3390/coatings10111123
APA StyleLei, J., Niu, S., Hou, S., Wang, D., & Li, X. (2020). Temperature Sensing Utilizing Stimulate Brillouin Scattering Fast Light in Liquid-Filled Photonic Crystal Fibers. Coatings, 10(11), 1123. https://doi.org/10.3390/coatings10111123



