Incidence Angle Effects on the Fabrication of Microstructures Using Six-Beam Laser Interference Lithography

Abstract

This paper presents a theoretical demonstration of diverse microstructure fabrication by changing the angle of incidence of a six-beam laser interference lithography system. Different combinations are formed with transverse electric (TE) and transverse magnetic (TM) polarizations and various microstructures are simulated by controlling the high-reflectivity mirror group to adjust the incidence angle. This study indicates that the incidence angle has a considerable influence on the shape and period of the lattice, thereby contributing to the fabrication of microstructures with different arrangements. These structures include donut, circle, D-type, rectangular, triangular, U-type, and honeycomb lattices. The six-beam laser interference lithography technique is expected to benefit microstructure fabrication because of its simple operation, large writing area, and low cost, thereby promoting the development of micro-optics.

1. Introduction

Micro- and nanostructures play key roles in innovative applications (such as plasmonics [1,2] and solar absorbers [3,4]) and the industrialization of micro- and nanofabrication technologies allows major industries to establish and maintain global leadership positions in key technology fields such as materials science [5], physics [6,7], and chemistry [8]. New trends in the development of micro- and nanomanufacturing guide strategic future investment and development to maintain and enhance the manufacturing industry. In recent years, various micro- and nanostructures have renewed interest in surface-enhanced Raman scattering [9,10], sensors [11,12], photocatalysis [13], and light absorption [14,15]. There are several ways to fabricate micro- and nanostructures, including chemical and physical methods, but chemical methods have drawbacks due to uncontrollable periods and irregular shapes. Instead, most researchers have been attracted to the photolithography of physical methods, which includes extreme ultraviolet (EUV) lithography [16], repeated-step projection lithography [17], X-ray lithography [18], and laser interference lithography (LIL) [19,20,21]. Over 30 years, EUV lithography has developed from a next-generation concept to high-volume manufacturing with high resolutions achieved at a wavelength of 13.5 nm [22], but its disadvantages are expensive sources and a complex exposure system. Although repeated-step projection lithography can provide a relatively small periodic structure, its alignment technique is complex, and X-ray lithography has relatively high requirements for its mask and photoresist, thereby inhibiting its widespread application. By contrast, LIL has the advantages of a large writing area, simple optical systems, and operations, thereby satisfying the requirements of microstructure fabrication.

Improvements in resolution have led to a new technological revolution in lithography with the introduction of various methods, the most popular being shortening the exposure wavelength, increasing the numerical aperture (NA), and decreasing the k-factor. The exposure wavelength reached 157 nm (F2) with the advent of excimer laser light sources in 2004, while the EUV exposure wavelength reached 13.5 nm and the k-factor is a constant associated with the optical lens [22]. Meanwhile, the NA depends on the refractive index and the angle of incidence (AOI). In general, the refractive index is unity except in immersion exposure. Therefore, the AOI is critical for improving resolution and fabricating micro- and nanostructures. To date, lithography research with a specified AOI has achieved meaningful results and has occupied a dominant position in the industry. For example, Chen et al. [23] studied dual-injection four-beam LIL at an AOI of 45°, Zhang et al. [24] investigated how the azimuth angle affected the written microstructure with two, three, and four beams with different polarization combinations under the same AOI, and Sarkar et al. [25] studied polarization effects in phase-controlled multi-beam interference lithography to realize submicron photonic structures. However, although the above research promoted the development of the microoptics industry, the influence of changes in the AOI has yet to be studied explicitly regarding the fabrication of micro- and nanostructures.

To fully explore the effects of the AOI when fabricating microstructures, we simulate herein six-beam LIL with different combinations of transverse electric (TE) and transverse magnetic (TM) polarizations. The results show that the AOI can affect the microstructure arrangement, lattice shape, and periodic value. This study promotes microstructure fabrication and plays a vital role in the field of microoptics.

2. Theoretical Analysis of Six-Beam Laser Interference Lithography

Figure 1 shows a schematic of the operation of a six-beam LIL system. The laser (L) reaches the collimator lens after through the aperture, then emits to beam splitter 1 (BS1, reflected energy: transmitted energy = 1:1) in the form of an approximate plane wave. The reflected light of BS1 will split into L1, L2, and L6, which are required for interference. Among them, L1 is the light transmitted by the beam splitter 3 (BS3, reflected energy: transmitted energy = 1:1), L2 is the reflected light by BS3, and L6 is the light reflected by beam splitter 2 (BS2, reflected energy: transmitted energy = 1:2). The transmitted light of BS1 which has the same way as the reflected light will split into L3, L4, and L5. Half-wave plates (HP1–HP3, HP1’–HP3’) can rotate polarized light and further modulate the polarization direction of the emitted light to achieve TE and TM polarization, and high-reflectively mirrors (R1–R5, R1’–R5’) adjust the AOI. The six beams are distributed uniformly in space, and the azimuth angle of adjacent beams remains at 60°. Note that the AOIs of the six beams are identical at each exposure. Finally, the six beams interfere at a point in the photoresist to form different lattice patterns.

The electric field vector of beam n (${\stackrel{\rightharpoonup }{E}}_n$) can be expressed as [26]

$${\stackrel{\rightharpoonup }{E}}_n=A_n{\stackrel{\rightharpoonup }{P}}_{n}cos\left({\stackrel{\rightharpoonup }{K}}_n\times {\stackrel{\rightharpoonup }{r}}_n-\omega t+{\phi }_n\right)$$

(1)

where $A_n$ is the amplitude, ${\stackrel{\rightharpoonup }{P}}_n$ is the unit polarization vector, ${\stackrel{\rightharpoonup }{K}}_n$ is the vector in the direction of propagation, ${\stackrel{\rightharpoonup }{r}}_n$ is the position vector, $\mathsf{\omega }$ is the frequency, t is the time, and ${\mathsf{\phi }}_n$ is the initial phase. In Equation (1), ${\stackrel{\rightharpoonup }{K}}_n$ is represented by [26]

$${\stackrel{\rightharpoonup }{K}}_n=K\left({\sin \mathsf{\theta }}_n\times \cos {\varnothing }_n\times \stackrel{\rightharpoonup }{i}-{\sin \mathsf{\theta }}_n\times \sin {\varnothing }_n\times \stackrel{\rightharpoonup }{j}-{\cos \mathsf{\theta }}_n\times \stackrel{\rightharpoonup }{k}\right)$$

(2)

The TE and TM polarizations are combined to investigate the results fully for all the beams for the six-beam LIL system. Thus, ${\stackrel{\rightharpoonup }{P}}_n$ can be written as

$${\stackrel{\rightharpoonup }{P}}_{\mathrm{TE}}={\sin \mathsf{\theta }}_n\times \stackrel{\rightharpoonup }{i}-{\cos \mathsf{\theta }}_n\times \stackrel{\rightharpoonup }{j}$$

(3)

$${\stackrel{\rightharpoonup }{P}}_{\mathrm{TM}}=-{\cos \mathsf{\theta }}_n\times \cos {\varnothing }_n\times \stackrel{\rightharpoonup }{i}-{\cos \mathsf{\theta }}_n\times \sin {\varnothing }_n\times \stackrel{\rightharpoonup }{j}-\sin {\varnothing }_n\times {\stackrel{\rightharpoonup }{k}}_{}$$

(4)

where $K$ is the wavenumber, ${\mathsf{\theta }}_n$ is the AOI, and ${\varnothing }_n$ is the azimuth angle. In the six-beam interference field, the intensity distribution ($I$) can be described as

$$I=\left({\stackrel{\rightharpoonup }{E}}_1+\cdots +{\stackrel{\rightharpoonup }{E}}_6\right)\left({\stackrel{\rightharpoonup }{E}}_1^{*}+\cdots +{\stackrel{\rightharpoonup }{E}}_6^{*}\right)$$

(5)

where ${\stackrel{\rightharpoonup }{E}}_n^{*}$ is the complex conjugate of the corresponding electric field ${\stackrel{\rightharpoonup }{E}}_n$.

3. Simulation Results and Discussion

During the numerical simulation, the six beams are set with a wavelength of 442 nm and an initial phase of zero. To intuitively observe the periodic structure of a microstructure, the calculation range is 10 times wavelength in the X- and Y-directions. The Z-direction is perpendicular to the photoresist, and its range is not considered under ideal conditions. The polarization is decomposed into X-, Y-, and Z-directions according to Equations (3) and (4), which can be expressed by the matrix. In the calculation process, the corresponding polarization component and the optical field component are calculated by matrix operation. Finally, the light field intensity distribution is obtained via summation according to Equation (5). To investigate further how the AOI affects microstructure fabrication, five polarization combinations are formed by combining the TE and TM polarizations, namely, (i) six TE beams, (ii) six TM beams, (iii) TE-TM-TM-TE-TM-TM, (iv) TM-TE-TE-TM-TE-TE, and (v) TM-TE-TM-TE-TM-TE.

Based on the above theoretical analysis, we begin with polarization combination (iii) and analyze the microstructures using numerical simulations for AOIs of 15°, 30°, 45°, 60°, 75°, and 85°. Figure 2 illustrates the microstructures fabricated using the six-beam LIL with polarization combination (iii). A three-dimensional illustration of a single-period microstructure is shown in the upper-right corner of the corresponding two-dimensional field distribution pattern. As shown in Figure 2a, triangular lattices are obtained with an AOI of 15°. The azimuth of the two triangular lattices parallel to the X-axis is inverted from the other four, thereby leading to six adjacent triangular lattices that form a hexagon with unequal sides. Upon increasing the AOI to 30°, the lattices are compressed horizontally to form D-type lattices, as shown in Figure 2b. Based on theoretical analysis and previous research, the microstructure arrangement is affected by the number of beams and incident azimuth angle, and the lattice shape is determined by the electric field components of the TE and TM polarizations in all directions [25,26,27]. Thus, the increased AOI affects the magnitude of the electric field components and further compresses the lattice.

To explain this phenomenon further, we increase the AOI to 45°, whereupon the horizontal direction of the lattices compresses to form rectangular lattices, as shown in Figure 2c. Although the lattice shape changes, the arrangement of the hexagonal microstructure with unequal sides remains invariant. Upon increasing the AOI to 60°, the rectangular lattices are connected successively to form U-type lattices [28] (Figure 2d). For larger AOI (75° or 85°), the lattices are again compressed horizontally so that the bottom of the U-shaped lattices break to form rectangular lattices arranged horizontally, as shown in Figure 2e,f. Although rectangular lattices can be obtained in both cases, their parallelism is higher at larger AOI.

Herein, we also consider other polarization combinations for fabricating microstructures.

Table 1. Optical field distributions of microstructures with a six-beam LIL system.

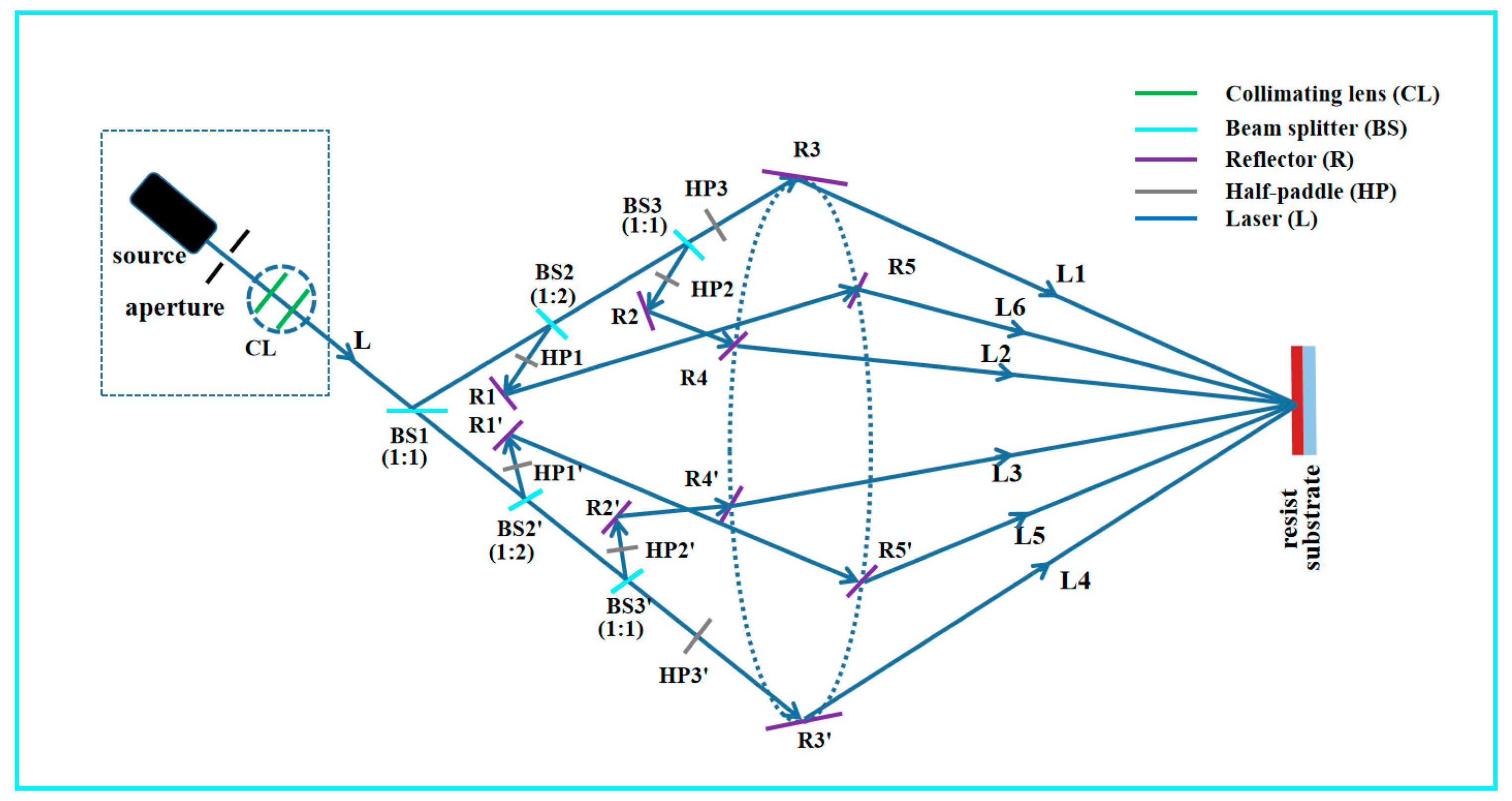
	Mode	Six TE Beam	Six TM Beam	TM-TE-TE TM-TE-TE	TE-TM-TM TE-TM-TM	TM-TE-TM TE-TM-TE
θ
θ = 15°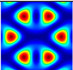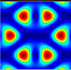
		Donut	Donut	Triangular	Triangular	Honeycomb
θ = 30°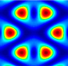
		Donut	Donut	Triangular	D-type	Honeycomb
θ = 45°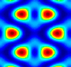
		Donut	Circle	D-type	Rectangle	Honeycomb
θ = 60°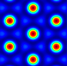
		Donut	Circle	D-type	U-type	Circle
θ = 75°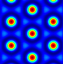
		Donut	Circle	Circle	Rectangle	Circle
θ = 85°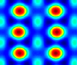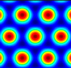
		Donut	Circle	Circle	Rectangle	Circle

shows the single-period microstructures that are fabricated using the six-beam LIL system. We begin by investigating how the AOI affects the fabrication of microstructures under TE or TM polarization conditions. TE polarization produces a donut lattice [25] in which the remaining six adjacent lattices form an equilateral hexagon. The period decreases with the AOI, which does not impact the lattice shape or microstructure arrangement because of the uniform distribution of the electric field as generated by TE polarization in the incident direction. Although TM polarization can also produce donut lattices, it has a higher fill factor [25] as the AOI increases. Besides, the arrangement of the equilateral hexagon remains unchanged, but the donut lattices evolve into circular lattices, which are called Kagome-type lattices [25]. This is because the electric field component of TM polarization is decomposed into the remaining two directions, and the electric fields of the components are related to the AOI. Therefore, microstructures with various lattice shapes can be fabricated by changing the AOI in conjunction with using TE and TM polarization. This conclusion is confirmed by polarization combination (iii).

Next, we study polarization combinations (iv) and (v) to explain this effect further and fabricate additional microstructure types. For polarization combination (iv), triangular lattices are formed at an AOI of 15° or 30°, and the periodic microstructures are identical to those with polarization combination (iii) at an AOI of 15°. When the AOI increases to 45° or 60°, the triangular lattices are compressed horizontally to form D-type lattices. Although circular lattices can be obtained for larger AOI (75° or 85°), the microstructure becomes more ordered with increasing AOI. For polarization combination (v), the fabricated microstructures are identical to those formed by three TM-polarized beams with an azimuth angle of 120° [29]. Honeycomb lattices are fabricated at an AOI of less than 45° and circular lattices are fabricated at an AOI of more than 60°. This is because of the irrelevance of the two polarized beams (TM and TE) on the same axis and the uniform spatial distribution of the same type of polarization. Photolysis of the negative photoresist film takes place in the unexposed resist, while positive photoresist has the opposite effect. However, because these two microstructures are complementary, both can be fabricated with either photoresist.

4. Conclusions

Herein, we have provided a theoretical presentation of a six-beam LIL system for fabricating microstructures. The results of numerical simulations showed that the AOI strongly affects the lattice shape, period, and microstructure arrangement. Various microstructures were obtained by changing the AOI with different polarization combinations for the six beams, and consequently, donut, circle, D-type, rectangular, triangular, U-type, and honeycomb lattices could be fabricated. Through adjusting the polarization and AOI, the proposed method can achieve the desired microstructure. This simple and inexpensive system can provide an effective way for promoting the development of micro- and nanostructures in the future.