An Atomization Model of Air Spraying Using the Volume-of-Fluid Method and Large Eddy Simulation
Abstract
:1. Introduction
2. Paint Atomization Model of Air Spray
2.1. Basic Governing Equations
2.2. Interface Capture Model
2.3. Turbulence Model
3. Numerical Simulation
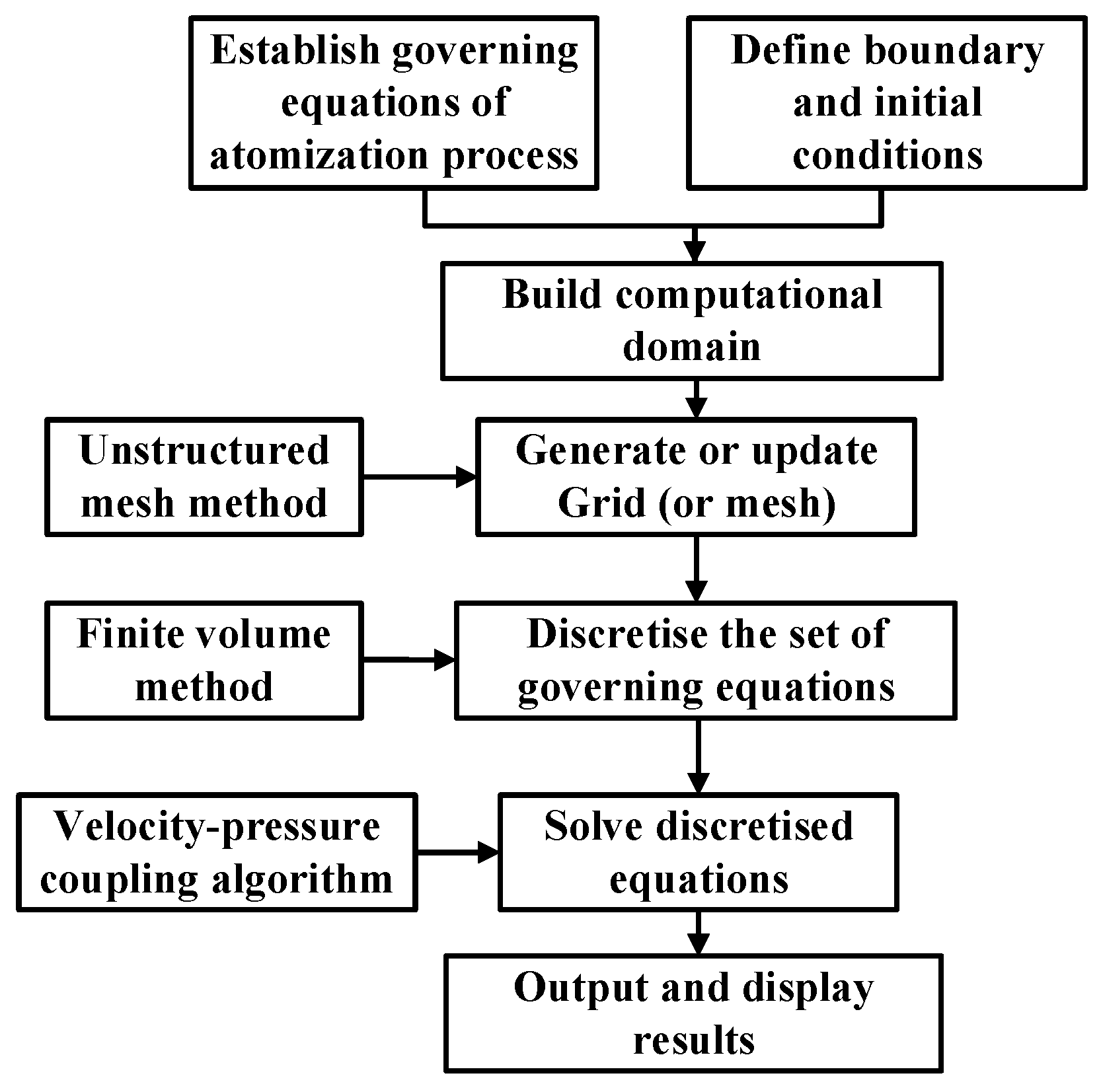
3.1. Simulation Process
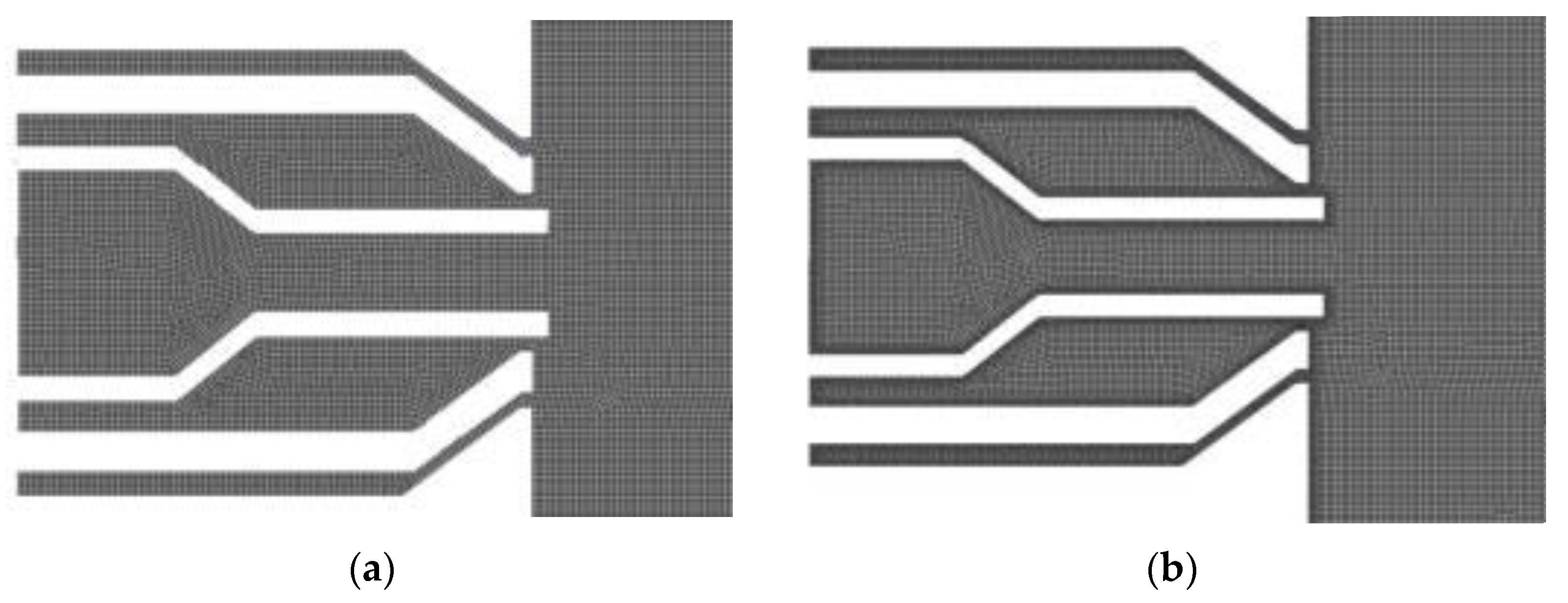
3.2. Computational Domain and Initial Mesh
3.3. Parameter Settings of Atomization Simulation
4. Model Verification
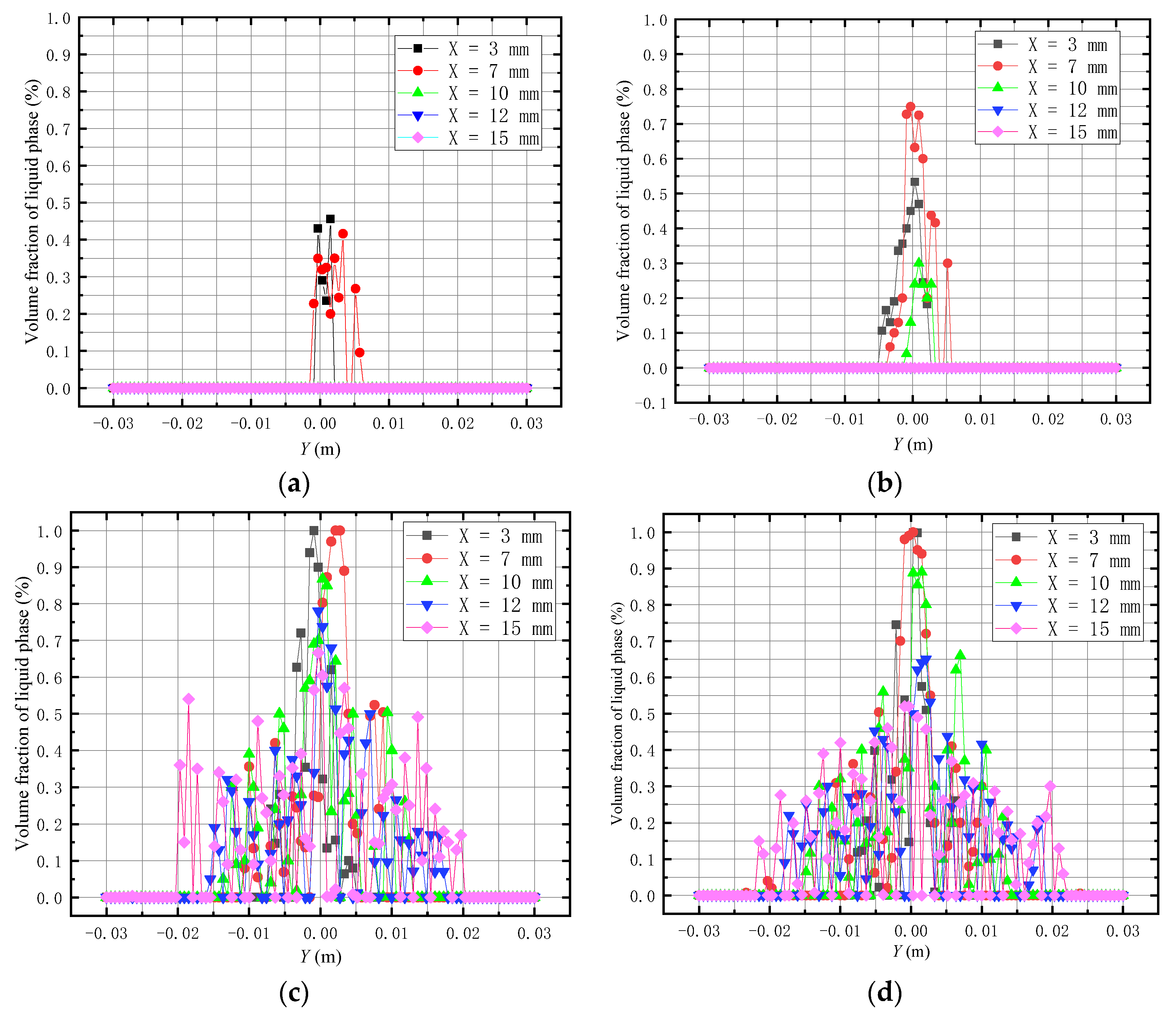
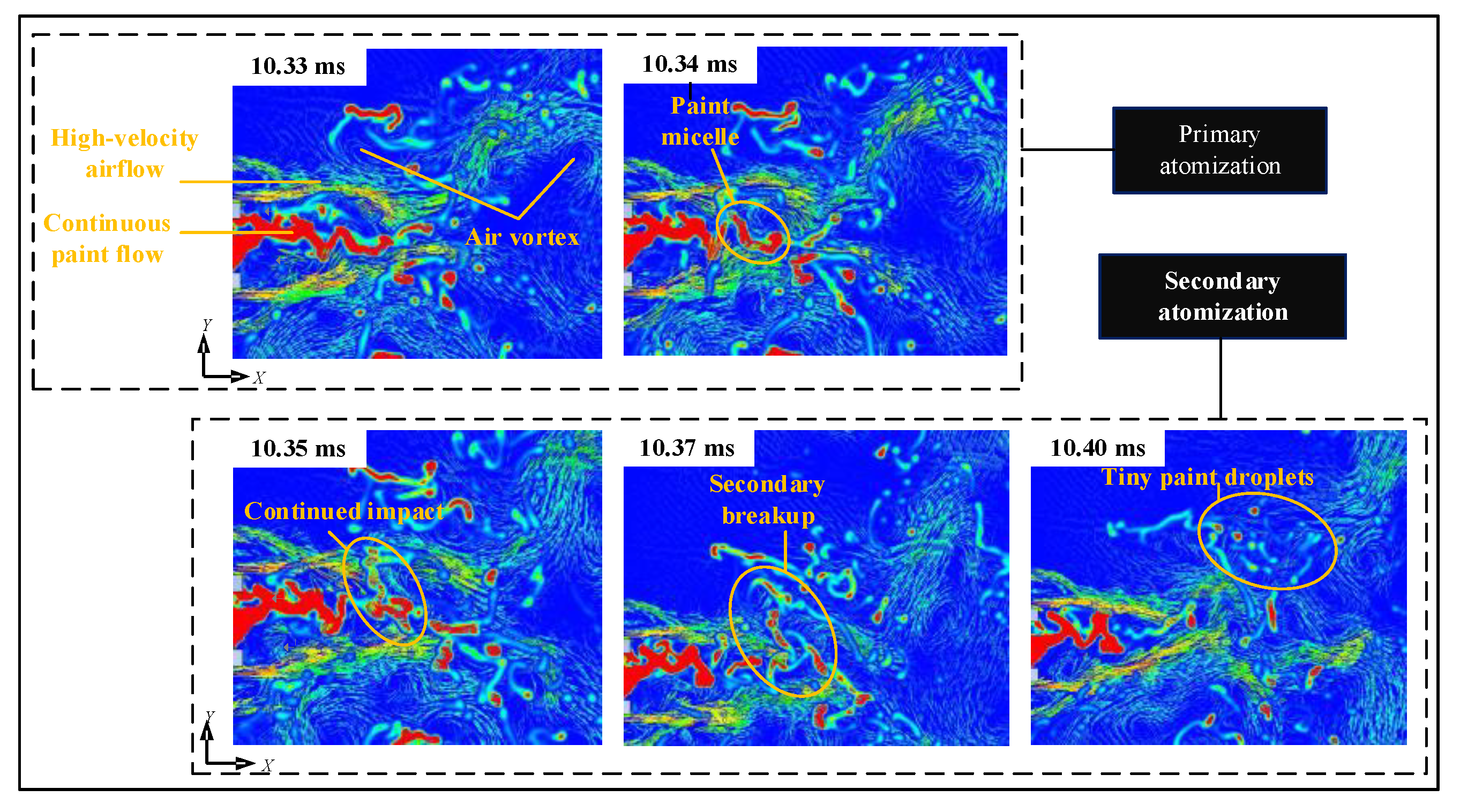
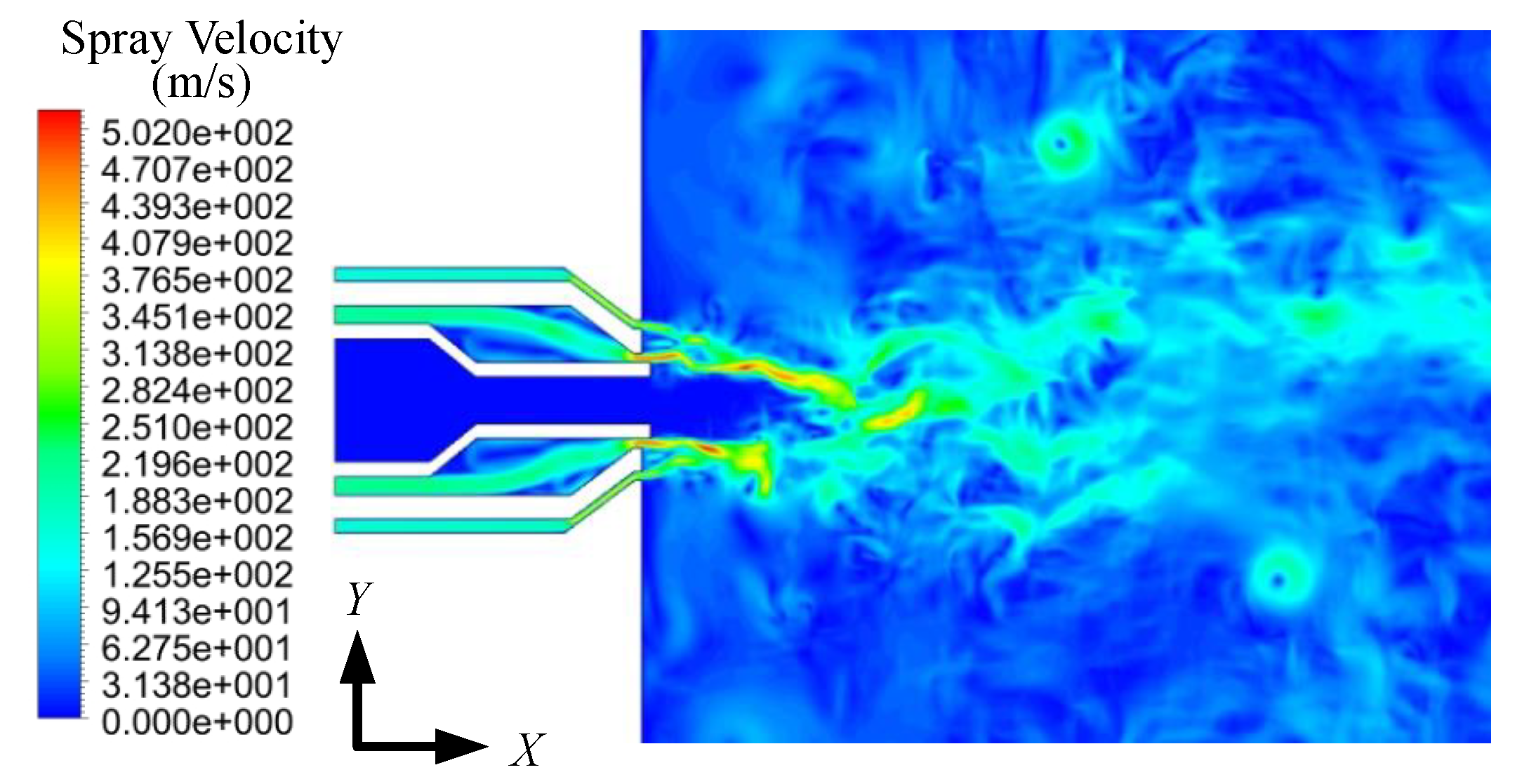
4.1. Numerical Simulation Results
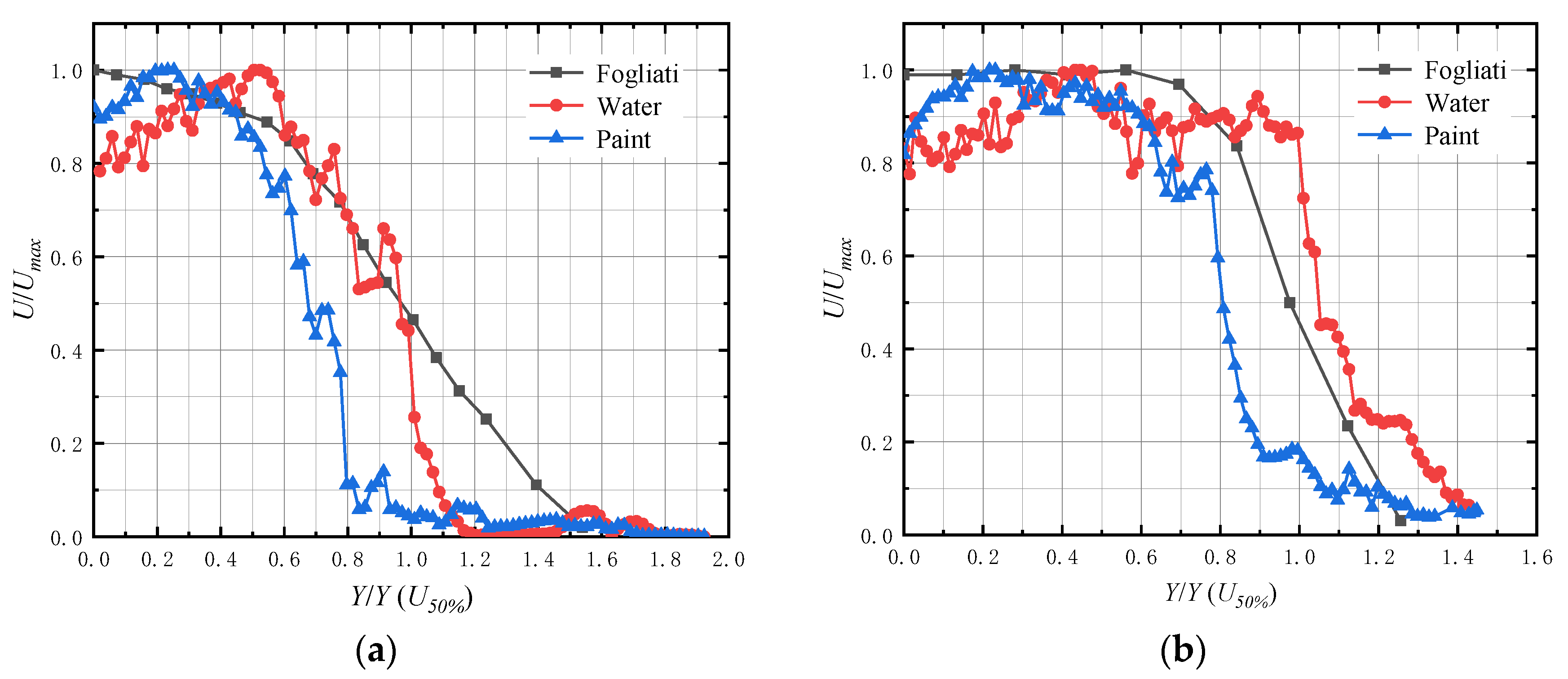
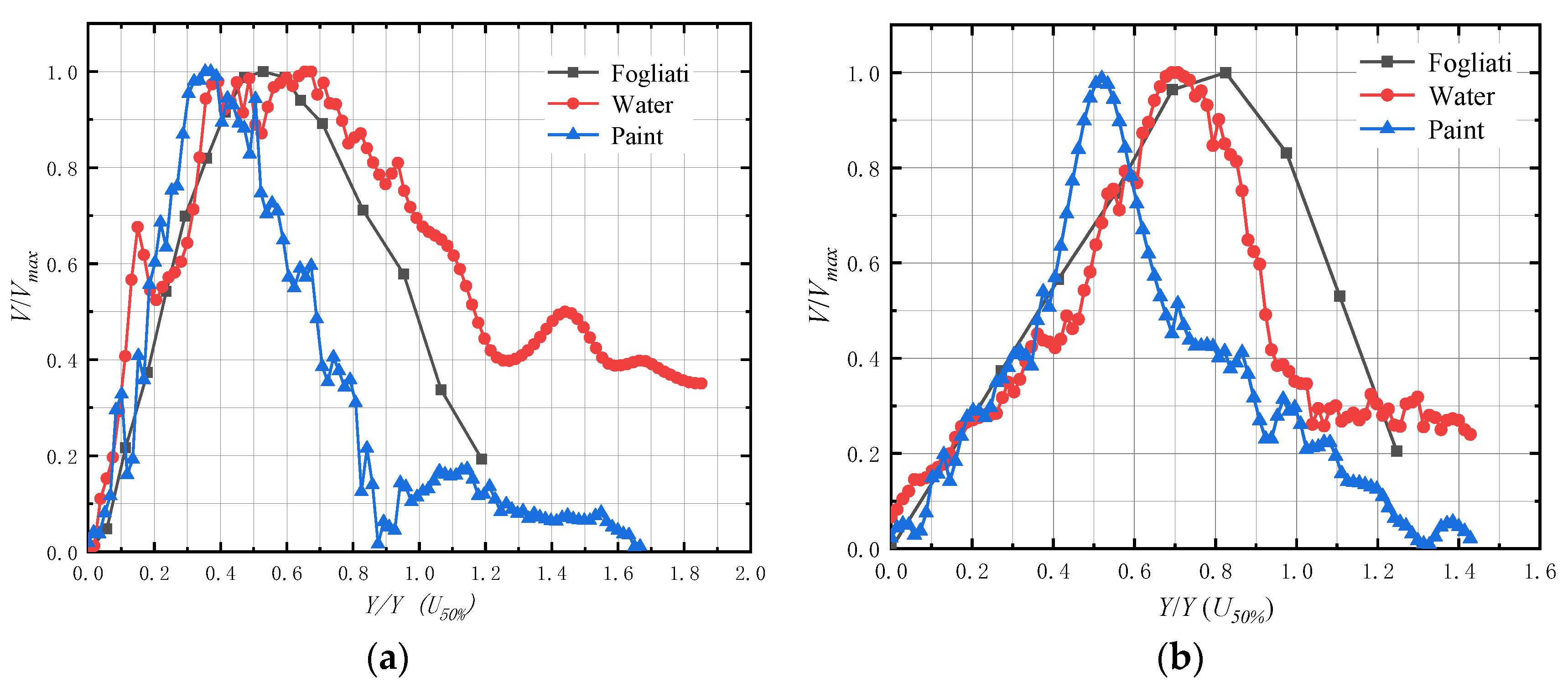
4.2. Result Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Neal, A.S.; Jonathan, A.B.; Ron, K.F. Precision robotic coating application and thickness control optimization for f-35 final finishes. SAE Int. J. Aerosp. 2009, 2, 284–290. [Google Scholar]
- Chen, H.P.; Xi, N. Automated tool trajectory planning of industrial robots for painting composite surfaces. Int. J. Adv. Manuf. Technol. 2008, 35, 680–696. [Google Scholar] [CrossRef]
- Chen, W.; Chen, Y.; Li, B.; Zhang, W.; Chen, K. Design of redundant robot painting system for long non-regular duct. Ind. Robot Int. J. 2016, 43, 58–64. [Google Scholar] [CrossRef]
- Xie, F.G.; Liu, X.J.; Wu, C.; Zhang, P. A novel spray painting robotic device for the coating process in automotive industry. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 2081–2093. [Google Scholar] [CrossRef]
- Stephan, S.; Hasse, H. Enrichment at vapour–liquid interfaces of mixtures: Establishing a link between nanoscopic and macroscopic properties. Int. Rev. Phys. Chem. 2020, 39, 319–349. [Google Scholar] [CrossRef]
- Colbert, S.A.; Cairncross, R.A. A discrete droplet transport model for predicting spray coating patterns of an electrostatic rotary atomizer. J Electrost. 2006, 64, 234–246. [Google Scholar] [CrossRef]
- Domnick, J.; Lindenthal, A.; Tropea, C.; Xu, T.H. Application of phase doppler anemometry in paint sprays. At. Sprays. 1994, 4, 437–450. [Google Scholar]
- Luo, H.; Nishida, K.; Uchitomi, S.; Ogata, Y.; Zhang, W.; Fujikawa, T. Microscopic behavior of spray droplets under flat-wall impinging condition. Fuel 2018, 219, 467–476. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Park, S. Atomization characteristics of aerosol spray from hair spray vessel with various design parameters. J. Aerosol Sci. 2019, 133, 24–36. [Google Scholar] [CrossRef]
- Chen, W.Z.; Chen, Y.; Zhang, W.M.; He, S.W.; Li, B.; Jiang, J.Z. Paint thickness simulation for robotic painting of curved surfaces based on Euler–Euler approach. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 199. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, W.Z.; Li, B.; Zhang, G.; Zhang, W.M. Paint thickness simulation for painting robot trajectory planning: A review. Ind. Robot. Int. J. 2017, 44, 629–638. [Google Scholar] [CrossRef]
- Fogliati, M.; Fontana, D.; Garbero, M.; Vanni, M.; Baldi, G.; Donde, R. CFD simulation of paint deposition in an air spray process. JCT Res. 2006, 3, 117–125. [Google Scholar] [CrossRef]
- Ye, Q.; Pulli, K. Numerical and experimental investigation on the spray coating process using a pneumatic atomizer: Influences of operating conditions and target geometries. Coatings. 2017, 7, 13. [Google Scholar] [CrossRef] [Green Version]
- Shin, J.; Kim, D.; Seo, J.; Park, S. Effects of the physical properties of fuel on spray characteristics from a gas turbine nozzle. Energy. 2020, 205, 118090. [Google Scholar] [CrossRef]
- AlZahrani, A.A.; Dincer, I. Modeling of n-Hexane and n-Octane liquid fuel jets in gaseous crossflow for evaporation, combustion and breakup evaluation. Int. Commun. Heat Mass Transf. 2017, 88, 203–210. [Google Scholar] [CrossRef]
- Li, W.; Qian, L.; Song, S.; Zhong, X. Numerical study on the influence of shaping air holes on atomization performance in pneumatic atomizers. Coatings. 2019, 9, 410. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.A.; Xie, X.P.; Lu, X.H. Design of a double-nozzle air spray gun and numerical research in the interference spray flow field. Coatings. 2020, 10, 475. [Google Scholar] [CrossRef]
- Ghate, K.; Muthuselvan, G.; Sundararajan, T. Modeling of primary and secondary atomization with simplex atomizers. Multiph. Sci. Technol. 2020, 32, 237–258. [Google Scholar] [CrossRef]
- Giussani, F.; Piscaglia, F.; Saez-Mischlich, G.; Hèlie, J. A three-phase VOF solver for the simulation of in-nozzle cavitation effects on liquid atomization. J. Comput. Phys. 2020, 406, 109068. [Google Scholar] [CrossRef]
- Gurakov, N.I.; Zubrilin, I.A.; Abrashkin, V.Y.; Morales, M.H.; Yakushkin, D.V.; Yastrebov, V.V.; Kolomzarov, O.V.; Idrisov, D.V. Validation of the VOF method for liquid spray process simulation from a pressure-swirl atomizer. AIP Conf. Proc. 2020, 2304, 020031. [Google Scholar]
- Payri, R.; Giraldo, J.S.; Ayyapureddi, S.; Versey, Z. Experimental and analytical study on vapor phase and liquid penetration for a high pressure diesel injector. Appl. Therm. Eng. 2018, 137, 721–728. [Google Scholar] [CrossRef]
- Jacobsohn, G.L.; Mohapatra, C.K.; Grover, R.O.; Duke, D.J.; Schmidt, D.P. Comparison of turbulence modeling methods for evaluating GDI sprays with transient needle motion. Presented at the SAE World Congress Exper (WCX2019), Detroit, MI, USA, 9–11 April 2019. [Google Scholar]
- Xiao, F.; Dianat, M.; McGuirk, J.J. LES of turbulent liquid jet primary breakup in turbulent coaxial air flow. Int. J. Multiph. Flow. 2013, 60, 103–118. [Google Scholar] [CrossRef] [Green Version]
- Zou, W.; He, Z.; Gu, X. Viscous Fluid Dynamics, 1st ed.; National Defense Industry Press: Beijing, China, 2013; pp. 128–133. [Google Scholar]

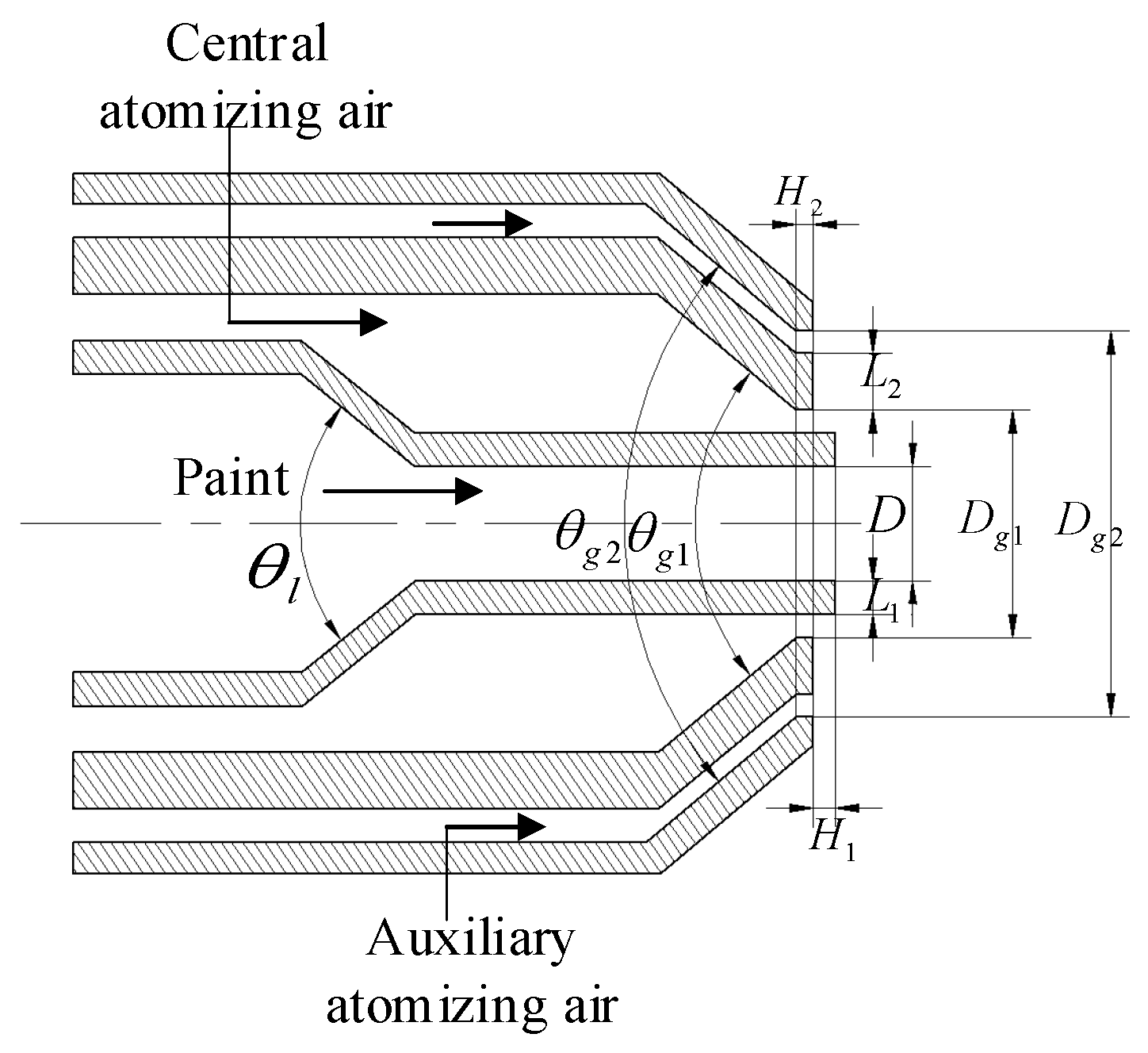




| Parameter Symbol | D | Dg1 | Dg2 | L1 | L2 | H1 | H2 | θ1 | θg1 | θg2 |
|---|---|---|---|---|---|---|---|---|---|---|
| Size | 2.0 mm | 4.0 mm | 7.6 mm | 0.6 mm | 1.0 mm | 0.4 mm | 0.3 mm | 78° | 80° | 80° |
| Substance | Density | Viscosity | Surface Tension | Reference Temperature |
|---|---|---|---|---|
| Paint | 1200 kg/m3 | 0.097 kg/(m·s) | 0.0287194 N/m | 298.15 K |
| Air | 1.225 kg/m3 | 0.000017894 kg/(m·s) | – | 298.15 K |
| Water | 998.2 kg/m3 | 0.001003 kg/(m·s) | 0.0719404 N/m | 298.15 K |
| Type | Ejection Conditions of Liquid Phase | Ejection Conditions of Central Atomizing Air | Ejection Conditions of Auxiliary Atomizing Air | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Medium Type | MI | TI | HD | PI | TI | HD | PI | TI | HD | |
| Simulation 1 | Paint | 1.42 m/s | 5% | 1 mm | 121 kPa | 5% | 0.5 mm | 81 kPa | 5% | 0.4 mm |
| Simulation 2 | Water | 3 cm3/s | 10% | 1 mm | 152 kPa | 10% | 0.5 mm | 121 kPa | 10% | 0.4 mm |
| Fogliati | Water | 3 cm3/s | 10% | 2 mm | 150 kPa | 10% | 0.5 mm | 120 kPa | 10% | 0.5 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Chen, S.; Chen, W.; Hu, J.; Jiang, J. An Atomization Model of Air Spraying Using the Volume-of-Fluid Method and Large Eddy Simulation. Coatings 2021, 11, 1400. https://doi.org/10.3390/coatings11111400
Chen Y, Chen S, Chen W, Hu J, Jiang J. An Atomization Model of Air Spraying Using the Volume-of-Fluid Method and Large Eddy Simulation. Coatings. 2021; 11(11):1400. https://doi.org/10.3390/coatings11111400
Chicago/Turabian StyleChen, Yan, Shiming Chen, Wenzhuo Chen, Jun Hu, and Junze Jiang. 2021. "An Atomization Model of Air Spraying Using the Volume-of-Fluid Method and Large Eddy Simulation" Coatings 11, no. 11: 1400. https://doi.org/10.3390/coatings11111400





