Sliding Dispersion Entropy-Based Fault State Detection for Diaphragm Pump Parts
Abstract
:1. Introduction
2. Methodology
2.1. Sliding Dispersion Entropy (SDE)
2.2. State Warning Line Based on SDE
2.3. Fault State Detection Method
3. Results and Discussion
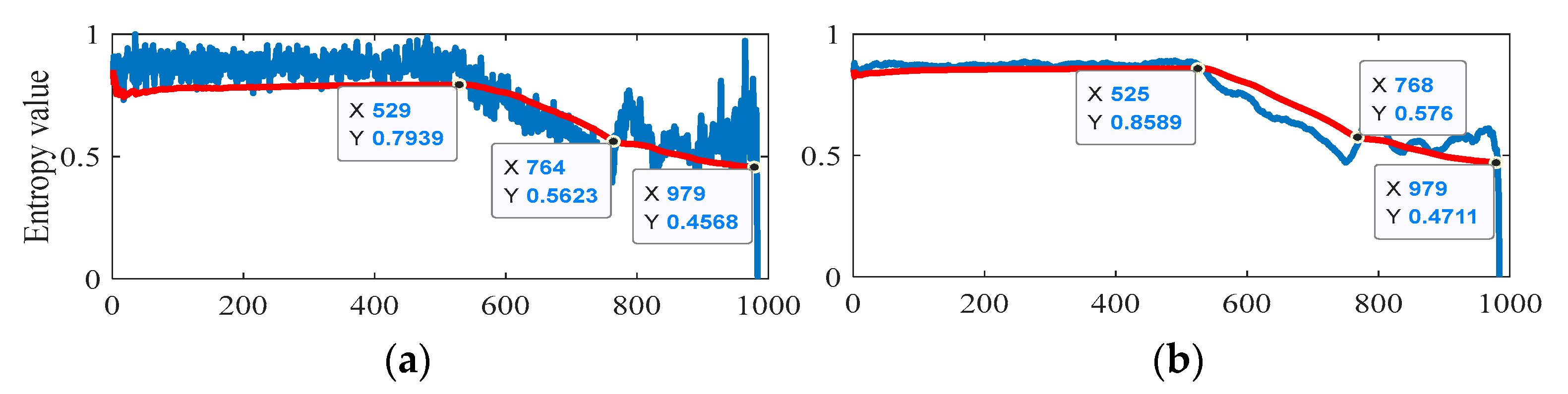
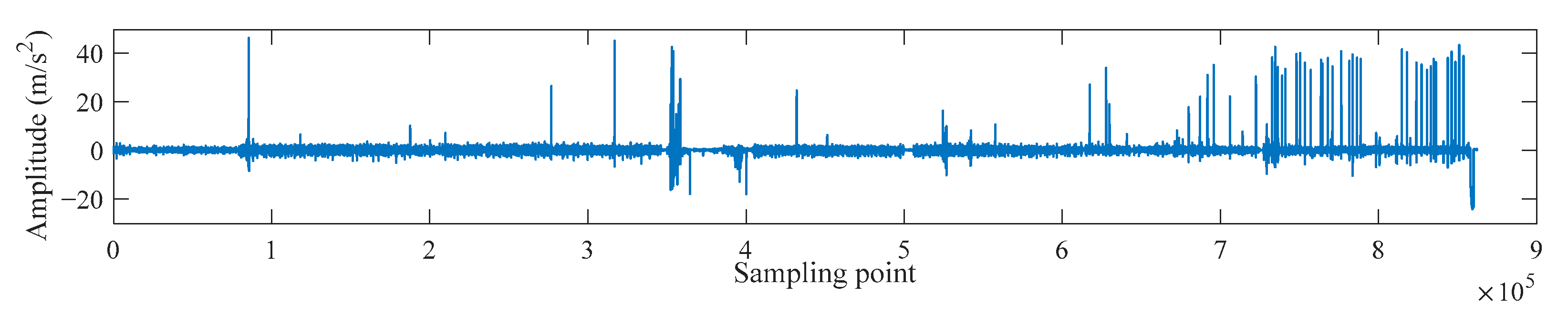
3.1. Bearing Fault Detection and Comparative Analysis
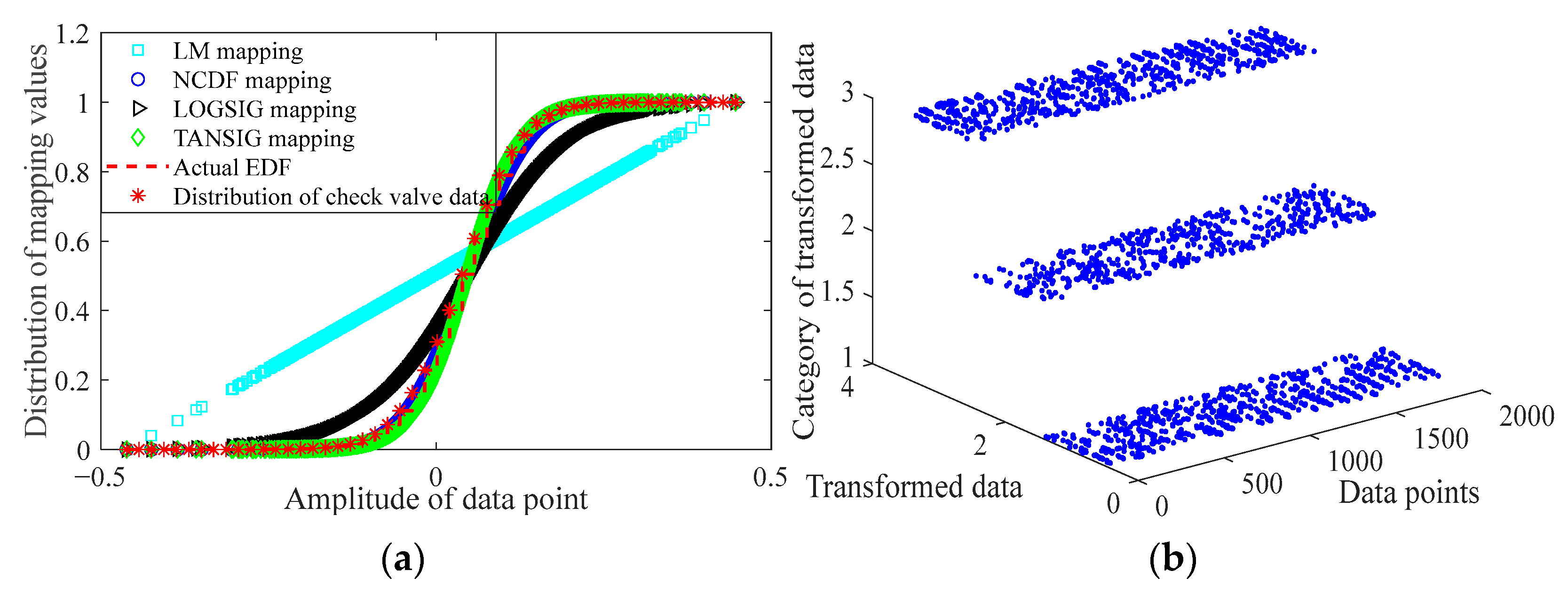
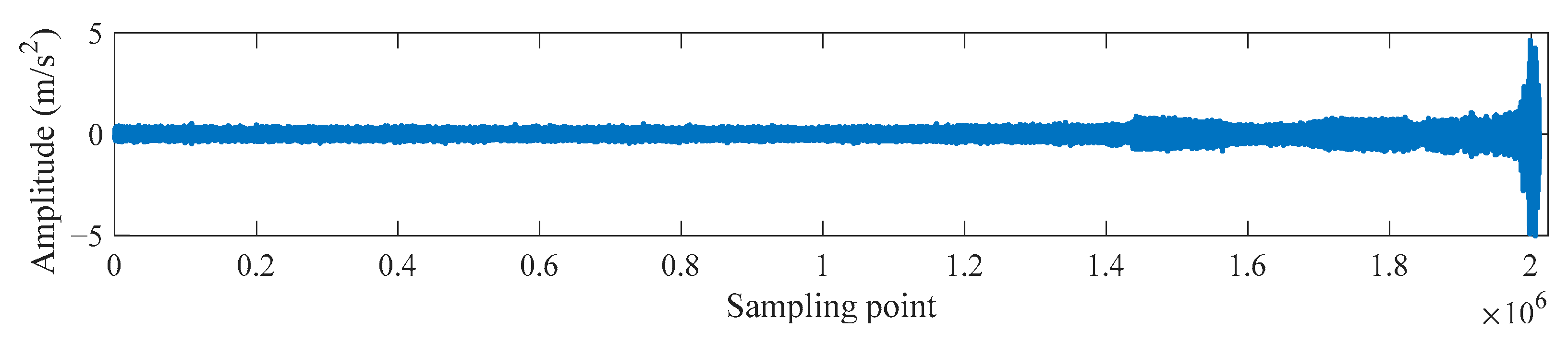
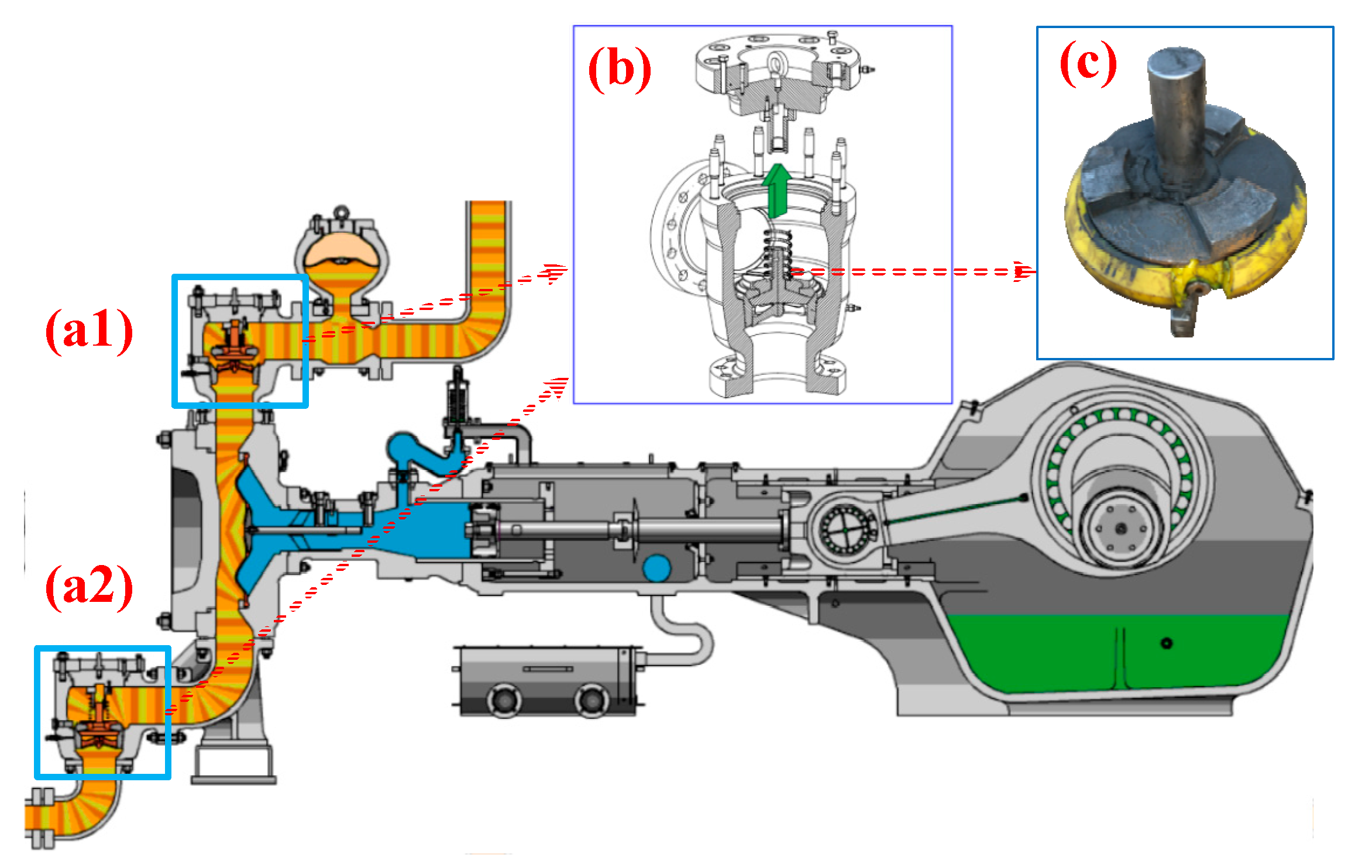
3.2. Check Valve Fault Detection and Practical Application
3.3. Comparison and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, W.; Mckeown, A.; Yu, Z. Correction of cavitation with thermodynamic effect for a diaphragm pump in organic Rankine cycle systems. Energy Rep. 2020, 6, 2956–2972. [Google Scholar] [CrossRef]
- Xiao, L.; Liu, Z.; Zhang, Y.; Zheng, Y.; Cheng, C. Degradation assessment of bearings with trend-reconstruct-based features selection and gated recurrent unit network. Measurement 2020, 165, 108064. [Google Scholar] [CrossRef]
- Gao, S.; Zhang, S.; Zhang, Y.; Gao, Y. Operational reliability evaluation and prediction of rolling bearing based on isometric mapping and NoCuSa-LSSVM. Reliab. Eng. Syst. Saf. 2020, 201, 106968. [Google Scholar] [CrossRef]
- Hua, Z.; Xiao, Y.; Cao, J. Misalignment Fault Prediction of Wind Turbines Based on Improved Artificial Fish Swarm Algorithm. Entropy 2021, 23, 692. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhang, X.; Kari, T.; Hu, W. Health Assessment and Remaining Useful Life Prediction of Wind Turbine High-Speed Shaft Bearings. Energies 2021, 14, 4612. [Google Scholar] [CrossRef]
- Bilendo, F.; Badihi, H.; Lu, N.; Jiang, B. A data-driven prognostics method for explicit health index assessment and improved remaining useful life prediction of bearings. ISA Trans. 2021. [Google Scholar] [CrossRef] [PubMed]
- He, M.; Zhou, Y.; Li, Y.; Wu, G.; Tang, G. Long short-term memory network with multi-resolution singular value decomposition for prediction of bearing performance degradation. Measurement 2020, 156, 107582. [Google Scholar] [CrossRef]
- Ding, N.; Li, H.; Yin, Z.; Jiang, F. A novel method for journal bearing degradation evaluation and remaining useful life prediction under different working conditions. Measurement 2021, 177, 109273. [Google Scholar] [CrossRef]
- Hu, M.; Wang, G.; Ma, K.; Cao, Z.; Yang, S. Bearing performance degradation assessment based on optimized EWT and CNN. Measurement 2021, 172, 108868. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Qin, A.-S.; Mao, H.-L.; Hu, Q. Cross-domain fault diagnosis of rolling bearing using similar features-based transfer approach. Measurement 2021, 172, 108900. [Google Scholar] [CrossRef]
- Kumar, P.S.; Kumaraswamidhas, L.; Laha, S. Selection of efficient degradation features for rolling element bearing prognosis using Gaussian Process Regression method. ISA Trans. 2021, 112, 386–401. [Google Scholar] [CrossRef] [PubMed]
- Noman, K.; Wang, D.; Peng, Z.; He, Q. Oscillation based permutation entropy calculation as a dynamic nonlinear feature for health monitoring of rolling element bearing. Measurement 2021, 172, 108891. [Google Scholar] [CrossRef]
- Minhas, A.S.; Kankar, P.; Kumar, N.; Singh, S. Bearing fault detection and recognition methodology based on weighted multiscale entropy approach. Mech. Syst. Signal Process. 2021, 147, 107073. [Google Scholar] [CrossRef]
- Li, H.; Sun, J.; Ma, H.; Tian, Z.; Li, Y. A novel method based upon modified composite spectrum and relative entropy for degradation feature extraction of hydraulic pump. Mech. Syst. Signal Process. 2019, 114, 399–412. [Google Scholar] [CrossRef]
- Mostafa, R.; Reza, A.M.; Hamed, A. Application of dispersion entropy to status characterization of rotary machines. J. Sound Vib. 2018, 438, 291–308. [Google Scholar]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, S.; Li, W. Bearing performance degradation assessment using long short-term memory recurrent network. Comput. Ind. 2019, 106, 14–29. [Google Scholar] [CrossRef]
- Azami, H.; Rostaghi, M.; Escudero, J. Refined composite multiscale dispersion entropy: A fast measure of complexity. IEEE Trans. Bio-Med. Eng. 2016, 99, 1–5. [Google Scholar]
- Cleveland, W.S. LOWESS: A Program for Smoothing Scatterplots by Robust Locally Weighted Regression. Am. Stat. 1981, 35, 54. [Google Scholar] [CrossRef]
- Duong, P.B.; Khan, A.S.; Shon, D.; Im, K. A Reliable Health Indicator for Fault Prognosis of Bearings. Sensors 2018, 18, 3740. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Z.; Liu, Y.; Wang, Q.; Wang, J.; Luo, Y. Ensemble empirical mode decomposition energy moment entropy and enhanced long short-term memory for early fault prediction of bearing. Measurement 2021, 110417. [Google Scholar] [CrossRef]
- Haidong, S.; Junsheng, C.; Hongkai, J.; Yu, Y.; Zhantao, W. Enhanced deep gated recurrent unit and complex wavelet packet energy moment entropy for early fault prognosis of bearing. Knowl. Based Syst. 2020, 188, 105022. [Google Scholar] [CrossRef]





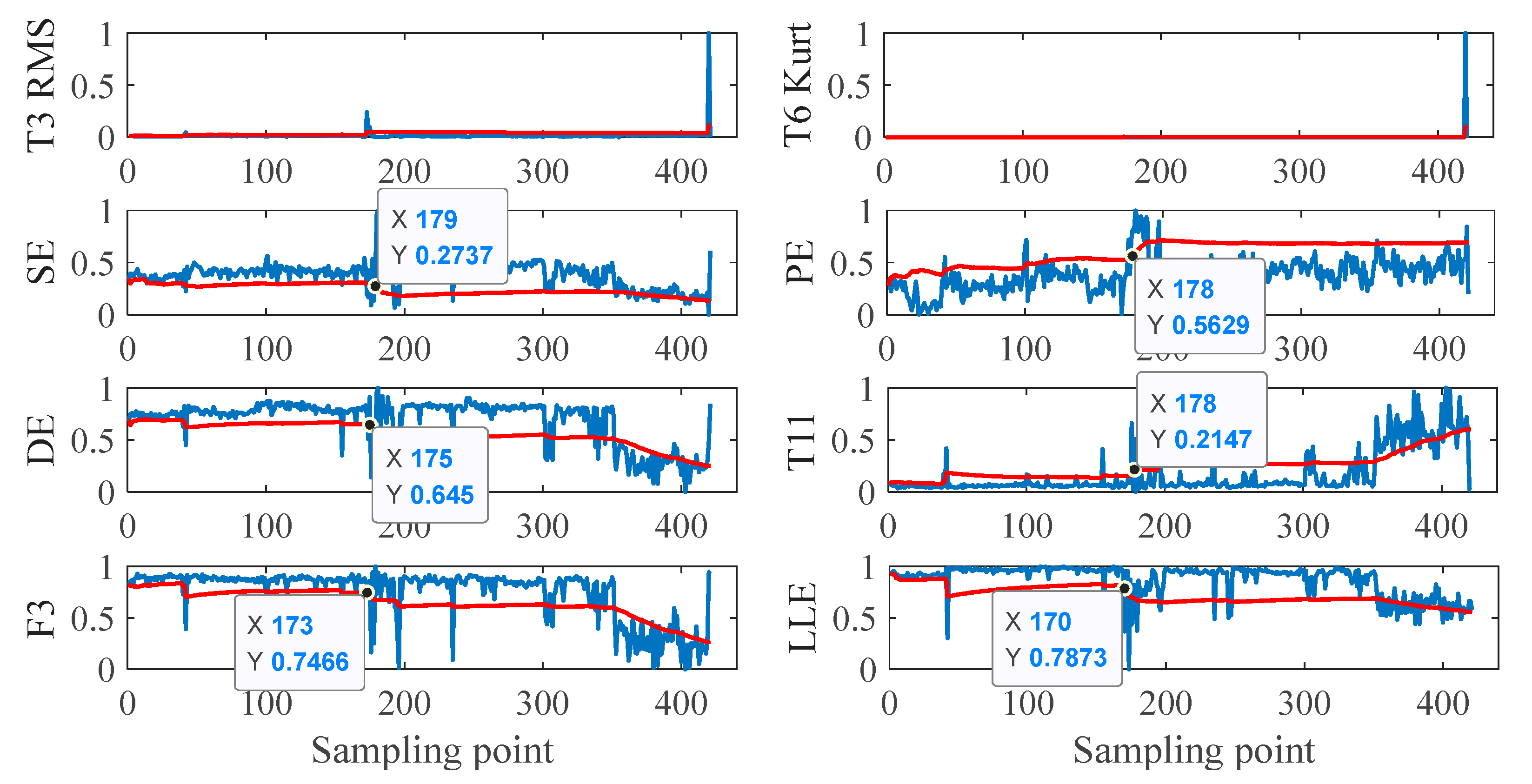
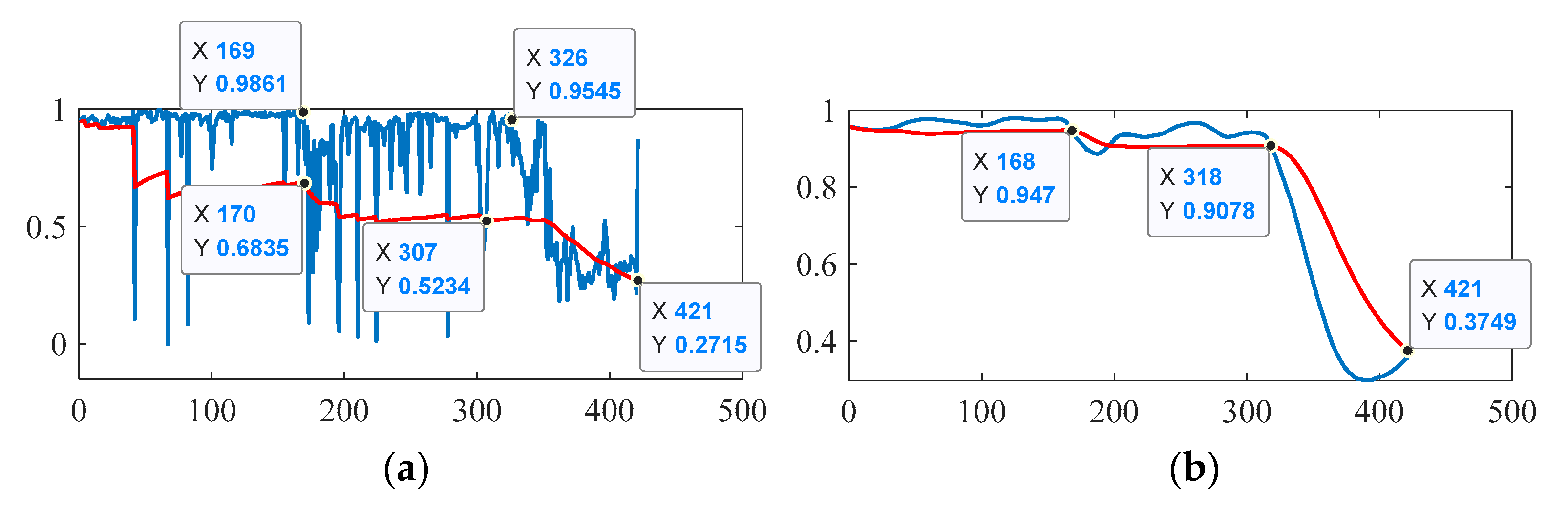
| Feature | Mon | Rob | Tre | MEI | Feature | Mon | Rob | Tre | MEI |
|---|---|---|---|---|---|---|---|---|---|
| T1 | 0.0193 | 0.9628 | 0.6334 | 0.4252 | F7 | 0.0030 | 0.9857 | 0.7152 | 0.4403 |
| T2 | 0.0010 | 0.9640 | 0.6269 | 0.4151 | F8 | 0.0050 | 0.9929 | 0.6680 | 0.4340 |
| T3 RMS | 0.0233 | 0.9594 | 0.6301 | 0.4255 | F9 | 0.0030 | 0.9898 | 0.7144 | 0.4413 |
| T4 | 0.0193 | 0.9628 | 0.6334 | 0.4252 | F10 | 0.0417 | 0.9720 | 0.7189 | 0.4562 |
| T5 | 0.0010 | 0.8725 | 0.1857 | 0.2994 | F11 | 0.0193 | 0.9696 | 0.0374 | 0.3080 |
| T6 Kurt | 0.0091 | 0.8050 | 0.1129 | 0.2686 | F12 | 0.0050 | 0.9689 | 0.0160 | 0.2964 |
| T7 | 0.0111 | 0.9107 | 0.5107 | 0.3809 | F13 | 0.0152 | 0.9713 | 0.6083 | 0.4206 |
| T8 | 0.0111 | 0.9110 | 0.5112 | 0.3811 | TF1 | 0.0356 | 0.9939 | 0.6055 | 0.4370 |
| T9 | 0.0010 | 0.6239 | 0.3618 | 0.2600 | TF2 | 0.0030 | 0.9205 | 0.1400 | 0.3057 |
| T10 | 0.0233 | 0.9240 | 0.3962 | 0.3681 | TF3 | 0.0233 | 0.9197 | 0.6577 | 0.4191 |
| T11 | 0.0050 | 0.9919 | 0.6207 | 0.4242 | TF4 | 0.0111 | 0.9286 | 0.4078 | 0.3657 |
| T12 | 0.0111 | 0.9247 | 0.1883 | 0.3206 | TF5 | 0.0071 | 0.8813 | 0.3607 | 0.3400 |
| T13 | 0.0030 | 0.9211 | 0.3240 | 0.3426 | TF6 | 0.0172 | 0.8879 | 0.7433 | 0.4236 |
| T14 | 0.0050 | 0.9192 | 0.3784 | 0.3540 | TF7 | 0.0010 | 0.9140 | 0.7462 | 0.4239 |
| T15 | 0.0030 | 0.9775 | 0.5957 | 0.4139 | TF8 | 0.0010 | 0.9069 | 0.7589 | 0.4243 |
| T16 | 0.0132 | 0.9429 | 0.5453 | 0.3985 | PCA | 0.0050 | 0.5864 | 0.0114 | 0.1807 |
| F1 | 0.0132 | 0.9634 | 0.5547 | 0.4065 | LLE | 0.0030 | 0.9999 | 0.8071 | 0.4629 |
| F2 | 0.0132 | 0.9260 | 0.4199 | 0.3684 | LLTSA | 0.0010 | 0.5866 | 0.4686 | 0.2702 |
| F3 | 0.0172 | 0.9885 | 0.6996 | 0.4451 | SE | 0.0091 | 0.9135 | 0.5620 | 0.3910 |
| F4 | 0.0193 | 0.9833 | 0.6986 | 0.4443 | PE | 0.0091 | 0.9925 | 0.7807 | 0.4584 |
| F5 | 0.0172 | 0.9814 | 0.7183 | 0.4467 | DE | 0.0111 | 0.9903 | 0.7028 | 0.4432 |
| F6 | 0.0254 | 0.9813 | 0.5552 | 0.4181 | SDE | 0.0193 | 0.9958 | 0.8166 | 0.4717 |
| Feature | Mon | Rob | Tre | MEI | Feature | Mon | Rob | Tre | MEI |
|---|---|---|---|---|---|---|---|---|---|
| T1 | 0.0380 | 0.8520 | 0.0652 | 0.2877 | F7 | 0.0571 | 0.9479 | 0.3254 | 0.3780 |
| T2 | 0.0285 | 0.8501 | 0.0620 | 0.2817 | F8 | 0.0333 | 0.9745 | 0.3589 | 0.3808 |
| T3 RMS | 0.0142 | 0.8411 | 0.1026 | 0.2800 | F9 | 0.0333 | 0.9621 | 0.2066 | 0.3466 |
| T4 | 0.0380 | 0.8520 | 0.0652 | 0.2877 | F10 | 0.0380 | 0.8982 | 0.3893 | 0.3663 |
| T5 | 0.0428 | 0.6580 | 0.0841 | 0.2356 | F11 | 0.0095 | 0.8498 | 0.3105 | 0.3218 |
| T6 Kurt | 0.0571 | 0.5694 | 0.0840 | 0.2162 | F12 | 0.0190 | 0.7823 | 0.1837 | 0.2809 |
| T7 | 0.0095 | 0.7583 | 0.5998 | 0.3522 | F13 | 0.0047 | 0.8443 | 0.3905 | 0.3338 |
| T8 | 0.0142 | 0.7584 | 0.5962 | 0.3539 | TF1 | 0.0285 | 0.7802 | 0.6846 | 0.3952 |
| T9 | 0.0190 | 0.6151 | 0.0824 | 0.2105 | TF2 | 0.0238 | 0.7716 | 0.6425 | 0.3719 |
| T10 | 0.0142 | 0.7518 | 0.0836 | 0.2494 | TF3 | 0.0047 | 0.7035 | 0.4003 | 0.2935 |
| T11 | 0.0047 | 0.9547 | 0.6221 | 0.4132 | TF4 | 0.0047 | 0.7427 | 0.5321 | 0.3316 |
| T12 | 0.0380 | 0.7902 | 0.6644 | 0.3889 | TF5 | 0.0428 | 0.6275 | 0.4898 | 0.3076 |
| T13 | 0.0095 | 0.7778 | 0.6722 | 0.3725 | TF6 | 0.0047 | 0.6974 | 0.4431 | 0.3002 |
| T14 | 0.0047 | 0.7746 | 0.6716 | 0.3691 | TF7 | 0.0190 | 0.7107 | 0.3904 | 0.3008 |
| T15 | 0.0142 | 0.8359 | 0.6561 | 0.3891 | TF8 | 0.0047 | 0.7117 | 0.4510 | 0.3061 |
| T16 | 0.0190 | 0.7838 | 0.6324 | 0.3711 | PCA | 0.0428 | 0.9920 | 0.0840 | 0.3358 |
| F1 | 0.0142 | 0.8139 | 0.3309 | 0.3175 | LLE | 0.0071 | 0.9999 | 0.5083 | 0.4052 |
| F2 | 0.0190 | 0.7601 | 0.0829 | 0.2541 | LLTSA | 0.0095 | 0.6520 | 0.1708 | 0.2345 |
| F3 | 0.0047 | 0.9328 | 0.6328 | 0.4087 | SE | 0.0095 | 0.8861 | 0.3336 | 0.3373 |
| F4 | 0.0142 | 0.9112 | 0.6350 | 0.4055 | PE | 0.0238 | 0.9742 | 0.4658 | 0.3973 |
| F5 | 0.0761 | 0.9338 | 0.3794 | 0.3941 | DE | 0.0285 | 0.9581 | 0.5538 | 0.4125 |
| F6 | 0.0285 | 0.8726 | 0.4408 | 0.3642 | SDE | 0.0666 | 0.9494 | 0.6001 | 0.4382 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Jia, Y.; Bai, H.; Xing, L.; Yang, Y. Sliding Dispersion Entropy-Based Fault State Detection for Diaphragm Pump Parts. Coatings 2021, 11, 1536. https://doi.org/10.3390/coatings11121536
Zhou C, Jia Y, Bai H, Xing L, Yang Y. Sliding Dispersion Entropy-Based Fault State Detection for Diaphragm Pump Parts. Coatings. 2021; 11(12):1536. https://doi.org/10.3390/coatings11121536
Chicago/Turabian StyleZhou, Chengjiang, Yunhua Jia, Haicheng Bai, Ling Xing, and Yang Yang. 2021. "Sliding Dispersion Entropy-Based Fault State Detection for Diaphragm Pump Parts" Coatings 11, no. 12: 1536. https://doi.org/10.3390/coatings11121536
APA StyleZhou, C., Jia, Y., Bai, H., Xing, L., & Yang, Y. (2021). Sliding Dispersion Entropy-Based Fault State Detection for Diaphragm Pump Parts. Coatings, 11(12), 1536. https://doi.org/10.3390/coatings11121536






