Computational Simulations of Nanoconfined Argon Film through Adsorption–Desorption in a Uniform Slit Pore
Abstract
:1. Introduction
2. Simulation Models and Methods
3. Results and Discussion
3.1. Commensurate Contact Simulations
3.2. Incommensurate Contact Simulations
4. Summary and Further Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
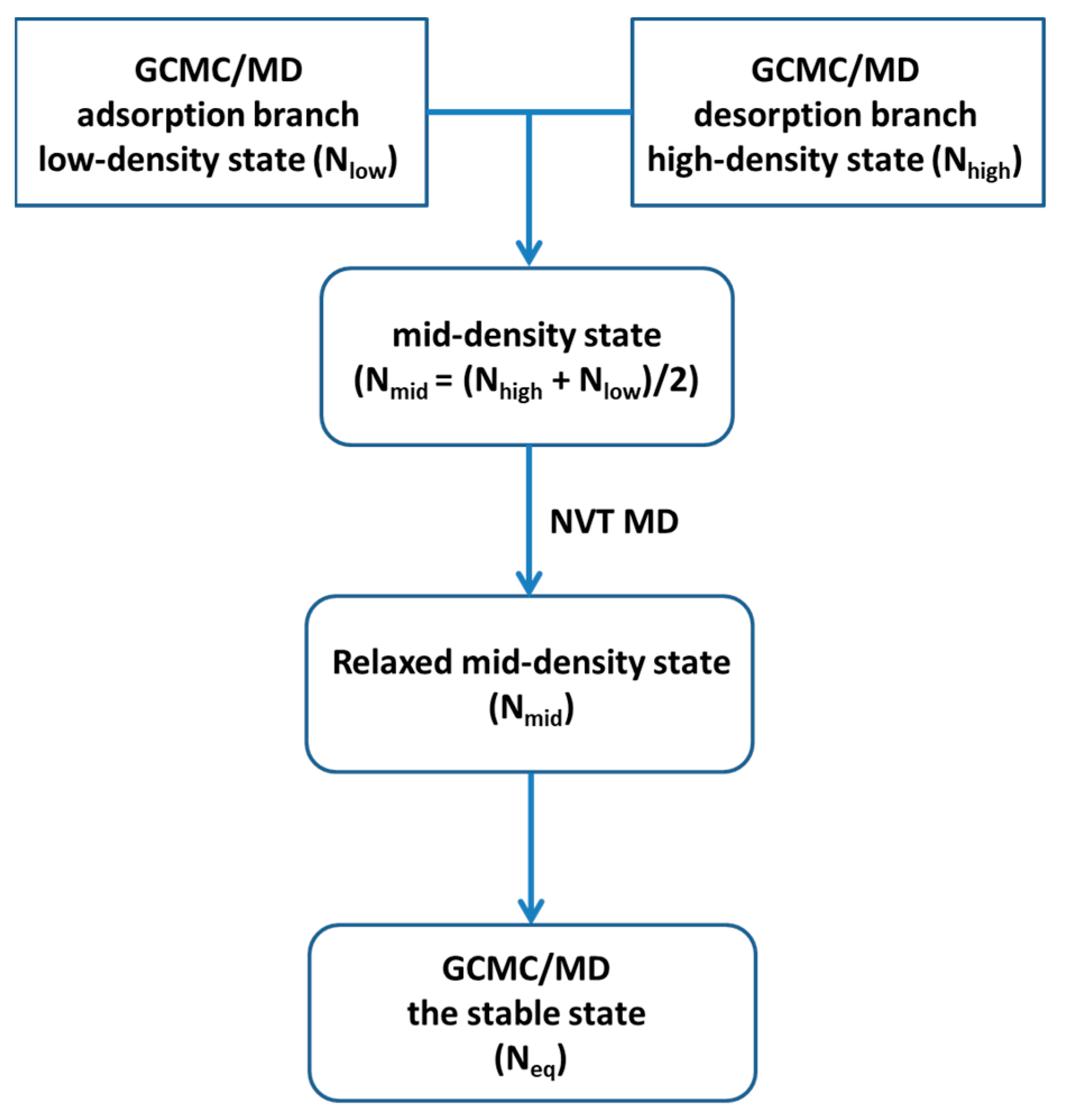
Appendix A. Equilibrium Phase in LVMD Simulations
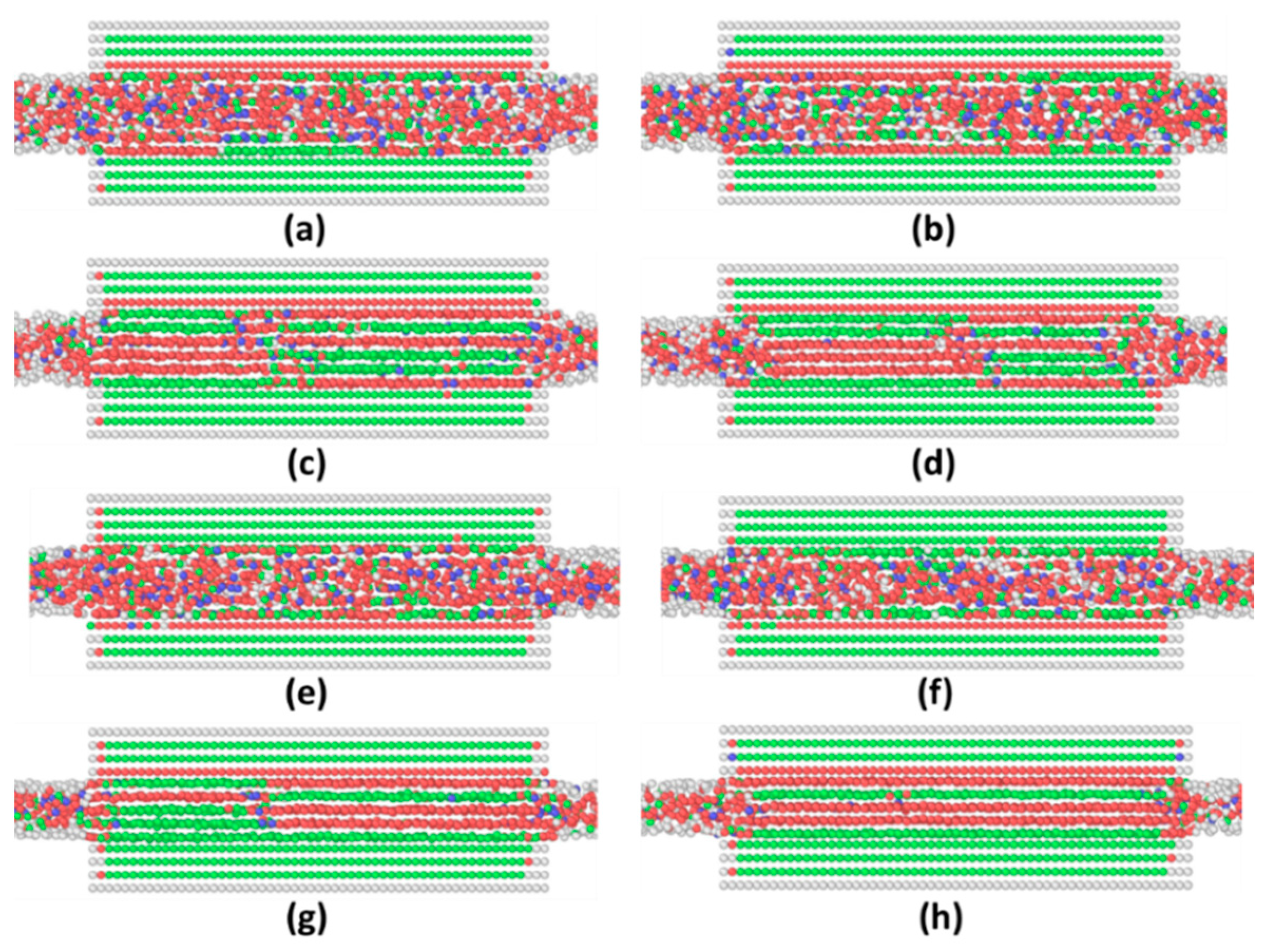
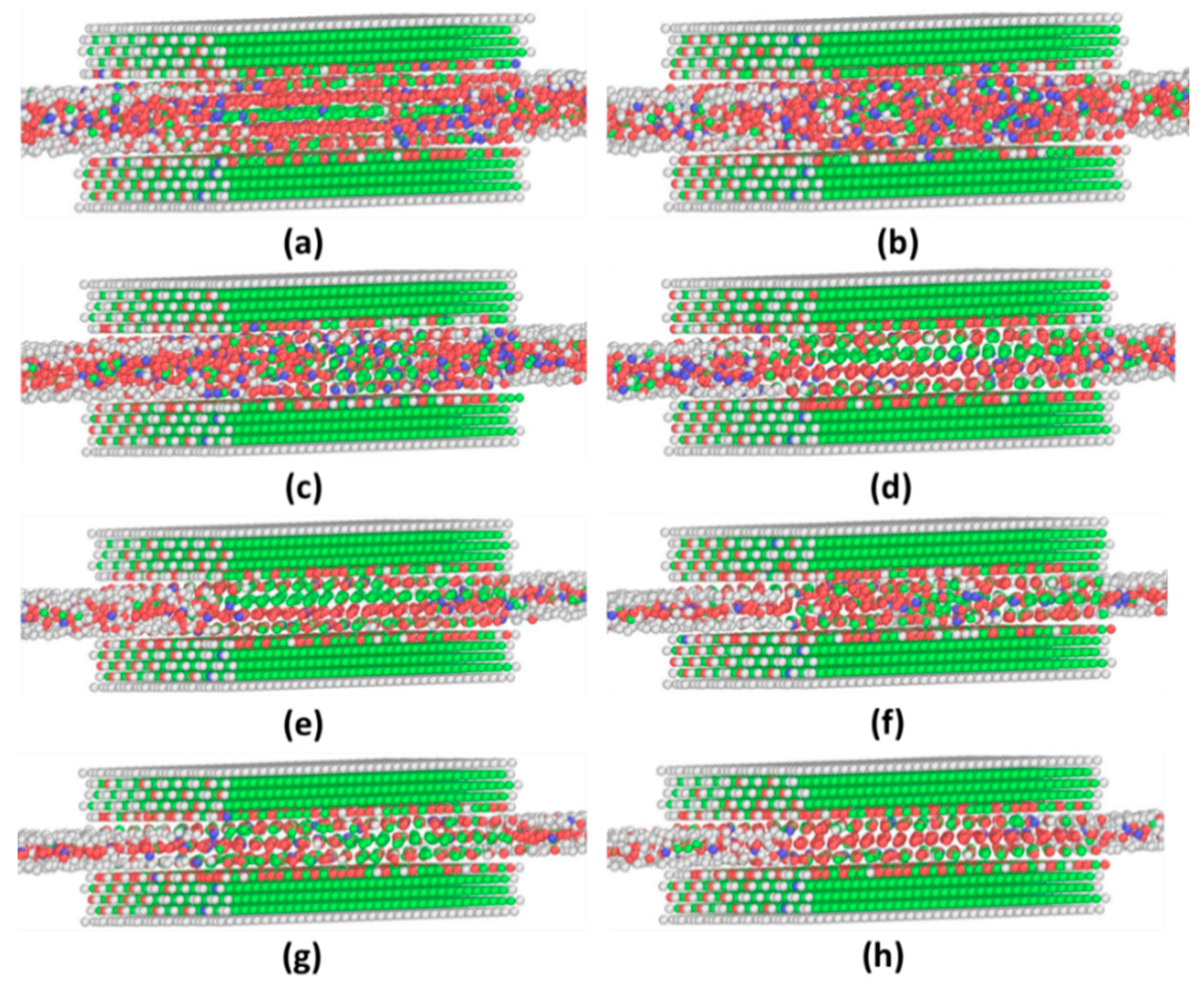
References
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier, Academic Press, Inc.: San Diego, CA, USA, 2011. [Google Scholar]
- Klein, J.; Kumacheva, E. Confinement-induced phase transitions in simple liquids. Science 1995, 269, 816–819. [Google Scholar] [CrossRef] [PubMed]
- Klein, J.; Kumacheva, E. Simple liquids confined to molecularly thin layers. I. Confinement-induced liquid-to-solid phase transitions. J. Chem. Phys. 1998, 108, 6996–7009. [Google Scholar] [CrossRef]
- Kumacheva, E.; Klein, J. Simple liquids confined to molecularly thin layers. II. Shear and frictional behavior of solidified films. J. Chem. Phys. 1998, 108, 7010–7022. [Google Scholar] [CrossRef]
- Demirel, A.L.; Granick, S. Glasslike transition of a confined simple fluid. Phys. Rev. Lett. 1996, 77, 2261–2264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thompson, P.A.; Robbins, M.O. Origin of stick-slip motion in boundary lubrication. Science 1990, 250, 792–794. [Google Scholar] [CrossRef]
- Docherty, H.; Cummings, P.T. Direct evidence for fluid–solid transition of nanoconfined fluids. Soft Matter 2010, 6, 1640–1643. [Google Scholar] [CrossRef]
- Rosenhek-Goldian, I.; Kampf, N.; Yeredor, A.; Klein, J. On the question of whether lubricants fluidize in stick–slip friction. Proc. Natl. Acad. Sci. USA 2015, 112, 7117–7122. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.M.; Hallett, J.E.; Perkin, S. Solidification and superlubricity with molecular alkane films. Proc. Natl. Acad. Sci. USA 2019, 116, 25418–25423. [Google Scholar] [CrossRef] [Green Version]
- Gooneie, A.; Balmer, T.E.; Heuberger, M. Seclusion of molecular layers in a confined simple liquid. Phys. Rev. Res. 2020, 2, 022026. [Google Scholar] [CrossRef]
- Gao, H.; Müser, M.H. Why liquids can appear to solidify during squeeze-out–Even when they don’t. J. Colloid Interface Sci. 2020, 562, 273–278. [Google Scholar] [CrossRef]
- Lei, Y.; Leng, Y. Force oscillation and phase transition of simple fluids under confinement. Phys. Rev. E 2010, 82, 040501. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Leng, Y. Stick-slip friction and energy dissipation in boundary lubrication. Phys. Rev. Lett. 2011, 107, 147801. [Google Scholar] [CrossRef] [PubMed]
- Leng, Y.; Xiang, Y.; Lei, Y.; Rao, Q. A comparative study by the grand canonical Monte Carlo and molecular dynamics simulations on the squeezing behavior of nanometers confined liquid films. J. Chem. Phys. 2013, 139, 074704. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.-G.; Leng, Y. Squeezing and stick–slip friction behaviors of lubricants in boundary lubrication. Proc. Natl. Acad. Sci. USA 2018, 115, 6560–6565. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.-G.; Xiang, Y.; Papanikolaou, S.; Leng, Y. On the shear dilation of polycrystalline lubricant films in boundary lubricated contacts. J. Chem. Phys. 2020, 152, 104708. [Google Scholar] [CrossRef]
- Xu, R.-G.; Leng, Y. Solvation force simulations in atomic force microscopy. J. Chem. Phys. 2014, 140, 214702. [Google Scholar] [CrossRef]
- Xu, R.-G.; Leng, Y. Contact stiffness and damping of liquid films in dynamic atomic force microscope. J. Chem. Phys. 2016, 144, 154702. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.-G.; Xiang, Y.; Leng, Y. Computational simulations of solvation force and squeezing out of dodecane chain molecules in an atomic force microscope. J. Chem. Phys. 2017, 147, 054705. [Google Scholar] [CrossRef] [Green Version]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [Green Version]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [Green Version]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Lechner, W.; Dellago, C. Accurate determination of crystal structures based on averaged local bond order parameters. J. Chem. Phys. 2008, 129, 114707. [Google Scholar] [CrossRef]
- Tribello, G.A.; Giberti, F.; Sosso, G.C.; Salvalaglio, M.; Parrinello, M. Analyzing and driving cluster formation in atomistic simulations. J. Chem. Theory Comput. 2017, 13, 1317–1327. [Google Scholar] [CrossRef]
- Giberti, F.; Salvalaglio, M.; Parrinello, M. Metadynamics studies of crystal nucleation. IUCrJ 2015, 2, 256–266. [Google Scholar] [CrossRef] [Green Version]
- Tambach, T.J.; Bolhuis, P.G.; Hensen, E.J.; Smit, B. Hysteresis in clay swelling induced by hydrogen bonding: Accurate prediction of swelling states. Langmuir 2006, 22, 1223–1234. [Google Scholar] [CrossRef]
- Rao, Q.; Xiang, Y.; Leng, Y. Molecular simulations on the structure and dynamics of water–methane fluids between Na-montmorillonite clay surfaces at elevated temperature and pressure. J. Phys. Chem. C 2013, 117, 14061–14069. [Google Scholar] [CrossRef]
- Rao, Q.; Leng, Y. Methane aqueous fluids in montmorillonite clay interlayer under near-surface geological conditions: A grand canonical Monte Carlo and molecular dynamics simulation study. J. Phys. Chem. B 2014, 118, 10956–10965. [Google Scholar] [CrossRef]
- Rao, Q.; Leng, Y. Molecular understanding of CO2 and H2O in a montmorillonite clay interlayer under CO2 geological sequestration conditions. J. Phys. Chem. C 2016, 120, 2642–2654. [Google Scholar] [CrossRef]
- Fedyanin, I.; Pertsin, A.; Grunze, M. Quasistatic computer simulations of shear behavior of water nanoconfined between mica surfaces. J. Chem. Phys. 2011, 135, 174704. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Herrera, L.; Nguyen, V.T.; Do, D.; Nicholson, D. A Monte Carlo scheme based on mid-density in a hysteresis loop to determine equilibrium phase transition. Mol. Simul. 2011, 37, 932–939. [Google Scholar] [CrossRef]
- Peterson, B.K.; Gubbins, K.E. Phase transitions in a cylindrical pore: Grand canonical Monte Carlo, mean field theory and the Kelvin equation. Mol. Phys. 1987, 62, 215–226. [Google Scholar] [CrossRef]
- Peterson, B.K.; Gubbins, K.E.; Heffelfinger, G.S.; Marini Bettolo Marconi, U.; van Swol, F. Lennard-Jones fluids in cylindrical pores: Nonlocal theory and computer simulation. J. Chem. Phys. 1988, 88, 6487–6500. [Google Scholar] [CrossRef]
- Neimark, A.V.; Vishnyakov, A. Gauge cell method for simulation studies of phase transitions in confined systems. Phys. Rev. E 2000, 62, 4611–4622. [Google Scholar] [CrossRef] [Green Version]
- Vishnyakov, A.; Neimark, A.V. Studies of Liquid—Vapor Equilibria, Criticality, and Spinodal Transitions in Nanopores by the Gauge Cell Monte Carlo Simulation Method. J. Phys. Chem. B 2001, 105, 7009–7020. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the open visualization tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mater. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Liu, Z.; Do, D.D.; Nicholson, D. A thermodynamic study of the mid-density scheme to determine the equilibrium phase transition in cylindrical pores. Mol. Simul. 2012, 38, 189–199. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Do, D.; Nicholson, D. Reconciliation of different simulation methods in the determination of the equilibrium branch for adsorption in pores. Mol. Simul. 2014, 40, 713–720. [Google Scholar] [CrossRef] [Green Version]
- Ustinov, E.A.; Do, D. Application of kinetic Monte Carlo method to equilibrium systems: Vapour–liquid equilibria. J. Colloid Interface Sci. 2012, 366, 216–223. [Google Scholar] [CrossRef]
- Fan, C.; Do, D.; Nicholson, D.; Ustinov, E. Chemical potential, Helmholtz free energy and entropy of argon with kinetic Monte Carlo simulation. Mol. Phys. 2014, 112, 60–73. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.T.; Do, D.; Nicholson, D. Monte Carlo simulation of the gas-phase volumetric adsorption system: Effects of dosing volume size, incremental dosing amount, pore shape and size, and temperature. J. Phys. Chem. B 2011, 115, 7862–7871. [Google Scholar] [CrossRef]
- Kast, S.M. Combinations of simulation and integral equation theory. Phys. Chem. Chem. Phys. 2001, 3, 5087–5092. [Google Scholar] [CrossRef]

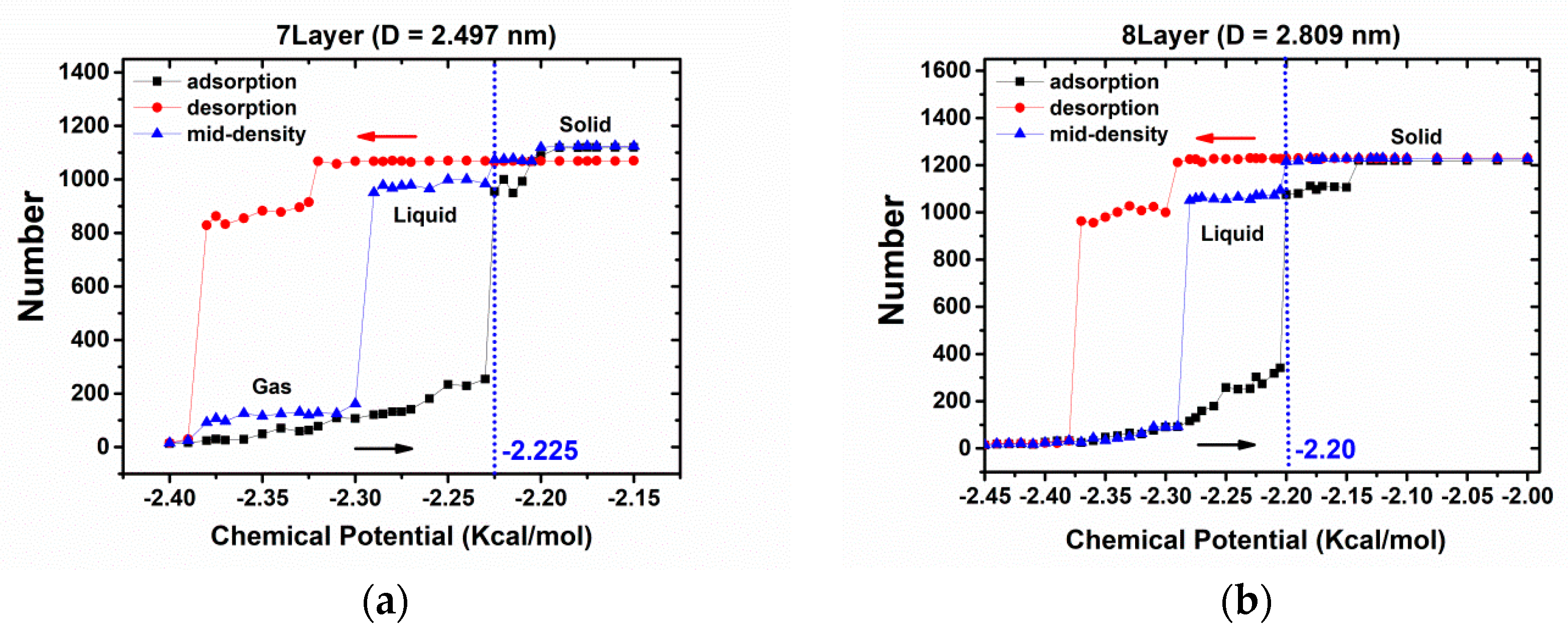






| Lattice Constant (nm) | σw | σwf | εwf | Lateral Dimensions (nm × nm) | |
|---|---|---|---|---|---|
| Commensurate | 0.5405 | σ | σ | ε | 6.12 × 3.31 |
| Incommensurate | 0.408 | 0.755σ | 0.887σ | ε | 6.92 × 4.50 |
| Thickness | GCMC | LVMD |
|---|---|---|
| 6.5 Layer + 1.0Å | Liquid | Liquid |
| 6.5 Layer + 0.5Å | Liquid | Liquid |
| 6.5 Layer | Solid | Solid |
| 6 Layer | Solid | Solid |
| 5.5 Layer + 1.0Å | Liquid | Liquid |
| 5.5 Layer + 0.5Å | Liquid | Liquid |
| 5.5 Layer | Solid | Solid |
| 5 Layer | Solid | Solid |
| Thickness | GCMC | LVMD |
|---|---|---|
| 18.5 Å | Solid | Solid |
| 17.5 Å | Liquid | Liquid |
| 17.0 Å | Liquid | Liquid |
| 16.0 Å | Solid | Solid |
| 15.0 Å | Solid | Solid |
| 14.0 Å | Liquid | Liquid |
| 13.0 Å | Solid | Solid |
| 12.5 Å | Solid | Solid |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.-G.; Rao, Q.; Xiang, Y.; Bian, M.; Leng, Y. Computational Simulations of Nanoconfined Argon Film through Adsorption–Desorption in a Uniform Slit Pore. Coatings 2021, 11, 177. https://doi.org/10.3390/coatings11020177
Xu R-G, Rao Q, Xiang Y, Bian M, Leng Y. Computational Simulations of Nanoconfined Argon Film through Adsorption–Desorption in a Uniform Slit Pore. Coatings. 2021; 11(2):177. https://doi.org/10.3390/coatings11020177
Chicago/Turabian StyleXu, Rong-Guang, Qi Rao, Yuan Xiang, Motong Bian, and Yongsheng Leng. 2021. "Computational Simulations of Nanoconfined Argon Film through Adsorption–Desorption in a Uniform Slit Pore" Coatings 11, no. 2: 177. https://doi.org/10.3390/coatings11020177
APA StyleXu, R.-G., Rao, Q., Xiang, Y., Bian, M., & Leng, Y. (2021). Computational Simulations of Nanoconfined Argon Film through Adsorption–Desorption in a Uniform Slit Pore. Coatings, 11(2), 177. https://doi.org/10.3390/coatings11020177





