Next Article in Journal
Highly Conductive Co-Doped Ga2O3:Si-In Grown by MOCVD
Previous Article in Journal
Comparative Study of Corrosion Properties of Different Graphene Nanoplate/Epoxy Composite Coatings for Enhanced Surface Barrier Protection
Previous Article in Special Issue
Effect of Plating Current Density on the Ball-On-Disc Wear of Sn-Plated Ni Coatings on Cu Foils
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Coatings
Volume 11
Issue 3
10.3390/coatings11030286
coatings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Molecular Dynamics Simulation on the Interaction between Palygorskite Coating and Linear Chain Alkane Base Lubricant

by
Jin Zhang
1,2,
Lv Yang
1,*,
Yue Wang
1,
Huaichao Wu
1,
Jiabin Cai
1 and
Shusheng Xu
2,*
1
School of Mechanical Engineering, Guizhou University, Guiyang 550025, China
2
State Key Laboratory of Solid Lubrication, Lanzhou Institute of Chemical Physics, Chinese Academy of Sciences, Lanzhou 730000, China
*
Authors to whom correspondence should be addressed.
Coatings 2021, 11(3), 286; https://doi.org/10.3390/coatings11030286
Submission received: 27 January 2021 / Revised: 23 February 2021 / Accepted: 25 February 2021 / Published: 1 March 2021
(This article belongs to the Special Issue Selected Papers from the K-TRIB2020)
Browse Figures
Versions Notes

Abstract

:
Molecular dynamics (MD) simulations were conducted to investigate the interactions between a palygorskite coating and linear chain alkanes (dodecane C12, tetradecane C14, hexadecane C16, and octadecane C18), representing base oils in this study. The simulation models were built by placing the alkane molecules on the surface of the palygorskite coating. These systems were annealed and geometrically optimized to obtain the corresponding stable configurations, followed by the analysis of the structural changes occurring during the MD process. The interfacial interaction energies, mean square displacements, and self-diffusion coefficients of the systems were evaluated to characterize the interactions between base lubricant molecules and palygorskite coating. It was found that the alkanes exhibited self-arrangement ability after equilibrium. The interfacial interaction was attractive, and the electrostatic energy was the main component of the binding energy. The chain length of the linear alkanes had a significant impact on the intensity of the interfacial interactions and the molecular diffusion behavior. Moreover, the C12 molecule exhibited higher self-diffusion coefficient values than C14, C16 and C18. Therefore, it could be the best candidate to form an orderliness and stable lubricant film on the surface of the palygorskite coating. The present work provides new insight into the optimization of the structure and composition of coatings and lubricants, which will guide the experimental development of these systems for practical applications.

Graphical Abstract

1. Introduction

Palygorskite, also named attapulgite, has a layered chain-like structure with ideal chemical formula Mg5(H2O)4(Si4O10)2(OH)2·4(H2O) [1,2]. This mineral shows a 2:1 (TOT)-type crystal structure [3,4] with wide channels. Three main forms of water are present in the palygorskite crystal: zeolitic water in the channels, structural water coordinated to octahedral cations at the edge of the layered structure, and hydroxyl (–OH) groups combined with octahedral cations [5]. The channel structure and water components inside the channels endow this mineral with a large specific surface area and high crystal structure stability. Previous research on palygorskite has attracted great interest in the fields of surface engineering, protective coatings, green chemistry, and catalysis [6,7,8,9,10,11,12]. Pei et al. [13] first proposed a hydrophilic–hydrophobic reversal mechanism for the surface of a modified palygorskite coating and attributed it to the treatment of modifier chains with different solvents. When palygorskite was modified by solid-state grinding, acid or heat activation, the corresponding coatings achieved excellent superamphiphobicity and mechanical robustness, and could even be applied on aluminum foil, polytetrafluoroethylene (PTFE) plates, or polyester textile substrates [14,15,16,17]. The superior superhydrophobic and superamphiphobic properties of palygorskite-based coatings [18,19], the high adsorption capacity and reusability of palygorskite-based adsorbents [20], and the excellent photocatalytic performance of catalysts based on palygorskite benefit from the high aspect ratio of its nanorod structure, as well as from its excellent mechanical, chemical, and thermal stability [21,22,23].
One of the main ways to reduce energy consumption, material loss, and NOx or CO2 emissions is to reduce the friction and wear of the counterpart surfaces of the moving components of a machine. Over the past few years, extensive efforts have been dedicated to evaluate the performance of palygorskite as a lubricant additive, which confirmed its excellent anti-wear properties. PTFE doped by an appropriate amount of palygorskite additive treated with hydrochloric acid exhibited excellent wear and fracture resistances. It was reported that the high heat absorption capacity of composites filled with nano-palygorskite was critical for achieving enhanced performances [24]. A very low wear rate was observed for liquid lubricants upon blending them with nanosized metal (Mo or Ag)-dotted palygorskite additives, to form desirable tribofilms on the wear tracks of counterpart surfaces via possible mechanochemistry and mechanophysics mechanisms [25,26]. It is worth noting that palygorskite, as an anti-wear and self-healing phase combined with an organic matrix, is also a desirable candidate to improve tribological properties in the surface engineering field. However, experimental studies of the microscopic interaction mechanism between palygorskite coatings and lubricants are scarce, because the in situ characterization of the formation and removal process of a tribofilm is still a challenge for current analytical techniques. On this basis, the development of simulation approaches is still an important requirement to investigate the interactions between palygorskite coatings and base oil.
In recent years, the molecular dynamics (MD) simulation approach has emerged as an important alternative in the nanomaterial field and played a significant role in the study of the microstructure and properties of materials on a molecular scale. The exploration of the intermolecular and intramolecular interaction behaviors of nanomaterials has attracted widespread interests in simulation approaches, which can serve as effective strategies to explore novel and promising nanomaterials for industrial applications. Owing to the complex structure of layered and chain-like clay minerals, MD simulations have been widely used to model the microstructure of these systems and further elucidate their intrinsic mechanisms, with the aim to improve the performance of composite materials. Using molecular models based on monoclinic and orthogonal systems, it was found that strong hydrogen bonds are formed between the C=O group of the indigo molecule and the structural water present in the palygorskite channels, which could be located in the channels without any obstacle [27,28]. Based on this finding, a previous study investigated the structural evolution during the dehydration process of palygorskite with various water contents (H2O/Mg = 4, 2, 1, 0) at different temperatures [29]. Nevertheless, simulation studies of the interaction between palygorskite coatings and organic lubricants, as well as of the corresponding mechanism, are still scarce. MD simulation approaches based on the Materials Studio (MS) package have opened a new avenue for the further exploration of the microscopic mechanisms of organic processes. This method was employed by Bu et al. [30] to model the adsorption mechanism of radioactive cesium ions on calcium silicate hydrates of different sizes. The results showed that the structure of the surface layer and the competitive mechanism between crystal water and cesium ions could significantly influence the adsorption process. Turning to lubricant materials, Zhang et al. [31] used MD simulations to determine the adsorption mechanism of ricinoleic acid on the surface of an iron substrate in glycerin-based lubricant oil, the crucial effects of the interaction between zinc dialkyl dithiophosphate (ZDDP) and the adsorbed hexadecane lubricant on the mechanical and thermal slips were also clarified.
Herein, we first built molecular models of a palygorskite solid coating and typical mineral base oils (linear chain alkanes) and then carried out MD simulations to determine their interaction mechanism via the MS package. The molecular structures of palygorskite and linear chain alkanes (C12–C18) were optimized by molecular mechanics. Furthermore, the structural and energy changes were systematically investigated. The analysis included the characterization of the structure, chain length, and distribution of the base oil molecules on the crystal surface of the palygorskite coating. We identified the interaction mechanism between palygorskite surface and base oil (linear chain alkane molecules) by analyzing the binding energies, mean square displacements (MSDs), and self-diffusion coefficients (D) of the alkane molecules and the relative concentration of water molecules on the palygorskite coating surface. More importantly, the present simulations provide insight into the intrinsic interactions between a typical palygorskite crystal and mineral base oil molecules, which can support further experimental studies on palygorskite coatings and lubricants used in practical applications.

2. Models and Simulation Methods

2.1. Model Construction

Palygorskite possesses a monoclinic crystal structure with 2/m symmetry, and the C2/m space group was employed for the present models, using the MS program [32]. A single palygorskite crystal with lattice parameters a = 13.2858 Å, b = 17.8476 Å, c = 5.2419 Å, α = γ = 90°, and β = 107.560° was obtained from the American Mineralogist Crystal Structure Database [28,33,34], and the unit cell model is shown in Figure 1a. Then, the relevant MS module was applied to expand the single crystal into a 2a × 2b × 6c palygorskite supercell, which was then cleaved along the (100) surface, with a thickness of 19 Å. The obtained palygorskite supercell had a size of 19 Å × 35.6952 Å × 31.4514 Å and contained 2196 atoms. Periodic boundary conditions were applied in the x, y, and z directions. Then, the palygorskite supercell was geometry-optimized and used for building the interfacial interaction model.
Mineral base oil is mainly composed of multi-carbon linear alkanes, isoparaffins, cycloalkanes, and aromatic hydrocarbons. To efficiently assess the interactions between carbon chains of different length and the palygorskite coating surface, typical linear alkanes such as dodecane (C12H26, labeled as C12), tetradecane (C14H30, C14), hexadecane (C16H34, C16), and octadecane (C18H38, C18) were employed in this study [35,36]. The linear structures of all alkanes were optimized and used for building an amorphous cell. In order to build an amorphous cell of size compatible with the (100) surface of palygorskite, the lattice type of the cell was set to orthorhombic, with a = 35.695 Å and b = 31.451 Å, and the c parameter was automatically adjusted according to the density and number of alkane molecules. The melting points of C12-C18 are all less than 30 °C, which is 303.15 K. The simulated temperature was set to 303.15K to simulate the amorphous state of alkane molecules in this study. According to the actual density of C12-C18 alkanes (approximately 0.75–0.77 g/dm3), the density of all amorphous cells and number of alkane molecules were set to 0.75 g/dm3 and 30, respectively. The amorphous cells were then subjected to 1000 steps at a temperature of 303.15 K and simultaneous geometry optimization. Then, a frame was extracted from the MD trajectory and annealed to obtain a more stable structure.
To investigate the intrinsic interactions between linear alkane molecules and the surface of the palygorskite coating, interfacial interaction models were built by placing alkanes with different chain length on the (100) plane of the palygorskite crystal (the corresponding models are labeled Pal/C12, Pal/C14, Pal/C16, and Pal/C18). The amorphous cell of the alkanes with the lowest energy obtained during the annealing process (as shown in Figure 2) and the geometry-optimized palygorskite supercell were assembled in layers. In particular, the first layer was the palygorskite supercell and the second was the alkane amorphous cell, and a distance of 5 Å was set between the two. Next, the two layers were built into a surface, and a 30 Å-thick vacuum layer was added to minimize the effect of periodic boundary conditions. The as-built simulation systems are shown in Figure 1b and Figure 3, and the detailed parameters of the models are listed in Table 1. Geometry optimizations were then performed on all as-built models to produce the initial configurations of the MD simulations.

2.2. Simulation Methods

Before the build-up of the palygorskite supercell and alkane amorphous cell models, a unit cell of palygorskite and the four alkane molecules were created and used to calculate the atomic charges using the density functional theory (DFT) method [27]. The calculations were performed with the Energy task in CASTEP module based on MS package, using the GGA-PBE functional with quality set to ultrafine. The energy cutoff was set as 310 eV with the SCF tolerance of 5.0 × 10−7 eV/atom and the maximum SCF cycles was 500. Furthermore, the quality of k-point set was fine and the ultrasoft pseudo-potentials were used. The final charges of the simulated structures are shown in Figure 4.
The initially built structures are not stable configurations. Therefore, all initial models of alkanes, palygorskite, and as-built systems were subjected to geometry optimization before further use. The molecular mechanics method was used to perform the geometry optimizations, which were carried out using the Forcite module of MS. The optimizations were performed with the COMPASS force field, using the Ewald summation for electrostatic interactions with a tolerances of 1 × 10−4 kcal/mol, along with the atom-based van der Waals method with the cutoff distance of 12.5 Å. The corresponding spline and buffer widths were 1 Å and 0.5 Å, respectively [37,38,39,40,41]. Atomic charges were calculated by DFT, as discussed above, and the forcefield atom types were determined automatically. Energy and displacement convergence tolerances were set to 1 × 10−4 kcal/mol and 5 × 10−5 Å, respectively. The energies of the simulation systems were minimized using the smart minimization algorithm, combining the steepest descent, conjugate gradient, and Newton algorithms to remove unfavorable interactions and reach the lowest energy state. The number of iterations for all of the as-built systems was 5000, whereas that used for the isolated alkanes and the palygorskite supercell was 1000.
The annealing process of the amorphous cell of the alkanes was completed according to the following methods [40]. The initial and highest temperatures of the simulated annealing algorithm were set to 303.15 K and 800 K, respectively. The annealing process was carried out for 5 cycles, and the temperature was changed 10 times from heating to cooling in each cycle and the dynamics steps were 10,000 at each time. Thus, the total number of dynamics steps was 1 × 106 with a time steps of 1 fs, and structural optimization was carried out after each cycle. The COMPASS forcefield and the canonical (constant number of particles, volume, and temperature, NVT) ensemble were used for the annealing dynamics, and the temperature was controlled by the Berendsen method. At the end of the annealing process, the output configuration with the lowest energy was used to build the simulation systems.
The geometry-optimized configurations of the as-built systems were used as input systems for the MD simulations. Because the pressure was not a crucial factor in our systems, all MD simulations were carried out in the NVT ensemble [40]. In order for the alkane molecules to fully interact with the palygorskite coating, all surfaces of palygorskite were in a free state. The MD simulations of the interfacial interaction systems included two steps. The first was a relaxation stage, which was started by selecting random velocities from a Maxwell distribution and setting the temperature to 303.15 K. The Newtonian equations of motion were solved under periodic boundary conditions, and time averages were used as ensemble averages. The Verlet velocity integration algorithm was applied with a time steps of 1 fs. The system was coupled to a heat bath using the Berendsen method with a total relaxation time of 1 ns, and snapshots of the systems were extracted from the MD trajectory every 5000 time steps. The trajectory file included forces and velocities. The COMPASS force field was applied to describe atomic interactions. The non-bonded electrostatic interactions were described by the Ewald summation algorithm [42], with accuracy set to 0.001 kcal/mol. Van der Waals interactions were calculated by the atom-based summation method with a cutoff radius of 12.5 Å, and the spline and buffer widths were set to 1 Å and 0.5 Å, respectively. The second step of the MD simulations was the equilibrium stage, which was performed by selecting the lowest-energy structure in the final 300 ps (which was close to equilibrium in the first step) as the MD input configuration. The MD simulation was then started using the current velocities from the above structure, and the Nose-Hoover thermostat was adopted to control the temperature. The accuracy of electrostatic interactions was set to a higher value of 0.0001 kcal/mol. The simulation was carried out for 500 ps with a time steps of 1 fs, and the trajectory was recorded every 5000 steps in the production run. The other parameters employed in the second step of the MD run were the same used in the first stage. The all above MD simulations were conducted three times for each system with different configurations generated by amorphous cell, and the average energies were used in this work.

3. Results and Discussion

3.1. MD Simulation and System Equilibrium Process

The relaxation process at four different time points of the MD simulation is illustrated in Figure 5. At 0 ps, which corresponds to the initial structure after geometry optimization, the distance between the alkanes and the (100) surface of palygorskite was approximately 5 Å, while after 50 ps of MD relaxation the alkanes were fully adsorbed on the surface and arranged in a disordered configuration, similar to the initial structure. However, after 500 ps, all alkane molecules formed an ordered and layered arrangement. Up to the final 1000 ps, the distribution of the alkanes remained in a stable state similar to the configuration at 500 ps, which reflects their self- arrangement abilities.
The system energy and temperature are crucial factors to assess the thermodynamic state of a system in MD simulations. The system is considered to be in equilibrium when the fluctuations of both temperature and energy are in the 5%–10% range [40,43,44]. The potential energy and temperature profiles of the simulation systems in the equilibrium stage are presented in Figure 6a,b respectively. In the 500 ps long equilibrium trajectory, both the potential energy and temperature stayed in a relatively stable range, with fluctuations of less than 10%. This suggests that the simulation systems had reached the equilibrium state. Moreover, the average potential energy values of Pal/C12, Pal/C14, Pal/C16, and Pal/C18 were −380,679.12, −381,124.73, −380,648.69 and −380,932.99 kcal/mol, respectively, indicating that the length of the linear alkanes affected the equilibrium state in these systems.
The structures of the simulation systems in the equilibrium state are shown in Figure 7. The spatial distance between the alkanes and the (100) plane of the palygorskite coating was further reduced in the equilibrium state compared with the initial systems (as shown in Figure 3). This confirms that the alkane molecules tended to be adsorbed on the (100) plane of the palygorskite coating in the equilibrium state, and then formed stable layered structures. The equilibrium configurations of the alkanes were almost the same as those at 1000 ps in the relaxation stage, which indicates that the structure of the systems tended to remain stable after equilibrium. Figure 7e–h displays top views of the corresponding structures in equilibrium, showing that the alkane molecules were evenly distributed on the palygorskite (100) surface and arranged regularly. This indicates that the alkane molecules can self-arrange after the system is in equilibrium. It can be concluded that the linear alkanes and the surface of the palygorskite coating have excellent compatibility. Thus, the nano-palygorskite substrate might serve as solid coating of solid–liquid lubrication systems with alkane-based lubricants.

3.2. Interaction Energies

In this study, all energy calculations were performed on the last 500 ps of the MD trajectory of the equilibrium stage, and the energies of production stage were calculated using a self-compiled code and their average values were used as energy parameters. The binding energy and interaction energies (Ebind and E, respectively) between the linear chain alkanes and the crystal surface of palygorskite were calculated by the following formula [45,46]:
Ebind = −E = (Epal + Ealkane) − Etotal
where Epal and Ealkane are the single-point energies of the individual palygorskite crystal and alkane molecules, respectively. Ebind > 0 (E < 0) indicates that the interaction force between the alkane molecules and the (100) plane of palygorskite is attractive, rather than repulsive. A higher binding energy denotes a stronger attractive force. The binding energies of all linear alkane systems in the equilibrium state are listed in Table 2. The table shows that all systems exhibited positive energy values, which indicates that the alkanes adsorbed on the surface of palygorskite through attractive forces. Moreover, the binding energies of Pal/C12 and Pal/C16 were significantly greater than those of Pal/C14 and Pal/C18, which indicates that the binding energy did not increase with increasing chain length of the alkanes.
To further investigate the intrinsic of the interaction between alkane molecules and the surface of palygorskite, the intermolecular interaction energies (Einter) in all linear alkane systems were calculated, which were used to compare with the corresponding binging energies listed in Table 2. The Einters under system equilibrium were calculated from the cohesive energy density, and the results are listed in Table 3. A higher absolute value of Einter denotes a stronger strength of interaction. Table 2 and Table 3 show that the binding energy of Pal/C12 is greater than the Einter, which indicates that alkane molecules can overcome the obstacles of intermolecular interactions and stably adsorb on the surface of palygorskite. At the same time, intermolecular interaction energy provides a certain strength and thickness of the adsorbed alkane molecules film. On account for that the shear slip preferentially occurs between C12 alkane molecules during frictional sliding, the adsorbed C12 alkane molecules film plays roles of lubrication and antiwear. In the regime of boundary lubrication, a thick and stable adsorbed lubrication film is beneficial to isolate direct contact of peaks on the surface of counterparts. The effects of friction reducing and antiwear mainly depend on the thickness and stability of the adsorbed film. However, the overlarge intermolecular interaction energy of the lubricating film will increase the resistance when the molecules move together, thereby reducing the effect of friction reduction. Therefore, a higher binding energy between C12 and palygorskite surface and certain strength of intermolecular interaction energy are helpful to form stable adsorbed lubrication film. Table 3 also shows that the Einter among alkane molecules in the presented systems mainly comes from van der Waals energy, which indicates that the main driving force for molecules to form a stable lubrication film is van der Waals force.
The main components of the total energy in the equilibrium systems are listed in Table 4. The total energy of the system is mainly composed of valence energy (Evalence) and non-bonding energy (Enon-bond) contributions. The non-bonding term includes the van der Waals energy (EvdW) produced by van der Waals interactions and the electrostatic energy (Eelect) associated with Coulomb interactions. Table 4 shows that the main contribution to the total energy of the equilibrium structure was the non-bonding term, which mainly derived from the electrostatic energy. This indicates that the interaction between alkane molecules and palygorskite mainly originated from Coulomb forces in non-bonding interactions.

3.3. Mean Square Displacement and Diffusion Coefficient

In MD simulations, the MSD is generally used to evaluate the dynamic behavior of a molecule, and can be expressed as follows [47]:
MSD = 〈 | r ( t ) − r | 2 〉 = 1 n ∑ i = 1 n | r i ( t + t 0 ) − r i ( t 0 ) | 2
where r i ( t 0 )   and r i ( t + t 0 )   are the positions of the i particle at t 0   and t + t 0 , respectively. The self-diffusion coefficient can then be obtained by fitting the MSD curve with the Einstein’s formula [48]:
D = lim t → ∞ 1 6 t 〈 | r ( t ) − r ( 0 ) | 2 〉
The MSDs of the linear alkanes in the equilibrium stage are shown in Figure 8a. Obviously, in the equilibrium stage, the mobility of C12 and C14 is much higher than that of C16 and C18, The shorter the carbon chain length of the alkane molecule, the higher its mobility. In order to accurately reflect the dynamic characteristics of a molecule in a simulation, the diffusion coefficient is usually obtained by fitting the relatively stable central region of the MSD curve. Using Equation (3), the middle 400ps region of the equilibrium trajectory was fitted by the least-squares method, and the fitted MSD curve of each system is shown in Figure 9a–d. The fitted parameters of the MSD curve and the obtained diffusion coefficients are listed in Table 5. Generally, the higher diffusion coefficient of alkane molecules indicates that it has strong diffusion ability on the surface of palygorskite and is easy to form a uniformly distributed lubricant film. For all simulated systems, the self-diffusion coefficients of the linear chain alkanes in the equilibrium stage are shown in Figure 8. The D values decrease firstly and then increase with increasing chain length, with C12 and C14 having higher diffusion coefficients of 0.03499 Å2/ps and 0.01254 Å2/ps, respectively. This confirms that the chain length of the linear alkanes has a great impact on their diffusion coefficient. Based on our MD simulation, to achieve optimal evenly lubricant film, C12 would be the best candidate due to its highest diffusion coefficient.

3.4. Water Molecules in Palygorskite

The analysis of water molecules on the palygorskite crystal surface has often been used to elucidate the interaction between the clay (palygorskite) and the surrounding environment, because water hosted in the channels of the clay has a significant influence on its properties [49,50,51,52]. To further evaluate the properties of water molecules on the palygorskite surface, the binding energies between alkanes and water molecules on the (100) surface of palygorskite were calculated and reported in Table 6. The Ews and Ealkane values in the table are the single-point energies of individual water and alkane molecules, respectively. The interaction energies of all systems were low and the binding energies were negative, which indicates a small repulsive force between alkane and water molecules. This behavior is consistent with the hydrophobicity of alkanes, thus confirming the reliability of the present simulations. Based on the results in Section 3.2, the absolute values of the alkane–palygorskite binding energies were much higher than the alkane–water ones. Hence, the attractive force between alkanes and palygorskite was much higher than the repulsion between alkanes and water molecules, so that the alkane molecules could be firmly adsorbed on the surface of palygorskite and form stable molecular layers.
The above results show that, despite the presence of a repulsive force between alkane and water molecules in the equilibrium systems, as shown in Figure 7, water molecules remained adsorbed on the surface of palygorskite after the MD simulation. The relative concentration of water molecules on the surface of palygorskite in the Pal/C12 system was then calculated, and the values along the X, Y, and Z axes are presented in Figure 10. Along the X axis direction, which is perpendicular to the (100) plane, the water molecules were distributed in one layer, with a higher relative concentration. Two obvious peaks at Y = 9 Å and Y = 27 Å (corresponding to the positions of the channels) were observed along the Y axis, and a certain concentration of water molecules was also present at other positions. An almost uniform distribution of water molecules was observed along the Z axis. These results indicate that, without the constraints of the adjacent channels, water molecules were dispersed more evenly on the palygorskite surface and were not repelled by the alkane molecules.
The interaction energy between water molecules on the palygorskite surface and the palygorskite framework was further calculated, and the results are listed in Table 7. In the table, Ews denotes the single-point energy of individual water molecules on the palygorskite surface and Ep is the energy of the isolated palygorskite framework, without the surface water layers. The results indicate a high adsorption energy between the water layers and palygorskite. On the one hand, strong hydrogen bonds were formed between the water molecules of palygorskite and the oxygen atoms in the silicon tetrahedron, as previously reported [29,51,52,53]. Hence, the zeolitic water molecules were stably fixed in the channels and on the palygorskite surface. On the other hand, strong van der Waals and electrostatic interactions were present between the water molecules and the palygorskite framework, resulting in a large adsorption energy of water molecules on the palygorskite substrate. This interaction enables the water molecules to maintain a stable distribution on the surface of palygorskite, even under the repulsive forces of alkane molecules.
It is well established that molecular interaction models and simulations can shed light on the design of experiments in most fields related to materials, including lubricants and crystalline materials. This study provides a theoretical basis for developing new solid-liquid composite lubricant phases consisting of linear chain alkanes (C12–C18) and a palygorskite coating. With respect to the as-built Pal/Cx systems, all alkane molecules shifted toward the palygorskite surface during the MD process. The geometry optimization of the systems played an important role in the present simulations. Based on these calculations, the interaction energies, mean square displacements, and self-diffusion coefficients of the alkanes, as well as the relative concentrations of water molecules on the palygorskite coating surface, were analyzed to determine the interaction mechanism between base oil and palygorskite. The potential energy and temperature of the system reached steady state during the equilibrium stage. At the same time, the chain length of the linear alkanes affected their binding energy, with the Pal/C12 system showing the highest value. The binding energy results and the relaxation process further confirmed that the linear chain alkanes were adsorbed to the (100) plane of the palygorskite coating in the equilibrium state, suggesting the palygorskite coating has good compatibility with the studied alkanes. The binding energy was mainly composed of van der Waals and electrostatic interactions, and the intermolecular interaction energy of alkanes was mainly contributed by van der Waals force. Therefore, the stable and order configuration of alkanes can be attributed to the synergy of the Coulomb force between alkane molecules and the surface of palygorskite as well as the van der Waals forces among alkane molecules. The MSD and D values of the simulated systems were significantly affected by the chain length of the alkanes. For all simulated systems, the highest diffusion coefficient of C12 molecules indicates that it has strong diffusion ability on the surface of palygorskite and is easy to form a uniformly distributed lubricant film. In this study, C12 presented strong adsorption capacity and relatively uniform distribution on the surface of palygorskite. Therefore, to achieve excellent orderliness and form a stable lubricant film on the surface of the palygorskite coating, C12 should be the best candidate among the four alkanes. On the surface of palygorskite, the water molecules formed weak repulsive interactions with the alkane molecules, along with strong attractive interactions with the palygorskite framework. As a result, the water molecules were adsorbed on the palygorskite coating surface. These findings provide new insight into the intrinsic interactions and potential dispersion behaviors in linear chain alkane/palygorskite systems and can shed light on the design of experiments for solid-liquid composite lubricant systems.

4. Conclusions

In summary, molecular models of the interaction between the crystal surface of a palygorskite coating and C12-C18 linear alkanes were built and subjected to molecular dynamics simulations. The structures of the alkanes and palygorskite were optimized and MD simulations were started from the geometry-optimized structures. The results of the structural changes during the MD process showed that alkanes with linear chains exhibited self-arrangement on the (100) palygorskite plane after equilibrium. The interaction between alkanes and palygorskite coating was attractive rather than repulsive, it was mainly derived from Coulomb and van der Waals forces, and the intermolecular interaction energy of alkanes was mainly contributed by van der Waals force. This resulted in the alkane molecules being adsorbed on the (100) plane of the palygorskite coating evenly and formed stable layered structures. The C12 exhibited highest diffusion ability on the surface of the palygorskite coating, which would be the best candidate to form an orderliness and stable lubricant film. The water molecules formed weak repulsive interactions with the alkane molecules, along with strong attractive interactions with the palygorskite framework. As a result, the water molecules were adsorbed on the palygorskite coating surface and were not repelled by the alkane molecules. The present results shed light on the interactions between linear chain alkanes (base oil) and the crystal surface of a palygorskite coating. These findings can be an important reference in the development of solid-liquid composite lubricant systems for practical applications, and will facilitate the optimization of the selection of chain alkane molecules, the form of interaction, and the dispersion of the alkane base oil on the palygorskite surface.

Author Contributions

Conceptualization, J.Z. and L.Y.; methodology, J.Z., L.Y., and S.X.; software, J.Z.; validation, J.Z., L.Y., and S.X.; formal analysis, J.Z.; investigation, J.Z., H.W., and J.C.; resources, L.Y., Y.W., and J.C.; data curation, J.Z., L.Y., and S.X.; writing—original draft preparation, J.Z.; writing—review and editing, J.Z., L.Y., and S.X.; visualization, J.Z. and J.C.; supervision, H.W.; project administration, Y.W.; funding acquisition, J.Z., Y.W., and S.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by National Natural Science Foundation of China (Grant No. 51965009, 52075521), Department of Education of Guizhou Province (Grant No. Q.J.H.YJSCXJH(2019)014), Science and Technology Planning Project in Guizhou Province (Grant No. Q.K.H.LH(2017)7245).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data is contained within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yang, L.; Li, Y.; Cai, J.; Ding, X.; Cao, Y. The formation mechanisms for auto-restoration tribofilm at the presence of palygorskite-Ag nanoparticles. Integr. Ferroelectr. 2017, 182, 110–118. [Google Scholar] [CrossRef]
  2. Gaines, R.V.; Skinner, H.C.W.; Foord, E.E.; Mason, B.; Rosenzweig, A. Dana’s New Mineralogy, 8th ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
  3. Galan, E. Properties and applications of palygorskite-sepiolite clays. Clay Miner. 1996, 31, 443–453. [Google Scholar] [CrossRef]
  4. Galán, E. A New Approach to Compositional Limits for Sepiolite and Palygorskite. Clays Clay Miner. 1999, 47, 399–409. [Google Scholar] [CrossRef]
  5. Pan, Z.; Zhao, A.; Pan, R. The Crystallography and Mineralogy; Geological Press: Beijing, China, 1998. [Google Scholar]
  6. Middea, A.; Fernandes, T.L.; Neumann, R.; Gomes, O.D.F.; Spinelli, L.S. Evaluation of Fe(III) adsorption onto palygorskite surfaces. Appl. Surf. Sci. 2013, 282, 253–258. [Google Scholar] [CrossRef] [Green Version]
  7. Zhu, J.; Zhang, P.; Wang, Y.; Wen, K.; Su, X.; Zhu, R.; He, H.; Xi, Y. Effect of acid activation of palygorskite on their toluene adsorption behaviors. Appl. Clay Sci. 2018, 159, 60–67. [Google Scholar] [CrossRef]
  8. Sarkar, B.; Megharaj, M.; Xi, Y.; Naidu, R. Surface charge characteristics of organo-palygorskites and adsorption of p-nitrophenol in flow-through reactor system. Chem. Eng. J. 2012, 185–186, 35–43. [Google Scholar] [CrossRef]
  9. Silva, A.F.; Burggraeve, A.; Denon, Q.; Van Der Meeren, P.; Sandler, N.; Kerkhof, T.V.D.; Hellings, M.; Vervaet, C.; Remon, J.P.; Lopes, J.A.; et al. Particle sizing measurements in pharmaceutical applications: Comparison of in-process methods versus off-line methods. Eur. J. Pharm. Biopharm. 2013, 85, 1006–1018. [Google Scholar] [CrossRef]
  10. Chen, M.; Jiang, W.; Wang, F.; Shen, P.; Ma, P.; Gu, J.; Mao, J.; Li, F. Synthesis of highly hydrophobic floating magnetic polymer nanocomposites for the removal of oils from water surface. Appl. Surf. Sci. 2013, 286, 249–256. [Google Scholar] [CrossRef]
  11. Li, X.; Zhang, Z.; Yao, C.; Lu, X.; Zhao, X.; Ni, C. Attapulgite-CeO2/MoS2 ternary nanocomposite for photocatalytic oxidative desulfurization. Appl. Surf. Sci. 2016, 364, 589–596. [Google Scholar] [CrossRef]
  12. Zhang, J.; Wang, Q.; Wang, A. Synthesis and characterization of chitosan-g-poly(acrylic acid)/attapulgite superabsorbent composites. Carbohydr. Polym. 2007, 68, 367–374. [Google Scholar] [CrossRef]
  13. Pei, M.; Pan, C.; Wu, D.; Liu, P. Surface hydrophilic-hydrophobic reversal coatings of polydimethylsiloxane-palygorskite nanosponges. Appl. Clay Sci. 2020, 189, 105546. [Google Scholar] [CrossRef]
  14. Zhang, P.; Tian, N.; Zhang, J.; Wang, A. Effects of modification of palygorskite on superamphiphobicity and microstructure of palygorskite@fluorinated polysiloxane superamphiphobic coatings. Appl. Clay Sci. 2018, 160, 144–152. [Google Scholar] [CrossRef]
  15. Li, B.; Zhang, J. Durable and self-healing superamphiphobic coatings repellent even to hot liquids. Chem. Commun. 2016, 52, 2744–2747. [Google Scholar] [CrossRef] [PubMed]
  16. Li, F.; Du, M.; Zheng, Q. Dopamine/Silica Nanoparticle Assembled, Microscale Porous Structure for Versatile Superamphiphobic Coating. ACS Nano 2016, 10, 2910–2921. [Google Scholar] [CrossRef]
  17. Dong, J.; Wang, Q.; Zhang, Y.; Zhu, Z.; Xu, X.; Zhang, J.; Wang, A. Colorful Superamphiphobic Coatings with Low Sliding Angles and High Durability Based on Natural Nanorods. ACS Appl. Mater. Interfaces 2017, 9, 1941–1952. [Google Scholar] [CrossRef] [PubMed]
  18. Zhang, P.; Dong, S.; Li, B.; Wei, X.; Zhang, J. Durable and fluorine-free superhydrophobic coatings from palygorskite-rich spent bleaching earth. Appl. Clay Sci. 2018, 157, 237–247. [Google Scholar] [CrossRef]
  19. Dong, J.; Zhu, Q.; Wei, Q.; Zheng, B.; Li, S.; Zhang, J. A comparative study about superamphiphobicity and stability of superamphiphobic coatings based on Palygorskite. Appl. Clay Sci. 2018, 165, 8–16. [Google Scholar] [CrossRef]
  20. Li, X.-J.; Yan, C.-J.; Luo, W.-J.; Gao, Q.; Zhou, Q.; Liu, C.; Zhou, S. Exceptional cerium(III) adsorption performance of poly(acrylic acid) brushes-decorated attapulgite with abundant and highly accessible binding sites. Chem. Eng. J. 2016, 284, 333–342. [Google Scholar] [CrossRef]
  21. Lakbita, O.; Rhouta, B.; Maury, F.; Senocq, F.; Amjoud, M.; Daoudi, L. Influence of the crystal structure of Ag2CO3 on the photocatalytic activity under visible light of Ag2CO3-Palygorskite nanocomposite material. Appl. Surf. Sci. 2019, 464, 205–211. [Google Scholar] [CrossRef] [Green Version]
  22. Xu, J.; Wang, A. Electrokinetic and Colloidal Properties of Homogenized and Unhomogenized Palygorskite in the Presence of Electrolytes. J. Chem. Eng. Data 2012, 57, 1586–1593. [Google Scholar] [CrossRef]
  23. Huang, D.; Wang, W.; Xu, J.; Wang, A. Mechanical and water resistance properties of chitosan/poly(vinyl alcohol) films reinforced with attapulgite dispersed by high-pressure homogenization. Chem. Eng. J. 2012, 210, 166–172. [Google Scholar] [CrossRef]
  24. Lai, S.-Q.; Li, T.-S.; Liu, X.-J.; Lv, R.-G. A Study on the Friction and Wear Behavior of PTFE Filled with Acid Treated Nano-Attapulgite. Macromol. Mater. Eng. 2004, 289, 916–922. [Google Scholar] [CrossRef]
  25. Wang, K.; Wu, H.; Wang, H.; Liu, Y.; Yang, L.; Zhao, L. Tribological properties of novel palygorskite nanoplatelets used as oil-based lubricant additives. Friction 2021, 9, 332–343. [Google Scholar] [CrossRef]
  26. Yang, L.; Zhou, Y.; Li, Y.; Cai, J.; Cao, Y. Effect of Ag Content in Palygorskite/Ag Blending Nanocomposite on Friction and Wear Properties of 45 Mild Steel Tribopair. Integr. Ferroelectr. 2013, 145, 10–16. [Google Scholar] [CrossRef]
  27. Fois, E.; Gamba, A.; Tilocca, A. On the unusual stability of Maya blue paint: Molecular dynamics simulations. Microporous Mesoporous Mater. 2003, 57, 263–272. [Google Scholar] [CrossRef]
  28. Chiari, G.; Giustetto, R.; Ricchiardi, G. Crystal structure refinements of palygorskite and Maya Blue from molecular modelling and powder synchrotron diffraction. Eur. J. Miner. 2003, 15, 21–33. [Google Scholar] [CrossRef]
  29. Giustetto, R.; Vitillo, J.G.; Corazzari, I.; Turci, F. Evolution and Reversibility of Host/Guest Interactions with Temperature Changes in a Methyl Red@Palygorskite Polyfunctional Hybrid Nanocomposite. J. Phys. Chem. C 2014, 118, 19322–19337. [Google Scholar] [CrossRef]
  30. Bu, J.; Teresa, R.G.; Brown, K.; Sanchez, F. Adsorption mechanisms of cesium at calcium-silicate-hydrate surfaces using molecular dynamics simulations. J. Nucl. Mater. 2019, 515, 35–51. [Google Scholar] [CrossRef]
  31. Zheng, D.; Wang, X.; Zhang, M.; Liu, Z.; Ju, C. Anticorrosion and lubricating properties of a fully green lubricant. Tribol. Int. 2019, 130, 324–333. [Google Scholar] [CrossRef]
  32. Accelrys Inc. Materials Studio Version 8.0; Accelrys Inc.: San Diego, CA, USA, 2014; Available online: https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/biovia-materials-studio/ (accessed on 27 February 2021).
  33. Post, J.E.; Heaney, P.J. Synchrotron powder X-ray diffraction study of the structure and dehydration behavior of palygorskite. Am. Miner. 2008, 93, 667–675. [Google Scholar] [CrossRef]
  34. Rajan, H.; Uchida, H.; Bryan, D.L.; Swaminathan, R.; Downs, R.T.; Hall-Wallace, M. The American mineralogist crystal structure database. Am. Miner. 2003, 88, 247–250. [Google Scholar]
  35. Berro, H.; Fillot, N.; Vergne, P. Molecular dynamics simulation of surface energy and ZDDP effects on friction in nano-scale lubricated contacts. Tribol. Int. 2010, 43, 1811–1822. [Google Scholar] [CrossRef]
  36. Jaishankar, A.; Jusufi, A.; Vreeland, J.L.; Deighton, S.P.; Pellettiere, J.R.; Schilowitz, A.M. Adsorption of Stearic Acid at the Iron Oxide/Oil Interface: Theory, Experiments, and Modeling. Langmuir 2019, 35, 2033–2046. [Google Scholar] [CrossRef]
  37. Toth, R.; Coslanich, A.; Ferrone, M.; Fermeglia, M.; Pricl, S.; Miertus, S.; Chiellini, E. Computer simulation of polypropylene/organoclay nanocomposites: Characterization of atomic scale structure and prediction of binding energy. Polymer 2004, 45, 8075–8083. [Google Scholar] [CrossRef]
  38. Castonguay, L.A.; Rappe, A.K. Ziegler-Natta catalysis. A theoretical study of the isotactic polymerization of propylene. J. Am. Chem. Soc. 1992, 114, 5832–5842. [Google Scholar] [CrossRef]
  39. Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
  40. Zhang, S.-G.; Wang, F.-Y.; Tan, X.-Y. Molecular dynamics simulation the hydroxyapatite scale inhibition mechanism of water-soluble polymers. J. Theor. Comput. Chem. 2010, 9, 889–902. [Google Scholar] [CrossRef]
  41. Zeng, J.-P.; Qian, X.-R.; Wang, F.-H.; Shao, J.-L.; Bai, Y.-S. Molecular dynamics simulation on the interaction mechanism between polymer inhibitors and calcium phosphate. J. Chem. Sci. 2014, 126, 649–658. [Google Scholar] [CrossRef]
  42. Nymand, T.M.; Linse, P. Ewald summation and reaction field methods for potentials with atomic charges, dipoles, and polarizabilities. J. Chem. Phys. 2000, 112, 6152–6160. [Google Scholar] [CrossRef]
  43. Bhowmik, R.; Katti, K.S.; Katti, D. Molecular dynamics simulation of hydroxyapatite–polyacrylic acid interfaces. Polymer 2007, 48, 664–674. [Google Scholar] [CrossRef]
  44. Tong, Z.; Xie, Y.; Zhang, Y. Molecular dynamics simulation on the interaction between polymer inhibitors and β-dicalcium silicate surface. J. Mol. Liq. 2018, 259, 65–75. [Google Scholar] [CrossRef]
  45. Zeng, J.; Zhang, J.; Gong, X. Molecular dynamics simulation of interaction between benzotriazoles and cuprous oxide crystal. Comput. Theor. Chem. 2011, 963, 110–114. [Google Scholar] [CrossRef]
  46. Zeng, J.-P.; Wang, F.-H.; Zhou, C.; Gong, X.-D. Molecular Dynamics Simulation on Scale Inhibition Mechanism of Polyepoxysuccinic Acid to Calcium Sulphate. Chin. J. Chem. Phys. 2012, 25, 219–225. [Google Scholar] [CrossRef] [Green Version]
  47. Wu, L.; Keer, L.M.; Lu, J.; Song, B.; Gu, L. Molecular dynamics simulations of the rheological properties of graphene–PAO nanofluids. J. Mater. Sci. 2018, 53, 15969–15976. [Google Scholar] [CrossRef]
  48. Kadota, K.; Furukawa, R.; Shirakawa, Y.; Shimosaka, A.; Hidaka, J. Effect of surface properties of calcium carbonate on aggregation process investigated by molecular dynamics simulation. J. Mater. Sci. 2013, 49, 1724–1733. [Google Scholar] [CrossRef]
  49. Post, J.E.; Bish, D.L.; Heaney, P.J. Synchrotron powder X-ray diffraction study of the structure and dehydration behavior of sepiolite. Am. Miner. 2007, 92, 91–97. [Google Scholar] [CrossRef]
  50. Brovchenko, I.; Geiger, A.; Oleinikova, A. Water in nanopores: II. The liquid–vapour phase transition near hydrophobic surfaces. J. Phys. Condens. Matter 2004, 16, S5345–S5370. [Google Scholar] [CrossRef]
  51. Zhou, J.; Lu, X.; Boek, E.S. Confined water in tunnel nanopores of sepiolite: Insights from molecular simulations. Am. Miner. 2016, 101, 713–718. [Google Scholar] [CrossRef]
  52. Ockwig, N.W.; Greathouse, J.A.; Durkin, J.S.; Cygan, R.T.; Daemen, L.L.; Nenoff, T.M. Nanoconfined Water in Magnesium-Rich 2:1 Phyllosilicates. J. Am. Chem. Soc. 2009, 131, 8155–8162. [Google Scholar] [CrossRef] [PubMed]
  53. Giustetto, R.; Levy, D.; Wahyudi, O.; Ricchiardi, G.; Vitillo, J.G. Crystal structure refinement of a sepiolite/indigo Maya Blue pigment using molecular modelling and synchrotron diffraction. Eur. J. Miner. 2011, 23, 449–466. [Google Scholar] [CrossRef]
Coatings 11 00286 g001 550
Figure 1. Simulation models of palygorskite coating: (a) unit cell model and (b) as-built configuration of the simulation system.
Figure 1. Simulation models of palygorskite coating: (a) unit cell model and (b) as-built configuration of the simulation system.
Coatings 11 00286 g001
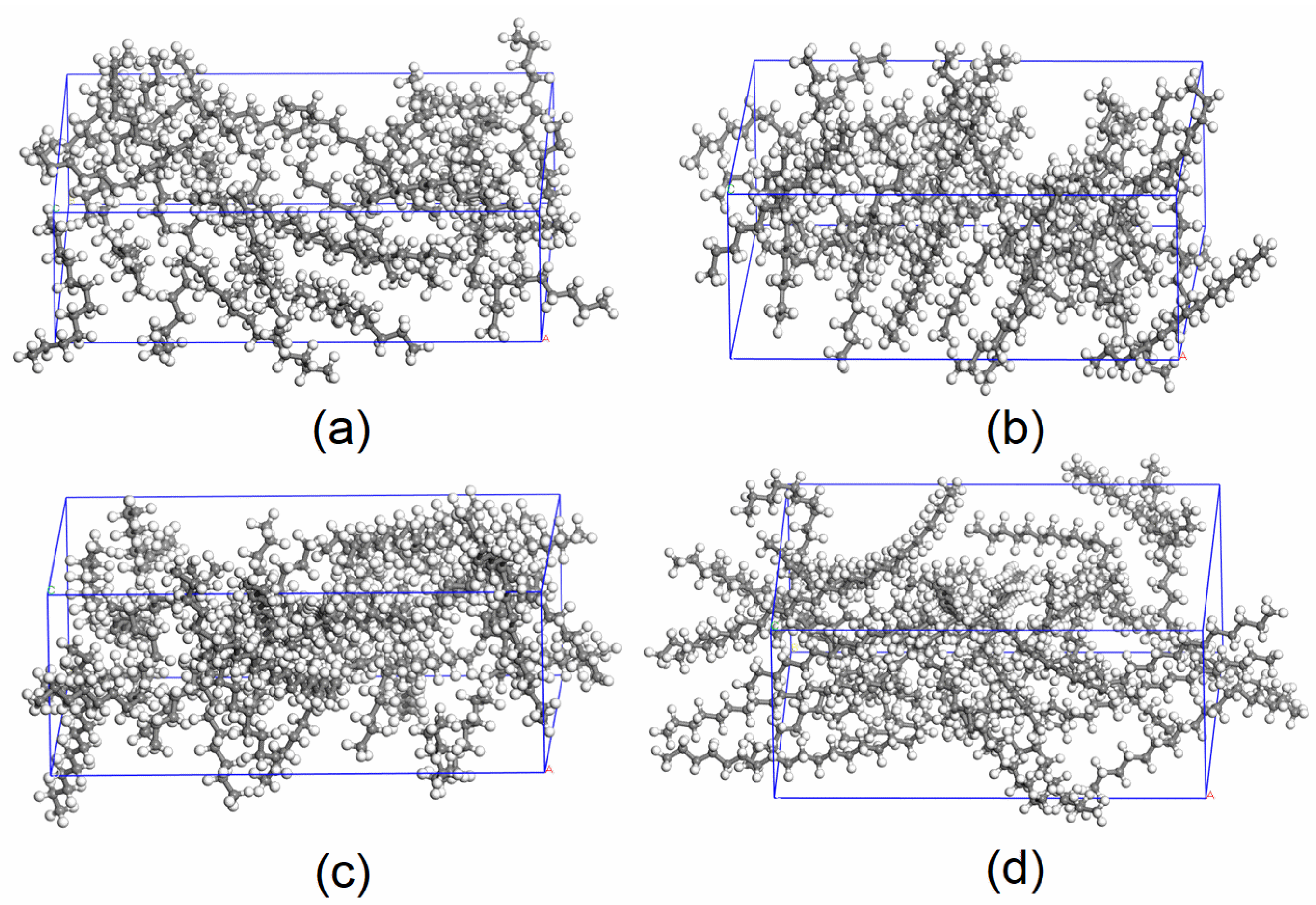
Coatings 11 00286 g002 550
Figure 2. Lowest-energy amorphous cells of the alkane molecules during annealing process: (a) C12, (b) C14, (c) C16, and (d) C18.
Figure 2. Lowest-energy amorphous cells of the alkane molecules during annealing process: (a) C12, (b) C14, (c) C16, and (d) C18.
Coatings 11 00286 g002
Coatings 11 00286 g003 550
Figure 3. Initial configurations of simulation systems: (a) Pal/C12, (b) Pal/C14, (c) Pal/C16 and (d) Pal/C18.
Figure 3. Initial configurations of simulation systems: (a) Pal/C12, (b) Pal/C14, (c) Pal/C16 and (d) Pal/C18.
Coatings 11 00286 g003
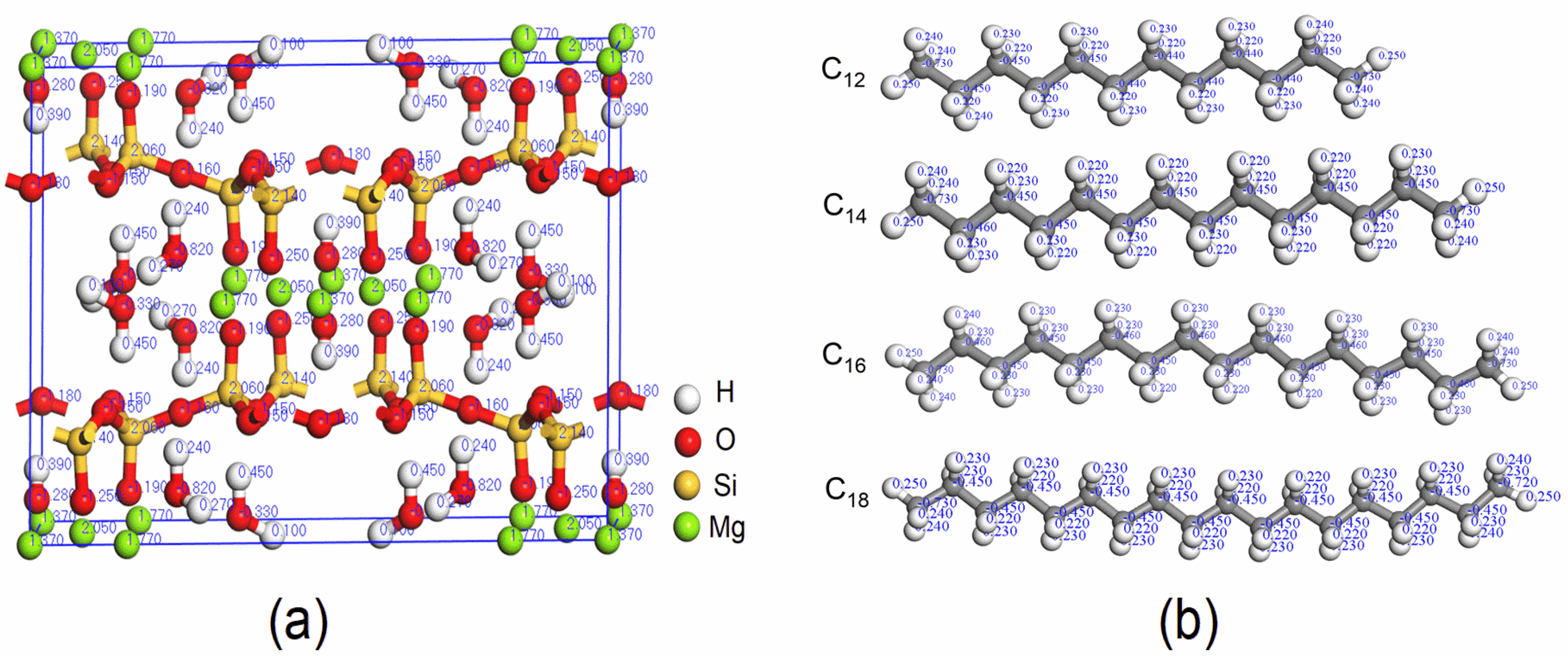
Coatings 11 00286 g004 550
Figure 4. Unit cell structures with charges calculated by the DFT method: (a) unit cell model of palygorskite and (b) linear alkane molecules for C12-C18.
Figure 4. Unit cell structures with charges calculated by the DFT method: (a) unit cell model of palygorskite and (b) linear alkane molecules for C12-C18.
Coatings 11 00286 g004
Coatings 11 00286 g005 550
Figure 5. Configurations of simulation systems at different MD times during the relaxation stage: (a) Pal/C12, (b) Pal/C14, (c) Pal/C16 and (d) Pal/C18.
Figure 5. Configurations of simulation systems at different MD times during the relaxation stage: (a) Pal/C12, (b) Pal/C14, (c) Pal/C16 and (d) Pal/C18.
Coatings 11 00286 g005
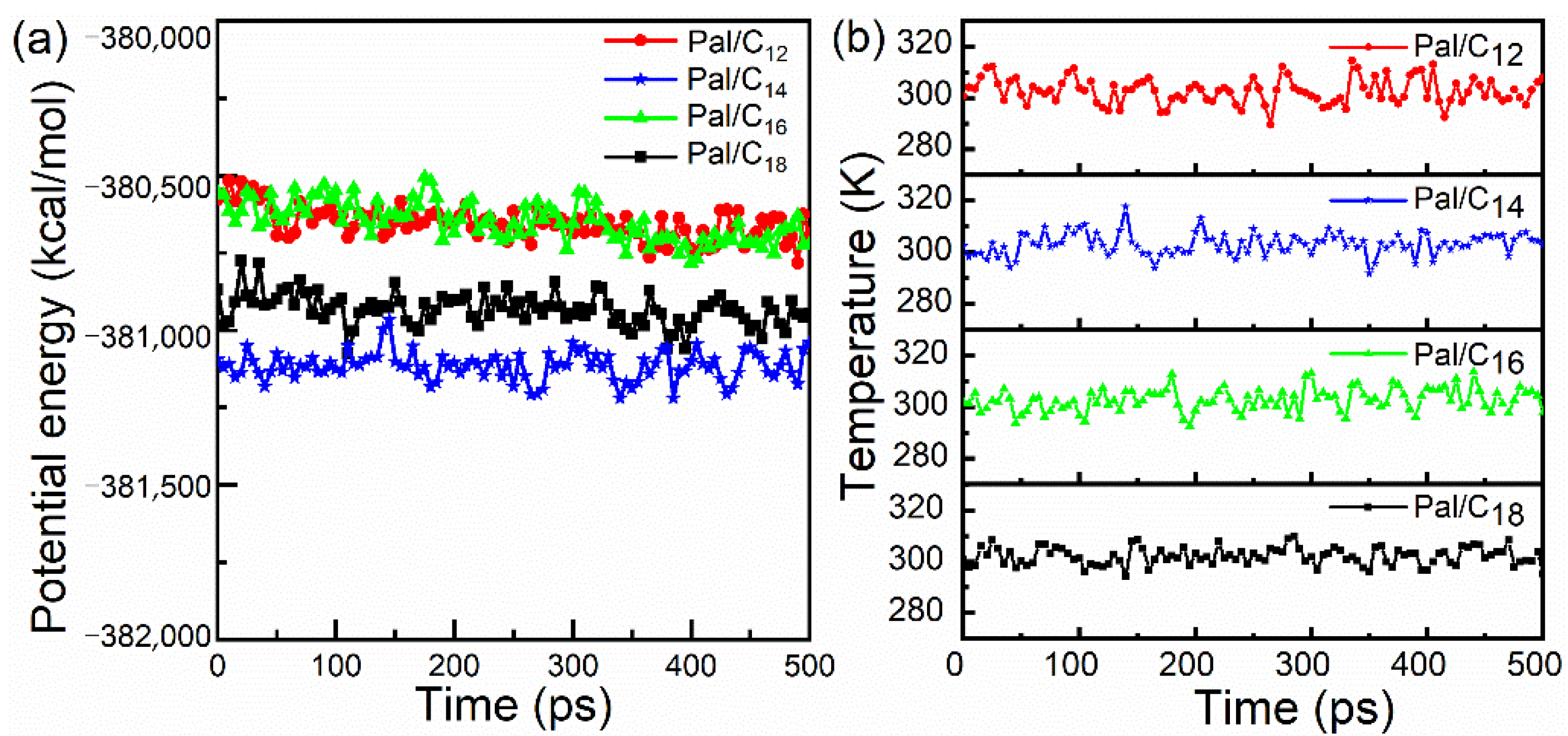
Coatings 11 00286 g006 550
Figure 6. (a) Potential energy and (b) temperature profiles of simulation systems in the equilibrium state.
Figure 6. (a) Potential energy and (b) temperature profiles of simulation systems in the equilibrium state.
Coatings 11 00286 g006
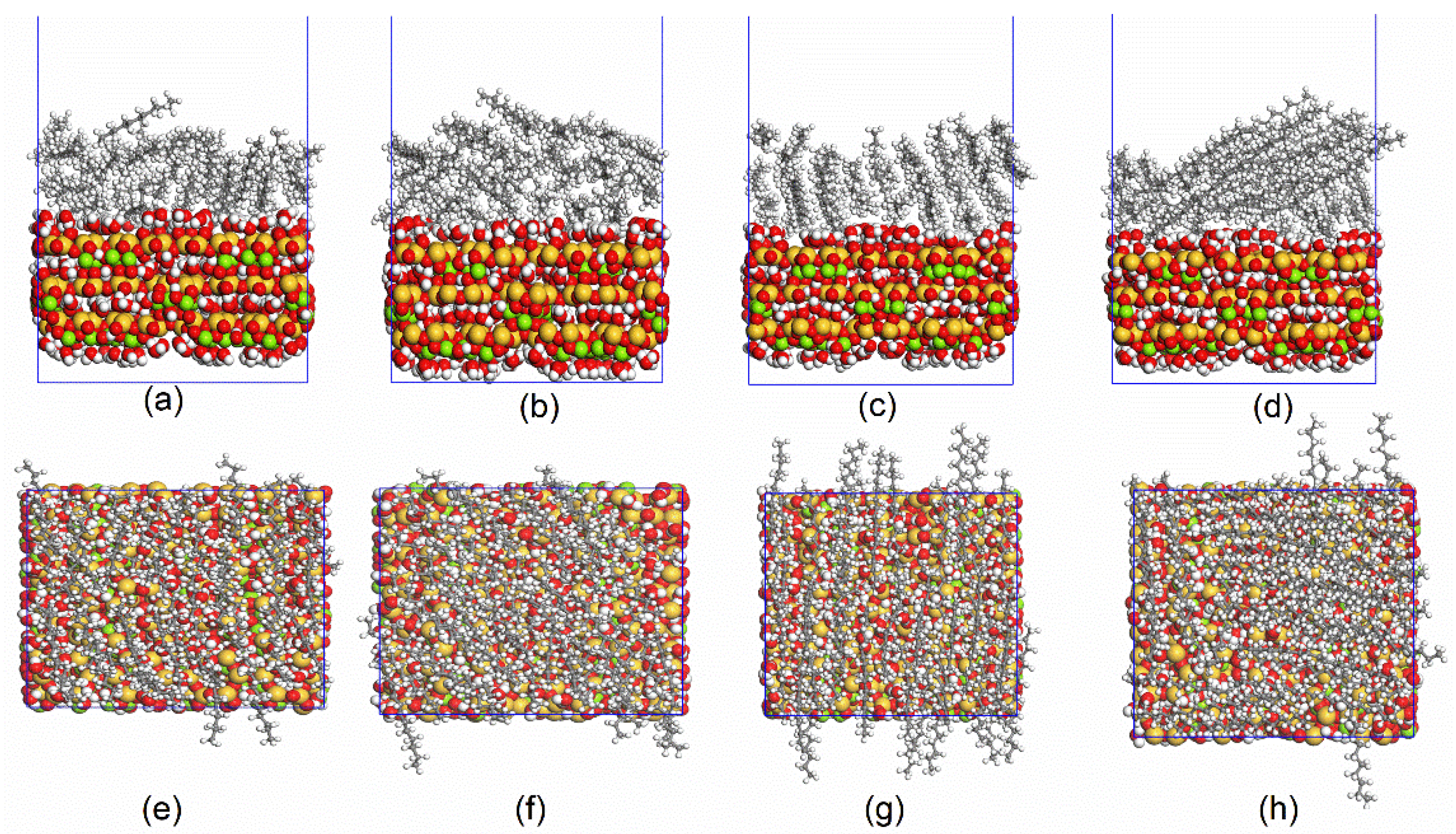
Coatings 11 00286 g007 550
Figure 7. Configurations of modeled systems in equilibrium state: (a) Pal/C12, (b) Pal/C14, (c) Pal/C16and (d) Pal/C18. The (e–h) panels show top views of the (a–d) structures.
Figure 7. Configurations of modeled systems in equilibrium state: (a) Pal/C12, (b) Pal/C14, (c) Pal/C16and (d) Pal/C18. The (e–h) panels show top views of the (a–d) structures.
Coatings 11 00286 g007
Coatings 11 00286 g008 550
Figure 8. MSD profiles (a) and self-diffusion coefficients (b) of alkanes in equilibrium systems.
Figure 8. MSD profiles (a) and self-diffusion coefficients (b) of alkanes in equilibrium systems.
Coatings 11 00286 g008
Coatings 11 00286 g009 550
Figure 9. Fitted MSD profiles in equilibrium systems: (a) C12, (b) C14, (c) C16, (d) C18.
Figure 9. Fitted MSD profiles in equilibrium systems: (a) C12, (b) C14, (c) C16, (d) C18.
Coatings 11 00286 g009
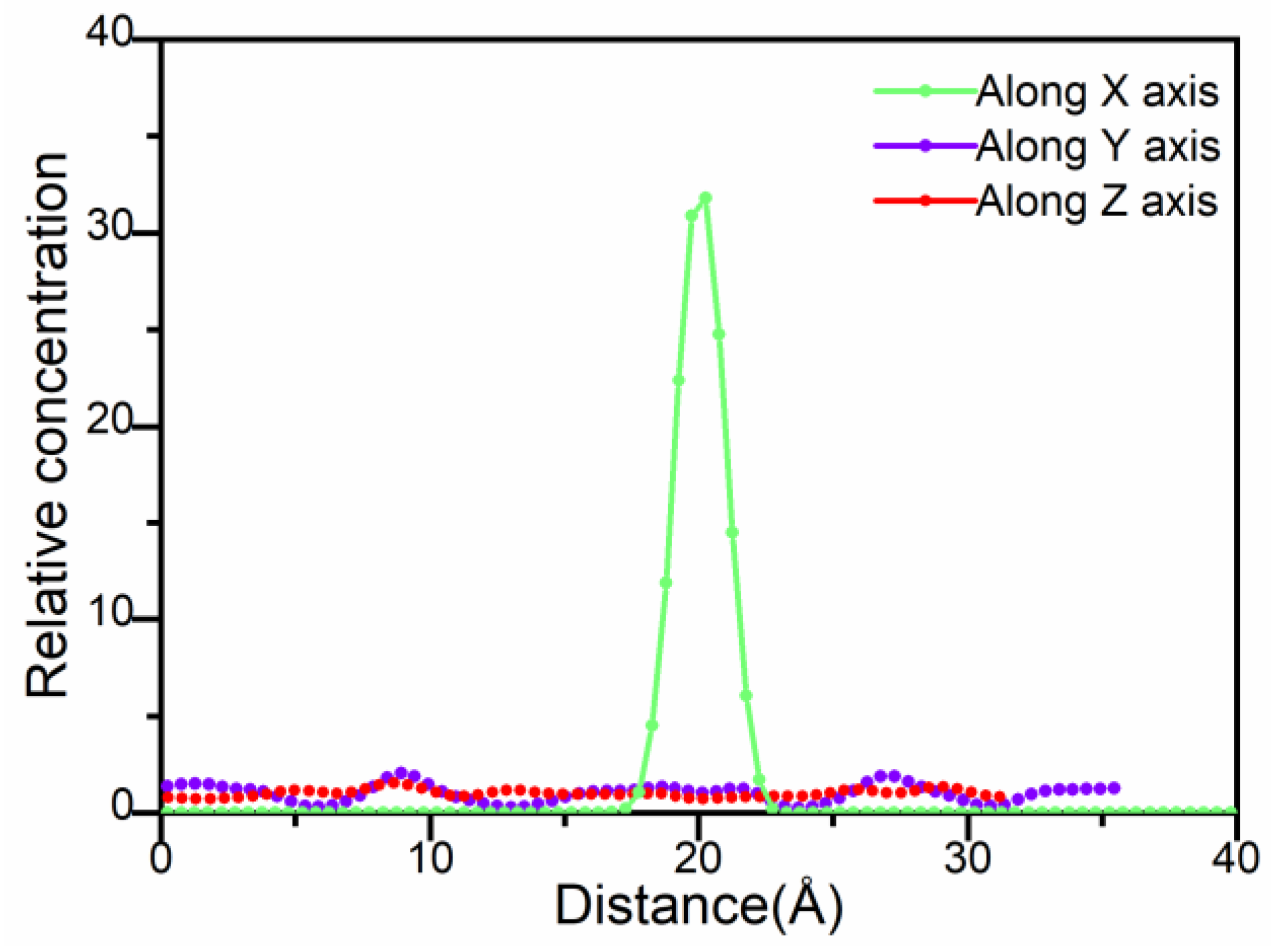
Coatings 11 00286 g010 550
Figure 10. Relative concentration of water molecules on the palygorskite surface in the Pal/C12 equilibrium system.
Figure 10. Relative concentration of water molecules on the palygorskite surface in the Pal/C12 equilibrium system.
Coatings 11 00286 g010
Table
Table 1. Parameters of the as-built simulation systems.
Table 1. Parameters of the as-built simulation systems.
SystemsAlkanesNumber of AlkanesDensity of Alkanes (g/cm3)Number of Total Atoms
Pal/C12Dodecane300.753336
Pal/C14Tetradecane300.753516
Pal/C16Hexadecane300.753696
Pal/C18Octadecane300.753876
Table
Table 2. Binding energies between linear alkanes and palygorskite surface (units: kcal/mol).
Table 2. Binding energies between linear alkanes and palygorskite surface (units: kcal/mol).
SchemeEtotalEpalEalkane△EEbind
Pal/C12−380,621.34−380,871.75616.13−365.72365.72
Pal/C14−381,071.52−381,017.62154.27−208.18208.18
Pal/C16−380,805.33−380,783.75318.03−339.61339.61
Pal/C18−381,207.72−380,957.772.64−252.59252.59
Table
Table 3. The intermolecular interaction energy of alkanes in the equilibrium systems (units: kcal/mol).
Table 3. The intermolecular interaction energy of alkanes in the equilibrium systems (units: kcal/mol).
SystemsEinter
(kcal/mol)		Contributions to Einter
(kcal/mol)
EvdWEelect
Pal/C12−278.23−301.8323.60
Pal/C14−406.04−386.53−19.51
Pal/C16−491.64−488.17−3.47
Pal/C18−606.81−570.37−36.43
Table
Table 4. The main components of the total energy in the equilibrium systems (units: kcal/mol).
Table 4. The main components of the total energy in the equilibrium systems (units: kcal/mol).
SystemsEvalence
(kcal/mol)		Contributions to Enon-bond
(kcal/mol)		Enon-bond
(kcal/mol)		Etotal
(kcal/mol)
EvdWEelect
Pal/C1231,880.0219,245.89−431,743.89−412,498−380,679.12
Pal/C1432,259.2219,357.32−432,677.23−413,319.92−381,124.73
Pal/C1631,939.4119,064.11−431,586.91−412,522.79−380,648.69
Pal/C1831,985.3819,171.35−432,020.58−412,849.23−380,932.99
Table
Table 5. The fitted parameters of the MSD curve and the obtained diffusion coefficients.
Table 5. The fitted parameters of the MSD curve and the obtained diffusion coefficients.
SystemsY = a + b*xD (Å2/ps)
abb/6
Pal/C1214.28218 ± 0.370.20993 ± 1.44 × 10−30.03499 ± 2.41 × 10−4
Pal/C1411.09352 ± 0.240.07525 ± 9.39 × 10−40.01254 ± 1.57 × 10−4
Pal/C167.48414 ± 0.187850.0257 ± 7.28 × 10−40.00428 ± 1.21 × 10−4
Pal/C188.0188 ± 0.170.03879 ± 6.67 × 10−40.00646 ± 1.11 × 10−4
Table
Table 6. The binding energies between alkanes and water molecules on the (100) surface of palygorskite (units: kcal/mol).
Table 6. The binding energies between alkanes and water molecules on the (100) surface of palygorskite (units: kcal/mol).
SystemsEtotalEwsEalkane△EEbind
Pal/C121045.94 395.97 616.13 33.84 −33.84
Pal/C14578.06 401.28 154.27 22.50 −22.50
Pal/C16822.52 468.67 318.03 35.82 −35.82
Pal/C18366.56 350.48 2.64 13.45 −13.45
Table
Table 7. The interaction energies between water molecules on the palygorskite surface and the palygorskite framework (units: kcal/mol).
Table 7. The interaction energies between water molecules on the palygorskite surface and the palygorskite framework (units: kcal/mol).
SystemsEtotalEwsEp△EEbind
Pal/C12−380,886.28395.97−377,686.59−3595.653595.65
Pal/C14−381,017.62401.28−377,804.38−3614.533614.53
Pal/C16−380,698.07468.67−377,259.93−3906.813906.81
Pal/C18−380,898.11350.48−377,857.79−3390.793390.79
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Zhang, J.; Yang, L.; Wang, Y.; Wu, H.; Cai, J.; Xu, S. Molecular Dynamics Simulation on the Interaction between Palygorskite Coating and Linear Chain Alkane Base Lubricant. Coatings 2021, 11, 286. https://doi.org/10.3390/coatings11030286

AMA Style

Zhang J, Yang L, Wang Y, Wu H, Cai J, Xu S. Molecular Dynamics Simulation on the Interaction between Palygorskite Coating and Linear Chain Alkane Base Lubricant. Coatings. 2021; 11(3):286. https://doi.org/10.3390/coatings11030286

Chicago/Turabian Style

Zhang, Jin, Lv Yang, Yue Wang, Huaichao Wu, Jiabin Cai, and Shusheng Xu. 2021. "Molecular Dynamics Simulation on the Interaction between Palygorskite Coating and Linear Chain Alkane Base Lubricant" Coatings 11, no. 3: 286. https://doi.org/10.3390/coatings11030286

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop