Repeated Laser Shock-Wave Adhesion Test for Metallic Coatings: Adhesion Durability and Its Mechanism Studied by Molecular Dynamics Simulation
Abstract
:1. Introduction
2. Experimental Methods and Specimen
2.1. LaSAT
2.2. Specimen
3. Results
3.1. Interfacial Crack Growth
3.1.1. Laser Ultrasonic Scanning (LUS)
3.1.2. FEM with Cohesive Zone Model (CZM)
3.2. Cyclic Irradiation Test
4. MD Study
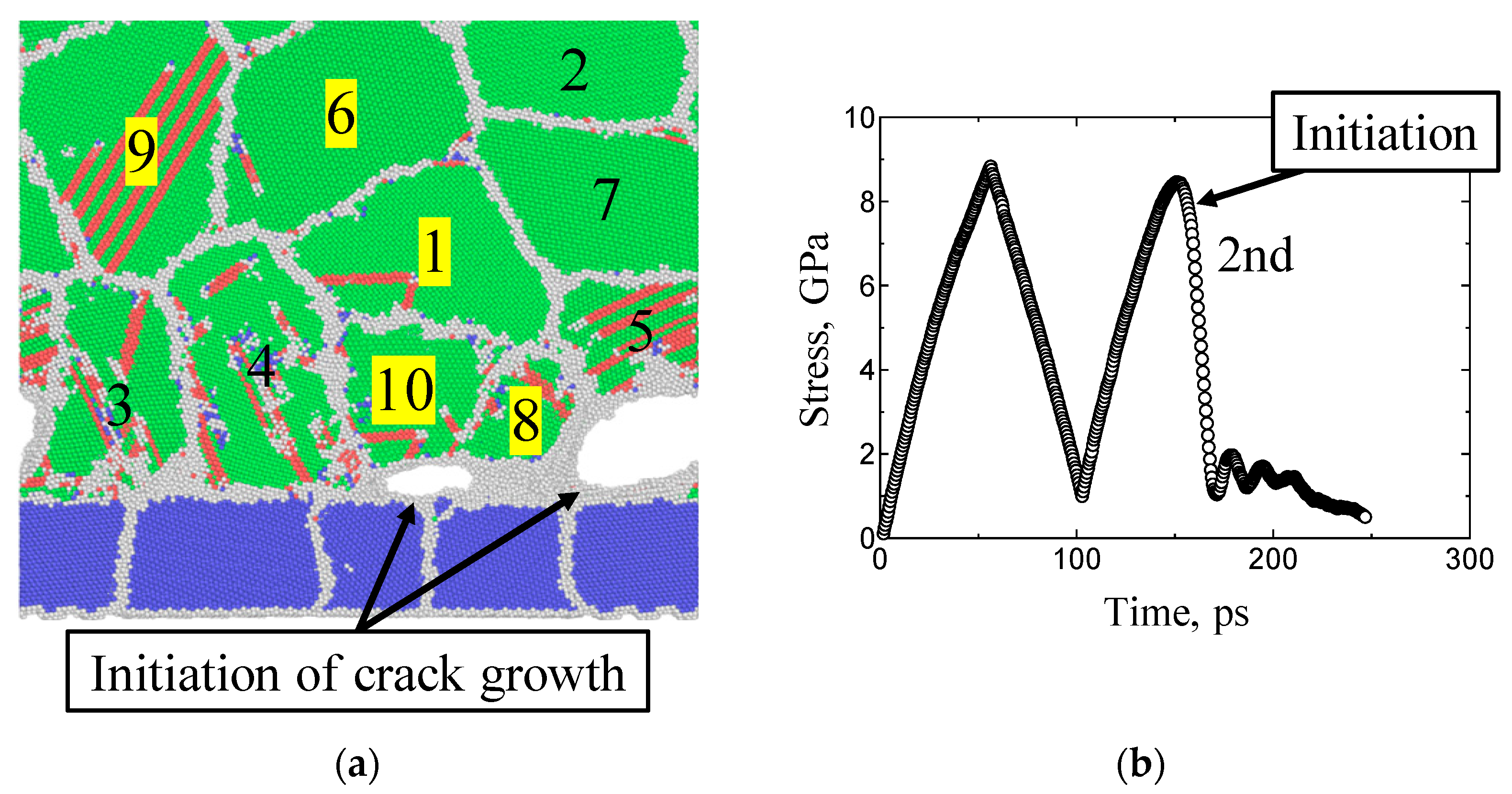
4.1. Crack Growth Simulation by MD
4.1.1. Simulation Condition
4.1.2. Estimation of Interfacial Fracture Toughness
4.2. Fatigue Loading Simulation
4.2.1. Simulation Condition
4.2.2. Simulation Results
4.2.3. Discussion
5. Conclusions
- (1)
- To evaluate interfacial fracture toughness, delamination growth tests for a Cu plate on SUS substrate were conducted using LaSAT. First, an initial delamination was created using LaSAT, and an additional LaSAT was conducted to enhance the initial delamination growth. The delamination area could be visualized non-destructively using LUS. FEM computation was carried out to compute the interfacial stress due to LaSAT. In addition, a CZM was used to estimate Kc.
- (2)
- Repeated LaSAT was conducted to evaluate the adhesion durability of Cu coating. The tests were performed at various laser energies to investigate the number of loading cycles required for delamination. The results indicated a fatigue fracture tendency similar to that of a common homogeneous metal material: The coating life of delamination increased as the applied stress decreased.
- (3)
- Using MD simulations of the Cu/Fe interface, we calculated the interfacial fracture toughness using the displacement extrapolation method. The interfacial fracture toughness ranged from 1.6 to 3.0 MPa√m, values that are comparable to those calculated from the LaSAT experiment, 0.91 MPa√m and 2.0 MPa√m. This suggests that the delamination growth at the interface is dominated by local plastic deformation in a small region on the nanometer scale around the crack tip. In addition, we verified our MD simulation from the LaSAT experiments.
- (4)
- MD simulations were also done to perform stress-controlled cyclic loadings in a Cu/Fe interfacial polycrystalline model. This model was an infinite-flat-plate interface model without interface edges. Unlike conventional fatigue mechanisms, the model did not induce any intrusion or extrusion. Even in the interface model, we found that the accumulation of microscopic plastic deformations (dislocations) in each grain resulted in fatigue fracture.
- (5)
- We found that there are active grains that preferentially slip, and dislocations in the grains propagate up toward the grain boundaries and/or interface. This results in an accumulation of dislocations, increasing the dislocation density. Therefore, a source of stress concentration forms, resulting in the initiation of fatigue cracks. Thus, interfacial fatigue cracks may initiate from the inside along the interface, and interfacial edges are not always necessary for interfacial fatigue fracture.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, N.; Jia, R.; Zhang, H.; Sha, W.; Li, Y.; Jiang, Z. In-situ Cu Coating on Steel Surface after Oxidizing at High Temperature. Materials 2019, 12, 3536. (In English) [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fukumoto, S.; Ohta, K.; Yanagimoto, T.; Kashiba, Y.; Kikuchi, M.; Matsushima, M.; Fujimoto, K. Characteristics and Microstructural Development of Cold-Sprayed Copper Coating on Aluminum. Mater. Trans. 2019, 60, 602–610. [Google Scholar] [CrossRef] [Green Version]
- Wan, Y.; Hu, X.; Xu, T.; Li, Y.; Jiang, X. Interfacial IMC growth of SAC305/Cu joint with a novel dual-layer of Ni(P)/Cu plating during solid-state aging. Microelectron. Eng. 2018, 199, 69–79. [Google Scholar] [CrossRef]
- Yang, L.; Atanasova, T.; Radisic, A.; Deconinck, J.; West, A.C.; Vereecken, P. Wafer-scale Cu plating uniformity on thin Cu seed layers. Electrochim. Acta 2013, 104, 242–248. [Google Scholar] [CrossRef]
- Lee, P.T.; Wu, Y.S.; Lin, P.C.; Chen, C.C.; Hsieh, W.Z.; Ho, C.E. High-speed Cu electrodeposition and its solderability. Surf. Coat. Technol. 2017, 320, 559–567. [Google Scholar] [CrossRef]
- Watanabe, M.; Kuroda, S.; Yokoyama, K.; Inoue, T.; Gotoh, Y. Modified tensile adhesion test for evaluation of interfacial toughness of HVOF sprayed coatings. Surf. Coat. Technol. 2008, 202, 1746–1752. [Google Scholar] [CrossRef]
- Dayani, S.B.; Shaha, S.K.; Ghelichi, R.; Wang, J.F.; Jahed, H. The impact of AA7075 cold spray coating on the fatigue life of AZ31B cast alloy. Surf. Coat. Technol. 2018, 337, 150–158. [Google Scholar] [CrossRef]
- Piveteau, L.-D.; Gasser, B.; Schlapbach, L. Evaluating mechanical adhesion of sol–gel titanium dioxide coatings containing calcium phosphate for metal implant application. Biomaterials 2000, 21, 2193–2201. [Google Scholar] [CrossRef]
- Mead, J.L.; Lu, M.; Huang, H. Inducing stable interfacial delamination in a multilayer system by four-point bending of microbridges. Surf. Coat. Technol. 2017, 320, 478–482. [Google Scholar] [CrossRef] [Green Version]
- Hirakata, H.; Kitazawa, M.; Kitamura, T. Fatigue crack growth along interface between metal and ceramics submicron-thick films in inert environment. Acta Mater. 2006, 54, 89–97. [Google Scholar] [CrossRef]
- Ito, H.; Kiminami, S.; Cho, H. Evaluation of adhesion quality of oxide scale on low carbon steel at high temperature using a laser spallation technique. Trans. JSME 2015, 81, 14-00493. (In Japanese) [Google Scholar] [CrossRef]
- Mittal, K.L. Adhesion Measurement of Thin Films, Thick Films, and Bulk Coatings; ASTM International: West Conshohocken, PA, USA, 1978. [Google Scholar]
- Yuan, J.; Gupta, V. Measurement of interface strength by the modified laser spallation technique. I. Experiment and simulation of the spallation process. J. Appl. Phys. 1993, 74, 2388–2396. [Google Scholar] [CrossRef]
- Berthe, L.; Arrigoni, M.; Boustie, M.; Cuq-Lelandais, J.P.; Broussillou, C.; Fabre, G.; Jeandin, M.; Guipont, V.; Nivard, M. State-of-the-art laser adhesion test (LASAT). Nondestruct. Test. Eval. 2011, 26, 303–317. [Google Scholar] [CrossRef]
- Bolis, C.; Berthe, L.; Boustie, M.; Arrigoni, M.; Barradas, S.; Jeandin, M. Physical approach to adhesion testing using laser-driven shock waves. J. Phys. D Appl. Phys. 2007, 40, 3155–3163. [Google Scholar] [CrossRef]
- Bégué, G.; Fabre, G.; Guipont, V.; Jeandin, M.; Bilhe, P.; Guedou, J.Y.; Lepoutre, F. Laser Shock Adhesion Test (LASAT) of EB-PVD TBCs: Towards an industrial application. Surf. Coat. Technol. 2013, 237, 305–312. [Google Scholar] [CrossRef]
- Arrigoni, M.; Kruger, S.E.; Blouin, A.; Lévesque, D.; Arsenault, B.; Monchalin, J.P.; Boustie, M.; Berthe, L. Adhesive Bond Testing By Laser Induced Shock Waves. In Proceedings of the 17th World Conference on Nondestructive Testing, Shanghai, China, 25–28 October 2008. [Google Scholar]
- Kanamori, K.; Saito, Y.; Yamada, T.; Yonezu, A.; Chen, X. Development of Adhesion Durability Evaluation of Surface Coatings Using Repeated Laser Shock-wave Adhesion Test. J. Nondestruct. Eval. 2020, 39, 87. [Google Scholar] [CrossRef]
- Ostrowicki, G.T.; Sitaraman, S.K. Cyclic magnetic actuation technique for thin film interfacial fatigue crack propagation. Eng. Fract. Mech. 2016, 168, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Shen, F.; Yeo, A.; Liu, B.; Xue, M.; Xu, H.; Zhou, K. Characterization of interfacial delamination in multi-layered integrated circuit packaging. Surf. Coat. Technol. 2017, 320, 349–356. [Google Scholar] [CrossRef]
- Yashiro, K.; Nimura, K.; Naito, K. Molecular Dynamics Study on Adhesion of Various Ni/Al Interface for Ni-Plated Aluminum Alloys. Mater. Trans. 2018, 59, 1753–1760. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Xiao, S.; Deng, H.; Hu, W. Molecular dynamics simulation of fatigue crack propagation in bcc iron under cyclic loading. Int. J. Fatigue 2014, 68, 253–259. [Google Scholar] [CrossRef]
- Wu, W.-P.; Li, Y.-L.; Sun, X.-Y. Molecular dynamics simulation-based cohesive zone representation of fatigue crack growth in a single crystal nickel. Comput. Mater. Sci. 2015, 109, 66–75. [Google Scholar] [CrossRef]
- Kanamori, K.; Kimoto, Y.; Toriumi, S.; Yonezu, A. Evaluation of Adhesion Durability of Ni–P Coating using Repeated Laser Shock Adhesion Test. Surf. Coat. Technol. 2020, 396, 125953. [Google Scholar]
- Watanabe, Y.; Yonezu, A.; Chen, X. Measurement of interfacial fracture toughness of surface coatings using pulsed-laser-induced ultrasonic waves. J. Nondestruct. Eval. 2018, 37, 2. [Google Scholar] [CrossRef]
- van Hal, B.; Peerlings, R.H.; Geers, M.G.; van der Sluis, O. Cohesive zone modeling for structural integrity analysis of IC interconnects. Microelectron. Reliab. 2007, 47, 1251–1261. [Google Scholar] [CrossRef]
- Watanabe, Y.; Fujisawa, S.; Yonezu, A.; Chen, X. Quantitative evaluation of adhesion quality of surface coating by using pulse laser-induced ultrasonic waves. Surf. Coat. Technol. 2016, 286, 231–238. [Google Scholar] [CrossRef] [Green Version]
- Yuuki, R.; Liu, J.-Q.; Xu, J.-Q.; Ohara, T.; Ono, T. Evaluation of the Fatigue Strength of Adhesive Joints Based on Interfacial Fracture Toughness. J. Soc. Mat. Sci. Jpn. 1992, 41, 1299–1304. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Bazhirov, T. Data-centric online ecosystem for digital materials science. arXiv 2019, arXiv:1902.10838. [Google Scholar]
- Bonny, G.; Pasianot, R.C.; Castin, N.; Malerba, L. Ternary Fe–Cu–Ni many-body potential to model reactor pressure vessel steels: First validation by simulated thermal annealing. Philos. Mag. 2009, 89, 3531–3546. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]




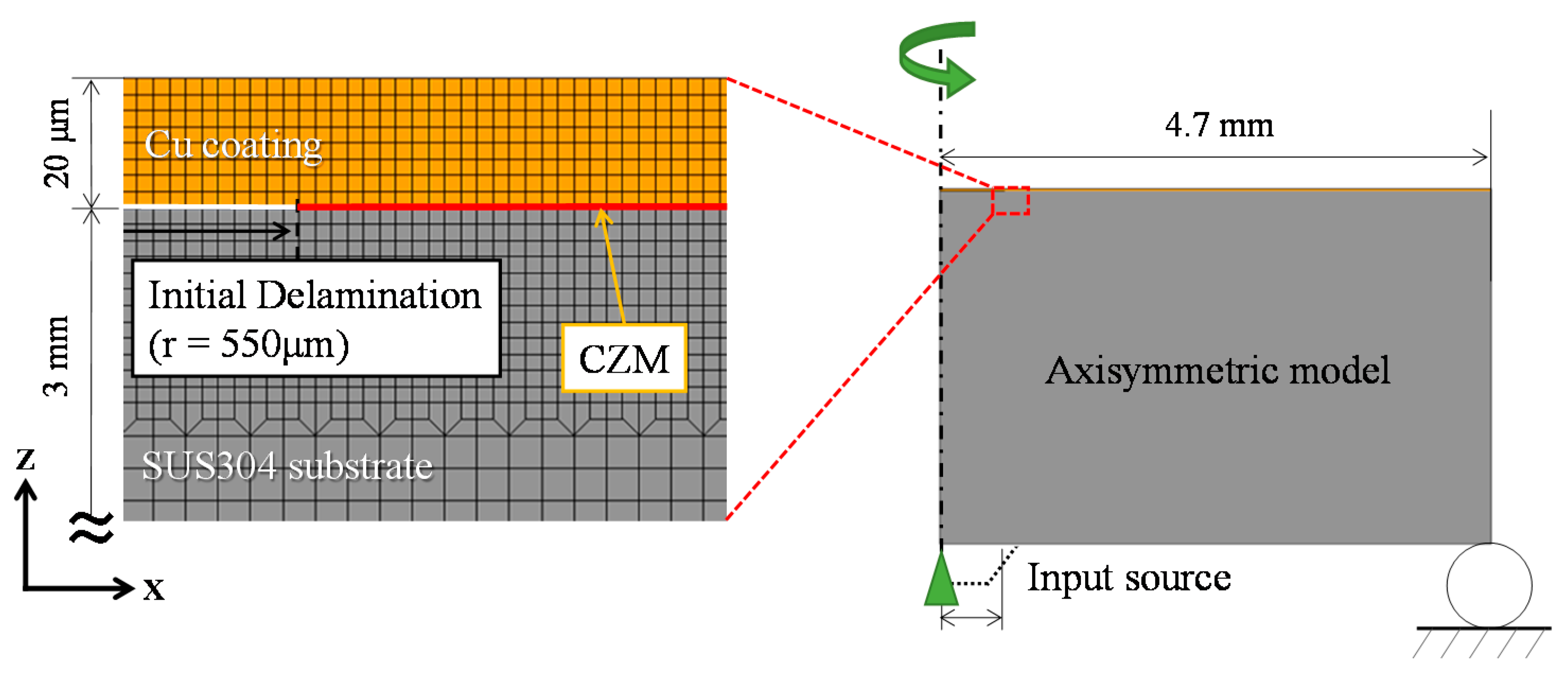












| Material | SUS304 Substrate | Cu Coating |
|---|---|---|
| Young’s modulus E, GPa | 197 | 110 |
| Density ρ, kg/m3 | 8000 | 8960 |
| Longitudinal wave velocity CL, m/s | 5757 | 4346 |
| Transverse wave velocity CS, m/s | 4352 | 3026 |
| Poisson’s ratio ν | 0.30 | 0.34 |
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
|---|---|---|---|---|---|
| KI, MPa√m | 1.55 | 2.30 | 2.31 | 1.80 | 1.75 |
| KII, MPa√m | 0.35 | 1.84 | 1.53 | 1.50 | 0.66 |
| KC, MPa√m | 1.59 | 2.95 | 2.77 | 2.34 | 1.87 |
| (a) | |||
|---|---|---|---|
| Grain Number | MSF | Slip System | |
| Slip Plane Normal | Slip Direction | ||
| No. 1 | −0.49 | (1−11) | [110] |
| No. 2 | −0.47 | (11−1) | [11] |
| No. 3 | −0.45 | (−111) | [0−11] |
| No. 4 | −0.49 | (−111) | [101] |
| No. 5 | −0.45 | (111) | [0−11] |
| No. 6 | 0.37 | (1−11) | [−101] |
| No. 7 | 0.47 | (−111) | [110] |
| No. 8 | 0.47 | (111) | [−110] |
| No. 9 | −0.47 | (1−11) | [110] |
| No. 10 | −0.43 | (111) | [−101] |
| (b) | |||
| Grain Number | MSF | Slip System | |
| Slip Plane Normal | Slip Direction | ||
| No. 1 | −0.46 | (1−11) | [11] |
| No. 2 | 0.31 | (−111) | [0−11] |
| No. 3 | 0.41 | (−111) | [0−11] |
| No. 4 | −0.39 | (1−11) | [110] |
| No. 5 | −0.42 | (1−11) | [110] |
| No. 6 | 0.46 | (111) | [−110] |
| No. 7 | −0.42 | (−111) | [0−11] |
| No. 8 | 0.46 | (11–1) | [−110] |
| No. 9 | −0.46 | (11−1) | [−110] |
| No. 10 | 0.45 | (111) | [0−11] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanamori, K.; Toriumi, S.; Kimoto, Y.; Yonezu, A. Repeated Laser Shock-Wave Adhesion Test for Metallic Coatings: Adhesion Durability and Its Mechanism Studied by Molecular Dynamics Simulation. Coatings 2021, 11, 291. https://doi.org/10.3390/coatings11030291
Kanamori K, Toriumi S, Kimoto Y, Yonezu A. Repeated Laser Shock-Wave Adhesion Test for Metallic Coatings: Adhesion Durability and Its Mechanism Studied by Molecular Dynamics Simulation. Coatings. 2021; 11(3):291. https://doi.org/10.3390/coatings11030291
Chicago/Turabian StyleKanamori, Kohei, Shuto Toriumi, Yoshikatsu Kimoto, and Akio Yonezu. 2021. "Repeated Laser Shock-Wave Adhesion Test for Metallic Coatings: Adhesion Durability and Its Mechanism Studied by Molecular Dynamics Simulation" Coatings 11, no. 3: 291. https://doi.org/10.3390/coatings11030291
APA StyleKanamori, K., Toriumi, S., Kimoto, Y., & Yonezu, A. (2021). Repeated Laser Shock-Wave Adhesion Test for Metallic Coatings: Adhesion Durability and Its Mechanism Studied by Molecular Dynamics Simulation. Coatings, 11(3), 291. https://doi.org/10.3390/coatings11030291






