Machine Learning Model to Map Tribocorrosion Regimes in Feature Space
Abstract
:1. Introduction
2. Methodology
2.1. Unsupervised Learning
2.2. Supervised Learning
3. Results and Discussion
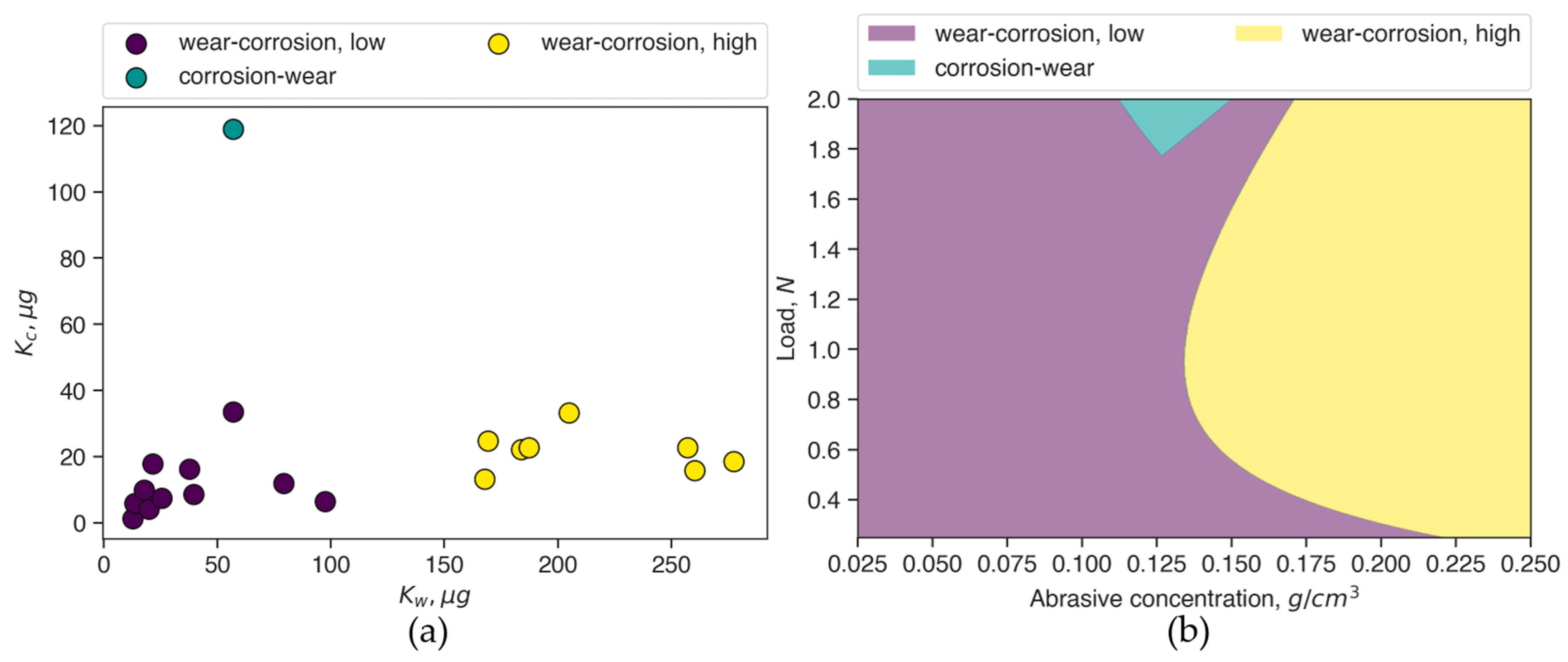
3.1. Identifying the Clusters
3.2. Tribocorrosion Maps
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Zhao, T.; Ju, W.; Shi, S. Materials discovery and design using machine learning. J. Mater. 2017, 3, 159–177. [Google Scholar] [CrossRef]
- Xie, H.; Wang, Z.; Qin, N.; Du, W.; Qian, L. Prediction of Friction Coefficients During Scratch Based on an Integrated Finite Element and Artificial Neural Network Method. J. Tribol. 2020, 142, 1–25. [Google Scholar] [CrossRef]
- Gyurova, L.A.; Friedrich, K. Artificial neural networks for predicting sliding friction and wear properties of polyphenylene sulfide composites. Tribol. Int. 2011, 44, 603–609. [Google Scholar] [CrossRef]
- Argatov, I.I.; Chai, Y.S. An artificial neural network supported regression model for wear rate. Tribol. Int. 2019, 138, 211–214. [Google Scholar] [CrossRef]
- Velten, K.; Reinicke, R.; Friedrich, K. Wear volume prediction with artificial neural networks. Tribol. Int. 2000, 33, 731–736. [Google Scholar] [CrossRef]
- Bhaumik, S.; Pathak, S.D.; Dey, S.; Datta, S. Artificial intelligence based design of multiple friction modifiers dispersed castor oil and evaluating its tribological properties. Tribol. Int. 2019, 140, 105813. [Google Scholar] [CrossRef]
- Rashmi, W.; Osama, M.; Khalid, M.; Rasheed, A.K.; Bhaumik, S.; Wong, W.Y.; Datta, S.; TCSM, G. Tribological performance of nanographite-based metalworking fluid and parametric investigation using artificial neural network. Int. J. Adv. Manuf. Technol. 2019, 104, 359–374. [Google Scholar] [CrossRef]
- Humelnicu, C.; Ciortan, S.; Amortila, V. Artificial Neural Network-Based Analysis of the Tribological Behavior of Vegetable Oil–Diesel Fuel Mixtures. Lubricants 2019, 7, 32. [Google Scholar] [CrossRef] [Green Version]
- Vinoth, A.; Datta, S. Design of the ultrahigh molecular weight polyethylene composites with multiple nanoparticles: An artificial intelligence approach. J. Compos. Mater. 2019, 54, 179–192. [Google Scholar] [CrossRef]
- Pai, P.S.; Mathew, M.T.; Stack, M.M.; Rocha, L.A. Some thoughts on neural network modelling of microabrasion–corrosion processes. Tribol. Int. 2008, 41, 672–681. [Google Scholar] [CrossRef] [Green Version]
- Buj-Corral, I.; Sivatte-Adroer, M.; Llanas-Parra, X. Adaptive indirect neural network model for roughness in honing processes. Tribol. Int. 2020, 141, 105891. [Google Scholar] [CrossRef]
- Peng, Y.; Cai, J.; Wu, T.; Cao, G.; Kwok, N.; Zhou, S.; Peng, Z. A hybrid convolutional neural network for intelligent wear particle classification. Tribol. Int. 2019, 138, 166–173. [Google Scholar] [CrossRef]
- Kamrunnahar, M.; Urquidi-Macdonald, M. Prediction of corrosion behavior using neural network as a data mining tool. Corros. Sci. 2010, 52, 669–677. [Google Scholar] [CrossRef]
- Mareci, D.; Suditu, G.D.; Chelariu, R.; Trincă, L.C.; Curteanu, S. Prediction of corrosion resistance of some dental metallic materials applying artificial neural networks. Mater. Corros. 2016, 67, 1213–1219. [Google Scholar] [CrossRef]
- Jiménez-Come, M.J.; Turias, I.J.; Ruiz-Aguilar, J.J.; Trujillo, F.J. Characterization of pitting corrosion of stainless steel using artificial neural networks. Mater. Corros. 2015, 66, 1084–1091. [Google Scholar] [CrossRef] [Green Version]
- Mareci, D.; Dragoi, E.-N.; Bolat, G.; Chelariu, R.; Gordin, D.; Curteanu, S. Modelling the influence of pH, fluoride, and caffeine on the corrosion resistance of TiMo alloys by artificial neural networks developed with differential evolution algorithm. Mater. Corros. 2015, 66, 982–994. [Google Scholar] [CrossRef]
- Chelariu, R.; Suditu, G.D.; Mareci, D.; Bolat, G.; Cimpoesu, N.; Leon, F.; Curteanu, S. Prediction of Corrosion Resistance of Some Dental Metallic Materials with an Adaptive Regression Model. JOM 2015, 67, 767–774. [Google Scholar] [CrossRef]
- Xu, K.; Luxmoore, A.R.; Deravi, F. Comparison of shape features for the classification of wear particles. Eng. Appl. Artif. Intell. 1997, 10, 485–493. [Google Scholar] [CrossRef]
- Chou, J.-S.; Ngo, N.-T.; Chong, W.K. The use of artificial intelligence combiners for modeling steel pitting risk and corrosion rate. Eng. Appl. Artif. Intell. 2017, 65, 471–483. [Google Scholar] [CrossRef]
- Yılmaz, A. Shoulder Implant Manufacturer Detection by Using Deep Learning: Proposed Channel Selection Layer. Coatings 2021, 11, 346. [Google Scholar] [CrossRef]
- Landolt, D. Electrochemical and materials aspects of tribocorrosion systems. J. Phys. D Appl. Phys. 2006, 39, 3121–3127. [Google Scholar] [CrossRef]
- Richard, C. 19—Tribocorrosion at elevated temperatures in the metal working industry. In Woodhead Publishing Series in Metals and Surface Engineering; Landolt, D., Mischler, S., Eds.; Woodhead Publishing: Cambridge, UK, 2011; pp. 517–536. ISBN 978-1-84569-966-6. [Google Scholar]
- Bai, H.-D.; Zheng, B.-C.; Li, W.; Tu, X.-H. Failure analysis of ring die of a feed pellet machine. China Foundry 2020, 17, 167–172. [Google Scholar] [CrossRef]
- Behrens, B.-A.; Brunotte, K.; Wester, H.; Rothgänger, M.; Müller, F. Multi-Layer Wear and Tool Life Calculation for Forging Applications Considering Dynamical Hardness Modeling and Nitrided Layer Degradation. Materials 2020, 14, 104. [Google Scholar] [CrossRef]
- Karakaş, M.S. Tribocorrosion behavior of surface-modified AISI D2 steel. Surf. Coat. Technol. 2020, 394, 125884. [Google Scholar] [CrossRef]
- Zavieh, A.H.; Espallargas, N. Effect of 4-point bending and normal load on the tribocorrosion-fatigue (multi-degradation) of stainless steels. Tribol. Int. 2016, 99, 96–106. [Google Scholar] [CrossRef]
- Kasar, A.K.; Siddaiah, A.; Ramachandran, R.; Menezes, P.L. Tribocorrosion Performance of Tool Steel for Rock Drilling Process. J. Bio. Tribo-Corros. 2019, 5, 44. [Google Scholar] [CrossRef]
- Wood, R.J.K.; Herd, S.; Thakare, M.R. A critical review of the tribocorrosion of cemented and thermal sprayed tungsten carbide. Tribol. Int. 2018, 119, 491–509. [Google Scholar] [CrossRef]
- Kowalski, M.; Stachowiak, A. Tribocorrosion Performance of Cr/CrN Hybrid Layer as a Coating for Machine Components Used in a Chloride Ions Environment. Coatings 2021, 11, 242. [Google Scholar] [CrossRef]
- Rasool, G.; El Shafei, Y.; Stack, M.M. Mapping Tribo-Corrosion Behaviour of TI-6AL-4V Eli in Laboratory Simulated Hip Joint Environments. Lubricants 2020, 8, 69. [Google Scholar] [CrossRef]
- Siddaiah, A.; Khan, Z.A.; Ramachandran, R.; Menezes, P.L. Performance Analysis of Retrofitted Tribo-Corrosion Test Rig for Monitoring in Situ Oil Conditions. Materials 2017, 10, 1145. [Google Scholar] [CrossRef] [Green Version]
- Yue, Z.; Zhou, P.; Shi, J. Some Factors Influencing Corrosion-Erosion Performance of Materials. In Proceedings of the Wear of Materials, Houston, TX, USA, 5 April 1987; Luedema, K.C., Ed.; ASME: New York, NY, USA, 1987; pp. 763–770. [Google Scholar]
- Stack, M.M.; Zhou, S.; Newman, R.C. Effects of particle velocity and applied potential on erosion of mild steel in carbonate/bicarbonate slurry. Mater. Sci. Technol. 1996, 12, 261–268. [Google Scholar] [CrossRef]
- Wood, R.J.K. Tribo-corrosion of coatings: A review. J. Phys. D Appl. Phys. 2007, 40, 5502–5521. [Google Scholar] [CrossRef]
- Kent, D.; Wang, G.; Yu, Z.; Dargusch, M.S. Pseudoelastic behaviour of a β Ti–25Nb–3Zr–3Mo–2Sn alloy. Mater. Sci. Eng. A 2010, 527, 2246–2252. [Google Scholar] [CrossRef]
- Huang, W.; Wang, Z.; Liu, C.; Yu, Y. Wear and Electrochemical Corrosion Behavior of Biomedical Ti–25Nb–3Mo–3Zr–2Sn Alloy in Simulated Physiological Solutions. J. Bio. Tribo-Corros. 2015, 1, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, P.; Das, S.K.; Davim, J.P. Tribology of materials for biomedical applications. In Mechanical Behaviour of Biomaterials; Davim, J.P., Ed.; Woodhead Publishing: Cambridge, UK, 2019; pp. 1–45. [Google Scholar]
- Qiu, J.; Yu, W.-Q.; Zhang, F.-Q.; Smales, R.J.; Zhang, Y.-L.; Lu, C.-H. Corrosion behaviour and surface analysis of a Co-Cr and two Ni-Cr dental alloys before and after simulated porcelain firing. Eur. J. Oral Sci. 2011, 119, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Li, Y.; Huang, W.; Chen, X.; He, H. Micro-abrasion–corrosion behaviour of a biomedical Ti–25Nb–3Mo–3Zr–2Sn alloy in simulated physiological fluid. J. Mech. Behav. Biomed. Mater. 2016, 63, 361–374. [Google Scholar] [CrossRef] [PubMed]
- Stack, M.M.; Rodling, J.; Mathew, M.T.; Jawan, H.; Huang, W.; Park, G.; Hodge, C. Micro-abrasion–corrosion of a Co–Cr/UHMWPE couple in Ringer’s solution: An approach to construction of mechanism and synergism maps for application to bio-implants. Wear 2010, 269, 376–382. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometirka 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Naganna, S.R.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support. Vector Classification. Available online: https://www.csie.ntu.edu.tw/~cjlin/papers/guide/guide.pdf (accessed on 15 December 2020).
- Brownlee, J. How to Use One-vs-Rest and One-vs-One for Multi-Class Classification. Available online: https://machinelearningmastery.com/one-vs-rest-and-one-vs-one-for-multi-class-classification/ (accessed on 10 January 2021).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramachandran, R. Machine Learning Model to Map Tribocorrosion Regimes in Feature Space. Coatings 2021, 11, 450. https://doi.org/10.3390/coatings11040450
Ramachandran R. Machine Learning Model to Map Tribocorrosion Regimes in Feature Space. Coatings. 2021; 11(4):450. https://doi.org/10.3390/coatings11040450
Chicago/Turabian StyleRamachandran, Rahul. 2021. "Machine Learning Model to Map Tribocorrosion Regimes in Feature Space" Coatings 11, no. 4: 450. https://doi.org/10.3390/coatings11040450
APA StyleRamachandran, R. (2021). Machine Learning Model to Map Tribocorrosion Regimes in Feature Space. Coatings, 11(4), 450. https://doi.org/10.3390/coatings11040450





