Langmuir Probe Technique for Plasma Characterization during Pulsed Laser Deposition Process
Abstract
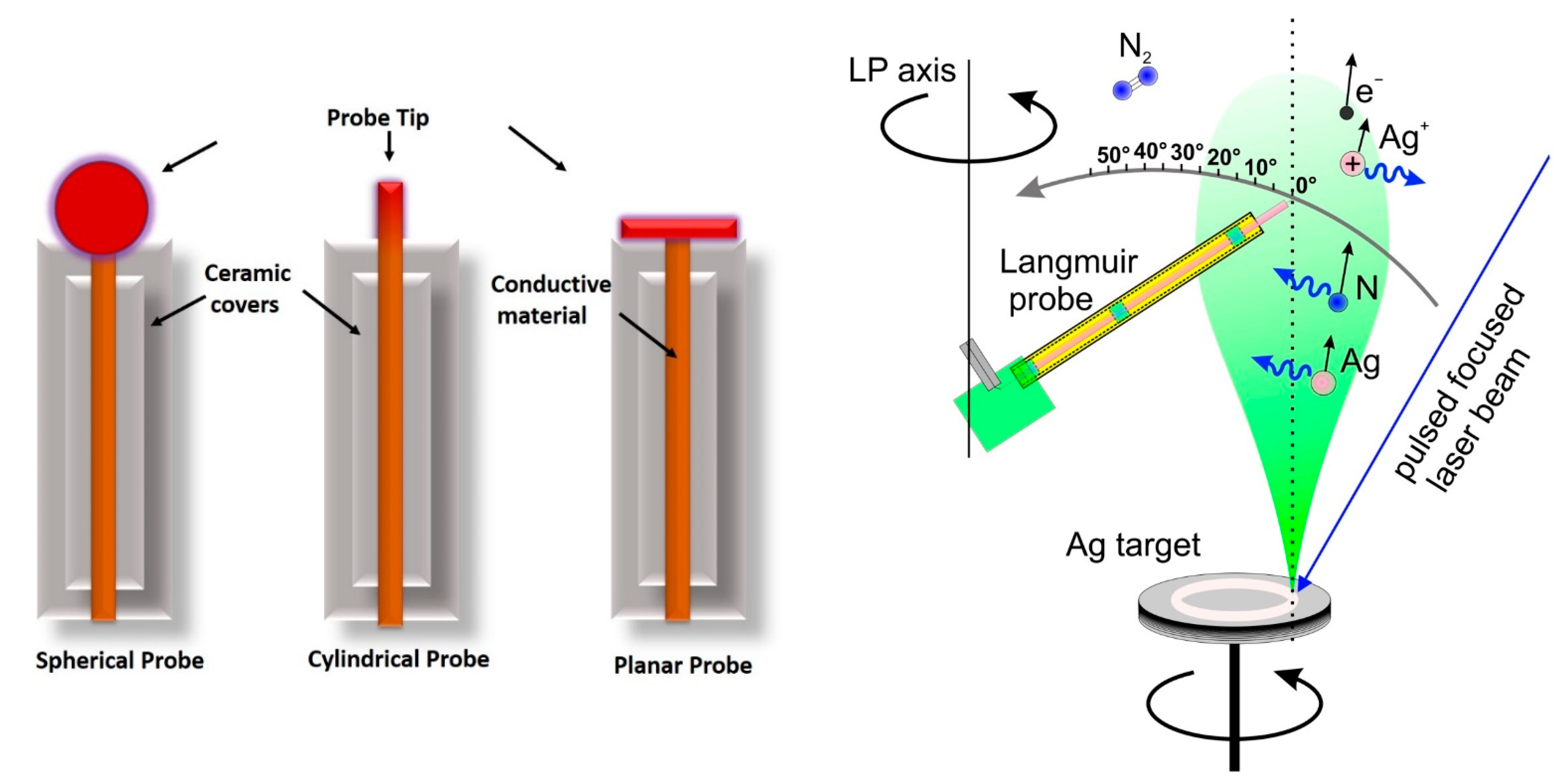
:1. Introduction: A History of Measurements
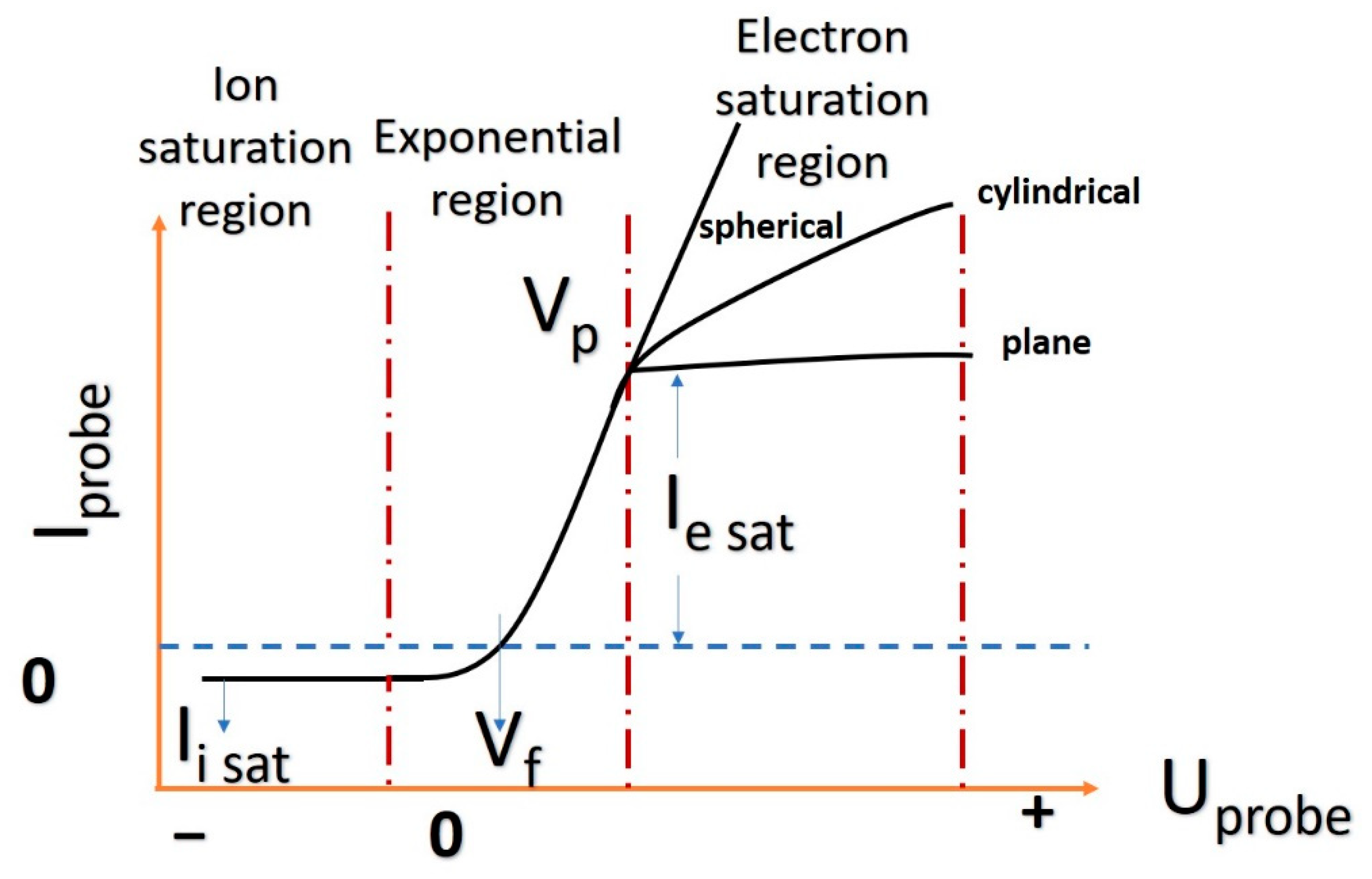
2. Classical Theory of Langmuir Probe Adapted for Transient Plasmas
- a)
- The saturation ionic region is defined by a small current amplitude and a relatively fast saturation for the ionic current. The saturation current is defined as (where A is the probe area, e is the electron charge, ni is the ionic density, Te the electron temperature and mi the ionic mass);
- b)
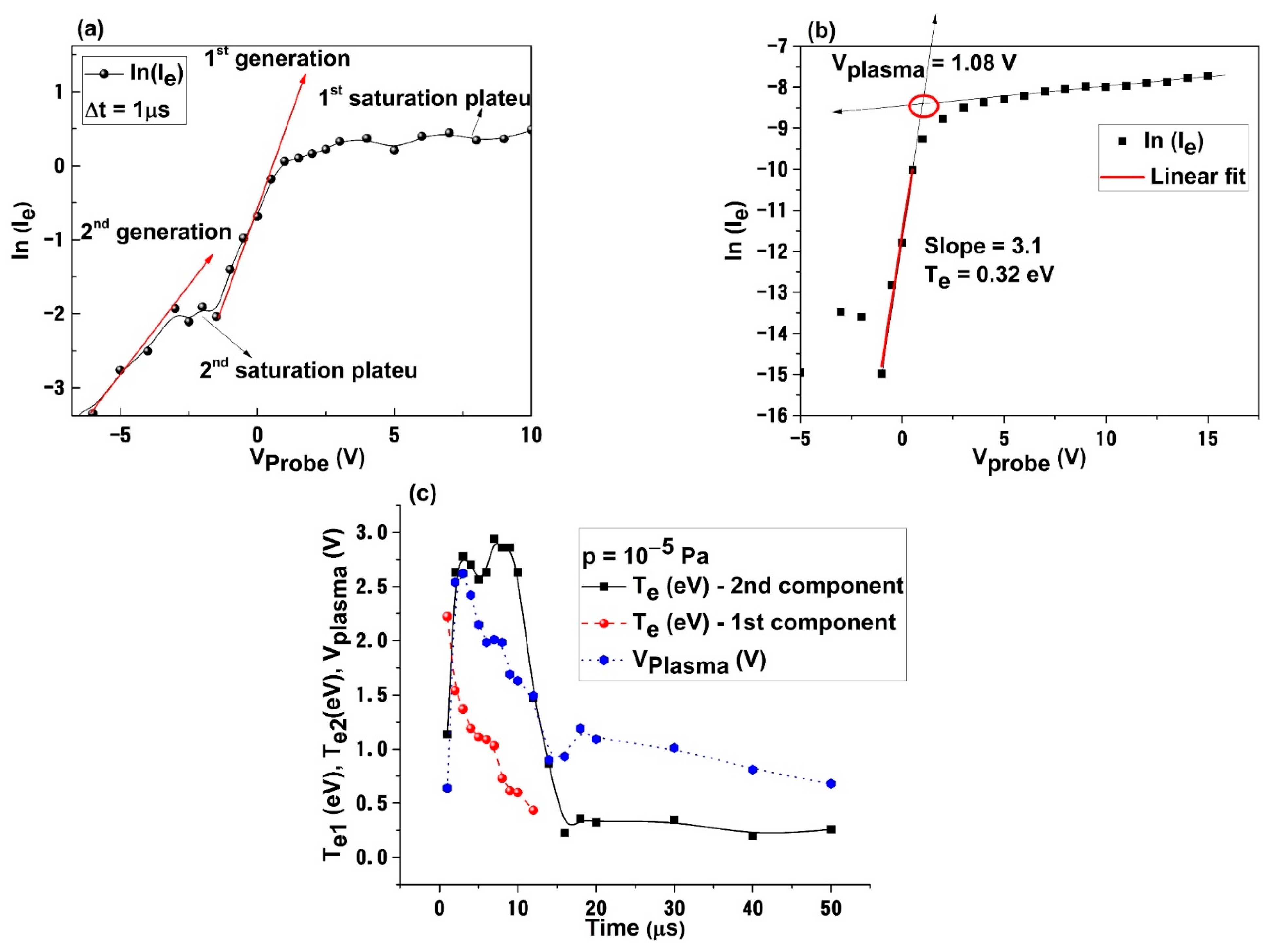
- The transition part, where the floating potential (Vf) can be found as the voltage for which the current on the probe equals zero, is followed by an exponential increase of the electronic current. The inflection point of the characteristic, where the current changes from an exponential dependence on the VProbe to a squared root one, will define the plasma potential VPlasma;
- c)
- The saturation electronic region is defined by a maximum electronic current collected by the probe. The saturation current is defined as . This region is particularly characteristic to the planar probe, whereas for other configurations the electron saturation is not reached. This is due to the increase of the space charge surface around the LP.
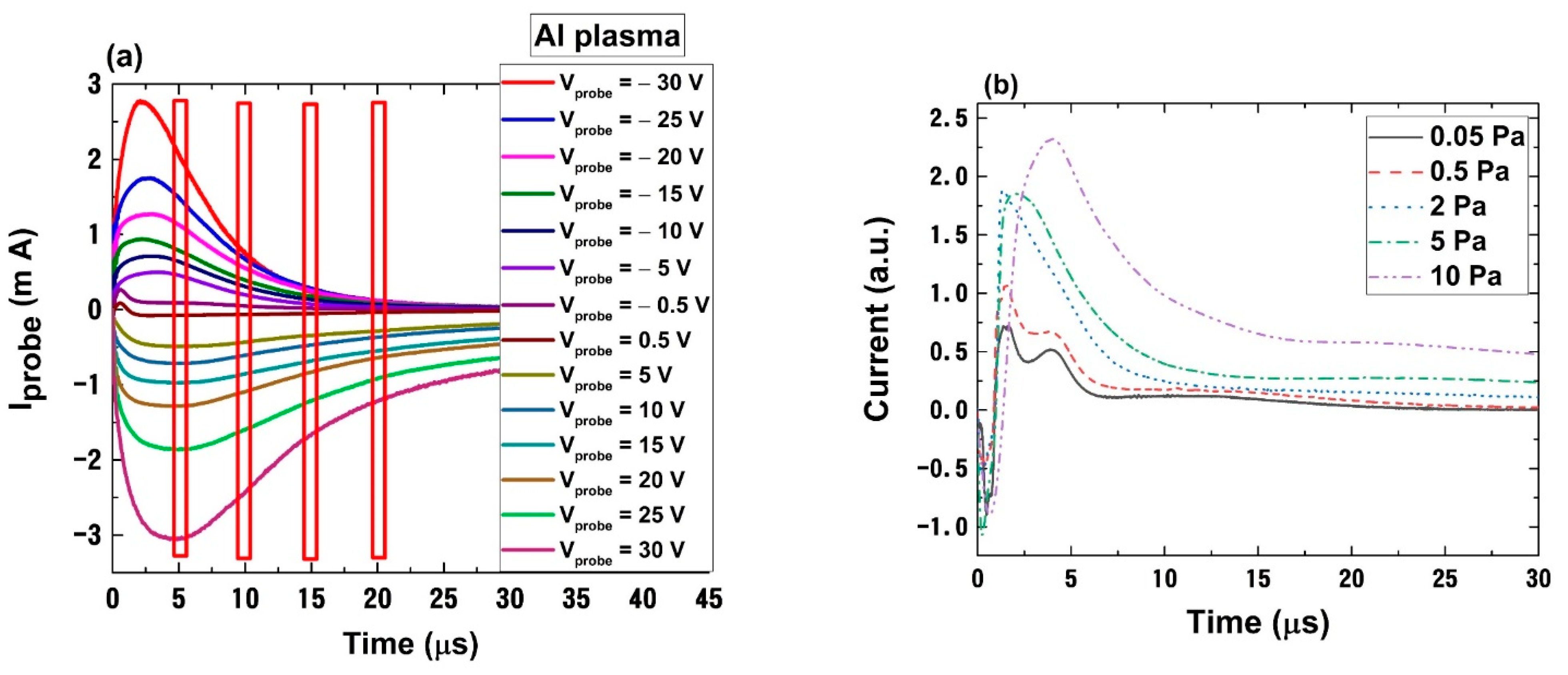
3. Time-of-Flight Analysis of Charge Fluxes in LPP
4. Limitation for Langmuir Probe Method: Perturbative Regimes and Misinterpretation of Fluctuations in the Plasma
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miller, C.J. Laser Ablation; Miller, C.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; Volume 28, ISBN 978-3-642-78722-5. [Google Scholar]
- Askar’yan, G.A.; Moroz, E.M. Pressure on evaporation of matter in a radiation beam. Sov. Phys. 1963, 13, 1638–1639. [Google Scholar]
- Honig, R.E.; Woolston, J.R. Laser-induced emission of electrons, ions, and neutral atoms from solid surfaces. Appl. Phys. Lett. 1963, 2, 138. [Google Scholar] [CrossRef]
- Lichtman, D.; Ready, J.F. Laser beam induced electron emission. Phys. Rev. Lett. 1963, 10, 342–345. [Google Scholar] [CrossRef]
- Ready, J.F. Development of plume of material vaporized by giant-pulse laser. Appl. Phys. Lett. 1963, 3, 11–13. [Google Scholar] [CrossRef]
- Howe, J.A. Observations on the maser-induced graphite. Jet. J. Chem. Phys. 1963, 39, 1362–1363. [Google Scholar] [CrossRef]
- Berkowitz, J.; Chupka, W.A. mass spectrometric study of vapor ejected from graphite and other solids by focused laser beams. J. Chem. Phys. 1964, 40, 2735–2736. [Google Scholar] [CrossRef]
- Neuman, F. Momentum transfer and cratering effects produced by giant laser pulses. Appl. Phys. Lett. 1964, 4, 167–169. [Google Scholar] [CrossRef]
- Benavides, O.; de la Cruz May, L.; Mejia, E.B.; Ruz Hernandez, J.A.; Flores Gil, A. Laser wavelength effect on nanosecond laser light reflection in ablation of metals. Laser Phys. 2016, 26, 126101. [Google Scholar] [CrossRef]
- Ehler, A.W.; Weissler, G.L. Vacuum ultraviolet radiation from plasmas formed by a laser on metal surfaces. Appl. Phys. Lett. 1966, 8, 89. [Google Scholar] [CrossRef]
- Archbold, E.; Hughes, T.P. Electron temperature in a laser-heated plasma. Nature 1964, 204, 670. [Google Scholar] [CrossRef]
- Sonnenberg, H.; Heffner, H.; Spicer, W. two-photon photoelectric effect in Cs3Sb1. Appl. Phys. Lett. 1964, 5, 95–96. [Google Scholar] [CrossRef]
- Smith, H.M.; Turner, A.F. Vacuum deposited thin films using a ruby laser. Appl. Opt. 1965, 4, 147. [Google Scholar] [CrossRef]
- Dijkkamp, D.; Venkatesan, T.; Wu, X.D.; Shaheen, S.A.; Jisrawi, N.; Min-Lee, Y.H.; McLean, W.L.; Croft, M. Preparation of Y-Ba-Cu oxide superconductor thin films using pulsed laser evaporation from high Tc bulk material. Appl. Phys. Lett. 1987, 51, 619–621. [Google Scholar] [CrossRef]
- Eason, R. Pulsed Laser Deposition of Thin Films: Applications-Led Growth of Functional Materials; John Wiley & Sons: New York, NY, USA, 2007; ISBN 0471447099. [Google Scholar]
- Itina, T. Laser Ablation From fundamentals to Applications; In Tech Open: Rijeka, Croatia, 2017; ISBN 978-953-51-3700-9. [Google Scholar]
- Loiseleur, P.; Hansen, T.N.; Larour, J.; Lunney, J.G. Time-resolved EUV spectroscopy in the early stage of laser ablation of carbon. Appl. Surf. Sci. 2002, 197–198, 164–168. [Google Scholar] [CrossRef]
- Morales, L. A laser ablation method for the synthesis of crystalline semiconductor nanowires. Science 1998, 279, 208–211. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, D.; Han, S.; Li, C.; Tang, T.; Jin, W.; Liu, X.; Lei, B.; Zhou, C. Laser ablation synthesis and electron transport studies of tin oxide nanowires. Adv. Mater. 2003, 15, 1754–1757. [Google Scholar] [CrossRef]
- Sotelo, J.G.; Bonilla-Ríos, J.; García-Escobar, F.; Gordillo, J.L. Film growth of tetragonal SnO2 on glass substrate by dip-coating technique for ethanol sensing applications. Coatings 2021, 11, 303. [Google Scholar] [CrossRef]
- Marra, A.; Rollo, G.; Cimmino, S.; Silvestre, C. Assessment on the effects of ZnO and Coated ZnO particles on iPP and PLA properties for application in food packaging. Coatings 2017, 7, 29. [Google Scholar] [CrossRef] [Green Version]
- Savu, R.; Joanni, E. Low-temperature, self-nucleated growth of indium–tin oxide nanostructures by pulsed laser deposition on amorphous substrates. Scripta Mat. 2006, 55, 979–981. [Google Scholar] [CrossRef]
- Craciun, V.; Craciun, D.; Wang, X.; Anderson, T.J.; Singh, R.K. Highly conducting indium tin oxide films grown by ultraviolet-assisted pulsed laser deposition at low temperatures. J. Optoelectron. Adv. Mat. 2003, 5, 401–408. [Google Scholar] [CrossRef]
- Eisenhawer, B.; Zhang, D.; Clavel, R.; Berger, A.; Michler, J.; Christiansen, S. Growth of doped silicon nanowires by pulsed laser deposition and their analysis by electron beam induced current imaging. Nanotechnology 2011, 22, 075706. [Google Scholar] [CrossRef]
- Pappas, D.L.; Saenger, K.L.; Cuomo, J.J.; Dreyfus, R.W. Characterization of laser vaporization plasmas generated for the deposition of diamond-like carbon. J. Appl. Phys. 1992, 72, 3966–3970. [Google Scholar] [CrossRef]
- Voevodin, A.A.; Donley, M.S. Preparation of amorphous diamond-like carbon by pulsed laser deposition: A critical review. Surf. Coat. Technol. 1996, 82, 199–213. [Google Scholar] [CrossRef]
- Voevodin, A.A.; Jones, J.G.; Zabinski, J.S.; Hultman, L. Plasma characterization during laser ablation of graphite in nitrogen for the growth of fullerene-like CNx films. J. Appl. Phys. 2002, 92, 724–735. [Google Scholar] [CrossRef]
- Voevodin, A.A.; Laube, S.J.P. In situ plasma monitoring of pulsed laser deposition of diamond-like carbon films. Surf. Coat. Technol. 1995, 76–77, 670–674. [Google Scholar] [CrossRef]
- Grigoriev, S.N.; Fominski, V.Y.; Gnedovets, A.G.; Romanov, R.I. Experimental and numerical study of the chemical composition of WSex thin films obtained by pulsed laser deposition in vacuum and in a buffer gas atmosphere. Appl. Surf. Sci. 2012, 258, 7000–7007. [Google Scholar] [CrossRef]
- Giuffreda, E.; Delle Side, D.; Nassisi, V.; Krása, J. Plasma production in carbon-based materials. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 406, 225–228. [Google Scholar] [CrossRef]
- Krása, J.; Delle Side, D.; Giuffreda, E.; Nassisi, V. Characteristics of target polarization by laser ablation. Laser Part. Beams 2015, 33, 601–605. [Google Scholar] [CrossRef] [Green Version]
- Fominski, V.; Demin, M.; Fominski, D.; Romanov, R.; Goikhman, A.; Maksimova, K. Comparative study of the structure, composition, and electrocatalytic performance of hydrogen evolution in mosx~2+δ/mo and mosx~3+δ films obtained by pulsed laser deposition. Nanomaterials 2020, 10, 201. [Google Scholar] [CrossRef] [Green Version]
- Salimian, A.; Hasnath, A.; Anguilano, L.; Onwukwe, U.; Aminishahsavarani, A.; Sachez, C.; Upadhyaya, H. Highly conductive zinc oxide based transparent conductive oxide films prepared using RF plasma sputtering under reducing atmosphere. Coatings 2020, 10, 472. [Google Scholar] [CrossRef]
- Salimian, A.; Haghpanahan, R.; Hasnath, A.; Upadhyaya, H. Optical analysis of RF sputtering plasma through colour characterization. Coatings 2019, 9, 315. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, Y.L.; Kau, L.H.; Huang, H.J.; Lee, C.C.; Fuh, Y.K.; Li, T.T. In situ plasma monitoring of PECVD nc-Si:H Films and the influence of dilution ratio on structural evolution. Coatings 2018, 8, 238. [Google Scholar] [CrossRef] [Green Version]
- Song, J.B.; Kim, J.T.; Oh, S.G.; Yun, J.Y. Contamination particles and plasma etching behavior of atmospheric plasma sprayed Y2O3 and YF3 coatings under NF3 plasma. Coatings 2019, 9, 102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Mack, D.E.; Mauer, G.; Vaßen, R. Laser cladding of embedded sensors for thermal barrier coating applications. Coatings 2018, 8, 176. [Google Scholar] [CrossRef] [Green Version]
- Zavestovskaya, I.N.; Glazov, O.A.; Demchenko, N.N. Threshold characteristics of ultrashort laser pulse ablation of metals. Proc. 3rd Int. Conf. Front. Plasma Phys. Technol. 2008, 3, 10–18. [Google Scholar]
- Hermann, J.; Mercadier, L.; Axente, E.; Noël, S. Properties of plasmas produced by short double pulse laser ablation of metals. J. Phys. Conf. Ser. 2012, 399, 012006. [Google Scholar] [CrossRef]
- Williams, G.O.; O’Connor, G.M.; Mannion, P.T.; Glynn, T.J. Langmuir probe investigation of surface contamination effects on metals during femtosecond laser ablation. Appl. Surf. Sci. 2008, 254, 5921–5926. [Google Scholar] [CrossRef]
- Geohegan, D.B.; Puretzky, A.A. Dynamics of laser ablation plume penetration through low pressure background gases. Appl. Phys. Lett. 1995, 67, 197–199. [Google Scholar] [CrossRef] [Green Version]
- Geohegan, D.B.; Puretzky, A.A. Laser ablation plume thermalization dynamics in background gases: Combined imaging, optical absorption and emission spectroscopy, and ion probe measurements. Appl. Surf. Sci. 1996, 96–98, 131–138. [Google Scholar] [CrossRef] [Green Version]
- Leboeuf, J.N.; Chen, K.R.; Donato, J.M.; Geohegan, D.B.; Liu, C.L.; Puretzky, A.A.; Wood, R.F. Modeling of dynamical processes in laser ablation. Appl. Surf. Sci. 1996, 96–98, 14–23. [Google Scholar] [CrossRef] [Green Version]
- Harilal, S.S.; Bindhu, C.V.; Tillack, M.S.; Najmabadi, F.; Gaeris, A.C. Plume splitting and sharpening in laser-produced aluminium plasma. J. Phys. D Appl. Phys. 2002, 35, 2935–2938. [Google Scholar] [CrossRef] [Green Version]
- Harilal, S.S.; Bindhu, C.V.; Tillack, M.S.; Najmabadi, F.; Gaeris, A.C. Internal structure and expansion dynamics of laser ablation plumes into ambient gases. J. Appl. Phys. 2003, 93, 2380–2388. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Li, X.; Wei, W.; Jia, S.; Qiu, A. Understanding plume splitting of laser ablated plasma: A view from ion distribution dynamics. Phys. Plasmas 2013, 20, 113512. [Google Scholar] [CrossRef]
- Amoruso, S.; Toftmann, B.; Schou, J. Broadening and attenuation of UV laser ablation plumes in background gases. Appl. Surf. Sci. 2005, 248, 323–328. [Google Scholar] [CrossRef]
- Yoo, J.H.; Jeong, S.H.; Mao, X.L.; Greif, R.; Russo, R.E. Evidence for phase-explosion and generation of large particles during high power nanosecond laser ablation of silicon. Appl. Phys. Lett. 2000, 76, 783. [Google Scholar] [CrossRef]
- Lahm, S.H. Unified theory of langmuir probe in a collisionless plasma. Phys. Fluids 1965, 8, 73. [Google Scholar] [CrossRef]
- Koopman, D.W. Langmuir probe and microwave measurements of the properties of streaming plasmas generated by focused laser pulses. Phys. Fluids 1971, 14, 1707. [Google Scholar] [CrossRef]
- Merlino, R.L. Understanding Langmuir probe current-voltage characteristics. Am. J. Phys. 2007, 75, 1078. [Google Scholar] [CrossRef] [Green Version]
- Lunney, J.G.; Doggett, B.; Kaufman, Y. Langmuir probe diagnosis of laser ablation plasmas. J. Phys. Conf. Ser. 2007, 59, 470–474. [Google Scholar] [CrossRef]
- Donnelly, T.; Lunney, J.G.; Amoruso, S.; Bruzzese, R.; Wang, X.; Ni, X. Dynamics of the plumes produced by ultrafast laser ablation of metals. J. Appl. Phys. 2010, 108, 043309. [Google Scholar] [CrossRef] [Green Version]
- Ovsyannikov, A.A.; Zhukov, M.F. Plasma Diagnostics; Cambridge International Science Publishing: Cambridge, UK, 2000. [Google Scholar]
- Chen, F.F. Introduction to Plasma Physics; Springer: Boston, MA, USA, 1974; pp. 1–16. [Google Scholar]
- Doggett, B.; Lunney, J.G. Langmuir probe characterization of laser ablation plasmas. J. Appl. Phys. 2009, 105, 033306. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Gurlui, S.; Bulai, G.; Nica, P.; Agop, M.; Focsa, C. Langmuir probe investigation of transient plasmas generated by femtosecond laser ablation of several metals: Influence of the target physical properties on the plume dynamics. Appl. Surf. Sci. 2017, 417, 108–118. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Chertopalov, S.; Craciun, V.; Novotný, M.; Lancok, J. Investigation of laser-produced plasma multistructuring by floating probe measurements and optical emission spectroscopy. Plasma Process. Polym. 2020, 17, 2000136. [Google Scholar] [CrossRef]
- Focsa, C.; Gurlui, S.; Nica, P.; Agop, M.; Ziskind, M. Plume splitting and oscillatory behavior in transient plasmas generated by high-fluence laser ablation in vacuum. Appl. Surf. Sci. 2017, 424, 299–309. [Google Scholar] [CrossRef]
- Nica, P.; Agop, M.; Gurlui, S.; Bejinariu, C.; Focsa, C. Characterization of aluminum laser produced plasma by target current measurements. Jpn. J. Appl. Phys. 2012, 51, 106102. [Google Scholar] [CrossRef]
- Anoop, K.K.; Polek, M.P.; Bruzzese, R.; Amoruso, S.; Harilal, S.S. Multidiagnostic analysis of ion dynamics in ultrafast laser ablation of metals over a large fluence range. J. Appl. Phys. 2015, 117, 083108. [Google Scholar] [CrossRef] [Green Version]
- Donnelly, T.; Lunney, J.G.; Amoruso, S.; Bruzzese, R.; Wang, X.; Ni, X. Angular distributions of plume components in ultrafast laser ablation of metal targets. Appl. Phys. A Mater. Sci. Process. 2010, 100, 569–574. [Google Scholar] [CrossRef]
- Amoruso, S.; Schou, J.; Lunney, J.G.; Phipps, C. Ablation plume dynamics in a background gas. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2010; pp. 665–676. [Google Scholar]
- Irimiciuc, S.; Boidin, R.; Bulai, G.; Gurlui, S.; Nemec, P.; Nazabal, V.; Focsa, C. Laser ablation of (GeSe2)100−x(Sb2Se3)x chalcogenide glasses: Influence of the target composition on the plasma plume dynamics. Appl. Surf. Sci. 2017, 418, 594–600. [Google Scholar] [CrossRef]
- Caridi, F.; Torrisi, L.; Margarone, D.; Borrielli, A. Investigations on low temperature laser-generated plasmas. Laser Part. Beams 2008, 26, 265–271. [Google Scholar] [CrossRef]
- Krása, J.; Lorusso, A.; Doria, D.; Belloni, F.; Nassisi, V.; Rohlena, K. Time-of-flight profile of multiply-charged ion currents produced by a pulse laser. Plasma Phys. Control. Fusion 2005, 47, 1339–1349. [Google Scholar] [CrossRef]
- Gurlui, S.; Agop, M.; Nica, P.; Ziskind, M.; Focsa, C. Experimental and theoretical investigations of a laser-produced aluminum plasma. Phys. Rev. E 2008, 78, 026405. [Google Scholar] [CrossRef]
- Focsa, C.; Nemec, P.; Ziskind, M.; Ursu, C.; Gurlui, S.; Nazabal, V. Laser ablation of AsxSe100−x chalcogenide glasses: Plume investigations. Appl. Surf. Sci. 2009, 255, 5307–5311. [Google Scholar] [CrossRef]
- Ursu, C.; Gurlui, S.; Focsa, C.; Popa, G. Space and time-resolved optical diagnosis for the study of laser ablation plasma dynamics. Nucl. Instruments Methods Phys. Res. Sect. B Beam Interact. with Mater. Atoms 2009, 267, 446–450. [Google Scholar]
- Kelly, R.; Dreyfus, R.W. On the effect of Knudsen-layer formation on studies of vaporization, sputtering, and desorption. Surf. Sci. 1988, 198, 263–276. [Google Scholar] [CrossRef]
- Mihesan, C.; Lebrun, N.; Ziskind, M.; Chazallon, B.; Focsa, C.; Destombes, J.L. IR laser resonant desorption of formaldehyde-H2O ices: Hydrated cluster formation and velocity distribution. Surf. Sci. 2004, 566–568, 650–658. [Google Scholar] [CrossRef]
- Zimmermann, F.M.; Ho, W. State resolved studies of photochemical dynamics at surfaces. Surf. Sci. Rep. 1995, 22, 127–247. [Google Scholar] [CrossRef]
- Dogar, A.H.; Ilyas, B.; Ullah, S.; Nadeem, A.; Qayyum, A. Langmuir probe measurements of Nd-YAG laser-produced copper plasmas. IEEE Trans. Plasma Sci. 2011, 39, 897–900. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Mihaila, I.; Agop, M. Experimental and theoretical aspects of a laser produced plasma. Phys. Plasmas 2014, 21, 093509. [Google Scholar] [CrossRef]
- Cutroneo, M.; Mackova, A.; Malinsky, P.; Matousek, J.; Torrisi, L.; Ullschmied, J. High-intensity laser for Ta and Ag implantation into different substrates for plasma diagnostics. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2015, 354, 56–59. [Google Scholar] [CrossRef]
- Láska, L.; Krása, J.; Pfeifer, M.; Rohlena, K.; Gammino, S.; Torrisi, L.; Andò, L.; Ciavola, G. Generation of intense streams of metallic ions with a charge state up to 10+ in a laser ion source. Rev. Sci. Instrum. 2004, 75, 1575–1578. [Google Scholar] [CrossRef]
- Láska, L.; Badziak, J.; Boody, F.P.; Gammino, S.; Jungwirth, K.; Krása, J.; Pfeifer, M.; Rohlena, K.; Ullschmied, J.; Parys, P. Laser production of highly charged ions. Braz. J. Phys. 2004, 34, 1615–1620. [Google Scholar] [CrossRef]
- Bulgakov, A.; Bulgakova, N.M. Dynamics of laser-induced plume expansion into an ambient gas during film deposition. J. Phys. D Appl. Phys. 1999, 28, 1710–1718. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Hodoroaba, B.C.; Bulai, G.; Gurlui, S.; Craciun, V. Multiple structure formation and molecule dynamics in transient plasmas generated by laser ablation of graphite. Spectrochim. Acta Part B At. Spectrosc. 2020, 165, 105774. [Google Scholar] [CrossRef]
- Mascali, D.; Gambino, N.; Miracoli, R.; Gammino, S.; Torrisi, L.; Maimone, F.; Tumino, L. Plasma parameters measurements by means of Langmuir probe. Radiat. Eff. Defects Solids 2008, 163, 471–478. [Google Scholar] [CrossRef]
- Dimitriu, D.G.; Irimiciuc, S.A.; Popescu, S.; Agop, M.; Ionita, C.; Schrittwieser, R.W. On the interaction between two fireballs in low-temperature plasma. Phys. Plasmas 2015, 22, 113511. [Google Scholar] [CrossRef]
- Borowitz, J.L.; Eliezer, S.; Gazit, Y.; Givon, M.; Jackel, S.; Ludmirsky, A.; Salzmann, D.; Yarkoni, E.; Zigler, A.; Arad, B. Temporally resolved target potential measurements in laser-target interactions. J. Phys. D Appl. Phys. 1987, 20, 210–214. [Google Scholar] [CrossRef]
- Ludmirsky, A.; Givon, M.; Eliezer, S.; Gazit, Y.; Jackel, S.; Krumbein, A.; Szichman, H. Electro-optical measurements of high potentials in laser produced plasmas with fast time resolution. Laser Part. Beams 1984, 2, 245–250. [Google Scholar] [CrossRef]
- Ludmirsky, A.; Eliezer, S.; Arad, B.; Borowitz, A.; Gazit, Y.; Jackel, S.; Krumbein, A.D.; Salzmann, D.; Szichman, H. Experimental Evidence of Charge Separation (Double Layer) in Laser-Produced Plasmas. IEEE Trans. Plasma Sci. 1985, 13, 132–134. [Google Scholar] [CrossRef]
- Pearlman, J.S.; Dahlbacka, G.H. Charge separation and target voltages in laser-produced plasmas. Appl. Phys. Lett. 1977, 31, 414–417. [Google Scholar] [CrossRef]
- Eliezer, S.; Hora, H. Surface waves in laser-produced plasma double layers. Fusion Technol. 1989, 17, 290–294. [Google Scholar] [CrossRef]
- Nica, P.; Agop, M.; Gurlui, S.; Focsa, C. Oscillatory Langmuir probe ion current in laser-produced plasma expansion. EPL (Europhys. Lett.) 2010, 89, 65001. [Google Scholar] [CrossRef]
- Gurlui, S.; Sanduloviciu, M.; Mihesan, C.; Ziskind, M.; Focsa, C. Periodic phenomena in laser-ablation plasma plumes: A self-organization scenario. In AIP Conference Proceedings; American Institute of Physics: Melville, NY, USA, 2009; Volume 821, pp. 279–282. [Google Scholar]
- Irimiciuc, S.A.; Agop, M.; Nica, P.; Gurlui, S.; Mihaileanu, D.; Toma, Ş.; Focşa, C. Dispersive effects in laser ablation plasmas. Jpn. J. Appl. Phys. 2014, 53, 116202. [Google Scholar] [CrossRef]
- Nica, P.; Vizureanu, P.; Agop, M.; Gurlui, S.; Focsa, C.; Forna, N.; Ioannou, P.D.; Borsos, Z. Experimental and theoretical aspects of aluminum expanding laser plasma. Jpn. J. Appl. Phys. 2009, 48, 066001. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irimiciuc, S.A.; Chertopalov, S.; Lancok, J.; Craciun, V. Langmuir Probe Technique for Plasma Characterization during Pulsed Laser Deposition Process. Coatings 2021, 11, 762. https://doi.org/10.3390/coatings11070762
Irimiciuc SA, Chertopalov S, Lancok J, Craciun V. Langmuir Probe Technique for Plasma Characterization during Pulsed Laser Deposition Process. Coatings. 2021; 11(7):762. https://doi.org/10.3390/coatings11070762
Chicago/Turabian StyleIrimiciuc, Stefan Andrei, Sergii Chertopalov, Jan Lancok, and Valentin Craciun. 2021. "Langmuir Probe Technique for Plasma Characterization during Pulsed Laser Deposition Process" Coatings 11, no. 7: 762. https://doi.org/10.3390/coatings11070762
APA StyleIrimiciuc, S. A., Chertopalov, S., Lancok, J., & Craciun, V. (2021). Langmuir Probe Technique for Plasma Characterization during Pulsed Laser Deposition Process. Coatings, 11(7), 762. https://doi.org/10.3390/coatings11070762







