Multi-Objective Optimization of MIG Welding and Preheat Parameters for 6061-T6 Al Alloy T-Joints Using Artificial Neural Networks Based on FEM
Abstract
:1. Introduction
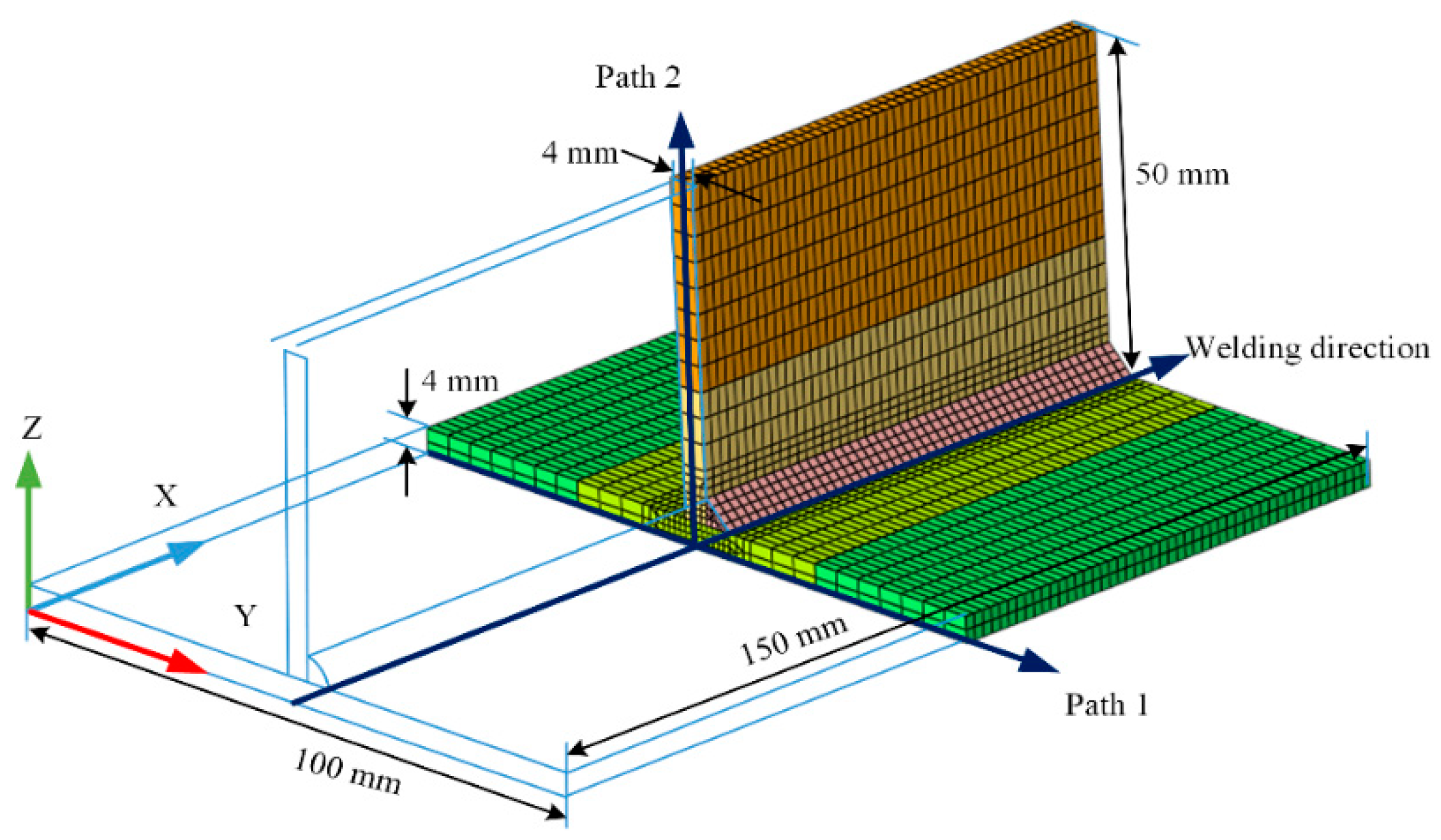
2. Finite Element Simulation
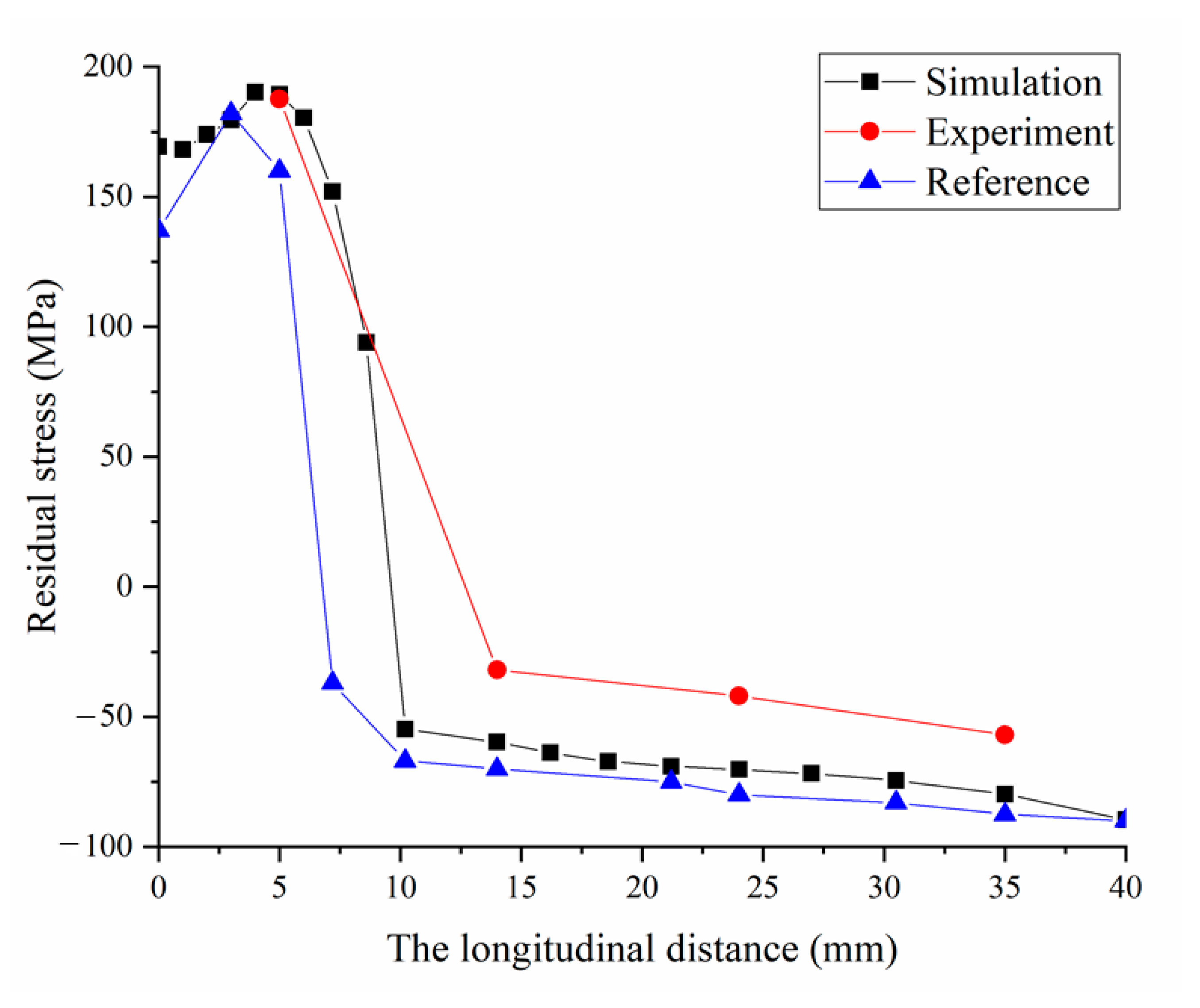
3. Experiments and Finite Element Model Validation
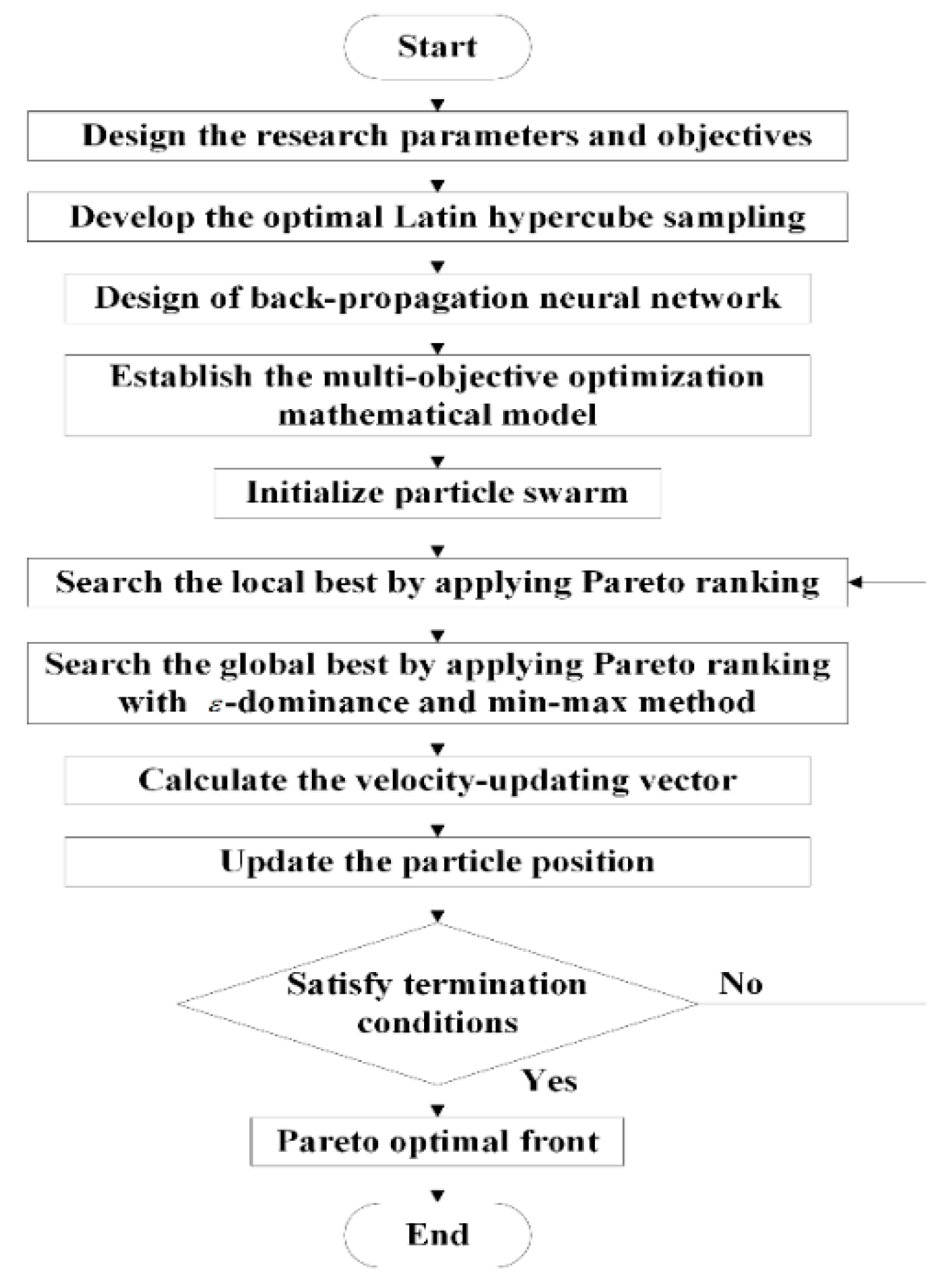
4. Multi-Objective Optimization Problem
4.1. Selection of the Process Parameter Combination Based on OLHS
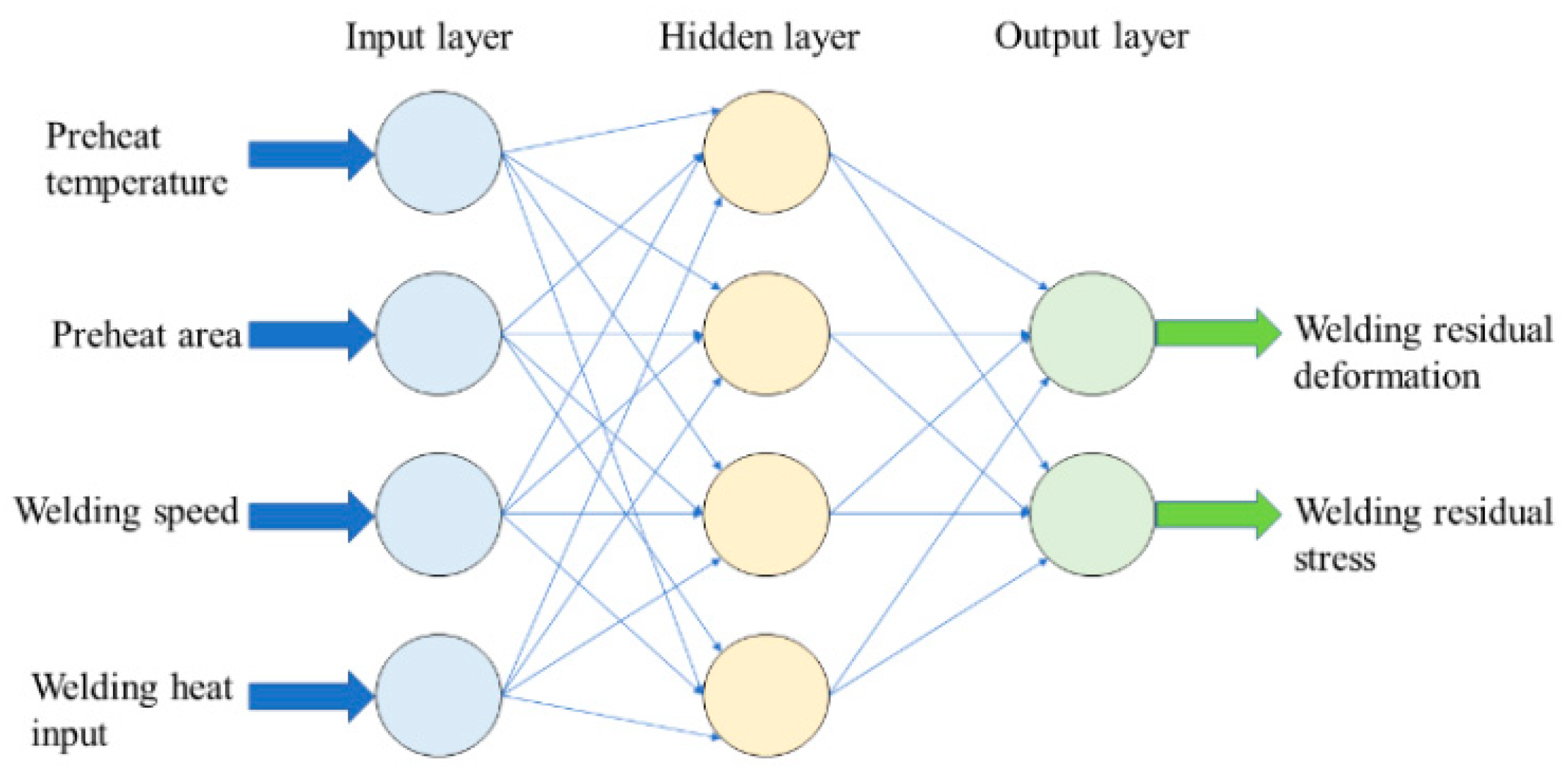
4.2. Design of a Back-Propagation Neural Network
4.3. Multi-Objective Particle Swarm Optimization Algorithm
4.3.1. Definition of Optimization
4.3.2. The Pareto Front
5. Results and Discussion
5.1. Results of OLHS Table
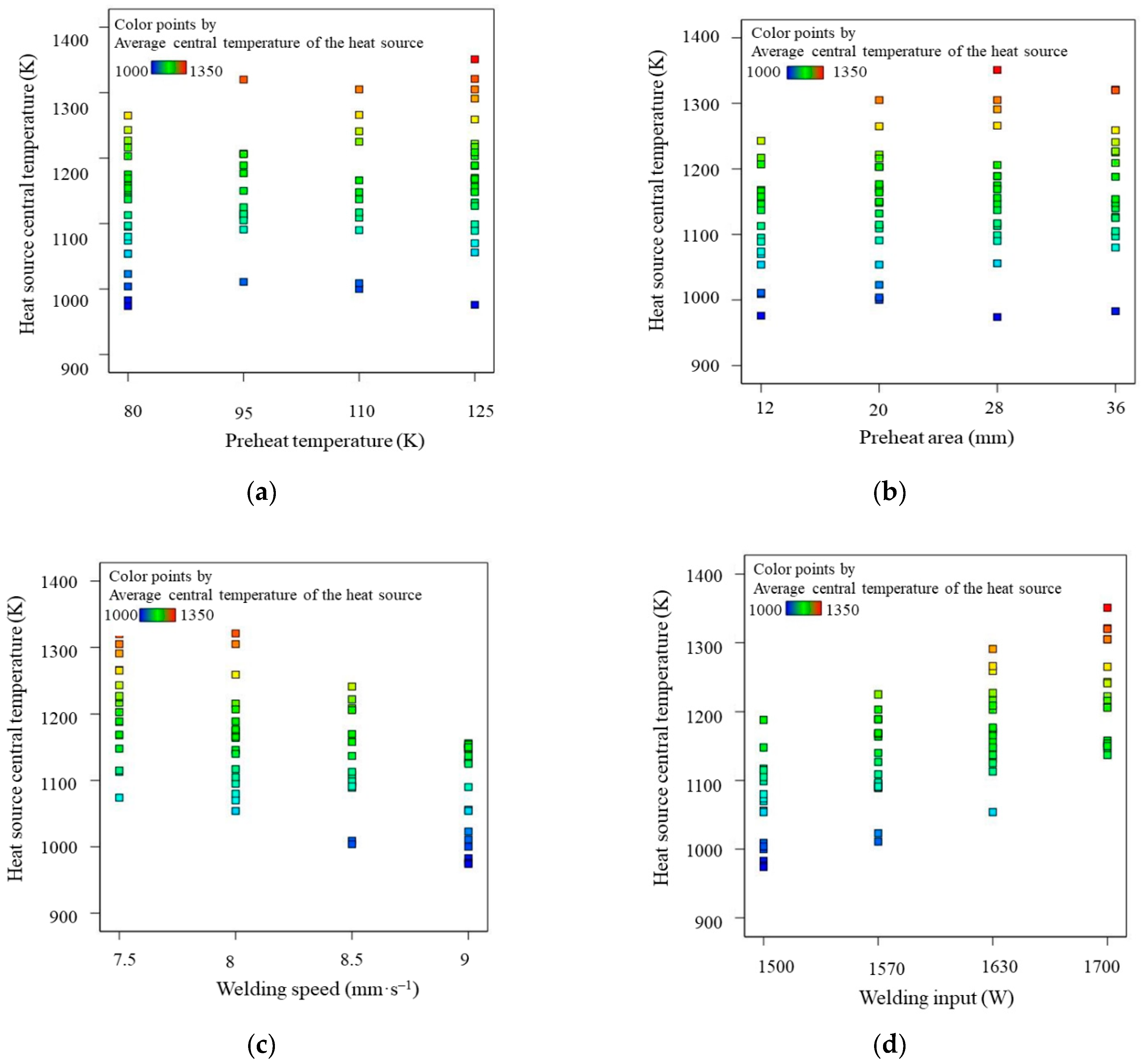
5.2. Influence of Welding Parameters
5.2.1. ANOVA for Heat Source Central Temperature, Welding Residual Deformation and Welding Residual Stress
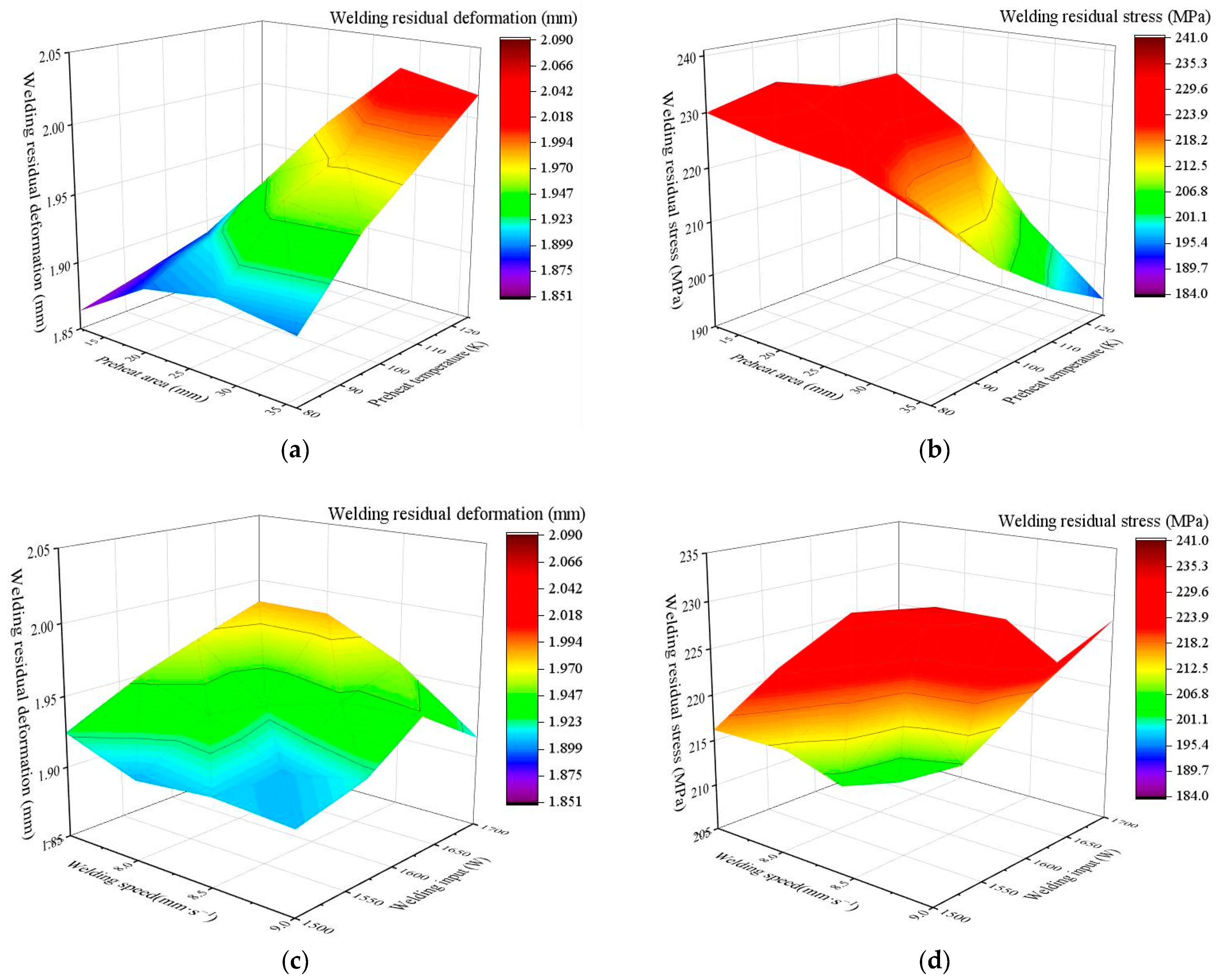
5.2.2. Discussion of Welding Residual Deformation and Stress
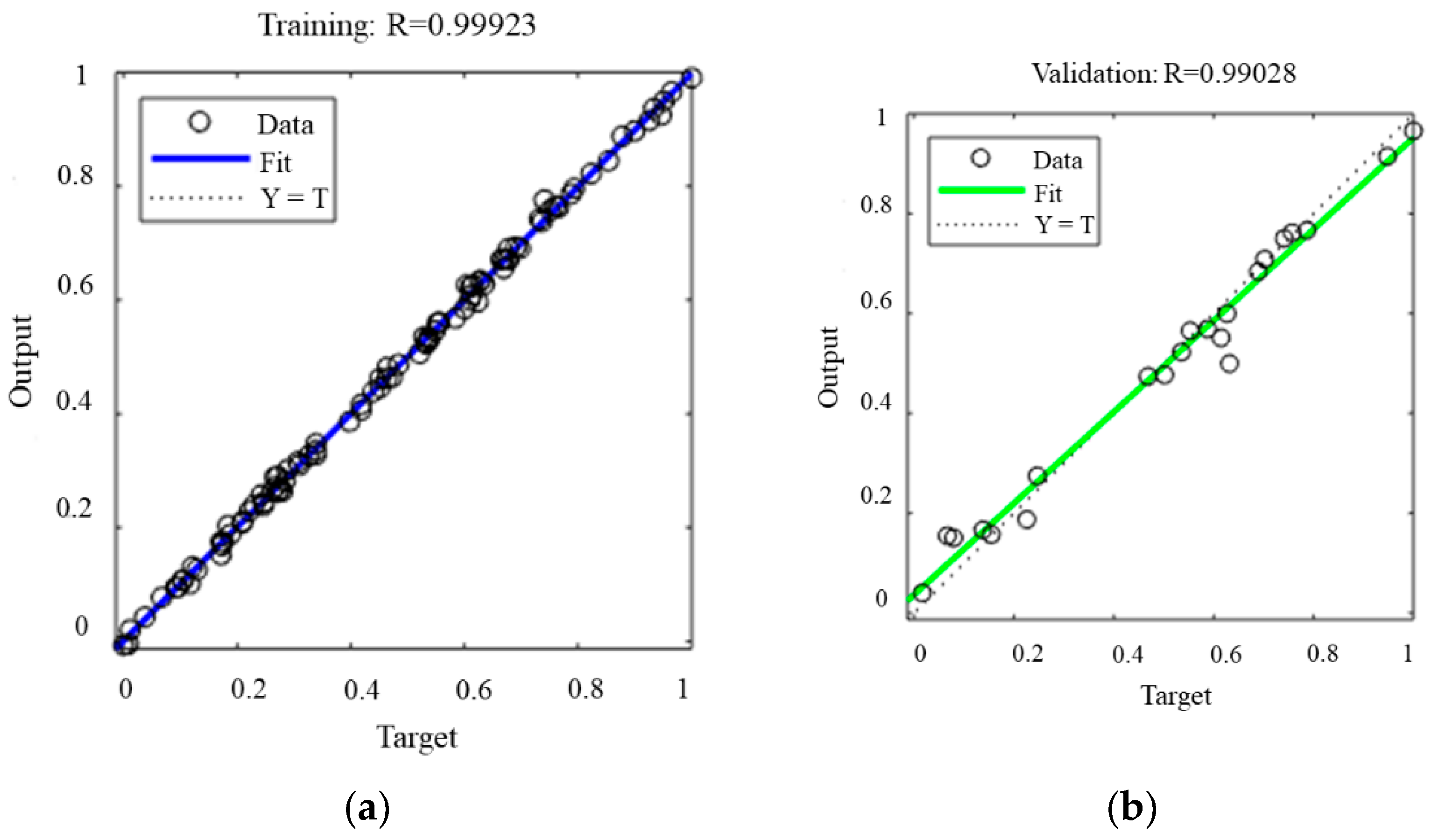
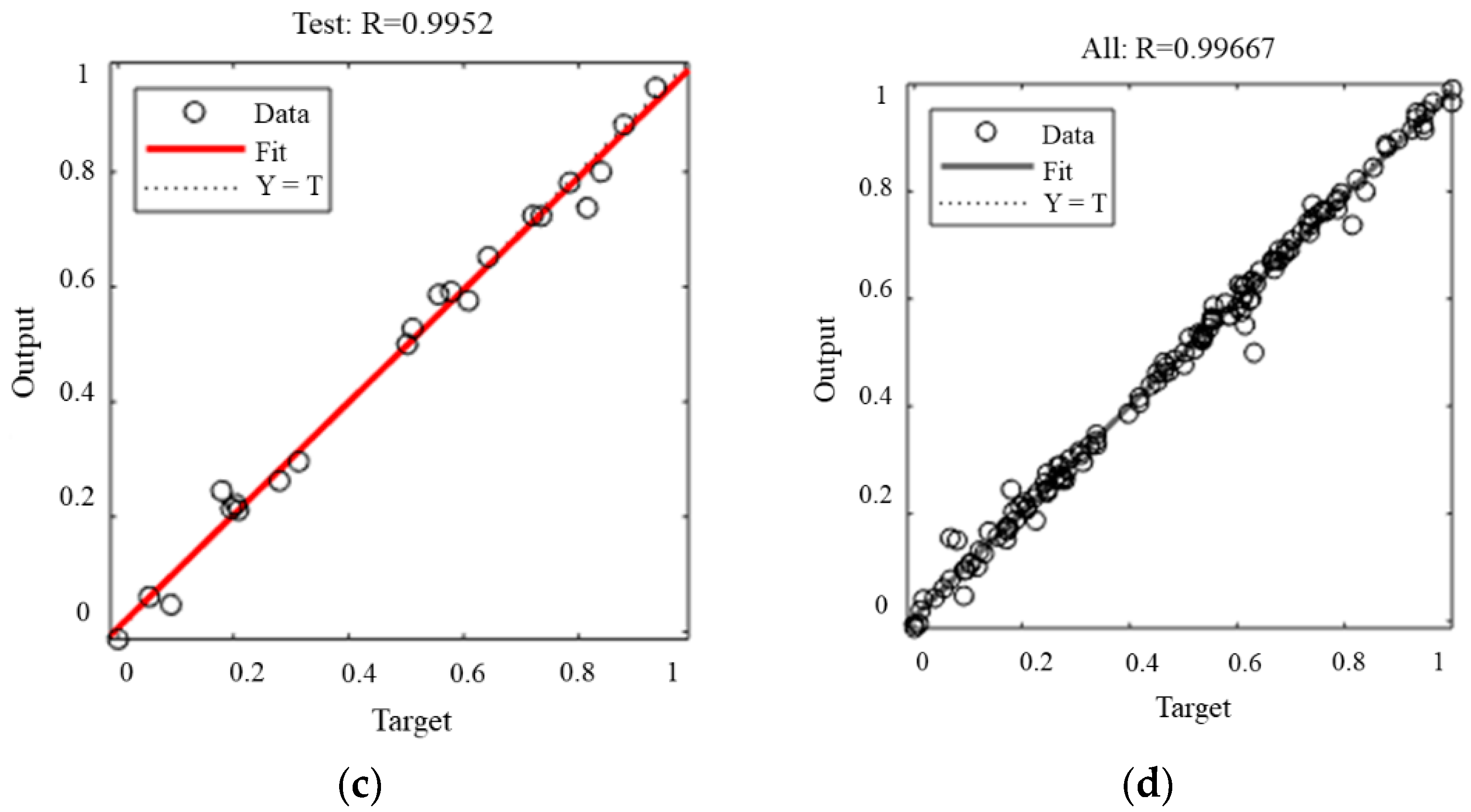
5.3. Performance of BPNN
5.4. Optimal Values of Design Parameters for Minimizing Objective Functions
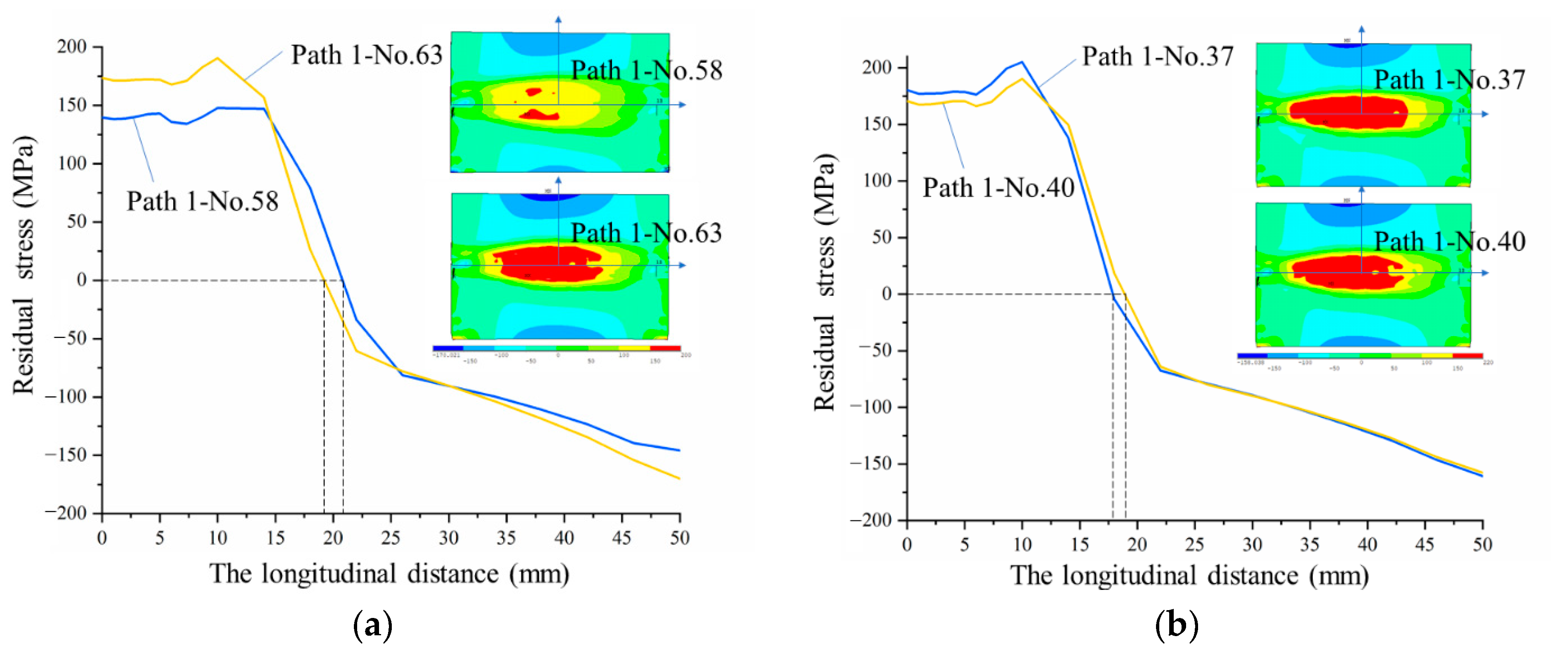
5.5. Simulation Experiments Confirmation
6. Conclusions
- (1)
- The thermal elastoplastic method was used to simulate the residual deformation and stress of 6061-T6 aluminum alloy T-joint in ANSYS. The simulation results are basically consistent with the measured data, and the error is within 5%.
- (2)
- The OLHS and ANOVA method were adopted to sample with uniformity and find the influence degree. The results showed that preheat temperature and welding speed had the greatest effect on the minimization of welding residual deformation and stress, respectively, followed by the preheat area.
- (3)
- Preheating can reduce the temperature gradient and cooling rate after welding and reduced the welding stress to prevent the formation of cracks. However, the higher the preheat temperature is, the larger the residual deformation is. Furthermore, the simulation results showed that preheating can reduce the longitudinal residual stress near the welding beam. However, the wider preheat area can increase the area of tensile stress, which is not good for the fatigue strength of parts. In addition, the faster the welding speed is, the higher the welding residual stress is, but the wider the distribution of welding residual compressive stress is.
- (4)
- Artificial neural network-based MOPSO was used to optimize the effective parameters to minimize welding deformation and stress. The BPNN was selected to predict the value of the objective functions. The R values were 0.990 and 0.995, respectively, indicating that the prediction model had a good prediction effect.
- (5)
- Welding residual deformation and stress are at the minimum at the same time, when the welding parameters are selected as preheating temperature 85 °C and preheating area 12 mm, welding speed 8.8 mm/s and heat input 1535 W, respectively. The Pareto front was obtained by using the MOPSO algorithm with ε-dominance. The error between the FE results and the Pareto optimal compromise solutions is less than 12.5%. The designers can select one solution from many Pareto solutions according to practical needs.
- (6)
- Further, in order to further verify the reliability of the prediction, we will test and verify the welding results in the test group in the future, and obtain more useful conclusions by comparing the change rules of welding heat curve, residual deformation and stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Miao, B. Development trend and prospect of key technologies for next generation high speed trains. Electri. Drive Locomot. 2018, 1, 1–12. [Google Scholar]
- Yang, S.; Zhang, D.; Tuo, W.; Yu, Z. Microstructures and properties of extruded Al-0.6Mg-0.6Si aluminium alloy for high-speed vehicle. Procedia Eng. 2014, 81, 598–603. [Google Scholar] [CrossRef] [Green Version]
- Çam, G.; İpekoğlu, G. Recent developments in joining of aluminum alloys. Int. J. Adv. Manuf. Technol. 2017, 91, 1851–1866. [Google Scholar] [CrossRef]
- Rozumek, D.; Lewandowski, J.; Lesiuk, G.; Correia, J. The influence of heat treatment on the behavior of fatigue crack growth in welded joints made of S355 under bending loading. Int. J. Fatigue 2020, 131, 105328. [Google Scholar] [CrossRef]
- Yi, J.; Zhang, J.; Cao, S.; Guo, P. Effect of welding sequence on residual stress and deformation of 6061-T6 aluminium alloy automobile component. Trans. Nonferrous Met. Soc. Chin. 2019, 29, 287–295. [Google Scholar] [CrossRef]
- Shao, Q.; Xu, T.; Yoshino, T.; Song, N. Multi-objective optimization of gas metal arc welding parameters and sequences for low-carbon steel (Q345D) T joints. J. Iron Steel Res. 2017, 24, 544–555. [Google Scholar] [CrossRef]
- Maneiah, D.; Debashis, M.; Prahlada, R.K.; Brahma, R.K. Process parameters optimization of friction stir welding for optimum tensile strength in Al 6061-T6 alloy butt welded joints. Mate. Today 2020, 27, 904–908. [Google Scholar] [CrossRef]
- Yang, X.; Chen, H.; Zhu, Z.; Cai, C.; Zhang, C. Effect of shielding gas flow on welding process of laser-arc hybrid welding and MIG welding. J. Manuf. Process. 2019, 38, 530–542. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, R. Optimization of process parameters of metal inert gas welding with preheating on AISI 1018 mild steel using grey based Taguchi method. Measurement 2019, 148, 106924. [Google Scholar] [CrossRef]
- Matthew, R.K.; Steven, R.S.; Daniel, C.A.; Jeffrey, F.; Ryan, H. Experimental investigation of linear friction welding of AISI 1020 steel with pre-heating. J. Manuf. Processes 2019, 39, 26–39. [Google Scholar]
- Aalami-Aleagha, M.E.; Foroutan, M.; Feli, S.; Nikabadi, S. Analysis preheat effect on thermal cycle and residual stress in a welded connection by FE simulation. Int. J. Pres. Ves. Pip. 2014, 114, 69–75. [Google Scholar] [CrossRef]
- Khoshroyan, A.; Darvazi, A.R. Effects of welding parameters and welding sequence on residual stress and distortion in Al6061-T6 aluminum alloy for T-shaped welded joint. Trans. Nonferrous Met. Soc. Chin. 2020, 30, 76–89. [Google Scholar] [CrossRef]
- Ashu, G.; Madhav, R.; Anirban, B. Metallurgical behavior and variation of vibro-acoustic signal during preheating assisted friction stir welding between AA6061-T6 and AA7075-T651 alloys. Trans. Nonferrous Met. Soc. Chin. 2019, 29, 1610–1620. [Google Scholar]
- Zhu, C.; Tang, X.; He, Y.; Lu, F.; Cui, H. Effect of preheating on the defects and microstructure in NG-GMA welding of 5083 Al-alloy. J. Mate. Process. Technol. 2018, 251, 214–224. [Google Scholar] [CrossRef]
- Asadi, P.; Alimohammadi, S.; Kohantorabi, O.; Fazli, A.; Akbari, M. Effects of material type, preheating and weld pass number on residual stress of welded steel pipes by multi-pass TIG welding. Therm. Sci. Eng. Prog. 2020, 16, 100462. [Google Scholar] [CrossRef]
- Fallahi, A.; Jafarpur, A.; Nami, M.R. Analysis of welding conditions based on induced thermal irreversibilities in welded structures: Cases of welding sequences and preheating treatment. Sci. Iran 2011, 18, 398–406. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Wang, M.; Wang, J.; Chen, X.; P, G.E. Effect of pre-heating on residual stress in aluminum alloy joint for healthcare applications. Electr. Weld. Mach. 2015, 45, 54–58. [Google Scholar]
- Liu, B. The Research of Synchronizing Process of Preheating and Welding for High Strength Steel. Master’s Thesis, Hehai university, Jiangsu, China, June 2016. [Google Scholar]
- Wu, C.; Kim, J.W. Numerical prediction of deformation in thin-plate welded joints using equivalent thermal strain method. Thin Walled Struct. 2020, 157, 107033. [Google Scholar] [CrossRef]
- Chang, Y.; Yue, J.; Guo, R.; Liu, W.; Li, L. Penetration quality prediction of asymmetrical fillet root welding based on optimized BP neural network. J. Manuf. Process. 2020, 50, 247–254. [Google Scholar] [CrossRef]
- Kshirsagar, R.; Jones, S.; Lawrence, J.; Kanfoud, J. Effect of the Addition of Nitrogen through Shielding Gas on TIG Welds Made Homogenously and Heterogeneously on 300 Series Austenitic Stainless Steels. J. Manuf. Mater. Process. 2021, 5, 72. [Google Scholar]
- Bunaziv, I.; Akselsen, O.M.; Frostevarg, J.; Kaplan, A.F.H. Deep penetration fiber laser-arc hybrid welding of thick HSLA steel. J. Mater. Process. Technol. 2018, 256, 216–228. [Google Scholar] [CrossRef]
- Moradi, M.; Moghadam, M.K.; Shamsborhan, V.; Beiranvand, Z.M.; Bodaghi, M. Simulation, statistical modeling, and optimization of CO2 laser cutting process of polycarbonate sheets. Optik 2021, 225, 164932. [Google Scholar] [CrossRef]
- Bai, R.; Guo, Z.; Lei, Z.; Wu, W.; Yan, C. Hybrid inversion method and sensitivity analysis of inherent deformations of welded joints. Adv. Eng. Software 2019, 131, 186–195. [Google Scholar] [CrossRef]
- Huang, H.; Wang, J.; Li, L.; Ma, N. Prediction of laser welding induced deformation in thin sheets by efficient numerical modeling. J. Mater. Process. Technol. 2016, 227, 117–128. [Google Scholar] [CrossRef]
- Zhang, W.; Fu, H.; Fan, J.; Li, R.; Xu, H.; Liu, F.; Qi, B. Influence of multi-beam preheating temperature and stress on the buckling distortion in electron beam welding. Mater. Design 2018, 139, 439–446. [Google Scholar] [CrossRef]
- Yi, J.; Cao, S.; Li, L.; Guo, P.; Liu, K. Effect of welding current on morphology and microstructure of Al alloy T-joint in double-pulsed MIG welding. Trans. Nonferrous Met. Soc. Chin. 2015, 25, 3204–3211. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. New finite element model for welding heat sources. Metall. Mater. Trans. B 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Xu, T.; Liu, G.; Ge, H.; Zhang, W.; Yu, Z. Research for Modeling Heat Source of Dynamic Welding with Local Coordinate Curve Path. J.-L. Univ. (Eng. Tech. Ed.) 2014, 44, 1704–1709. [Google Scholar]
- Shao, Q.; Xu, T.; Yoshino, T.; Song, N.; Yu, Z. Optimization of the welding sequence and direction for the side beam of a bogie frame based on the discrete particle swarm algorithm. Proc. Inst. Mech. Eng. B-J. Eng. 2018, 232, 1423–1435. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 5th ed.; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Mostaghim, S.; Teich, L. The role of ε-dominance in multi objective particle swarm optimization methods. In Proceedings of the 2003 Congress on Evolutionary Computation, Canberra, ACT, Australia, 8–12 December 2003; IEEE: New York, NY, USA, 2004; Volume 3, pp. 1764–1771. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Winter Simulation Conference, Perth, WA, Australia, 27 November–1 December 1995; IEEE: New York, NY, USA, 1995; Volume 11, pp. 1942–1948. [Google Scholar]
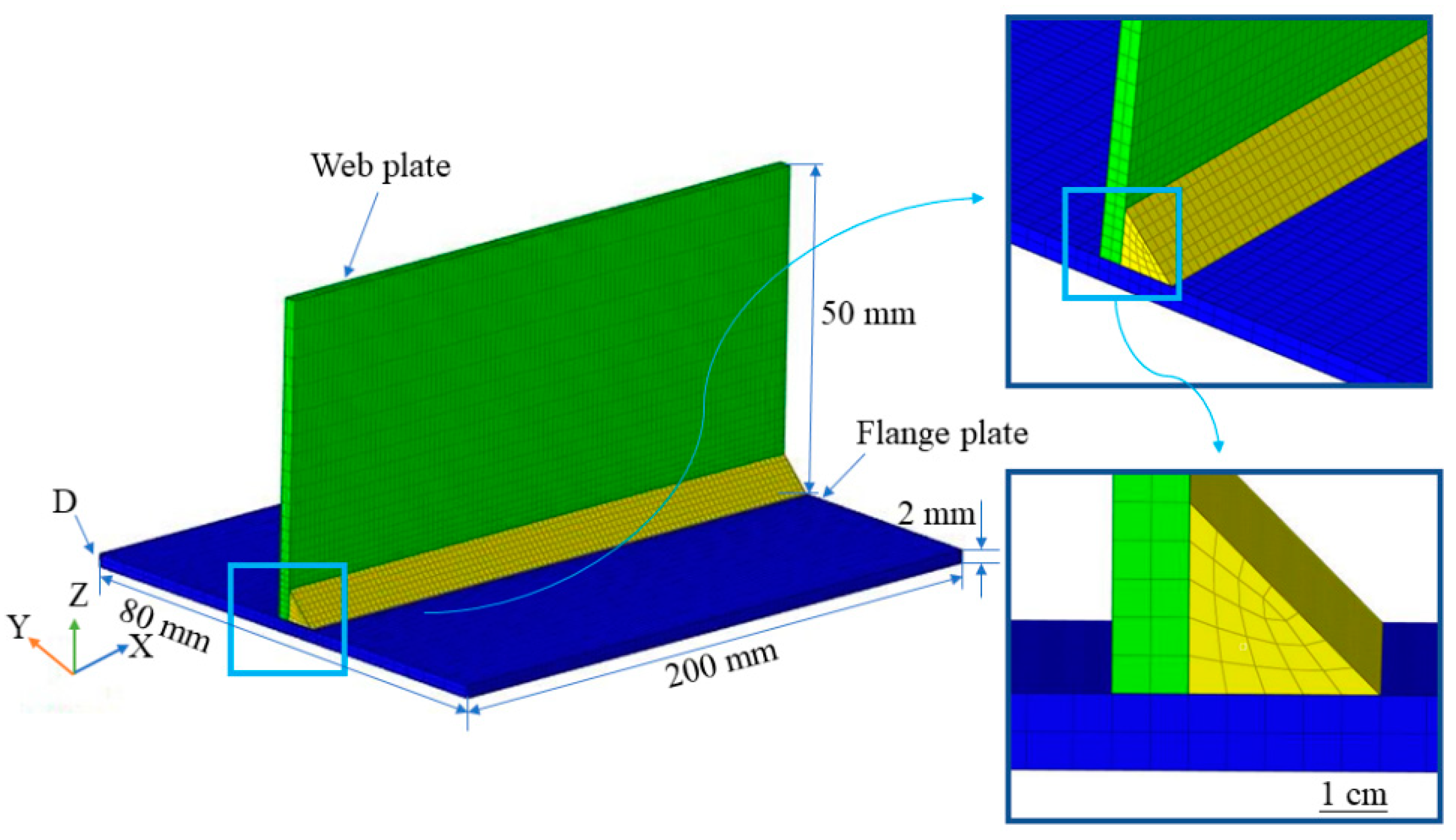
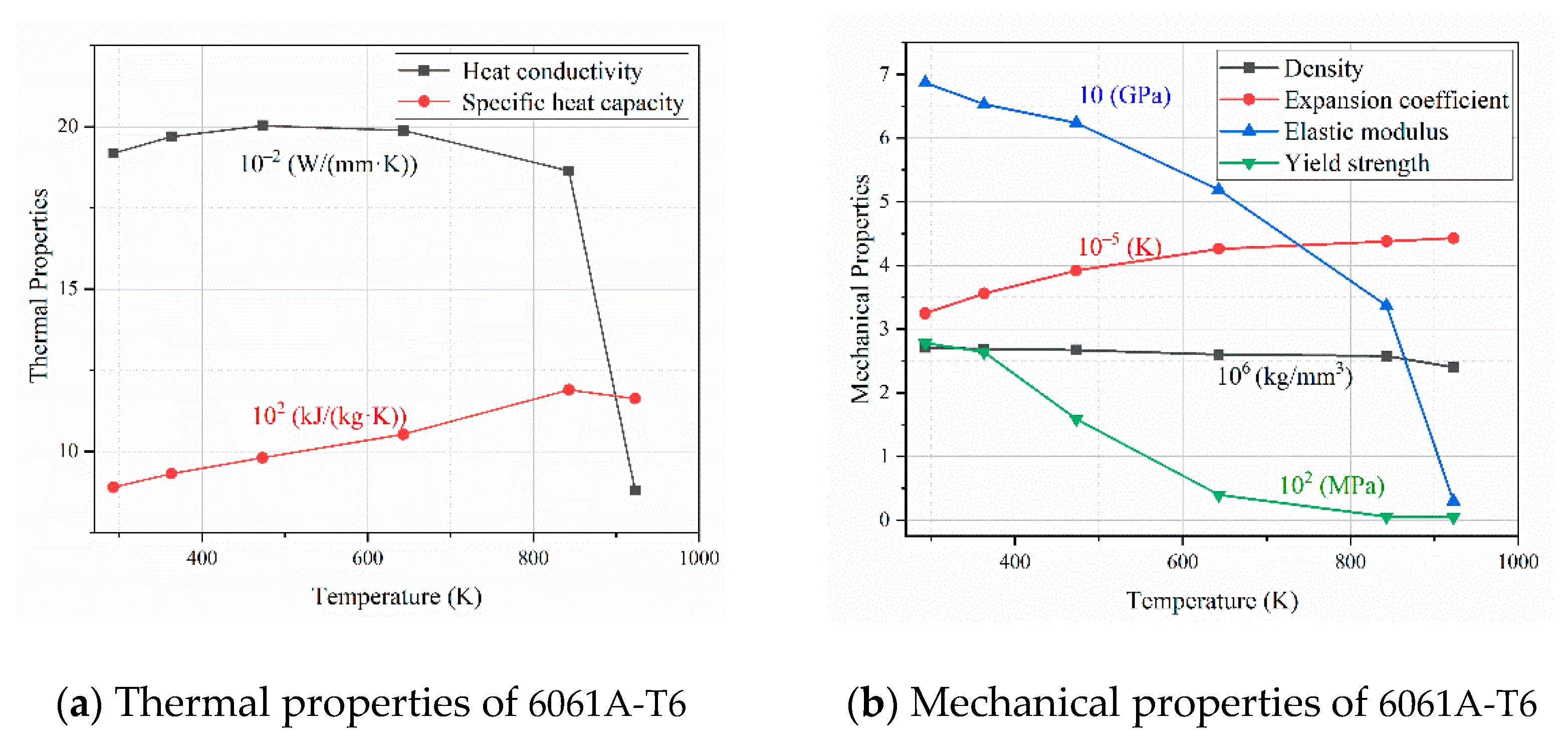






| Mg | Si | Fe | Cu | Cr | Mn | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|
| 0.8–1.2 | 0.4–0.8 | 0.70 | 0.15–0.40 | 0.04–0.35 | 0.15 | 0.25 | 0.15 | Balance |
| Result | Experiment [27] | Simulation | Deviation | Simulation [27] | Deviation |
|---|---|---|---|---|---|
| Distance along Z direction (mm) | 1.1 | 1.08 | 1.8% | 1.05 | 4.5% |
| Angular deformation (°) | 1.61 | 1.54 | 4.3% | 1.50 | 6.8% |
| Research Parameters | Selected Range |
|---|---|
| Preheat temperature | 80–125 °C |
| Preheat area | 12–36 mm |
| Welding speed | 7.5–9 mm/s |
| Welding heat input | 1500–1700 W |
| No | Optimization Variable | Objective Variable | |||||
|---|---|---|---|---|---|---|---|
| Preheat Temperature (X1) (°C) | Preheat Area (X2) (mm) | Welding Speed (X3) (mm/s) | Welding Heat Input (X4) (W) | Heat Source Central Temperature (°C) | Welding Residual Deformation (Y1) (mm) | Welding Residual Stress (Y2) (MPa) | |
| 1 | 95 | 20 | 8.5 | 1570 | 1091 | 1.904 | 186.36 |
| 2 | 95 | 20 | 9 | 1700 | 1150 | 1.926 | 181.74 |
| 3 | 95 | 36 | 7.5 | 1700 | 1320 | 2.002 | 129.12 |
| 4 | 95 | 36 | 9 | 1630 | 1125 | 1.929 | 173.30 |
| 5 | 95 | 12 | 8 | 1700 | 1207 | 1.896 | 171.43 |
| 6 | 95 | 28 | 8.5 | 1700 | 1206 | 1.962 | 165.51 |
| 7 | 95 | 36 | 8 | 1500 | 1105 | 1.917 | 171.88 |
| 8 | 95 | 28 | 7.5 | 1570 | 1189 | 1.951 | 159.43 |
| 9 | 95 | 20 | 7.5 | 1500 | 1115 | 1.909 | 176.34 |
| 10 | 95 | 20 | 8 | 1630 | 1177 | 1.925 | 171.97 |
| 11 | 95 | 12 | 8.5 | 1630 | 1113 | 1.873 | 185.90 |
| 12 | 95 | 12 | 9 | 1570 | 1011 | 1.860 | 199.86 |
| 13 | 80 | 36 | 9 | 1700 | 1154 | 1.910 | 173.22 |
| 14 | 80 | 20 | 8.5 | 1500 | 1004 | 1.879 | 197.36 |
| 15 | 80 | 28 | 9 | 1500 | 974 | 1.880 | 198.75 |
| 16 | 80 | 20 | 8 | 1700 | 1216 | 1.910 | 167.56 |
| 17 | 80 | 36 | 7.5 | 1630 | 1227 | 1.920 | 148.05 |
| 18 | 80 | 12 | 7.5 | 1500 | 1074 | 1.851 | 184.19 |
| 19 | 80 | 28 | 8.5 | 1630 | 1137 | 1.905 | 179.16 |
| 20 | 80 | 20 | 7.5 | 1700 | 1265 | 1.932 | 155.23 |
| 21 | 80 | 28 | 7.5 | 1570 | 1169 | 1.916 | 166.15 |
| 22 | 80 | 12 | 8.5 | 1700 | 1158 | 1.867 | 181.54 |
| 23 | 80 | 36 | 8 | 1500 | 1080 | 1.888 | 178.16 |
| 24 | 80 | 28 | 8 | 1630 | 1175 | 1.918 | 169.41 |
| 25 | 110 | 20 | 9 | 1500 | 1000 | 1.915 | 198.42 |
| 26 | 110 | 36 | 9 | 1630 | 1148 | 1.964 | 166.27 |
| 27 | 110 | 36 | 8.5 | 1700 | 1241 | 2.000 | 145.53 |
| 28 | 110 | 12 | 9 | 1700 | 1137 | 1.900 | 185.61 |
| 29 | 110 | 28 | 9 | 1570 | 1090 | 1.959 | 182.17 |
| 30 | 110 | 20 | 8.5 | 1570 | 1109 | 1.932 | 183.01 |
| 31 | 110 | 12 | 8 | 1630 | 1166 | 1.901 | 176.75 |
| 32 | 110 | 36 | 7.5 | 1570 | 1225 | 1.984 | 137.67 |
| 33 | 110 | 28 | 7.5 | 1630 | 1266 | 2.013 | 141.98 |
| 34 | 110 | 20 | 7.5 | 1700 | 1305 | 2.001 | 144.46 |
| 35 | 110 | 28 | 8 | 1500 | 1117 | 1.956 | 173.91 |
| 36 | 110 | 12 | 8.5 | 1500 | 1009 | 1.870 | 198.54 |
| 37 | 80 | 12 | 8 | 1570 | 1095 | 1.855 | 185.84 |
| 38 | 80 | 28 | 7.5 | 1500 | 1113 | 1.901 | 174.49 |
| 39 | 80 | 28 | 9 | 1700 | 1147 | 1.916 | 178.30 |
| 40 | 80 | 36 | 8 | 1570 | 1140 | 1.901 | 169.89 |
| 41 | 80 | 36 | 9 | 1500 | 983 | 1.876 | 192.99 |
| 42 | 80 | 12 | 9 | 1630 | 1054 | 1.853 | 196.78 |
| 43 | 80 | 12 | 8 | 1630 | 1146 | 1.864 | 180.61 |
| 44 | 80 | 20 | 8 | 1500 | 1054 | 1.874 | 188.68 |
| 45 | 80 | 12 | 7.5 | 1700 | 1243 | 1.892 | 162.00 |
| 46 | 80 | 20 | 7.5 | 1630 | 1203 | 1.910 | 165.84 |
| 47 | 80 | 20 | 9 | 1570 | 1023 | 1.873 | 197.44 |
| 48 | 80 | 36 | 8.5 | 1570 | 1097 | 1.892 | 178.84 |
| 49 | 125 | 12 | 9 | 1700 | 1149 | 1.919 | 183.76 |
| 50 | 125 | 36 | 8 | 1630 | 1259 | 2.027 | 132.03 |
| 51 | 125 | 28 | 8 | 1700 | 1305 | 2.066 | 137.49 |
| 52 | 125 | 28 | 9 | 1500 | 1056 | 1.979 | 183.51 |
| 53 | 125 | 20 | 8.5 | 1630 | 1170 | 1.979 | 173.84 |
| 54 | 125 | 20 | 9 | 1630 | 1132 | 1.971 | 182.26 |
| 55 | 125 | 20 | 7.5 | 1570 | 1203 | 1.982 | 160.36 |
| 56 | 125 | 20 | 8.5 | 1700 | 1222 | 1.998 | 167.41 |
| 57 | 125 | 20 | 8 | 1570 | 1164 | 1.971 | 171.76 |
| 58 | 125 | 28 | 7.5 | 1630 | 1291 | 2.055 | 134.07 |
| 59 | 125 | 36 | 7.5 | 1500 | 1188 | 1.998 | 138.36 |
| 60 | 125 | 36 | 9 | 1570 | 1127 | 1.984 | 164.14 |
| 61 | 125 | 12 | 7.5 | 1570 | 1168 | 1.918 | 172.15 |
| 62 | 125 | 28 | 8.5 | 1500 | 1099 | 1.983 | 176.19 |
| 63 | 125 | 28 | 9 | 1630 | 1156 | 2.011 | 171.14 |
| 64 | 125 | 12 | 9 | 1500 | 976 | 1.884 | 202.62 |
| 65 | 125 | 12 | 8 | 1500 | 1070 | 1.894 | 188.02 |
| 66 | 125 | 36 | 8.5 | 1630 | 1209 | 2.013 | 144.84 |
| 67 | 125 | 12 | 7.5 | 1630 | 1217 | 1.932 | 164.90 |
| 68 | 125 | 28 | 8 | 1570 | 1189 | 2.013 | 156.82 |
| 69 | 125 | 36 | 8 | 1700 | 1321 | 2.061 | 123.87 |
| 70 | 125 | 12 | 8.5 | 1570 | 1089 | 1.898 | 189.93 |
| 71 | 125 | 28 | 7.5 | 1700 | 1351 | 2.090 | 124.79 |
| 72 | 125 | 20 | 7.5 | 1500 | 1185 | 1.963 | 170.15 |
| Source | Heat source Central Temperature | Welding Residual Deformation | Welding Residual Stress | ||||||
|---|---|---|---|---|---|---|---|---|---|
| F-Value | p-Value | – | F-Value | p-Value | – | F-Value | p-Value | – | |
| Preheat temperature (A) | 883.33 | <0.0001 | significant | 11,116.15 | <0.0001 | significant | 239.05 | 0.0113 | – |
| Preheat area (B) | 515.71 | <0.0001 | significant | 4272.88 | <0.0001 | significant | 3955.25 | <0.0001 | significant |
| Welding speed (C) | 2400.74 | <0.0001 | significant | 651.98 | <0.0001 | significant | 4302.08 | <0.0001 | significant |
| Welding input (D) | 4125.25 | <0.0001 | significant | 2105.38 | <0.0001 | significant | 3097.19 | <0.0001 | significant |
| AB | 16.61 | 0.0032 | – | 181.84 | <0.0001 | significant | 166.65 | 0.0007 | – |
| AC | 1.17 | 0.4567 | – | 7.1 | 0.022 | – | 7.9 | 0.059 | – |
| AD | 0.4833 | 0.8381 | – | 23.23 | 0.0015 | – | 7.24 | 0.0676 | – |
| BC | 1.43 | 0.3613 | – | 11.75 | 0.0072 | – | 21.29 | 0.0153 | – |
| BD | 0.6517 | 0.7286 | – | 25.66 | 0.0012 | – | 11.12 | 0.0366 | – |
| CD | 1.33 | 0.3961 | – | 27.01 | 0.001 | – | 20.04 | 0.0165 | – |
| No. | Result Type | Preheat Temperature (°C) | Preheat Area (mm) | Welding Speed (mm/s) | Welding Heat Input (W) | Welding Residual Deformation | Welding Residual Stress |
|---|---|---|---|---|---|---|---|
| Case 1 | Optimization | 119 | 33 | 7.5 | 1692 | 0.985 | 0.616 |
| FE | 0.862 | 0.665 | |||||
| Case 2 | Optimization | 81 | 36 | 7.6 | 1653 | 0.886 | 1.000 |
| FE | 0.935 | 0.928 | |||||
| Case 3 | Optimization | 85 | 12 | 8.8 | 1535 | 0.927 | 0.721 |
| FE | 0.881 | 0.786 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, Q.; Tan, F.; Li, K.; Yoshino, T.; Guo, G. Multi-Objective Optimization of MIG Welding and Preheat Parameters for 6061-T6 Al Alloy T-Joints Using Artificial Neural Networks Based on FEM. Coatings 2021, 11, 998. https://doi.org/10.3390/coatings11080998
Shao Q, Tan F, Li K, Yoshino T, Guo G. Multi-Objective Optimization of MIG Welding and Preheat Parameters for 6061-T6 Al Alloy T-Joints Using Artificial Neural Networks Based on FEM. Coatings. 2021; 11(8):998. https://doi.org/10.3390/coatings11080998
Chicago/Turabian StyleShao, Qing, Fuxing Tan, Kai Li, Tatsuo Yoshino, and Guikai Guo. 2021. "Multi-Objective Optimization of MIG Welding and Preheat Parameters for 6061-T6 Al Alloy T-Joints Using Artificial Neural Networks Based on FEM" Coatings 11, no. 8: 998. https://doi.org/10.3390/coatings11080998





