Numerical Investigation on the Evaporation Performance of Desulfurization Wastewater in a Spray Drying Tower without Deflectors
Abstract
:1. Introduction
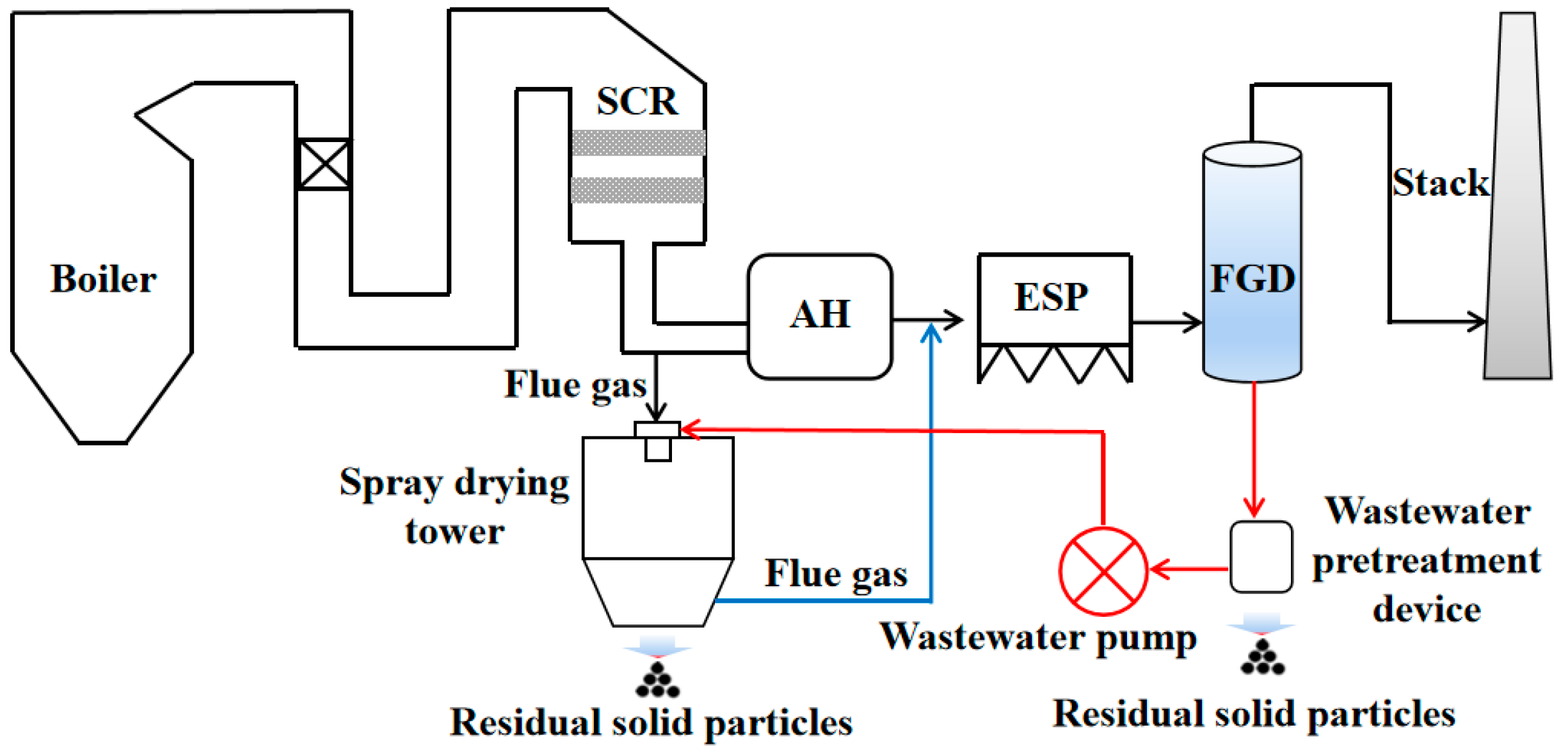
2. Physical Model and Numerical Method
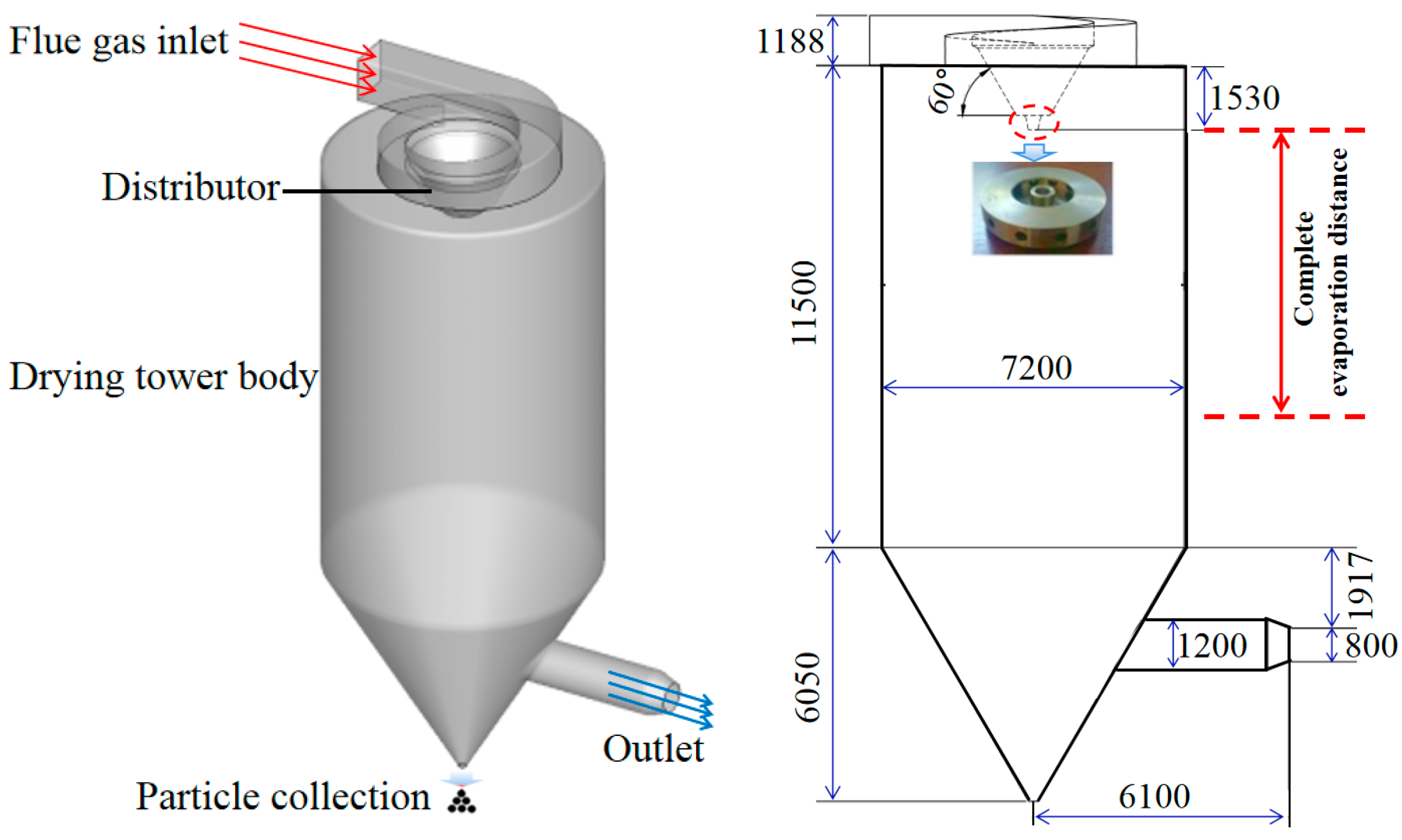
2.1. Spray Drying Tower Description
2.2. Numerical Method
2.3. Validation of the Simulated Results
3. Results and Discussion
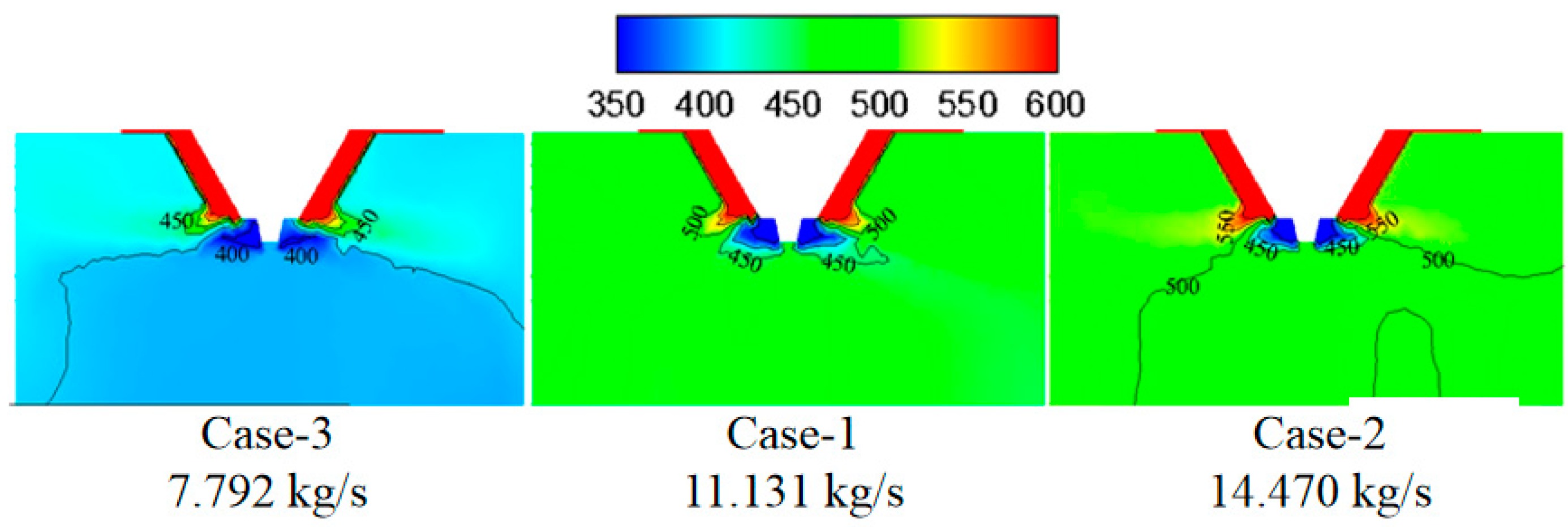
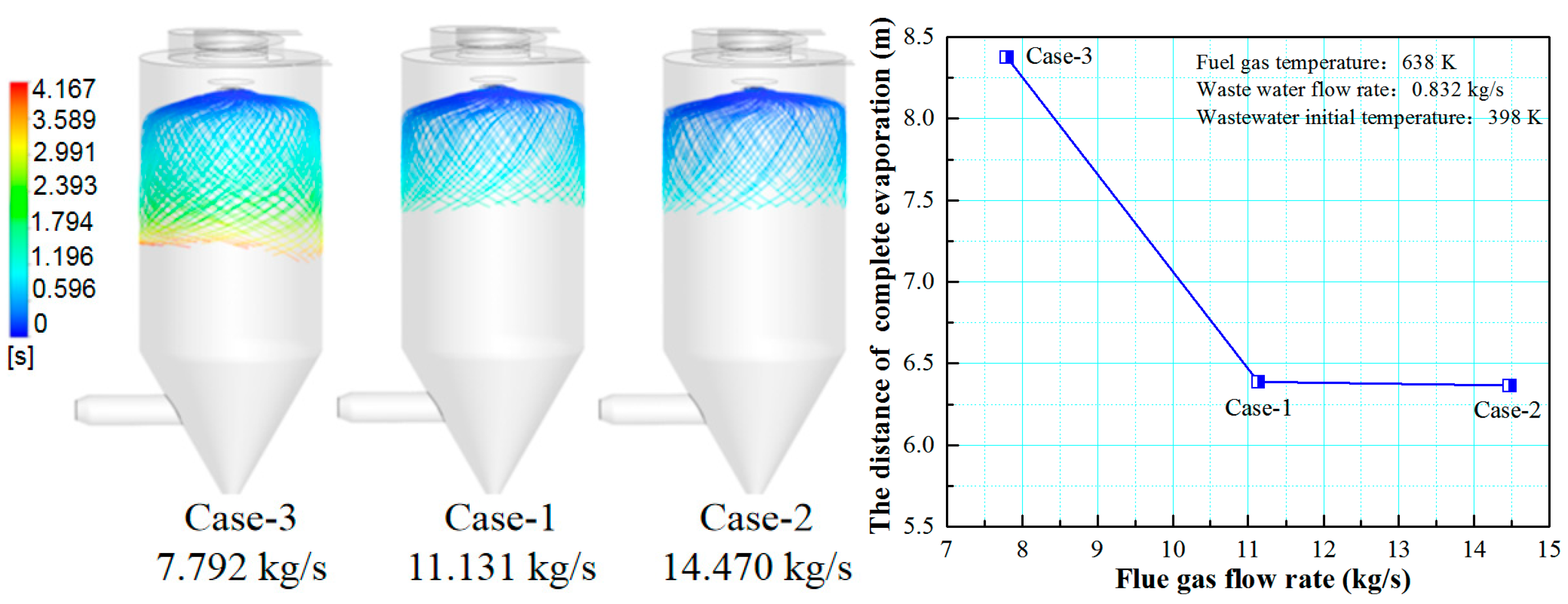
3.1. Effect of Flue Gas Flow Rate on the Evaporation Performance
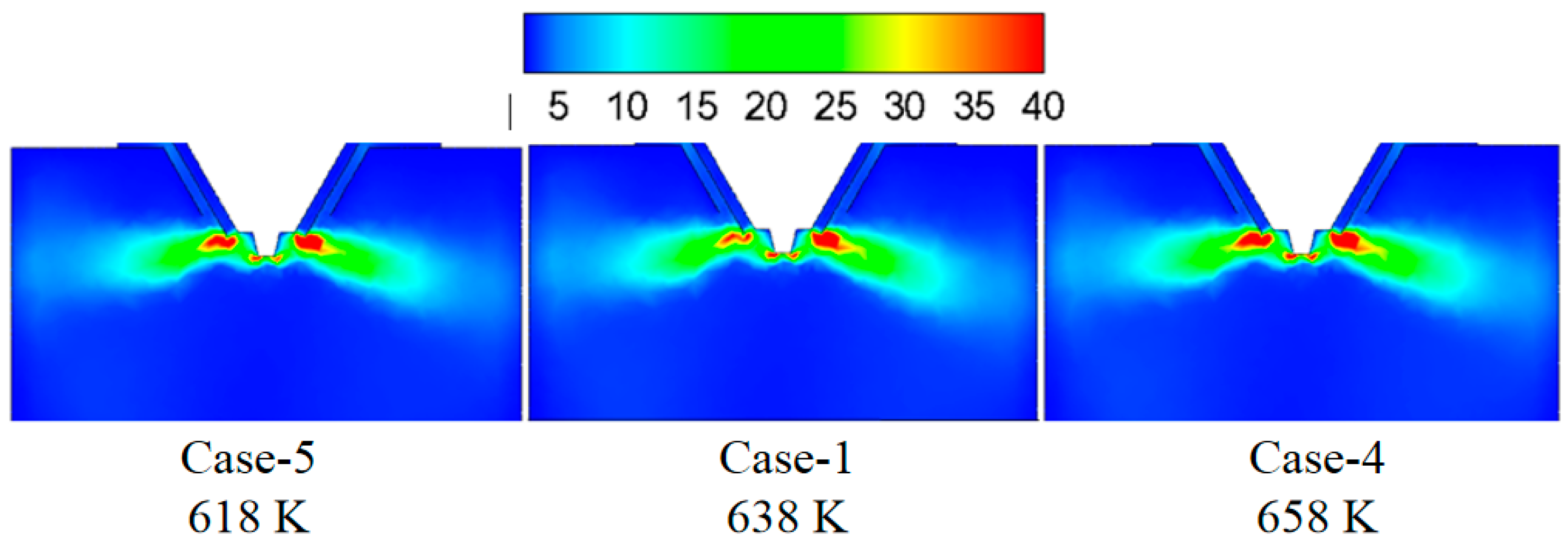
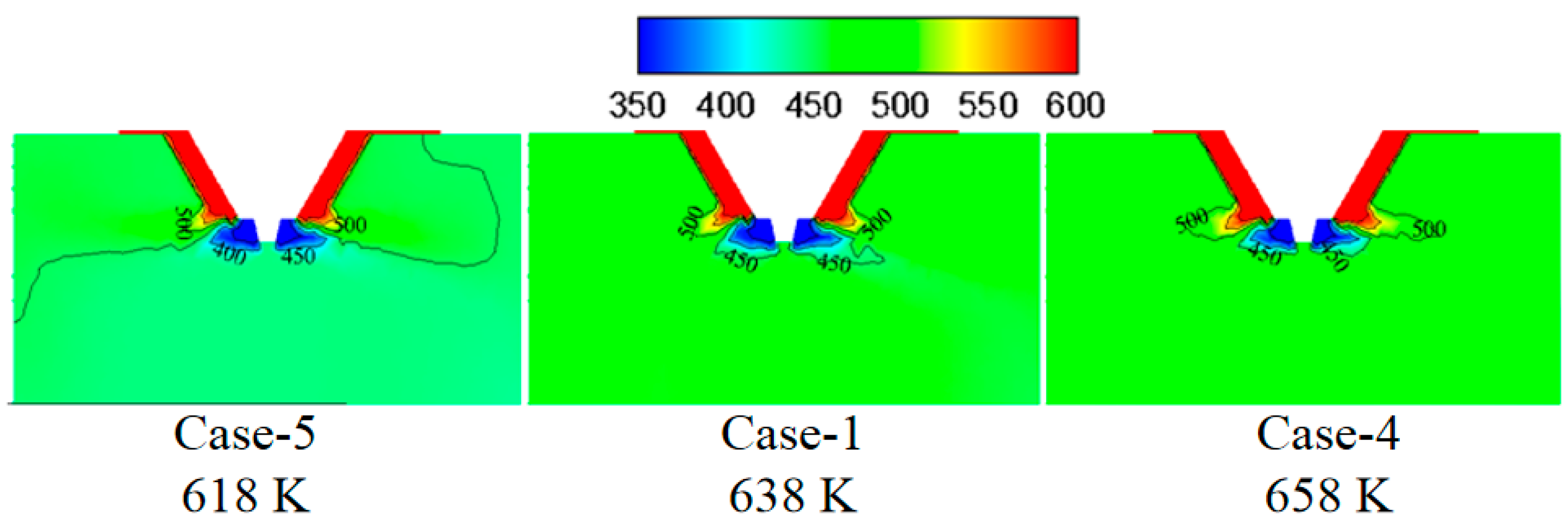
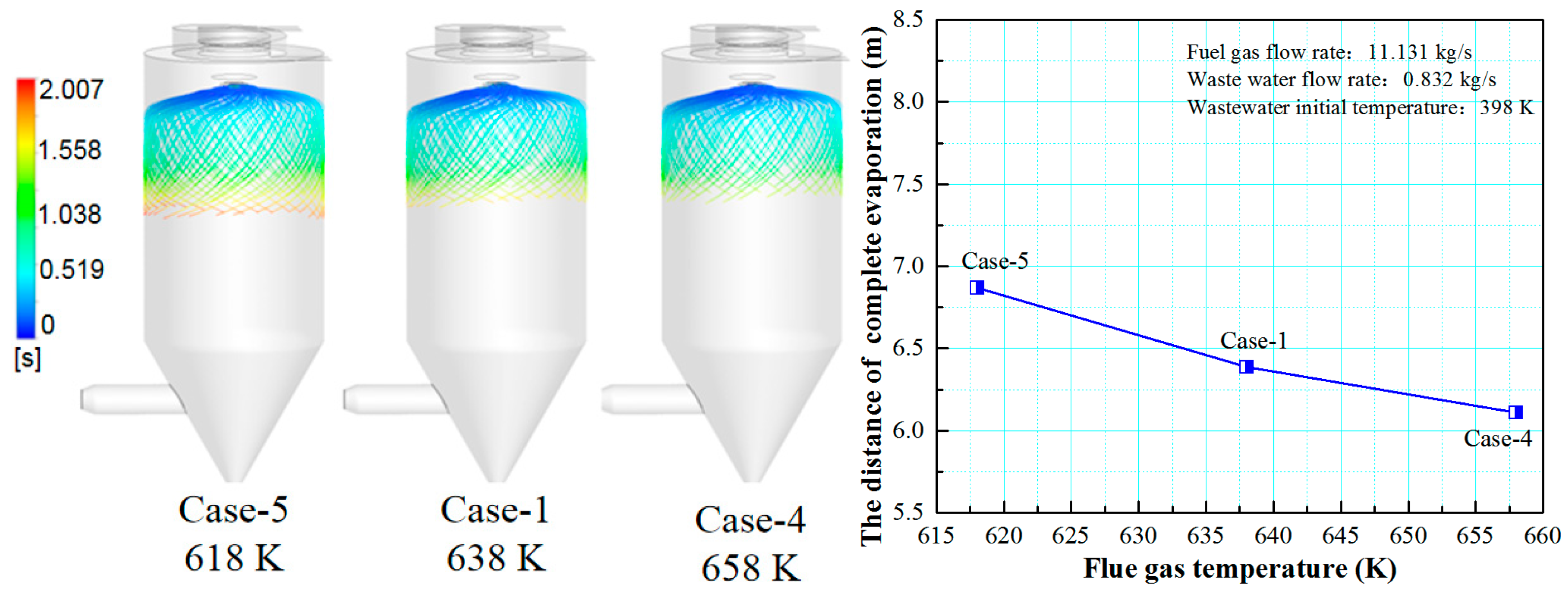
3.2. Effect of Flue Gas Temperature on the Evaporation Performance
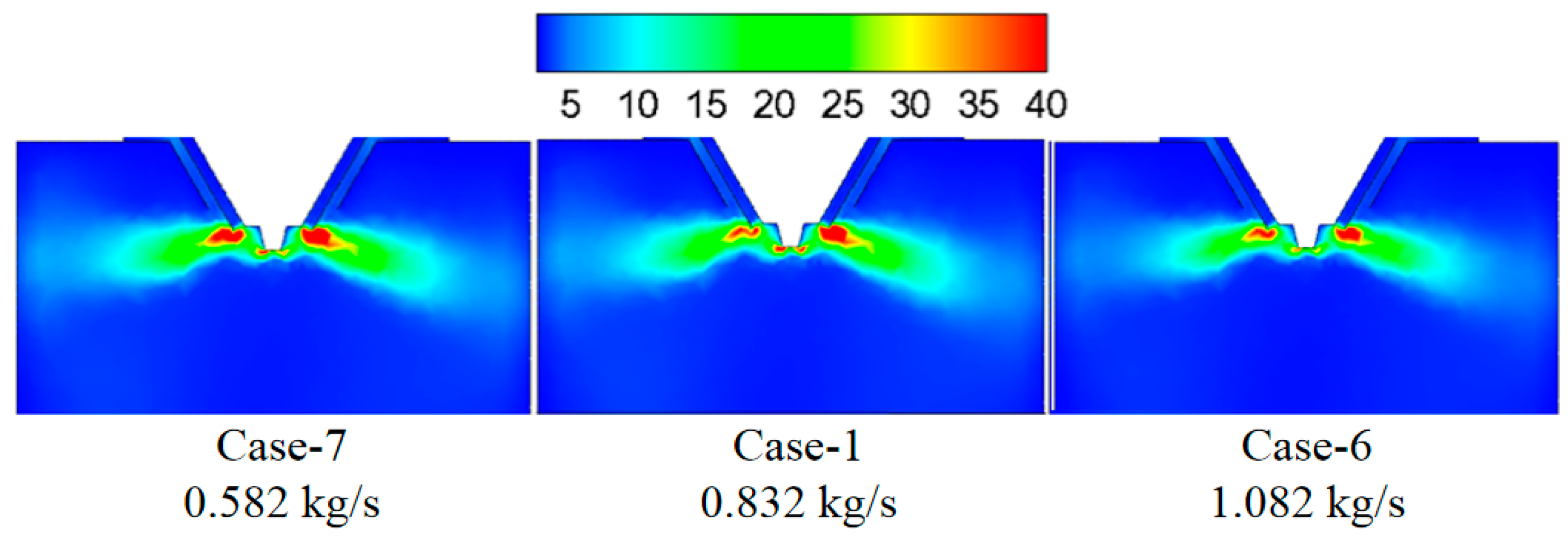
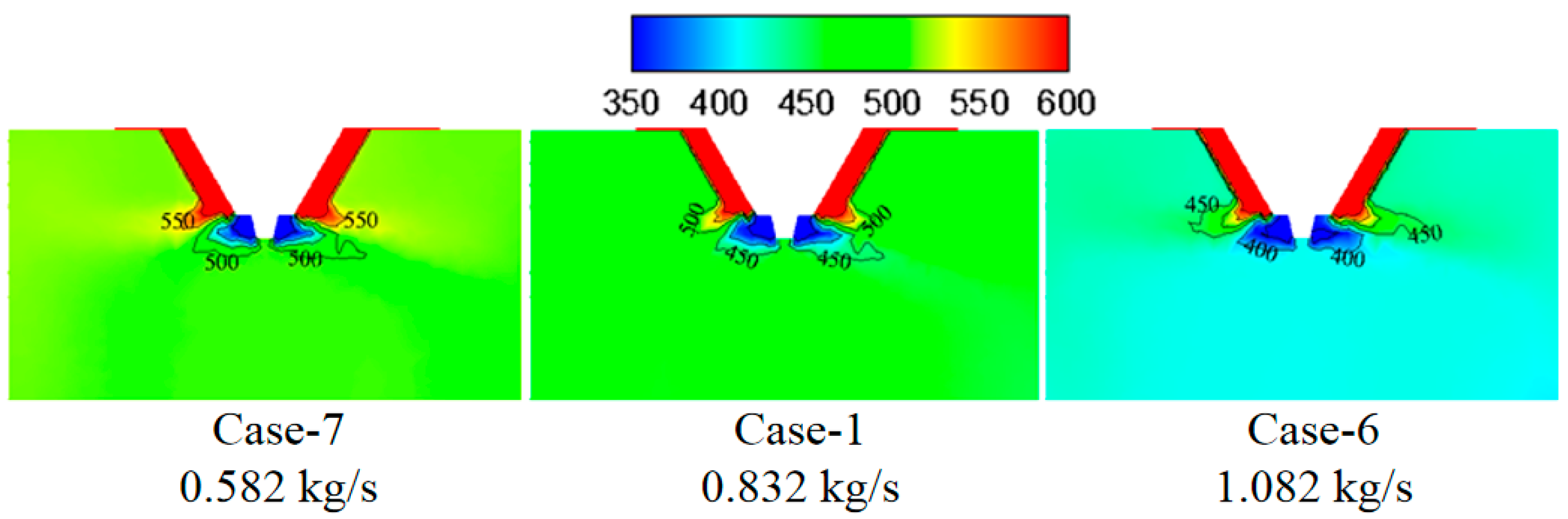
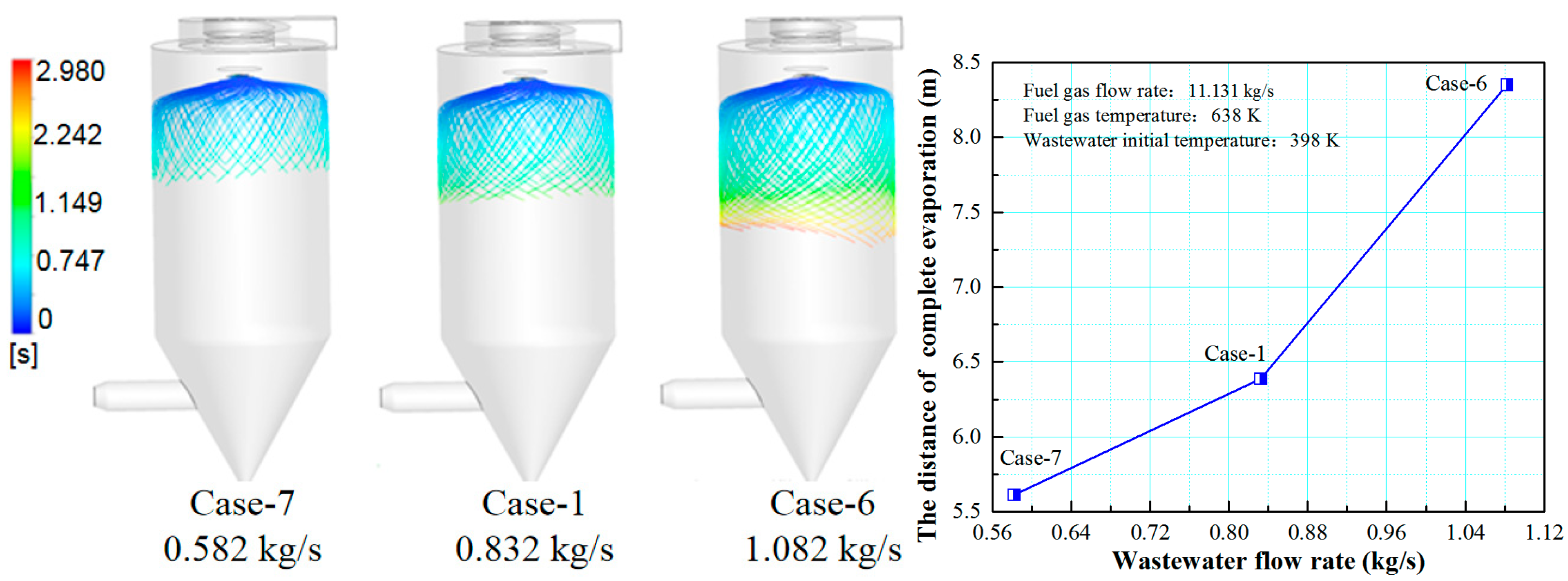
3.3. Effect of Wastewater Flow Rate on The Evaporation Performance
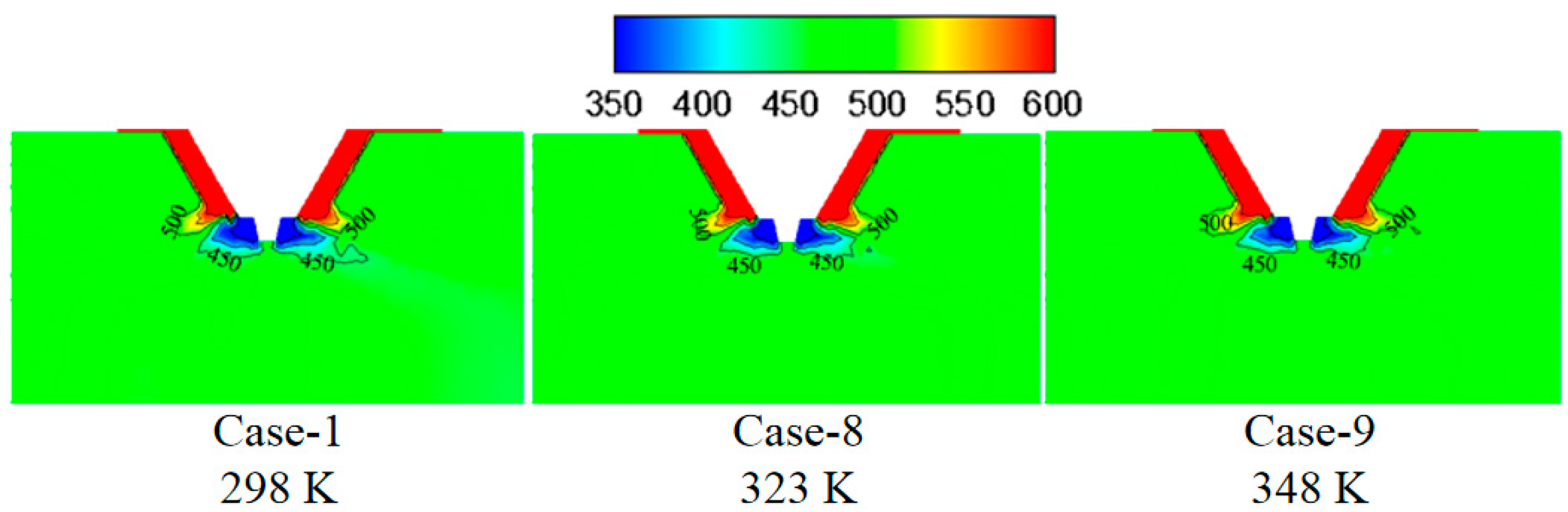
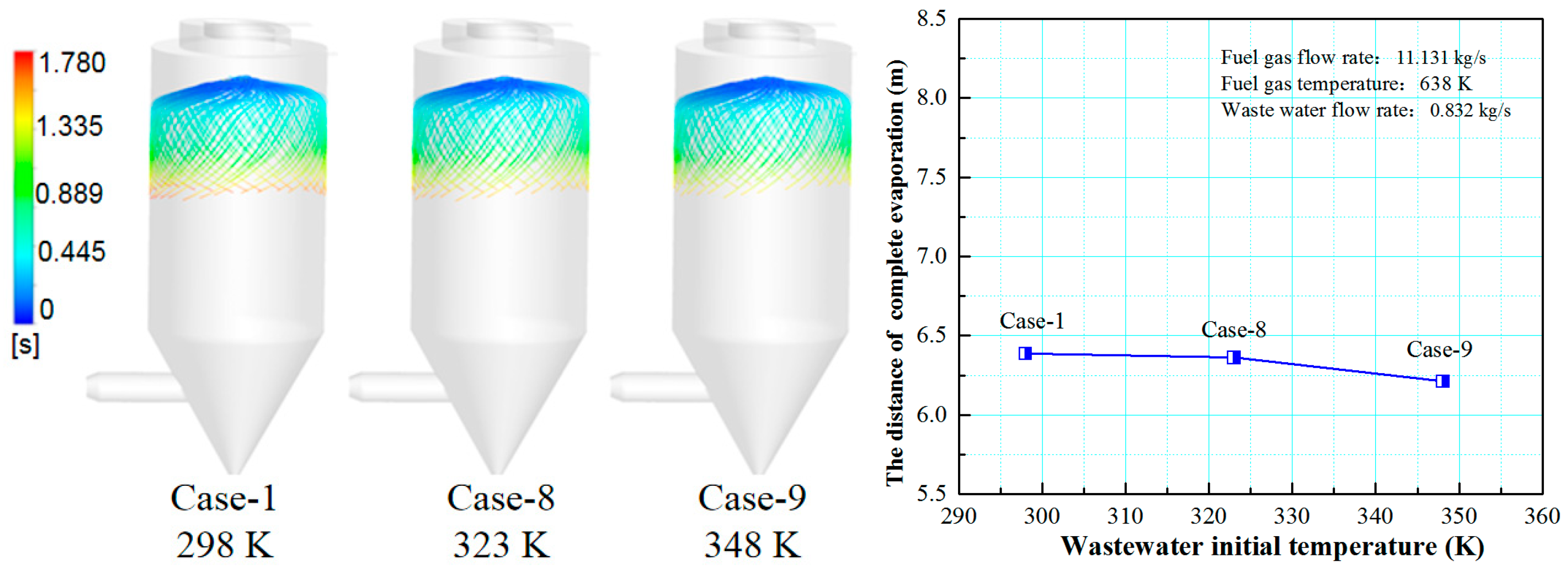
3.4. Effect of Wastewater Initial Temperature on the Evaporation Performance
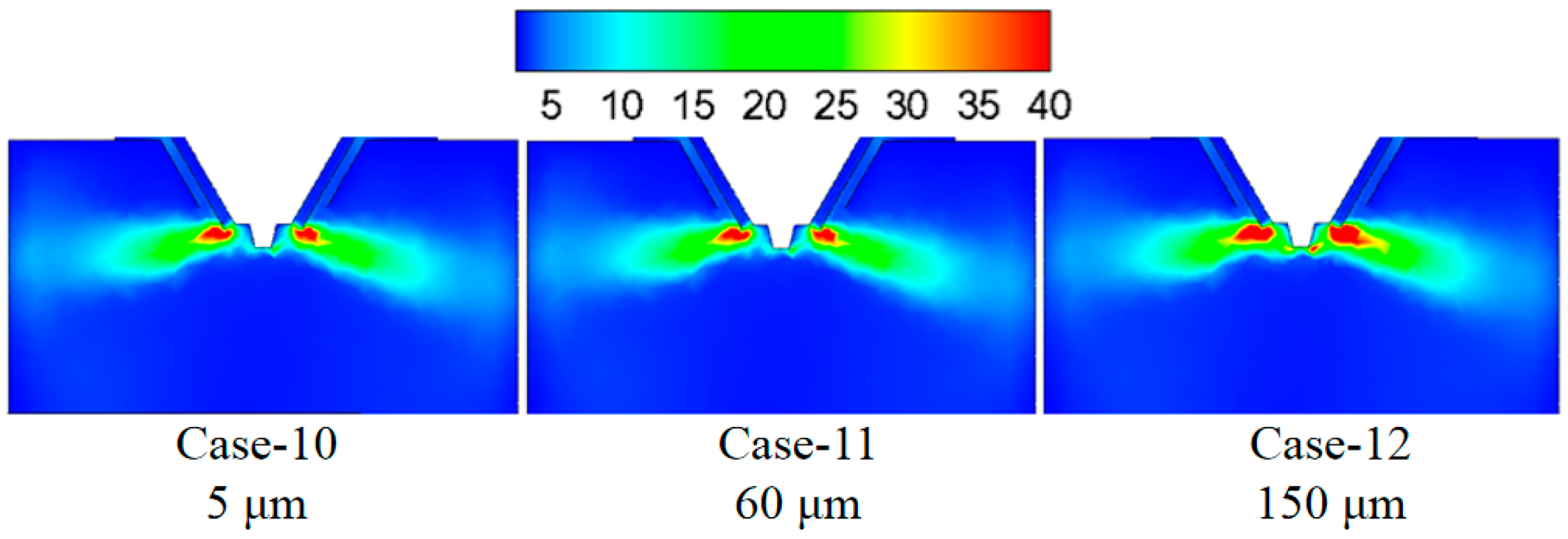
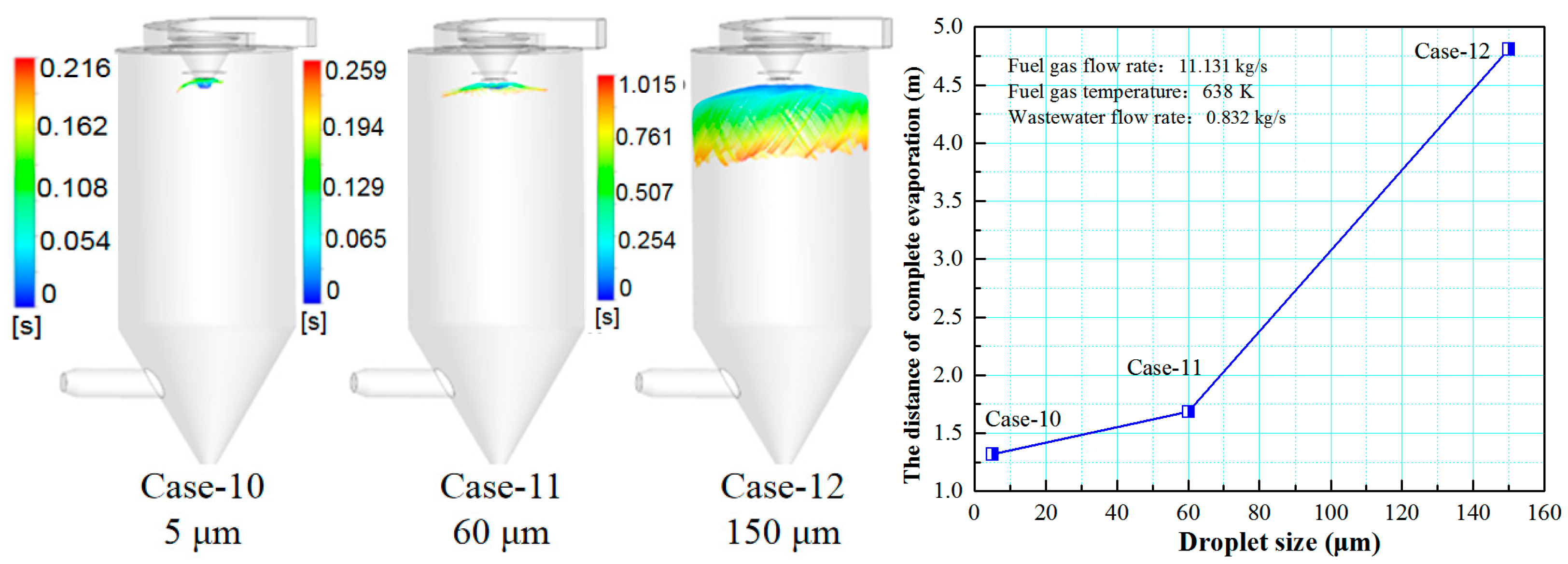
3.5. Effect of Droplet Size on the Evaporation Performance
3.6. Orthogonal Test of Evaporation Performance
4. Conclusions
- (1)
- The flue gas flow rate and temperature affect the evaporation performance of the desulfurization wastewater. The larger the flue gas flow rate and the higher the flue gas temperature, the faster the wastewater droplet evaporation and the shorter the complete evaporation distance. However, if the flue gas flow rate exceeds a certain level, the improvement of the droplet evaporation performance is not apparent. In actual operation, the effect of atomization and the safety of boiler operation should be considered simultaneously, an appropriate amount of flue gas flow should be extracted, and the wastewater flow of the spray drying tower should be practically designed.
- (2)
- The smaller the wastewater flow rate, the higher the initial wastewater temperature, the faster the wastewater droplet evaporation, and the shorter the complete evaporation distance.
- (3)
- Reducing the droplet size is beneficial to improving the evaporation effect of the desulfurization wastewater. Considering all factors, it is more economical and practical to choose a droplet size of 60 μm.
- (4)
- The orthogonal test results of various factors show that the factors affecting droplet evaporation performance are as follows: flue gas flow rate > wastewater flow rate > flue gas temperature > initial wastewater temperature > droplet size. Considering the evaporation ratio and the distance of complete evaporation, the optimal setting is 14.470 kg/s for flue gas flow rate, 385 °C for flue gas temperature, 0.582 kg/s for wastewater flow rate, 25 °C for initial wastewater temperature, and 60 μm for droplet size.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Córdoba, P. Status of flue gas desulphurisation (FGD) systems from coal-fired power plants: Overview of the physic-chemical control processes of wet limestone FGDs. Fuel 2015, 144, 274–286. [Google Scholar] [CrossRef]
- Guo, Y.; Xu, Z.; Zheng, C.; Shu, J.; Dong, H.; Zhang, Y.; Weng, W.; Gao, X. Modeling and optimization of wet flue gas desulfurization system based on a hybrid modeling method. J. Air Waste Manag. 2019, 69, 565–575. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez Ortiz, F.J.; Vidal, F.; Ollero, P.; Salvador, L.; Cortés, V.; Gimenez, A. Pilot-plant technical assessment of wet flue gas desulfu-rization using limestone. Ind. Eng. Chem. Res. 2006, 45, 1466–1477. [Google Scholar] [CrossRef]
- Srivastava, R.K.; Jozewicz, W. Flue gas desulfurization: The state of the art. J. Air Waste Manage. 2001, 51, 1676–1688. [Google Scholar] [CrossRef]
- Ma, S.; Chai, J.; Chen, G.; Wu, K.; Xiang, Y.; Wan, Z.; Zhang, J.; Zhu, H. Partitioning characteristic of chlorine ion in gas and solid phases in process of desulfurization waste water evaporation: Model development and calculation. Environ. Sci. Pollut. Res. 2019, 26, 8257–8265. [Google Scholar] [CrossRef] [PubMed]
- Shafiq, I.; Hussain, M.; Shehzad, N.; Maafa, I.M.; Akhter, P.; Amjad, U.; Razzaq, S.S.A.; Yang, W.; Tahir, M.; Russo, N. The effect of crystal facets and induced porosity on the performance of monoclinic BiVO4 for the enhanced visible-light driven photocatalytic abatement of methylene blue. J. Environ. Chem. Eng. 2019, 7, 103265. [Google Scholar] [CrossRef]
- Azam, K.; Raza, R.; Shezad, N.; Shabir, M.; Yang, W.; Ahmad, N.; Shafiq, I.; Akhter, P.; Razzaq, A.; Hussain, M. Development of recoverable magnetic mesoporous carbon ad-sorbent for removal of methyl blue and methyl orange from waste water. J. Environ. Chem. Eng. 2020, 8, 104220. [Google Scholar] [CrossRef]
- Ma, S.; Chai, J.; Chen, J.; Wu, K.; Wan, Z.; Zhang, J. Numerical simulation of bypass evaporation system treating FGD waste water using high temperature flue gas. Environ. Technol. 2018, 5, 1–24. [Google Scholar]
- Guo, J.; Shu, S.; Liu, X.; Wang, X.; Yin, H.; Chu, Y. Influence of Fe loadings on desulfurization performance of activated carbon treated by nitric acid. Environ. Technol. 2017, 38, 266–276. [Google Scholar] [CrossRef]
- Ma, S.; Chai, J.; Chen, G.; Yu, W.; Zhu, S. Research on desulfurization waste water evaporation: Present and future perspectives. Renew. Sust. Energ. Rev. 2016, 58, 1143–1151. [Google Scholar]
- Cui, L.; Li, G.; Li, Y.; Yang, B.; Zhang, L.; Dong, Y.; Ma, C. Electrolysis-electrodialysis process for removing chloride ion in wet flue gas desulfurization waste water (DW): Influencing factors and energy consumption analysis. Chem. Eng. Res. Des. 2017, 123, 240–247. [Google Scholar] [CrossRef]
- Enoch, G.D.; Spiering, W.; Tigchelaar, P.; de Niet, J.; Lefers, J.B. Treatment of waste water from wet lime (stone) flue gas desulfurization plants with aid of crossflow microfiltration. Sep. Sci. Technol. 1990, 25, 1587–1605. [Google Scholar] [CrossRef]
- Ye, C.S.; Huang, J.W.; Liu, T. Technology progress and treatment methods of flue Gas desulfurization waste water in coal-fired plants. Environ. Eng. 2017, 35, 10–13. [Google Scholar]
- Liu, Z.; Wey, M.; Lin, C. Reaction characteristics of Ca(OH)2, HCl and SO2 at low temperature in a spray dryer integrated with a fabric filter. J. Hazard Mater. 2002, 95, 291–304. [Google Scholar] [CrossRef]
- Ukai, N.; Nagayasu, T.; Kamiyama, N.; Fukuda, T. Spray-Drying Device for Dehydrated Filtrate from Desulfurization Waste Water, Air Pollution Control System and Flue Gas Treatment Method. U.S. Patent No. 9,555,341, 31 January 2017. [Google Scholar]
- Shaw, W.A. Fundamentals of zero liquid discharge system design. Power 2011, 155, 56–58. [Google Scholar]
- Shaw, W.A. Benefits of evaporation FGD purge water. Power 2008, 152, 60–63. [Google Scholar]
- Mosti, C.; Cenci, V. ZLD systens applied to ENEL coal-fired power plants. Power Tech. 2012, 92, 69–73. [Google Scholar]
- Xu, Y.; Jin, B.S.; Zhou, Z.; Fang, W. Experimental and numerical investigations of desulfurization waste water evaporation in a lab-scale flue gas duct: Evaporation and HCl release characteristics. Environ. Technol. 2021, 42, 1411–1427. [Google Scholar] [CrossRef]
- Liang, Z.; Zhang, L.; Yang, Z.; Qiang, T.; Pu, G.; Ran, J. Evaporation and crystallization of a droplet of desulfurization waste water from a coal-fired power plant. Appl. Therm. Eng. 2017, 119, 52–62. [Google Scholar] [CrossRef]
- Deng, J.J.; Pan, L.M.; Chen, D.Q.; Dong, Y.Q.; Wang, C.M.; Liu, H.; Kang, M.Q. Numerical simulation and field test study of desulfuriza-tion waste water evaporation treatment through flue gas. Water Sci. Technol. 2014, 70, 1285–1291. [Google Scholar] [CrossRef]
- Zheng, C.; Zheng, H.; Yang, Z.; Liu, S.; Li, X.; Zhang, Y.; Weng, W.; Gao, X. Experimental study on the evaporation and chlorine migration of desulfurization waste water in flue gas. Environ. Sci. Pollut. Res. 2019, 26, 4791–4800. [Google Scholar] [CrossRef] [PubMed]
- Jen, T.C.; Li, L.; Cui, W.; Chen, Q.; Zhang, X. Numerical investigations on cold gas dynamic spray process with nano- and microsize particles. Int. J. Heat Mass Tran. 2005, 48, 4384–4396. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathe-Matical Models of Turbulence; Von Karman In-stitutefor Fluid Dynamics: Sint-Genesius-Rode, Belgium, 1972. [Google Scholar]
- ANSYS. Ver A F 16.0—User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Orourke, P.J.; Amsden, A.A. The TAB method for numerical calculation of spray droplet breakup. In Proceedings of the International Fuels and Lubricants Meeting and Exposition, Toronto, ON, Canada, 2 November 1987. [Google Scholar]
- Miura, K.; Miura, T.; Ohtani, S. Heat and mass transfer to and from droplets. Chem. Eng. Prog. Sym. Ser. 1977, 163, 95–102. [Google Scholar]
- Sazhin, S.S. Advanced models of fuel droplet heating and evaporation. Prog. Energ. Combust. Sci. 2006, 32, 162–214. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, M.; Wang, C.; Gao, Z. Optimal design of diversion piers of lateral intake pumping station based on orthogonal test. Shock Vib. 2021, 5, 1–9. [Google Scholar]




| Item | Value |
|---|---|
| Volume flow of flue gas (Nm3/h) | 32,315 |
| Temperature (K) | 638 |
| Density (kg/m3) | 1.24 |
| viscosity (kg/m·s) | 3.22 × 10−5 |
| Specific heat capacity at constant pressure (J/kg·k) | 1159.2 |
| Components (%) | |
| N2 | 73.00 |
| O2 | 3.00 |
| CO2 | 13.00 |
| H2O(g) | 11.00 |
| Cases | Flow Rate of Flue Gas | Temperature of Flue Gas | Flow Rate of Wastewater | Initial Temperature of Wastewater | Droplet Size |
|---|---|---|---|---|---|
| kg/s | K | kg/s | K | μm | |
| 1 | 11.131 | 638 | 0.832 | 298 | size range: 10–200 μm, an average diameter: 60 μm, spread parameter: 1.2 |
| 2 | 14.470 | 638 | 0.832 | 298 | |
| 3 | 7.792 | 638 | 0.832 | 298 | |
| 4 | 11.131 | 658 | 0.832 | 298 | |
| 5 | 11.131 | 618 | 0.832 | 298 | |
| 6 | 11.131 | 638 | 1.082 | 298 | |
| 7 | 11.131 | 638 | 0.582 | 298 | |
| 8 | 11.131 | 638 | 0.832 | 323 | |
| 9 | 11.131 | 638 | 0.832 | 348 | |
| 10 | 11.131 | 638 | 0.832 | 298 | 5 μm |
| 11 | 11.131 | 638 | 0.832 | 298 | 60 μm |
| 12 | 11.131 | 638 | 0.832 | 298 | 150 μm |
| 13–30 | Orthogonal test of evaporation performance | ||||
| Item | 100% Load (600 MW) | 66% Load (400 MW) | |
|---|---|---|---|
| Operation parameter | Flue gas temperature (K) | 638 | 610 |
| Flow rate of wastewater (kg/s) | 0.832 | 0.582 | |
| Inlet wastewater temperature (K) | 298 | 298 | |
| Temperature at the outlet (K) | Simulated | 460 | 446 |
| Measured | 453 | 432 | |
| H2O(g) concentration at the outlet (%) | Simulated | 17.5 | 16.9 |
| Measured | 17.1 | 16.3 | |
| Cases | Flue Gas Flow Rate | Flue Gas Temperature | Wastewater Flow Rate | Wastewater Initial Temperature | Droplet Size | Evaporation Ratio * | The Distance of Complete Evaporation |
|---|---|---|---|---|---|---|---|
| kg/s | °C | kg/s | °C | μm | % | m | |
| 13 | 14.470 | 385 | 1.082 | 75 | 150 | 100 | 4.774 |
| 14 | 14.470 | 365 | 0.832 | 50 | 60 | 100 | 1.888 |
| 15 | 14.470 | 345 | 0.582 | 25 | 5 | 100 | 2.504 |
| 16 | 11.131 | 385 | 1.082 | 50 | 60 | 100 | 2.021 |
| 17 | 11.131 | 365 | 0.832 | 25 | 5 | 100 | 2.664 |
| 18 | 11.131 | 345 | 0.582 | 75 | 150 | 100 | 3.854 |
| 19 | 7.792 | 385 | 0.832 | 75 | 5 | 96.51 | - |
| 20 | 7.792 | 365 | 0.582 | 50 | 150 | 100 | 3.687 |
| 21 | 7.792 | 345 | 1.082 | 25 | 60 | 90.39 | - |
| 22 | 14.470 | 385 | 0.582 | 25 | 60 | 100 | 1.780 |
| 23 | 14.470 | 365 | 1.082 | 75 | 150 | 100 | 5.107 |
| 24 | 14.470 | 345 | 0.832 | 50 | 5 | 98.68 | - |
| 25 | 11.131 | 385 | 0.832 | 25 | 150 | 100 | 4.480 |
| 26 | 11.131 | 365 | 0.582 | 75 | 60 | 100 | 1.783 |
| 27 | 11.131 | 345 | 1.082 | 50 | 5 | 98.34 | - |
| 28 | 7.792 | 385 | 0.582 | 50 | 5 | 99.71 | - |
| 29 | 7.792 | 365 | 1.082 | 25 | 150 | 97.04 | - |
| 30 | 7.792 | 345 | 0.832 | 75 | 60 | 100 | 2.153 |
| K1 | 598.68 | 596.22 | 585.77 | 596.51 | 597.04 | - | |
| K2 | 598.34 | 597.04 | 595.19 | 596.73 | 590.39 | - | - |
| K3 | 583.65 | 587.41 | 599.71 | 587.43 | 593.24 | - | - |
| k1 | 99.78 | 99.37 | 97.63 | 99.42 | 99.51 | - | - |
| k2 | 99.72 | 99.51 | 99.20 | 99.46 | 98.40 | - | - |
| k3 | 97.28 | 97.90 | 99.95 | 97.91 | 98.87 | - | - |
| R | 2.50 | 1.61 | 2.32 | 1.55 | 1.11 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Zhao, N.; Feng, Y.; Xie, Z. Numerical Investigation on the Evaporation Performance of Desulfurization Wastewater in a Spray Drying Tower without Deflectors. Coatings 2021, 11, 1022. https://doi.org/10.3390/coatings11091022
Li D, Zhao N, Feng Y, Xie Z. Numerical Investigation on the Evaporation Performance of Desulfurization Wastewater in a Spray Drying Tower without Deflectors. Coatings. 2021; 11(9):1022. https://doi.org/10.3390/coatings11091022
Chicago/Turabian StyleLi, Debo, Ning Zhao, Yongxin Feng, and Zhiwen Xie. 2021. "Numerical Investigation on the Evaporation Performance of Desulfurization Wastewater in a Spray Drying Tower without Deflectors" Coatings 11, no. 9: 1022. https://doi.org/10.3390/coatings11091022
APA StyleLi, D., Zhao, N., Feng, Y., & Xie, Z. (2021). Numerical Investigation on the Evaporation Performance of Desulfurization Wastewater in a Spray Drying Tower without Deflectors. Coatings, 11(9), 1022. https://doi.org/10.3390/coatings11091022





