Optical Absorption in Si:H Thin Films: Revisiting the Role of the Refractive Index and the Absorption Coefficient
Abstract
1. Introduction
2. Materials, Microstructure and Optical Characterization
3. Results and Discussion
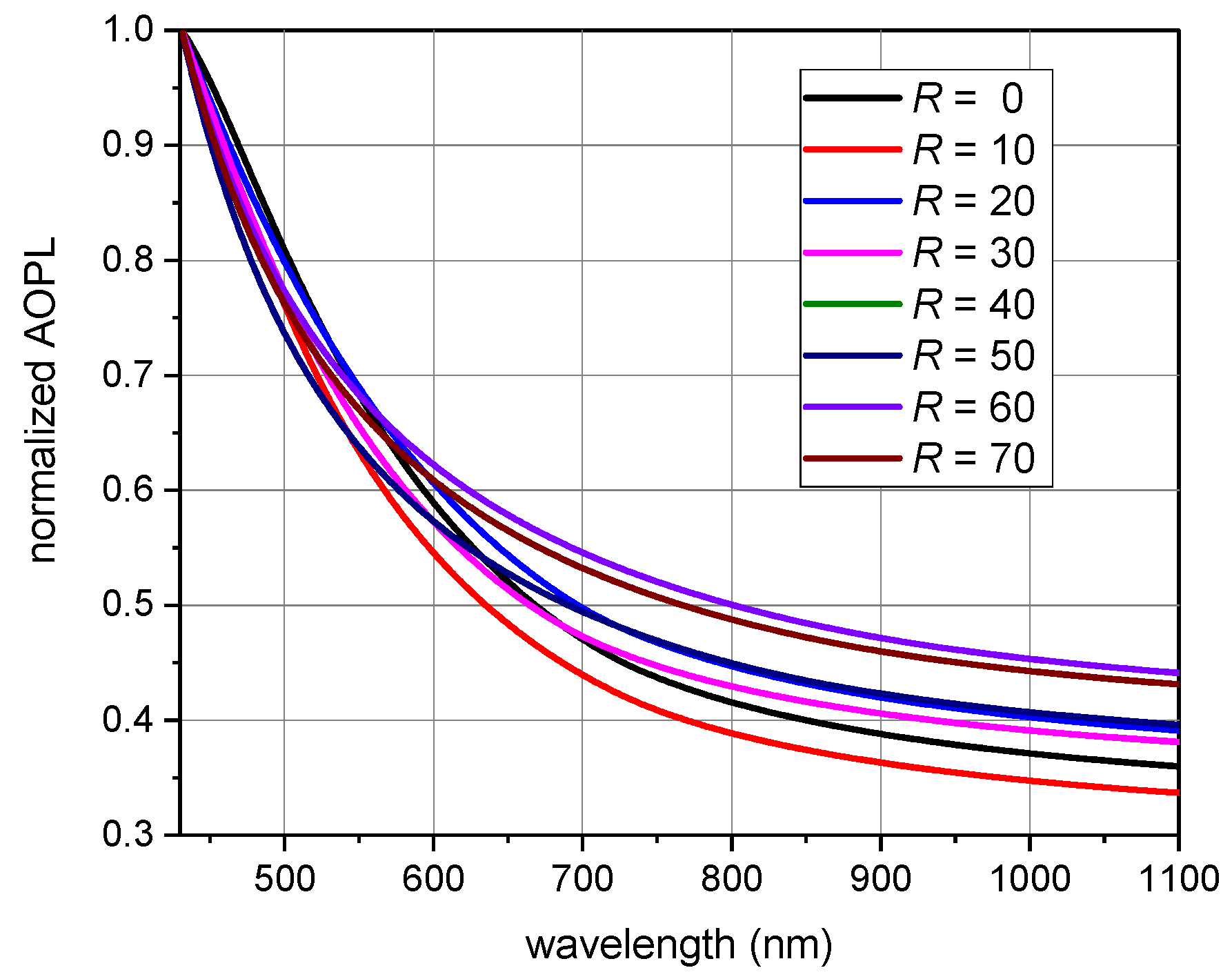
3.1. Single Pass Absorption and Optical Path Length
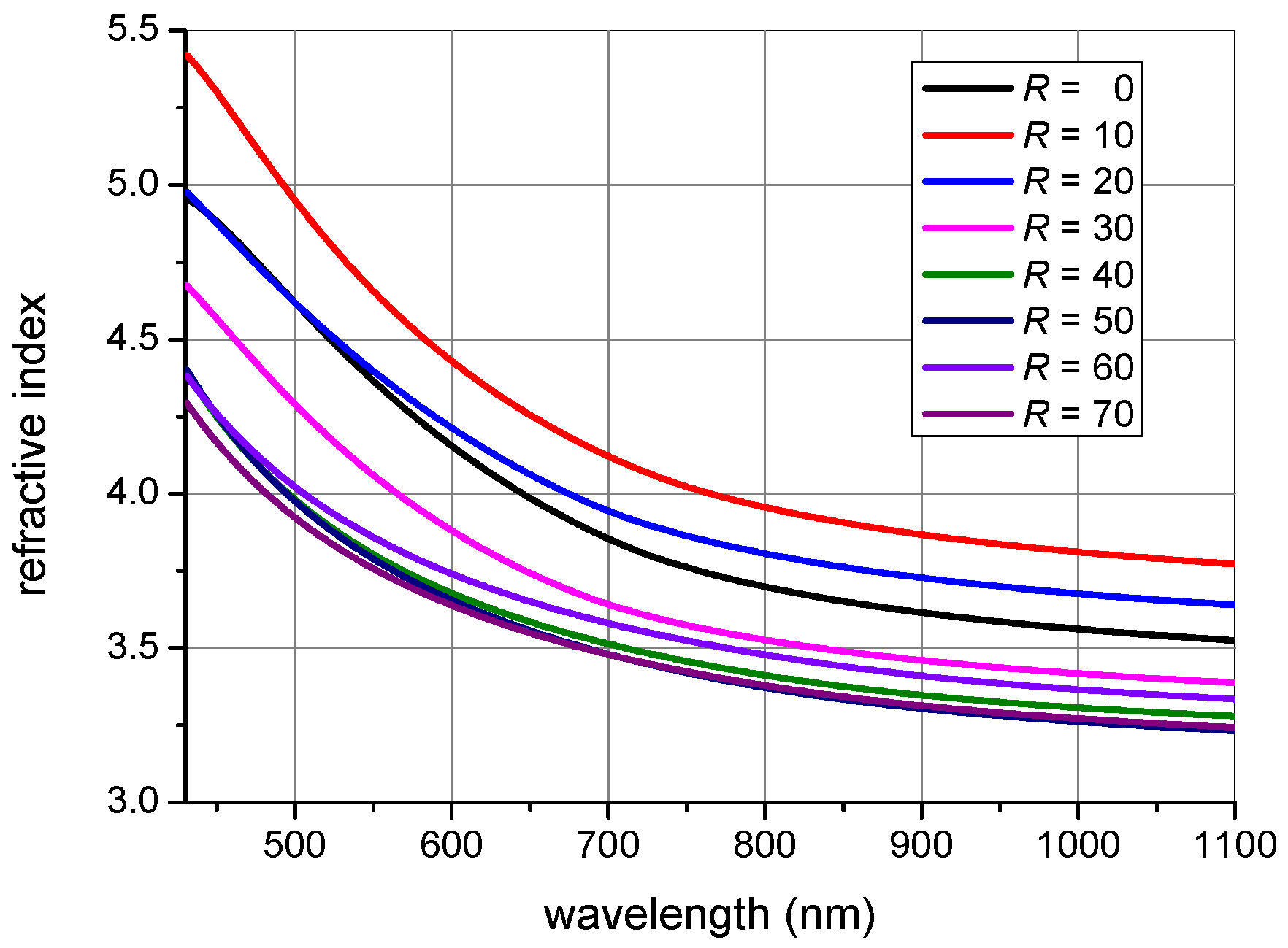
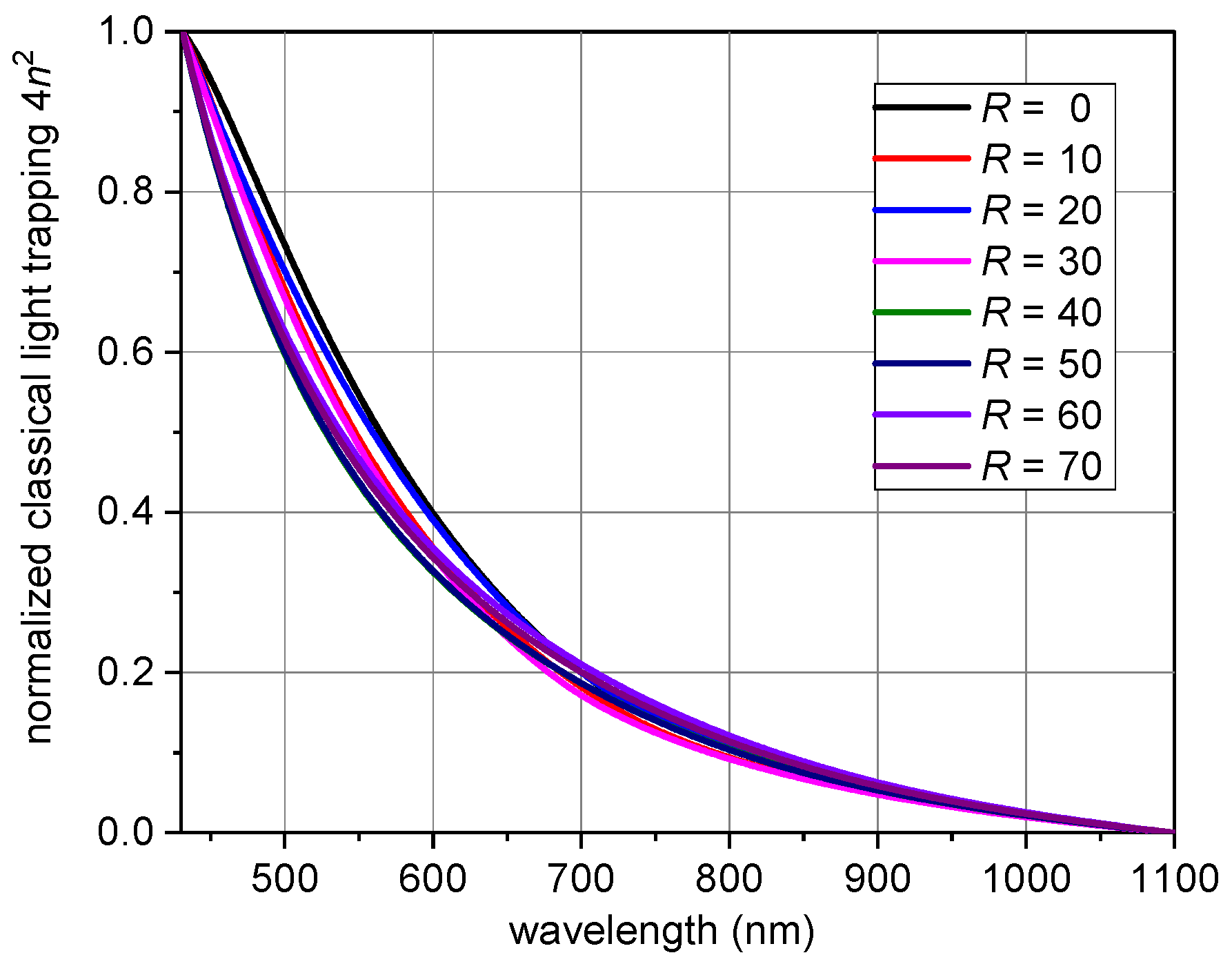
3.2. Refractive Indices and Absorption Coefficients in Light Trapping Limits
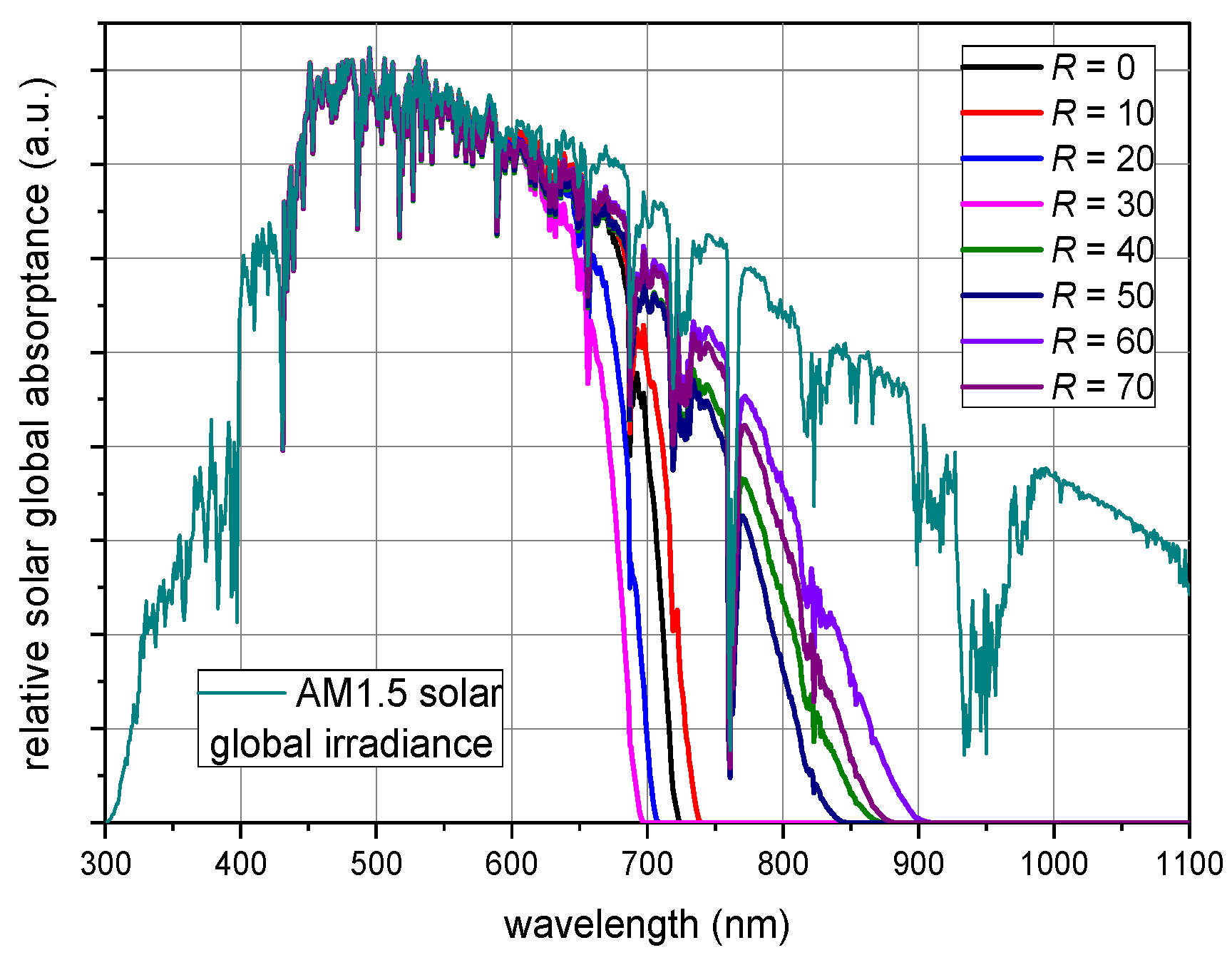
3.3. Absorption Characteristics versus Thin Film Structure and Microstructure
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ra’di, Y.; Simovski, C.R.; Tretyakov, S.A. Thin Perfect Absorbers for Electromagnetic Waves: Theory, Design, and Realizations. Phys. Rev. Appl. 2015, 3, 037001. [Google Scholar] [CrossRef]
- Dushaq, G.; Nayfeh, A.; Rasras, M. Tuning the optical properties of RF-PECVD grown μc-Si:H thin films using different hydrogen flow rate. Superlattices Microst. 2017, 107, 172–177. [Google Scholar] [CrossRef]
- Li, K.; Haque, S.; Martins, A.; Fortunato, E.; Martins, R.; Mendes, M.J.; Schuster, C.S. Light trapping in solar cells: Simple design rules to maximize absorption. Optica 2020, 7, 1377–1384. [Google Scholar] [CrossRef]
- Mohammed, M.A.; Melskens, J.; Stabile, R.; Pagliano, F.; Li, C.; Kessels, W.M.M.; Raz, O. Metastable Refractive Index Manipulation in Hydrogenated Amorphous Silicon for Reconfigurable Photonics. Adv. Opt. Mater. 2020, 8, 1901680. [Google Scholar] [CrossRef]
- Khan, A.D.; Rehman, Q.; Khan, A.D.; Subhan, F.E.; Noman, M.; Ahmed, S.; Khan, H.A. Broadband Solar Energy Absorption in Plasmonic Thin-Film Amorphous Silicon Solar Cell. Coatings 2019, 9, 638. [Google Scholar] [CrossRef]
- Fonash, S.J. Introduction to Light Trapping in Solar Cell and Photodetector Devices; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Abdellatif, S.; Kirah, K.; Ghannam, R.; Khalil, A.S.G.; Anis, W. Enhancing the absorption capabilities of thin-film solar cells using sandwiched light trapping structures. Appl. Opt. 2015, 54, 5534–5541. [Google Scholar] [CrossRef] [PubMed]
- Burresi, M.; Pratesi, F.; Riboli, F.; Wiersma, D.S. Complex photonic structures for light harvesting. Adv. Opt. Mater. 2015, 3, 722–743. [Google Scholar] [CrossRef] [PubMed]
- Zeman, M.; Isabella, O.; Jäger, K.; Santbergen, R.; Solntsev, S.; Topic, M.; Krc, J. advanced light management approaches for thin-film silicon solar cells. Energy Procedia 2012, 15, 189–199. [Google Scholar] [CrossRef]
- Mallick, S.B.; Sergeant, N.P.; Agrawal, M.; Lee, J.-Y.; Peumans, P. Coherent light trapping in thin-film photovoltaics. MRS Bull. 2011, 36, 453–460. [Google Scholar] [CrossRef]
- Agrawal, M.; Peumans, P. Broadband optical absorption enhancement through coherent light trapping in thin-film photovoltaic cells. Opt. Express 2008, 16, 5385–5396. [Google Scholar] [CrossRef]
- Durmaz, Z.; Husein, S.; Saive, R. Thin silicon interference solar cells for targeted or broadband wavelength absorption enhancement. Opt. Express 2021, 29, 4324–4337. [Google Scholar] [CrossRef] [PubMed]
- Müllerová, J.; Šutta, P.; Calta, P.; Netrvalová, M.; Medlín, R. Modifications of effective optical properties of a-Si:H/a-SiNx:H multilayers by means of multilayer design and sublayer thickness. OSA Contin. 2020, 3, 1385–1397. [Google Scholar] [CrossRef]
- Mupparapu, R.; Vynck, K.; Svensson, T.; Burresi, M.; Viersma, D.S. Path length enhancement in disordered media for increased absorption. Opt. Express 2015, 23, A1472–A1484. [Google Scholar] [CrossRef] [PubMed]
- Kats, M.A.; Capasso, F. Optical absorbers based on strong interference in ultra-thin films. Laser Photonics Rev. 2016, 10, 735–749. [Google Scholar] [CrossRef]
- Ajmal, H.M.S.; Khan, F.; Nam, K.; Kim, H.Y.; Kim, S.D. Ultraviolet photodetection based on high-performance Co-plus-Ni doped ZnO nanorods grown by hydrothermal method on transparent plastic substrate. Nanomaterials 2020, 10, 1225. [Google Scholar] [CrossRef] [PubMed]
- Ajmal, H.M.S.; Khan, F.; Huda, N.U.; Lee, S.; Nam, K.; Kim, H.Y.; Eom, T.-H.; Kim, S.D. High-performance flexible ultraviolet photodetectors with Ni/Cu-codoped ZnO nanorods grown on PET substrates. Nanomaterials 2019, 9, 1067. [Google Scholar] [CrossRef]
- Massiot, I.; Cattoni, A.; Collin, S. Progress and prospects for ultrathin solar cells. Nat. Energy 2020, 5, 959–972. [Google Scholar] [CrossRef]
- Müllerová, J.; Šutta, P.; Prušáková, L.; Netrvalová, M. Dispersive and BEMA investigation on optical properties of photovoltaic thin films. SPIE Proc. 2014, 9441, 94411J. [Google Scholar]
- Müllerová, J.; Šutta, P.; van Elzakker, G.; Zeman, M.; Mikula, M. Microstructure of hydrogenated silicon thin films prepared from silane diluted with hydrogen. Appl. Surf. Sci. 2008, 254, 3690–3695. [Google Scholar] [CrossRef]
- Gope, J.; Kumar, S.; Parashar, A.; Dayal, S.; Rauthan, C.M.S.; Srivastava, P.C. Effect of hydrogen content and bonding environment on mechanical properties of hydrogenated silicon films deposited by high-frequency PECVD process. ISRN Nanomater. 2012, 2012, 429348. [Google Scholar] [CrossRef]
- Schmidt, K.J.; Lin, Y.; Beaudoin, M.; Xia, G.; O’Leary, S.K.; Yue, G.; Yan, B. The mean crystallite size within a hydrogenated nanocrystalline silicon based photovoltaic solar cell and its role in determining the corresponding crystalline volume fraction. Can. J. Phys. 2014, 92, 857–861. [Google Scholar] [CrossRef]
- Park, Y.-B.; Rhee, Y.-B. Microstructure and initial growth characteristics of the low temperature microcrystalline silicon films on silicon nitride surface. J. Appl. Phys. 2001, 90, 217–221. [Google Scholar] [CrossRef][Green Version]
- Chen, S.-H.; Wang, H.-W.; Chang, T.-W. Absorption coefficient modeling of microcrystalline silicon thin film using Maxwell-Garnett effective medium theory. Opt. Express 2012, 20, A197–A2004. [Google Scholar] [CrossRef] [PubMed]
- Poruba, A.; Fejfar, A.; Remes, Z.; Springer, J.; Vanecek, M.; Kocka, J.; Meier, J.; Torres, P.; Shah, A. Optical absorption and light scattering in microcrystalline silicon thin films and solar cells. J. Appl. Phys. 2000, 88, 148–160. [Google Scholar] [CrossRef]
- Müllerová, J.; Šutta, P. On some ambiguities of the absorption edge and optical band gaps of amorphous and polycrystalline semiconductors. Commun. Sci. Lett. Univer. Zilina 2018, 19, 9–15. [Google Scholar]
- Yablonovitch, E.; Cody, G.D. Intensity enhancement in textured optical sheets for solar cells. IEEE Trans. Electron. Dev. 1982, 29, 300–305. [Google Scholar] [CrossRef]
- Andreani, L.C.; Bozzola, A.; Kowalczewski, P.; Liscidini, M.; Redorici, L. Silicon solar cells: Toward the efficiency limits. Adv. Phys. X 2019, 4, 1548305. [Google Scholar] [CrossRef]
- Zhao, H.; Schiff, E.A. A Light-trapping metric for solar cells with application to cadmium telluride and silicon. IEEE J. Photovolt. 2015, 5, 487–497. [Google Scholar] [CrossRef]
- Saive, R. Light trapping in thin silicon solar cells: A review on fundamentals and technologies. Prog. Photovolt. Res. Appl. 2021, 1–13. [Google Scholar]
- Cho, C.; Jeong, S.; Lee, J.-Y. Optical study of thin-film photovoltaic cells with apparent optical path length. J. Opt. 2016, 18, 094001. [Google Scholar] [CrossRef]
- Tiedje, T.; Yablonovitch, E.; Cody, G.D.; Brooks, B. Limiting Efficiency of Silicon Solar Cells. IEEE Trans. Electron. Dev. 1984, ED-31, 711–716. [Google Scholar] [CrossRef]
- Green, M.A. Lambertian light trapping in textured solar cells and light-emitting diodes: Analytical Solutions. Prog. Photovolt. Res. Appl. 2002, 10, 235–241. [Google Scholar] [CrossRef]
- Wang, K.X.; Yu, Z.; Liu, V.; Cui, Y.; Fan, S. Absorption enhancement in ultrathin crystalline silicon solar cells with antireflection and light-trapping nanocone gratings. Nano Lett. 2012, 12, 1616–1619. [Google Scholar] [CrossRef] [PubMed]
- Ingenito, A.; Isabella, O.; Zeman, M. Experimental demonstration of 4n2 classical absorption limit in nanotextured ultrathin solar cells with dielectric omnidirectional back reflector. ACS Photonics 2014, 1, 270–278. [Google Scholar] [CrossRef]
- Weinstein, L.A.; Hsu, W.-C.; Yerci, S.; Boriskina, S.V.; Chen, G. Enhanced absorption of thin-film photovoltaic cells using optical cavity. J. Opt. 2015, 17, 055901. [Google Scholar] [CrossRef]
- ASTM. Standard Tables for Reference Solar Spectral Irradiances, Standard G173-03; American Society for Testing and Materials: Philadelphia, PA, USA, 2012. [Google Scholar]
- Müllerová, J.; Prušáková, L.; Netrvalová, M.; Vavruňková, V.; Šutta, P. A study of optical absorption in amorphous hydrogenated silicon thin films of varied thickness. Appl. Surf. Sci. 2010, 256, 5567–5671. [Google Scholar] [CrossRef]
- Mazzarella, L.; Morales-Vilches, A.B.; Korte, L.; Schlatmann, R.; Stannowski, B. Versatility of nanocrystalline silicon films: From thin-film to perovskite/c-si tandem solar cell applications. Coatings 2021, 10, 759. [Google Scholar] [CrossRef]



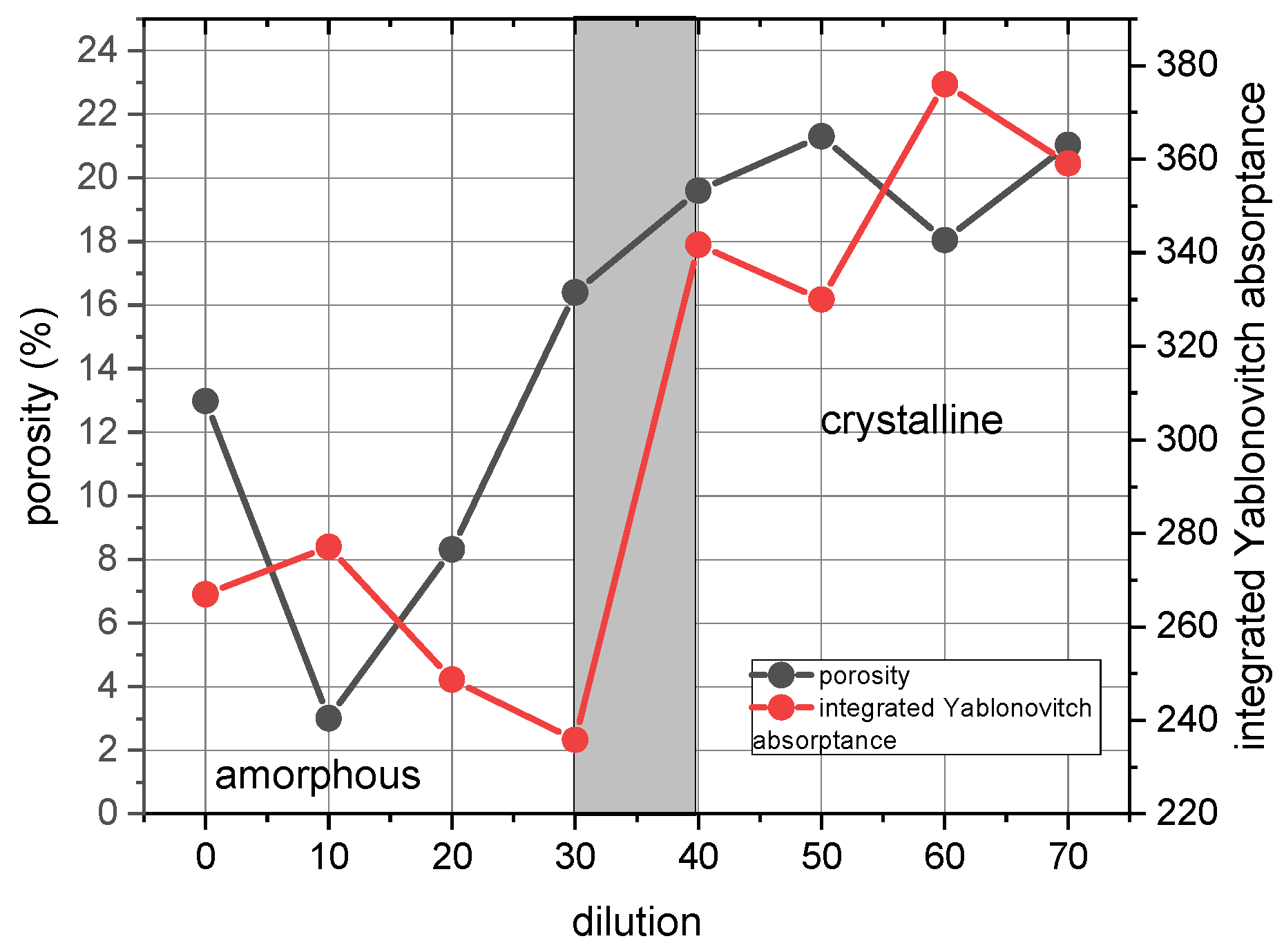
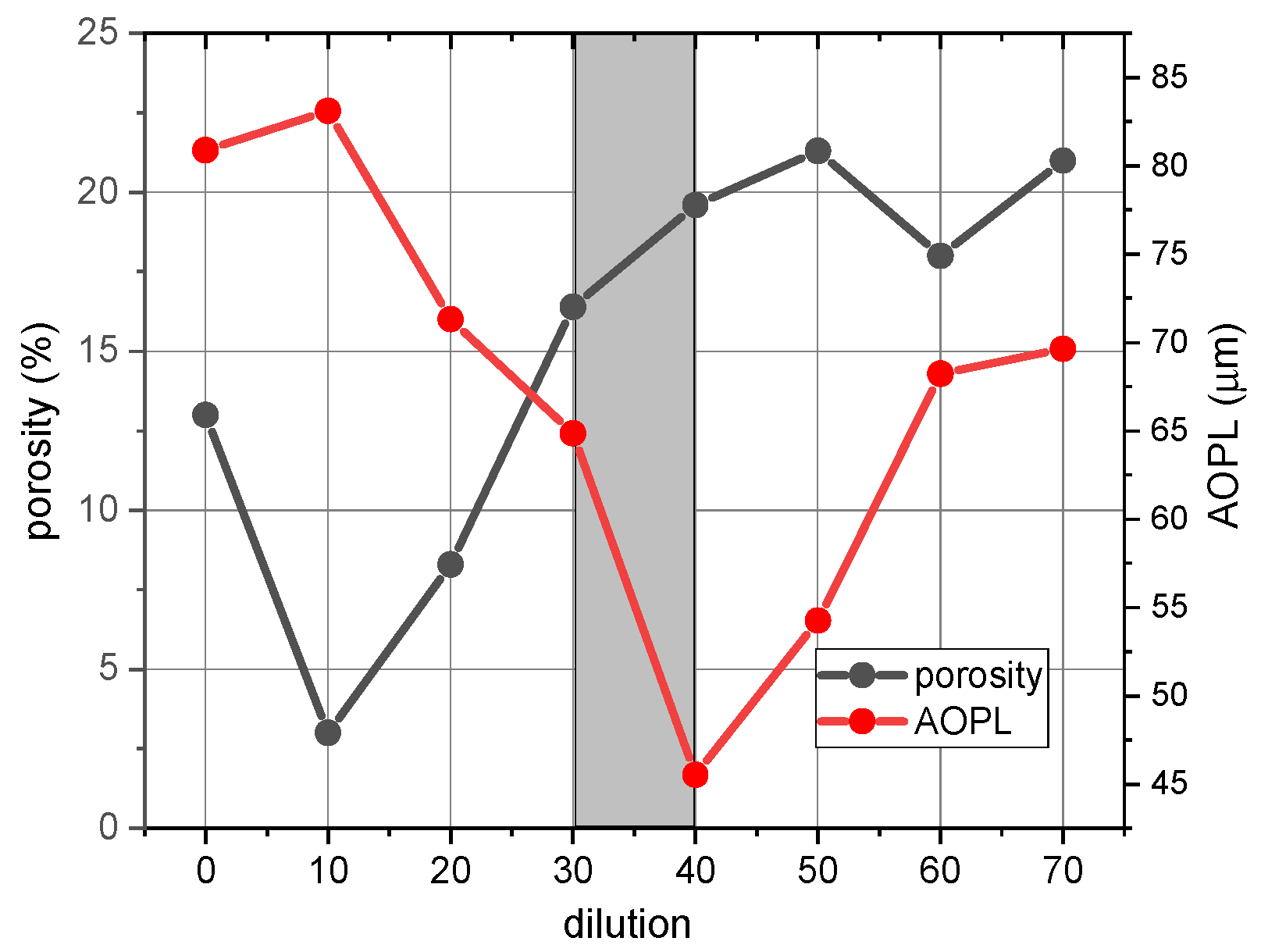
| R | d (nm) | pc/pa (%) | p (%) | cH (at.%) | LR (nm) | λb (nm) | AYin (a.u.) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 488 | 0 | 13.0 | 3.46 | 10.5 | - | 47.89 | 1689 | 705 | 267 |
| 10 | 400 | 0 | 3.0 | 3.73 | 12.6 | - | 55.65 | 1492 | 717 | 277 |
| 20 | 385 | 0 | 8.3 | 3.59 | 10.2 | - | 51.55 | 1382 | 688 | 249 |
| 30 | 427 | 0 | 16.4 | 3.36 | 7.8 | - | 45.16 | 1435 | 675 | 236 |
| 40 | 326 | 54 | 19.6 | 3.27 | 2.5 | 9.24 | 42.77 | 1066 | 791 | 342 |
| 50 | 406 | 63 | 21.3 | 3.22 | 2.3 | 9.25 | 41.47 | 1307 | 778 | 330 |
| 60 | 466 | 75 | 18.0 | 3.32 | 1.4 | 9.22 | 44.09 | 1547 | 827 | 376 |
| 70 | 517 | 77 | 21.0 | 3.23 | 2.2 | 9.27 | 41.73 | 1670 | 809 | 359 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Müllerová, J.; Šutta, P.; Holá, M. Optical Absorption in Si:H Thin Films: Revisiting the Role of the Refractive Index and the Absorption Coefficient. Coatings 2021, 11, 1081. https://doi.org/10.3390/coatings11091081
Müllerová J, Šutta P, Holá M. Optical Absorption in Si:H Thin Films: Revisiting the Role of the Refractive Index and the Absorption Coefficient. Coatings. 2021; 11(9):1081. https://doi.org/10.3390/coatings11091081
Chicago/Turabian StyleMüllerová, Jarmila, Pavol Šutta, and Michaela Holá. 2021. "Optical Absorption in Si:H Thin Films: Revisiting the Role of the Refractive Index and the Absorption Coefficient" Coatings 11, no. 9: 1081. https://doi.org/10.3390/coatings11091081
APA StyleMüllerová, J., Šutta, P., & Holá, M. (2021). Optical Absorption in Si:H Thin Films: Revisiting the Role of the Refractive Index and the Absorption Coefficient. Coatings, 11(9), 1081. https://doi.org/10.3390/coatings11091081





