On the Superconducting Critical Temperature of Heavily Disordered Interfaces Hosting Multi-Gap Superconductivity

Abstract

LaAlO${}_3$/SrTiO${}_3$ interfaces are a nice example of a two-dimensional electron gas, whose carrier density can be varied by top- and back-gating techniques. Due to the electron confinement near the interface, the two-dimensional band structure is split into sub-bands, and more than one sub-band can be filled when the carrier density increases. These interfaces also host superconductivity, and the interplay of two-dimensionality, multi-band character, with the possible occurrence of multi-gap superconductivity and disorder calls for a better understanding of finite-bandwidth effects on the superconducting critical temperature of heavily disordered multi-gap superconductors.

1. Introduction

Anderson’s theorem [1] states that superconductivity in a conventional s-wave superconductor is robust with respect to the introduction of (non-magnetic) impurities in the material, and the superconducting critical temperature $T_{\mathrm{c}}$ is, to some extent, independent of the amount of disorder in the system. On the other hand, an increase in $T_{\mathrm{c}}$ is generically expected when an increase in the number of superconducting carriers leads to the filling of additional conduction bands: the density of states increases, and the superconducting coupling increases accordingly with important effects on $T_{\mathrm{c}}$. So far, an increasing number of materials has been found to display multi-gap superconductivity, as for example, MgB${}_2$ [2], iron-based superconductors [3,4,5,6], and heavy fermions [7,8]. Owing to a large variety of behaviors and different sensitivity to the effects of disorders, the interplay between impurity scattering and multi-gap superconductivity has stimulated both experimental and theoretical reanalyses of this important issue. Here, we will consider the paradigmatic example of the SrTiO${}_3$-based interfaces as LaAlO${}_3$/SrTiO${}_3$ (LAO/STO), which are superconducting systems displaying various regimes as the number of carriers is changed by top- or back-gating. In particular, the confinement of carriers near the interface induces the splitting of the spectrum into discrete two-dimensional sub-bands. By changing the number of carriers and also depending on the orientation of the interface with respect to the crystal axes, different behaviors of $T_{\mathrm{c}}$ are observed. For (001)-oriented interfaces, the system is non-superconducting at low carrier densities, while the critical temperature rapidly increases above some filling threshold, which is likely related to the filling of some sub-band with a high density of states [9,10,11], so these make a case of their own. For (111)- or (110)-oriented interfaces, the system is always superconducting below a critical temperature. Although the situation is not completely settled as far as the absolute values of the carrier concentration is concerned, the various available results show that the critical temperature first slowly increases upon increasing the carrier density, while above an optimal carrier density (corresponding to the largest $T_{\mathrm{c}}$), it decreases more rapidly as an increasing number of charge carriers is introduced [12,13,14]. This decrease of $T_{\mathrm{c}}$ is intriguing because it is at odds with the idea that larger carrier density implies the involvement of more bands, and consequently, a larger density of states and a larger superconducting coupling. More specifically, it is found that a significant suppression of $T_{\mathrm{c}}$ takes place at a carrier density close to the value at which a Lifshitz transition occurs and an upper sub-band starts to be filled. One possible explanation for this counterintuitive behavior has been proposed in the Ref. [15], where a two-band system is considered, with an inter-band pairing interaction in the presence of elastic impurity scattering. In particular, for a repulsive inter-band interaction, one finds a strong pair-breaking effect when the chemical potential approaches the bottom of the upper band and this second band starts to interact with the first one. The aim of the present work is to systematically investigate the interplay of disorder, multi-band physics, and superconductivity in a range of parameters that is more pertinent to the LAO/STO interface, considering that while the lower band is in a BCS-like weak-coupling regime (henceforth, the acronym BCS stands for Bardeen-Cooper-Shrieffer), the second band enters the superconducting regime when the chemical potential approaches the bottom of the band by an energy of the order of the pairing energy cutoff $\Omega$ (set, for example, by the Debye frequency ${\omega }_{\mathrm{D}}$ of the phonons involved in pairing, $\Omega =\hslash {\omega }_{\mathrm{D}}$, where ℏ is the Planck constant). This is a situation typical of strong-coupling superconductivity with a Bose-Einstein condensation of Cooper pairs. This mixed regime for the two involved bands deserves a specific analysis, which we consider within our systematic investigation. In our work, we will also point out the crucial role of large-scale inhomogeneities to reproduce the $T_{\mathrm{c}}$ versus filling behavior experimentally observed. We neglect all weak-localization effects, but our interest is in the heavily disordered regime before weak-localization effects set in, but in a regime when the premises upon which Anderson’s theorem rests are violated.

The paper is organized as follows. In Section 2 we briefly summarize the theoretical model, particularly discussing the linearized gap equations from which we calculate the critical temperature. Albeit in a heavily disordered system the concept of multiple bands loses its meaning, as disorder mixes the band eigenstates, the eigenvalues of the clean system (and the corresponding densities of states) enter into the calculation, so we keep referring to the various bands in this loose sense. Since our goal here is to unravel all the ingredients that can trigger the observed suppression of the superconductivity one by one, the numerical results of Section 3 are grouped in subsections. We begin with the study of effects of a finite bandwidth and the effect of disorder in a single band, in Section 3.1. Then, in Section 3.2, we add a second uncoupled band to the system. The fully coupled s± disordered model is studied in Section 3.3. Finally, in Section 4 we will make our concluding remarks and discuss some perspectives of the present study.

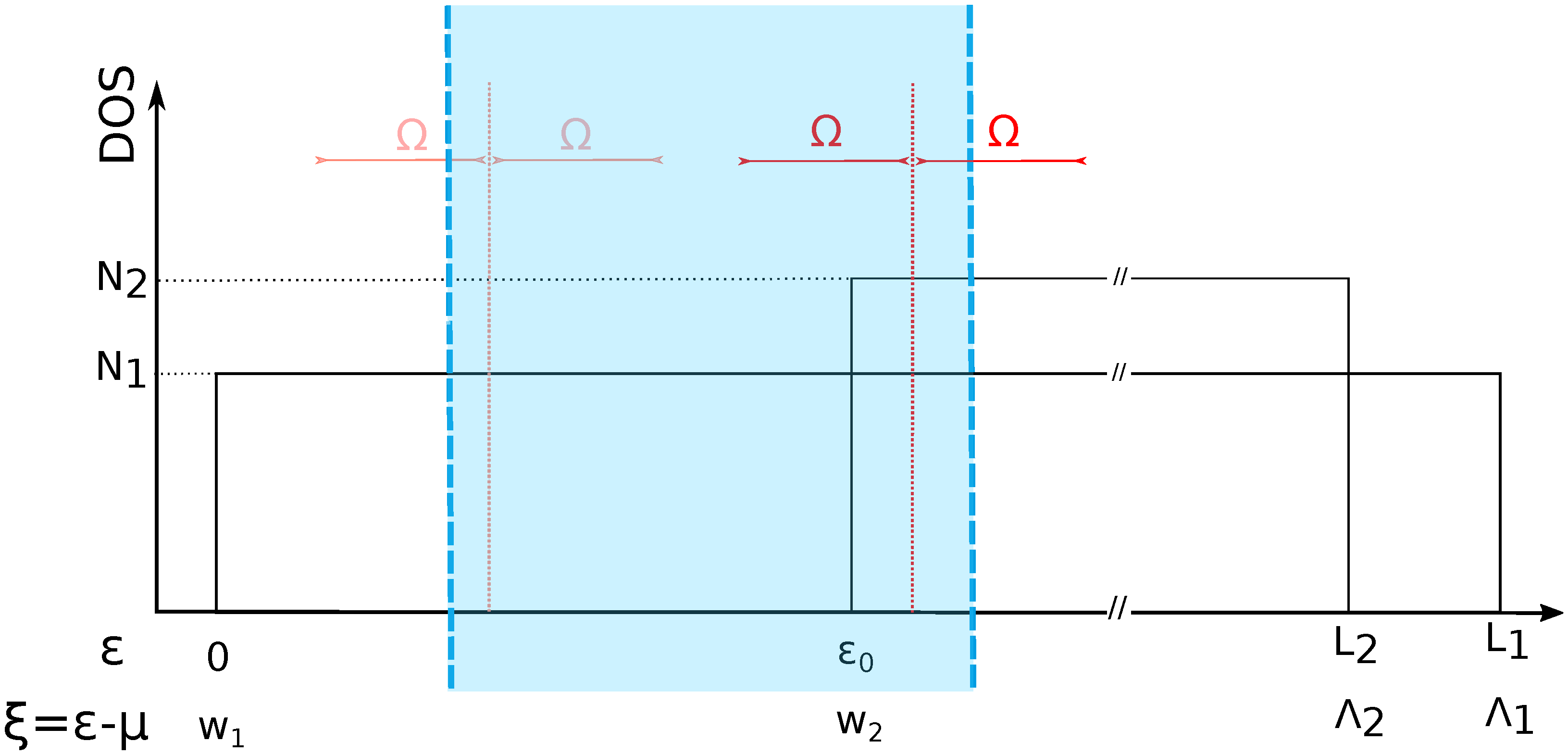
2. Two-Band Superconductor in the Presence of Disorder

Let us consider a two-band system, as in Figure 1, to represent the crudest possible description of a superconducting system where other bands come into play with increasing the carrier density. Here, both bands display a constant density of states (DOS), $N_1$ and $N_2$. We indicate the Debye energy (here meaning the characteristic cutoff scale of superconducting pairing) with $\Omega$ and

$$\lambda =\left(\begin{array}{cc}{\lambda }_{11}& {\lambda }_{12}\\ {\lambda }_{21}& {\lambda }_{22}\end{array}\right)$$

is the matrix of the bare coupling constant, the indices labeling the two bands of the clean system. We do not perform the self-consistent calculation of the matrix element of the pairing interaction starting from the exact electron wave functions in the potential well that confines the electrons and creates the sub-band structure, although it is known that this introduces further effects of modulation of $T_{\mathrm{c}}$ at the Lifshitz points, when a new band starts to be filled, or the topology of the Fermi surface changes [16,17,18]. Calling the edges of the two bands (with respect to the chemical potential, as it is suitable when dealing with superconducting systems) as $w_j$, for the lower band edge, and ${\Lambda }_j$ for the higher band edge, we have $w_1=-\mu$, $w_2={\epsilon }_0-\mu$ and ${\Lambda }_i=L_i-\mu$. As one can see, we are considering the system in an intermediate regime, where the lower band is described by the BCS theory since the pairing window $\mu \pm \Omega$ is fully contained within the band, while the upper band stays in Bose-Einstein condensation (henceforth, BEC) regime. This is because, when the chemical potential approaches the bottom of the upper band, the coupling between its carriers and the carriers in the lower band already starts to be effective when the chemical potential is below the Lifshitz point (which occurs when $\mu$ enters the upper band $\mu ={ϵ}_0$). This choice of parameter regime is motivated by the fact that, according to the experimental analyses [19,20], it is more appropriate to the LAO/STO interfaces [10,11,19] (see Section 3). We point out that in LAO/STO interfaces one of the two bands would be doubly degenerate—the upper, in the conventional (001) orientation, the lower, in the (110) orientation—so a three-band model would be more appropriate, at the expenses of a less transparent, and more heavily numerical, theoretical treatment. Since the main features of band interplay are already present in a two-band model, we keep our description as simple as possible, to highlight the crucial aspects.

Calculating the effect of disorder within the self-consistent Born approximation (see also the Refs. [15,21]), one finds the linearized gap equations

$$\left(\begin{array}{c}{\Delta }_1\\ {\Delta }_2\end{array}\right)=\left(\begin{array}{cc}{\lambda }_{11}& {\lambda }_{12}\\ {\lambda }_{21}& {\lambda }_{22}\end{array}\right)\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)\left(\begin{array}{c}{\Delta }_1\\ {\Delta }_2\end{array}\right),$$

(1)

which are needed to investigate the behavior of the critical temperature $T_{\mathrm{c}}$, identified as the first temperature at which the matrix on the right-hand side of Equation (1) develops an eigenvalue equal to one (coming from high temperature). The elements of the matrix A are given by

$$A_{ij}=k_{B}T\sum _n\frac{M_{ij}}{\det \left(M\right)}{\int }_{\max [-\Omega ,w_i]}^{\max [\Omega ,w_i]}\frac{d\xi }{{\tilde{\omega }}_n^2+{(\xi +h_n)}^2},$$

(2)

${\tilde{\omega }}_n$ and $h_n$ being, respectively, the Matsubara frequency shifted by disorder effects and the frequency-dependent correction to the chemical potential $\mu$, calculated self-consistently:

$$\left\{\begin{array}{c}{\tilde{\omega }}_n={\omega }_n+\frac{\Gamma {\tilde{\omega }}_n}{2}\sum _{j=1,2}{\tilde{f}}_{n,j}\hfill \\ \\ h_n=-\frac{\Gamma }{2}\sum _{j=1,2}{\tilde{g}}_{n,j},\hfill \end{array}\right.$$

(3)

where ${\omega }_n=(2n+1)\pi k_{B}T$, n ranging over integer numbers, is the Matsubara frequency of the clean system, $\Gamma$ is the disorder-induced broadening and sets the scale for the inverse lifetime of the charge carriers,

$${\tilde{f}}_{n,j}=\frac{1}{\pi }{\int }_{w_j}^{{\Lambda }_j}\frac{d\xi }{{\tilde{\omega }}_n^2+{(\xi +h_n)}^2},{\tilde{g}}_{n,j}=\frac{1}{\pi }{\int }_{w_j}^{{\Lambda }_j}\frac{(\xi +h_n)d\xi }{{\tilde{\omega }}_n^2+{(\xi +h_n)}^2},$$

and the matrix

$$M=\left(\begin{array}{cc}1-\frac{\Gamma }{2}{\tilde{f}}_{n,1}& \frac{\Gamma }{2}{\tilde{f}}_{n,1}\\ & \\ \frac{\Gamma }{2}{\tilde{f}}_{n,2}& 1-\frac{\Gamma }{2}{\tilde{f}}_{n,2}\end{array}\right)$$

(4)

introduces vertex corrections to the Cooper susceptibility due to disorder [22,23].

3. Results

The focus of this study is on the role of static impurity disorder on the Lifshitz transition of the multi-band system. As anticipated in Section 1, we neglect all weak-localization effects, but our interest is in the heavily disordered regime, which turns out to be pertinent to LAO/STO interfaces. In order to justify the last statement, we make some considerations about the order of magnitude of the main quantities involved, such as energies and temperatures, before showing our results. A reasonable estimate of disorder can be obtained from the mobilities $\overline{\mu }$ observed in LAO/STO interfaces. We use the standard relations $\Gamma =\frac{1}{2}\hslash {\tau }^{-1}$ and $\overline{\mu }=e\tau /m^{\ast }$, where $\tau$ is the scattering time, e the absolute value of the electron charge and $m^{\ast }$ is the electron effective mass. One should, however, keep in mind that the filling of different sub-bands, upon changing the carrier density, induces substantial variations of the mobility [20]. Then, for instance, in (110)-oriented LAO/STO interfaces, using the values of the experimentally determined mobilities, the energy scale associated with the inverse scattering time, $\hslash {\tau }^{-1}$, is found to range between approximately $0.3$ and 5 meV (so that $0.15$ meV $<\Gamma <2.5$ meV). In order to keep the model as simple as possible, we choose to keep $\tau$ constant, although it is clear that the above substantial variations in the mobility would imply a marked carrier density dependence of $\tau$.

Regarding the relevance the mixed BCS-BEC regime, this was chosen coherently with known experimental facts: on the one hand, the Debye energy in bulk STO is of the order of $\Omega =400$ K $·k_B=34.5$ meV [24], while multi-gap superconductivity is observed at a gate voltage corresponding approximately to ${\epsilon }_0=90$ meV. Using reasonable estimates for the DOS and filling in the various sub-bands (as obtained from Hall measurements and the known values of the dielectric constant one can translate the experimental range of gate potential in experiments into the corresponding excursion of the chemical potential: the observational window ranges from ∼40 meV up to ∼110 meV (blue dashed vertical line in Figure 1 for an experimental setup with back-gating in a (110)-oriented LAO/STO interface [19]). Lastly, the critical temperature we consider in this work corresponds to the point at which the inverse Cooper susceptibility vanishes, so typical values of this quantity at low carrier density are around hundreds of mK ($T_{\mathrm{c}}\approx 0.2÷0.25$ K [12,19]). Since $T_{\mathrm{c}}$ is set by the Debye energy $\Omega$, the coupling constants $\lambda$ and, as it will be clear below, the disorder-induced broadening $\Gamma$, one has to adjust the bare coupling constants (in particular, ${\lambda }_{11}$), to obtain the correct order of magnitude of the critical temperature. The unit of measures are then Kelvin for the calculated temperatures and meV for all the energies. Equation (1) is solved numerically in the following subsections, adding one element at a time, in order to discern the role of the different physical ingredients. We start with a simple toy model, with just one finite band in the presence of disorder, and then add the second uncoupled band. Finally the effect of coupling the two bands will be investigated.

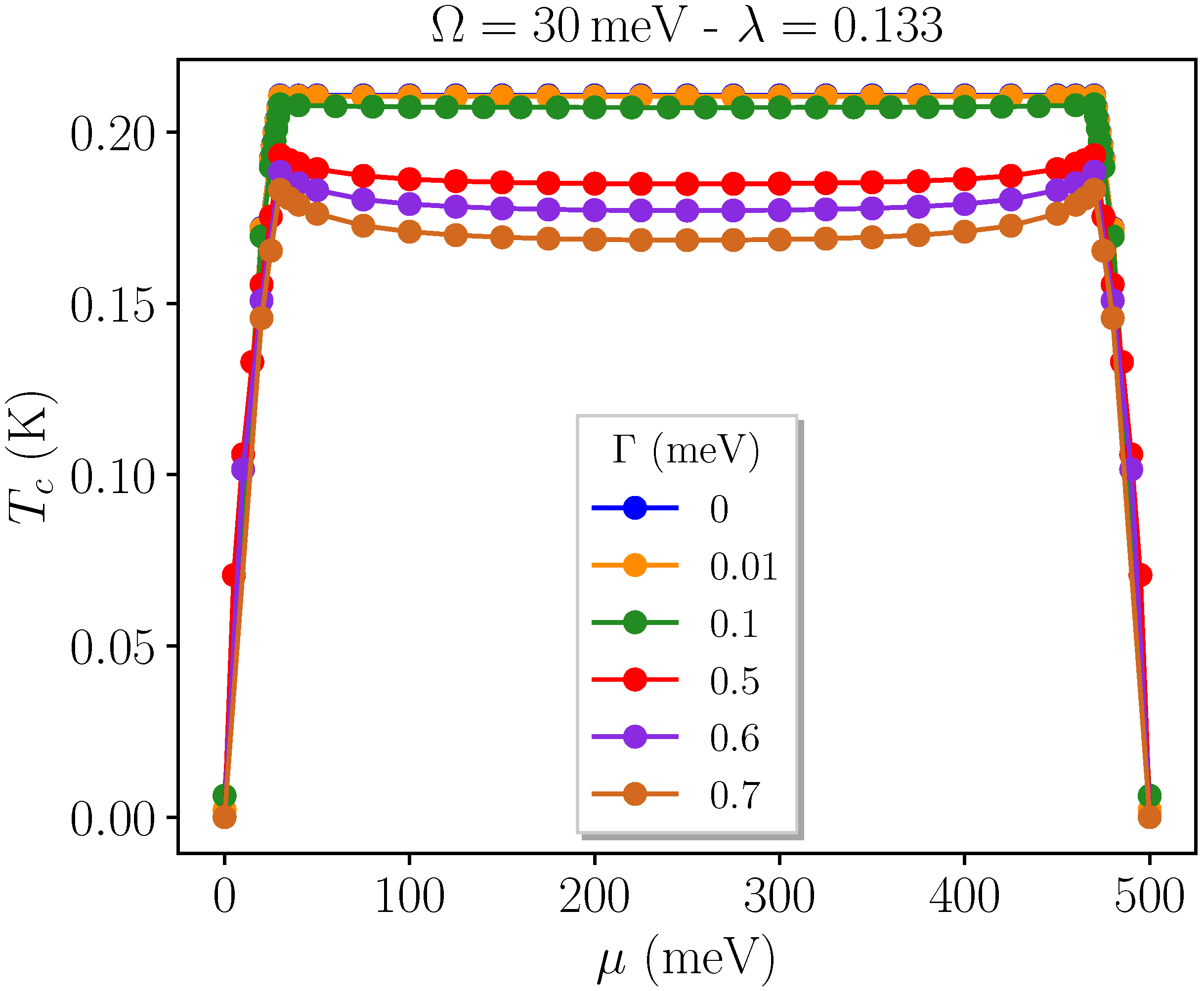
3.1. Toy Model: Finite-Bandwidth Effect in a Single-Band System

We first unravel the physics of the single-band system, observing both finite-bandwidth effects and the role of disorder-induced line and vertex corrections. Let us rewrite the equation for $T_{\mathrm{c}}$ as

$$1=\pi k_B{T}_{\mathrm{c}}\sum _{{\omega }_n}\frac{\lambda {\phi }_n}{1-\frac{\Gamma }{2}{\phi }_n},$$

(5)

where

$${\phi }_n=\frac{1}{\pi }{\int }_{\min \left(\max \right(-\Omega ,w),\Lambda )}^{\max \left(\max \right(\Omega ,\Lambda ),w)}\frac{d\xi }{{\tilde{\omega }}_n^2+{(\xi +h_n)}^2},$$

the band ranges from $w=-\mu$ to $\Lambda =L-\mu$, and $\Omega$ is the Debye energy. The corrected Matsubara frequency ${\tilde{\omega }}_n$ and the correction to the chemical potential $h_n$, are calculated from the coupled self-consistent equations:

$$\left\{\begin{array}{c}{\tilde{\omega }}_n={\omega }_n+\frac{\Gamma {\tilde{\omega }}_n}{2}{\tilde{f}}_n,\hfill \\ h_n=-\frac{\Gamma }{2}{\tilde{g}}_n.\hfill \end{array}\right.$$

(6)

In Figure 2 the critical temperature $T_{\mathrm{c}}$ is plotted as a function of the chemical potential $\mu$ for a finite band ranging between 0 and 500 meV, with a constant DOS. Clearly, finite bandwidth effects are important at the edges of the band, in particular in an energy range that is set by the Debye energy $\Omega$. We used here $\Omega =30$ meV and $\lambda =0.133$, so $T_{\mathrm{c}}\approx 0.21$ K in the clean case (blue circles in Figure 2). In agreement with Anderson’s theorem, a small amount of disorder, $\Gamma =0.01$ meV, does not change the value of the superconducting critical temperature $T_{\mathrm{c}}$. On the other hand, when $\Gamma$ is at least 50 times greater, $\Gamma >0.5$ meV, a substantial suppression of $T_{\mathrm{c}}$ is found. We would also like to highlight the more pronounced kink in the suppression of superconductivity, observed when both disorder and finite-bandwidth effects are present, at $\mu =w+\Omega$ and $\mu =\Lambda -\Omega$. More on this will be discussed in Section 4.

The role of both line and vertex corrections is shown in Figure 3, where larger values of the Debye energy $\Omega$ and of the coupling constant $\lambda$ are considered to emphasize the effects. In particular, $\Omega$ = 60 meV enhances the finite bandwidth effects at the edges of the band, while the increase of the critical temperature, taking $\lambda =0.19$, was necessary in order to emphasize the effects of the corrections, in particular the effect of the vertex correction. Specifically, looking at Figure 3c, for $\Gamma$ = 0.5 meV the effect of the line correction alone (green line) is so important that it can drastically suppress the critical temperature. This is a trend that we observe also in Figure 3b and also slightly in Figure 3a, although the effect here is really small: the line correction, that is, the correction to the Matsubara frequency in Equation (3), lowers substantially the critical temperature while the vertex correction, that is, the matrix M in Equation (4), largely compensates the line correction almost completely restoring the clean value of the critical temperature $T_{\mathrm{c}}\left(\Gamma =0\right)$. This is a clear manifestation of Anderson’s theorem, which, as it is well-known, can be rephrased by stating that superconductivity is robust against disorder whenever self-energy (line) corrections coexist and get (largely) cancelled by vertex corrections. On the contrary, as it is again well-known, whenever the wave symmetry or the magnetic character of impurities leads to vanishing or small vertex corrections, the premises for Anderson’s theorem to apply no longer hold.

Finally, let us stress once again the importance of the numbers involved. It is in fact of great interest for both theoreticians, whose final goal is to describe real systems, and experimentalist to understand quantitatively how all the parameters and quantities involved interplay and contribute individually to the suppression of $T_{\mathrm{c}}$. In the case at issue here, we observe that the suppression of the critical temperature due to the presence of disorder is of the same order of magnitude, that is, few tens of mK, independently of the value of $T_{\mathrm{c}}$ in the clean case. Although this is not surprising, since $T_{\mathrm{c}}$ depends only on the Debye energy $\Omega$ and the coupling constant $\lambda$, which are unrelated to the disorder-induced broadening $\Gamma$, the relative suppression on $T_{\mathrm{c}}$ can be significant. Calling $\delta T_{\mathrm{c}}=T_{\mathrm{c}}\left(\Gamma =0\right)-T_{\mathrm{c}}(\Gamma )$ the difference between the critical temperature of the clean system and the one of the disordered system, and comparing our results for $\Gamma =0.5$ meV in Figure 2 (red dots), where $T_{\mathrm{c}}\left(\Gamma =0\right)=0.21$ K, and in Figure 3c (orange dots), where $T_{\mathrm{c}}\left(\Gamma =0\right)=4.03$ K, we find, respectively, $\delta T_{\mathrm{c}}/T_{\mathrm{c}}\left(\Gamma =0\right)\approx 0.1$ and $\delta T_{\mathrm{c}}/T_{\mathrm{c}}\left(\Gamma =0\right)=0.01$. This shows that the same disorder becomes relatively more important in systems with lower critical temperature.

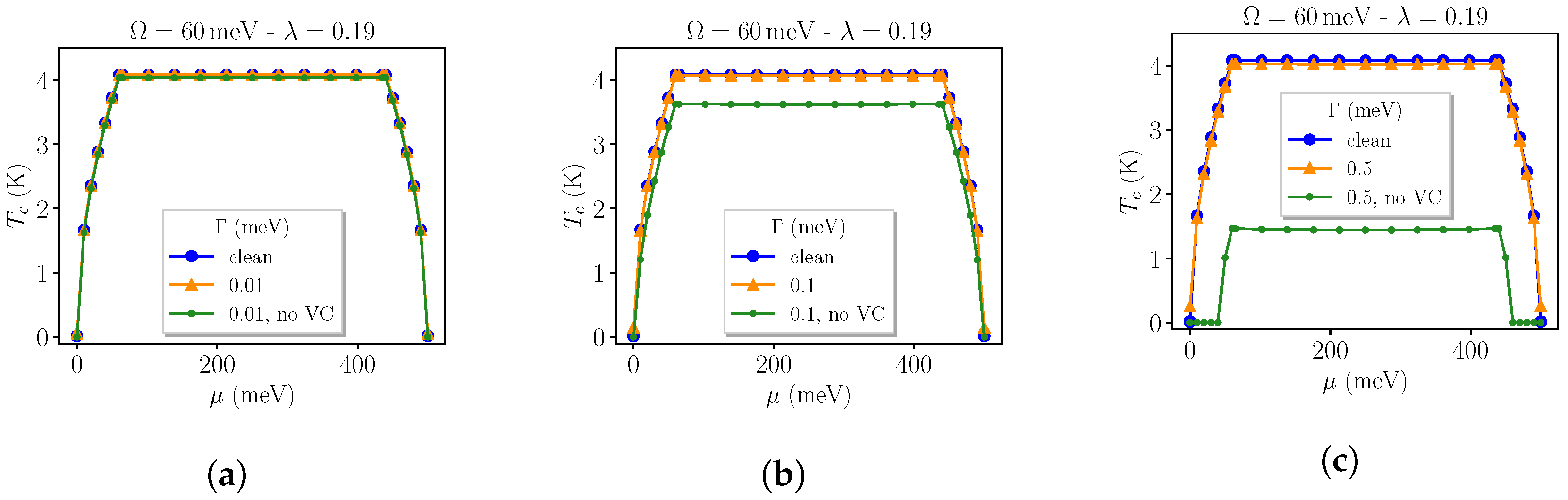
3.2. Two Uncoupled Disordered Bands

We present here the results of our calculations in an intermediate case between the one-band model studied above and the full two-band disordered model. In other words, we add the second band to the system, keeping the two bands uncoupled, that is, ${\lambda }_{12}={\lambda }_{21}=0$. Thus, Equation (1) reduces to

$$\left\{\begin{array}{c}{\Delta }_1={\lambda }_{11}(A_{11}{\Delta }_1+A_{12}{\Delta }_2)\hfill \\ {\Delta }_2={\lambda }_{22}(A_{21}{\Delta }_1+A_{22}{\Delta }_2)\hfill \end{array}\right.$$

(7)

Hence, even if formally, the inter-band couplings are set to zero, the disorder still couples the two bands because electrons can be scattered from one band to the other (hence, the loose meaning of the multi-band description in the presence of disorder), even though the pairs are still formed within each band separately. The parameters used are ${\lambda }_{11}={\lambda }_{22}=0.135$ and $\Omega =34.5$ meV, and the lower edge of the second band is ${\epsilon }_0$ = 90 meV. As one can see from Figure 4, increasing the chemical potential, a gradual decrease of the critical temperature is observed, coherently with the decrease observed in the toy model of Section 3.1, then a substantial suppression of the critical temperature is observed near the Lifshitz transition. Further increasing $\mu$, $T_{\mathrm{c}}$ starts to rise again, while the second band starts to be filled. Eventually, if the chemical potential enters well inside the second band, a situation similar to the one described in Section 3.1 should occur, albeit without particle-hole symmetry (for a generic relative position of the two bands), so that the maximum suppression of $T_{\mathrm{c}}$ (with respect to the value in the clean two-band system) due to finite-bandwidth effects is no longer expected to be located when the chemical potential reaches the middle of either bands.

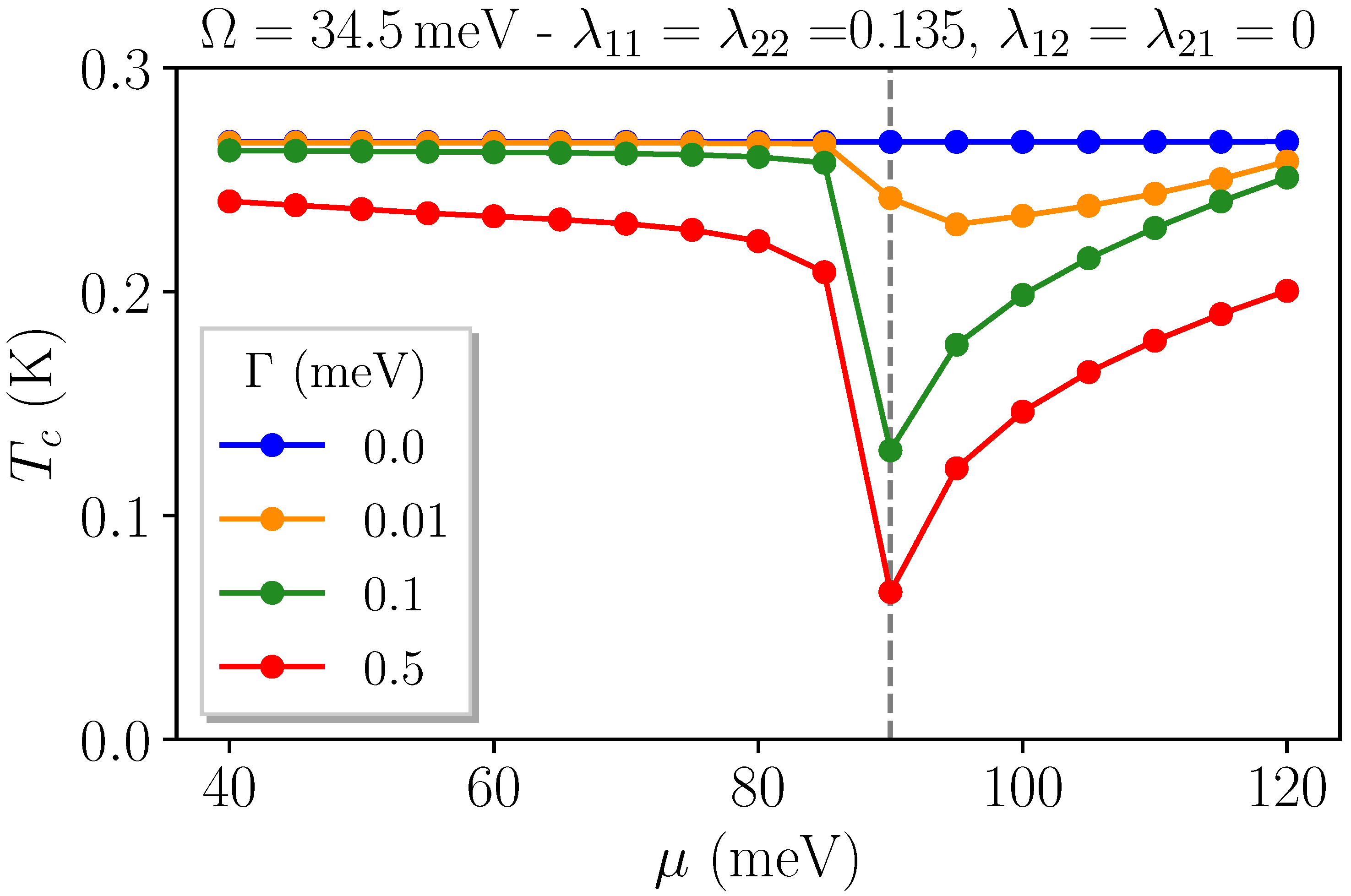
3.3. Two Coupled Disordered Bands

We finally discuss the complete model as presented in Section 2. We choose for the disorder-induced broadening the value $\Gamma =0.6$ meV, corresponding to $\hslash {\tau }^{-1}$ = 1.2 meV${}^{-1}$, and we tune the values of the coupling constants to obtain critical temperatures in the range of the values observed for LAO/STO. A further simplification we make, besides taking $\Gamma$ as independent of the carrier density, is to keep the two DOS equal $N_1=N_2$; otherwise, one should take the inter-band coupling constants obeying the relation ${\lambda }_{12}={\lambda }_{21}{N}_2/N_1$ [19]. Since in LAO/STO interfaces the DOS involved are typically of the same order, this simplification is not affecting substantially our results, with the noticeable exception of the (001) oriented interface, where the DOS of the lowermost sub-band is so much smaller than the DOS in the upper sub-bands, that superconductivity is suppressed altogether when the carrier concentration is not large enough to fill the upper sub-bands [9].

Setting $\Omega =34.5$ meV, the initial decrease of the critical temperature is due to finite bandwidth effects, as it was clear from the one band toy model presented in Section 3.1, while ${\lambda }_{11}$ tunes the order of magnitude of $T_{\mathrm{c}}$.

The depth and shape of the well at $\mu \approx {\epsilon }_0$ are strongly dependent both on the amount of disorder involved and on the values of the inter- and intra-band coupling constants. Similarly to ${\lambda }_{11}$, ${\lambda }_{22}$ rules the order of magnitude of $T_{\mathrm{c}}$ when the chemical potential is well inside the upper band ($\mu \gg {\epsilon }_0$), so necessarily it will affect both the minimum of the decrease of $T_{\mathrm{c}}$, at $\mu ={\epsilon }_0$, and its rise, for $\mu \gtrsim {\epsilon }_0$, as one can see from Figure 5a.

A subtler aspect is, however, the role of the inter-band coupling constants. As stated in the Ref. [15], sub-leading negative inter-band coupling constants, together with a small disorder, can induce the observed pair-breaking effect, while an attractive inter-band interaction only produce a much smaller suppression of $T_{\mathrm{c}}$ when the chemical potential approaches the edge of the second band. Nonetheless, in a strongly disordered system, this statement is not so clearcut. In Figure 5b we plot the curves $T_{\mathrm{c}}$ vs. $\mu$ for different values of the inter-band coupling constant. As one can see, while ${\lambda }_{12}={\lambda }_{21}=-{\lambda }_{11}·{10}^{-1}$ is indeed enough for the critical temperature to be zero in a wide range of values of the chemical potential (90 meV $<\mu <$ 100 meV, violet dots), a sub-leading positive coupling constant ${\lambda }_{12}={\lambda }_{21}=+{\lambda }_{11}·{10}^{-2}$ (lightblue dots) still generates a suppression of $T_{\mathrm{c}}$ at $\mu ={\epsilon }_0$ and the three curves with $-{\lambda }_{11}·{10}^{-2}<{\lambda }_{12}<+{\lambda }_{11}·{10}^{-2}$ (light blue, green, and yellow dots) present almost the same behavior in their increase inside the second band ($\mu >{\epsilon }_0$), stating the fact that the main pair-breaking effect is caused by the presence of a strong disorder.

4. Conclusions

Several theoretical concepts have been introduced to describe the non-monotonic behavior of the superconducting critical temperature at oxide interfaces as a function of the carrier concentration, highlighting, for example, the role of electron–electron correlations and spin–orbit interactions [14,24], or of the extended s-wave pairing symmetry [25].

In this work, we studied a two-gap model for a disordered two-band superconductor. Our scope was to highlight the role of disorder and inter-band scattering in the suppression of the superconducting critical temperature. In order to fully understand the details of the model, we studied it one step at a time. Owing to the obvious importance of the relative order of magnitude of the parameters describing the various physical regimes of the system under investigation, all these were approximately fixed according to the experimental measurement at our disposal in a specific relevant physical system, namely the LAO/STO interface.

As a matter of fact, although Anderson’s theorem is well satisfied in the weak-to-moderate disorder regime, the presence of a strong disorder is by itself an effective pair-breaking mechanism that suppresses superconductivity, even before single-particle localization effects set in. This effect becomes particularly relevant when a second band enters the game (even in the absence of a direct inter-band coupling). According to our model, once the scale of disorder is fixed to values compatible with transport measurements at the LAO/STO interface, the suppression of $T_{\mathrm{c}}$ seems to be of the order of few tens of mK, independently of the order of magnitude of $T_{\mathrm{c}}$ in the clean case. This leads to a relative suppression which is comparatively more and more important for those systems that have a low superconducting critical temperature: it is of about ten per cent, $\delta T_{\mathrm{c}}/T_{\mathrm{c}}\left(\Gamma =0\right)=0.1$, even in the one-band BCS system with a low clean critical temperature of a few hundreds of mK, that is, the same order of magnitude of $T_{\mathrm{c}}$ in LAO/STO heterostructures.

On the other hand, finite-bandwidth effects can also play a role in this framework: from the single band model, where the only element of pair-breaking is disorder, the variation of the chemical potential with respect to the band edges has a clear visible effect: considering, for instance, the lower edge to be at $w=0$ (Figure 1), the curve $T_{\mathrm{c}}$ vs. $\mu$ has different regimes. Initially, as it is well-known [9,10,11], it is rapidly increasing ($T_{\mathrm{c}}\sim \sqrt{\mu }$), as soon as the chemical potential enters the band and as long as its energy distance from the bottom of the band is smaller than the characteristic Debye energy ($\mu <\Omega$). Then, when $\mu$ increases, entering well inside the band ($\mu \gtrsim \Omega$), $T_{\mathrm{c}}$ slowly decreases as a consequence of finite-bandwidth effects. Further increasing $\mu$ leads to a nearly constant $T_{\mathrm{c}}$ when $\mu$ is around the center of the band, whereas $T_{\mathrm{c}}$ symmetrically increases slowly when the chemical potential enters the upper half of the band (because of particle-hole symmetry in a single band with constant DOS). These are rather weak effects that might obviously be overcome by other DOS details in real band structures (like, for example, van Hove singularities or Rashba spin-orbit couplings [26,27,28]), but they are often overlooked in theoretical analyses and it might be informative on some specific features (bandwidth, band edge positions, and so on) of the band structure specifically involved in experiments.

When adding the second band, this consideration is important in order to explain the first slow decrease (or possibly slow increase) in the $T_{\mathrm{c}}$ curve at low doping. Moreover, in Section 3.2 we also show that disorder alone can mix the two bands, scattering the electrons and generating a more pronounced suppression of the critical temperature in the vicinity of the Lifshitz point, where the second band starts to be filled.

Finally, we studied the effects of the coupling constants. In particular, once the disorder is set, the inter-band coupling is another key ingredient. It was already clear in the Ref. [15] that in the limit of weak disorder, a sub-leading repulsive interaction between bands is enough to observe the decrease of $T_{\mathrm{c}}$ at the Lifshitz transition. We are considering a much stronger disorder, with $\Gamma$ of the same order of magnitude as the one extracted from experiments on LAO/STO interfaces. On the one hand, we confirm that a repulsive coupling favors the suppression of $T_{\mathrm{c}}$, even bringing the critical temperature to vanish near ${\epsilon }_0$, over a finite chemical potential range, before it rises again when $\mu$ enters well inside the upper band. This happens already for ${\lambda }_{12}=-{\lambda }_{11}/10$. On the other hand, a small positive coupling between bands is still overcome by the disorder, especially near the Lifshitz transition.

We conclude our systematic analysis by noticing that in all cases the static point-like disorder due to quenched impurities creates a non-monotonic dip in $T_{\mathrm{c}}$ for $\mu$ around the Lifshitz point, bearing strong resemblance to the antiresonance phenomenon observed in clean systems when the pairing is calculated self-consistently [16,17,18]. This dip is substantially sharper than the rapid, yet smoother, decrease of $T_{\mathrm{c}}$ observed in LAO/STO interfaces [19]. To properly fit these data, it turned out to be important to consider of large-scale inhomogeneities in the density and in the superconducting properties of the interface. This not only confirmed the inhomogeneous character of LAO/STO interfaces [9,29,30,31,32,33], but naturally calls for further systematic investigation of the interplay between disorder due to quenched impurities and large-scale inhomogeneities in low-dimensional superconducting systems [34].