Patterning Configuration of Surface Hydrophilicity by Graphene Nanosheet towards the Inhibition of Ice Nucleation and Growth
Abstract
:1. Introduction
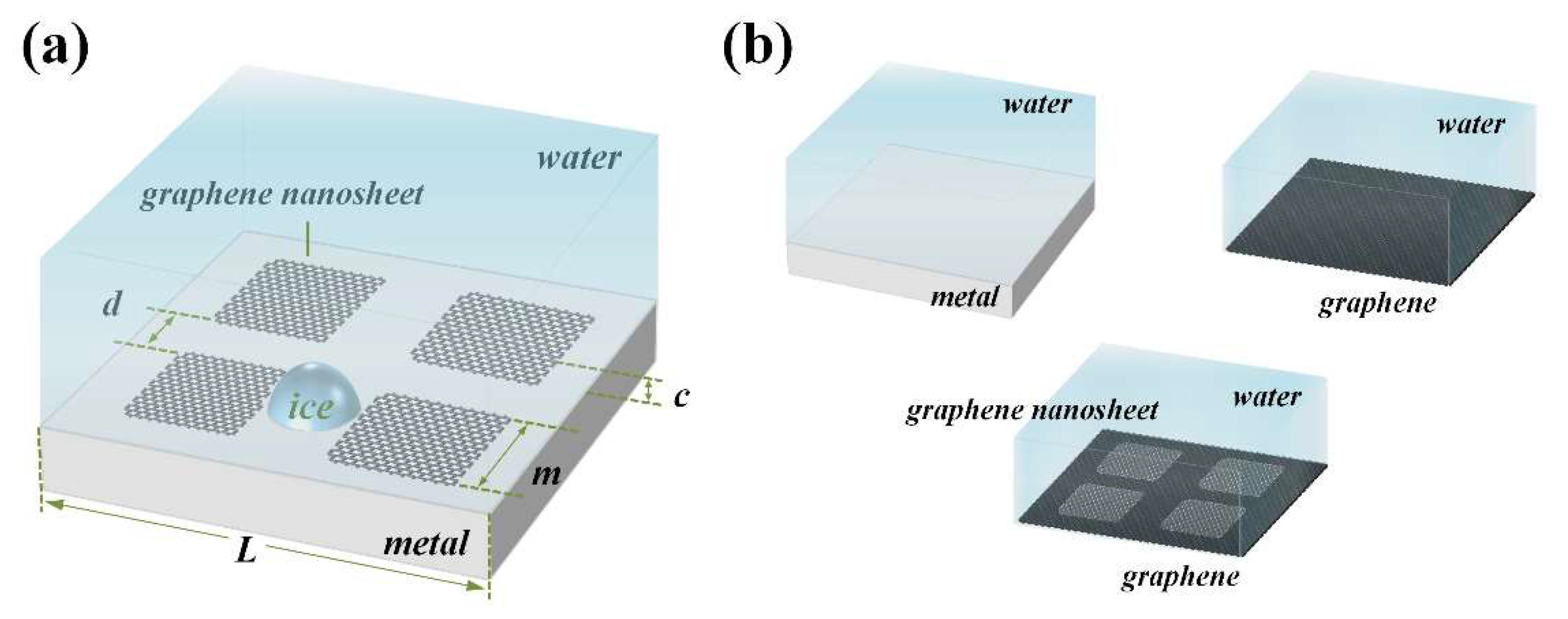
2. System and Simulations
3. Results and Discussion
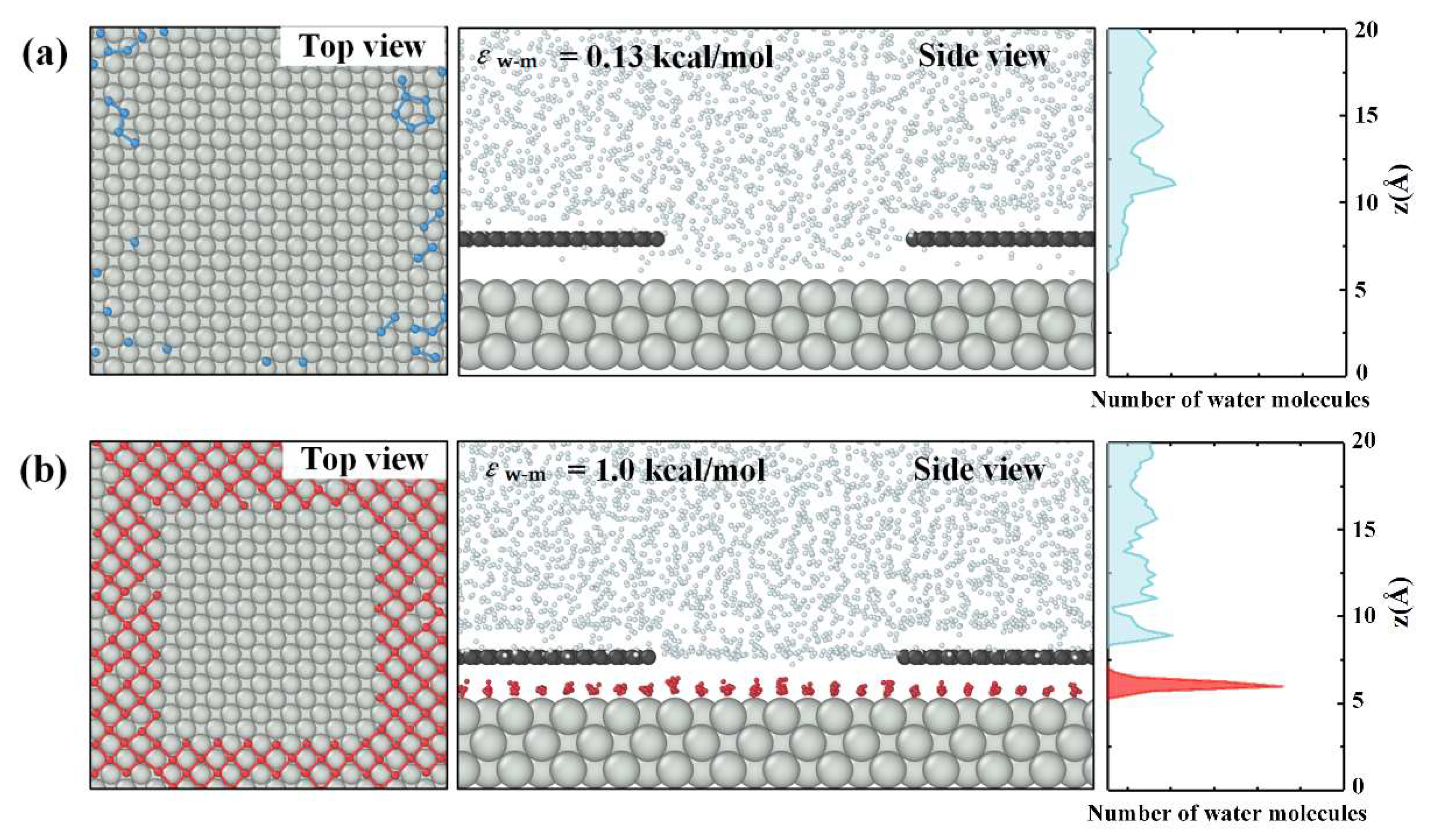
3.1. Surface Hydrophilicity and Ice Nucleation
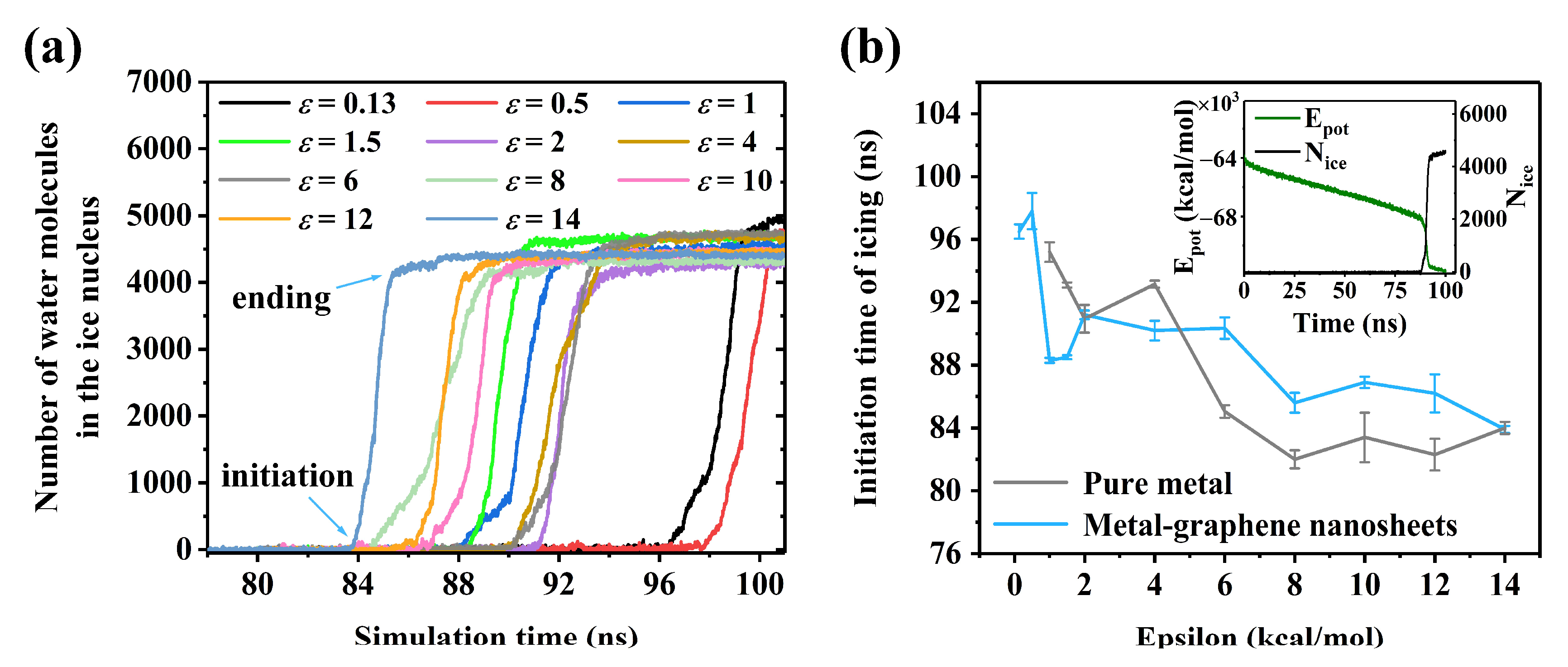
3.2. Priority of Ice Nucleation
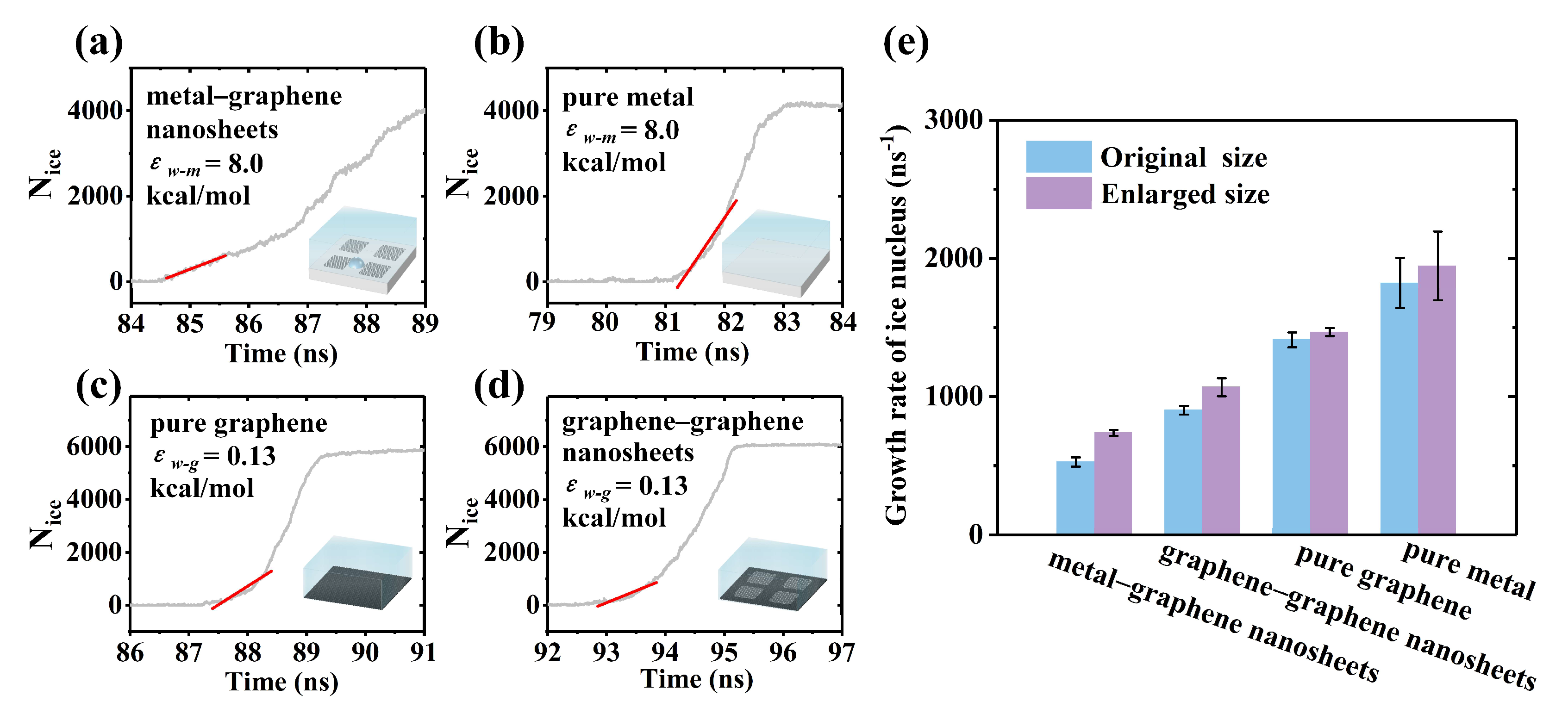
3.3. Ice Growth and Stunting Effect of Boundary Misorientation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, B.; Zhang, K.; Tao, C.; Zhao, Y.; Li, X.; Zhu, K.; Yuan, X. Strategies for anti-icing: Low surface energy or liquid-infused? RSC Adv. 2016, 6, 70251–70260. [Google Scholar] [CrossRef]
- Shen, Y.; Wu, X.; Tao, J.; Zhu, C.; Lai, Y.; Chen, Z. Icephobic materials: Fundamentals, performance evaluation, and applications. Prog. Mater. Sci. 2019, 103, 509–557. [Google Scholar] [CrossRef]
- Brini, E.; Fennell, C.J.; Fernandez-Serra, M.; Hribar-Lee, B.; Luksic, M.; Dill, K.A. How water’s properties are encoded in its molecular structure and energies. Chem. Rev. 2017, 117, 12385–12414. [Google Scholar]
- Fitzner, M.; Sosso, G.C.; Cox, S.J.; Michaelides, A. The many faces of heterogeneous ice nucleation: Interplay between surface morphology and hydrophobicity. J. Am. Chem. Soc. 2015, 137, 13658–13669. [Google Scholar] [CrossRef] [Green Version]
- Bayer, I.S. Mechanisms of surface icing and deicing technologies. Ice Adhes. Mech. Meas. Mitig. 2020, 325–359. [Google Scholar] [CrossRef]
- Ma, R.; Cao, D.; Zhu, C.; Tian, Y.; Peng, J.; Guo, J.; Chen, J.; Li, X.Z.; Francisco, J.S.; Zeng, X.C.; et al. Atomic imaging of the edge structure and growth of a two-dimensional hexagonal ice. Nature 2020, 577, 60–63. [Google Scholar] [CrossRef]
- Bi, Y.; Cabriolu, R.; Li, T. Heterogeneous Ice Nucleation controlled by the coupling of surface crystallinity and surface hydrophilicity. J. Phys. Chem. C 2016, 120, 1507–1514. [Google Scholar] [CrossRef] [Green Version]
- Jiang, J.; Li, G.X.; Sheng, Q.; Tang, G.H. Microscopic mechanism of ice nucleation: The effects of surface rough structure and wettability. Appl. Surf. Sci. 2020, 510, 145520. [Google Scholar] [CrossRef]
- Lin, Y.; Chen, H.; Wang, G.; Liu, A. Recent progress in preparation and anti-icing applications of superhydrophobic coatings. Coatings 2018, 8, 208. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Gao, X.; Li, Z. Roles of surface energy and temperature in heterogeneous ice nucleation. J. Phys. Chem. C 2017, 121, 11552–11559. [Google Scholar] [CrossRef]
- Li, C.; Gao, X.; Li, Z. Surface energy-mediated multistep pathways for heterogeneous ice nucleation. J. Phys. Chem. C 2018, 122, 9474–9479. [Google Scholar] [CrossRef]
- Luo, S.; Wang, J.; Li, Z. Homogeneous ice nucleation under shear. J. Phys. Chem. B 2020, 124, 3701–3708. [Google Scholar] [CrossRef] [PubMed]
- Metya, A.K.; Singh, J.K. Ice Nucleation on a graphite surface in the presence of nanoparticles. J. Phys. Chem. C 2018, 122, 19056–19066. [Google Scholar] [CrossRef]
- Matsuno, R.; Kokubo, Y.; Kumagai, S.; Takamatsu, S.; Hashimoto, K.; Takahara, A. Molecular design and characterization of ionic monomers with varying ion pair interaction energies. Macromolecules 2020, 53, 1629–1637. [Google Scholar] [CrossRef]
- Zhuo, Y.; Xiao, S.; Håkonsen, V.; He, J.; Zhang, Z. Anti-icing ionogel surfaces: Inhibiting ice nucleation, growth, and adhesion. ACS Mater. Lett. 2020, 2, 616–623. [Google Scholar] [CrossRef]
- Yue, X.; Liu, W.; Wang, Y. Effects of black silicon surface structures on wetting behaviors, single water droplet icing and frosting under natural convection conditions. Surf. Coat. Technol. 2016, 307, 278–286. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.-g. Sessile droplet freezing on polished and micro-micro-hierarchical silicon surfaces. Appl. Therm. Eng. 2018, 137, 66–73. [Google Scholar] [CrossRef]
- He, Z.Y.; Xie, W.J.; Liu, Z.Q.; Liu, G.M.; Wang, Z.W.; Gao, Y.Q.; Wang, J.J. Tuning ice nucleation with counterions on polyelectrolyte brush surfaces. Sci. Adv. 2016, 2, e1600345. [Google Scholar] [CrossRef] [Green Version]
- Kyrkjebø, S.; Cassidy, A.; Akhtar, N.; Balog, R.; Scheffler, M.; Hornekær, L.; Holst, B.; Flatabø, R. Graphene and graphene oxide on Ir(111) are transparent to wetting but not to icing. Carbon 2021, 174, 396–403. [Google Scholar] [CrossRef]
- Joghataei, M.; Ostovari, F.; Atabakhsh, S.; Tobeiha, N. Heterogeneous ice nucleation by graphene nanoparticles. Sci. Rep. 2020, 10, 9723. [Google Scholar] [CrossRef]
- Xue, H.; Lu, Y.; Geng, H.; Dong, B.; Wu, S.; Fan, Q.; Zhang, Z.; Li, X.; Zhou, X.; Wang, J. hydroxyl groups on the graphene surfaces facilitate ice nucleation. J. Phys. Chem. Lett. 2019, 10, 2458–2462. [Google Scholar] [CrossRef]
- Wang, Y.-R.; Xu, J.-Y.; Ma, C.-K.; Shi, M.-X.; Tu, Y.-B.; Sun, K.; Meng, S.; Wang, J.-Z. Ice II-like monolayer ice grown on graphite surface. J. Phys. Chem. C 2019, 123, 20297–20303. [Google Scholar] [CrossRef]
- Nasser, J.; Lin, J.; Zhang, L.; Sodano, H.A. Laser induced graphene printing of spatially controlled super-hydrophobic/hydrophilic surfaces. Carbon 2020, 162, 570–578. [Google Scholar] [CrossRef]
- Peng, W.J.; Li, H.Q.; Liu, Y.Y.; Song, S.X. A review on heavy metal ions adsorption from water by graphene oxide and its composites. J. Mol. Liq. 2017, 230, 496–504. [Google Scholar] [CrossRef]
- Babaahmadi, V.; Montazer, M.; Gao, W. Low temperature welding of graphene on PET with silver nanoparticles producing higher durable electro-conductive fabric. Carbon 2017, 118, 443–451. [Google Scholar] [CrossRef]
- Naumis, G.G.; Barraza-Lopez, S.; Oliva-Leyva, M.; Terrones, H. Electronic and optical properties of strained graphene and other strained 2D materials: A review. Rep. Prog. Phys. 2017, 80, 1–62. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.Y.; Wang, J.; Wu, H.; Liu, J.; Aksay, I.A.; Lin, Y.H. Graphene based electrochemical sensors and biosensors: A review. Electroanalysis 2010, 22, 1027–1036. [Google Scholar] [CrossRef]
- Akinwande, D.; Brennan, C.J.; Bunch, J.S.; Egberts, P.; Felts, J.R.; Gao, H.J.; Huang, R.; Kim, J.S.; Li, T.; Li, Y.; et al. A review on mechanics and mechanical properties of 2D materials-Graphene and beyond. Extrem. Mech. Lett. 2017, 13, 42–77. [Google Scholar] [CrossRef] [Green Version]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Wu, J.B.; Lin, M.L.; Cong, X.; Liu, H.N.; Tan, P.H. Raman spectroscopy of graphene-based materials and its applications in related devices. Chem. Soc. Rev. 2018, 47, 1822–1873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lupi, L.; Hudait, A.; Molinero, V. Heterogeneous nucleation of ice on carbon surfaces. J. Am. Chem. Soc. 2014, 136, 3156–3164. [Google Scholar] [CrossRef] [PubMed]
- Lupi, L.; Kastelowitz, N.; Molinero, V. Vapor deposition of water on graphitic surfaces: Formation of amorphous ice, bilayer ice, ice I, and liquid water. J. Chem. Phys. 2014, 141, 18C508. [Google Scholar] [CrossRef] [PubMed]
- Carrasco, J.; Hodgson, A.; Michaelides, A. A molecular perspective of water at metal interfaces. Nat. Mater. 2012, 11, 667–674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zokaie, M.; Foroutan, M. Confinement effects of graphene oxide nanosheets on liquid–solid phase transition of water. RSC Adv. 2015, 5, 97446–97457. [Google Scholar] [CrossRef]
- Redondo, O.; Prolongo, S.G.; Campo, M.; Sbarufatti, C.; Giglio, M. Anti-icing and de-icing coatings based Joule’s heating of graphene nanoplatelets. Compos. Sci. Technol. 2018, 164, 65–73. [Google Scholar] [CrossRef]
- Vertuccio, L.; De Santis, F.; Pantani, R.; Lafdi, K.; Guadagno, L. Effective de-icing skin using graphene-based flexible heater. Compos. Part B Eng. 2019, 162, 600–610. [Google Scholar] [CrossRef]
- Karim, N.; Zhang, M.; Afroj, S.; Koncherry, V.; Potluri, P.; Novoselov, K.S. Graphene-based surface heater for de-icing applications. RSC Adv. 2018, 8, 16815–16823. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Zhang, Y.; Wu, Q. Effect of graphene coating on the heat transfer performance of a composite anti-/deicing component. Coatings 2017, 7, 158. [Google Scholar] [CrossRef]
- Liu, K.; Wang, C.; Ma, J.; Shi, G.; Yao, X.; Fang, H.; Song, Y.; Wang, J. Janus effect of antifreeze proteins on ice nucleation. Proc. Natl. Acad. Sci. USA 2016, 113, 14739–14744. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Liu, K.; Wang, J. Bioinspired materials for controlling ice nucleation, growth, and recrystallization. Acc. Chem. Res. 2018, 51, 1082–1091. [Google Scholar] [CrossRef]
- Hudait, A.; Odendahl, N.; Qiu, Y.; Paesani, F.; Molinero, V. Ice-nucleating and antifreeze proteins recognize ice through a diversity of anchored clathrate and ice-like motifs. J. Am. Chem. Soc. 2018, 140, 4905–4912. [Google Scholar] [CrossRef]
- Geng, H.; Liu, X.; Shi, G.; Bai, G.; Ma, J.; Chen, J.; Wu, Z.; Song, Y.; Fang, H.; Wang, J. Graphene oxide restricts growth and recrystallization of ice crystals. Angew Chem. Int. Ed. Engl. 2017, 56, 997–1001. [Google Scholar] [CrossRef]
- Knight, C.A. Structural biology—Adding to the antifreeze agenda. Nature 2000, 406, 249–251. [Google Scholar] [CrossRef]
- Bai, G.; Gao, D.; Liu, Z.; Zhou, X.; Wang, J. Probing the critical nucleus size for ice formation with graphene oxide nanosheets. Nature 2019, 576, 437–441. [Google Scholar] [CrossRef]
- Zhang, X.-X.; Chen, M. Icephobicity of functionalized graphene surfaces. J. Nanomater. 2016, 2016, e1600345. [Google Scholar] [CrossRef] [Green Version]
- Akhtar, N.; Anemone, G.; Farias, D.; Holst, B. Fluorinated graphene provides long lasting ice inhibition in high humidity. Carbon 2019, 141, 451–456. [Google Scholar] [CrossRef]
- Ribeiro, I.d.A.; Koning, M.d. Grain-boundary sliding in ice ih: Tribology and rheology at the nanoscale. J. Phys. Chem. C 2021, 125, 627–634. [Google Scholar] [CrossRef]
- Liu, X.; Geng, H.; Sheng, N.; Wang, J.; Shi, G. Suppressing ice growth by integrating the dual characteristics of antifreeze proteins into biomimetic two-dimensional graphene derivatives. J. Mater. Chem. A 2020, 8, 23555–23562. [Google Scholar] [CrossRef]
- Molinero, V.; Moore, E.B. Water modeled as an intermediate element between carbon and silicon. J. Phys. Chem. B 2009, 113, 4008–4016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malkin, T.L.; Murray, B.J.; Salzmann, C.G.; Molinero, V.; Pickering, S.J.; Whale, T.F. Stacking disorder in ice I. Phys. Chem. Chem. Phys. 2015, 17, 60–76. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.S.; Roy, A.K.; Varshney, V.; Wohlwend, J.L.; Putnam, S.A. Temperature dependence of thermal conductance between aluminum and water. Int. J. Therm. Sci. 2012, 59, 17–20. [Google Scholar] [CrossRef]
- Maras, E.; Trushin, O.; Stukowski, A.; Ala-Nissila, T.; Jónsson, H. Global transition path search for dislocation formation in Ge on Si(001). Comput. Phys. Commun. 2016, 205, 13–21. [Google Scholar] [CrossRef] [Green Version]
- Metya, A.K.; Singh, J.K.; Muller-Plathe, F. Ice nucleation on nanotextured surfaces: The influence of surface fraction, pillar height and wetting states. Phys. Chem. Chem. Phys. 2016, 18, 26796–26806. [Google Scholar] [CrossRef] [PubMed]
- Qiu, H.; Guo, W. phase diagram of nanoscale water on solid surfaces with various wettabilities. J. Phys. Chem. Lett. 2019, 10, 6316–6323. [Google Scholar] [CrossRef]
- Kreder, M.J.; Alvarenga, J.; Kim, P.; Aizenberg, J. Design of anti-icing surfaces: Smooth, textured or slippery? Nat. Rev. Mater. 2016, 1, 15003. [Google Scholar] [CrossRef]
- Guo, P.; Zheng, Y.M.; Wen, M.X.; Song, C.; Lin, Y.C.; Jiang, L. Icephobic/anti-icing properties of micro/nanostructured surfaces. Adv. Mater. 2012, 24, 2642–2648. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhu, C.; Liu, K.; Jiang, Y.; Song, Y.; Francisco, J.S.; Zeng, X.C.; Wang, J. Distinct ice patterns on solid surfaces with various wettabilities. Proc. Natl. Acad. Sci. USA 2017, 114, 11285–11290. [Google Scholar] [CrossRef] [Green Version]
- Cox, S.J.; Kathmann, S.M.; Slater, B.; Michaelides, A. Molecular simulations of heterogeneous ice nucleation. II. Peeling back the layers. J. Chem. Phys. 2015, 142, 184705. [Google Scholar] [PubMed] [Green Version]
- Matsumoto, M.; Saito, S.; Ohmine, I. Molecular dynamics simulation of the ice nucleation and growth process leading to water freezing. Nature 2002, 416, 409–413. [Google Scholar] [CrossRef]
- Moore, E.B.; Molinero, V. Structural transformation in supercooled water controls the crystallization rate of ice. Nature 2011, 479, 506–508. [Google Scholar] [CrossRef]
- Lu, N.; Yin, D.; Li, Z.; Yang, J. Structure of graphene oxide: Thermodynamics versus kinetics. J. Phys. Chem. C 2011, 115, 11991–11995. [Google Scholar] [CrossRef] [Green Version]
- Perez, M. Gibbs-Thomson effects in phase transformations. Scr. Mater. 2005, 52, 709–712. [Google Scholar] [CrossRef]
- Wu, T.; Chen, Y.Z. Analytical studies of Gibbs-Thomson effect on the diffusion controlled spherical phase growth in a subcooled medium. Heat Mass Transf. 2003, 39, 665–674. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Shen, Y.; Tao, J.; Xu, Y.; Chen, H.; Liu, S.; Liu, W.; Xie, X. Patterning Configuration of Surface Hydrophilicity by Graphene Nanosheet towards the Inhibition of Ice Nucleation and Growth. Coatings 2022, 12, 52. https://doi.org/10.3390/coatings12010052
Jiang B, Shen Y, Tao J, Xu Y, Chen H, Liu S, Liu W, Xie X. Patterning Configuration of Surface Hydrophilicity by Graphene Nanosheet towards the Inhibition of Ice Nucleation and Growth. Coatings. 2022; 12(1):52. https://doi.org/10.3390/coatings12010052
Chicago/Turabian StyleJiang, Biao, Yizhou Shen, Jie Tao, Yangjiangshan Xu, Haifeng Chen, Senyun Liu, Weilan Liu, and Xinyu Xie. 2022. "Patterning Configuration of Surface Hydrophilicity by Graphene Nanosheet towards the Inhibition of Ice Nucleation and Growth" Coatings 12, no. 1: 52. https://doi.org/10.3390/coatings12010052
APA StyleJiang, B., Shen, Y., Tao, J., Xu, Y., Chen, H., Liu, S., Liu, W., & Xie, X. (2022). Patterning Configuration of Surface Hydrophilicity by Graphene Nanosheet towards the Inhibition of Ice Nucleation and Growth. Coatings, 12(1), 52. https://doi.org/10.3390/coatings12010052






