Stiffness Data of High-Modulus Asphalt Concretes for Road Pavements: Predictive Modeling by Machine-Learning
Abstract
:1. Introduction
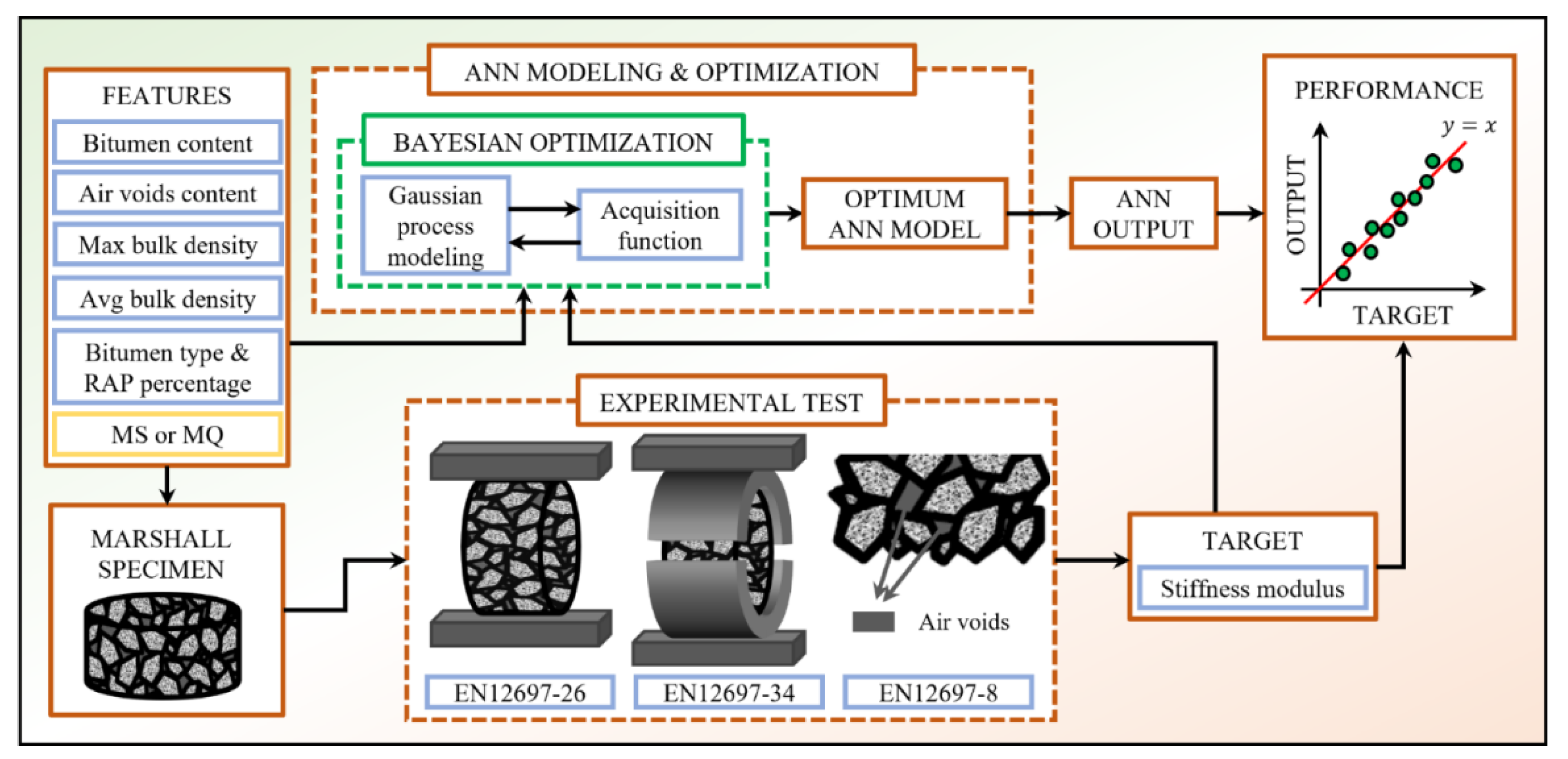
2. Materials and Methods
High Modulus Asphalt Concrete Characterization
3. Methodology
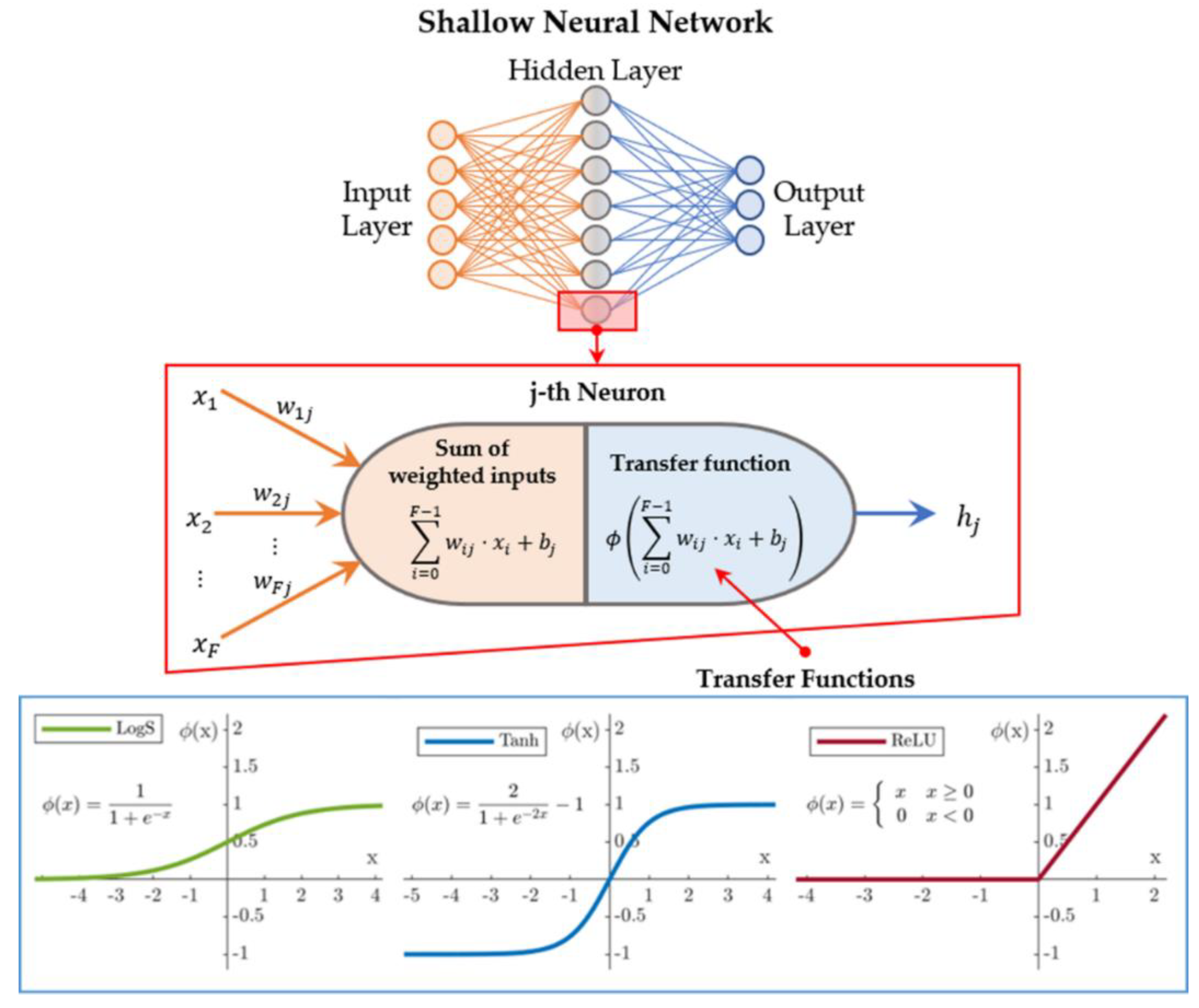
3.1. Shallow Neural Networks with Backpropagation Algorithm
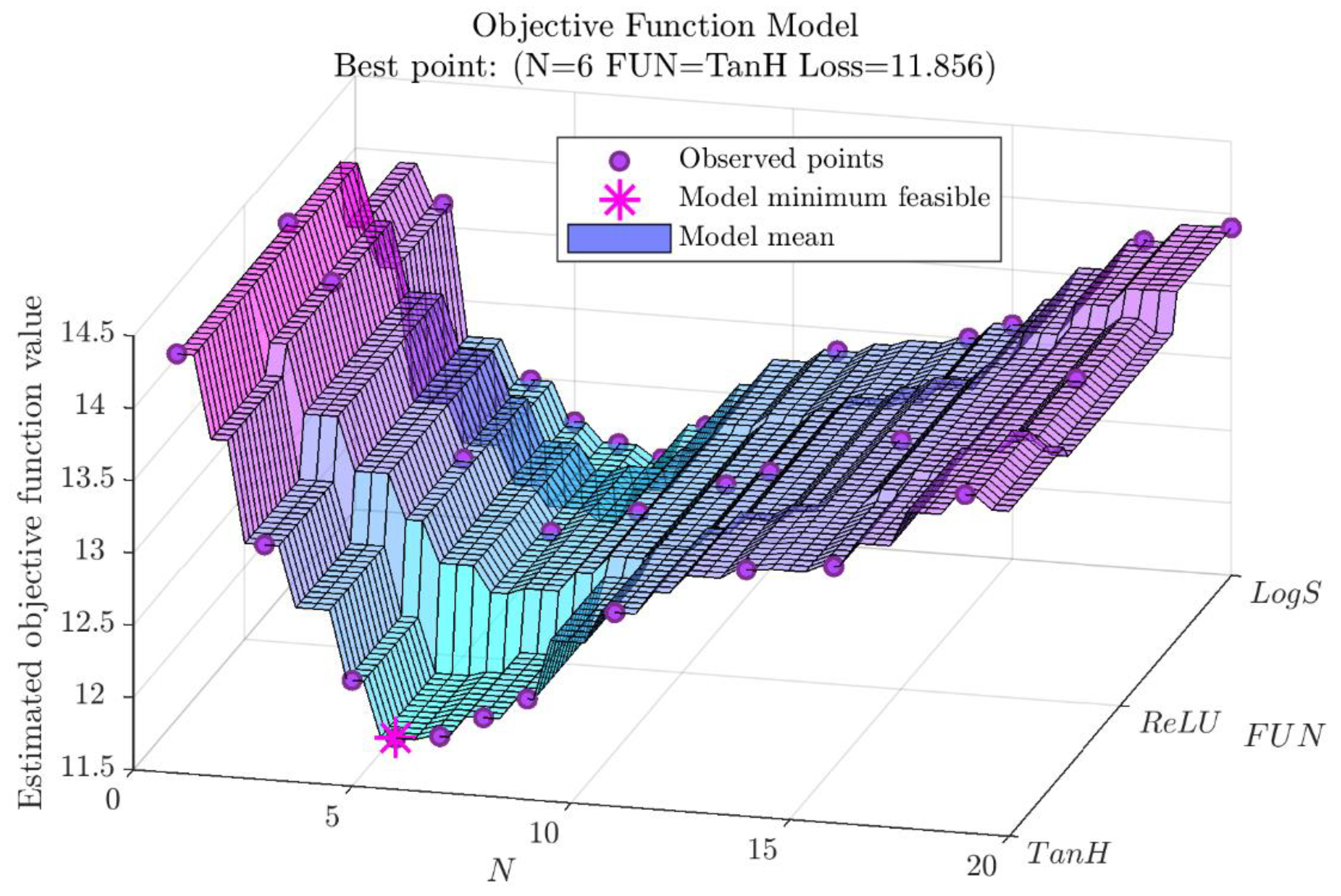
3.2. Bayesian Optimization
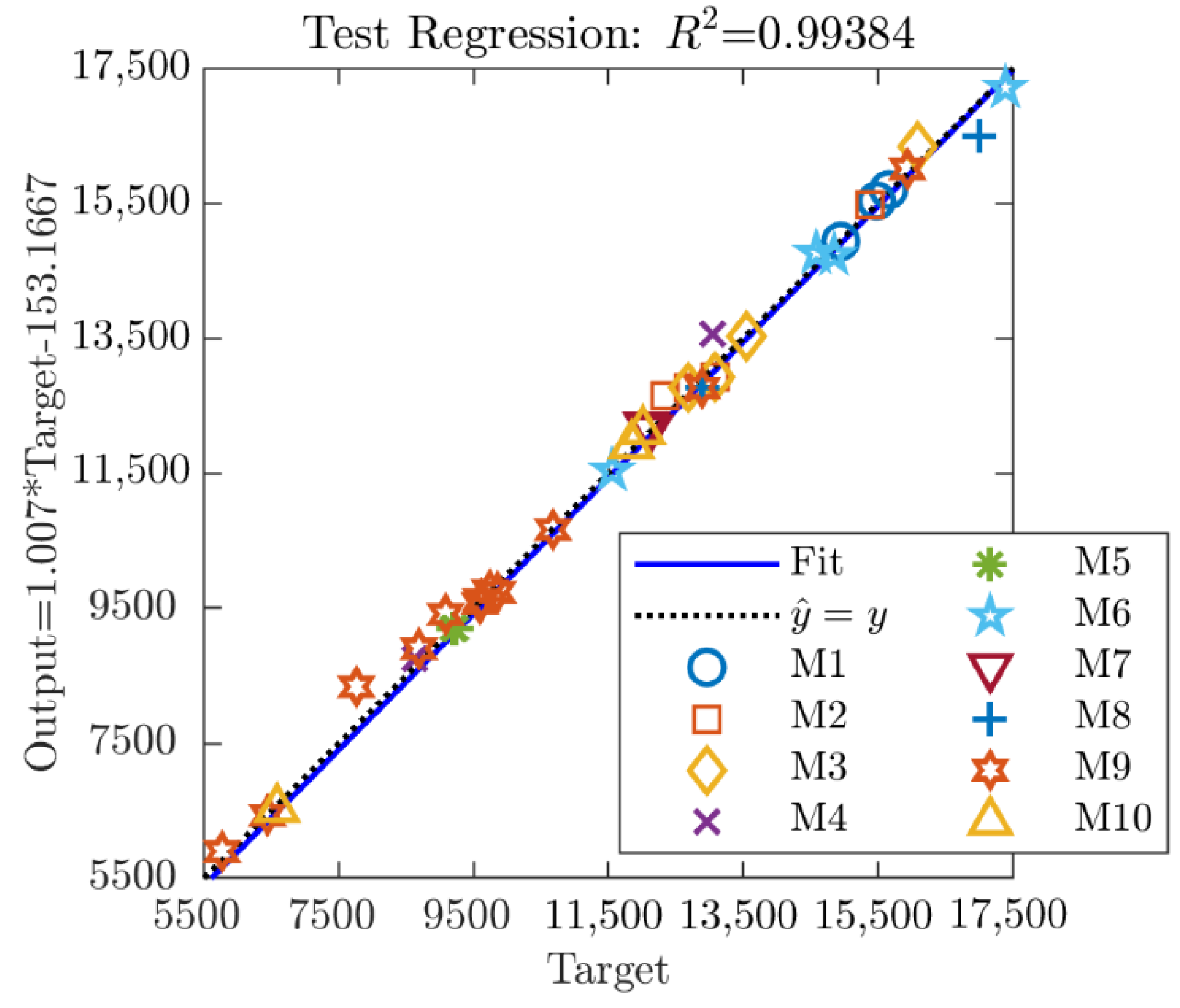
3.3. Input Features Selection and Models Evaluation
4. Discussion
5. Conclusions
- The IT-CY Stiffness Modulus of 115 Marshall test specimens of high-modulus asphalt mixtures prepared in the laboratory with reclaimed asphalt pavement or polymer-modified bitumen has been investigated, according to EN 12697-26 Annex C, as part of real case-mix design processes.
- There were good correlation strengths between the Stiffness Modulus and the Marshall test results, with high stiffness levels associated with high stability or quotient levels. Therefore, one of these empirical parameters could be used as an input feature, along with some parameters related to the HMAC composition, to improve the performance of a predictive model.
- Machine Learning approaches have been employed for the development of a predictive model of the HMACs’ stiffness modulus: the focus was particularly on Shallow Neural Networks, given their simple structure and good computational power even with respect to small data sets.
- A Bayesian optimization process was used to identify the neural topology, as well as the transfer function, optimal for the required modeling. In addition, a data augmentation strategy was designed for the case of the IT-CY test.
- By employing different performance metrics, it was possible to compare the optimal models obtained by varying the input feature related to the empirical Marshall test results. The SNN, which showed the best prediction accuracy of the average mechanical response of HMAC variants, receives as input a 6-component features vector, i.e., the Marshall stability (kN), the bitumen content (% by mass of mix), the air voids content (%), maximum and average bulk density (g/cm3), along with a categorical variable that distinguishes the bitumen type and RAP percentages (values from 0 to 10); such input features vector is processed by 6 neurons in the hidden layer characterized by a hyperbolic tangent activation unit.
- A worthwhile future development could be an in-depth investigation of aggregate grading curves’ influence on stiffness predictions by including additional inputs connected with mixture proportion. Another valuable alternative would be to replace during the modeling phase, variables referring to empirical properties (i.e., Marshall Stability) with those referring to pavement performance. In this way, it would be possible to predict by machine learning approaches fatigue life and/or permanent deformation resistance. Such an attempt would represent a significant step toward performance-based mixture design.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Espersson, M. Effect in the high modulus asphalt concrete with the temperature. Constr. Build. Mater. 2014, 71, 638–643. [Google Scholar] [CrossRef]
- Miró, R.; Valdés, G.; Martínez, A.; Segura, P.; Rodríguez, C. Evaluation of high modulus mixture behaviour with high reclaimed asphalt pavement (RAP) percentages for sustainable road construction. Constr. Build. Mater. 2011, 25, 3854–3862. [Google Scholar] [CrossRef]
- Rys, D.; Judycki, J.; Pszczola, M.; Jaczewski, M.; Mejlun, L. Comparison of low-temperature cracks intensity on pavements with high modulus asphalt concrete and conventional asphalt concrete bases. Constr. Build. Mater. 2017, 147, 478–487. [Google Scholar] [CrossRef]
- Corté, J.F. Development and uses of hard-grade asphalt and of high-modulus asphalt mixes in France. Transp. Res. Circ. 2001, 503, 12–31. [Google Scholar]
- Newcomb, D.E.; Willis, R.; Timm, D.H. Perpetual Asphalt Pavements—A Synthesis; Asphalt Pavement Association of Michigan: Okemos, MI, USA, 2002. [Google Scholar]
- Geng, H.; Clopotel, C.S.; Bahia, H.U. Effects of high modulus asphalt binders on performance of typical asphalt pavement structures. Constr. Build. Mater. 2013, 44, 207–213. [Google Scholar] [CrossRef]
- Marvila, M.T.; Azevedo, A.R.G.; Alexandre, J.; Zanelato, E.B.; Azeredo, N.G.; Simonassi, N.T.; Monteiro, S.N. Correlation between the properties of structural clay blocks obtained by destructive tests and Ultrasonic Pulse Tests. J. Build. Eng. 2019, 26, 100869. [Google Scholar] [CrossRef]
- Pasetto, M.; Baldo, N. Re-use of industrial wastes in cement bound mixtures for road construction. Environ. Eng. Manag. J. 2018, 17, 417–426. [Google Scholar] [CrossRef]
- Wang, L.; Song, Z.; Zeng, S.; Liu, J.; Ma, K. Exploration of the load fatigue test method for cement concrete wheels. Case Stud. Constr. Mater. 2022, 16, e00793. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, J.H.; Park, H.M. Performance evaluation of high modulus asphalt mixtures for long life asphalt pavements. Constr. Build. Mater. 2007, 21, 1079–1087. [Google Scholar] [CrossRef]
- Moghaddam, T.; Baaj, H. Rheological characterization of high-modulus asphalt mix with modified asphalt binders. Constr. Build. Mater. 2018, 193, 142–152. [Google Scholar] [CrossRef]
- Si, C.; Zhou, Y.; You, Z.; He, Y.; Chen, E.; Zhang, R. Micro-mechanical analysis of high modulus asphalt concrete pavement. Constr. Build. Mater. 2019, 220, 128–141. [Google Scholar] [CrossRef]
- Zaumanis, M.; Arraigada, M.; Poulikakos, L.D. 100% recycled high-modulus asphalt concrete mixture design and validation using vehicle simulator. Constr. Build. Mater. 2020, 260, 119891. [Google Scholar] [CrossRef]
- Baldo, N.; Valentin, J.; Manthos, E.; Miani, M. Numerical Characterization of High Modulus Asphalt Concrete Containing RAP: A Comparison among Optimized Shallow Neural Models. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 5th World Multidisciplinary Civil Engineering-Architecture-Urban Planning Symposium, Prague, Czech Republic, 15–19 June 2020; IOP Publishing: Bristol, UK, 2020. [Google Scholar] [CrossRef]
- Yun, T.; Kim, Y.R. Viscoelastoplastic modeling of the behavior of hot mix asphalt in compression. KSCE J. Civ. Eng. 2013, 17, 1323–1332. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Sauzéat, C.; Clec’h, P. Anisotropy of bituminous mixture in the linear viscoelastic domain. Mech. Time-Depend. Mater. 2016, 20, 281–297. [Google Scholar] [CrossRef]
- Rahmani, E.; Darabi, M.K.; Little, D.N.; Masad, E.A. Constitutive modeling of coupled aging-viscoelastic response of asphalt concrete. Constr. Build. Mater. 2017, 131, 1–15. [Google Scholar] [CrossRef]
- Darabi, M.K.; Huang, C.W.; Bazzaz, M.; Masad, E.A.; Little, D.N. Characterization and validation of the nonlinear viscoelastic-viscoplastic with hardening-relaxation constitutive relationship for asphalt mixtures. Constr. Build. Mater. 2019, 216, 648–660. [Google Scholar] [CrossRef]
- Specht, L.P.; Khatchatourian, O.; Brito, L.A.T.; Ceratti, J.A.P. Modeling of asphalt-rubber rotational viscosity by statistical analysis and neural networks. Mater. Res. 2007, 10, 69–74. [Google Scholar] [CrossRef]
- Mirzahosseini, M.R.; Aghaeifar, A.; Alavi, A.H.; Gandomi, A.H.; Seyednour, R. Permanent deformation analysis of asphalt mixtures using soft computing techniques. Expert Syst. Appl. 2011, 38, 6081–6100. [Google Scholar] [CrossRef]
- Androjić, I.; Marović, I. Development of artificial neural network and multiple linear regression models in the prediction process of the hot mix asphalt properties. Can. J. Civ. Eng. 2017, 44, 994–1004. [Google Scholar] [CrossRef]
- Alrashydah, E.I.; Abo-Qudais, S.A. Modeling of creep compliance behavior in asphalt mixes using multiple regression and artificial neural networks. Constr. Build. Mater. 2018, 159, 635–641. [Google Scholar] [CrossRef]
- Ziari, H.; Amini, A.; Goli, A.; Mirzaiyan, D. Predicting rutting performance of carbon nano tube (CNT) asphalt binders using regression models and neural networks. Constr. Build. Mater. 2018, 160, 415–426. [Google Scholar] [CrossRef]
- Montoya, M.A.; Haddock, J.E. Estimating asphalt mixture volumetric properties using seemingly unrelated regression equations approaches. Constr. Build. Mater. 2019, 225, 829–837. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Pasetto, M. Analysis of the mechanical behaviour of asphalt concretes using artificial neural networks. Adv. Civ. Eng. 2018, 2018, 1650945. [Google Scholar] [CrossRef] [Green Version]
- Ozsahin, T.S.; Oruc, S. Neural network model for resilient modulus of emulsified asphalt mixtures. Constr. Build. Mater. 2008, 22, 1436–1445. [Google Scholar] [CrossRef]
- Tapkın, S.; Çevik, A.; Uşar, Ü. Accumulated strain prediction of polypropylene modified marshall specimens in repeated creep test using artificial neural networks. Expert Syst. Appl. 2009, 36, 11186–11197. [Google Scholar] [CrossRef]
- Saoudi, B.S.; Haddadi, S.H. Predicting creep deformation of asphalts modified with polymer using artificial neural networks. Mag. Civ. Eng. 2021, 101, 10106. [Google Scholar] [CrossRef]
- Xiao, F.; Amirkhanian, S.; Juang, C.H. Prediction of fatigue life of rubberized asphalt concrete mixtures containing reclaimed asphalt pavement using artificial neural networks. J. Mater. Civ. Eng. 2009, 21, 253–261. [Google Scholar] [CrossRef]
- Ahmed, T.M.; Green, P.L.; Khalid, H.A. Predicting fatigue performance of hot mix asphalt using artificial neural networks. Road Mater. Pavement Des. 2017, 18, 141–154. [Google Scholar] [CrossRef]
- Ceylan, H.; Schwartz, C.W.; Kim, S.; Gopalakrishnan, K. Accuracy of predictive models for dynamic modulus of hot-mix asphalt. J. Mater. Civ. Eng. 2009, 21, 286–293. [Google Scholar] [CrossRef] [Green Version]
- Gong, H.; Sun, Y.; Dong, Y.; Han, B.; Polaczyk, P.; Hu, W.; Huang, B. Improved estimation of dynamic modulus for hot mix asphalt using deep learning. Constr. Build. Mater. 2020, 263, 119912. [Google Scholar] [CrossRef]
- Zavrtanik, N.; Prosen, J.; Tušar, M.; Turk, G. The use of artificial neural networks for modeling air void content in aggregate mixture. Autom. Constr. 2016, 63, 155–161. [Google Scholar] [CrossRef]
- Hussain, F.; Ali, Y.; Irfan, M. Quantifying the Differential Phase Angle Behaviour of Asphalt Concrete Mixtures Using Artificial Neural Networks. Int. J. Pavement Res. Technol. 2021, 121235, 1–19. [Google Scholar] [CrossRef]
- Baldo, N.; Manthos, E.; Miani, M. Stiffness modulus and marshall parameters of hot mix asphalts: Laboratory data modeling by artificial neural networks characterized by cross-validation. Appl. Sci. 2019, 9, 3502. [Google Scholar] [CrossRef] [Green Version]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2015, 104, 148–175. [Google Scholar] [CrossRef] [Green Version]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the 25th Annual Conference on Neural Information Processing Systems (NIPS 2011), Granada, Spain, 12–14 December 2011; Neural Information Processing Systems Foundation: La Jolla, CA, USA, 2011; Volume 24. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Hoang, V.H.; Nguyen, Q.T.; Tran, A.T.; Tran, T.C.H.; Do, T.A. Mechanical behavior of the asphalt wearing surface on an orthotropic steel bridge deck under cyclic loading. Case Stud. Constr. Mater. 2022, 16, e00836. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Signal Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Demuth, H.B.; Beale, M.H.; De Jess, O.; Hagan, M.T. Neural Network Design; Martin Hagan: Stillwater, OK, USA, 2014. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Neurocomputing: Foundations of Research; MIT Press: Cambridge, MA, USA, 1988; pp. 696–699. [Google Scholar]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Miani, M.; Dunnhofer, M.; Rondinella, F.; Manthos, E.; Valentin, J.; Micheloni, C.; Baldo, N. Bituminous Mixtures Experimental Data Modeling Using a Hyperparameters-Optimized Machine Learning Approach. Appl. Sci. 2021, 11, 11710. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 13–16 December 2012; pp. 2951–2959. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kushner, H.J. A New Method of Locating the Maximum Point of an Arbitrary Multipeak Curve in the Presence of Noise. J. Basic Eng. 1964, 86, 97–106. [Google Scholar] [CrossRef]
- Srinivas, N.; Krause, A.; Kakade, S.M.; Seeger, M. Gaussian Process Optimization in the Bandit Setting: No Regret and Experimental Design. arXiv 2009, arXiv:0912.3995. Available online: https://arxiv.org/abs/0912.3995 (accessed on 11 June 2021).
- Mockus, J.; Tiešis, V.; Zilinskas, A. The application of Bayesian methods for seeking the extremum. In Towards Global Optimization, 2nd ed.; Dixon, L.C.W., Szego, G.P., Eds.; North Holland Publishing Co.: Amsterdam, The Netherlands, 1978; pp. 117–129. [Google Scholar]
- Bull, A.D. Convergence Rates of Efficient Global Optimization Algorithms. J. Mach. Learn. Res. 2011, 12, 2879–2904. Available online: https://arxiv.org/abs/1101.3501 (accessed on 11 June 2021).
- Qi, M.; Zhang, G.P. An investigation of model selection criteria for neural network time series forecasting. Eur. J. Oper. Res. 2001, 132, 666–680. [Google Scholar] [CrossRef]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input determination for neural network models in water resources applications. Part 2. Case study: Forecasting salinity in a river. J. Hydrol. 2005, 301, 93–107. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning. Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Tapkın, S.; Çevik, A.; Uşar, Ü. Prediction of Marshall test results for polypropylene modified dense bituminous mixtures using neural networks. Expert Syst. Appl. 2010, 37, 4660–4670. [Google Scholar] [CrossRef]
- Ozgan, E. Artificial neural network based modelling of the Marshall Stability of asphalt concrete. Expert Syst. Appl. 2011, 38, 6025–6030. [Google Scholar] [CrossRef]
- Zumrawi, M.M.; Khalill, F.O. Experimental study of steel slag used as aggregate in asphalt mixture. Am. J. Constr. Build. Mater. 2017, 2, 26–32. [Google Scholar] [CrossRef]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Biecek, P.; Burzykowski, T. Explanatory Model Analysis. Explore, Explain, and Examine Predictive Models; Chapman and Hall/CRC: New York, NY, USA, 2021. [Google Scholar]
- Legates, D.R.; McCabe, G.J. A refined index of model performance: A rejoinder. Int. J. Climatol. 2013, 33, 1053–1056. [Google Scholar] [CrossRef]

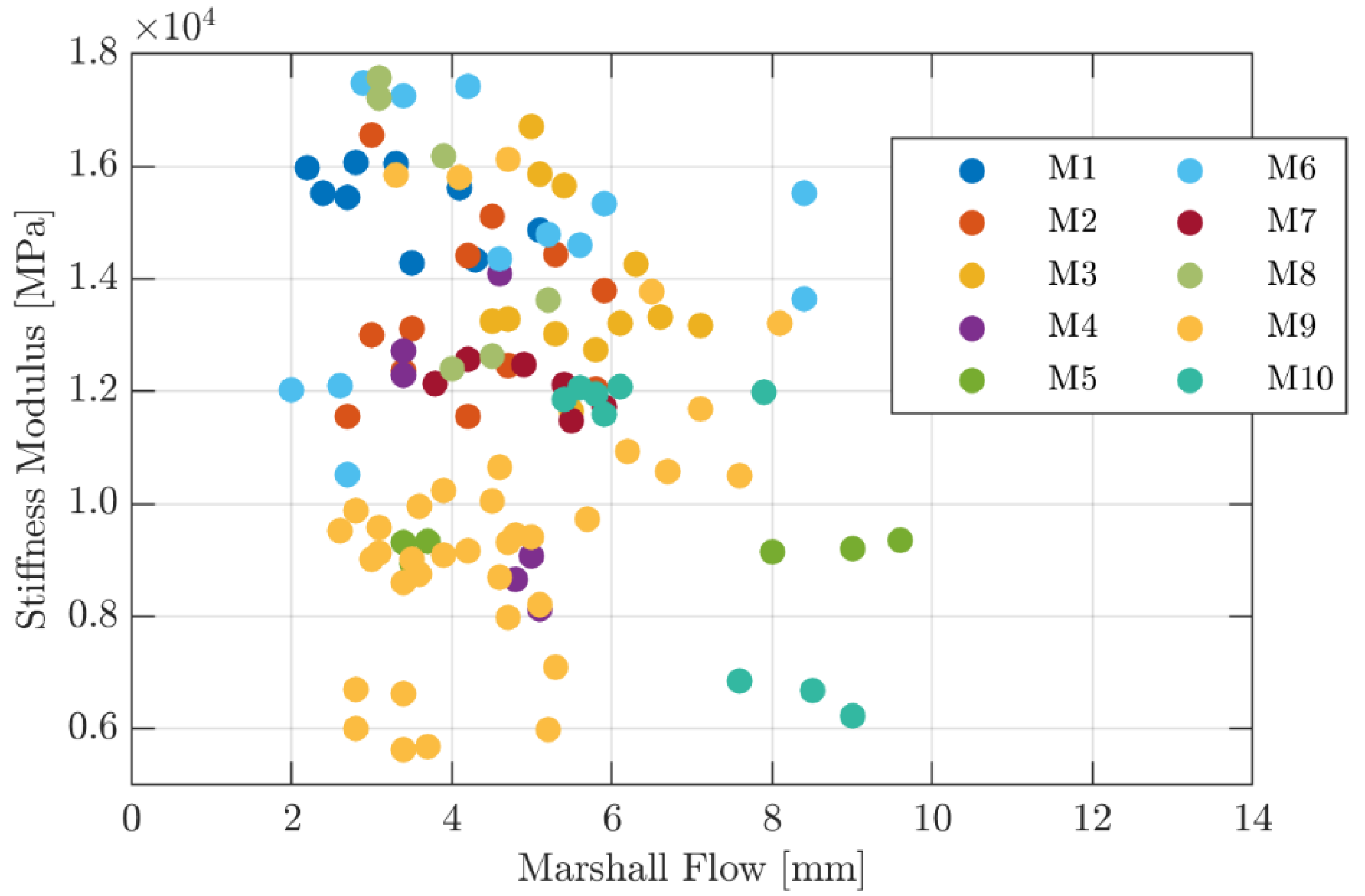


| Mix | Bitumen Type | ID | Bulk Density | Max Bulk Density | Binder Content | Voids Content | Maximum Strength | Marshall Stability | Marshall Flow | IT-CY 15 °C |
|---|---|---|---|---|---|---|---|---|---|---|
| (g/cm3) | (g/cm3) | (%) | (%) | kN | kN | (0.1 mm) | (MPa) | |||
| VMT 22 with 30% RA (Froněk-A) | 20/30 | M1 | 2.455 | 2.640 | 4.9 | 7.0 | 20.6 | 20.0 | 33 | 16,062 |
| 2.429 | 4.9 | 8.0 | 22.4 | 22.7 | 35 | 14,283 | ||||
| 2.456 | 4.9 | 7.0 | 21.6 | 23.1 | 28 | 16,078 | ||||
| VMT 22 with 30% RA (Froněk-B) | 20/30 | M1 | 2.459 | 2.647 | 4.6 | 7.1 | 20.7 | 20.9 | 51 | 14,867 |
| 2.453 | 4.6 | 7.3 | 19.6 | 20.5 | 41 | 15,616 | ||||
| 2.456 | 4.6 | 7.2 | 21.0 | 21.4 | 43 | 14,350 | ||||
| VMT 22 with 30% RA (Froněk-C) | 20/30 | M1 | 2.473 | 2.663 | 4.3 | 7.2 | 22.8 | 22.4 | 22 | 15,974 |
| 2.475 | 4.3 | 7.0 | 24.7 | 25.9 | 24 | 15,535 | ||||
| 2.485 | 4.3 | 6.7 | 24.1 | 24.6 | 27 | 15,452 | ||||
| VMT 22 with 20% RA (Froněk-1) | 20/30 | M2 | 2.467 | 2.676 | 4.3 | 7.8 | 20.1 | 20.5 | 58 | 12,049 |
| 2.463 | 4.3 | 8.0 | 19.0 | 19.8 | 42 | 14,419 | ||||
| 2.461 | 4.3 | 8.0 | 20.2 | 21.0 | 30 | 13,003 | ||||
| VMT 22 with 20% RA (Froněk-2) | 20/30 | M2 | 2.486 | 2.682 | 4.6 | 7.3 | 20.7 | 21.7 | 59 | 13,792 |
| 2.462 | 4.6 | 8.2 | 18.9 | 20.0 | 42 | 11,559 | ||||
| 2.480 | 4.6 | 7.5 | 19.6 | 19.8 | 47 | 12,452 | ||||
| VMT 22 with 20% RA (Froněk-4) | 20/30 | M2 | 2.460 | 2.678 | 4.9 | 8.1 | 23.5 | 23.5 | 53 | 14,441 |
| 2.460 | 4.9 | 8.1 | 24.3 | 23.9 | 45 | 15,113 | ||||
| 2.443 | 4.9 | 8.8 | 23.9 | 24.6 | 30 | 16,558 | ||||
| VMT 22 with 20% RA (Froněk-6) | 20/30 | M2 | 2.422 | 2.667 | 5.2 | 9.2 | 18.6 | 21.8 | 35 | 13,116 |
| 2.411 | 5.2 | 9.6 | 19.1 | 22.2 | 27 | 11,548 | ||||
| 2.422 | 5.2 | 9.2 | 22.3 | 25.4 | 34 | 12,370 | ||||
| VMT 22 with 30% RA var. 5.1 | 50/70 | M3 | 2.547 | 2.617 | 5.1 | 2.7 | 17.1 | 19.7 | 71 | 13,171 |
| 2.554 | 5.1 | 2.4 | 17.2 | 20.0 | 55 | 11,659 | ||||
| 2.538 | 5.1 | 3.0 | 19.6 | 21.9 | 45 | 13,242 | ||||
| VMT 22 with 30% RA. var. 4.8 | 50/70 | M3 | 2.538 | 2.607 | 4.8 | 2.6 | 17.4 | 19.9 | 58 | 12,739 |
| 2.535 | 4.8 | 2.8 | 14.8 | 16.9 | 47 | 13,287 | ||||
| 2.539 | 4.8 | 2.6 | 22.7 | 25.5 | 61 | 13,217 | ||||
| VMT 22 with 30% RA (Froněk) | 50/70 | M3 | 2.549 | 2.602 | 4.8 | 2.0 | 17.4 | 20.2 | 53 | 13,025 |
| 2.539 | 4.8 | 2.4 | 15.3 | 17.9 | 63 | 14,267 | ||||
| 2.548 | 4.8 | 2.1 | 16.8 | 19.0 | 66 | 13,325 | ||||
| VMT 22 with 30% RA (Froněk) | 50/70 | M3 | 2.553 | 2.626 | 4.6 | 2.8 | 20.6 | 20.7 | 51 | 15,871 |
| 2.548 | 4.6 | 3.0 | 18.6 | 21.0 | 54 | 15,666 | ||||
| 2.548 | 4.6 | 3.0 | 20.2 | 23.4 | 50 | 16,707 | ||||
| VMT 22 with 20% RA (Froněk-3) | 50/70 | M4 | 2.473 | 2.639 | 4.8 | 6.3 | 18.1 | 19.0 | 34 | 12,729 |
| 2.495 | 4.8 | 5.4 | 20.2 | 21.6 | 34 | 12,282 | ||||
| 2.477 | 4.8 | 6.1 | 21.5 | 22.3 | 46 | 14,101 | ||||
| VMT 22 with 20% RA (PKB-A) | 50/70 | M4 | 2.397 | 2.496 | 4.4 | 4.0 | 14.2 | 13.6 | 48 | 8666 |
| 2.421 | 4.4 | 3.0 | 13.4 | 13.4 | 50 | 9064 | ||||
| 2.412 | 4.4 | 3.4 | 12.2 | 12.4 | 51 | 8135 | ||||
| VMT 22 with 10% RA (PKB-101) | 50/70 | M5 | 2.358 | 2.559 | 4.6 | 7.9 | 12.1 | 11.4 | 35 | 8950 |
| 2.351 | 4.6 | 8.1 | 15.3 | 14.1 | 37 | 9339 | ||||
| 2.355 | 4.6 | 8.0 | 12.8 | 14.5 | 34 | 9311 | ||||
| VMT 22 with 10% RA (PKB-102) | 50/70 | M5 | 2.341 | 2.559 | 4.5 | 8.5 | 17.1 | 16.2 | 90 | 9203 |
| 2.343 | 4.5 | 8.4 | 17.1 | 16.1 | 80 | 9142 | ||||
| 2.323 | 4.5 | 9.2 | 15.1 | 14.2 | 96 | 9361 | ||||
| VMT 22 NT | 20/30 | M6 | 2.362 | 2.490 | 4.7 | 5.1 | 18.9 | 17.1 | 46 | 14,357 |
| 2.409 | 4.7 | 3.2 | 21.4 | 20.3 | 56 | 14,601 | ||||
| 2.409 | 4.7 | 3.3 | 20.8 | 19.7 | 52 | 14,784 | ||||
| VMT 22 NT | 20/30 | M6 | 2.296 | 2.490 | 4.7 | 7.8 | 19.4 | 16.3 | 84 | 13,653 |
| 2.313 | 4.7 | 7.1 | 20.8 | 18.8 | 84 | 15,529 | ||||
| 2.296 | 4.7 | 7.8 | 19.7 | 16.5 | 59 | 15,345 | ||||
| VMT 22 (SK-1) | 20/30 | M6 | 2.330 | 2.449 | 4.6 | 4.9 | 25.4 | 24.1 | 26 | 12,102 |
| 2.324 | 4.6 | 5.1 | 24.5 | 23.2 | 20 | 12,027 | ||||
| 2.305 | 4.6 | 5.9 | 22.5 | 20.5 | 27 | 10,528 | ||||
| VMT 22 (VIA-1) | 20/30 | M6 | 2.702 | 2.789 | 4.7 | 3.1 | 21.1 | 22.8 | 42 | 17,417 |
| 2.691 | 4.7 | 3.5 | 19.2 | 21.3 | 34 | 17,262 | ||||
| 2.680 | 4.7 | 3.9 | 20.5 | 23.0 | 29 | 17,478 | ||||
| VMT 22 (SK-2) | 30/45 | M7 | 2.414 | 2.490 | 4.6 | 3.1 | 22.0 | 20.6 | 49 | 12,483 |
| 2.416 | 4.6 | 3.0 | 20.8 | 19.6 | 54 | 12,129 | ||||
| 2.396 | 4.6 | 3.8 | 21.7 | 20.6 | 59 | 11,734 | ||||
| VMT 22 (VHS) | 30/45 | M7 | 2.641 | 2.747 | 4.7 | 3.9 | 11.5 | 14.7 | 38 | 12,136 |
| 2.648 | 4.7 | 3.6 | 14.4 | 15.8 | 55 | 11,478 | ||||
| 2.650 | 4.7 | 3.5 | 14.2 | 15.6 | 42 | 12,566 | ||||
| VMT 22 (VIA-2) | TSA 15/25 | M8 | 2.709 | 2.818 | 4.8 | 3.9 | 19.7 | 22.8 | 39 | 16,182 |
| 2.724 | 4.8 | 3.3 | 18.0 | 21.6 | 31 | 17,571 | ||||
| 2.712 | 4.8 | 3.8 | 18.4 | 22.3 | 31 | 17,227 | ||||
| VMT 22 (TPA-1) | TSA 15/25 | M8 | 2.458 | 2.566 | 4.6 | 4.2 | 21.5 | 21.5 | 45 | 12,629 |
| 2.454 | 4.6 | 4.4 | 22.5 | 21.8 | 40 | 12,412 | ||||
| 2.460 | 4.6 | 4.1 | 23.5 | 23.0 | 52 | 13,627 | ||||
| VMT 22 (EV) | PMB 25/55–60 | M9 | 2.574 | 2.655 | 4.9 | 3.0 | 24.8 | 25.1 | 81 | 13,203 |
| 2.567 | 4.9 | 3.3 | 23.2 | 23.6 | 71 | 11,688 | ||||
| 2.576 | 4.9 | 3.0 | 27.2 | 27.7 | 65 | 13,772 | ||||
| VMT 22 (SK-3) | PMB 25/55–60 | M9 | 2.357 | 2.436 | 4.7 | 3.2 | 19.7 | 19.9 | 67 | 10,581 |
| 2.362 | 4.7 | 3.0 | 20.4 | 20.6 | 62 | 10,940 | ||||
| 2.363 | 4.7 | 3.0 | 20.9 | 21.1 | 76 | 10,505 | ||||
| VMT 22 (SK-4) | PMB 25/55–60 | M9 | 2.366 | 2.436 | 4.9 | 2.9 | 11.8 | 18.5 | 34 | 6632 |
| 2.367 | 4.9 | 2.8 | 10.8 | 17.3 | 28 | 6001 | ||||
| 2.358 | 4.9 | 3.2 | 11.3 | 17.8 | 28 | 6699 | ||||
| VMT 22 (TPA-2) | PMB 25/55–60 | M9 | 2.338 | 2.457 | 4.8 | 4.8 | 16.3 | 16.1 | 30 | 9024 |
| 2.329 | 4.8 | 5.2 | 20.2 | 20.4 | 31 | 9134 | ||||
| 2.334 | 4.8 | 5.0 | 17.6 | 17.4 | 39 | 9097 | ||||
| VMT 22 (ESLAB) | PMB 25/55–60 | M9 | 2.476 | 2.558 | 4.7 | 3.2 | 18.4 | 19.5 | 31 | 9585 |
| 2.485 | 4.7 | 2.9 | 17.9 | 18.4 | 47 | 9322 | ||||
| 2.481 | 4.7 | 3.0 | 17.2 | 17.4 | 46 | 10,656 | ||||
| VMT 22 (TPA-3) | PMB 25/55–60 | M9 | 2.415 | 2.632 | 4.9 | 8.3 | 20.8 | 19.7 | 53 | 7102 |
| 2.427 | 4.9 | 7.8 | 18.8 | 17.8 | 51 | 8203 | ||||
| 2.430 | 4.9 | 7.7 | 19.4 | 18.5 | 47 | 7986 | ||||
| VMT 22 (TPA-4) | PMB 25/55–60 | M9 | 2.416 | 2.485 | 4.9 | 2.8 | 21.1 | 21.7 | 42 | 9174 |
| 2.408 | 4.9 | 3.1 | 19.4 | 19.6 | 39 | 10,245 | ||||
| 2.404 | 4.9 | 3.3 | 19.6 | 19.8 | 50 | 9421 | ||||
| VMT 22 (VIA-3) | PMB 25/55–60 | M9 | 2.415 | 2.510 | 4.8 | 3.8 | 18.4 | 17.5 | 57 | 9731 |
| 2.416 | 4.8 | 3.7 | 18.1 | 16.9 | 45 | 10,044 | ||||
| 2.415 | 4.8 | 3.8 | 19.2 | 17.7 | 48 | 9446 | ||||
| VMT 22 (TPA-5) | PMB 25/55–60 | M9 | 2.338 | 2.457 | 5.0 | 4.8 | 18.7 | 18.9 | 46 | 8691 |
| 2.329 | 5.0 | 5.2 | 20.7 | 20.9 | 36 | 8759 | ||||
| 2.334 | 5.0 | 5.0 | 17.4 | 17.6 | 34 | 8611 | ||||
| VMT 22 (TPA-6) | PMB 25/55–60 | M9 | 2.335 | 2.467 | 4.8 | 5.3 | 18.2 | 18.8 | 36 | 9953 |
| 2.332 | 4.8 | 5.5 | 16.5 | 18.0 | 35 | 9018 | ||||
| 2.339 | 4.8 | 5.2 | 17.5 | 17.9 | 28 | 9884 | ||||
| 2.330 | 4.8 | 5.5 | 16.3 | 16.4 | 26 | 9521 | ||||
| VMT 22 (Chvaletice) | PMB 25/55–60 | M9 | 2.392 | 2.532 | 4.7 | 5.5 | 28.3 | 26.3 | 47 | 16,134 |
| 2.397 | 4.7 | 5.3 | 25.6 | 23.8 | 41 | 15,808 | ||||
| 2.386 | 4.7 | 5.8 | 28.3 | 26.8 | 33 | 15,855 | ||||
| VMT 22 (SK-5) | PMB 25/55–60 | M9 | 2.373 | 2.460 | 4.9 | 3.5 | 14.5 | 12.9 | 37 | 5685 |
| 2.362 | 4.9 | 4.0 | 14.2 | 12.0 | 34 | 5636 | ||||
| 2.378 | 4.9 | 3.3 | 15.2 | 13.7 | 52 | 5991 | ||||
| VMT 22 (TPA-7) | PMB 25/55–65 | M10 | 2.439 | 2.610 | 5.1 | 6.6 | 15.1 | 14.8 | 85 | 6686 |
| 2.441 | 5.1 | 6.5 | 15.8 | 14.9 | 90 | 6223 | ||||
| 2.433 | 5.1 | 6.8 | 14.1 | 13.6 | 76 | 6848 | ||||
| VMT 22 (TPA-8) | PMB 25/55–65 | M10 | 2.553 | 2.648 | 4.8 | 3.6 | 19.8 | 19.2 | 79 | 11,989 |
| 2.556 | 4.8 | 3.5 | 21.8 | 22.0 | 61 | 12,075 | ||||
| 2.545 | 4.8 | 3.9 | 18.9 | 19.1 | 58 | 11,958 | ||||
| VMT 22 (TPA-9) | PMB 25/55–65 | M10 | 2.554 | 2.629 | 5.0 | 2.8 | 21.8 | 22.7 | 54 | 11,849 |
| 2.548 | 5.0 | 3.1 | 19.8 | 20.2 | 59 | 11,603 | ||||
| 2.543 | 5.0 | 3.3 | 19.5 | 19.3 | 56 | 12,071 |
| ID | Features | N | MAE | RMSE | R2 | R2adj | ||
|---|---|---|---|---|---|---|---|---|
| MIXSNN | 5 | 6 | TanH | 12.093 | 209.12 | 293.56 | 0.9909 | 0.9894 |
| MSSNN | 6 | 6 | TanH | 11.856 | 160.17 | 241.54 | 0.9938 | 0.9923 |
| MQSNN | 6 | 8 | LogS | 12.373 | 174.91 | 272.61 | 0.9922 | 0.9902 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldo, N.; Miani, M.; Rondinella, F.; Valentin, J.; Vackcová, P.; Manthos, E. Stiffness Data of High-Modulus Asphalt Concretes for Road Pavements: Predictive Modeling by Machine-Learning. Coatings 2022, 12, 54. https://doi.org/10.3390/coatings12010054
Baldo N, Miani M, Rondinella F, Valentin J, Vackcová P, Manthos E. Stiffness Data of High-Modulus Asphalt Concretes for Road Pavements: Predictive Modeling by Machine-Learning. Coatings. 2022; 12(1):54. https://doi.org/10.3390/coatings12010054
Chicago/Turabian StyleBaldo, Nicola, Matteo Miani, Fabio Rondinella, Jan Valentin, Pavla Vackcová, and Evangelos Manthos. 2022. "Stiffness Data of High-Modulus Asphalt Concretes for Road Pavements: Predictive Modeling by Machine-Learning" Coatings 12, no. 1: 54. https://doi.org/10.3390/coatings12010054
APA StyleBaldo, N., Miani, M., Rondinella, F., Valentin, J., Vackcová, P., & Manthos, E. (2022). Stiffness Data of High-Modulus Asphalt Concretes for Road Pavements: Predictive Modeling by Machine-Learning. Coatings, 12(1), 54. https://doi.org/10.3390/coatings12010054










