Ultra-Narrow Gap Fiber Laser Conduction Welding Technology for 304 Stainless Steel Thick Plates and the Mechanical Properties of Welding Joints

Abstract

The application of thick metal plates is increasing, and the welding problem is becoming more and more prominent. Narrow gap laser welding is one of the important methods, and it is also a research hotspot. The stainless steel thick plates were welded using the ultra-narrow gap fiber laser conduction welding with filler wire. Results show that the ranges of technological parameters for the achievement of the weld seam with no defects are smaller when the gap width is comparatively larger. Using the optimized technological parameters, the butt welding with no defects on the 3 mm gap between two 304 stainless steel plates with 60 mm thickness was achieved through the filling 20 times. This welding method of 304 metal with large thickness is rare in the literature. The tensile strength of the welding joint can be up to 87% of that of the base metal, and the micro-hardness and yield strength of the joint are comparable with those of the base metal.

1. Introduction

The thick plates now are widely used as the global industrialization advances. Moreover, it has set much higher requirements on the welding quality. For example, in the project of International Thermonuclear Experimental Reactor (ITER), many structures should be welded together by the stainless steel thick plates, with the thickness up to 60 mm [1,2,3]. Both the low-temperature liquid oxygen and hydrogen fuel tank and the phased array radar substrates used in the Delta II rocket manufactured by the Boeing Company were made of thick aluminum alloy plates [4,5]. Due to great thicknesses and large sizes, these components can hardly be manufactured through some common machining methods such as cutting or rolling, and can only be welded together. Moreover, the manufacturing of these sets quite high requirements on the quality of welding joints and welding deformation. The applications of thick plates in industry at the present stage have brought new demands on welding techniques [6,7].

Narrow-gap argon arc welding [8], narrow-gap submerged-arc welding [9], and narrow-gap gas metal arc welding [10,11] are the conventional methods of thick plate welding in industry. The ultra-narrow gap welding method generally has a gap width of not more than 5 mm. However, the application of these methods exhibits a series of shortcomings such as great heat input and large welding deformations. Compared with these conventional welding methods, narrow-gap laser welding with filler wire integrates the double advantages of laser welding and narrow-gap welding, and exhibits many advantages such as relatively moderate heat input and small welding deformation, which has made this method receive more and more attention [12,13,14]. However, some problems also appear in the application of narrow-gap laser welding method with filler wire, mainly including incomplete fusion of side walls, keyhole-induced porosity, and welding deformation [14,15]. A small range of laser spot action is the main reason leading to the incomplete fusion of side walls, and the appearance of incomplete fused side walls can be inhibited using the combination of laser spots or beam weaving [16,17,18]. Unfortunately, this welding method can also bring about many problems such as the noticeable increase of welding gap and deformation. Using the narrow-gap laser conduction welding method with filler wire, Phaoniam et al. [19] welded the 304 stainless steel plates with the thickness of 10 mm and acquired the pore-free welded joints. The incomplete fusion of side walls also existed at the corner of groove bottom.

Aiming at solving the problems in the narrow-gap welding of thick plates such as pores, incomplete fusion of side walls, and welding deformation, the 304 stainless steel thick plates were welded by using the ultra-narrow gap fiber laser conduction welding with filler wire in this study. This welding method of 304 metal with large thickness is rare in the literature.

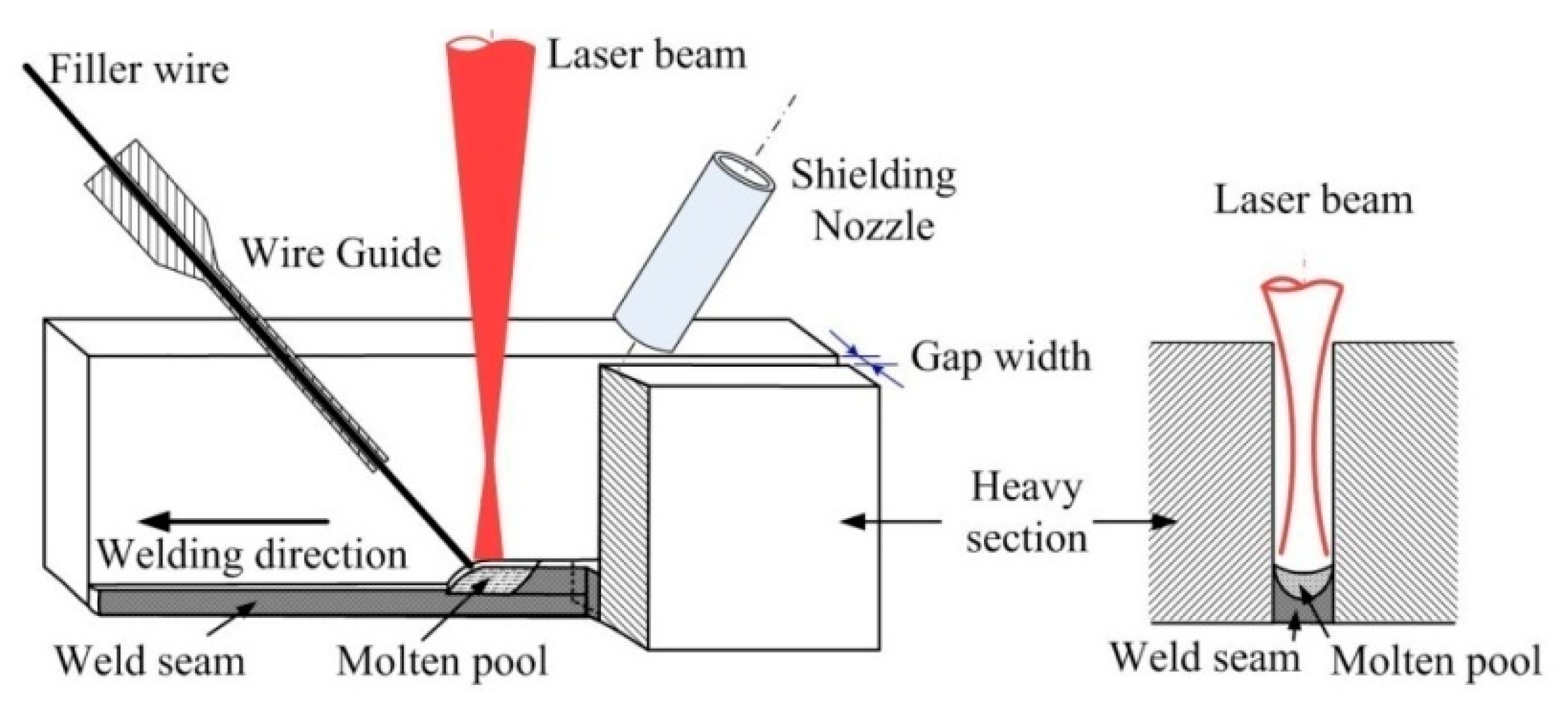
2. Experimental Method and Set-Up

The principle of the ultra-narrow gap laser conduction welding with filler wires is to reduce heat input and lower welding deformation by taking advantage of the ultra-narrow gap. The positive defocusing mode is used for ensuring a conduction welding mode, so that the keyhole-induced porosity in deep penetration welding can be avoided. During the welding process, the laser beam is used to heat the side and bottom parts of groove simultaneously and make them be fused at the same time, i.e., the incomplete fusion of side walls can be avoided [20]. In addition, in a front wire feeding mode, the molten pool is heated by the laser beam, and meanwhile the welding wires insert into the molten pool for heat adsorption and fusion. Accordingly, the instability in the transmission of laser energy and welding process induced by the swing of welding wires in the gap when the laser beam directly irradiates the welding wires can be avoided. Figure 1 displays the experimental layout.

The parameters of laser, external optical system, the chemical compositions of welding materials, and filler wires as well as the processing method in the welding have been described in the previous study in detail [20] and need not be repeated here. The adopted 304 stainless steel plates have two sizes, 250 mm × 200 mm × 60 mm and 250 mm × 200 mm × 20 mm, respectively. After the section of the weld seam was ground, polished, and corroded, the microscopic structure of the welding joint was observed using a GX51 Olympus optical microscope (Olympus Corporation, Tokyo, Japan), and the hardness in the middle of the welding joint was measured using an FM-300e Vickers micro-hardness meter (Future-tech corp, Tokyo, Japan). This test was carried out at room temperature, according to the Chinese standard GB/T 228.1-2010 [21]. During the measurement, the loads on the samples were 200 g, with the loading time of 15 s. The tensile strength, yield strength, and elongation ratio of the welding joint were measured by the MTS810.22M/Test Star TMHS electro-hydraulic servo universal material testing machine (Mechanical Testing & Simulation, MN, USA). The test adopts an axial load with tensile clamping force of 5 MPa, tensile speed of 3 mm/min, and gauge distance of 65 mm, respectively. The tensile samples were selected from the middle parts of the weld seams, with the size of 175 mm × 25 mm × 3 mm. During the bending tests, the diameter of the pressure roller is 20 mm and the distance between the supporting rollers is 20 mm.

3. Experimental Results and Analysis

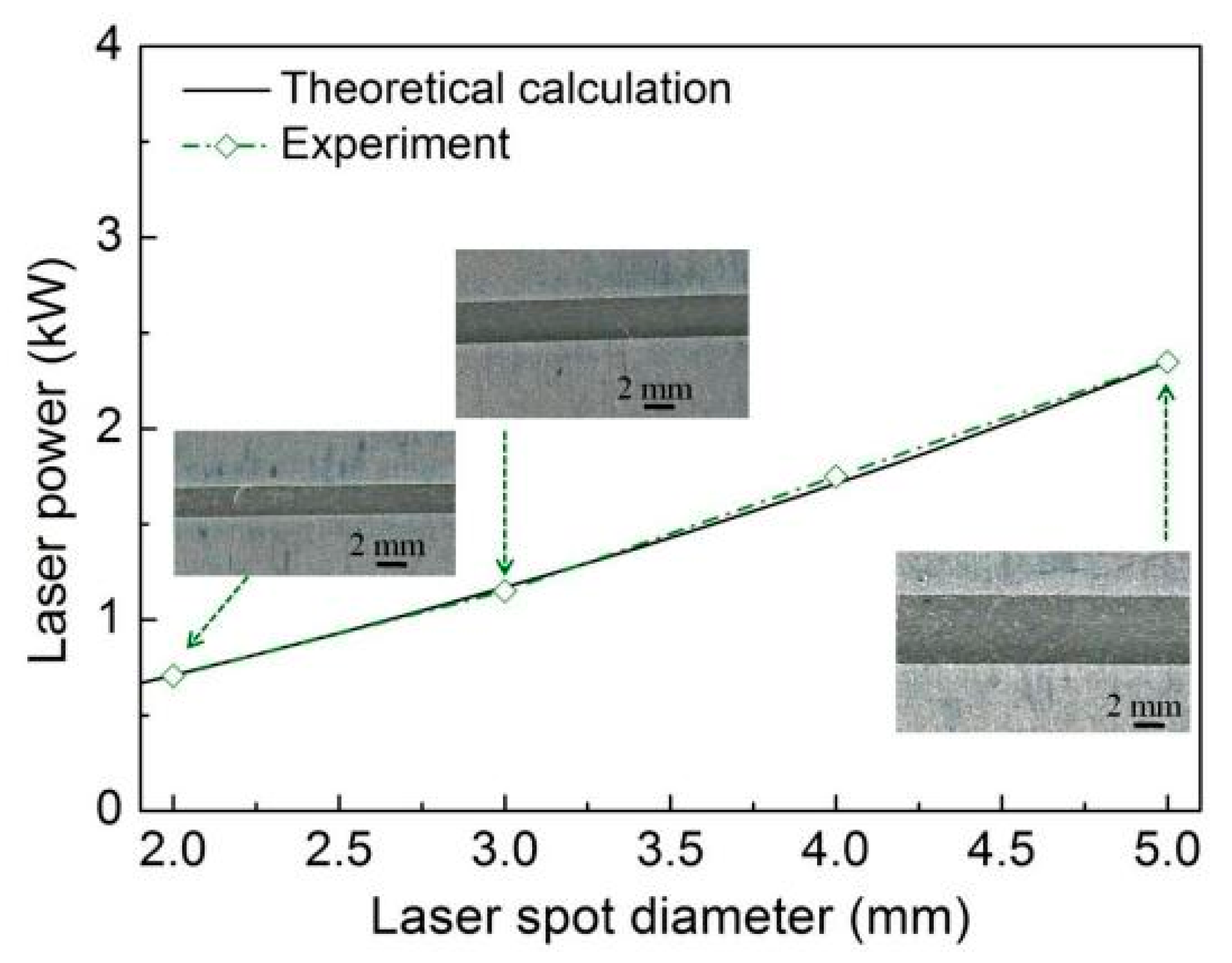
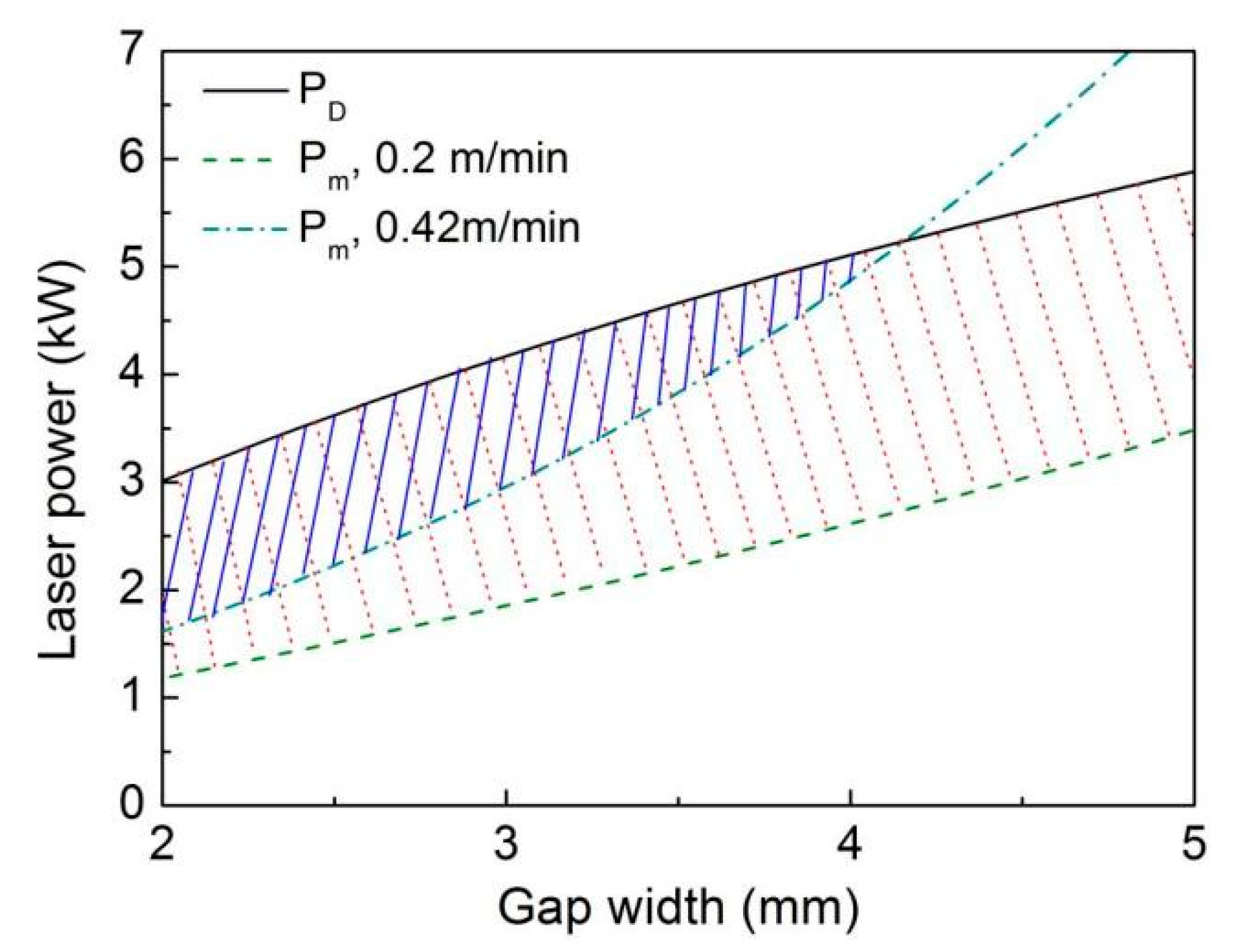
3.1. Physical Properties of the Ultra-Narrow Gap and the Technological Parameters’ Theoretical Value Ranges for Heat Conduction Welding

In the ultra-narrow gap, the laser welding was conducted in a heat conduction mode, and the laser energy should be smaller than the penetration threshold and larger than the fusion threshold for the plates on the edge of light spot. In-depth insights into the fusion and penetration threshold power are the key to the determination of the technological parameters’ value ranges during ultra-narrow gap laser conduction welding with filler wire theoretically. The heat dissipation of ultra-narrow gap differs from that of the flat-plate, whose structural parameters can be acquired by comparing the fusion threshold powers for the plates on the edge of light spot during flat-plate welding and ultra-narrow gap welding (i.e., the diameter of light spot equals to the weld width). The 304 stainless steel plates were welded at a speed of 0. 12 m/min. Figure 2 displays the variation of laser power with the diameter of light spot when the weld width equals the spot diameter during flat-plate welding.

Assuming a semi-infinite body (i.e., the flat thick plate) under the laser’s vertical action, the temperature on the metal surface at a distance of r far away from the center of light spot can be expressed as [22]:

$$T\left(r\right)-T_0=\frac{AP}{2\pi {\lambda }_{t}r}\exp \left[-\left(\frac{vr}{2a_t}\right)\right]$$

(1)

where $T\left(r\right)$ denotes the temperature at the radius of r, T₀ denotes room temperature ($T_0=300 \mathrm{K}$), A denotes the material’s laser absorptivity, v denotes the welding speed, ${\lambda }_t$ denotes the thermal conductivity, P denotes the laser’s power, at denotes the material’s thermal diffusivity ($a_t={\lambda }_t/\rho c$), $\rho$ denotes the density of welding material, and c denotes the thermal capacity of the welding material. In the present work, laser entered into the ultra-narrow gap and acted on the bottom of groove. Therefore, the welding materials can be regarded as being between semi-infinite thick plates and infinite thick plates. According to Equation (1), when the temperature on the edge of light spot reaches the melting point, the fusion threshold power $P_m$ can be written as:

$$P_m=\frac{2\pi \overline{{\lambda }_s}r\left(z\right)\left(T_{\mathrm{m}}-T_0\right)}{b\overline{A_s}}\exp \left(\frac{\overline{{\rho }_s}\overline{c_s}vr}{2\overline{{\lambda }_s}}\right)$$

(2)

where b denotes the structural parameters (b = 0.5 for an infinite body and b = 1 for a semi-infinite body), $T_m$ denotes the melting temperature of welded material, $\overline{{\lambda }_s}$ denotes the mean thermal conductivity at solid state, $r$ denotes the radius of laser beam spot radius, $\overline{A_s}$ denotes the mean absorptivity of solid metal, $\overline{c_s}$ and $\overline{{\rho }_s}$ denote the mean thermal capacity and density of the solid metal, and $v$ denotes the welding speed. For a simplified calculation, it can be assumed that the physical parameters are linear with temperature and the average temperature was then selected. For 304 stainless steel, $T_m=1670 \mathrm{K}$. According to the data in Ref. [23], $\overline{{\lambda }_s}=25 \mathrm{W}/\mathrm{Km}$, $\overline{c_s}\approx 600 \mathrm{j}/\mathrm{kg} \mathrm{K}$, $\overline{{\rho }_s}=7.35\times {10}^3 \mathrm{kg}/{\mathrm{m}}^3$ can be calculated. In addition, $\overline{A_s}\approx 0.4$ [24]. During the flat-plate welding (i.e., it can be assumed that the plate is a semi-infinite body), b = 1 and then the variation of laser power with the diameter of light spot when the edge of light spot begins to melt at a welding speed of 0.12 m/min can be calculated and presented in Figure 2. The measured values agree well with the theoretical calculating values (see Figure 2). This suggests that the selected values of the physical parameters of 304 stainless steel are appropriate.

The ultra-narrow gaps whose gaps are 2 mm, 3 mm, 4 and 5 mm, respectively, but the depths are all 15 mm were manufactured on a 304 stainless steel plate with the thickness of 20 mm, and the welding experiments were conducted in these ultra-narrow gaps at a welding speed of 0.12 m/min. Figure 3 displays the variation rule of the weld width in the ultra-narrow gap with the increase of laser power when the gap width and the diameter of light spot are both 2 mm. One can observe that, when the laser power is 1.1 kW, the weld width in the ultra-narrow gap equals the diameter of light spot, 2 mm; and the plate on the edge of the light spot begins to melt at this moment. Under the same conditions, when the welding was performed on a stainless steel flat plate, the laser power for the fusion of the plate on the edge of light spot was 0.704 W (see Figure 2). According to Equation (2), one can calculate that the structural coefficient of a 2-mm ultra-narrow gap is 0.64 (i.e., b = 0.64). The welding experiments were repeated on the ultra-narrow gaps with the gap widths of 3 mm, 4 mm, and 5 mm, respectively, using the laser with the diameters of light spot of 3 mm, 4 mm, and 5 mm, respectively. The laser power when the weld width equals to the diameter of laser spot was measured. In combination with the laser power when the stainless steel flat plate on the edge of light spot begins to melt under the same conditions as shown in Figure 2, the structural coefficients of different ultra-narrow gaps can be calculated according to Equation (2), as denoted by the green line in Figure 3.

Assuming that the vertical axis on the right side of Figure 3 is denoted as b (i.e., the structural coefficient) and the horizontal axis on the top of Figure 3 is denoted as x (i.e., the width of the ultra-narrow width), we made a linear regression fitting on b and x in accordance with the structural coefficients corresponding to different gap widths as shown in Figure 3, and the obtained fitting function can be described as:

$$b=0.5+0.076\mathrm{x}$$

(3)

where x denotes the gap width, with the unit of mm. One can observe that the structural coefficient of the ultra-narrow gap increases with the increasing gap width. When the gap width equals to 0 mm, b = 0.5, suggesting that the thick plate with center heated can be regarded as an infinite body; when the gap width equals to 6.74 mm, b = 1, suggesting that the ultra-narrow gap can be regarded as a semi-infinite body if the gap width exceeds 6.74 mm. The threshold power values for the fusion in the ultra-narrow gaps with different gap widths can be calculated according to Equations (2) and (3). As to the penetration threshold power in an ultra-narrow gap, assuming Pd denotes the penetration threshold power for the flat plates’ welding and PD denotes the penetration threshold power in the ultra-narrow gap, the following relation can be derived according to Equation (2):

$$P_D=\frac{P_d}{b}$$

(4)

By measuring the penetration threshold values during the flat plates welding of with the use of different light spot diameters, the penetration threshold powers of the ultra-narrow gap with different gap widths can be calculated according to Equations (3) and (4). As demonstrated in our team’s previous studies [25], the penetration threshold value is irrelevant to the diameter of light spot and welding speed when the welding is performed at a low speed. The penetration threshold of a 304 stainless steel flat plate during fiber laser welding remains to be 0.94 kW/mm at different welding speeds and light spots [20]. Based on Equations (2)–(4), the variations of fusion/penetration threshold powers with the gap width can be calculated, as shown in Figure 4 (in which the diameter of the laser spot acting on the bottom of groove exceeds the gap width by 0.1 mm).

The welding was conducted in the ultra-narrow gap using a heat conduction welding mode and the laser’s input power should be between the fusion threshold power and penetration threshold power, i.e., the technological parameters were selected from the oblique line section in Figure 4. When the laser’s input power exceeded the penetration threshold power, the keyholes-induced pores would appear; when the laser’s input power was smaller than the power for the fusion of the plate on the edge of the light spot, the incomplete fusion of side walls would appear. The power has a relative smaller selection range at a higher welding speed, and the parameter’s range decreases as the ultra-narrow gap width increases.

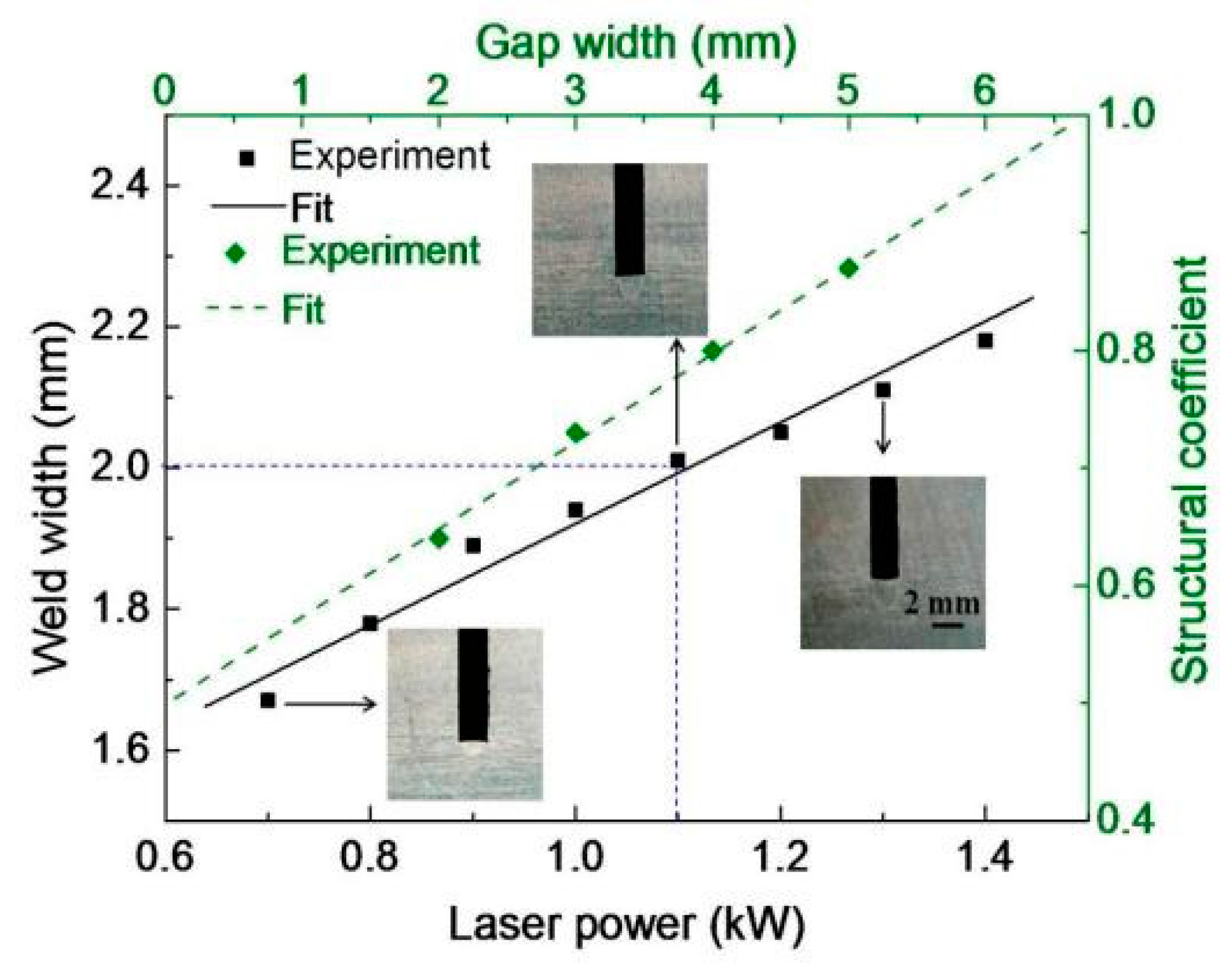
3.2. The Effects of the Technological Parameters on Weld Defects

The ultra-narrow gaps with the depth of 15 mm and different widths, respectively, were manufactured on a 304 stainless steel plate with the thickness of 20 mm. The filler wire welding experiments were conducted in the ultra-narrow gaps with the width of 4.2 mm, 3.2 mm and 2.2 mm, respectively. During the filler wire welding experiments (in which the diameter of the laser spot acting on the bottom of groove exceeds the gap width by 0.1 mm), different technological parameters were used; specifically, three sets of technological parameters (P = 4.9 kW,$\mathrm{v}=0.42 \mathrm{m}/\min$,$v_w=4.5 \mathrm{m}/\min$), (P = 3.3 kW, $\mathrm{v}=0.5 \mathrm{m}/\min$,$v_w=3.4 \mathrm{m}/\min$), and (P = 3 kW, $\mathrm{v}=0.5 \mathrm{m}/\min$,$v_w=2.5 \mathrm{m}/\min$), in which P denotes the laser’s input power, v denotes the welding speed, and $v_w$ denotes the wire feeding speed. Figure 5 displays the sections of the weld seams using the above-described three sets of welding technological parameters. One can observe that, in the gaps with the width of 4.2 mm, 3.2 mm, and 2.2 mm, the connections were achieved after the filling six, seven, and seven times, respectively. However, in two weld seams with comparatively large gap widths, incomplete fusion of side walls appears.

For the ultra-narrow gap laser conduction welding using filler wire, the following relation can be derived based on the energy balance relation:

$${\rho }_w{v}_w\frac{\pi {d_w}^2}{4}\left[L_m+\left(T_m-T_0\right)\right]+P_Q\le AP$$

(5)

where the first item on the left denotes the energy required for the fusion of wires, ${\rho }_w$ denotes the welding wire’s density, $L_m$ denotes the welding wire’s latent heat of fusion, $d_w$ denotes the welding wire’s diameter, and $P_Q$ denotes the energy lost in heat conduction. The maximum value of wire feeding speed under the conditions with different welding technological parameters and ultra-narrow gap widths can be calculated according to Equation (5). The volume of the wire fusion in the ultra-narrow gap equals the volume of the ultra-narrow gap:

$$v_w\frac{\mathsf{\pi }{{\mathrm{d}}_{\mathrm{w}}}^2}{4}=\mathrm{vGh}$$

(6)

where G denotes the gap width and h denotes the height for each fire feeding. According to Equation (6), the number of times for filing the ultra-narrow gap can be expressed as:

$$n=\frac{4\mathrm{vGH}}{v_w\mathsf{\pi }{{\mathrm{d}}_{\mathrm{w}}}^2}$$

(7)

where H denotes depth of the ultra-narrow gap. Given the technological parameters, the numbers of times for filling the ultra-narrow gaps with the width of 4.2 mm, 3.2 mm, and 2.2 mm are calculated to be 6.18, 7.12, and 6.9 according to Equation (7). The results are in good consistency with the time for filling in Figure 5.

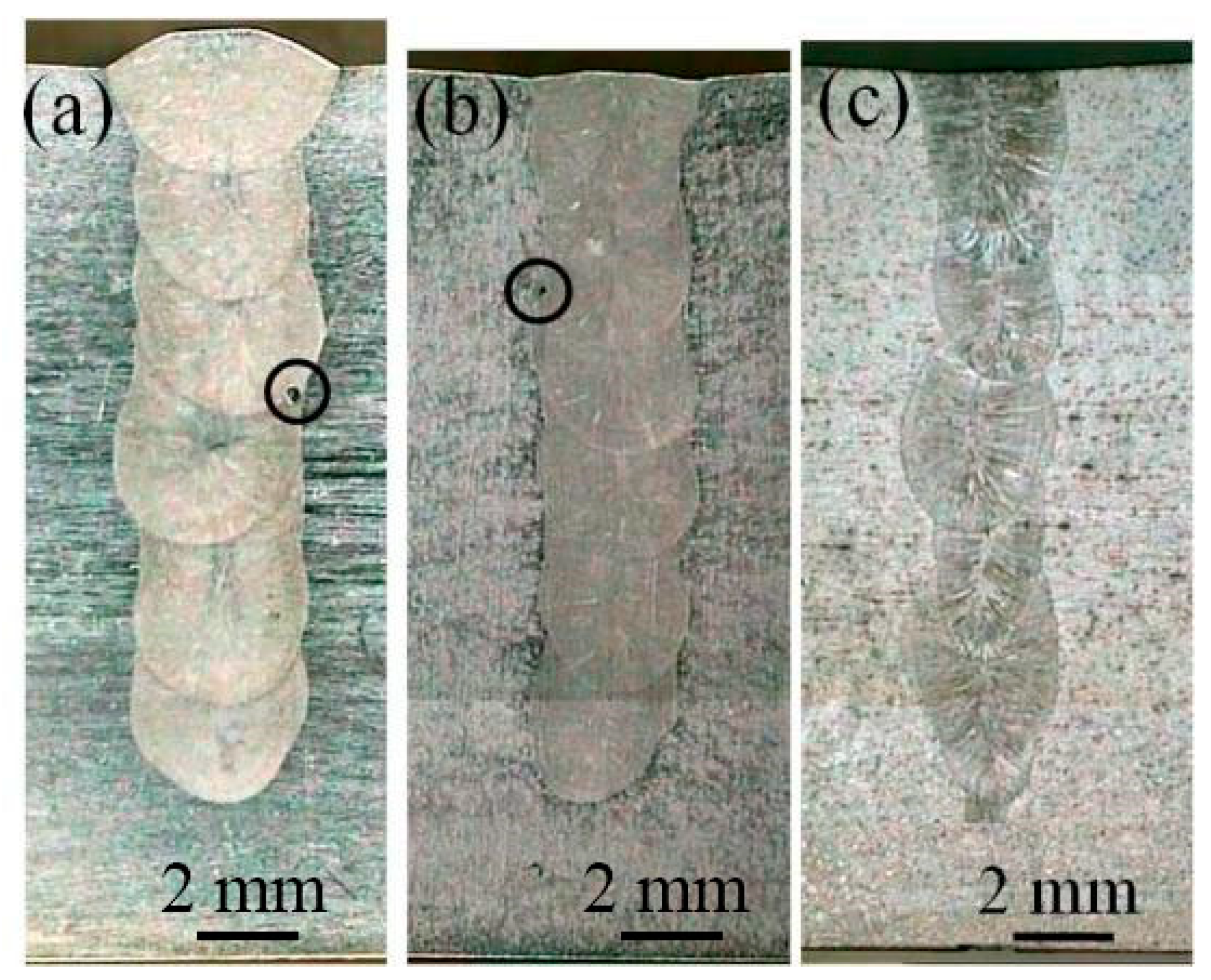
3.3. Micro-Structures of the Welding Joints

According to the results in Figure 4, the ultra-narrow gap with the width of 3 mm between two 304 stainless steel plates with the thickness of 60 mm was welded under the follow condition: P = 3.5 kW,$\mathrm{v}=0.42 \mathrm{m}/\min$, $v_w=3.4 \mathrm{m}/\min$. Figure 6 presents the welding results. The weld seam was acquired through 20 times of filling, with a regular pattern and no defects such as the incomplete fusion of side walls and pores. The depth of each filling is approximately 3 mm, and the width of the weld seam is approximately 3.8 mm.

Figure 7a shows the local microstructure of an ultra-narrow gap laser weld of 60 mm stainless steel thick plate. From the figure, it can be seen that the weld has typical characteristics of rapid solidification structure, and the columnar structure grows vertically from the edge of the fusion line to the center of the weld. The high-power microscopic observation results of the marked areas in Figure 7a are shown in Figure 7b–g. Figure 7b shows the microstructure of the base metal, which shows that long ferrite is uniformly distributed in the austenite matrix, which is the high-temperature ferrite produced by the segregation of ferrite-forming elements (mainly chromium) during hot rolling solidification of the base metal. Figure 7c shows the microstructure of the fusion line and heat affected zone. It can be seen that the grains in the heat affected zone have not grown obviously, which indicates that repeated heating of multi-pass welding has not caused obvious changes in the microstructure of heat affected zone. The ferrite content increases obviously near the fusion line of the base metal, showing the form of extending from the fusion zone to the base metal. Figure 7d shows the microstructure of the weld zone, which consists of columnar austenite and skeleton ferrite formed by rapid cooling, and the ferrite dendrite spacing is about 10 μm. Figure 7e shows the lath ferrite appearing at the grain boundary of columnar austenite, which shows that the ferrite of ultra-narrow gap laser weld is in the form of skeleton and lath ferrite coexisting. Figure 7f shows the microstructure of the weld center, which is a non-directional and non-uniform equiaxed crystal region and massive columnar crystal cluster, which is related to the smaller temperature gradient of the weld edge and the faster flow velocity of the weld pool compared with the central region of the weld pool. Figure 7g shows the microstructure of the interface between weld beads, where two parts of columnar crystals are formed vertically and horizontally, and the columnar crystals at the interface are closely connected and have no defects such as pores. The multidirectional columnar crystals are beneficial to improve the comprehensive mechanical properties of the joint.

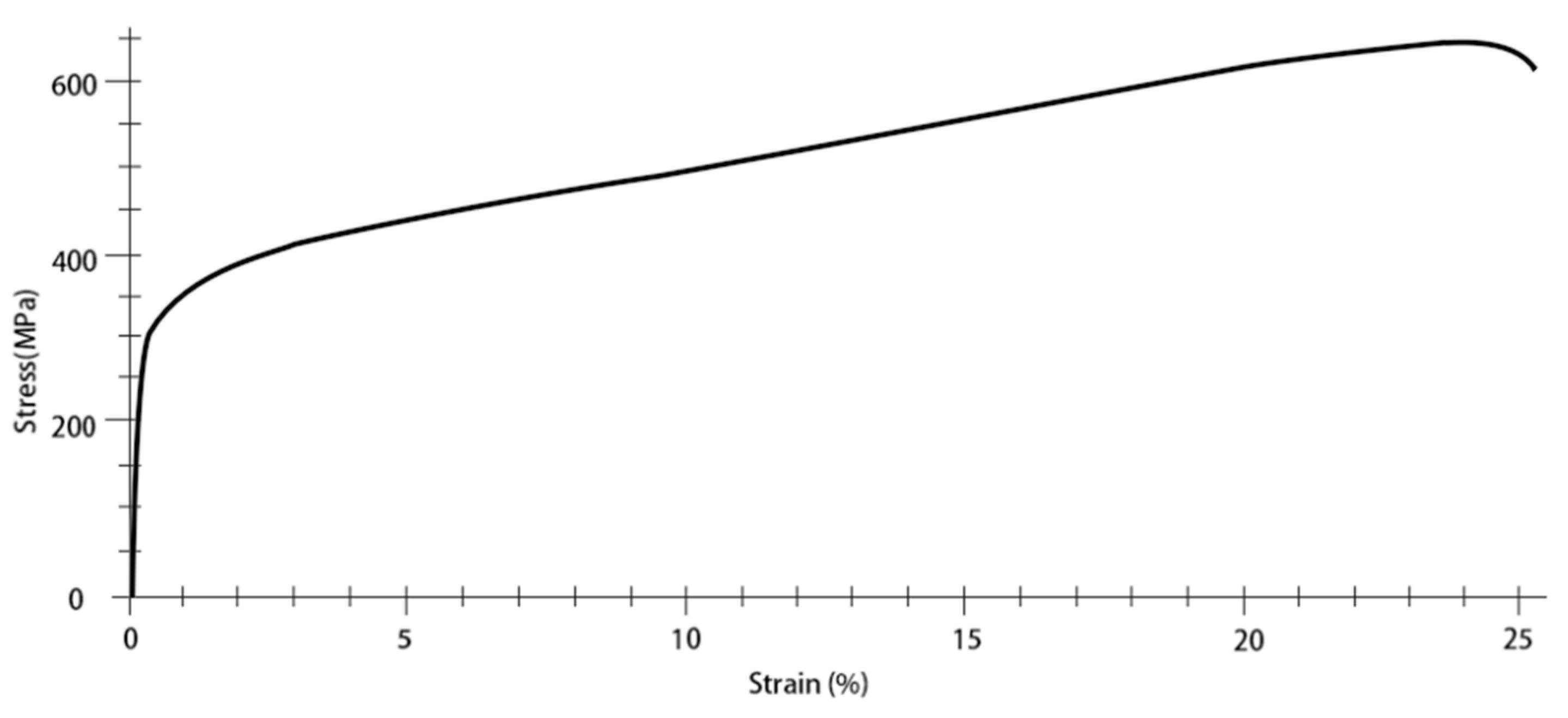
3.4. Mechanical Properties of the Welding Joints

Figure 8 displays the micro-hardness distribution in the middle of weld seam. One can observe that the micro-hardness of the weld seam is approximately 280 Hv, which is slightly smaller than that of the base metal (300 Hv). The micro-hardness of HAZ can reach up to 340 Hv. This is due to the fact that, when the HAZ was heated to the temperature near the alloy’s solidus curve, the precipitates in the base metal were dissolved and resulted in the supersaturation of austenite; therefore, various carbides and nitrides were re-precipitated during the rapid cooling process, leading to the increase of hardness in HAZ. According to the micro-hardness measurement results, the welding joint between two 304 stainless steel plates (with the thickness of 60 mm) using ultra-narrow laser conduction welding with filler wire exhibits slight differences in different regions in terms of hardness. No noticeable softening phenomenon can be observed, i.e., a narrow HAZ imposed little effects on the joint’s performance.

Figure 9 presents the tensile test results of the stainless steel welding joint. Figure 10 shows the stress–strain curves of the sample for the tensile test. One can observe that the tensile failure occurred in the weld seam; the average tensile strength of the welding joint is 651 MPa, which is 87% of the tensile strength of the base metal (745 MPa); the average yield strength of the welding joint is 315 MPa, which is approximately equal to that of the base metal (307 MPa); the average elongation ratio of the welding joint is approximately 24.7%, which is significantly lower than that of the base metal (48.6%). Since the filler wires are different from the base metal in terms of chemical components (the ferrite content in ER347 welding wires is higher), the strength of the weld seam decreases to a certain extent; however, the reduction of tension strength is mainly related to the fact that the weld seam is made up of the as-cast structures without hot rolling and strengthening. In addition, the weld seam underwent several times of thermal cycles due to the multi-layer filling process, which can be regarded the tempering process. Therefore, the strength of the welding joint became non-uniform, leading to the decline in overall strength. The significant reduction of elongation ratio is mainly due to the fact that the weld seam is inferior to the base metal in terms of tensile strength.

Figure 11 shows the effect of 180-degree bending of welding samples. As shown in Figure 11, all the tested bending samples can reach 180-degree bending without cracks and other defects, which indicates that the weld has good bending resistance and plasticity.

Figure 12 displays the scanning electron microscope (SEM) images of the tensile facture of the welding joint. It can be seen that the tensile fracture of the welding joint sample is characterized by the typical equal-axis dimples. These dimples lack directionality and vary slightly in size. No second-phase particles are found at the bottom of the dimple, so it can be judged that the fracture mode of the sample is a typical plastic fracture, also known as dimple fracture. The fracture principle is that, under the action of slip, the micro-cavities in the material itself grow up or gather continuously during the plastic deformation of the tensile specimen, and the thickness of the free surface between the micro-holes gradually decreases. When the plastic deformation reaches a certain degree, the micro-holes are connected together to form dimple fracture, which finally leads to the fracture separation of the specimen and fracture.

4. Conclusions

In this paper, the 304 stainless steel thick plates were welded using the ultra-narrow gap fiber laser conduction welding with filler wire, and the following conclusions can be reached:

• Using the optimized parameters and a gap with 3 mm width, two 304 stainless steel plates with 60 mm thickness were welding through the 20 times of filling. The obtained weld seam has the uniform widths from the top to bottom (being approximately 3.8 mm), with favorable formation, and no defects such as the incomplete fusion of sidewalls and keyhole-induced porosity can be observed.
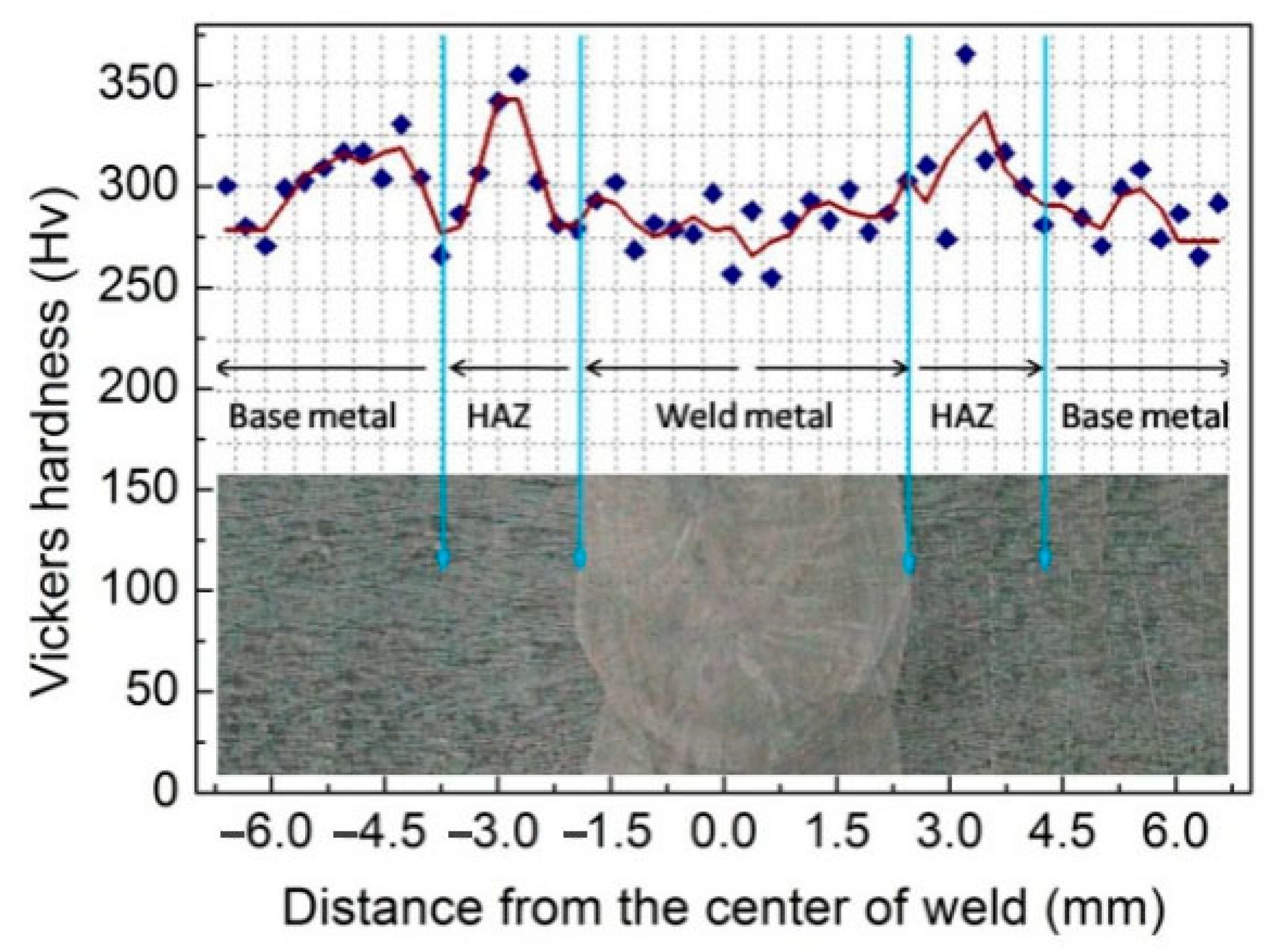
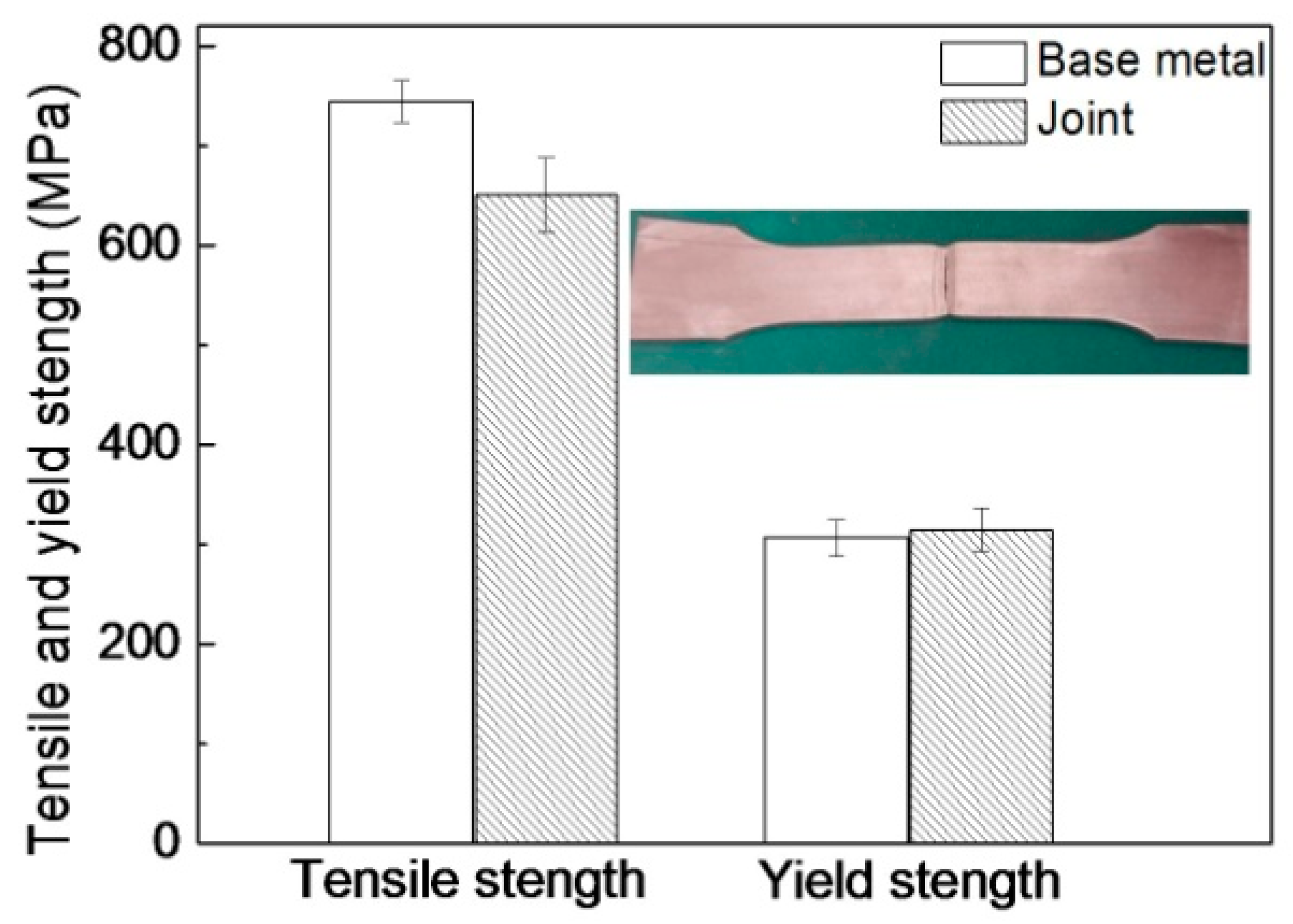
• The micro-hardness of the weld seam is almost equal to that of the base metal, which is slightly lower than that of HAZ. The tensile strength of the welding joint is 87% of that of the base metal, while the yield strength of the joint is slightly higher than that of the base metal.