Application of ANN Weighted by Optimization Algorithms to Predict the Color Coordinates of Cellulosic Fabric in Dyeing with Binary Mix of Natural Dyes
Abstract
:1. Introduction
2. Material and Method
2.1. Materials
2.2. Methods
2.3. ANN
2.4. GA
2.5. PSO
2.6. GWO
2.7. FMINCON
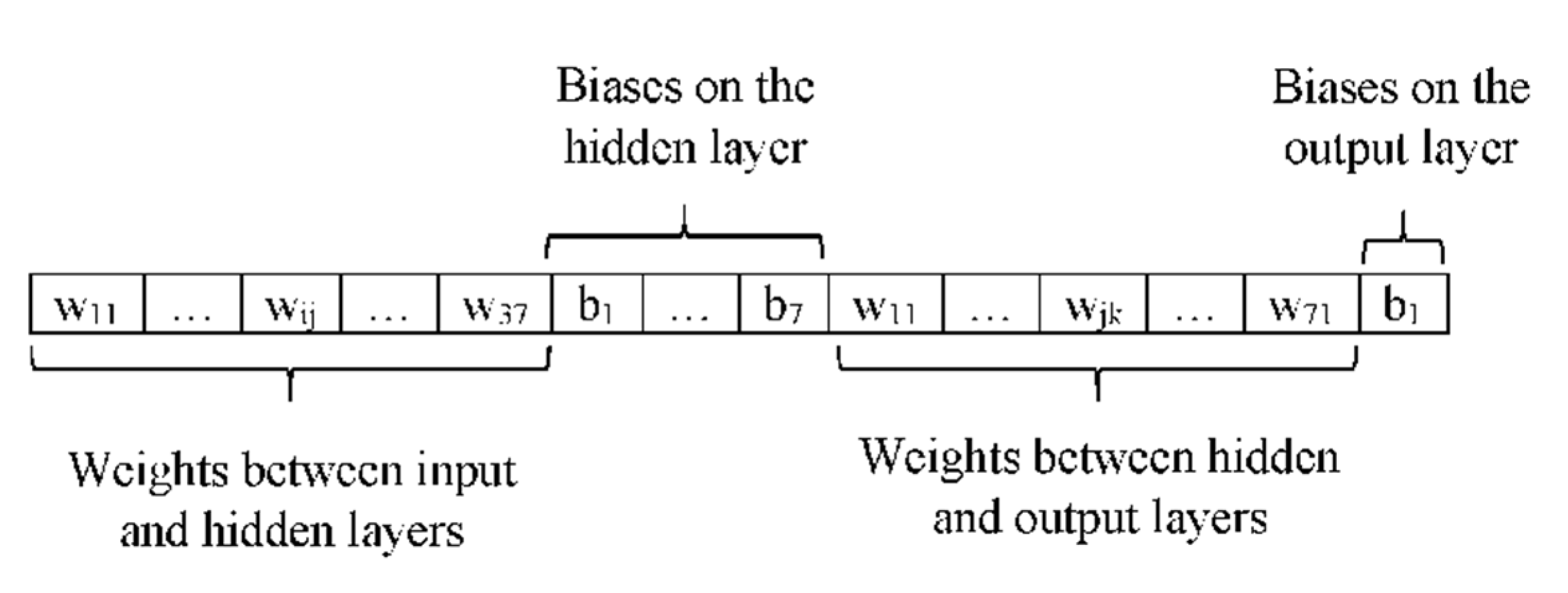
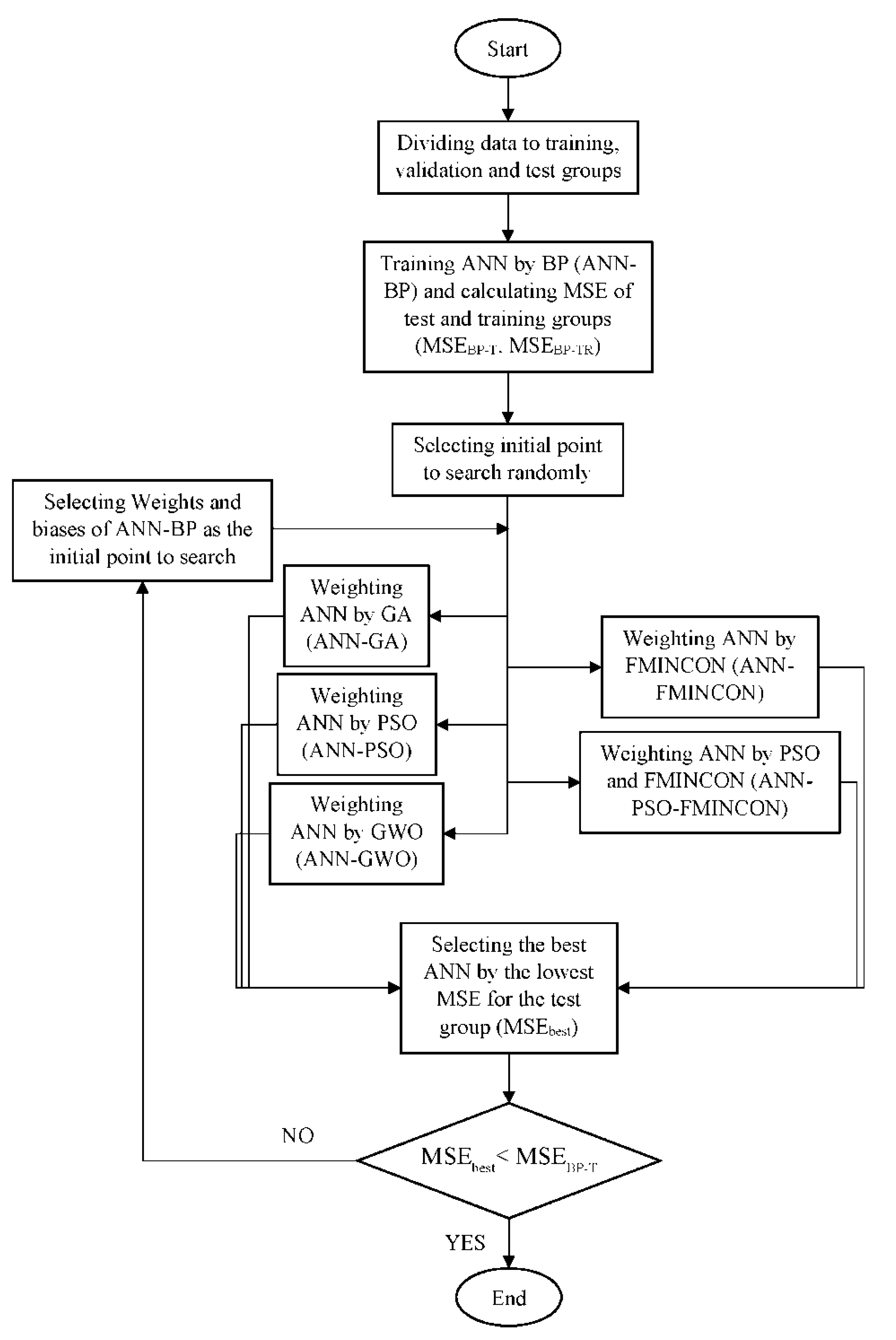
2.8. Weighting ANN
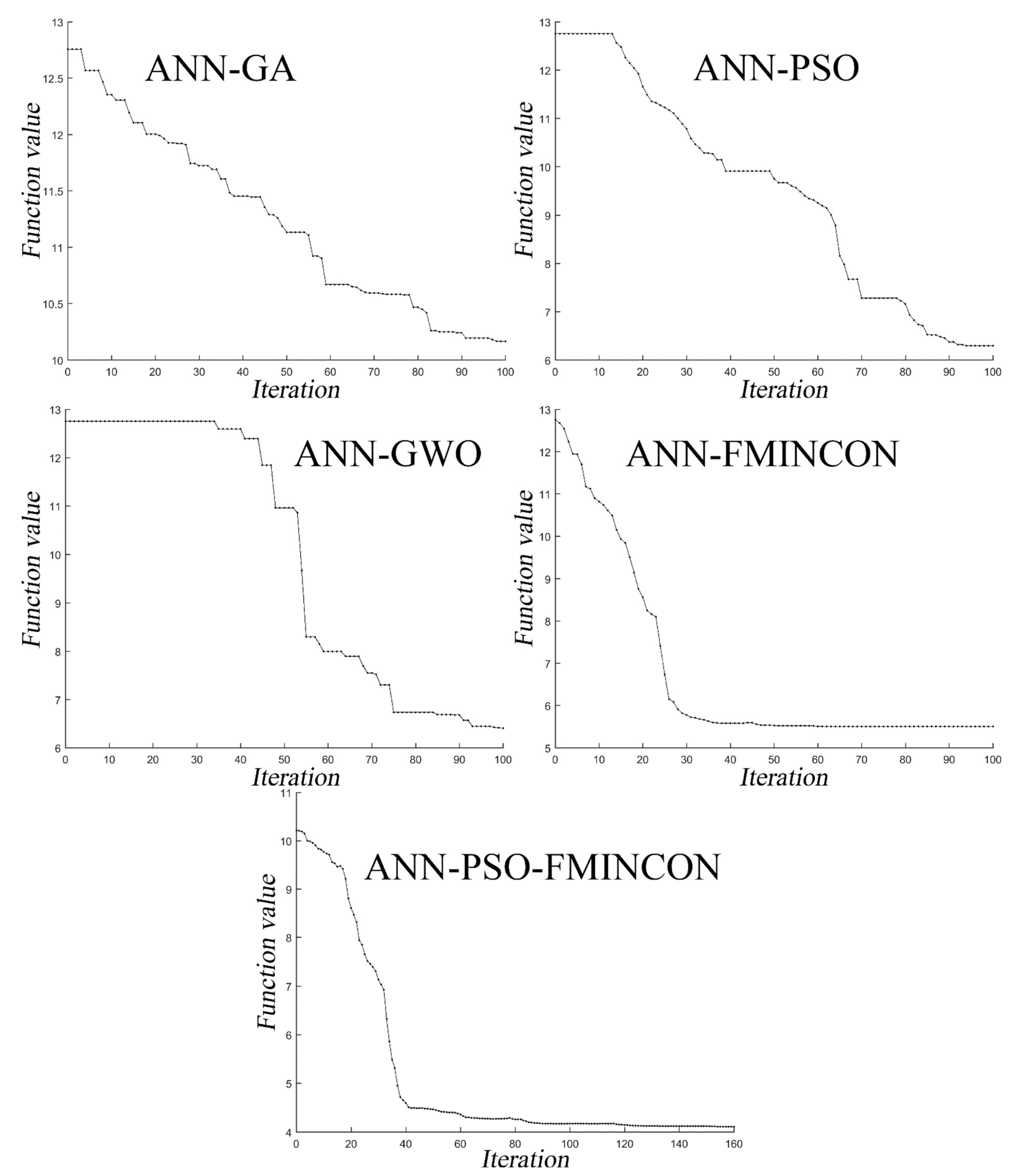
3. Result and Discussion
4. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rafiq, A.; Ikram, M.; Ali, S.; Niaz, F.; Khan, M.; Khan, Q.; Maqbool, M. Photocatalytic degradation of dyes using semiconductor photocatalysts to clean industrial water pollution. J. Ind. Eng. Chem. 2021, 97, 111–128. [Google Scholar] [CrossRef]
- Benli, H.; Paşayev, N.; Bahtiyari, M.İ.; Tugay, O. Investigation of the Possibilities of Using Rhapon-ticoides Iconiensis in Wool Dyeing. Text. Leather Rev. 2022, 5, 268–279. [Google Scholar] [CrossRef]
- Sk, S.; Mia, R.; Haque, A.; Shamim, A.M. Review on Extraction and Application of Natural Dyes. Text. Leather Rev. 2021, 4, 218–233. [Google Scholar] [CrossRef]
- Singh, M.; Vajpayee, M.; Ledwani, L. Eco-friendly surface modification of natural fibres to improve dye uptake using natural dyes and application of natural dyes in fabric finishing: A review. Mater. Today Proc. 2021, 43, 2868–2871. [Google Scholar] [CrossRef]
- Manyim, S.; Kiprop, A.K.; Mwasiagi, J.I.; Achisa, C.M.; Odero, M.P. Dyeing of cotton fabric with Euclea divinorum extract using response surface optimization method. Res. J. Text. Appar. 2021, 5, 109–123. [Google Scholar] [CrossRef]
- Rani, J.; Singh, S. Antimicrobial Properties of Herbal Dyes of Indian Medicinal Plants. Text. Leather Rev. 2022, 5, 199–222. [Google Scholar] [CrossRef]
- Ben Ticha, M.; Meksi, N.; Attia, H.E.; Haddar, W.; Guesmi, A.; Ben Jannet, H.; Mhenni, M.F. Ultrasonic extraction of Parthenocissus quinquefolia colorants: Extract identification by HPLC-MS analysis and cleaner application on the phytodyeing of natural fibres. Dye. Pigment. 2017, 141, 103–111. [Google Scholar] [CrossRef]
- Benli, H.; Bahtiyari, M.I. Use of ultrasound in biopreparation and natural dyeing of cotton fabric in a single bath. Cellulose 2015, 22, 867–877. [Google Scholar] [CrossRef]
- Buyukakinci, B.Y.; Guzel, E.T.; Karadag, R. Organic Cotton Fabric Dyed with Dyer’s Oak and Bar-berry Dye by Microwave Irradiation and Conventional Methods. Ind. Text. 2021, 72, 30–38. [Google Scholar] [CrossRef]
- Kiran, S.; Adeel, S.; Yousaf, M.S.; Habib, N.; Hassan, A.; Qayyum, M.A.; Abdullah, M. Green dyeing of microwave treated silk using coconut coir based tannin natural dye. Ind. Textila 2020, 71, 227–234. [Google Scholar] [CrossRef]
- Rehman Ur, F.; Adeel, S.; Haddar, W.; Bibi, R.; Azeem, M.; Mia, R.; Ahmed, B. Micro-wave-Assisted Exploration of Yellow Natural Dyes for Nylon Fabric. Sustainability 2022, 14, 5599. [Google Scholar] [CrossRef]
- Ul-Islam, S.; Rather, L.J.; Shabbir, M.; Bukhari, M.N.; Khan, M.A.; Mohammad, F. First Application of Mix Metallic Salt Mordant Combinations to Develop Newer Shades on Wool with Bixa orellana Natural Dye Using Reflectance Spectroscopy. J. Nat. Fibers 2018, 15, 363–372. [Google Scholar] [CrossRef]
- Asım, D.; Benli, H.; Şen, Y.; Bahtiyari, M.İ. Dyeing of Cotton with Thyme and Pomegranate Peel. Cellulose 2014, 21, 4671–4680. [Google Scholar]
- Amin, N.; Rehman, F.-U.; Adeel, S.; Ahamd, T.; Muneer, M.; Haji, A. Sustainable application of cochineal-based anthraquinone dye for the coloration of bio-mordanted silk fabric. Environ. Sci. Pollut. Res. 2020, 27, 6851–6860. [Google Scholar] [CrossRef]
- Baseri, S. Eco-friendly production of anti-UV and antibacterial cotton fabrics via waste products. Cellulose 2020, 27, 10407–10423. [Google Scholar] [CrossRef]
- Haji, A.; Naebe, M. Cleaner dyeing of textiles using plasma treatment and natural dyes: A review. J. Clean. Prod. 2020, 265, 121866. [Google Scholar] [CrossRef]
- Haji, A. Plasma activation and chitosan attachment on cotton and wool for improvement of dyeability and fastness properties. Pigment Resin Technol. 2020, 49, 483–489. [Google Scholar] [CrossRef]
- Haji, A.; Ashraf, S.; Nasiriboroumand, M.; Lievens, C. Environmentally Friendly Surface Treatment of Wool Fiber with Plasma and Chitosan for Improved Coloration with Cochineal and Safflower Natural Dyes. Fibers Polym. 2020, 21, 743–750. [Google Scholar] [CrossRef]
- Sajed, T.; Haji, A.; Mehrizi, M.K.; Boroumand, M.N. Modification of wool protein fiber with plasma and dendrimer: Effects on dyeing with cochineal. Int. J. Biol. Macromol. 2018, 107, 642–653. [Google Scholar] [CrossRef]
- Ainur, B.; Nurzhan, B.; Gani, Y.; Donyor, N. The improvement of bactericidal properties and change of colour characteristics of knitted materials at using nanosilver and carboxymethyl starch. Ind. Text. 2022, 73, 19–26. [Google Scholar] [CrossRef]
- Tripa, S.; Indrie, L.; Zlatev, Z.; Tripa, F. Customized clothes—A sustainable solution for textile waste generated by the clothing industry. Ind. Text. 2022, 73, 275–281. [Google Scholar] [CrossRef]
- Rosyida, A.; Masykuri, M. Minimisation of Pollution in the Cotton Fabric Dyeing Process with Natural Dyes by the Selection of Mordant Type. Res. J. Text. Appar. 2022, 26, 41–56. [Google Scholar] [CrossRef]
- Sikka, M.P.; Sarkar, A.; Garg, S. Artificial intelligence (AI) in textile industry operational modernization. Res. J. Text. Appar. 2022. ahead of print. [Google Scholar] [CrossRef]
- Gulihonenahali Rajkumar, A.; Hemath, M.; Kurki Nagaraja, B.; Neerakallu, S.; Thiagamani, S.M.K.; Asrofi, M. An Artificial Neural Network Prediction on Physical, Mechanical, and Thermal Char-acteristics of Giant Reed Fiber Reinforced Polyethylene Terephthalate Composite. J. Ind. Text. 2022, 51, 769S–803S. [Google Scholar] [CrossRef]
- Heydarian, P.; Vadood, M.; Yazdi, A.A.A. Modeling of bending length based on concentrated loading method. Indian J. Fibre Text. Res. 2020, 45, 220–223. [Google Scholar] [CrossRef]
- Karasawa, Y.; Uemae, M.; Yoshida, H.; Kamijo, M. Prediction of clothing comfort sensation of an undershirt using artificial neural networks with psychophysiological responses as input data. Text. Res. J. 2021, 92, 330–345. [Google Scholar] [CrossRef]
- Li, W.; Wei, Z.; Liu, Z.; Du, Y.; Zheng, J.; Wang, H.; Zhang, S. Qualitative identification of waste textiles based on near-infrared spectroscopy and the back propagation artificial neural network. Text. Res. J. 2021, 91, 2459–2467. [Google Scholar] [CrossRef]
- Majumdar, A. Modelling of thermal conductivity of knitted fabrics made of cotton–bamboo yarns using artificial neural network. J. Text. Inst. 2011, 102, 752–762. [Google Scholar] [CrossRef]
- Paknejad, S.H.; Vadood, M.; Soltani, P.; Ghane, M. Modeling the sound absorption behavior of carpets using artificial intelligence. J. Text. Inst. 2021, 112, 1763–1771. [Google Scholar] [CrossRef]
- Sumesh, K.; Kanthavel, K. Optimizing various parameters influencing mechanical properties of banana/coir natural fiber composites using grey relational analysis and artificial neural network models. J. Ind. Text. 2020, 51, 6705S–6727S. [Google Scholar] [CrossRef]
- Monticeli, F.M.; Neves, R.M.; Júnior, H.L.O. Using an artificial neural network (ANN) for prediction of thermal degradation from kinetics parameters of vegetable fibers. Cellulose 2021, 28, 1961–1971. [Google Scholar] [CrossRef]
- Jun, L.Y.; Karri, R.R.; Yon, L.S.; Mubarak, N.; Bing, C.H.; Mohammad, K.; Jagadish, P.; Abdullah, E. Modeling and optimization by particle swarm embedded neural network for adsorption of methylene blue by jicama peroxidase immobilized on buckypaper/polyvinyl alcohol membrane. Environ. Res. 2020, 183, 109158. [Google Scholar] [CrossRef] [PubMed]
- Picos-Benítez, A.R.; Martínez-Vargas, B.L.; Duron-Torres, S.M.; Brillas, E.; Peralta-Hernández, J.M. The use of artificial intelligence models in the prediction of optimum operational conditions for the treatment of dye wastewaters with similar structural characteristics. Process Saf. Environ. Prot. 2020, 143, 36–44. [Google Scholar] [CrossRef]
- Aminoddin, H.; Vadood, M. Environmentally Benign Dyeing of Polyester Fabric with Madder: Modelling by Artificial Neural Network and Fuzzy Logic Optimized by Genetic Algorithm. Fibers Polym. 2021, 22, 3351–3357. [Google Scholar]
- Vadood, M.; Haji, A. A hybrid artificial intelligence model to predict the color coordinates of polyester fabric dyed with madder natural dye. Expert Syst. Appl. 2022, 193, 116514. [Google Scholar] [CrossRef]
- Haji, A.; Payvandy, P. Application of ANN and ANFIS in prediction of color strength of plasma-treated wool yarns dyed with a natural colorant. Pigment Resin Technol. 2020, 49, 171–180. [Google Scholar] [CrossRef]
- Kheirkhah, B.P.; Vadood, M.; Safar, J.M. Modeling the Properties of Core-Compact Spun Yarn Using Artificial Neural Network. J. Text. Polym. 2016, 4, 101–105. [Google Scholar]
- Fausett, V. Fundamentals of Neural Networks: Architectures, Algorithms and Applications; Prentice Hall International: Hoboken, NJ, USA, 1994. [Google Scholar]
- Vle, N.F.L.; Najlona, E.V.I.; Umetne, Z.U.M. Predicting the Physical Properties of Drawn Nyylon-6 Fibers Using an Artificial-Neural-Network Model. Mater. Tehnol. 2015, 49, 325–332. [Google Scholar]
- Moazeni, N.; Vadood, M.; Semnani, D.; Hasani, H. Modeling the compliance of polyurethane nanofiber tubes for artificial common bile duct. Mater. Res. Express 2018, 5, 025004. [Google Scholar] [CrossRef]
- Hadavandi, E.; Mostafayi, S.; Soltani, P. A Grey Wolf Optimizer-based neural network coupled with response surface method for modeling the strength of siro-spun yarn in spinning mills. Appl. Soft Comput. 2018, 72, 1–13. [Google Scholar] [CrossRef]
- Erdem İşmal, Ö. Greener Natural Dyeing Pathway Using a by-Product of Olive Oil; Prina and Biomordants. Fibers Polym 2017, 18, 773–785. [Google Scholar] [CrossRef]
- Chipperfield, A.J.; Fleming, P.J. The Matlab Genetic Algorithm Toolbox. In Proceedings of the IEE Colloquium on Applied Control Techniques Using MATLAB, London, UK, 26 January 1995. [Google Scholar]
- Birge, B. Psot-a Particle Swarm Optimization Toolbox for Use with Matlab. In Proceedings of the 2003 IEEE Swarm Intelligence Symposium. SIS’03 (Cat. No. 03EX706), Indianapolis, IN, USA, 26 April 2003. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Coleman, T.; Branch, M.A.; Grace, A. Optimization Toolbox, 2nd ed.; For Use with Matlab. User’s Guide for Matlab 5; The MathWorks, Inc.: Natick, MA, USA, 1999. [Google Scholar]
- Saxén, A.; Bernander, K.B. Parallel Global Optimization Abb’s Metal Process Models Using Matlab. Project Rep. 2014, 1–30. [Google Scholar]
- Demuth, H.; Beale, M. Neural Network Toolbox, 4th ed.; The MathWorks Inc.: Natick, MA, USA, 2005. [Google Scholar]


| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Mordant | 3.00 | 2034.00 | 678.05 | 13.41 | 0.00 |
| Error | 116.00 | 5867.00 | 50.58 | - | - |
| Total | 119.00 | 7902.00 | - | - | - |
| Weld | 5.00 | 5432.00 | 1086.50 | 50.16 | 0.00 |
| Error | 114.00 | 2469.00 | 21.66 | - | - |
| Total | 119.00 | 7902.00 | - | - | - |
| Madder | 5.00 | 660.60 | 132.11 | 2.08 | 0.07 |
| Error | 114.00 | 7241.10 | 63.52 | - | - |
| Total | 119.00 | 7901.60 | - | - | - |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Mordant | 3.00 | 1092.00 | 363.89 | 5.68 | 0.00 |
| Error | 116.00 | 7432.00 | 64.07 | - | - |
| Total | 119.00 | 8524.00 | - | - | - |
| Weld | 5.00 | 6673.00 | 1334.51 | 82.17 | 0.00 |
| Error | 114.00 | 1851.00 | 16.24 | - | - |
| Total | 119.00 | 8524.00 | - | - | - |
| Madder | 5.00 | 769.50 | 153.91 | 2.26 | 0.05 |
| Error | 114.00 | 7754.50 | 68.02 | - | - |
| Total | 119.00 | 8524.00 | - | - | - |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|
| Mordant | 3.00 | 1473.00 | 491.10 | 12.94 | 0.00 |
| Error | 116.00 | 4402.00 | 37.95 | - | - |
| Total | 119.00 | 5875.00 | - | - | - |
| Weld | 5.00 | 1933.00 | 386.62 | 11.18 | 0.00 |
| Error | 114.00 | 3942.00 | 34.58 | - | - |
| Total | 119.00 | 5875.00 | - | - | - |
| Madder | 5.00 | 1103.00 | 220.59 | 5.27 | 0.00 |
| Error | 114.00 | 4772.00 | 41.86 | - | - |
| Total | 119.00 | 5875.00 | - | - | - |
| Number of Neurons | MSE for Training Group | MSE for Test Group | * MSE Change (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BP | GA | PSO | GWO | FMIN | PSO-FMIN | BP | GA | PSO | GWO | FMIN | PSO-FMIN | Training Group | Test Group | |
| 1 | 19.28 | 18.73 | 18.65 | 18.51 | 18.10 | 18.10 | 6.63 | 5.94 | 5.81 | 5.51 | 5.01α | 5.01 | 6.14 | 24.45 |
| 2 | 18.58 | 16.27 | 9.62 | 16.24 | 13.56 | 7.67 | 5.81 | 8.45 | 7.05 | 8.22 | 7.04 | 4.45 α | 58.73 | 23.48 |
| 3 | 12.76 | 10.17 | 6.30 | 6.41 | 5.51 | 4.11 | 3.60 | 4.55 | 7.02 | 7.97 | 10.76 | 2.02 α | 67.78 | 43.94 |
| 4 | 2.60 | 2.54 | 2.54 | 2.59 | 2.33 | 2.33 | 3.47 | 3.41 | 3.52 | 3.39 α | 3.39 | 3.39 | 0.18 | 2.28 |
| 5 | 1.91 | 1.90 | 1.89 | 1.91 | 1.73 | 1.73 | 3.63 | 3.64 | 3.66 | 3.63 α | 3.92 | 3.92 | 0.00 | 0.00 |
| 6 | 1.94 | 1.81 | 1.67 | 1.88 | 1.38 | 1.35 | 3.32 | 3.57 | 3.74 | 3.52 α | 4.62 | 4.10 | 3.52 | −5.89 |
| 7 | 2.37 | 2.21 | 2.12 | 2.25 | 1.18 | 1.15 | 4.36 | 4.37 | 4.79 | 4.15 α | 7.24 | 7.66 | 5.34 | 4.87 |
| Number of Neurons | MSE for Training Group | MSE for Test Group | * MSE Change (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BP | GA | PSO | GWO | FMIN | PSO-FMIN | BP | GA | PSO | GWO | FMIN | PSO-FMIN | Training Group | Test Group | |
| 1 | 17.52 | 16.50 | 16.44 | 16.46 | 16.50 | 16.44 | 4.44 | 4.89 α | 5.16 | 5.53 | 4.89 α | 5.19 | 5.82 | −10.06 |
| 2 | 10.61 | 10.56 | 10.55 | 10.57 | 10.56 | 10.49 | 3.94 | 4.31 | 4.31 | 4.26 | 4.31 | 3.77 α | 1.17 | 4.42 |
| 3 | 4.26 | 4.03 | 3.79 | 4.18 | 4.03 | 3.39 | 4.05 | 4.30 | 4.29 | 3.33 | 4.30 | 2.26 α | 20.38 | 44.09 |
| 4 | 1.59 | 1.59 | 1.58 | 1.59 | 1.59 | 1.49 | 2.18 | 2.18 | 2.24 | 2.18 | 2.18 | 1.68 α | 6.46 | 22.80 |
| 5 | 3.13 | 2.97 | 2.91 | 3.02 | 2.34 | 2.29 | 4.12 | 3.66 | 3.43 | 3.69 | 2.79 | 2.20 α | 26.73 | 46.69 |
| 6 | 3.62 | 3.30 | 3.14 | 3.49 | 2.21 | 2.15 | 13.67 | 13.26 | 13.60 | 11.83 | 3.81 | 3.44 α | 40.54 | 74.87 |
| 7 | 2.91 | 2.81 | 2.76 | 2.89 | 0.71 | 0.69 | 3.40 | 3.27 α | 3.64 | 3.39 | 4.52 | 4.12 | 3.23 | 3.70 |
| Number of Neurons | MSE for Training Group | MSE for Test Group | * MSE Change (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BP | GA | PSO | GWO | FMIN | PSO-FMIN | BP | GA | PSO | GWO | FMIN | PSO-FMIN | Training Group | Test Group | |
| 1 | 31.44 | 28.18 | 27.44 | 29.54 | 31.44 | 27.43 | 9.60 | 14.13 | 20.34 | 14.37 α | 20.85 | 20.85 | 6.04 | −49.75 |
| 2 | 25.25 | 24.99 | 24.67 | 25.03 | 25.25 | 11.33 | 23.47 | 26.25 | 28.06 | 26.58 | 16.48 α | 17.73 | 48.01 | 29.78 |
| 3 | 5.48 | 4.92 | 4.86 | 5.12 | 5.48 | 4.65 | 1.87 | 1.45 | 1.40 | 2.01 | 1.39 | 1.39 α | 15.02 | 25.81 |
| 4 | 4.37 | 4.21 | 4.18 | 4.28 | 4.37 | 3.41 | 2.05 | 1.42 | 1.41 | 1.31 α | 1.87 | 1.82 | 2.13 | 35.99 |
| 5 | 2.52 | 2.51 | 2.49 | 2.52 | 2.52 | 2.10 | 5.79 | 5.76 | 5.71 | 5.79 | 3.95 α | 4.71 | 23.35 | 31.72 |
| 6 | 21.39 | 16.18 | 13.04 | 14.18 | 21.39 | 2.09 | 16.85 | 13.50 | 15.91 | 17.83 | 5.94 | 5.43 α | 90.24 | 67.76 |
| 7 | 4.40 | 3.71 | 3.47 | 3.88 | 4.40 | 1.43 | 3.49 | 4.33 | 4.02 α | 4.96 | 6.80 | 5.61 | 21.27 | −15.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vadood, M.; Haji, A. Application of ANN Weighted by Optimization Algorithms to Predict the Color Coordinates of Cellulosic Fabric in Dyeing with Binary Mix of Natural Dyes. Coatings 2022, 12, 1519. https://doi.org/10.3390/coatings12101519
Vadood M, Haji A. Application of ANN Weighted by Optimization Algorithms to Predict the Color Coordinates of Cellulosic Fabric in Dyeing with Binary Mix of Natural Dyes. Coatings. 2022; 12(10):1519. https://doi.org/10.3390/coatings12101519
Chicago/Turabian StyleVadood, Morteza, and Aminoddin Haji. 2022. "Application of ANN Weighted by Optimization Algorithms to Predict the Color Coordinates of Cellulosic Fabric in Dyeing with Binary Mix of Natural Dyes" Coatings 12, no. 10: 1519. https://doi.org/10.3390/coatings12101519
APA StyleVadood, M., & Haji, A. (2022). Application of ANN Weighted by Optimization Algorithms to Predict the Color Coordinates of Cellulosic Fabric in Dyeing with Binary Mix of Natural Dyes. Coatings, 12(10), 1519. https://doi.org/10.3390/coatings12101519







