Comparative Study of the Mesomechanical Response of Asphalt Bridge Deck Pavement under Multiple Loads
Abstract
:1. Introduction
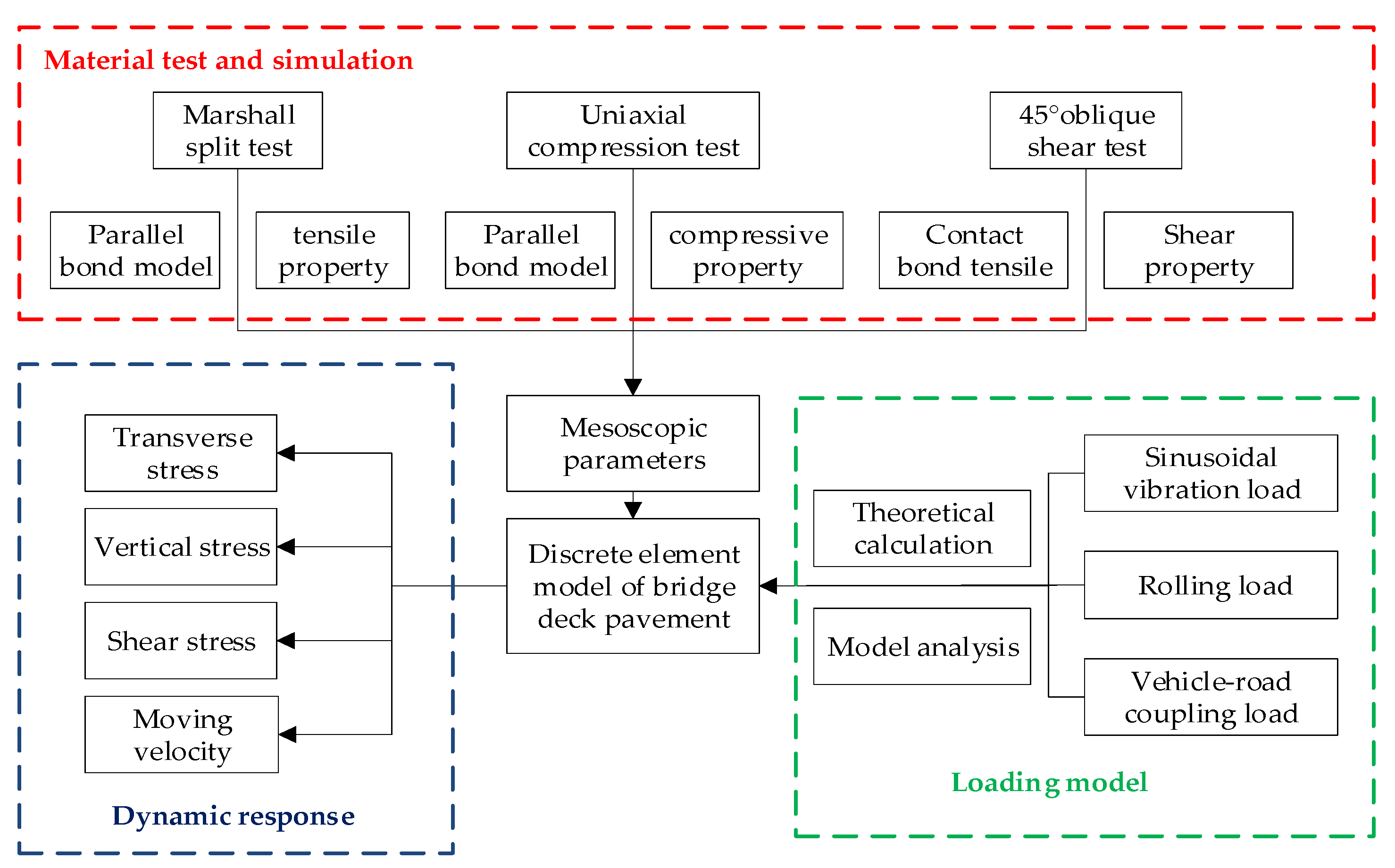
2. Material Experiment and Parameter Optimization
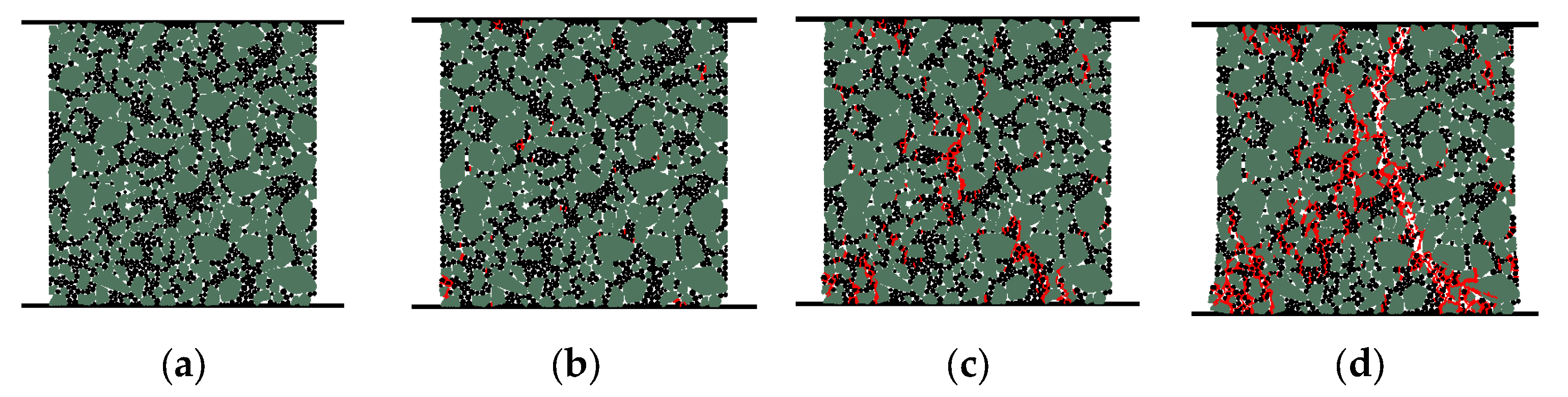
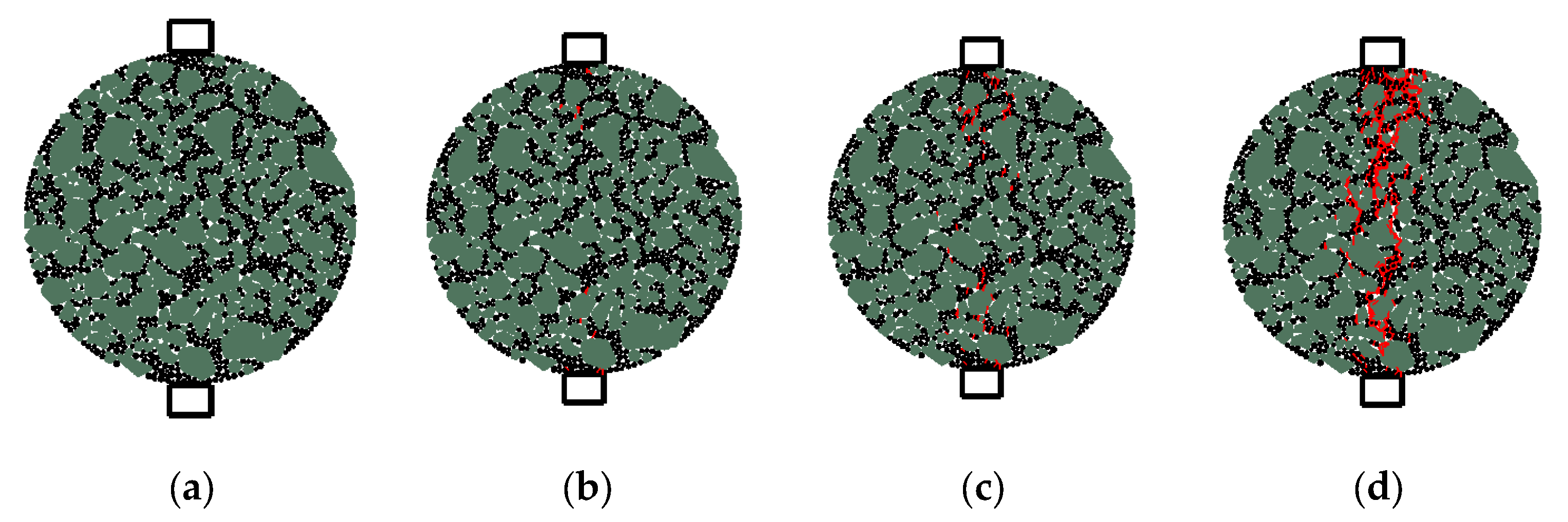
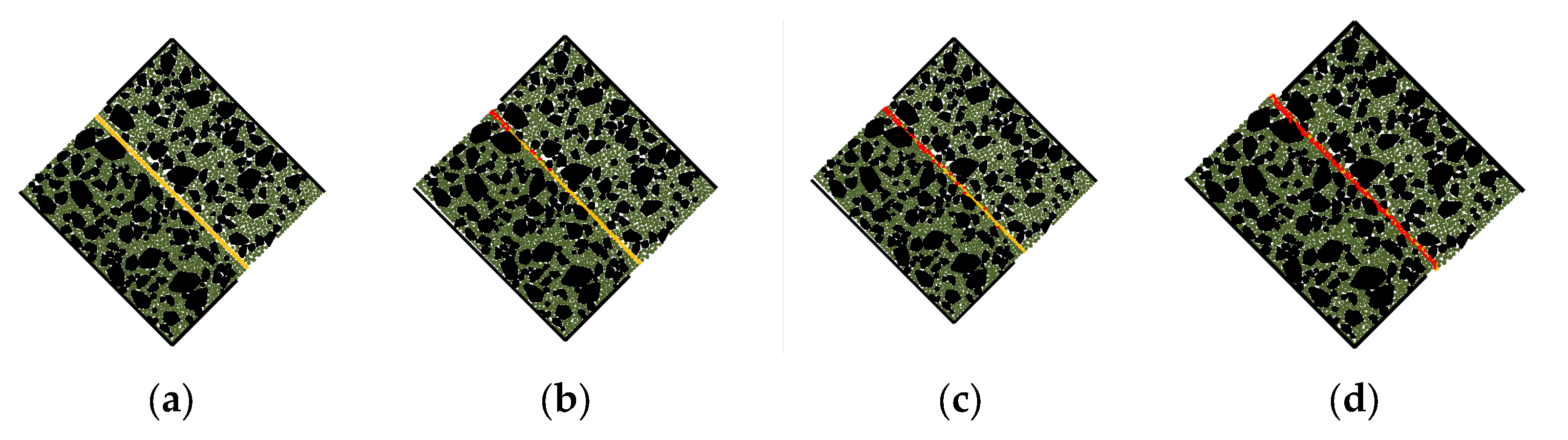
2.1. Material Experiment
2.2. Numerical Simulation and Parameter Optimization
3. Construction of Model and Realization of Dynamic Load
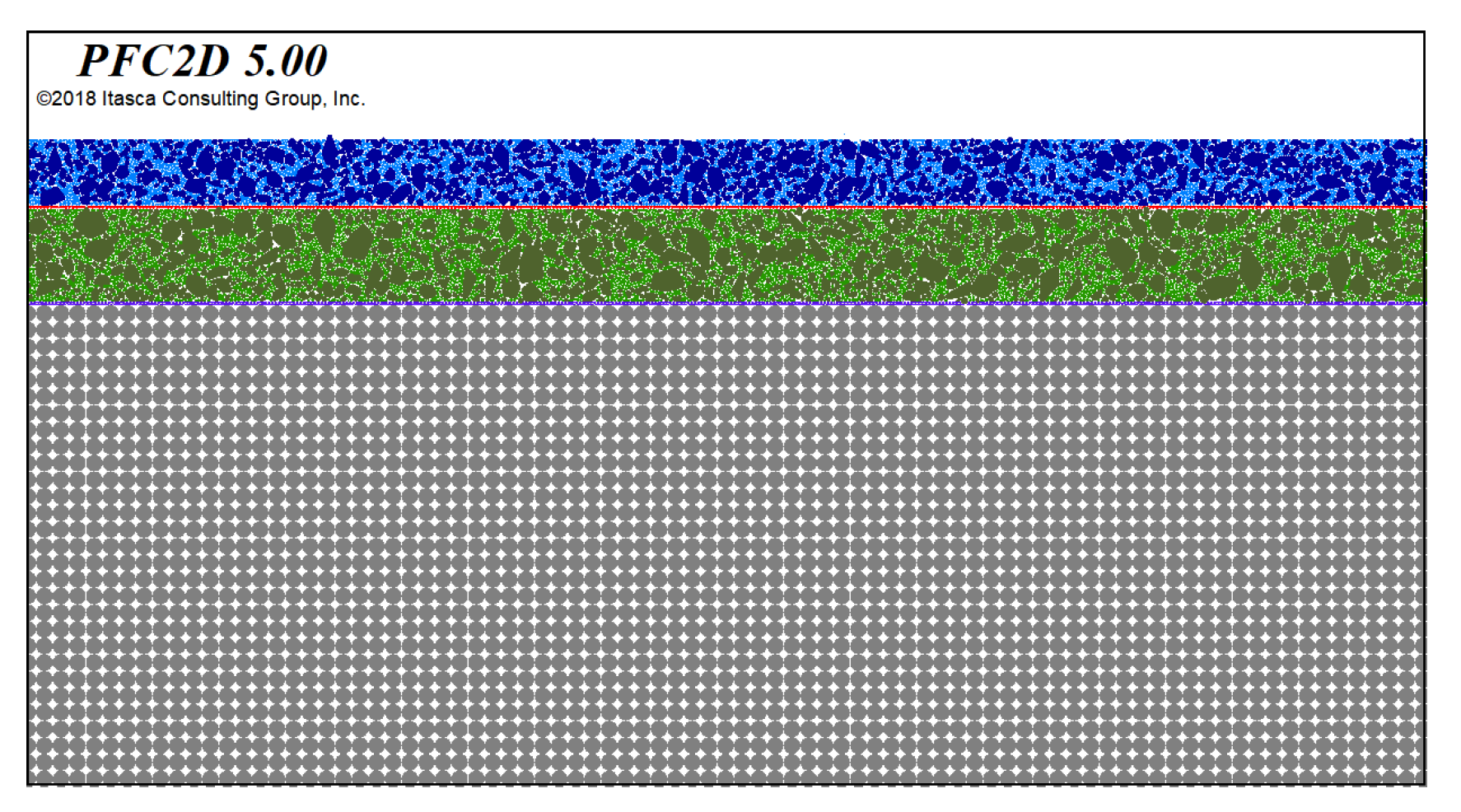
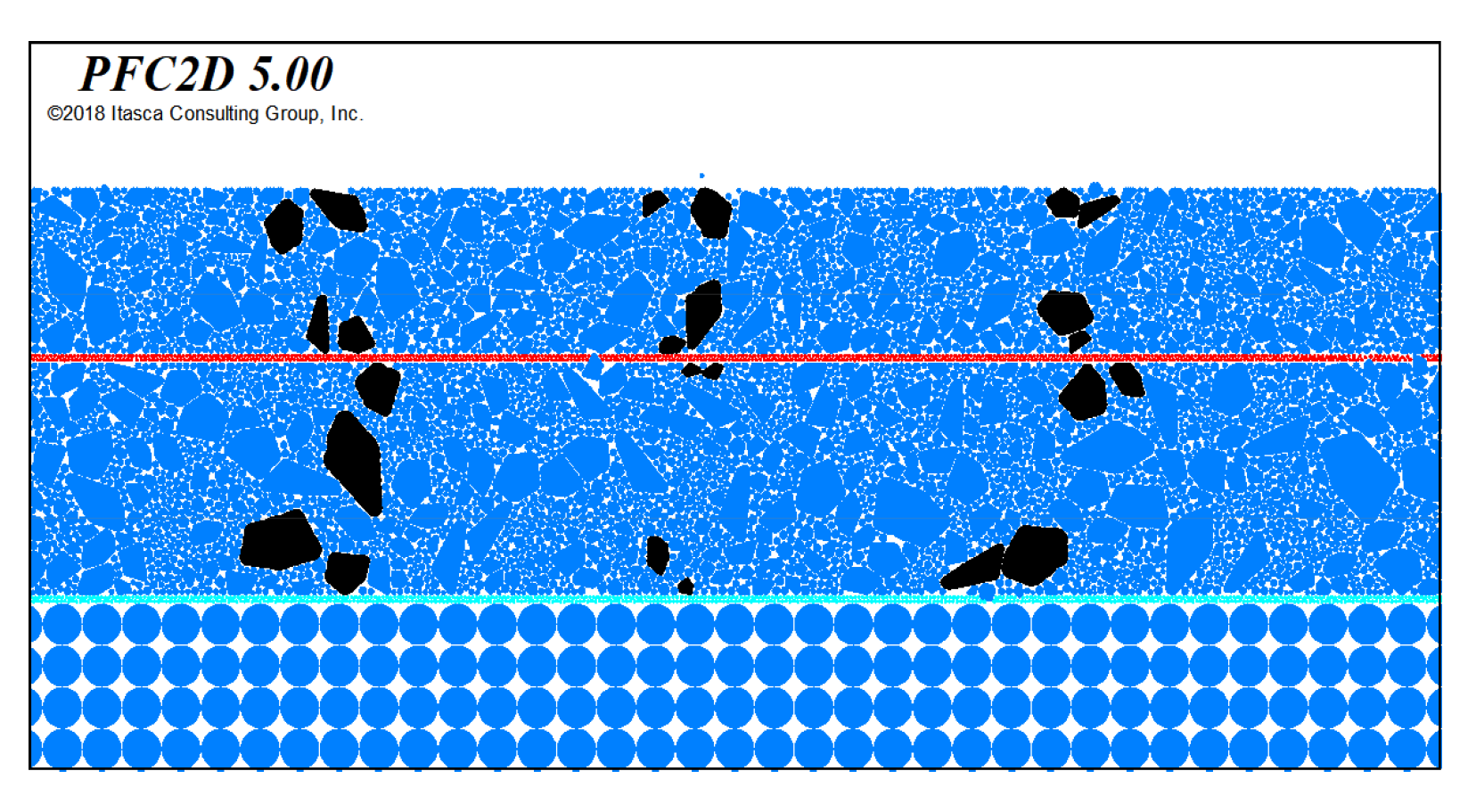
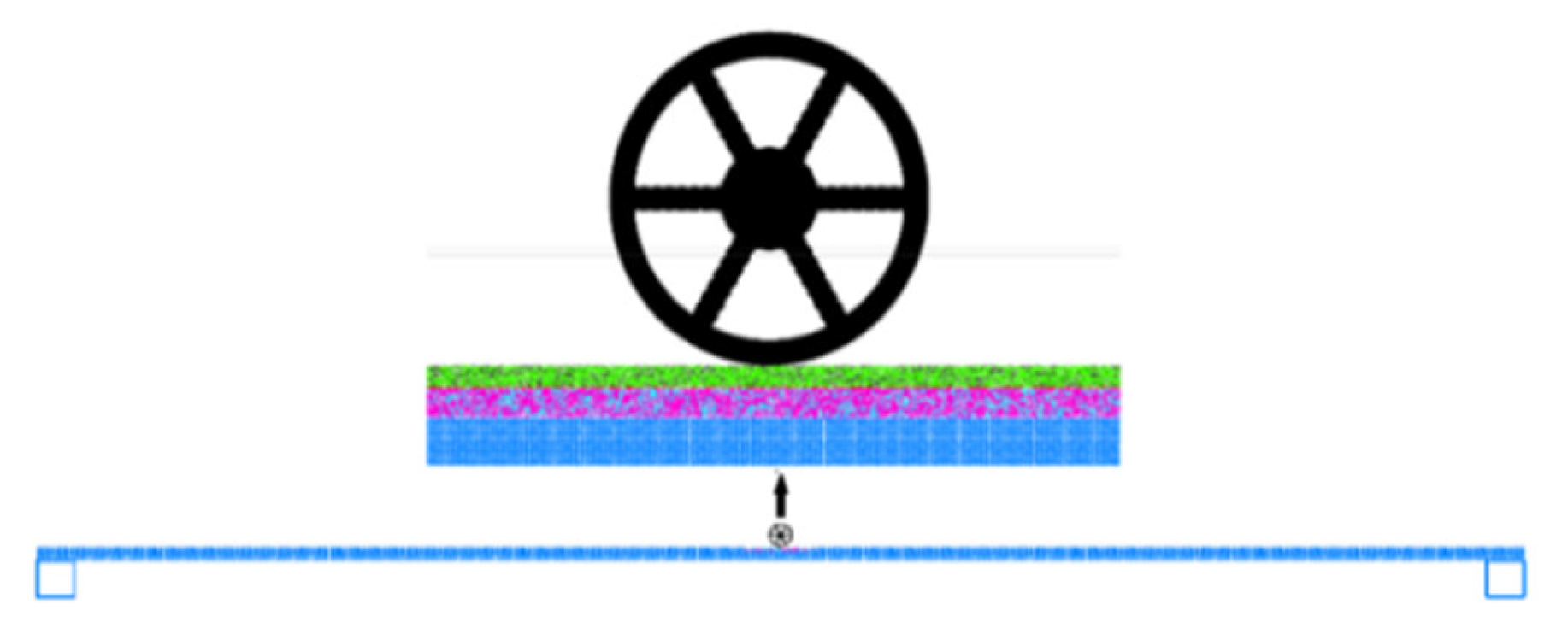
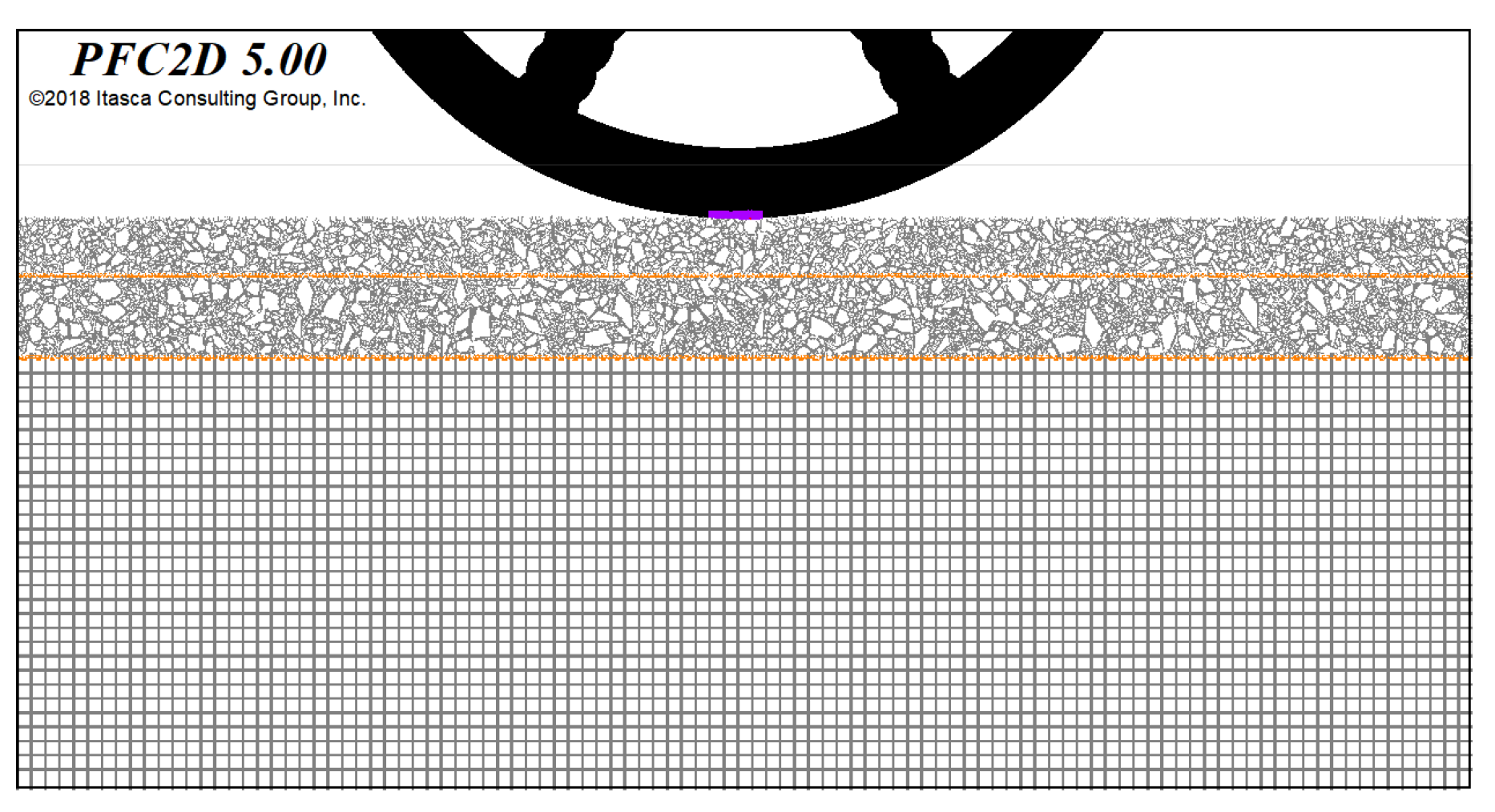
3.1. Construction of the Discrete Element Model
3.2. Multiple Loads
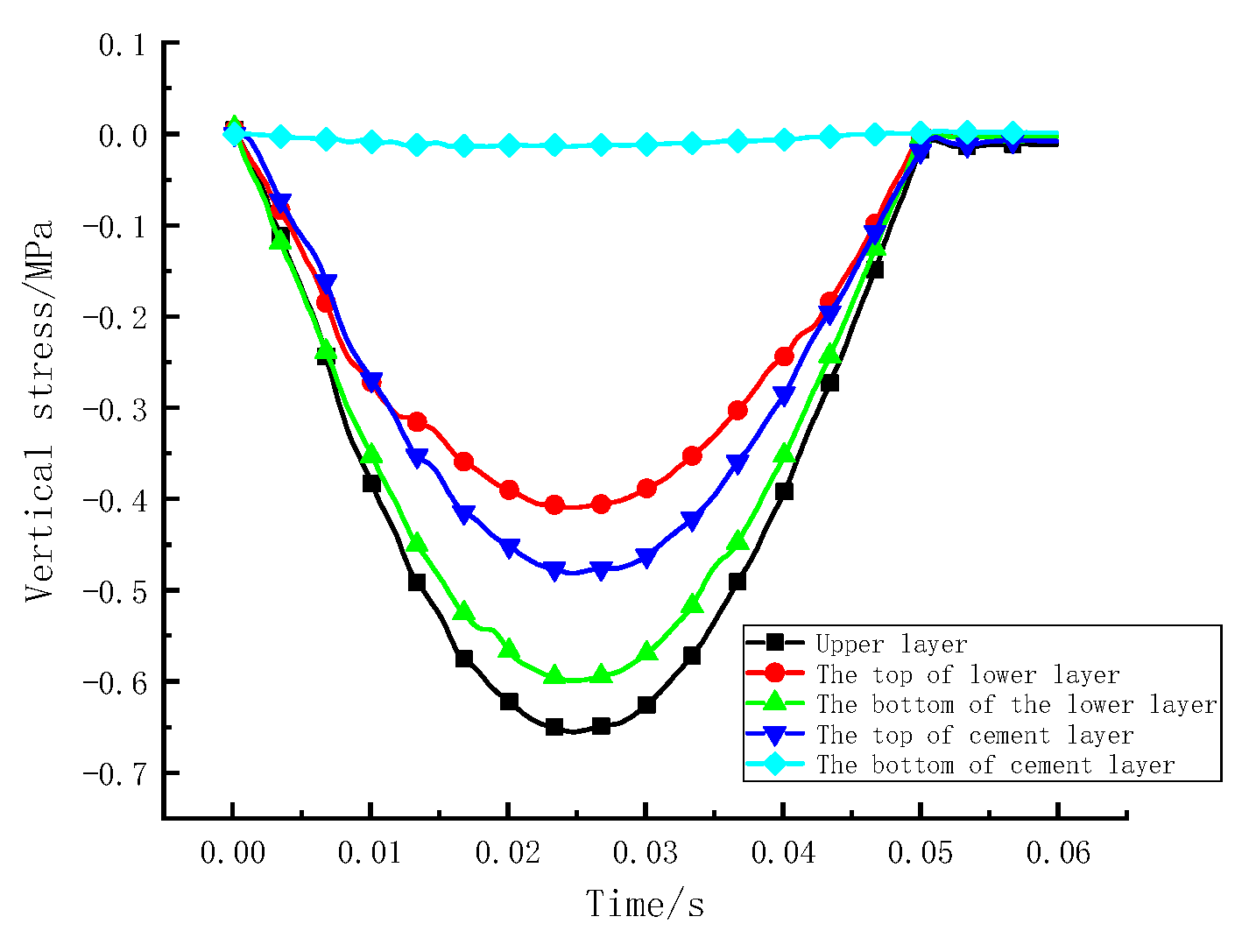
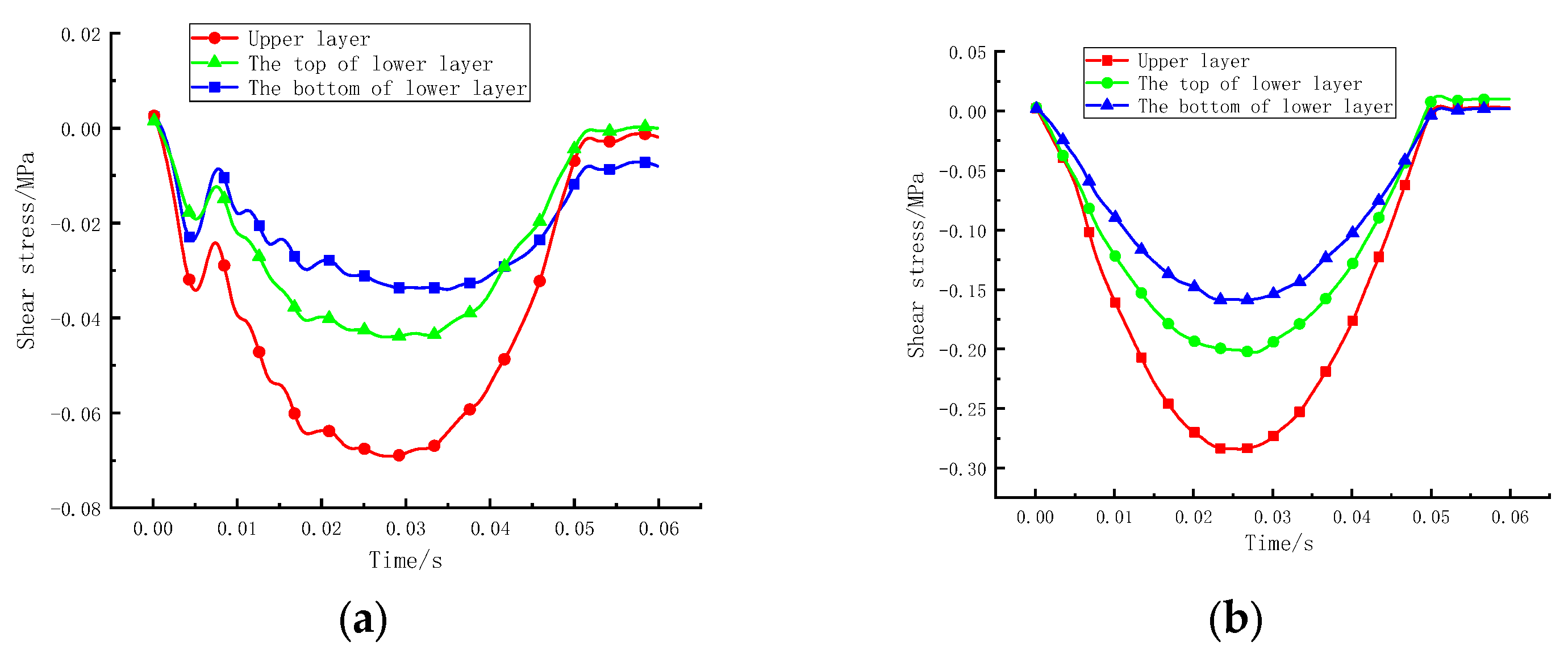
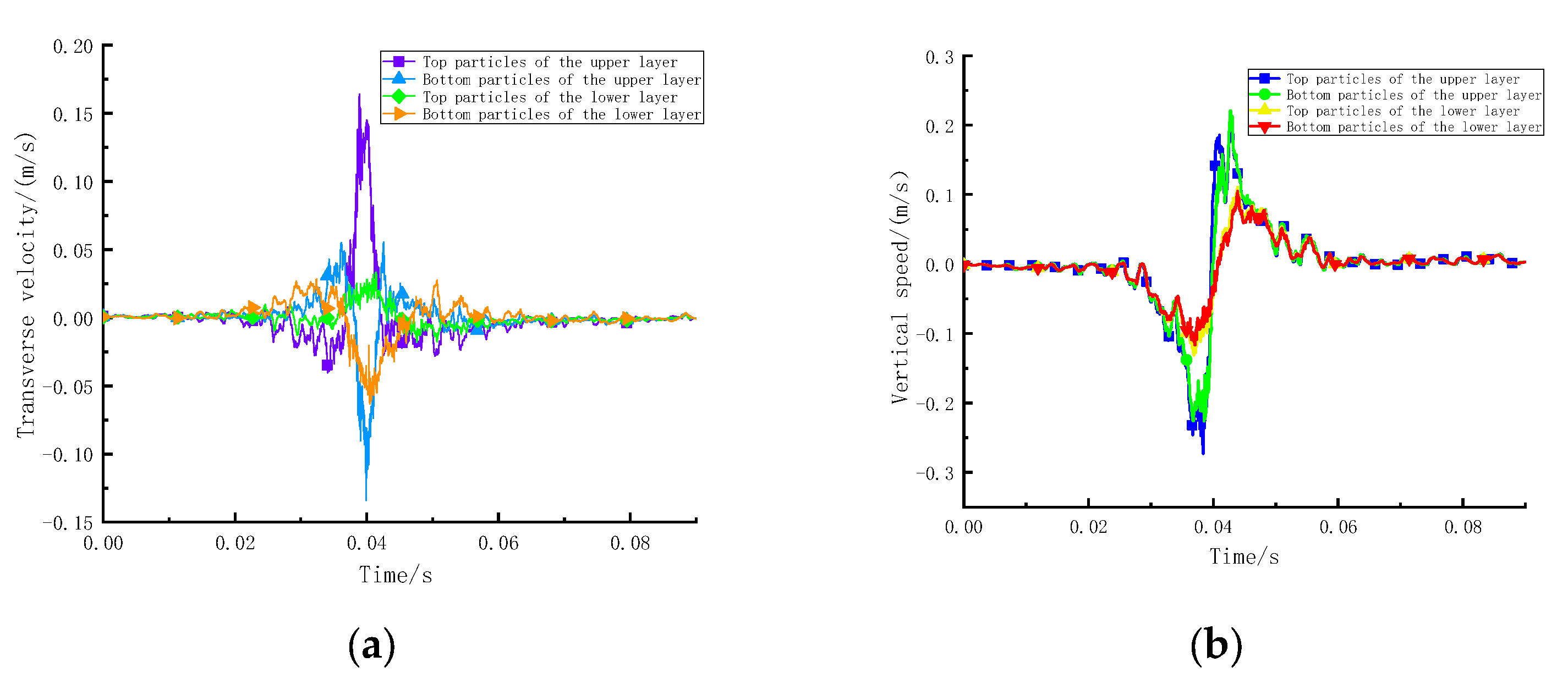
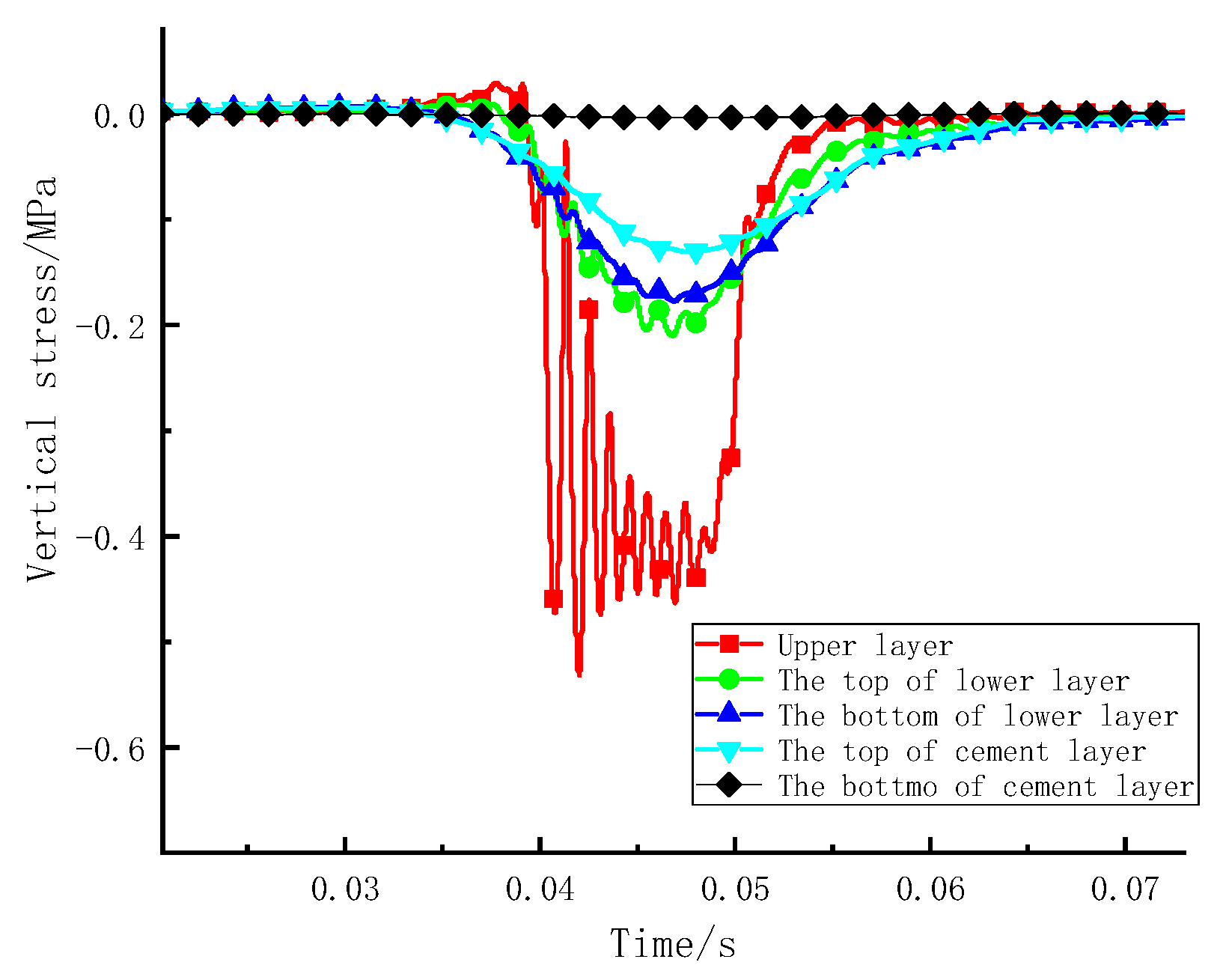
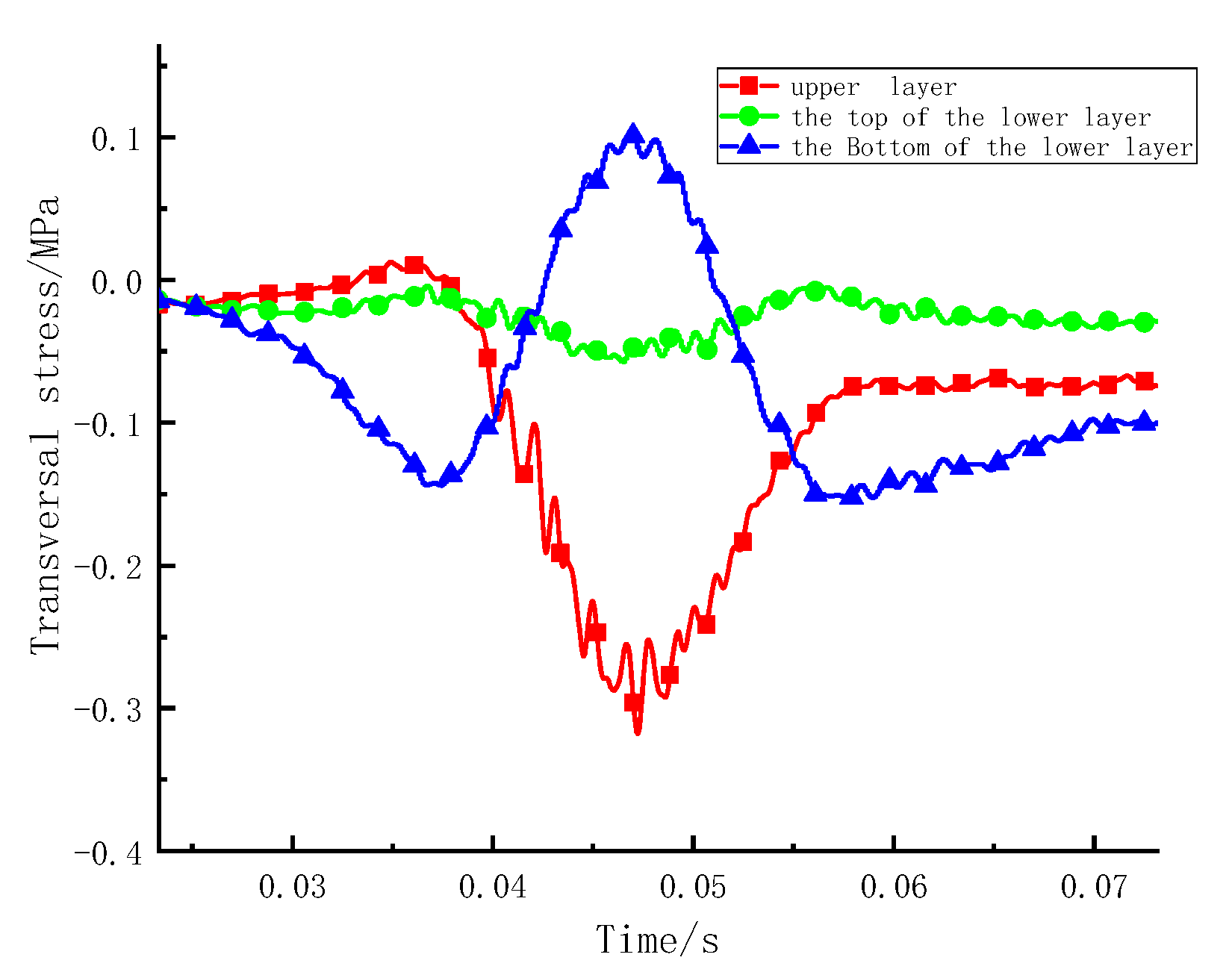
3.2.1. Vibration Load and Mechanical Response Analysis
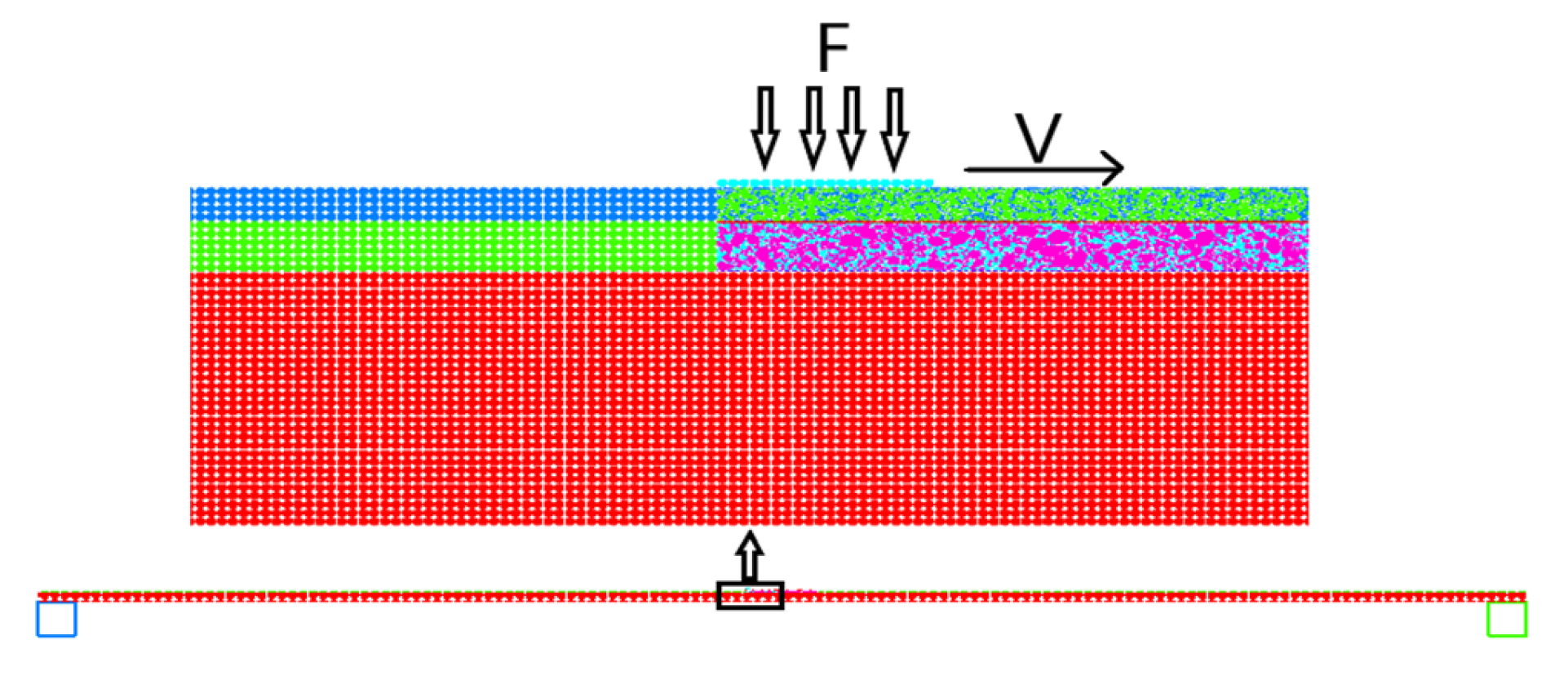
3.2.2. Rolling Load and Mechanical Response Analysis
3.2.3. Vehicle Road Coupling Load and Mechanical Response Analysis
4. Conclusions
- (1)
- There is a certain difference between the mechanical response under multiple loads. Therefore, it is significant to predict the damage behaviour of bridge deck pavement by considering multiple load forms.
- (2)
- Sinusoidal vibration loads can simply be the moving load. Under the action of vibration loading, the upper layer mainly bears compressive stress, and the lower layer mainly bears tensile stress. The shear stress at the edge of the loading area is approximately 4 times that at the centre of the loading area. Therefore, the edge of the wheel is a weak stress area and is prone to shear failure, and it is recommended to promote the shear resistance of the upper layer.
- (3)
- The rolling load considers the rolling friction force, applying horizontal force to the road, which can better reflect the rolling action of an actual wheel. The stress in the pavement structure increased and then gradually returned to its original stress before and after the vehicle travelled along the road. The direction of shear stress changes before and after the load passes through. The upper layer bears compressive stress, and the lower layer bears alternating tension and compression stress. It is suggested to improve the shear fatigue resistance of the upper layer and ensure the tensile fatigue resistance of the lower layer.
- (4)
- The stress response trend of the bridge deck pavement under a vehicle road coupling load and a rolling load is basically the same. However, when introducing the road roughness, the stress response value changes dramatically, which causes a significant effect on the upper layer. Therefore, the adhesion between the aggregate and asphalt should be improved to prevent pavement particles peeling from the upper layer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, I.K.; Kim, W.; Kang, H.T.; Seo, J.W. Analysis and Prediction of Highway Bridge Deck Slab Deterioration. J. Korea Inst. Struct. Maint. Insp. 2015, 19, 68–75. [Google Scholar] [CrossRef] [Green Version]
- Huang, W. Integrated Design Procedure for Epoxy Asphalt Concrete–Based Wearing Surface on Long-Span Orthotropic Steel Deck Bridges. J. Mater. Civ. Eng. 2015, 28, 04015189. [Google Scholar] [CrossRef]
- Wang, L.B.; Hou, Y.; Zhang, L.; Liu, G.J. A combined static-and-dynamics mechanics analysis on the bridge deck pavement. J. Clean. Prod. Sci. 2017, 166, 209–220. [Google Scholar] [CrossRef]
- Wang, L.; Kang, X.; Jiang, P. Vibration analysis of a multi-span continuous bridge subject to complex traffic loading and vehicle dynamic interaction. KSCE J. Civ. Eng. 2016, 20, 323–332. [Google Scholar] [CrossRef]
- Zhao, Y.; Fang, T.; Ni, F.; Cao, J. Mechanical response of thin layer asphalt mixture in bridge deck pavement. J. Transp. Eng. B-Pavements 2010, 10, 1–9. [Google Scholar]
- Si, C.; Su, X.; Cen, E. Comparative study on dynamic response of deck pavement of two kinds of box girder bridges under moving loads. Shock Vib. 2019, 2019, 6052745. [Google Scholar] [CrossRef] [Green Version]
- JTG D50-2017; Highway Asphalt Pavement Design Code. Ministry of Transport of the People’s Republic of China, People’s Communications Press: Beijing, China, 2017.
- Dong, Z.; Tan, Y.; Ou, J. Dynamic response analysis of asphalt pavement under three-directional nonuniform moving load. China Civ. Eng. J. 2013, 46, 122–130. [Google Scholar]
- Dong, Z.; Ni, F. Dynamic model and criteria indices of semi-rigid base asphalt pavement. Int. J. Pavement Eng. 2014, 15, 854–866. [Google Scholar] [CrossRef]
- Si, C.; Chen, E.; You, Z.; Yang, F. Dynamic response of temperature-seepage-stress coupling in asphalt pavement. Constr. Build Mater. 2019, 211, 824–836. [Google Scholar] [CrossRef]
- Gao, L.; Dan, H.; Li, L. Response Analysis of Asphalt Pavement under Dynamic Loadings: Loading Equivalence. Math. Probl. Eng. 2019, 2019, 7020298. [Google Scholar] [CrossRef] [Green Version]
- Gong, M.; Sun, Y.; Chen, J. Mechanical response analysis of asphalt pavement on curved concrete bridge deck using a mesostructure-based multi-scale method. Constr. Build Mater. 2021, 285, 122858. [Google Scholar] [CrossRef]
- Ye, Z.; Miao, Y.; Zhang, W.; Wang, L. Effects of random non-uniform load on asphalt pavement dynamic response. Int. J. Pavement Res. Technol. 2020, 14, 299–308. [Google Scholar] [CrossRef]
- Mejías-Santiago, M.; Doyle, J.D.; Rushing, J.F. Accelerated Pavement Testing of Warm-Mix Asphalt for Heavy-Traffic Airfields. Transport. Res. Rec. 2014, 2456, 11–20. [Google Scholar] [CrossRef]
- Tian, Y.; Lee, J.; Nantung, T.; Haddock, J. Development of a mid-depth profile monitoring system for accelerated pavement testing. Constr. Build Mater. 2017, 140, 1–9. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, X.; Ren, H.; Zhou, Z.; Wang, X.; Tang, S. Analysis of the Dynamic Responses of Asphalt Pavement Based on Full-Scale Accelerated Testing and Finite Element Simulation. Constr. Build Mater. 2022, 325, 126429. [Google Scholar] [CrossRef]
- Rafiq, W.; Musarat, M.A.; Altaf, M.; Napiah, M.; Sutanto, M.H.; Alaloul, W.S.; Javed, M.F.; Mosavi, A. Life Cycle Cost Analysis Comparison of Hot Mix Asphalt and Reclaimed Asphalt Pavement: A Case Study. Sustainability 2021, 13, 4411. [Google Scholar] [CrossRef]
- Mahmound, E.; Masad, E.; Nazarian, S. Discrete element analysis of the influences of aggregate properties and internal structure on fracture in asphalt mixture. J. Mater. Civ. Eng. 2010, 22, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Gao, Y.; Huang, X. Effects of aggregate size and specimen scale on asphalt mixture cracking using a micromechanical simulation approach. J. Wuhan Univ. Technol. 2017, 32, 1503–1510. [Google Scholar] [CrossRef]
- Tao, M.; Zhang, D.; Zhang, Y.; Zhang, Y. Simulation of wheel tracking test for asphalt mixture using discrete element modelling. Road Mater. Pavement 2018, 2, 367–384. [Google Scholar]
- Zhou, X.; Chen, S.; Ge, D.; You, Z. Investigation of asphalt mixture internal structure consistency in accelerated discrete element models. Constr. Build Mater. 2020, 244, 118272. [Google Scholar] [CrossRef]
- JTG E20-2011; Test Code for Asphalt and Asphalt Mixture in Highway Engineering. Ministry of Transport of the People’s Republic of China, People’s Communications Publishing House: Beijing, China, 2011.
- Awan, H.H.; Hussain, A.; Javed, M.F.; Qiu, Y.; Alrowais, R.; Mohamed, A.M.; Fathi, D.; Alzahrani, A.M. Predicting Marshall Flow and Marshall Stability of Asphalt Pavements Using Multi Expression Programming. Buildings 2022, 12, 314. [Google Scholar] [CrossRef]
- JTG/T 3364-02-2019; Technical Specification for Design and Construction of Highway Steel Bridge Deck Pavement. Ministry of Transport of the People’s Republic of China, People’s Communications Press: Beijing, China, 2019.
- You, Z.; Buttlar, W. Discrete element modeling to predict the modulus of asphalt concrete mixtures. J. Mater. Civ. Eng. 2004, 16, 140–146. [Google Scholar] [CrossRef]
- Chen, E.; Zhang, X.; Wang, G. Rigid-flexible coupled dynamic response of steel–concrete bridges on expressways considering vehicle–road–bridge interaction. Adv. Struct. Eng. 2020, 23, 160–173. [Google Scholar] [CrossRef]
- Yan, Z.; Chen, E.; Wang, Z.; Si, C. Research on Mesoscopic Response of Asphalt Pavement Structure under Vibration Load. Shock Vib. 2019, 2019, 2620305. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, R.; Sun, R.; Xu, Z. Macroscopic and mesoscopic correlation of granular materials based on rolling resistance linear contact model. Geotech. Mech. 2022, 4, 945–956+968. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, S.; Li, S.; Lu, Y.; Ding, H. Influence of vehicle-road coupled vibration on tire adhesion based on nonlinear foundation. Appl. Math. Mech.-Engl. 2021, 42, 607–624. [Google Scholar] [CrossRef]
- Yan, Z.; Wang, Z.; Chen, E. Dynamic response analysis of asphalt pavement vehicle-road based on discrete element method. Chin. J. Highw. 2019, 32, 51–60+79. [Google Scholar]











| Structure Layer | Grain Density (kg·m−3) | Stiffness Ratio | Parallel Bond Model Tensile Strength (Pa) | Parallel Bond Model Cohesion (Pa) | Elastic Modulus (Pa) | |
|---|---|---|---|---|---|---|
| Surface layer | Aggregate | 2450 | 2.5 | 2.22 × 106 | 2.65 × 106 | 1.2 × 109 |
| Asphalt mortar | 2100 | 2.5 | 1.36 × 106 | 1.85 × 106 | 7.2 × 107 | |
| Lower layer | Aggregate | 2450 | 2.0 | 1.8 × 106 | 2.3 × 106 | 1.2 × 109 |
| Asphalt mortar | 2100 | 2.0 | 1.3 × 106 | 1.8 × 106 | 5.2 × 107 | |
| Cement concrete layer | Aggregate | 2500 | 1 | 3.2 × 106 | 4.5 × 106 | 1.2 × 109 |
| Asphalt mortar | 2150 | 1 | 4.5 × 106 | 5.4 × 106 | 2.5 × 108 | |
| Structure Layer | Grain Density (kg/m3) | Stiffness Ratio | Contact Bond Tensile Strength (Pa) | Contact Bond Shear Strength (Pa) | Elastic Modulus (Pa) |
|---|---|---|---|---|---|
| Waterproof bonding layer | 2200 | 1 | 6.2 × 105 | 7.8 × 105 | 6.2 × 107 |
| Car Body Mass m1/kg | Vehicle Wheel Mass m2/kg | Suspension Stiffness Coefficient ks/(N·m−1) | Suspension Damping Coefficient Cs/(N·s·m−1) | Tire Stiffness Coefficient kt/(N·m−1) | Tire Damping Coefficient Ct/(N·s·m−1) |
|---|---|---|---|---|---|
| 2200 | 250 | 1 × 106 | 1.5 × 104 | 1.75 × 106 | 2000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Si, C.; Li, S.; Fan, T. Comparative Study of the Mesomechanical Response of Asphalt Bridge Deck Pavement under Multiple Loads. Coatings 2022, 12, 1665. https://doi.org/10.3390/coatings12111665
Cui Y, Si C, Li S, Fan T. Comparative Study of the Mesomechanical Response of Asphalt Bridge Deck Pavement under Multiple Loads. Coatings. 2022; 12(11):1665. https://doi.org/10.3390/coatings12111665
Chicago/Turabian StyleCui, Yaning, Chundi Si, Song Li, and Taotao Fan. 2022. "Comparative Study of the Mesomechanical Response of Asphalt Bridge Deck Pavement under Multiple Loads" Coatings 12, no. 11: 1665. https://doi.org/10.3390/coatings12111665
APA StyleCui, Y., Si, C., Li, S., & Fan, T. (2022). Comparative Study of the Mesomechanical Response of Asphalt Bridge Deck Pavement under Multiple Loads. Coatings, 12(11), 1665. https://doi.org/10.3390/coatings12111665






