Surface Potentials of Mixtures Containing Oddly Charged Colloids
Abstract
1. Introduction
2. Methods
3. Results
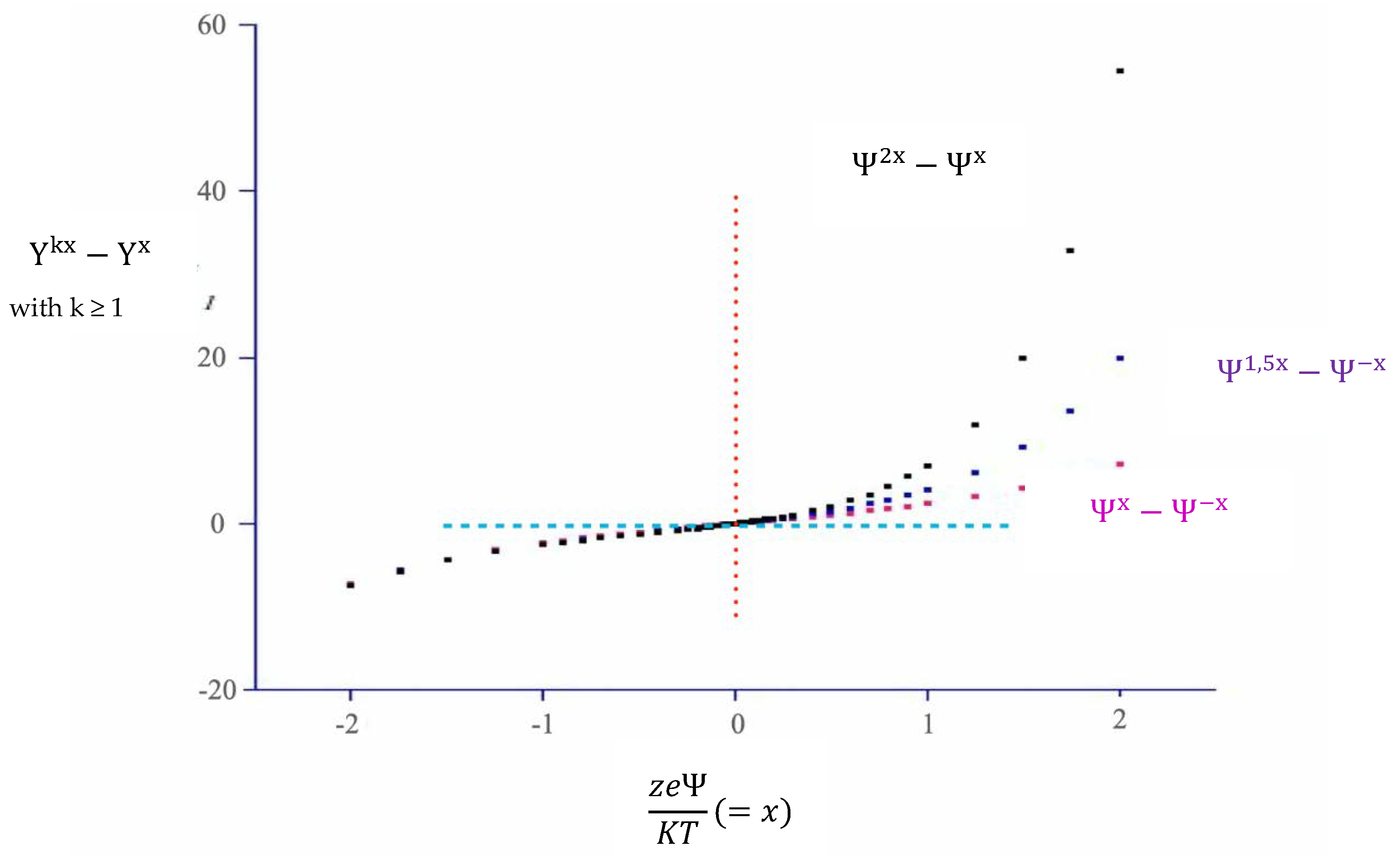
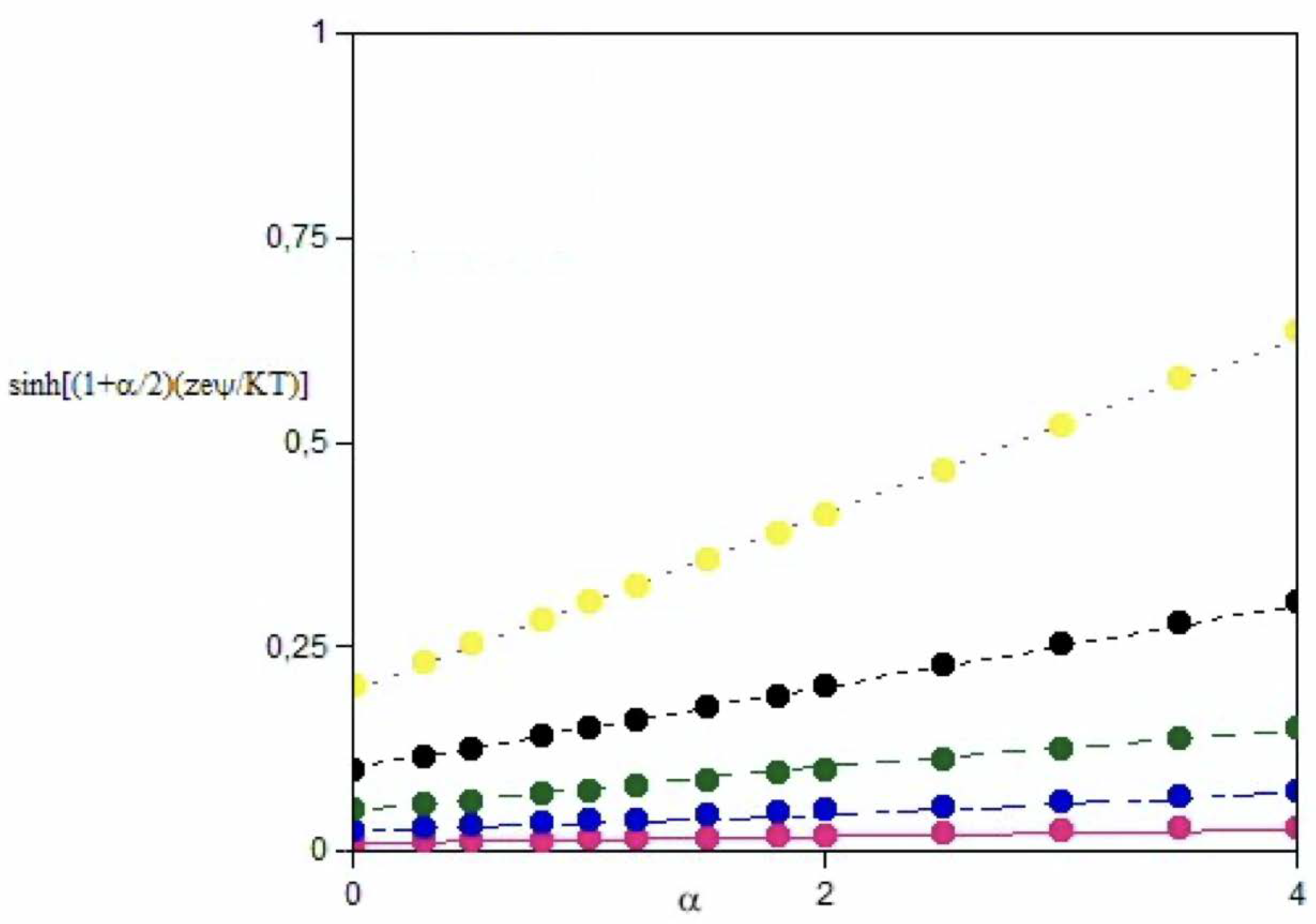
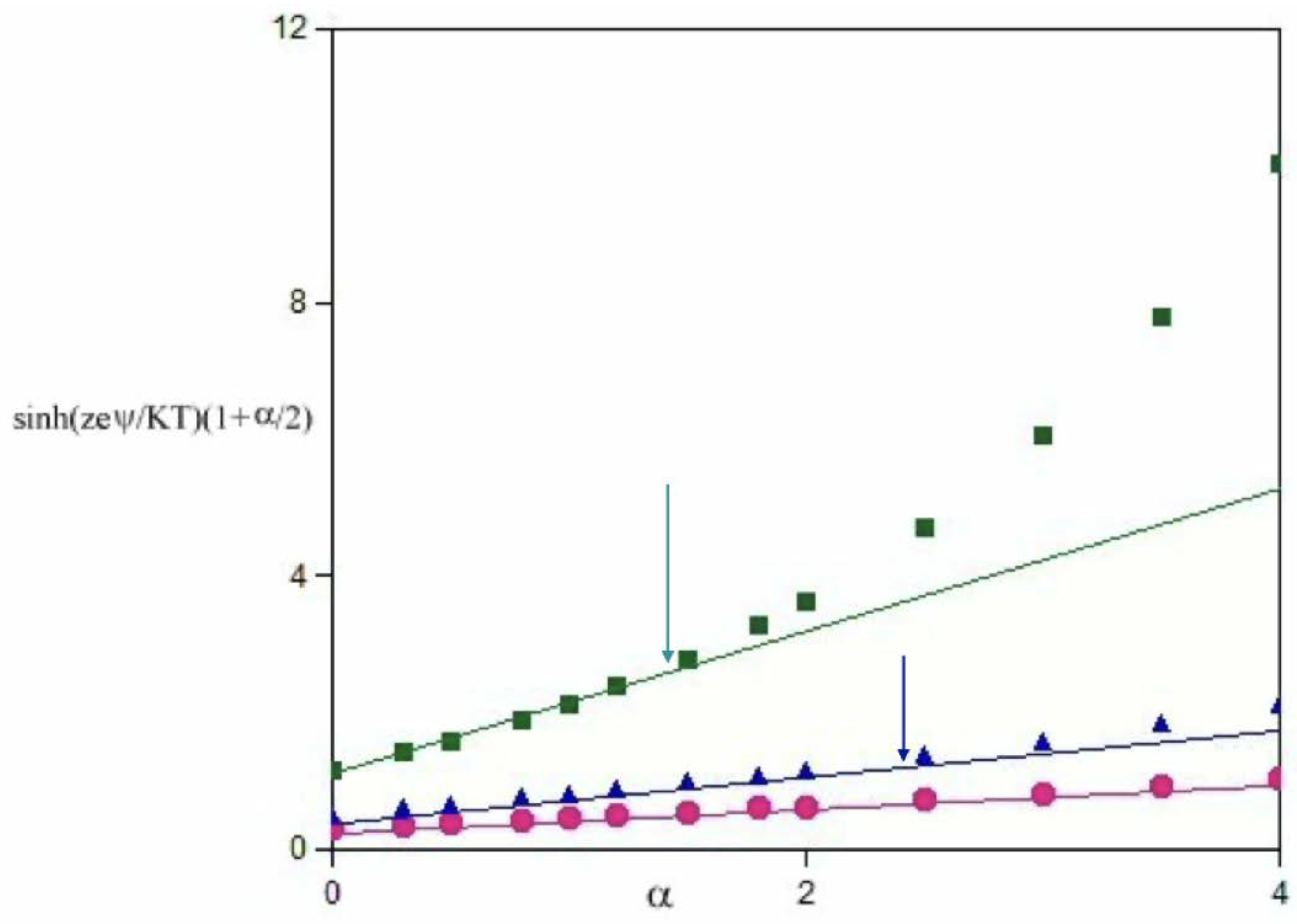
3.1. The Role of α
3.2. The Charge Transfer
4. Discussion
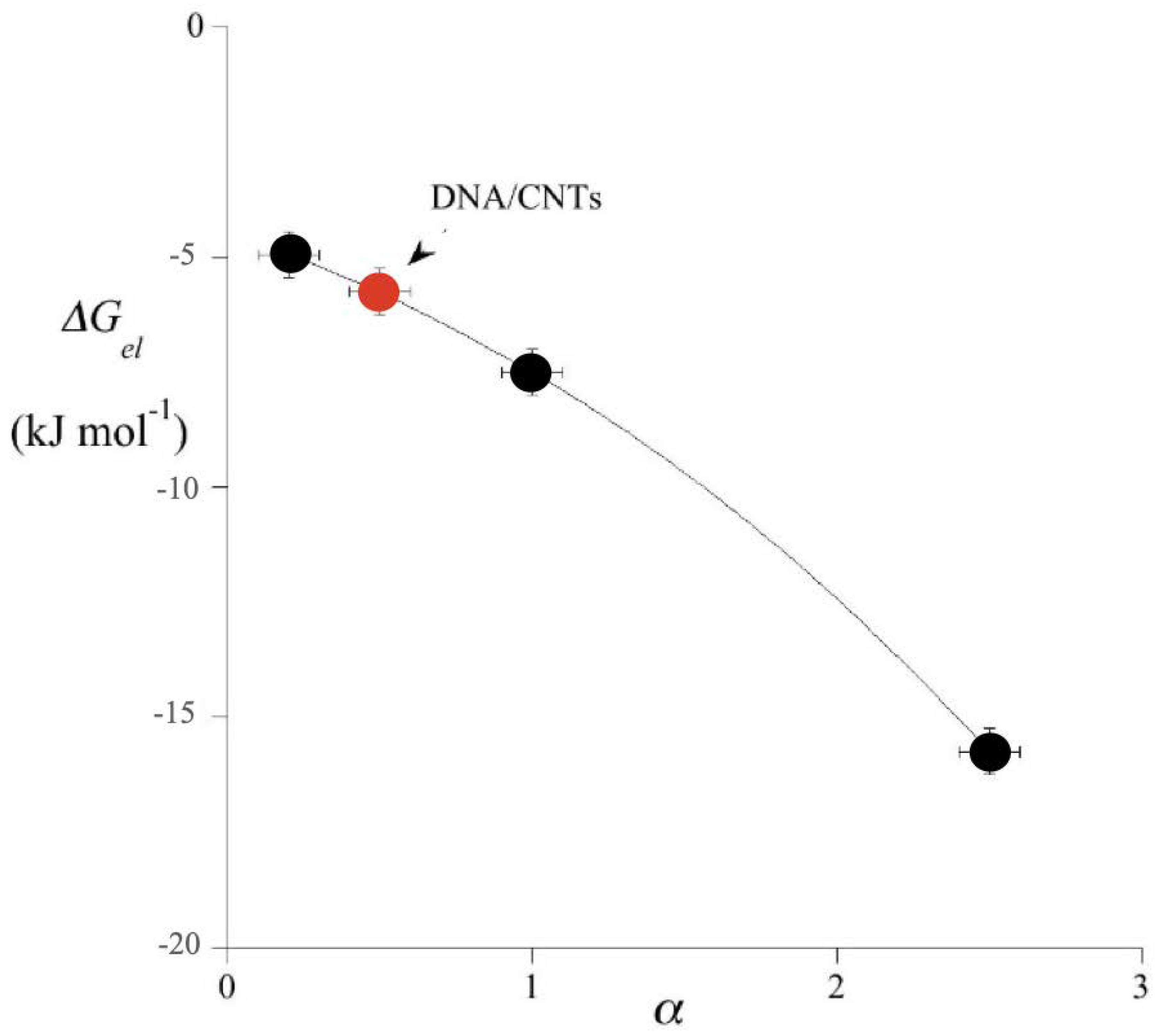
4.1. Colloid Crystals and Hybrid Colloids
4.2. Bio-Intended and Bio-Mimetic Systems
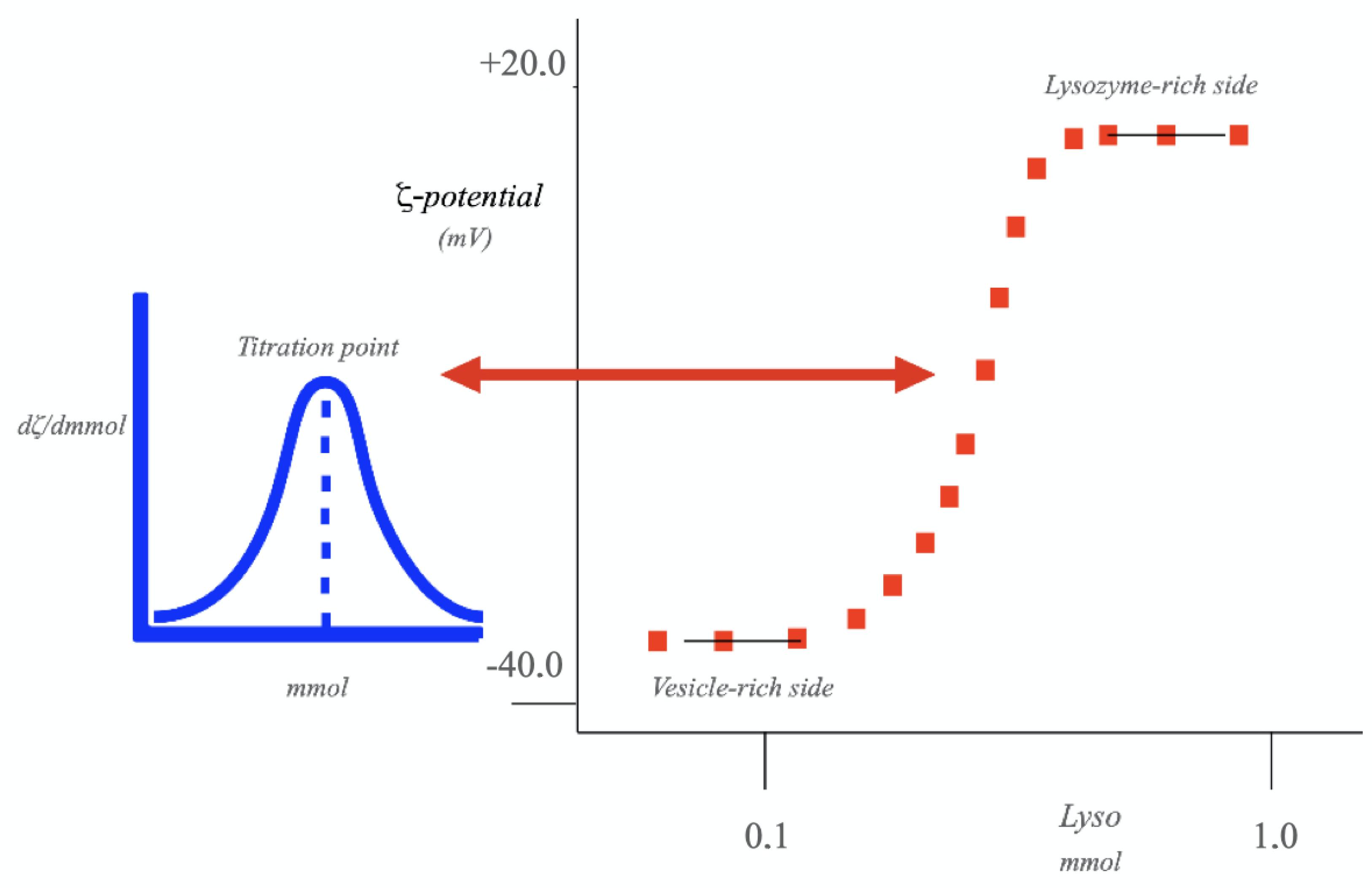
4.3. Colloid Titration
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oshima, H. Surface Charge Density/Surface Potential Relationship for a Spherical Colloidal Particle in a Salt-Free Medium. J. Colloid Interface Sci. 2002, 247, 18–23. [Google Scholar] [CrossRef]
- Lyklema, J.; Golub, T. Electrical Double Layer on Silver Iodide and Overcharging in the Presence of Hydrolyzable Cations. Croat. Chem. Acta 2007, 80, 303–311. [Google Scholar]
- Van Riemsdijk, V.H.; Bolt, G.H.; Koopal, L.K.; Blaakmeer, J. Electrolyte adsorption on heterogeneous surfaces: Adsorption models. J. Colloid Interface Sci. 1986, 109, 219–228. [Google Scholar] [CrossRef]
- Paria, S.; Khilar, K.C. A review on experimental studies of surfactant adsorption at the hydrophilic solid–water interface. Adv. Colloid Interface Sci. 2004, 110, 75–95. [Google Scholar] [CrossRef] [PubMed]
- Shubin, V. Adsorption of Cationic Polyacrylamide onto Monodisperse Colloidal Silica from Aqueous Electrolyte Solutions. J. Colloid Interface Sci. 1997, 191, 372–377. [Google Scholar] [CrossRef]
- Philipse, A.P. Colloidal sedimentation (and filtration). Curr. Opin. Colloid Interface Sci. 1997, 2, 200–206. [Google Scholar] [CrossRef]
- Robins, M.M. Emulsions-creaming phenomena. Curr. Opin. Colloid Interface Sci. 2000, 5, 265–272. [Google Scholar] [CrossRef]
- Ansell, G.C.; Dickinson, E. Brownian-dynamics simulation of the formation of colloidal aggregate and sediment structure. Faraday Discuss. Chem. Soc. 1987, 83, 167–177. [Google Scholar] [CrossRef]
- Deriaguin, R.V. Theory of the Stability of Colloids and Thin Films; Consultants Bureau: New York, NY, USA; London, UK, 1989. [Google Scholar]
- Landau, L.D. Collected Works; Nauka: Moscow, Russia, 1969; Volume I, pp. 386–411. [Google Scholar]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; N.B. It Is the Reprint of the 1948 Original Version; Dover Books on Chemistry: Mineola, NY, USA, 1999. [Google Scholar]
- Ninham, B.W. On progress in forces since DLVO theory. Adv. Colloid Interface Sci. 1999, 83, 1–17. [Google Scholar] [CrossRef]
- Clare, K.E.; Cruchley, A.E. Laboratory Experiments in The Stabilization of Clays With Hydrated Lime. Géotechnique 1957, 7, 97–111. [Google Scholar] [CrossRef]
- Sperling, R.A.; Parak, W.J. Surface modification, functionalization and bioconjugation of colloidal inorganic nanoparticles. Philos. Trans. R. Soc. A 2010, 368, 1333–1383. [Google Scholar] [CrossRef]
- Thompson, K.L.; Armes, S.P.; York, D.W.; Burdis, J.A. Synthesis of Sterically-Stabilized Latexes Using Well-Defined Poly(glycerol monomethacrylate) Macromonomers. Macromolecules 2010, 43, 2169–2177. [Google Scholar] [CrossRef]
- Byrnes, A.P.; Griffin, D.E. Binding of Sindbis Virus to Cell Surface Heparan Sulfate. J. Virol. 1998, 72, 7349–7356. [Google Scholar] [CrossRef] [PubMed]
- Fogolari, F.; Brigo, A.; Molinari, H. The Poisson-Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J. Mol. Recognit. 2002, 15, 377–392. [Google Scholar] [CrossRef] [PubMed]
- Parsegian, V.A.; Gingell, D. On the Electrostatic Interaction across a Salt Solution between Two Bodies Bearing Unequal Charges. Biophys. J. 1972, 12, 1192–1204. [Google Scholar] [CrossRef]
- Aranda-Espinoza, H.; Chen, Y.; Dan, N.; Lubensky, T.C.; Nelson, P.; Ramos, L.; Weitz, D.A. Electrostatic Repulsion of Positively Charged Vesicles and Negatively Charged Objects. Science 1999, 285, 394–397. [Google Scholar] [CrossRef] [PubMed]
- Lavi, E.D.; Crivellari, F.; Gagnon, Z. Dielectrophoretic detection of electrical property changes of stored human red blood cells. Electrophoresis 2022, 43, 1297–1308. [Google Scholar] [CrossRef] [PubMed]
- Hernando-Pérez, M.; Cartagena-Rivera, A.X.; Lošdorfer Božič, A.; Carrillo, P.J.P.; San Martín, C.; Mateu, M.G.; Raman, A.; Podgornik, R.; de Pablo, P.J. Quantitative nanoscale electrostatics of viruses. Nanoscale 2015, 7, 17289–17298. [Google Scholar] [CrossRef] [PubMed]
- Bu, W.; David Vaknin, D.; Travesset, A. How Accurate Is Poisson−Boltzmann Theory for Monovalent Ions near Highly Charged Interfaces? Langmuir 2006, 22, 5673–5681. [Google Scholar] [CrossRef]
- Outhwaite, C.W. A modified Poisson-Boltzmann approach to homogeneous ionic solutions. Condens. Matter Phys. 2004, 7, 719–733. [Google Scholar] [CrossRef]
- Vold, R.D.; Vold, M.J. Colloid and Interface Chemistry; Addison-Wesley Publ. Co.: Reading, MA, USA, 1983; Chapter VII; pp. 224–238. [Google Scholar]
- Manning, G.S. Counterion Condensation on Charged Spheres, Cylinders and Planes. J. Phys. Chem. B 2007, 111, 8554–8559. [Google Scholar]
- Adamson, A.W. Physical Chemistry of Surfaces, Vth ed.; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Evans, D.F.; Wennerstroem, H. The Colloidal Domain: Where Physics, Chemistry, Biology and Technology Meet; VCH: New York, NY, USA; Weinheim, Germany; Cambridge, UK, 1994; Chapter III; pp. 87–126. [Google Scholar]
- Gillespie, D.A.J.; Hallett, J.B.; Elujoba, O.; Hamzah, A.F.C.; Richardson, R.M.; Bartlett, P. Counterion Condensation on Spheres in the Salt-Free Limit. Soft Matter 2014, 10, 566–577. [Google Scholar] [PubMed]
- Leunissen, M.E.; Christova, C.G.; Hynninen, A.-P.; Royall, C.P.; Campbell, A.I.; Imhof, A.; Dijkstram, M.; van Roij, R.; van Blaaderen, A. Ionic colloidal crystals of oppositely charged particles. Nature 2005, 437, 235–240. [Google Scholar] [CrossRef]
- Bartlett, P.; Ottewill, R.H.; Pusey, P.N. Superlattice formation in binary mixtures of hard-sphere colloids. Phys. Rev. Lett. 1992, 68, 3801–3804. [Google Scholar] [CrossRef]
- Pieranski, P. Colloidal Crystals. Contemp. Phys. 1983, 24, 25–73. [Google Scholar] [CrossRef]
- Lumsdon, S.O.; Kaler, E.W.; Velev, O.D. Two-dimensional crystallization of microspheres by coplanar AC electric field. Langmuir 2004, 20, 2108–2116. [Google Scholar] [CrossRef]
- Bharti, B.; Findenegg, G.H.; Velev, O.D. Co-Assembly of Oppositely Charged Particles into Linear Clusters and Chains of Controllable Length. Sci. Rep. 2012, 2, 1004. [Google Scholar] [CrossRef] [PubMed]
- Gangwal, S.; Cayre, O.J.; Velev, O.D. Dielectrophoretic assembly of metallodielectric Janus particles in AC electric fields. Langmuir 2008, 24, 13312–31320. [Google Scholar] [CrossRef]
- Romio, M.; La Mesa, C. Hybrid nano-composites made of ss-DNA/wrapped carbon nanotubes and titania. Colloids Surf. B Biointerfaces 2017, 152, 12–17. [Google Scholar] [CrossRef]
- Ghofraniha, N.; Andreozzi, P.; Russo, J.; La Mesa, C.; Sciortino, F. Assembly Kinetics in Binary Mixtures of Strongly Attractive Colloids. J. Phys. Chem. B 2009, 113, 6775–6781. [Google Scholar] [CrossRef]
- Peppin, S.S.L.; Worster, M.G.; Wettlaufer, J.S. Morphological instability in freezing colloidal suspensions. Proc. R. Soc. A 2007, 463, 723–733. [Google Scholar] [CrossRef]
- Zerrouki, D.; Baudry, J.; Pine, D.; Chaikin, P.; Bibette, J. Chiral Colloidal clusters. Nature 2008, 455, 380–382. [Google Scholar] [CrossRef]
- Duisit, G.; Saleun, S.; Douthe, S.; Barsoum, J.; Chadeuf, G.; Moullier, P. Baculovirus vector requires electrostatic interactions including heparan sulfate for efficient gene transfer in mammalian cells. J. Gene Med. 1999, 1, 93–102. [Google Scholar] [CrossRef]
- Kwong, P.D.; Wyatt, R.; Sattentau, Q.J.; Sodroski, J.; Hendrickson, W.A. Oligomeric Modeling and Electrostatic Analysis of the gp120 Envelope Glycoprotein of Human Immunodeficiency Virus. J. Virol. 2000, 74, 1961–1972. [Google Scholar] [CrossRef] [PubMed]
- Rothman, J.E.; Kennedy, E.P. Asymmetrical distribution of phospholipids in the membrane of bacillus megaterium. J. Mol. Biol. 1977, 110, 603–618. [Google Scholar] [CrossRef]
- Ruigrok, R.W.H.; Barge, A.; Durrer, P.; Brunner, J.; Ma, K.; Whittaker, G.R. Membrane Interaction of Influenza Virus M1 Protein. Virology 2000, 267, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Pucci, C.; Scipioni, A.; La Mesa, C. Albumin binding onto synthetic vesicles. Soft Matter 2012, 8, 9669–9675. [Google Scholar] [CrossRef]
- Bonincontro, A.; La Mesa, C.; Proietti, C.; Risuleo, G. A Biophysical Investigation on the Binding and Controlled DNA Release in a Cetyltrimethylammonium Bromide-Sodium Octyl Sulfate Cat-Anionic Vesicle System. Biomacromolecules 2007, 8, 1824–1829. [Google Scholar] [CrossRef]
- van Voorthuizen, E.M.; Ashbolt, N.J.; Schäfer, A.I. Role of hydrophobic and electrostatic interactions for initial enteric virus retention by MF membranes. J. Membr. Sci. 2001, 194, 69–79. [Google Scholar] [CrossRef]
- Letizia, C.; Andreozzi, P.; Scipioni, A.; La Mesa, C.; Bonincontro, A.; Spigone, E. Protein Binding onto Surfactant-Based Synthetic Vesicles. J. Phys. Chem. B 2007, 111, 898–908. [Google Scholar] [CrossRef]
- Verma, A.; Stellacci, F. Effect of Surface Properties on Nanoparticle-Cell Interactions. Small 2010, 6, 12–21. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
La Mesa, C. Surface Potentials of Mixtures Containing Oddly Charged Colloids. Coatings 2022, 12, 1715. https://doi.org/10.3390/coatings12111715
La Mesa C. Surface Potentials of Mixtures Containing Oddly Charged Colloids. Coatings. 2022; 12(11):1715. https://doi.org/10.3390/coatings12111715
Chicago/Turabian StyleLa Mesa, Camillo. 2022. "Surface Potentials of Mixtures Containing Oddly Charged Colloids" Coatings 12, no. 11: 1715. https://doi.org/10.3390/coatings12111715
APA StyleLa Mesa, C. (2022). Surface Potentials of Mixtures Containing Oddly Charged Colloids. Coatings, 12(11), 1715. https://doi.org/10.3390/coatings12111715




