Asymmetrical Gaussian Potential Effects on Strongly Coupled Magnetopolaron Properties in Triangular Confinement Potential Quantum Wells
Abstract
:1. Introduction
2. Theoretical Model
3. The Effect of Temperature
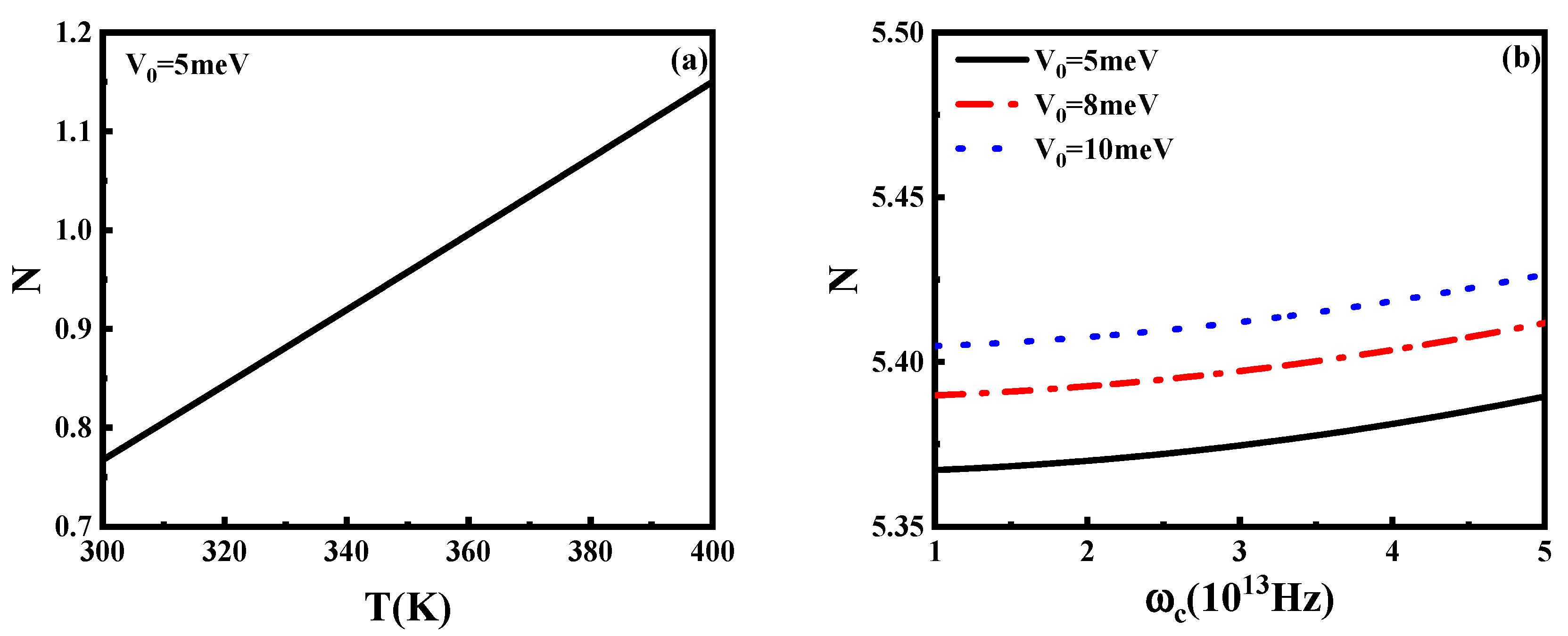
4. Results and Discussion
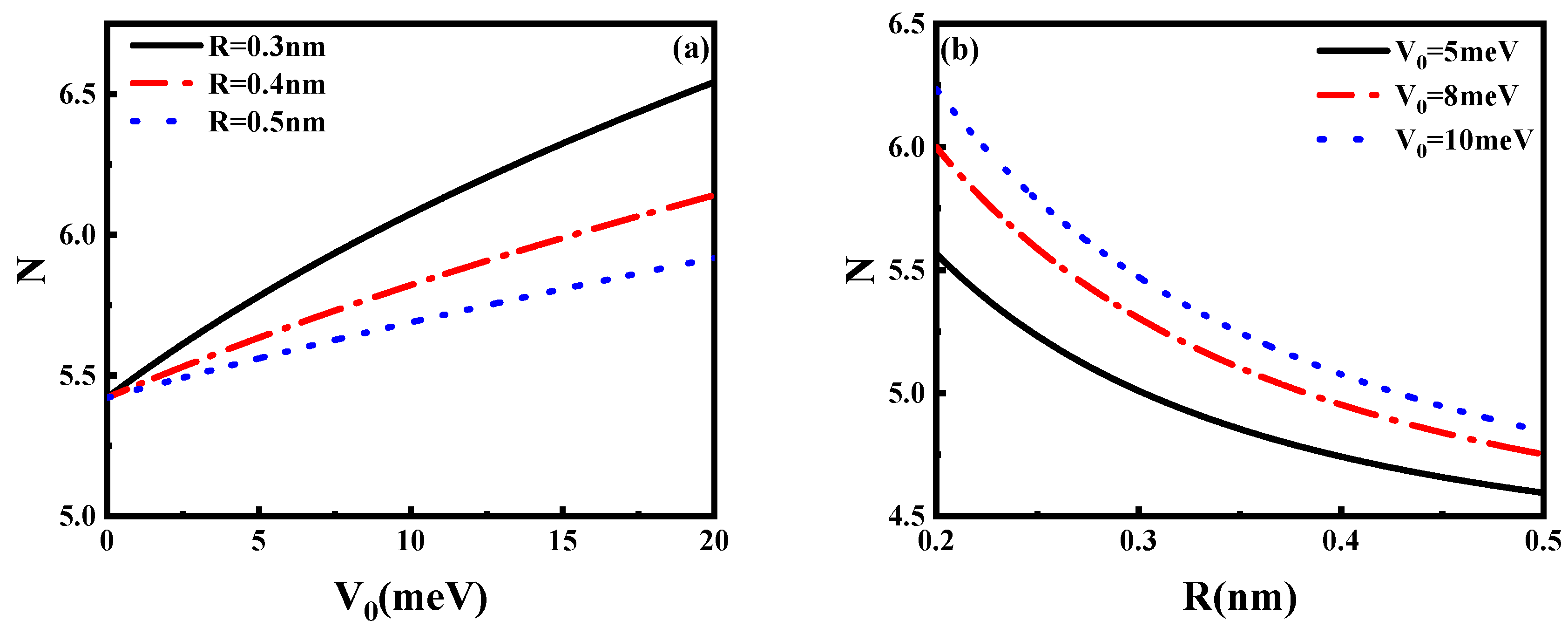
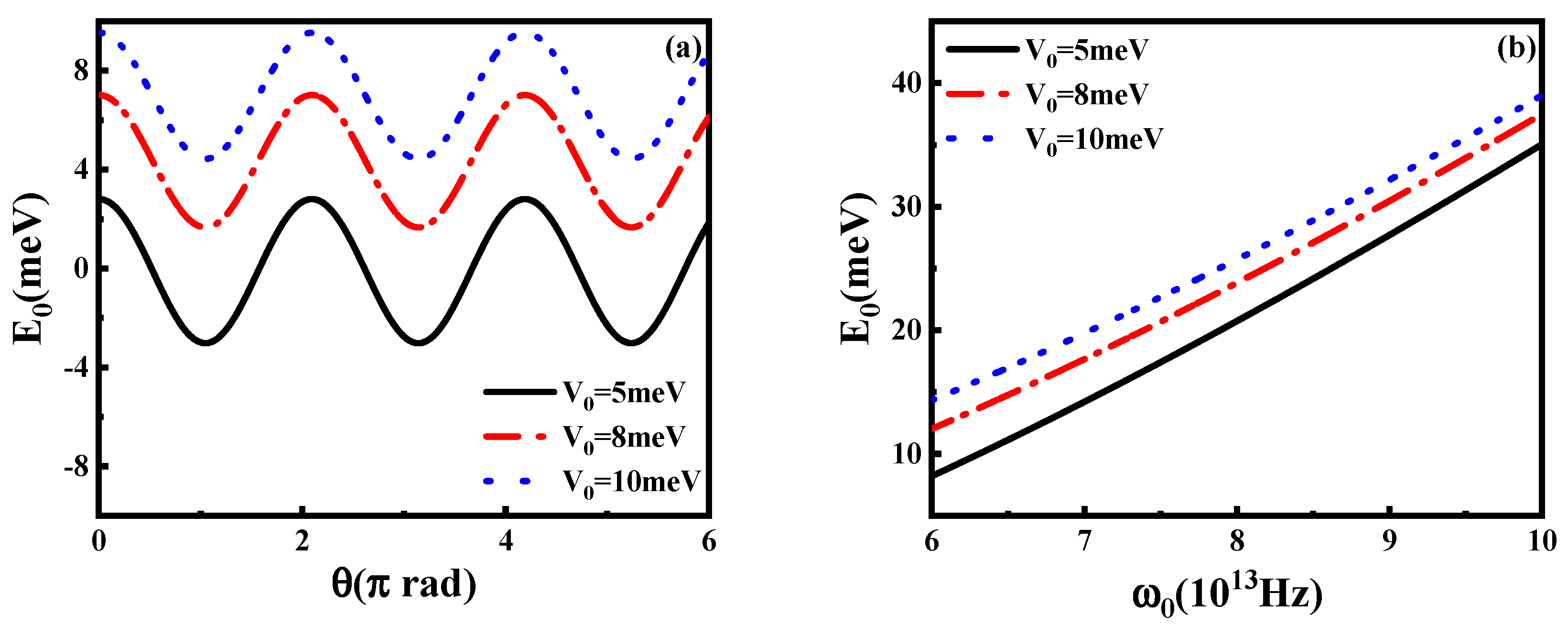
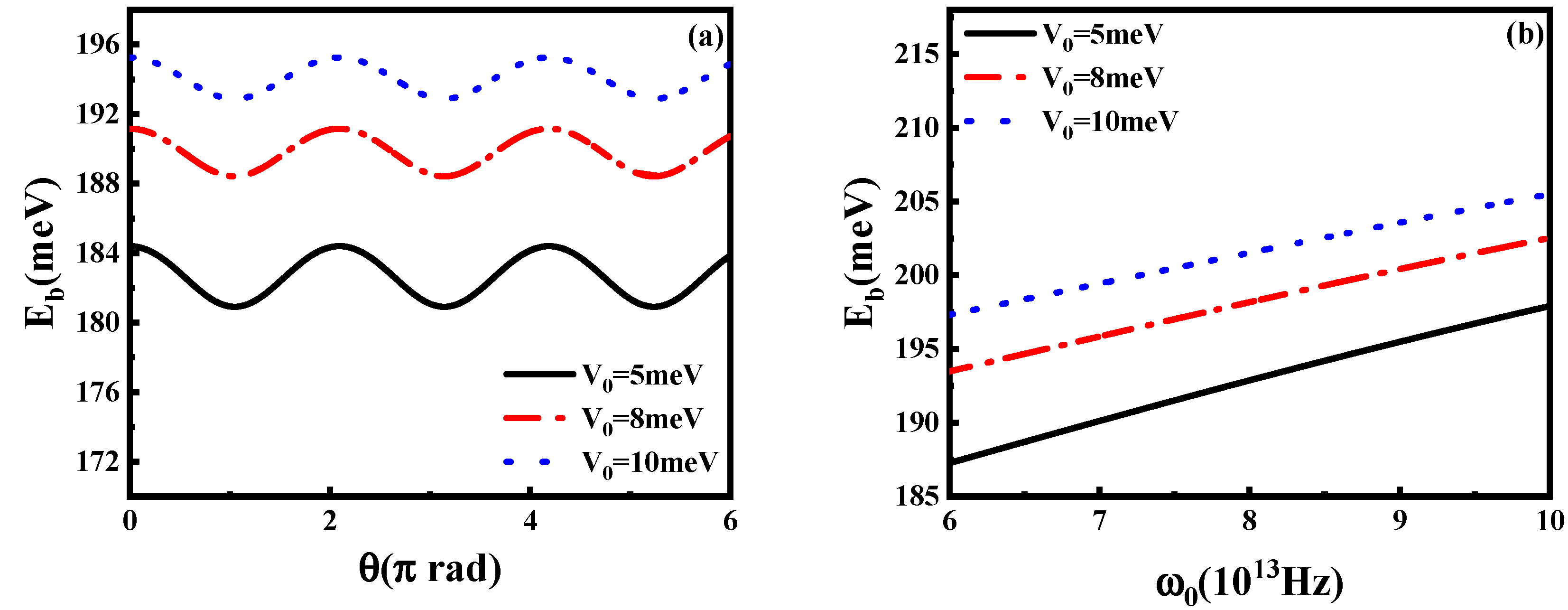
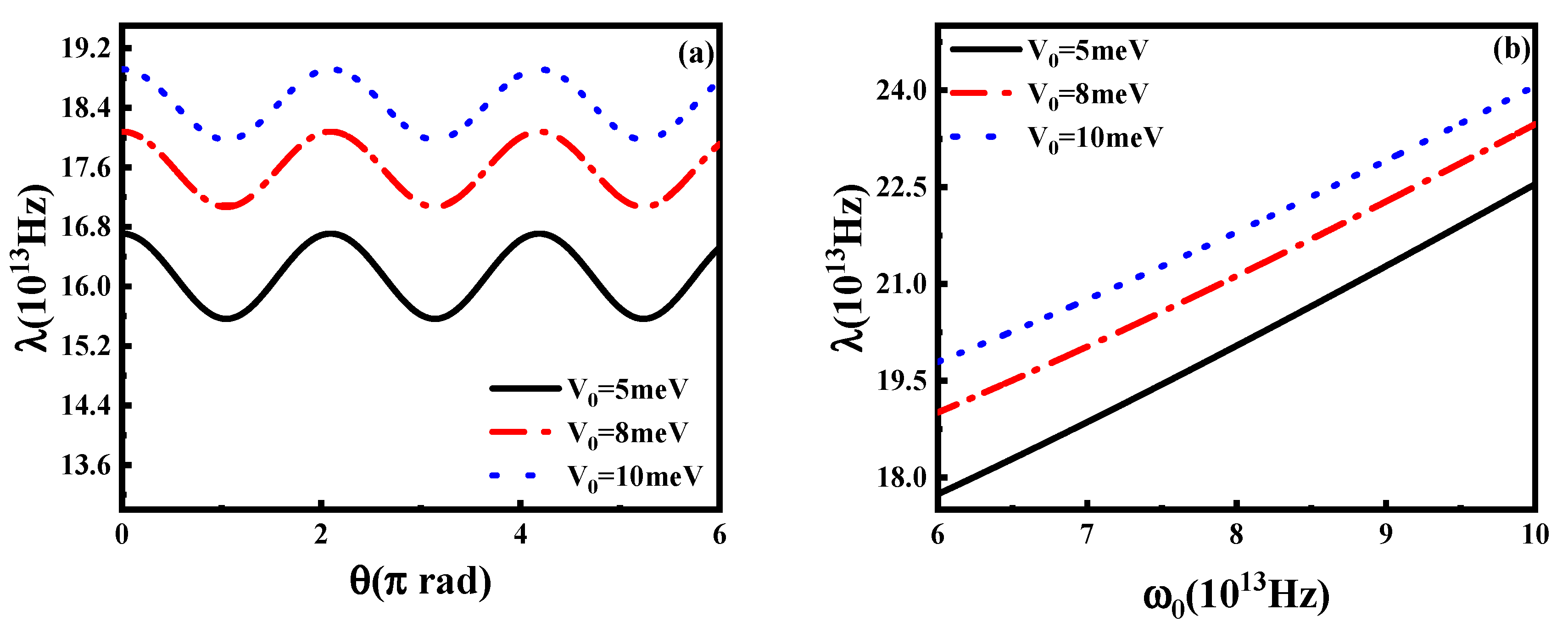



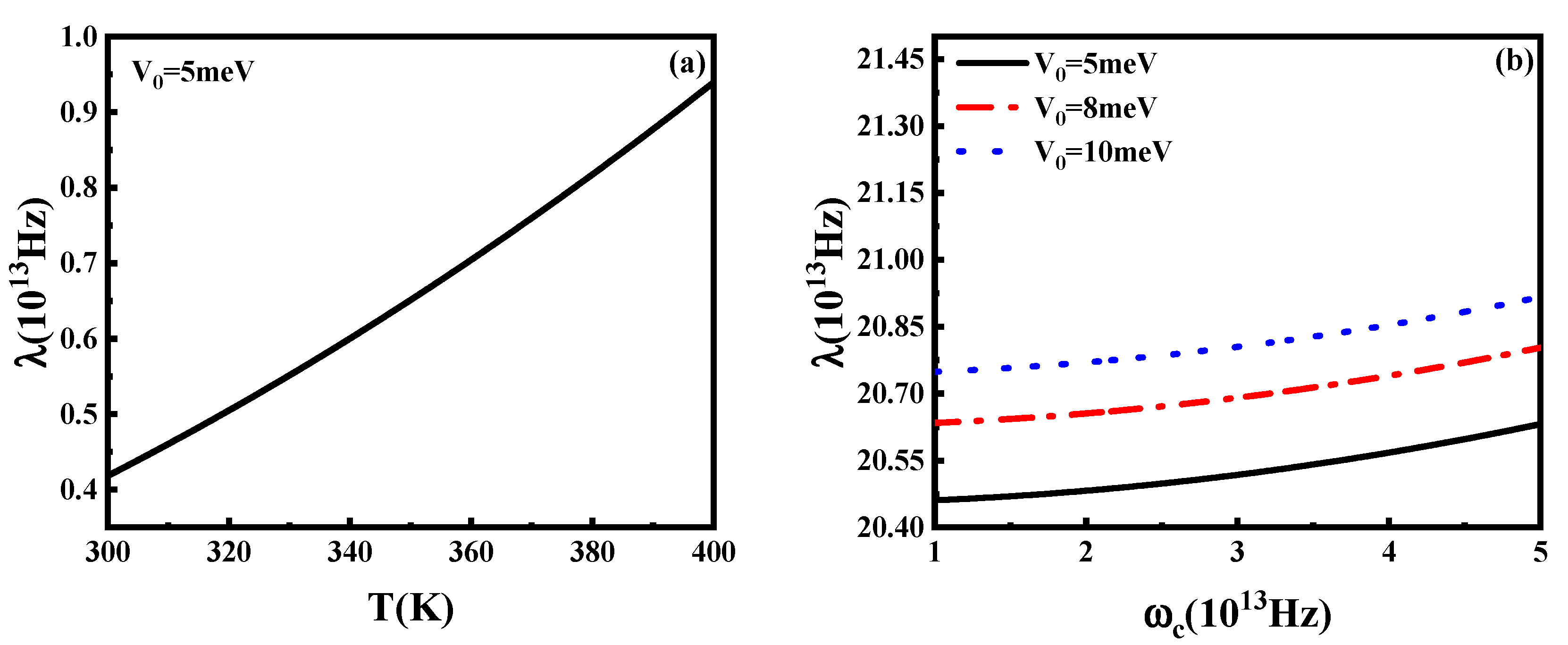
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QW | Quantum Well |
| AGCP | Asymmetrical Gaussian Confinement Potential |
| TCPQW | Triangular Confinement Potential Quantum Well |
| LO | Longitudinal Optical |
| LLP | Lee–Low–Pines |
| QST | Quantum Statistical Theory |
| GSE | Ground-State Energy |
| GSBE | Ground-State Binding Energy |
| VF | Vibrational Frequency |
References
- Camacho-Guardian, A.; Bruun, G.M. Landau effective interaction between quasiparticles in a Bose-Einstein condensate. Phys. Rev. X 2018, 8, 031042. [Google Scholar] [CrossRef] [Green Version]
- Franchini, C.; Reticcioli, M.; Setvin, M.; Diebold, U. Polarons in materials. Nat. Rev. Mater. 2021, 6, 560–586. [Google Scholar] [CrossRef]
- Emin, D. Polarons; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Abolfath, R.M.; Korkusinski, M.; Brabec, T.; Hawrylak, P. Spin textures in strongly coupled electron spin and magnetic or nuclear spin systems in quantum dots. Phys. Rev. Lett. 2012, 108, 247203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kaczmarkiewicz, P.; Machnikowski, P. Two-phonon polaron resonances in self-assembled quantum dots. Phys. Rev. B 2010, 81, 115317. [Google Scholar] [CrossRef] [Green Version]
- Pascual, G.; Boronat, J. Quasiparticle nature of the Bose polaron at finite temperature. Phys. Rev. Lett. 2021, 127, 205301. [Google Scholar] [CrossRef] [PubMed]
- Preisler, V.; Ferreira, R.; Hameau, S.; De Vaulchier, L.A.; Guldner, Y.; Sadowski, M.L.; Lemaître, A. Hole–LO phonon interaction in InAs/GaAs quantum dots. Phys. Rev. B 2005, 72, 115309. [Google Scholar] [CrossRef] [Green Version]
- Piekarz, P.; Legut, D.; Baldini, E.; Belvin, C.A.; Kołodziej, T.; Tabiś, W.; Kozłowski, A.; Kakol, Z.; Tarnawski, Z.; Lorenzana, J.; et al. Trimeron-phonon coupling in magnetite. Phys. Rev. B 2021, 103, 104303. [Google Scholar] [CrossRef]
- Koschorreck, M.; Pertot, D.; Vogt, E.; Fröhlich, B.; Feld, M.; Köhl, M. Attractive and repulsive Fermi polarons in two dimensions. Nature 2012, 485, 619–622. [Google Scholar] [CrossRef] [Green Version]
- Yamada, Y.; Kanemitsu, Y. Electron-phonon interactions in halide perovskites. NPG Asia Mater. 2022, 14, 48. [Google Scholar] [CrossRef]
- Lu, N.; Li, L.; Geng, D.; Liu, M. A review for polaron dependent charge transport in organic semiconductor. Org. Electron. 2018, 61, 223–234. [Google Scholar] [CrossRef]
- Cornelissen, L.J.; Oyanagi, K.; Kikkawa, T.; Qiu, Z.; Kuschel, T.; Bauer, G.E.W.; van Wees, B.J.; Saitoh, E. Nonlocal magnon-polaron transport in yttrium iron garnet. Phys. Rev. B 2017, 96, 104441. [Google Scholar] [CrossRef] [Green Version]
- Tan, L.B.; Cotlet, O.; Bergschneider, A.; Schmidt, R.; Back, P.; Shimazaki, Y.; Kroner, M.; İmamoğlu, A. Interacting polaron-polaritons. Phys. Rev. X 2020, 10, 021011. [Google Scholar] [CrossRef] [Green Version]
- Kandemir, B.S.; Cetin, A. Ground-and first-excited state energies of impurity magnetopolaron in an anisotropic quantum dot. Phys. Rev. B 2002, 65, 054303. [Google Scholar] [CrossRef]
- Ideue, T.; Hamamoto, K.; Koshikawa, S.; Ezawa, M.; Shimizu, S.; Kaneko, Y.; Tokura, Y.; Nagaosa, N.; Iwasa, Y. Bulk rectification effect in a polar semiconductor. Nat. Phys. 2017, 13, 578–583. [Google Scholar] [CrossRef]
- Wang, Z.; Reimann, K.; Woerner, M.; Elsaesser, T.; Hofstetter, D.; Hwang, J.; Schaff, W.J.; Eastman, L.F. Optical phonon sidebands of electronic intersubband absorption in strongly polar semiconductor heterostructures. Phys. Rev. Lett. 2005, 94, 037403. [Google Scholar] [CrossRef]
- Beljonne, D.; Cornil, J.; Sirringhaus, H.; Brown, P.J.; Shkunov, M.; Friend, R.H.; Brédas, J.L. Optical signature of delocalized polarons in conjugated polymers. Adv. Funct. Mater. 2001, 11, 229–234. [Google Scholar] [CrossRef]
- Hu, M.G.; Van de Graaff, M.J.; Kedar, D.; Corson, J.P.; Cornell, E.A.; Jin, D.S. Bose polarons in the strongly interacting regime. Phys. Rev. Lett. 2016, 117, 055301. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, S.M.; Endo, S.; Levinsen, J.; Parish, M.M. Universality of an impurity in a Bose-Einstein condensate. Phys. Rev. X 2018, 8, 011024. [Google Scholar] [CrossRef] [Green Version]
- De Teresa, J.M.; Ibarra, M.R.; Algarabel, P.A.; Ritter, C.; Marquina, C.; Blasco, J.; García, J.; Moral, A.; Arnold, Z. Evidence for magnetic polarons in the magnetoresistive perovskites. Nature 1997, 386, 256–259. [Google Scholar] [CrossRef]
- Zheng, F.; Wang, L. Large polaron formation and its effect on electron transport in hybrid perovskites. Energy Environ. Sci. 2019, 12, 1219–1230. [Google Scholar] [CrossRef]
- Sarma, S.D. Theory of two-dimensional magnetopolarons. Phys. Rev. Lett. 1984, 52, 859. [Google Scholar] [CrossRef]
- Boebinger, G.S.; Levi AF, J.; Schmitt-Rink, S.; Passner, A.; Pfeiffer, L.N.; West, K.W. Direct observation of two-dimensional magnetopolarons in a resonant tunnel junction. Phys. Rev. Lett. 1990, 65, 235. [Google Scholar] [CrossRef]
- Dietl, T.; Spałek, J. Effect of fluctuations of magnetization on the bound magnetic polaron: Comparison with experiment. Phys. Rev. Lett. 1982, 48, 355. [Google Scholar] [CrossRef]
- Wu, X.; Peeters, F.M.; Devreese, J.T. Two-dimensional polaron in a magnetic field. Phys. Rev. B 1985, 32, 7964. [Google Scholar]
- Hai, G.Q.; Peeters, F.M. Magnetopolaron effect in parabolic quantum wells in tilted magnetic fields. Phys. Rev. B 1999, 60, 8984. [Google Scholar] [CrossRef]
- Junior, L.A.R.; Stafström, S. Polaron stability in molecular semiconductors: Theoretical insight into the impact of the temperature, electric field and the system dimensionality. Phys. Chem. Chem. Phys. 2015, 17, 8973–8982. [Google Scholar] [CrossRef]
- Bonn, M.; Miyata, K.; Hendry, E.; Zhu, X.Y. Role of dielectric drag in polaron mobility in lead halide perovskites. ACS Energy Lett. 2017, 2, 2555–2562. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Ardila, L.A.P.; Schmidt, R.; Jachymski, K.; Negretti, A. Ionic polaron in a Bose-Einstein condensate. Commun. Phys. 2021, 4, 94. [Google Scholar] [CrossRef]
- Guenther, N.E.; Massignan, P.; Lewenstein, M.; Bruun, G.M. Bose polarons at finite temperature and strong coupling. Phys. Rev. Lett. 2018, 120, 050405. [Google Scholar] [CrossRef] [Green Version]
- Li, W.S.; Gu, S.W.; Au-Yeung, T.C.; Yeung, Y.Y. Effects of the parabolic potential and confined phonons on the polaron in a quantum wire. Phys. Rev. B 1992, 46, 4630. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Zhu, X.; Liu, Z.; Pan, S.H.; Li, X.Y. Polaron effects in asymmetric semiconductor quantum-well structures. Phys. Rev. B 1997, 55, 4670. [Google Scholar] [CrossRef]
- Fotue, A.J.; Kenfack, S.C.; Tiotsop, M.; Issofa, N.; Wirngo, A.V.; Djemmo, M.P.T.; Fotsin, H.; Fai, L.C. Shannon entropy and decoherence of bound magnetopolaron in a modified cylindrical quantum dot. Mod. Phys. Lett. B 2015, 29, 1550241. [Google Scholar] [CrossRef]
- Flebus, B.; Shen, K.; Kikkawa, T.; Uchida, K.; Qiu, Z.Y.; Saitoh, E.; Duine, R.A.; Bauer, G.E.W. Magnon-polaron transport in magnetic insulators. Phys. Rev. B 2017, 95, 144420. [Google Scholar] [CrossRef] [Green Version]
- Kikkawa, T.; Shen, K.; Flebus, B.; Duine, R.A.; Uchida, K.; Qiu, Z.Y.; Bauer, G.E.W.; Saitoh, E. Magnon polarons in the spin Seebeck effect. Phys. Rev. Lett. 2016, 117, 207203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Simensen, H.T.; Reitz, D.; Sun, Q.Y.; Yuan, W.; Li, C.; Tserkovnyak, Y.; Brataas, A.; Shi, J. Observation of magnon polarons in a uniaxial antiferromagnetic insulator. Phys. Rev. Lett. 2020, 125, 217201. [Google Scholar] [CrossRef] [PubMed]
- Mei, J.H.; Zhang, B.; Xiao, J.L.; Sun, Y.; Zhang, W.; Miao, X.J.; Sarengaowa; Ma, X.J. Effect of double-constrained potential on the ground-state binding energy of magnetopolaron in a quantum well. Int. J. Mod. Phys. B 2022, 2350072. [Google Scholar] [CrossRef]
- Qiu, W.; Sun, Y.; Xiao, J.L. Parabolic Potential Effect on Binding Energy of Impurity Polaron in Asymmetrical Semi-Exponential Quantum Wells. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 2233–2239. [Google Scholar] [CrossRef]
- Zhang, L.; Xie, H.J.; Chen, C.Y. Fröhlich electron-phonon interaction Hamiltonian in a quantum dot quantum well. Phys. Rev. B 2002, 66, 205326. [Google Scholar] [CrossRef]
- Melnikov, D.V.; Fowler, W.B. Electron-phonon interaction in a spherical quantum dot with finite potential barriers: The Fröhlich Hamiltonian. Phys. Rev. B 2001, 64, 245320. [Google Scholar] [CrossRef]
- Giustino, F. Electron-phonon interactions from first principles. Rev. Mod. Phys. 2017, 89, 015003. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.D.; Low, F.E.; Pines, D. The motion of slow electrons in a polar crystal. Phys. Rev. 1953, 90, 297. [Google Scholar] [CrossRef]
- Huybrechts, W.J. Internal excited state of the optical polaron. J. Phys. C Solid State Phys. 1977, 10, 3761. [Google Scholar] [CrossRef]
- Whitfield, G.; Engineer, M. Temperature dependence of the polaron. Phys. Rev. B 1975, 12, 5472. [Google Scholar] [CrossRef]
- Schilcher, M.J.; Robinson, P.J.; Abramovitch, D.J.; Tan, L.Z.; Rappe, A.M.; Reichman, D.R.; Egger, D.A. The significance of polarons and dynamic disorder in halide perovskites. ACS Energy Lett. 2021, 6, 2162–2173. [Google Scholar] [CrossRef]
- Zou, S.; Kamran, M.A.; Shi, L.J.; Liu, R.; Guo, S.; Kavokin, A.; Zou, B. Bosonic lasing from collective exciton magnetic polarons in diluted magnetic nanowires and nanobelts. ACS Photonics 2016, 3, 1809–1817. [Google Scholar] [CrossRef]
- Hackens, B.; Faniel, S.; Gustin, C.; Wallart, X.; Bollaert, S.; Cappy, A.; Bayot, V. Dwell-time-limited coherence in open quantum dots. Phys. Rev. Lett. 2005, 94, 146802. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Miao, X.J.; Sun, Y.; Ma, X.J.; Xiao, J.L. Parabolic Potential and Temperature Effects on the Magnetopolaron in a RbCl Asymmetrical Semi-exponential Quantum Well. J. Low Temp. Phys. 2022, 1–23. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, J.L. Coherence effects of the strongly-coupled optical polaron-level qubit in a quantum well with asymmetrical semi-exponential potential. Superlattices Microstruct. 2020, 145, 106617. [Google Scholar] [CrossRef]
- Miao, X.J.; Sun, Y.; Xiao, J.L. Anisotropic parabolic confinement potential effect on polaron ground state and phonon’s number in the RbCl asymmetrical quantum wells. Indian J. Phys. 2022, 96, 1969–1973. [Google Scholar] [CrossRef]
- Jo, I.; Hsu, I.K.; Lee, Y.J.; Sadeghi, M.M.; Kim, S.; Cronin, S.; Tutuc, E.; Banerjee, S.K.; Yao, Z.; Shi, L. Low-frequency acoustic phonon temperature distribution in electrically biased graphene. Nano Lett. 2011, 11, 85–90. [Google Scholar] [CrossRef]
| Material | Coupling Constants | ||
|---|---|---|---|
| RbCl | 0.432 | 3.81 | 21.45 |
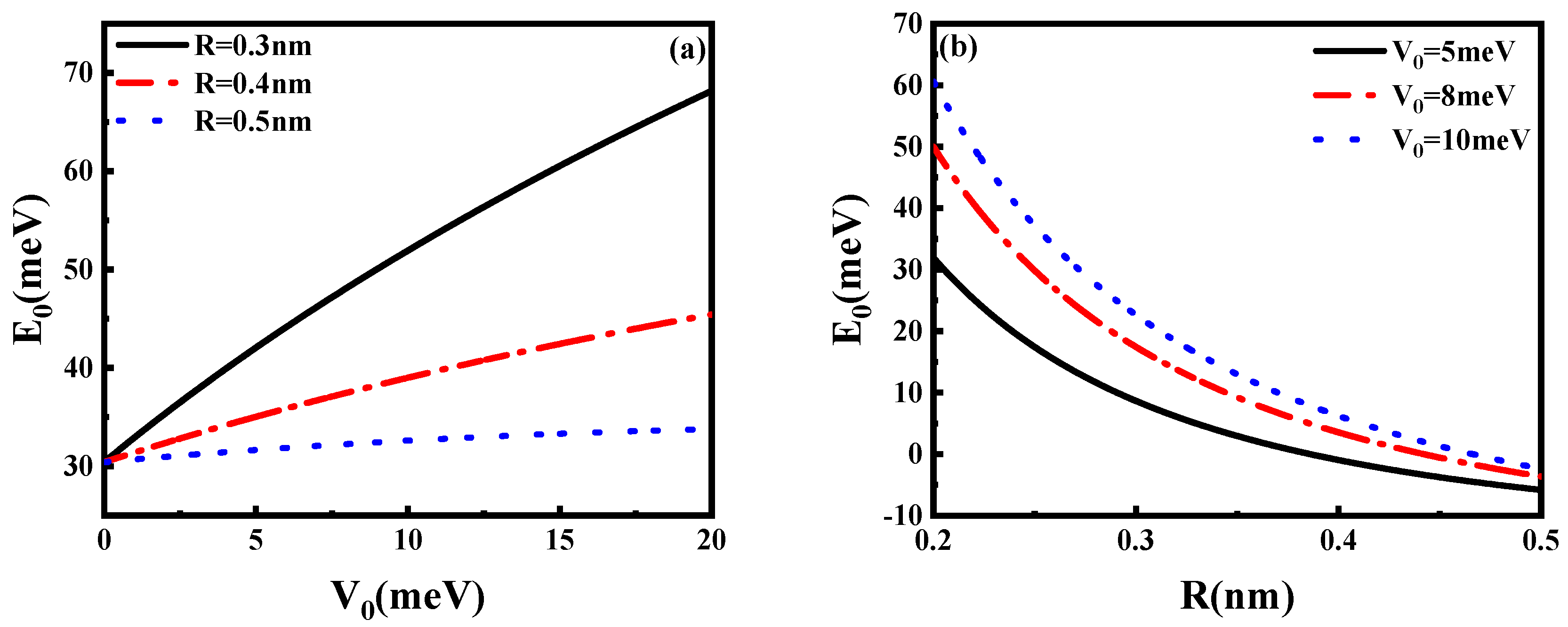
| Figure 1a, Figure 2a, Figure 3a and Figure 4a | |
| Figure 1b, Figure 2b, Figure 3b and Figure 4b | |
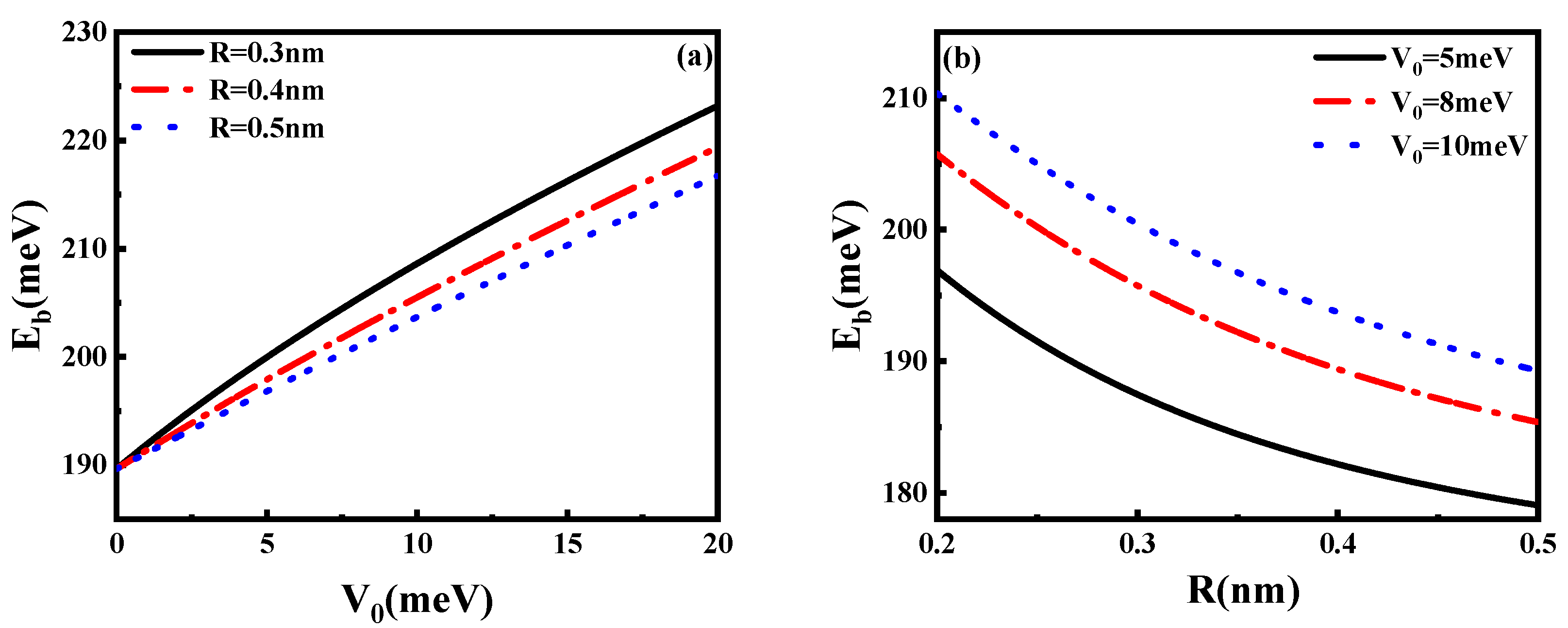
| Figure 5a, Figure 6a, Figure 7a and Figure 8a | |
| Figure 5b, Figure 6b, Figure 7b and Figure 8b | |
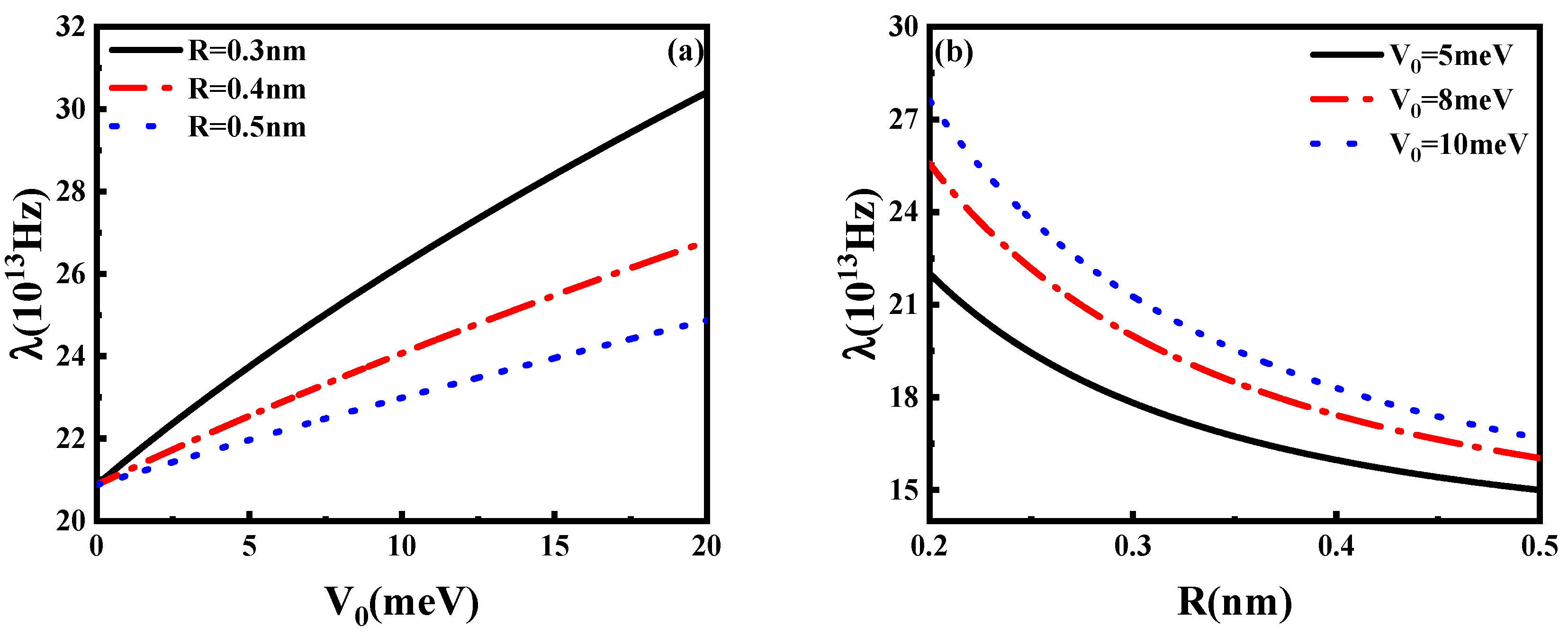
| Figure 9a, Figure 10a, Figure 11a and Figure 12a | |
| Figure 9b, Figure 10b, Figure 11b and Figure 12b |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, J.; Han, S.; Miao, X.; Sun, Y.; Xiao, J. Asymmetrical Gaussian Potential Effects on Strongly Coupled Magnetopolaron Properties in Triangular Confinement Potential Quantum Wells. Coatings 2022, 12, 1900. https://doi.org/10.3390/coatings12121900
Ge J, Han S, Miao X, Sun Y, Xiao J. Asymmetrical Gaussian Potential Effects on Strongly Coupled Magnetopolaron Properties in Triangular Confinement Potential Quantum Wells. Coatings. 2022; 12(12):1900. https://doi.org/10.3390/coatings12121900
Chicago/Turabian StyleGe, Jun, Shuang Han, Xiujuan Miao, Yong Sun, and Jinglin Xiao. 2022. "Asymmetrical Gaussian Potential Effects on Strongly Coupled Magnetopolaron Properties in Triangular Confinement Potential Quantum Wells" Coatings 12, no. 12: 1900. https://doi.org/10.3390/coatings12121900





