The Impurity and Decay-Magnetic Polaron Effects in III–V Compound Gaussian Quantum Wells
Abstract
:1. Introduction
2. Theoretical Method
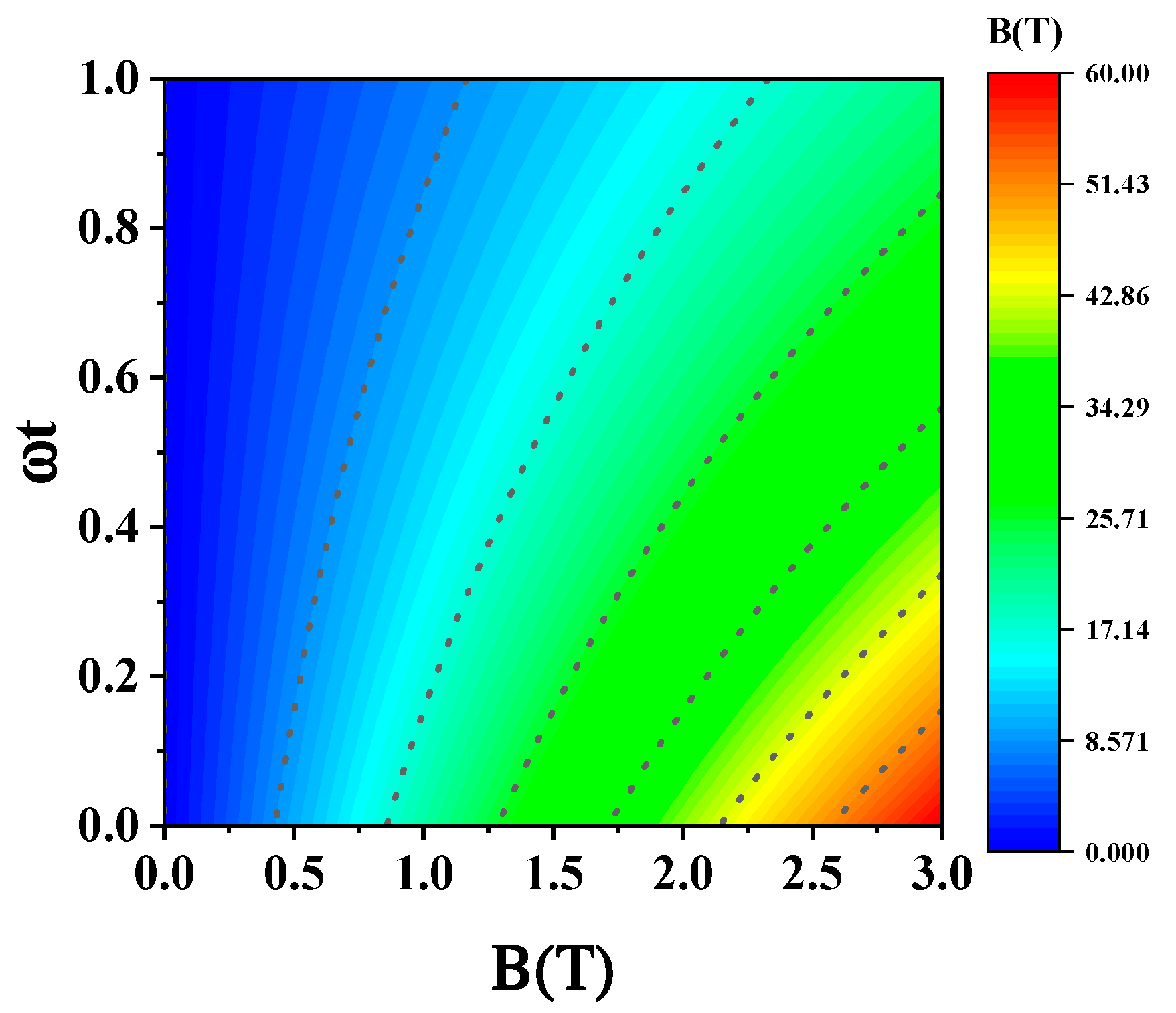
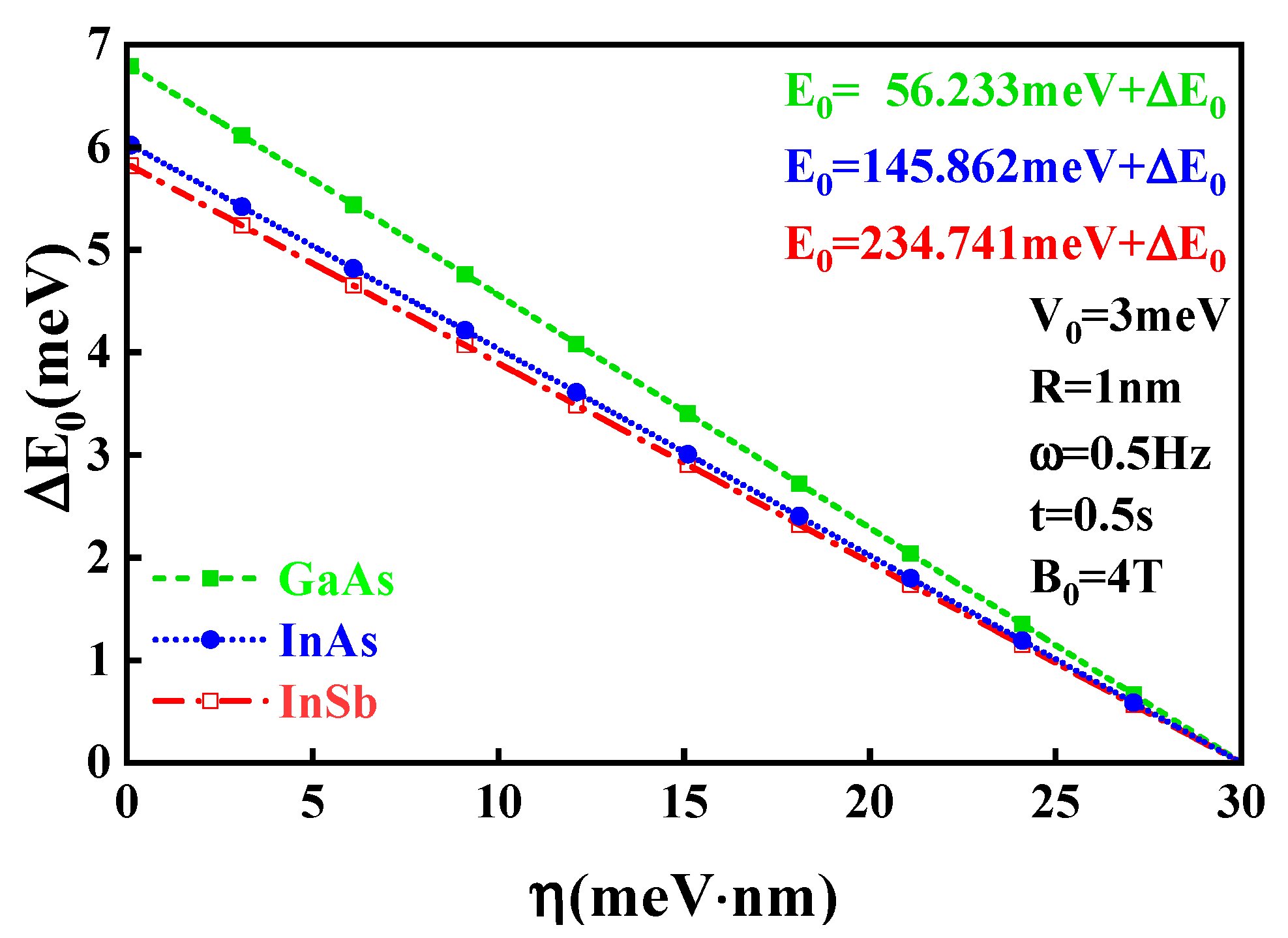
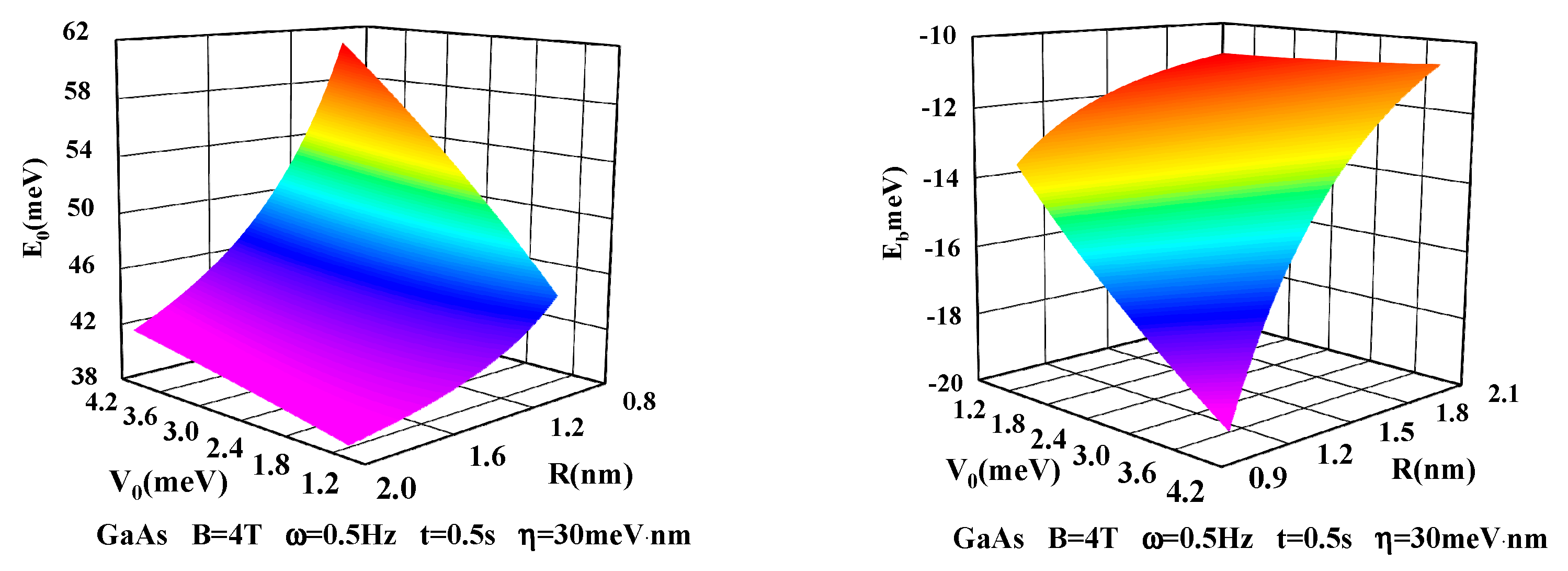
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Li, W.; Yin, L.; Liu, Y.; Guo, H.; Lai, J.; Han, Y.; Li, G.; Li, M.; Zhang, J.; et al. Full-color fluorescent carbon quantum dots. Sci. Adv. 2020, 6, eabb6772. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Wang, Y.-K.; Yuan, F.; Johnston, A.; Liu, Y.; Ma, D.; Choi, M.-J.; Chen, B.; Chekini, M.; Baek, S.-W.; et al. Bipolar-shell resurfacing for blue LEDs based on strongly confined perovskite quantum dots. Nat. Nanotechnol. 2020, 15, 668–674. [Google Scholar] [CrossRef] [PubMed]
- Topnani, N.B.; Nagaraja, P.; Musevic, I.; Ramarao, P. Fluorescence intermittency and spatial localization of core-shell quantum rod clusters in an inverse nematic gel. Phys. Rev. Mater. 2020, 4, 126002. [Google Scholar] [CrossRef]
- Cunha, S.M.; da Costa, D.R.; Felix, L.C.; Chaves, A.; Pereira, J.M., Jr. Electronic and transport properties of anisotropic semiconductor quantum wires. Phys. Rev. B 2020, 102, 045427. [Google Scholar] [CrossRef]
- Tummuru, T.; Can, O.; Franz, M. Chiral p-wave superconductivity in a twisted array of proximitized quantum wires. Phys. Rev. B 2021, 103, L100501. [Google Scholar] [CrossRef]
- Iyer, P.P.; DeCrescent, R.A.; Mohtashami, Y.; Lheureux, G.; Butakov, N.A.; Alhassan, A.; Weisbuch, C.; Nakamura, S.; DenBaars, S.P.; Schuller, J.A. Unidirectional luminescence from InGaN/GaN quantum-well metasurfaces. Nat. Photonics 2020, 14, 543–548. [Google Scholar] [CrossRef]
- Olusola, O.I.; Shomotun, O.P.; Vincent, U.E.; McClintock, P.V.E. Quantum vibrational resonance in a dual-frequency-driven Tietz-Hua quantum well. Phys. Rev. E 2020, 101, 052216. [Google Scholar] [CrossRef]
- Ridene, S. GaSbBi/GaSb quantum-well and wire laser diodes. Chem. Phys. Lett. 2018, 702, 44–48. [Google Scholar] [CrossRef]
- Zhao, Q.; Aqiqi, S.; You, J.-F.; Kria, M.; Guo, K.-X.; Feddi, E.; Zhang, Z.-H.; Yuan, J.-H. Influence of position-dependent effective mass on the nonlinear optical properties in AlxGa1−xAs/GaAs single and double triangular quantum wells. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 115, 113707. [Google Scholar] [CrossRef]
- De Silva, N.; Warnakula, T.; Gunapala, S.D.; Stockman, M.I.; Premaratne, M. Effect of logarithmic perturbations in ohmic like spectral densities in dynamics of electronic excitation using variational polaron transformation approach. J. Phys. Condens. Matter 2021, 33, 145304. [Google Scholar] [CrossRef]
- Asatryan, A.L.; Movsisyan, A.H.; Vartanian, A.L. External electric and magnetic field effects on the polaron in a wurtzite nitride nanowire embedded in a nonpolar matrix. Eur. Phys. J. B 2021, 94, 70. [Google Scholar] [CrossRef]
- Bahar, M.K.; Rodríguez-Magdaleno, K.A.; Martínez-Orozco, J.C.; Mora-Ramos, M.E.; Ungan, F. Optical properties of a triple AlGaAs/GaAs quantum well purported for quantum cascade laser active region. Mater. Today Commun. 2021, 26, 101936. [Google Scholar] [CrossRef]
- Yu, H.; Zhen, Z.; Shi, Y.-S.; Guo, K.-X.; Feddi, E.; Yuan, J.-H.; Zhang, Z.-H. The nonlinear optical absorption in AlxGa1−xAs/GaAs double-graded quantum wells: Magnetic field effect and the position-dependent effective mass effect. Eur. Phys. J. Plus 2021, 136, 555. [Google Scholar] [CrossRef]
- Frankerl, C.; Nippert, F.; Gomez-Iglesias, A.; Hoffmann, M.P.; Brandl, C.; Lugauer, H.-J.; Zeisel, R.; Hoffmann, A.; Davies, M.J. Origin of carrier localization in AlGaN-based quantum well structures and implications for efficiency droop. Appl. Phys. Lett. 2020, 117, 102107. [Google Scholar] [CrossRef]
- Gusev, G.M.; Olshanetsky, E.B.; Hernandez, F.G.G.; Raichev, O.E.; Mikhailov, N.N.; Dvoretsky, S.A. Two-dimensional topological insulator state in double HgTe quantum well. Phys. Rev. B 2020, 101, 241302. [Google Scholar] [CrossRef]
- Donmez, O.; Aydın, M.; Ardalı, Ş.; Yıldırım, S.; Tıraş, E.; Nutku, F.; Çetinkaya, Ç.; Çokduygulular, E.; Puustinen, J.; Hilska, J.; et al. Electronic transport in n-type modulation-doped AlGaAs/GaAsBi quantum well structures: Influence of Bi and thermal annealing on electron effective mass and electron mobility. Semicond. Sci. Technol. 2020, 35, 025009. [Google Scholar] [CrossRef]
- Sherly, I.J.; Nithiananthi, P. Tuning the dynamics of Bound Magnetic Polaron in asymmetric Cd1-x1Mnx1Te/Cd1-x2Mnx2Te Semimagnetic Concentric Double Quantum Rings: Through magnetic ion concentration and magnetic field. Phys. B Condens. Matter 2021, 600, 412615. [Google Scholar] [CrossRef]
- Korshunova, A.N.; Lakhno, V.D. Charge Transfer by Polarons in a Homogeneous Poly G/Poly C-Chain Subjected to a Constant Electric Field in Terms of the Peyrard–Bishop–Holstein Model. Tech. Phys. 2020, 65, 1467–1474. [Google Scholar] [CrossRef]
- Cai, C.-Y.; Qiu, W.; Sun, Y.; Zhao, C.-L.; Xiao, J.-L. Effects of an anisotropic parabolic potential and Coulomb’s impurity potential on the energy characteristics of asymmetrical semi-exponential CsI quantum wells. Commun. Theor. Phys. 2021, 73, 015701. [Google Scholar] [CrossRef]
- Selmi, M.; Smida, A.; El Kossi, S. Effect of Polaron formation in conduction and dielectric behavior in La0.7Sr0.25K0.05MnO3 oxide. J. Mater. Sci. Mater. Electron. 2021, 32, 6014–6027. [Google Scholar] [CrossRef]
- Fobasso, M.F.C.; Fotue, A.J.; Kenfack, S.C.; Ekengue, C.M.; Ngoufack, C.D.G.; Akay, D.; Fai, L.C. Laser light and external magnetic field control of polaron in asymmetric quantum dot. Superlattices Microstruct. 2019, 129, 77–90. [Google Scholar] [CrossRef]
- Phuc, H.V.; Tung, L.V.; Vinh, P.T.; Dinh, L. Nonlinear optical absorption via two-photon process in asymmetrical Gaussian potential quantum wells. Superlatt. Microstruct. 2015, 77, 267–275. [Google Scholar] [CrossRef]
- Zhai, W. A study of electric-field-induced second-harmonic generation in asymmetrical Gaussian potential quantum wells. Phys. B Condens. Matter 2014, 454, 50–55. [Google Scholar] [CrossRef]
- Wu, J.; Guo, K.; Liu, G. Polaron effects on nonlinear optical rectification in asymmetrical Gaussian potential quantum wells with applied electric fields. Phys. B Condens. Matter 2014, 446, 59–62. [Google Scholar] [CrossRef]
- Lee, T.D.; Low, F.E.; Pines, D. The Motion of Slow Electrons in a Polar Crystal. Phys. Rev. 1953, 90, 297. [Google Scholar] [CrossRef]
- Huybrechts, W.J. Internal excited state of the optical polaron. J. Phys. C Solid State Phys. 1977, 10, 3761. [Google Scholar] [CrossRef]
- Gharaati, A.; Khordad, R. Effects of magnetic field and spin-orbit interaction on energy levels in 1D quantum wire: Analytical solution. Opt. Quant. Electron. 2012, 44, 425–436. [Google Scholar] [CrossRef]


| Crystal | ||||
|---|---|---|---|---|
| InSb | 0.022 | 5.72 × 1013 Hz | 0.0138 | 1.26 × 10−32 kg |
| InAs | 0.052 | 4.55 × 1013 Hz | 0.0230 | 2.10 × 10−32 kg |
| GaAs | 0.068 | 5.50 × 1013 Hz | 0.0657 | 4.28 × 10−32 kg |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhang, W.; Ma, X.-J.; Li, P.-F.; Sun, Y.; Xiao, J.-L. The Impurity and Decay-Magnetic Polaron Effects in III–V Compound Gaussian Quantum Wells. Coatings 2022, 12, 1072. https://doi.org/10.3390/coatings12081072
Zhang X, Zhang W, Ma X-J, Li P-F, Sun Y, Xiao J-L. The Impurity and Decay-Magnetic Polaron Effects in III–V Compound Gaussian Quantum Wells. Coatings. 2022; 12(8):1072. https://doi.org/10.3390/coatings12081072
Chicago/Turabian StyleZhang, Xin, Wei Zhang, Xin-Jun Ma, Pei-Fang Li, Yong Sun, and Jing-Lin Xiao. 2022. "The Impurity and Decay-Magnetic Polaron Effects in III–V Compound Gaussian Quantum Wells" Coatings 12, no. 8: 1072. https://doi.org/10.3390/coatings12081072
APA StyleZhang, X., Zhang, W., Ma, X.-J., Li, P.-F., Sun, Y., & Xiao, J.-L. (2022). The Impurity and Decay-Magnetic Polaron Effects in III–V Compound Gaussian Quantum Wells. Coatings, 12(8), 1072. https://doi.org/10.3390/coatings12081072






