Structure and Characterization of Vacuum Arc Deposited Carbon Films—A Critical Overview
Abstract
1. Introduction
2. Characterization Methods
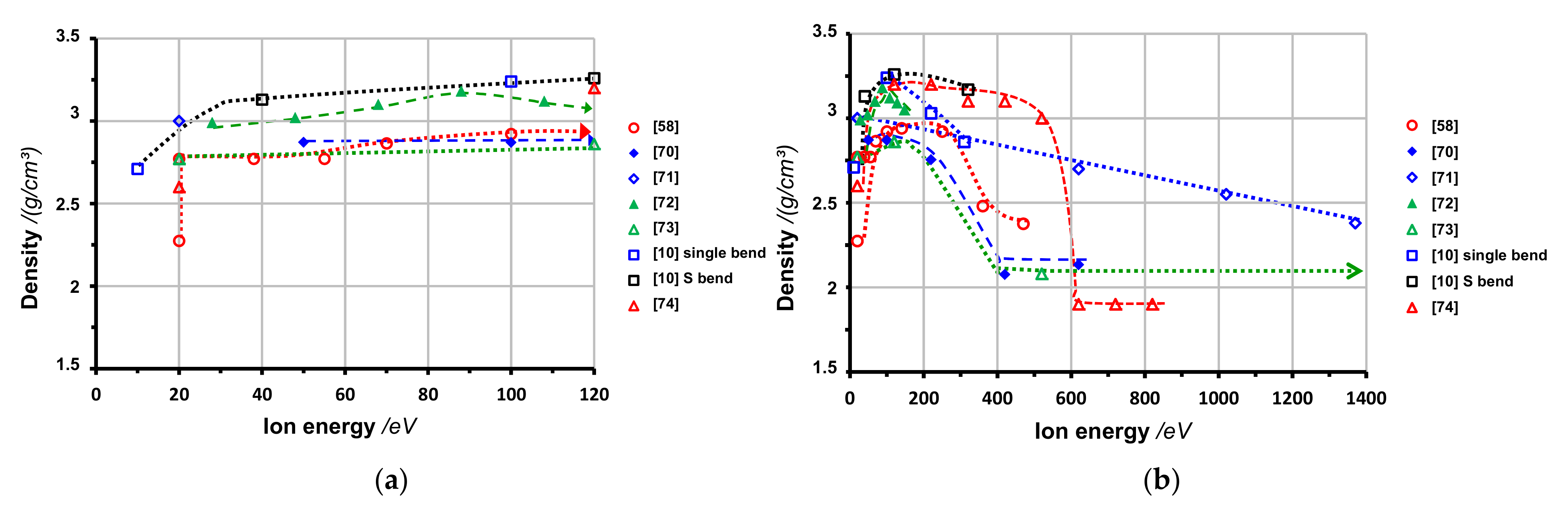
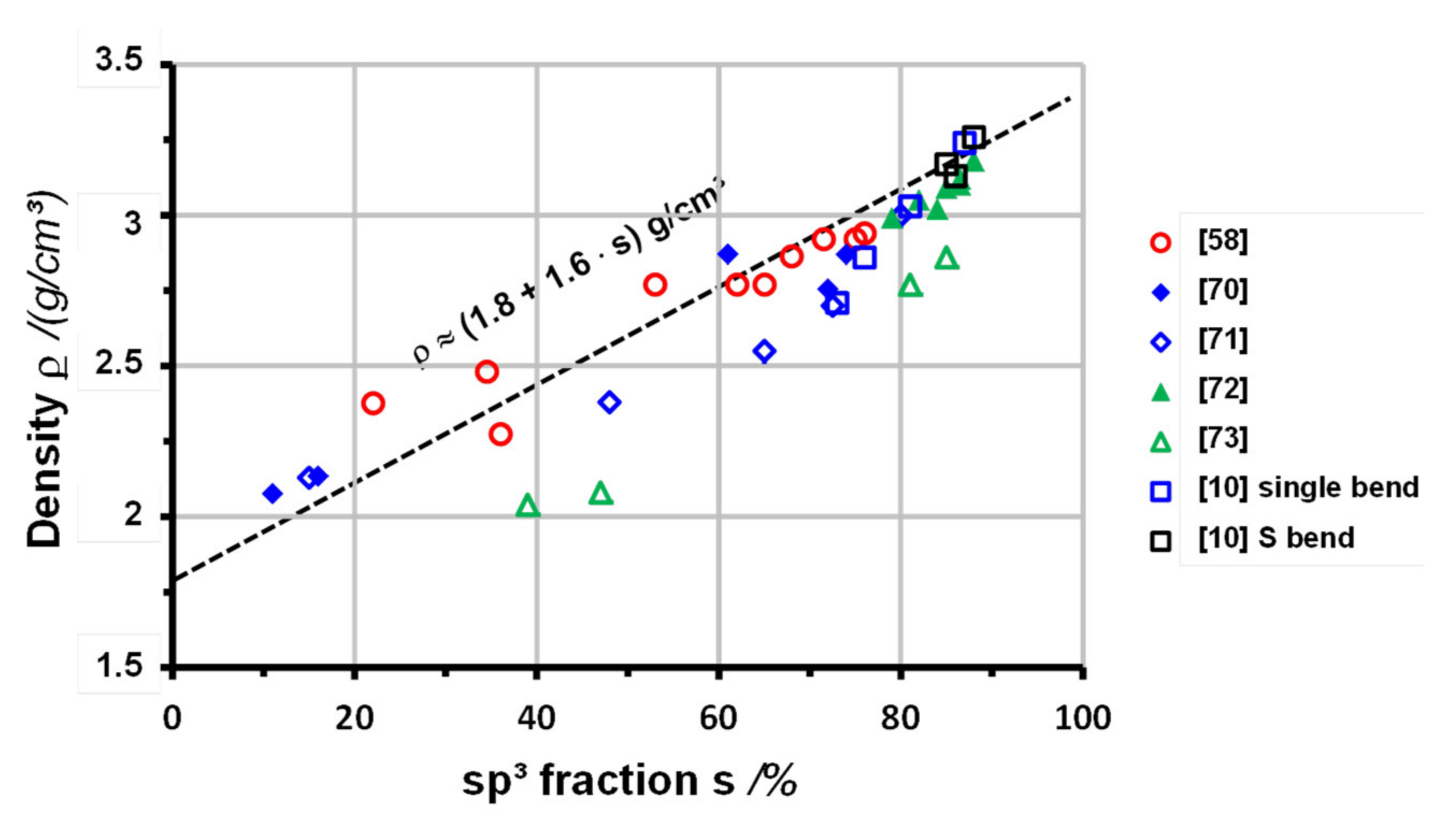
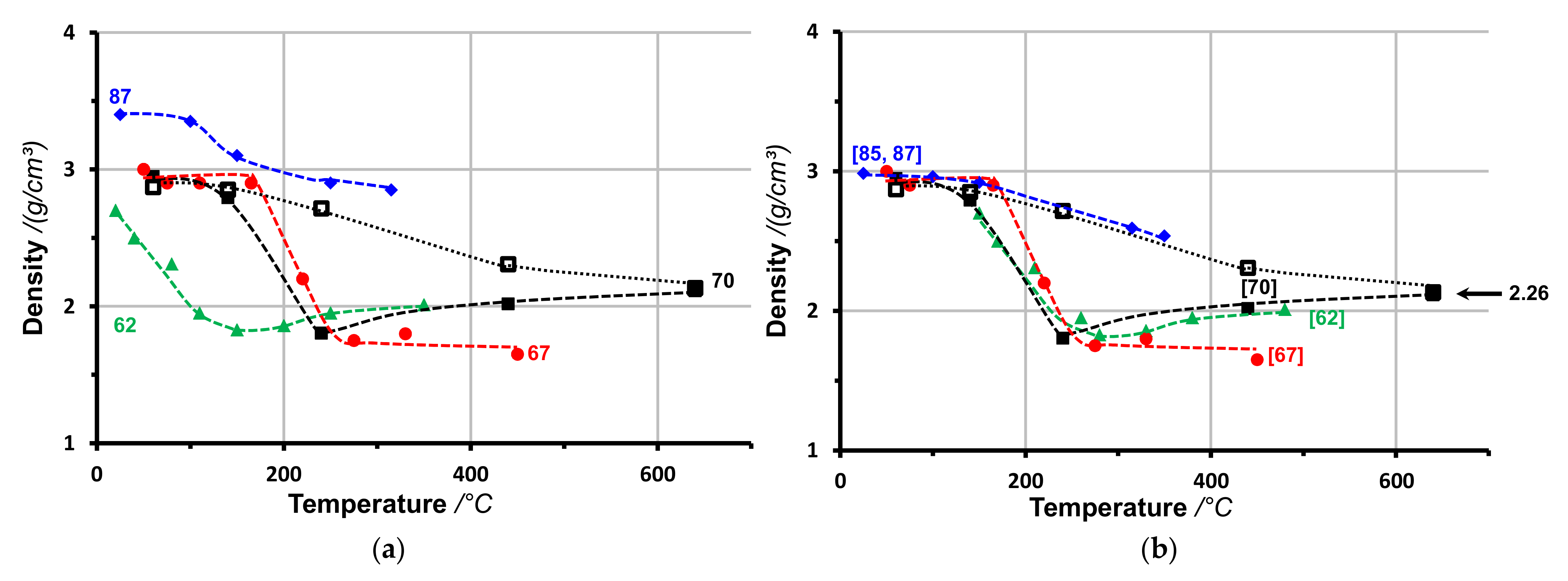
2.1. Mass Density
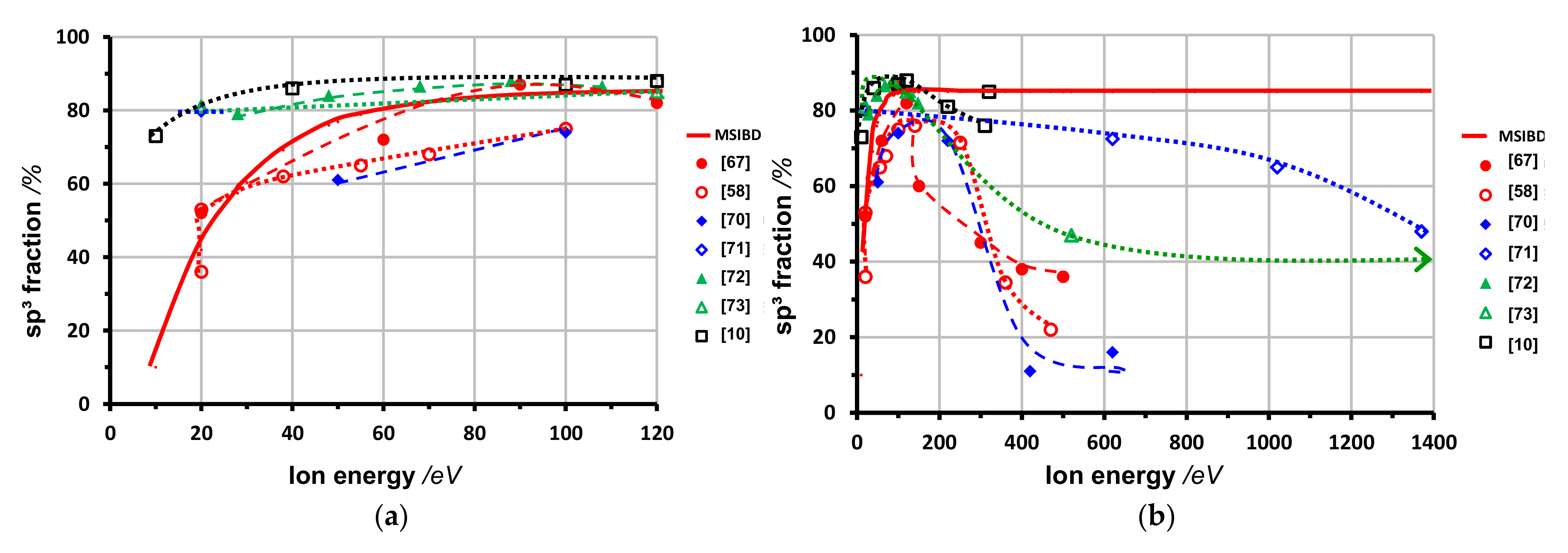
2.2. sp3 Fraction
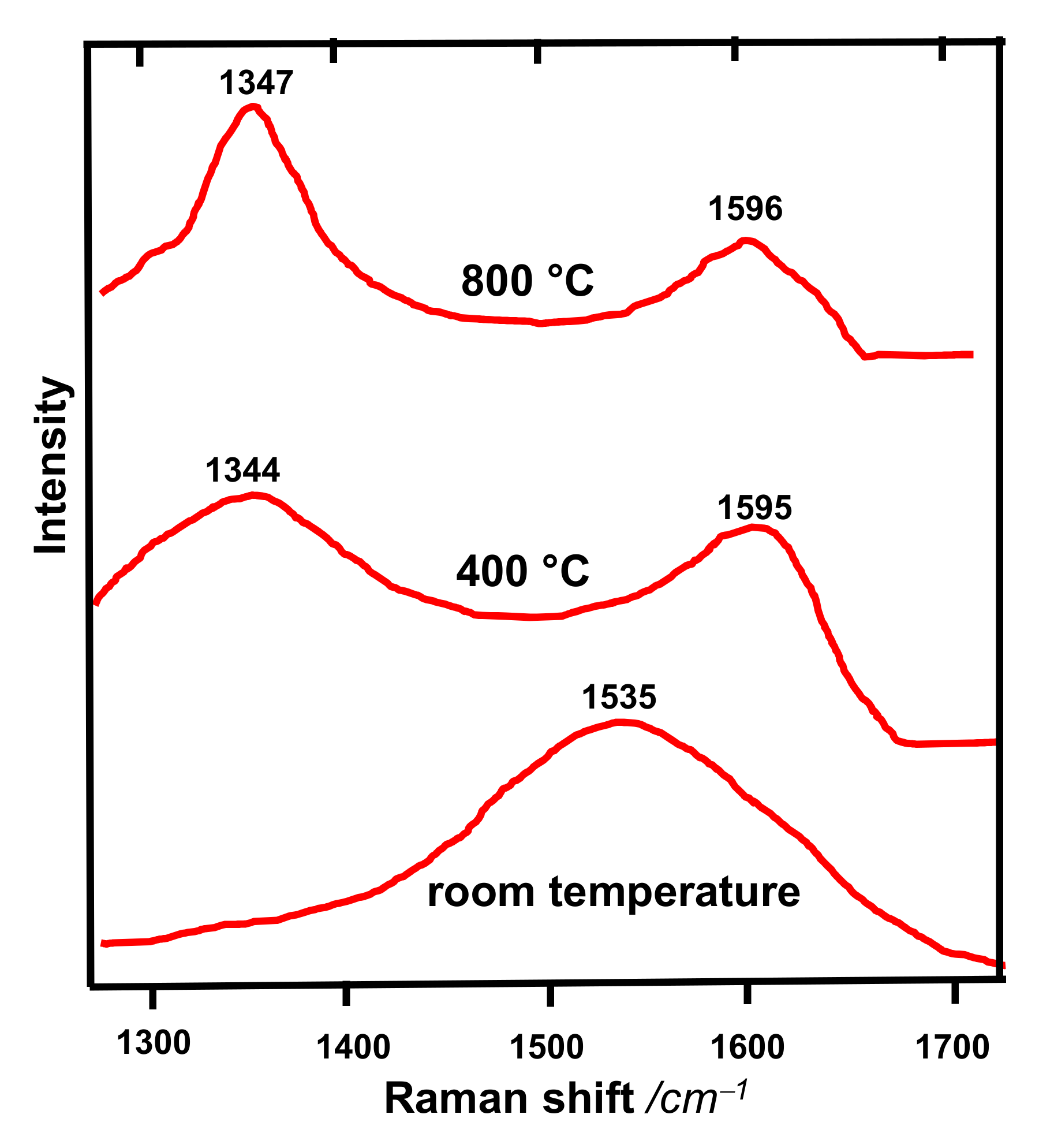
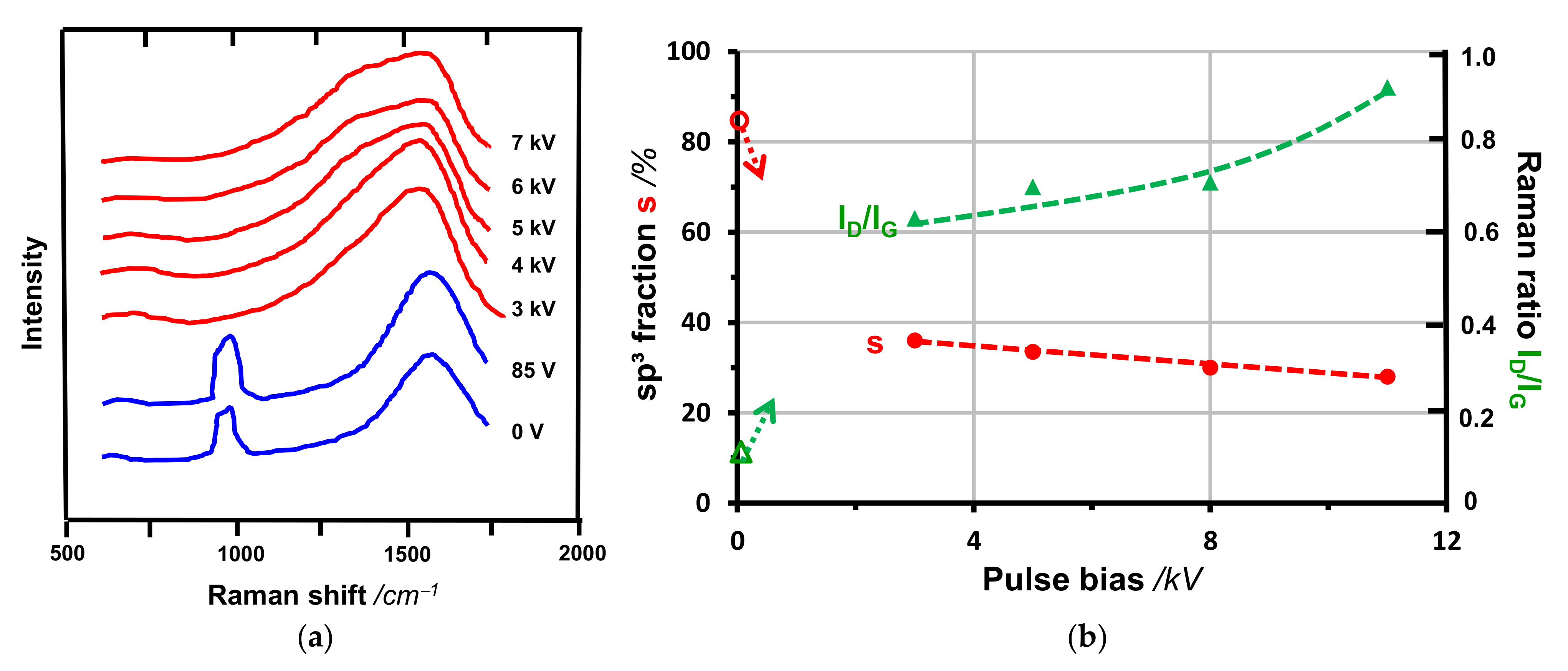
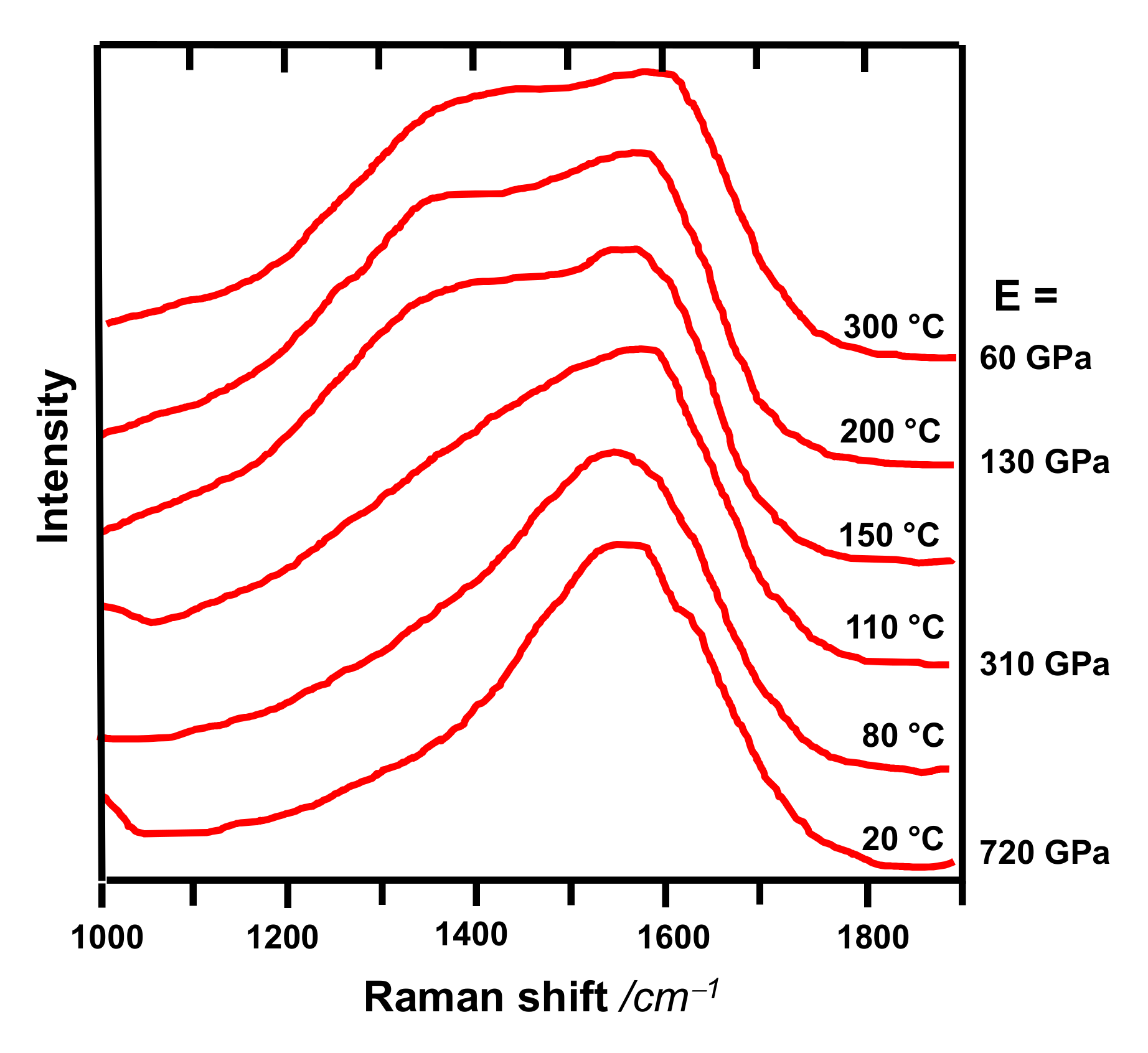
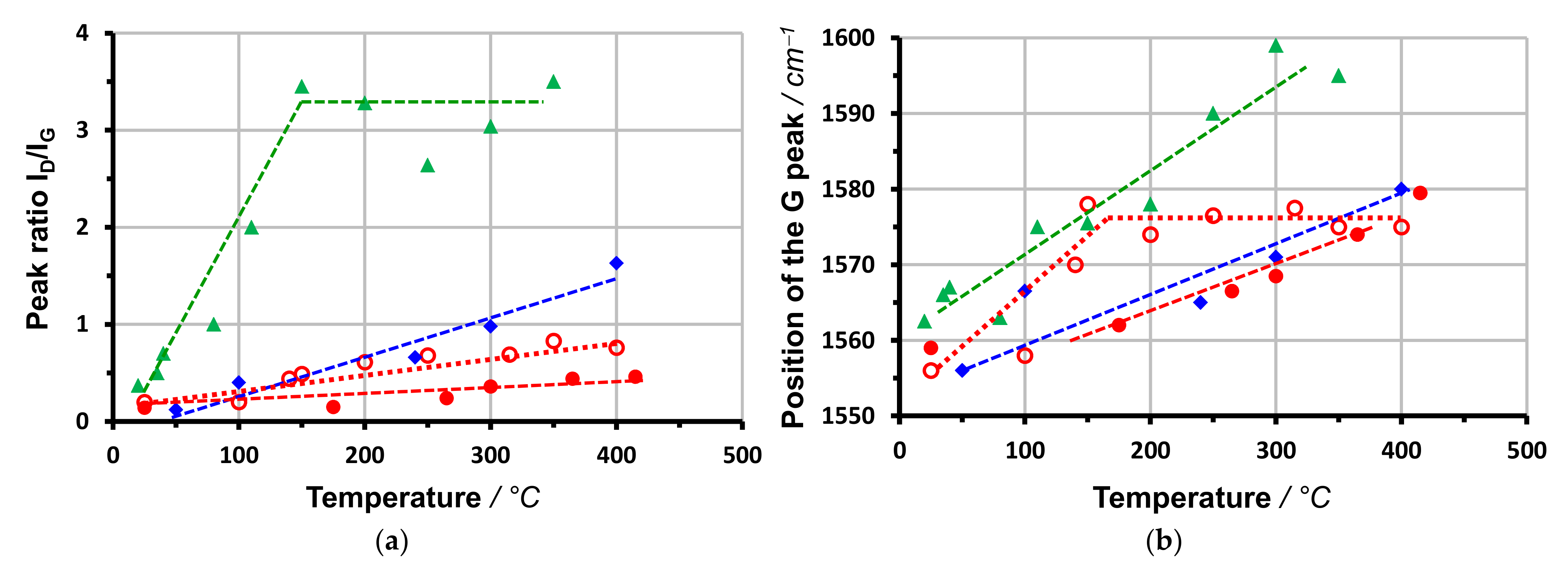
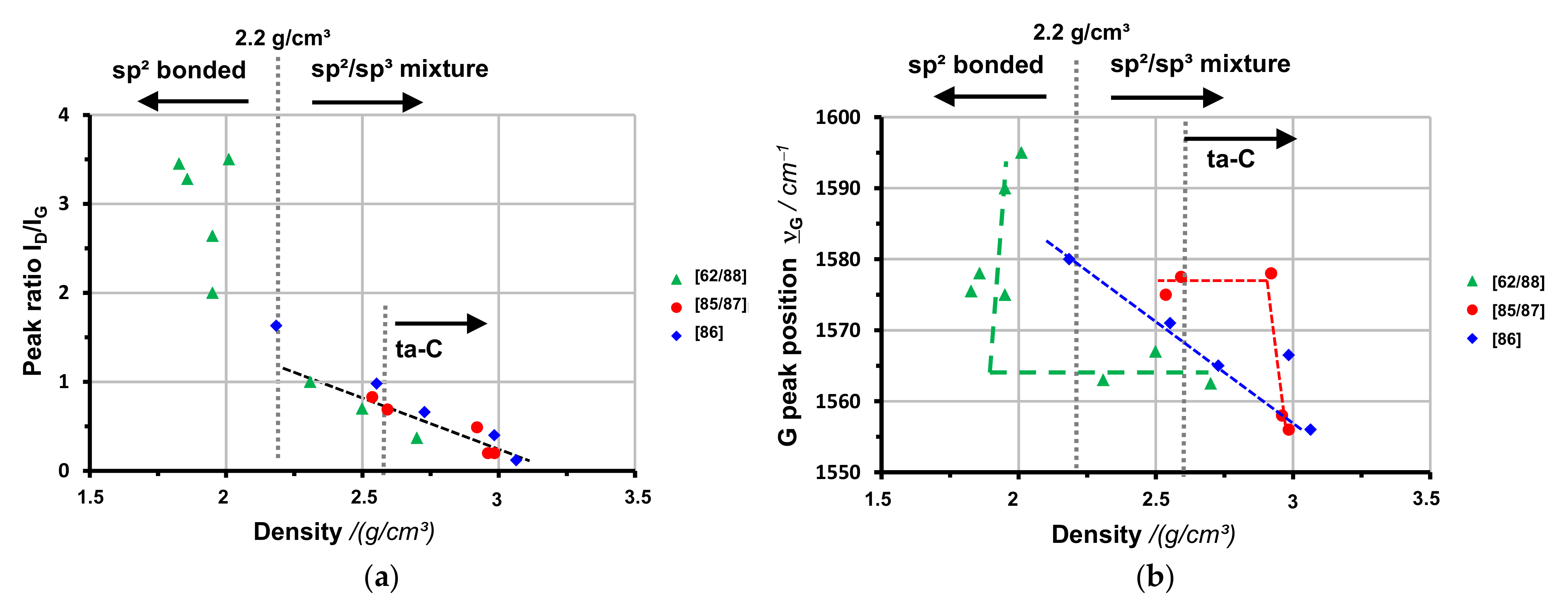
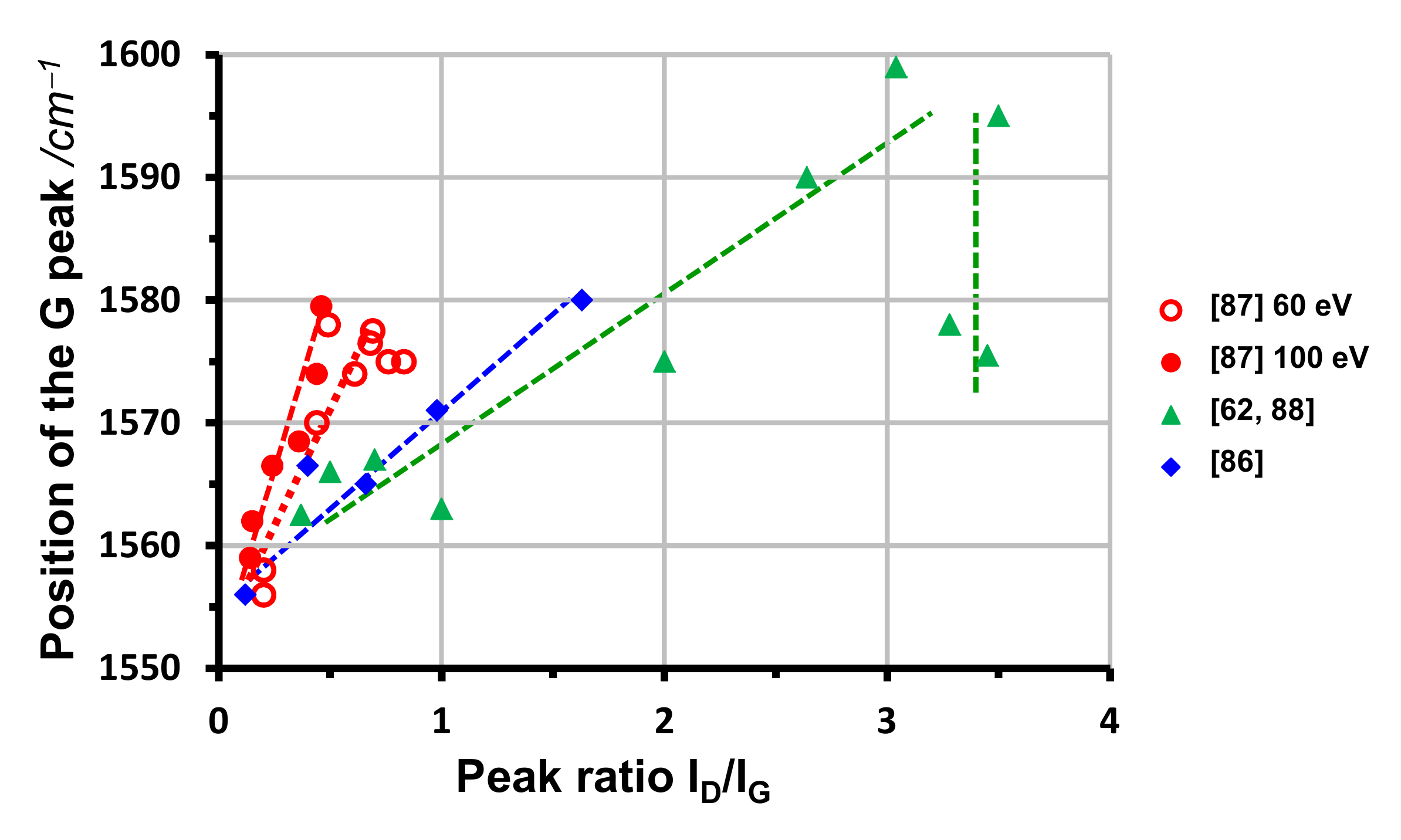
2.3. Raman Spectroscopy
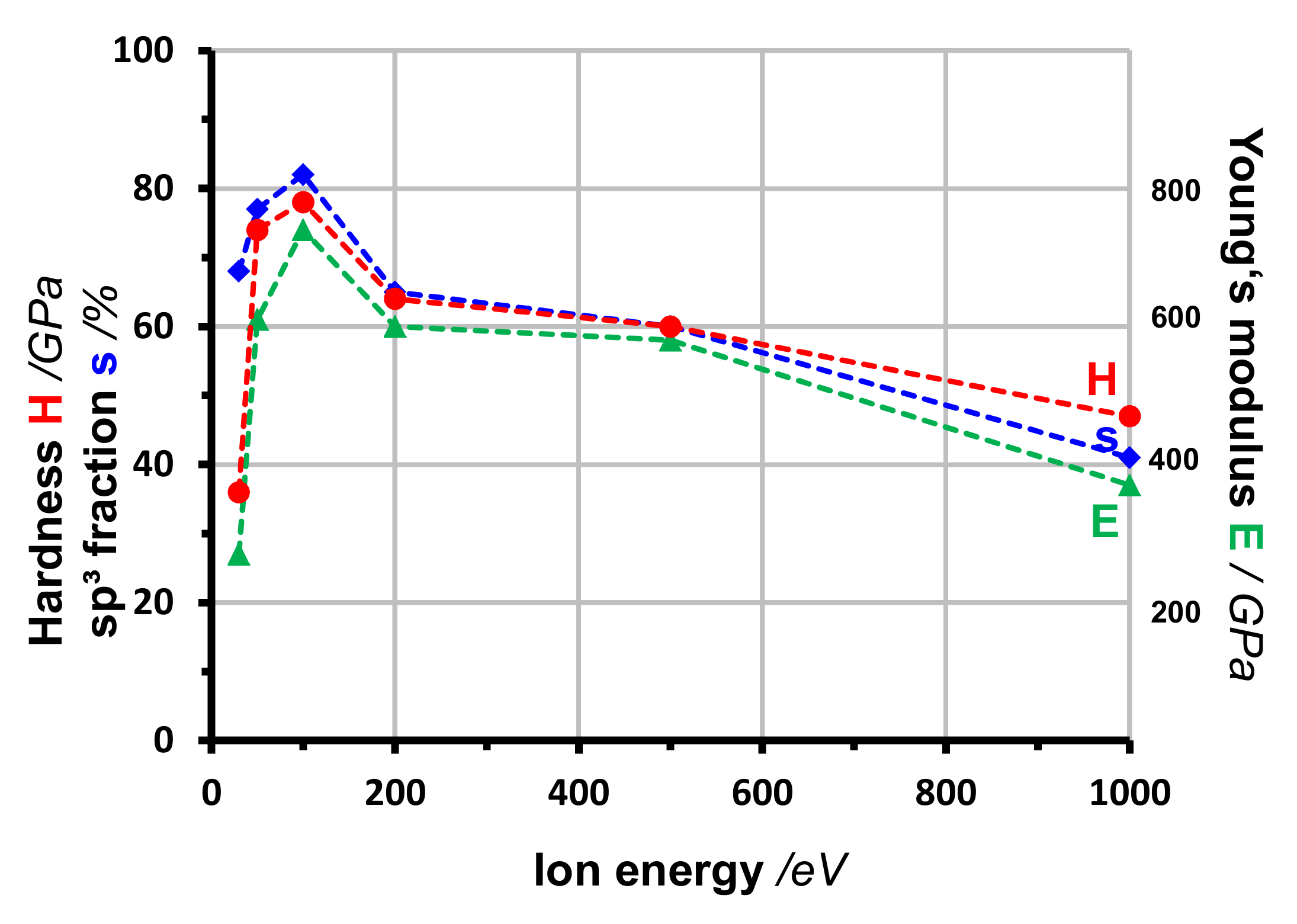
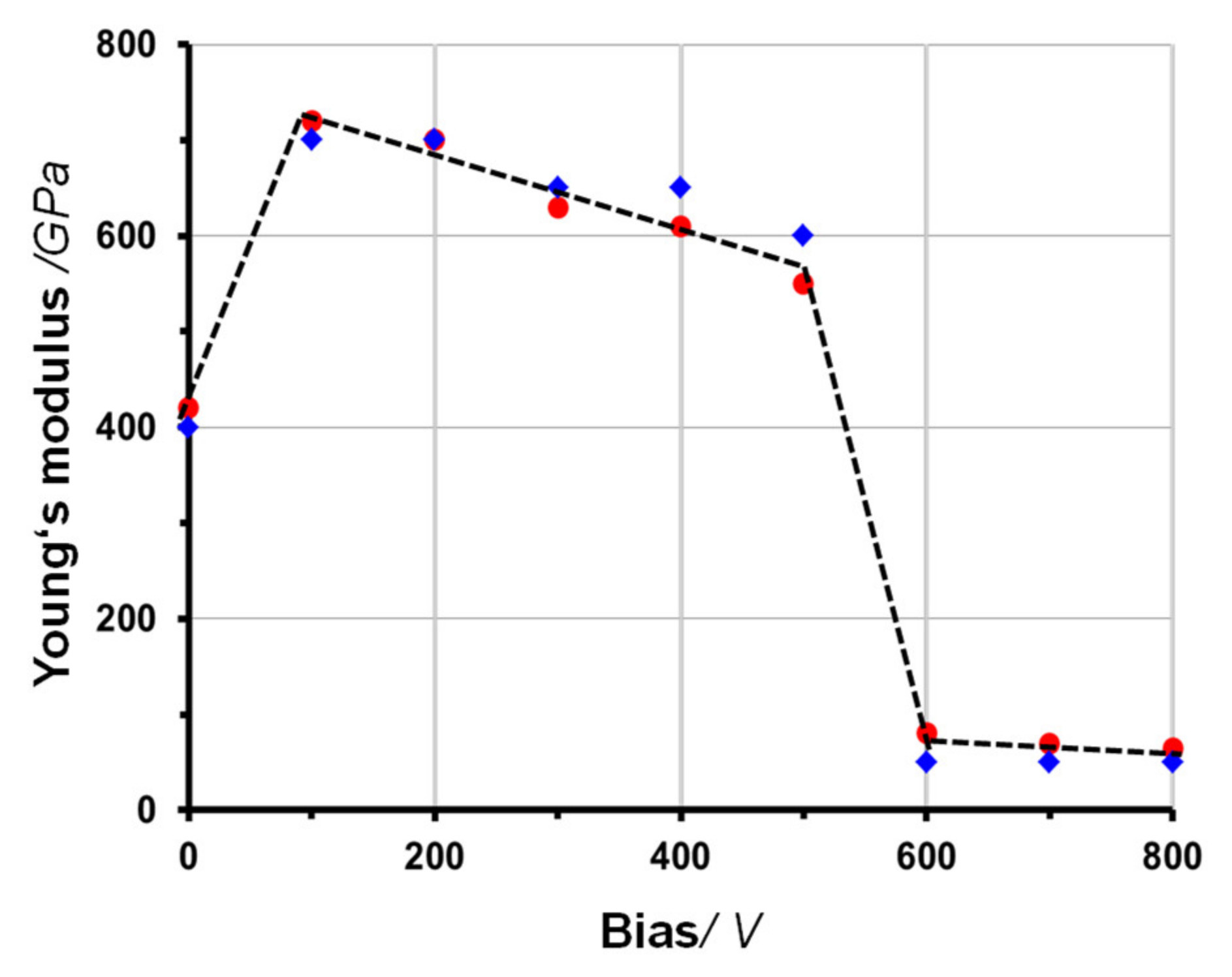
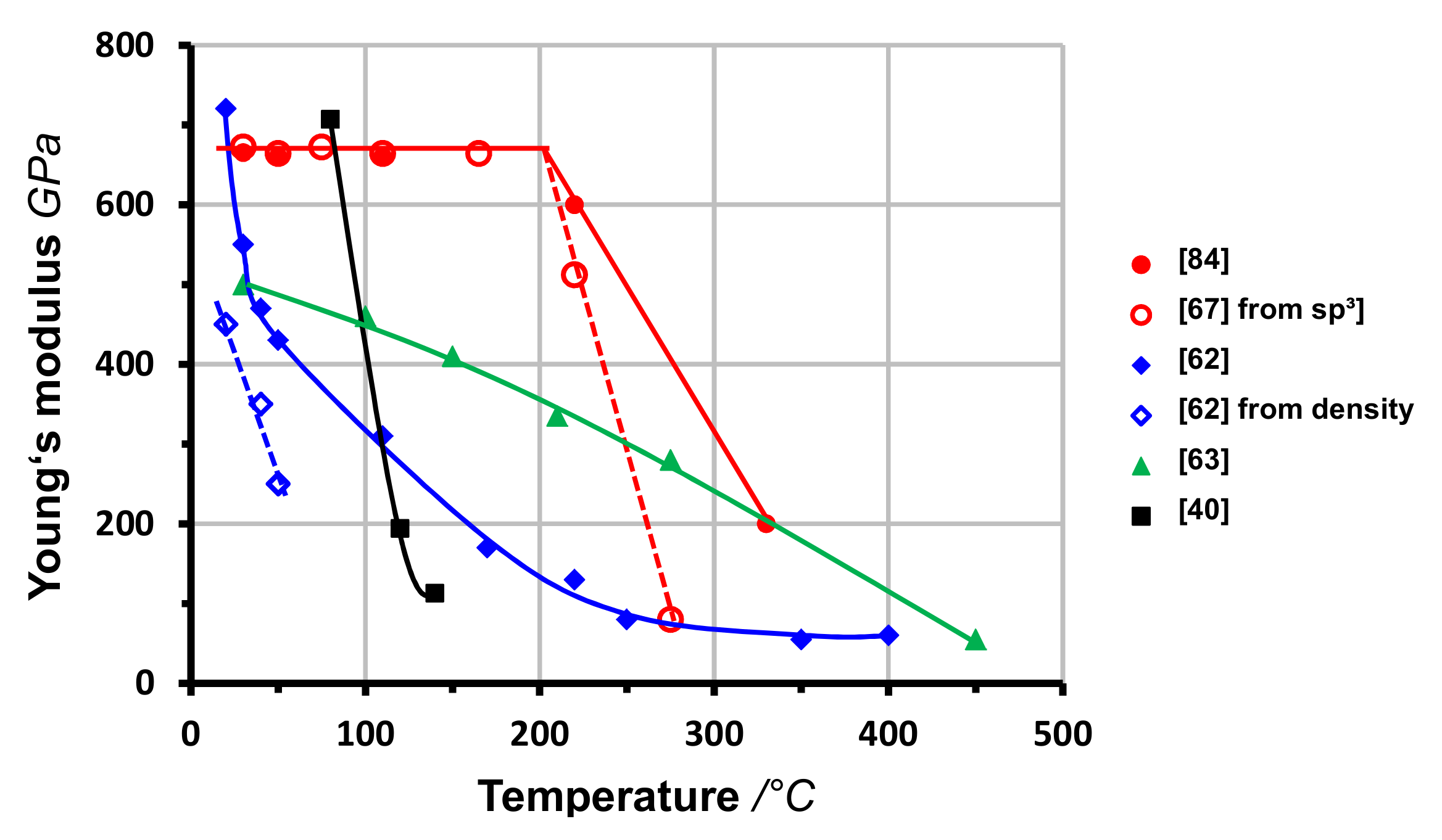
2.4. Young’s Modulus/Hardness
3. The Reference Case: Ion Beam Deposition
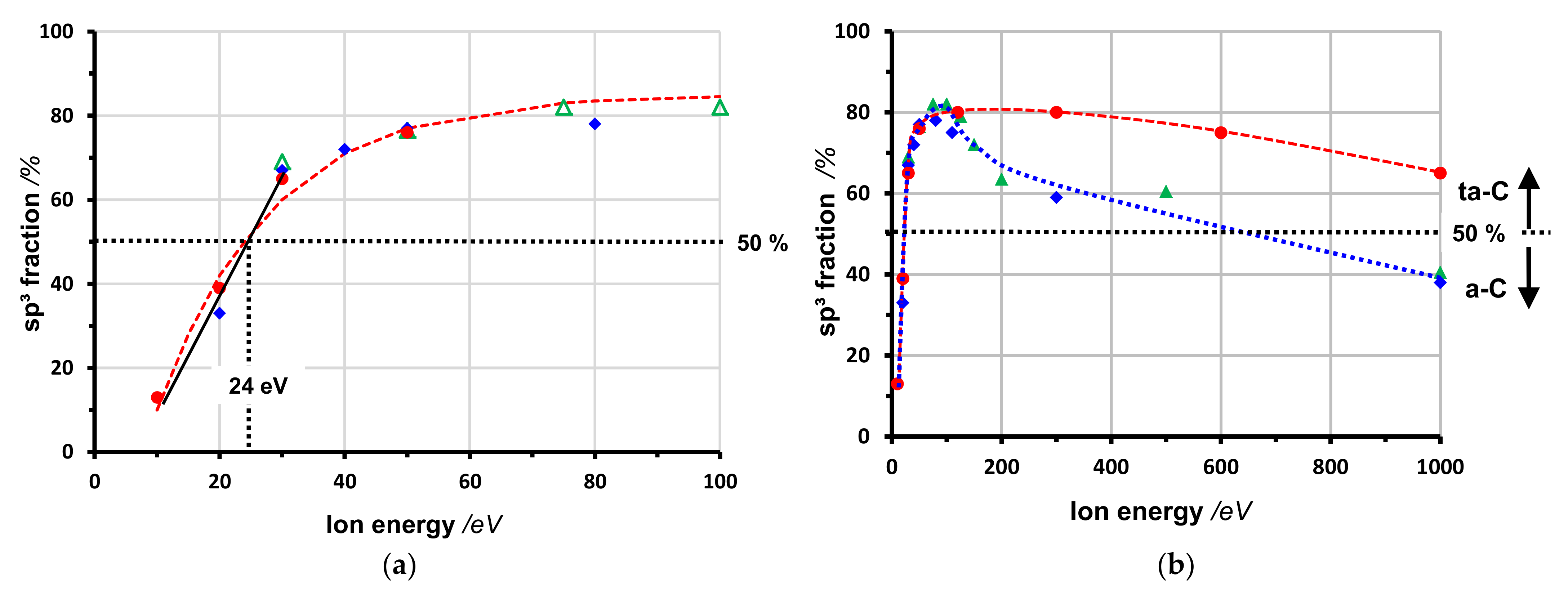
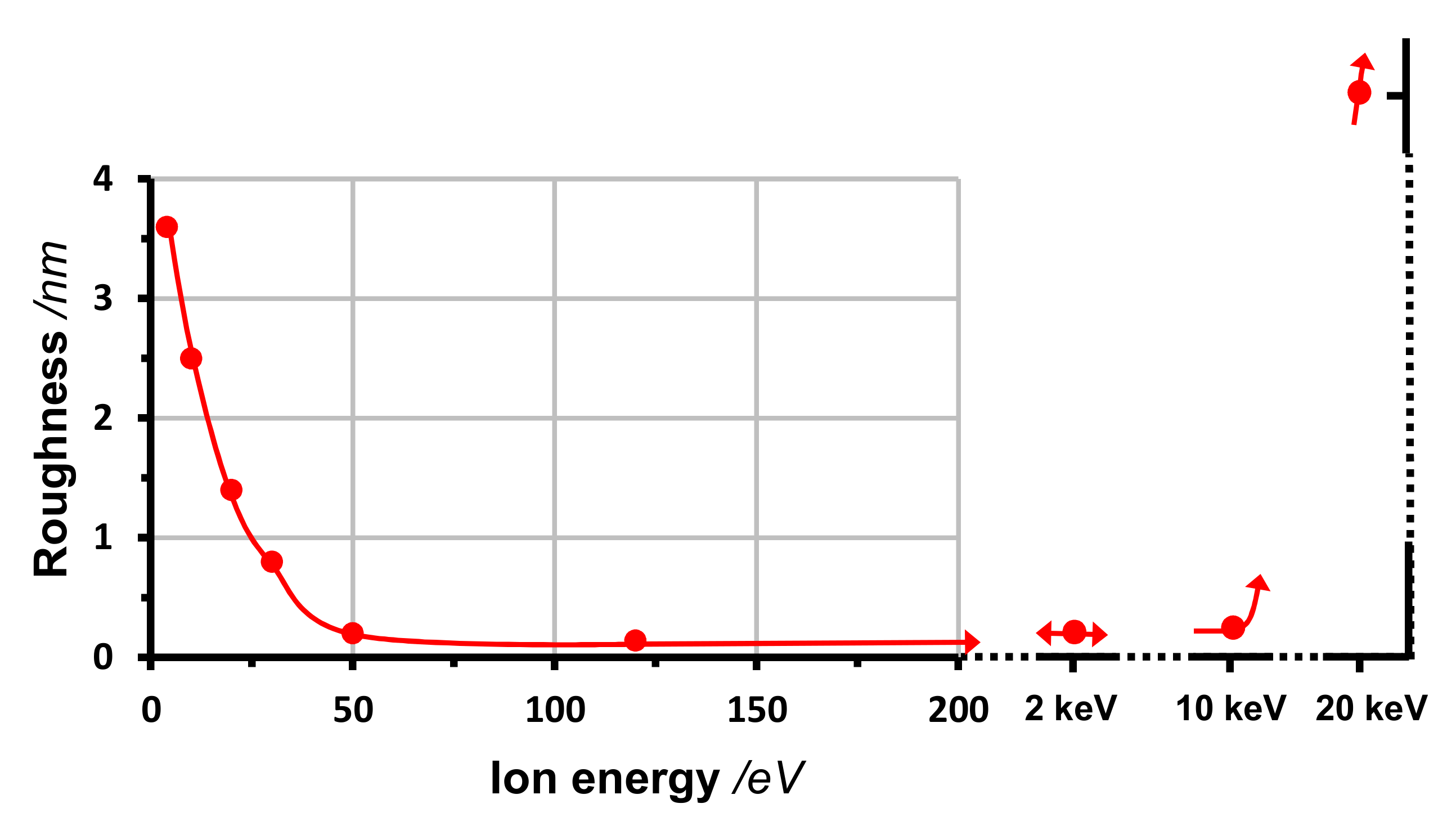
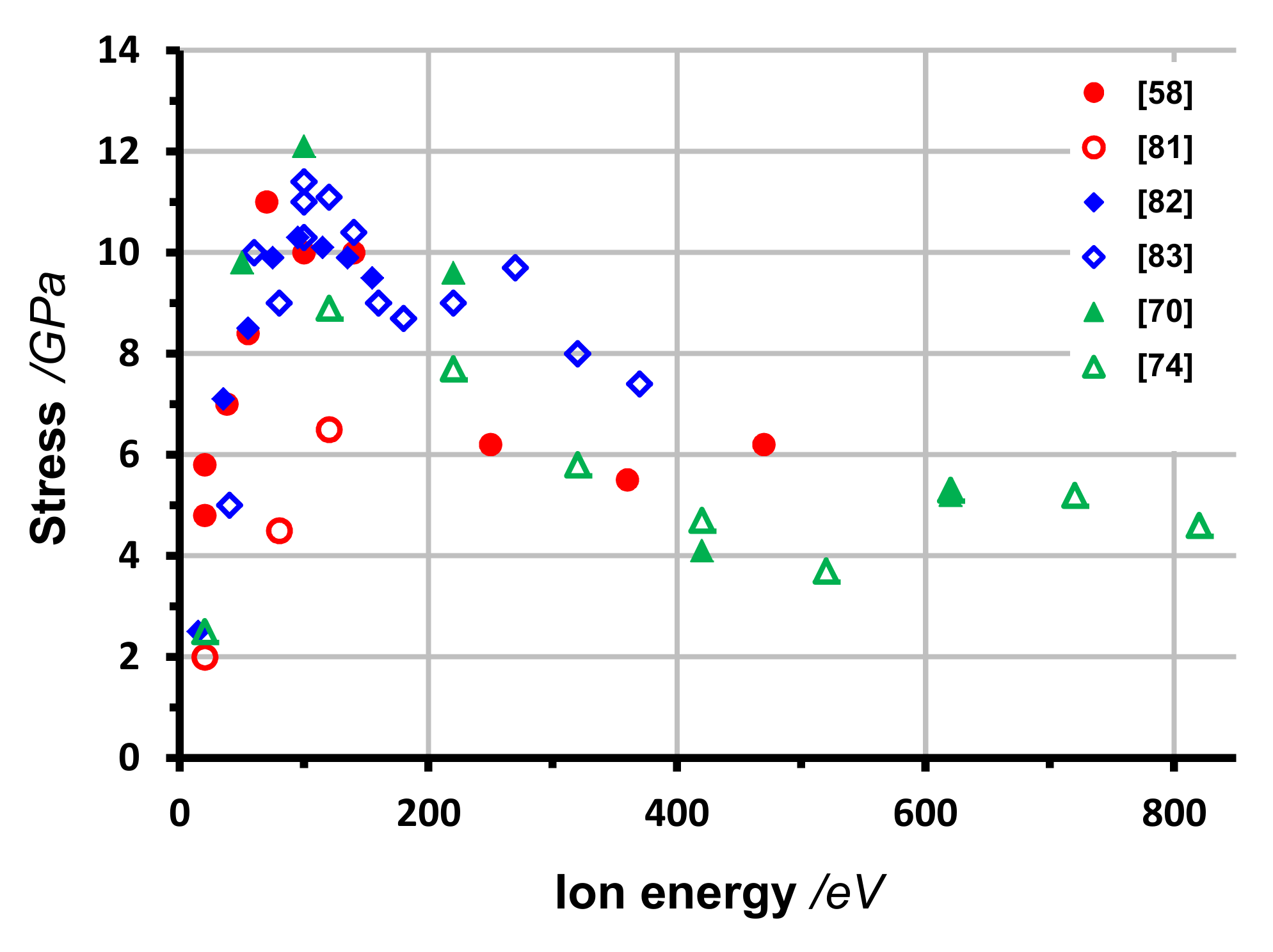
3.1. Ion Energy
≈ 0.1 + 0.75 {1 − exp(−(ε/eV − 10)/18)}
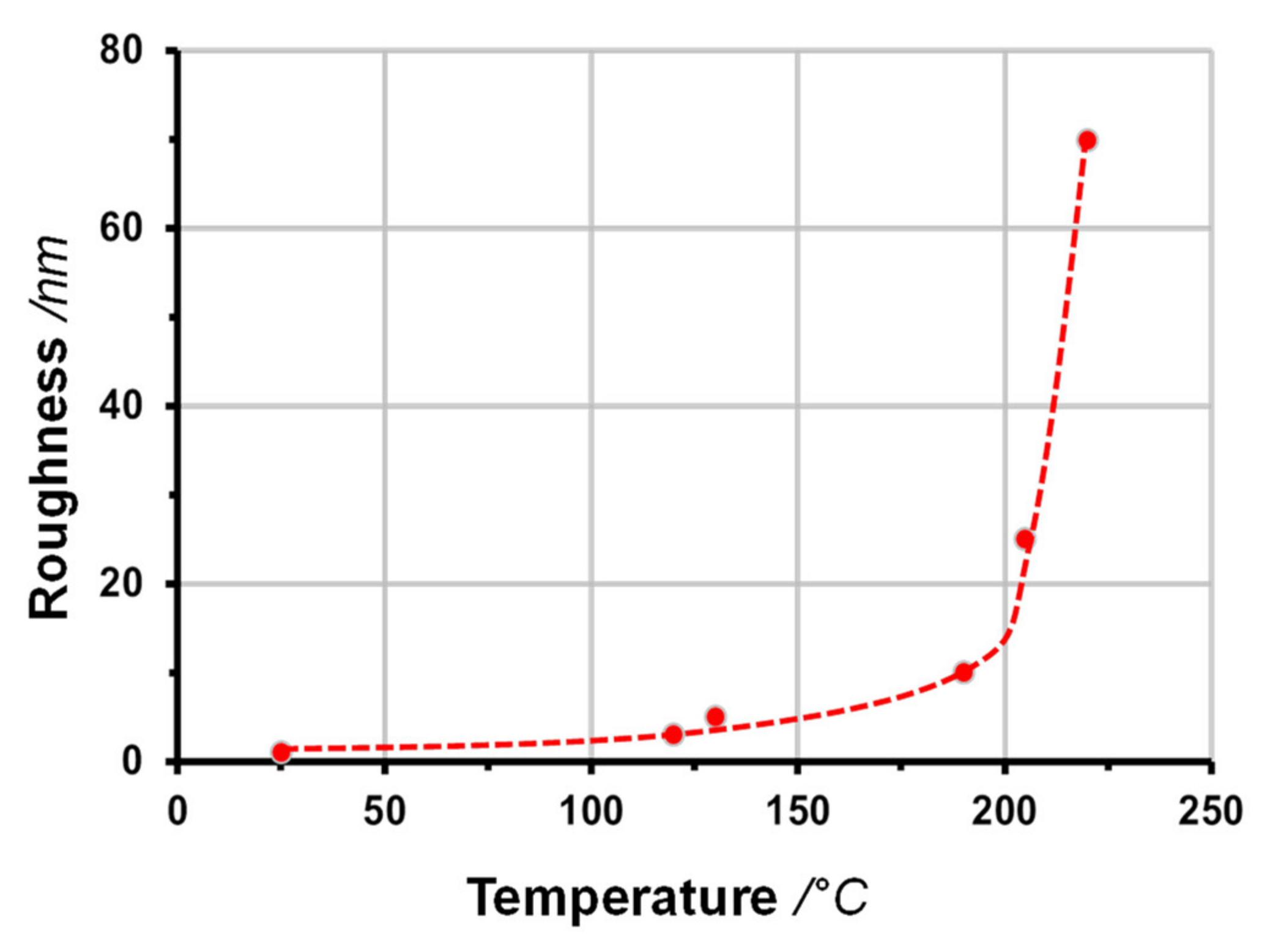
3.2. Deposition Temperature
4. Vacuum Arc Deposition
4.1. Deposition Conditions
- -
- dc arcs (arc current typically around 100 A) with strong magnetic fields and optimized cathode geometry;
- -
- pulsed arcs with high arc currents in the kiloampere range;
- -
- pulsed arcs with controllably displaced spot ignition (e.g., Laser-Arc);
- -
- separation of the macroparticles by curved magnetic fields (filtered arc).
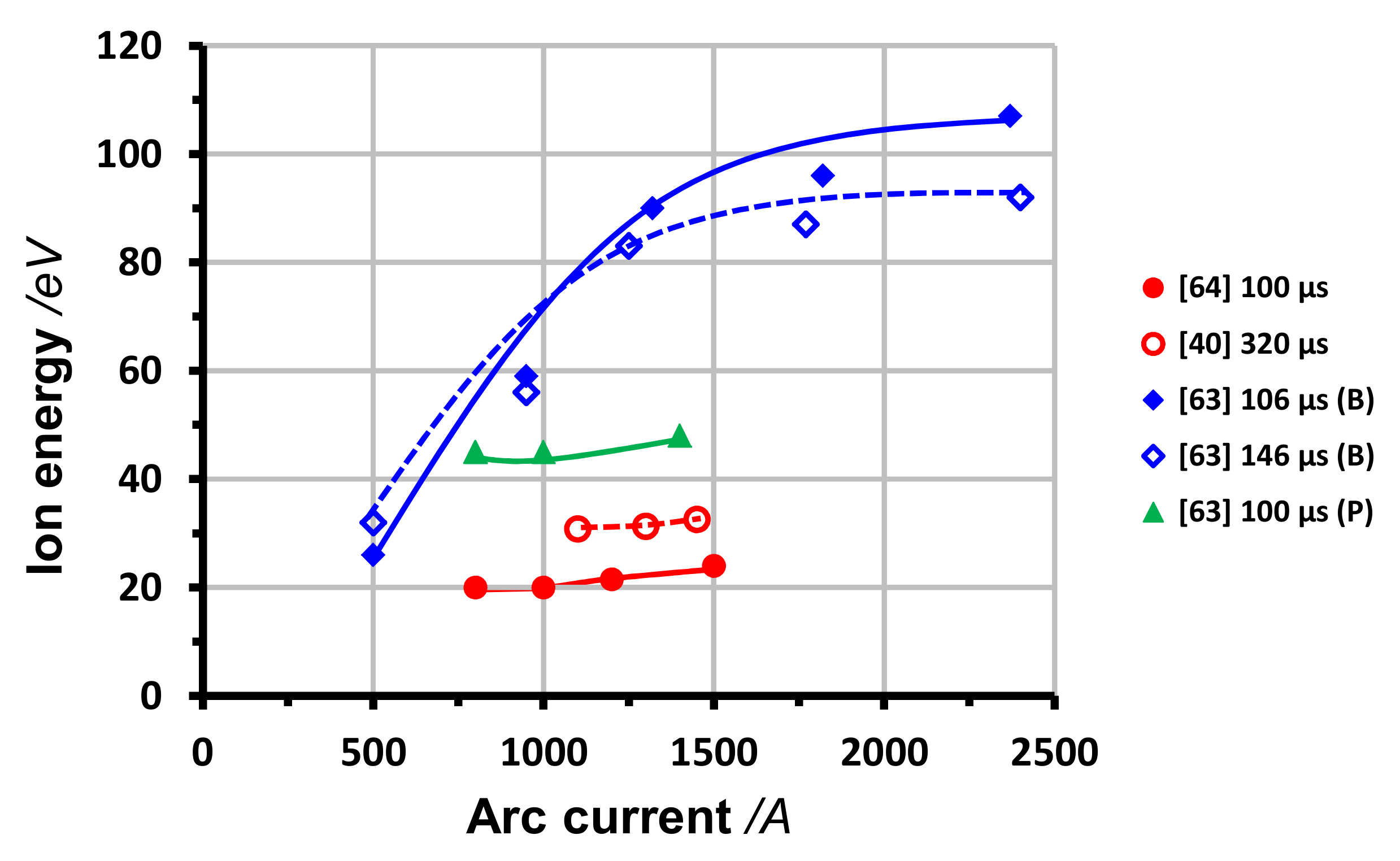
4.1.1. Ion Energy
- (1)
- The energy of the ions, impinging the substrate, is itself often not measured. Only the energy variation is controlled by the altered bias voltage. The additional energy on unbiased substrates is estimated, usually by about 20 eV, but may markedly deviates from this standard value.
- (2)
- Different widths of the energy distribution, especially the high-energy tail, may influence the film growth.
- (3)
- In the case of pulsed discharges and/or pulsed biasing, the instantaneous conditions vary during each pulse. They are only fragmentarily reflected by the mean ion energy.
- (4)
- Effects from an unintended substrate heating by the energetic ion flux may overlay the direct influence of higher ion energies.
4.1.2. Substrate Temperature
4.1.3. Further Factors
- -
- Inclined incidence: During the penetration of the energetic ions into the subsurface layer, they form transient sp3 bonds due to the local high-pressure conditions. However, the pressure gradient drives the carbon atoms towards the stress-free surface, so that they partially relax their bond state to sp2 [68]. Under inclined incidence with the angle ϑ against the surface normal, the penetration depth, i.e., the distance to the surface, is reduced by a factor cosϑ, thus shortening the diffusion path. Additionally, the superficial layer is damaged by the oblique ion tracks, stimulating the carbon mobility by means of the irradiation-induced diffusion. Inclined incidence occurs inevitably at the deposition of complex shaped parts and at the deposition with rotating substrate holders. In the latter case, the films represent a multilayer stack according to the periodically changing angle.
- -
- Deposition rate: Instantaneous very high deposition rates, as they are possible with pulsed high current arcs, limit the interval for structural relaxation. If they are combined with sufficient low repetition frequencies, additional heating by the intense ion impact can be minimized. For instance, for momentary rates of 1000 nm/s, the onset of the temperature-induced relaxation has been shifted from <200 °C up to 400 °C [69].
- -
- Hydrogen content: Hydrogen may be picked up from the residual gas, especially at only moderate base pressures and with larger carbon deposits in the deposition chamber. However, in the case of vacuum arc deposition, most of the entered hydrogen is again released by the intense ion bombardment. Usually the unintentionally incorporated hydrogen remains below 1–2% with a negligible influence on structure and properties.
- -
- Macroparticles: The graphitic macroparticles may not be completely eliminated from the plasma beam. Most of them are reflected, but some will be incorporated into the growing film. There they induce weakly embedded growth defects with a much larger volume. They may influence the film properties, especially the Raman spectra, the film roughness and the tribological behavior.
4.2. Ion Energy
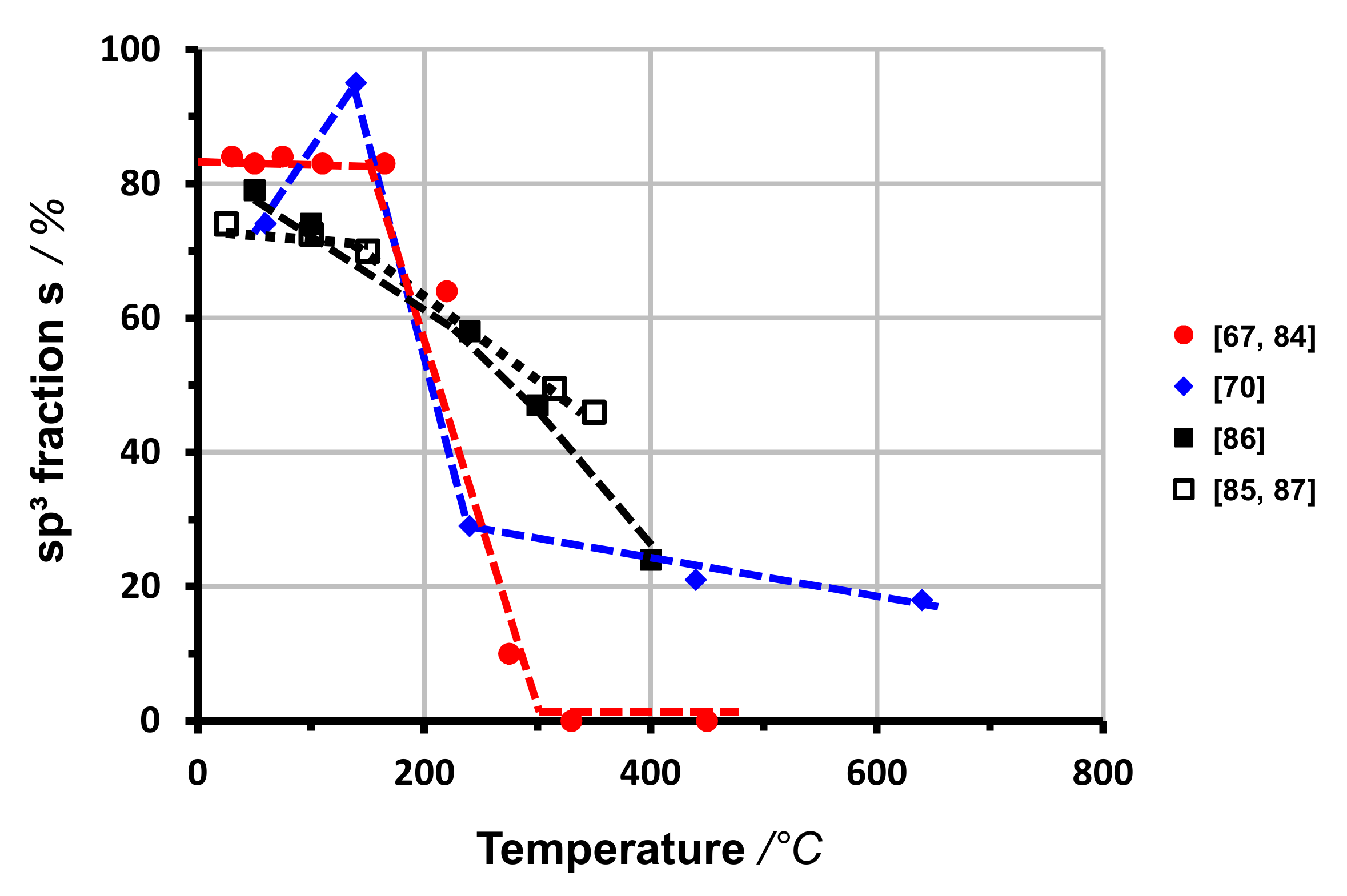
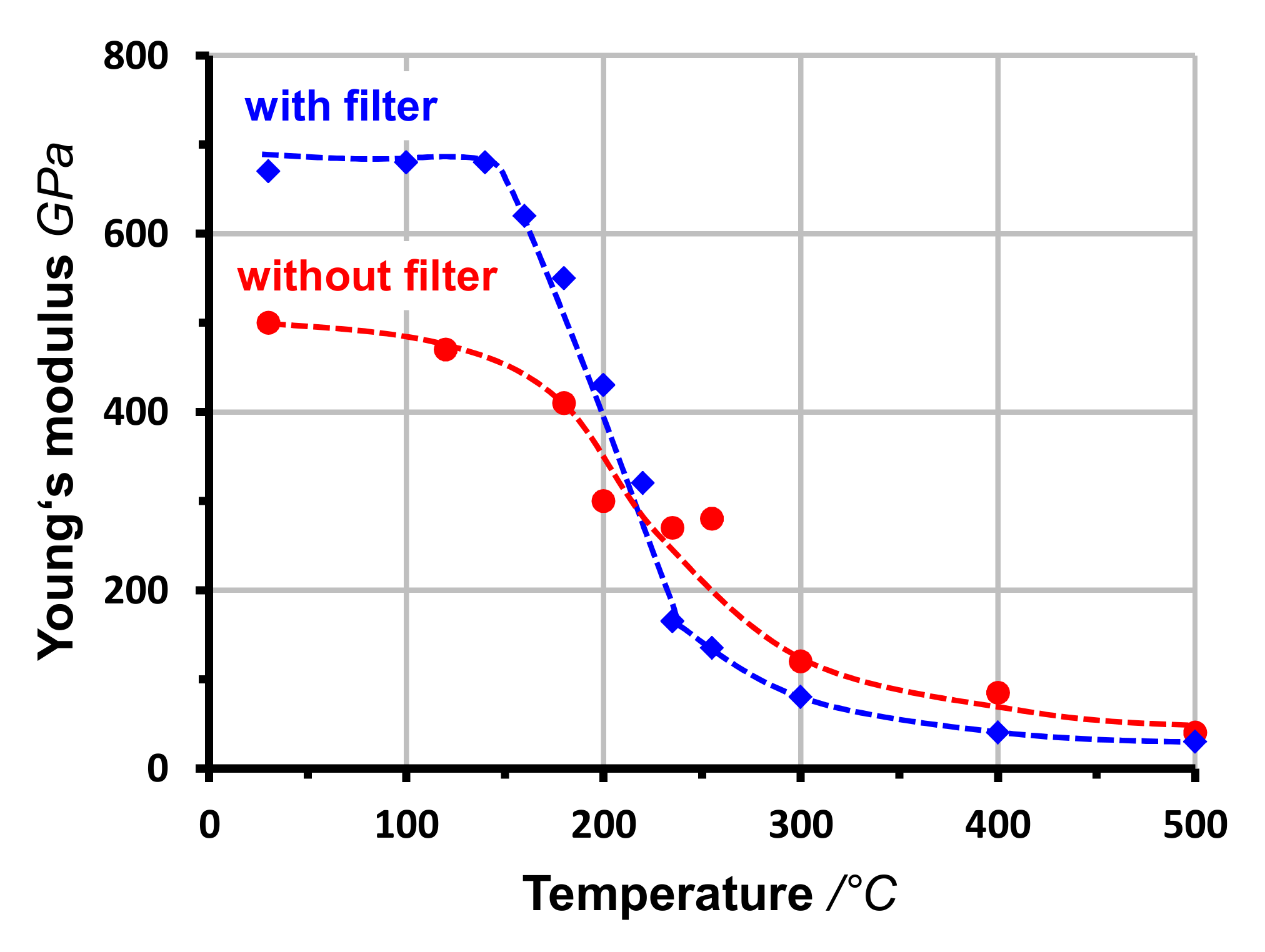
4.3. Deposition Temperature
- (1)
- The low temperature range below Tc with constant values of sp3 fraction s, density ρ, Young’s modulus E and stress σ. For varying ion energies, these quantities are related by Equations (1)–(4).
- (2)
- The transition range with strongly changing properties. The density decreases much more, and Young’s modulus and stress much less than it would expected according to the reduced sp3 fraction. Hence, the temperature-induced relaxation leads to other structures rather than the deposition with insufficient ion energies. The relations Equations (1)–(4) are not valid in the thermal transition range.
- (3)
- The high temperature range with nearly completely sp2-bonded films and constant density and stress.
- -
- High mean deposition rates, especially in combination with high ion energies, can lead to increasing temperatures in the surface region. The real deposition temperatures are then above the measured bulk temperatures. Hence, the observed critical substrate temperatures lie below the real surface values. The deposition induced surface heating is of especial importance for industrial technologies, where high deposition rates are usually an economic precondition.
- -
- Instantaneous very high deposition rates, as they are possible with pulsed high current arcs, limit the interval for structural relaxation. If they are combined with low repetition frequencies, additional heating by the ion impact can be avoided. For momentary rates of 1000 nm/s, critical temperatures Tc up to 400 °C have been realized [69].
- -
- The carbon ions in vacuum arc discharges are distributed over a certain energy range (Figure 9). Correspondingly, the transition may occur more gradually and extend over a broader temperature range.
5. Structure Map
- (1)
- Low ion energy deposition (≤10 eV)
- (2)
- Medium ion energy deposition (typically between 10 and 300 eV)
- (3)
- High ion energy deposition (typically between 300 and 500 eV)
- (4)
- Very high ion energy deposition (typically between 500 and 800 eV)
- (5)
- Ultrahigh ion energy deposition (typically above 800 eV)
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ferrari, A.C.; Robertson, J. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B 2000, 61, 14095–14107. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Robertson, J. Resonant Raman spectroscopy of disordered, amorphous and diamond-like carbon. Phys. Rev. B 2001, 64, 075414. [Google Scholar] [CrossRef]
- Schultrich, B. Tetrahedrally Bonded Amorphous Carbon Films I: Basics, Structure and Preparation; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Mößner, C.; Grant, P.; Tran, H.; Clarke, G.; Lockwood, D.J.; Labbe, H.J.; Mason, B.; Sproule, I. Characterization of diamond-like carbon by Raman spectroscopy, XPS and optical constants. Thin Solid Films 1998, 317, 397–401. [Google Scholar] [CrossRef]
- Robertson, J. Diamond-like amorphous carbon. Mater. Sci. Eng. R Rep. 2002, 37, 129–281. [Google Scholar] [CrossRef]
- Lifshitz, Y. Pitfalls in amorphous carbon studies. Diam. Relat. Mater. 2003, 12, 130–140. [Google Scholar] [CrossRef]
- Chu, P.K.; Li, L. Characterization of amorphous and nanocrystalline carbon films. Mater. Chem. Phys. 2006, 96, 253–277. [Google Scholar] [CrossRef]
- Ferrari, A.C. Non-destructive characterization of carbon films. In Tribology of Diamond-Like Carbon Films; Donnet, C., Erdemir, A., Eds.; Springer: Berlin, Germany, 2008; pp. 25–82. [Google Scholar]
- Ohtake, N.; Hiratsuka, M.; Kanda, K.; Akasaka, H.; Tsujioka, M.; Hirakuri, K.; Hirata, A.; Ohana, T.; Inaba, H.; Kano, M.; et al. Properties and classification of diamond-like carbon films. Materials 2021, 14, 315. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, A.C.; Libassi, A.; Tanner, B.K.; Stolojan, V.; Yuan, J.; Brown, L.M.; Rodil, S.E.; Kleinsorge, B.; Robertson, J. Density, sp³ fraction, and cross-sectional structure of amorphous carbon films determined by x-ray reflectivity and electron-energy-loss spectroscopy. Phys. Rev. B 2000, 62, 11089–11103. [Google Scholar] [CrossRef]
- Peng, J.L.; Fan, X.D.; Bursill, L.A. Combined HRTEM and PEELS analysis of nanoporous amorphous carbon. Int. J. Mod. Phys. B 1996, 10, 3875–3892. [Google Scholar] [CrossRef]
- Berger, S.D.; McKenzie, D.R.; Martin, P.J. EELS analysis of vacuum arc-deposited diamond-like films. Philos. Mag. Lett. 1988, 57, 285–290. [Google Scholar] [CrossRef]
- McKenzie, D.R.; Green, D.C.; Swift, P.D.; Cockayne, D.J.H.; Martin, P.J.; Netterfield, R.P.; Sainty, W.G. Electron optical techniques for microstructural and compositional analysis of thin films. Thin Solid Films 1990, 193, 418–430. [Google Scholar] [CrossRef]
- Kulik, J.; Lempert, G.D.; Grossmann, E.; Marton, D.; Rabalais, J.W.; Lifshitz, Y. sp³ content of mass-selected ion-beam-deposited carbon films determined by inelastic and elastic electron scattering. Phys. Rev. B 1995, 52, 15812–15822. [Google Scholar] [CrossRef] [PubMed]
- Papworth, A.J.; Kiely, C.J.; Burden, A.P.; Silva, S.R.P.; Amaratunga, G.A.J. Electron-energy-loss spectroscopy characterization of the sp2 bonding fraction within carbon thin films. Phys. Rev. B 2000, 62, 12628–12631. [Google Scholar] [CrossRef]
- Bernier, N.; Bocquet, F.; Allouche, A.; Saikaly, W.; Brosset, C.; Thibault, J.; Charaï, A. A methodology to optimize the quantification of sp2 carbon fraction from K edge EELS spectra. J. Electron. Spectrosc. Relat. Phenom. 2008, 164, 34–43. [Google Scholar] [CrossRef]
- Lifshitz, Y.; Lempert, G.D.; Rotter, S.; Avigal, I.; Uzan-Saguy, C.; Kalish, R.; Kulik, J.; Marton, D.; Rabalais, J.W. The effect of ion energy on the diamond-like/graphitic (sp³/sp²) nature of carbon films deposited by ion beams. Diam. Relat. Mater. 1994, 3, 542–546. [Google Scholar] [CrossRef]
- Merel, P.; Tabbal, M.; Chaker, M.; Moisa, S.; Margot, J. Direct evaluation of the sp3 content in diamond-like-carbon films by XPS. Appl. Surf. Sci. 1998, 136, 105–110. [Google Scholar] [CrossRef]
- Diaz, J.; Anders, S.; Zhou, X.; Moler, E.J.; Kellar, S.A.; Hussain, Z. Analysis of the π* and π* bands of the x-ray absorption spectrum of amorphous carbon. Phys. Rev. B 2001, 64, 125204. [Google Scholar] [CrossRef]
- Lesiak, B.; Kövér, L.; Tóth, J.; Zemek, J.; Jiricek, P.; Kromka, A.; Rangam, N.C. sp2/sp3 hybridisations in carbon nanomaterials—XPS and (X)AES study. Appl. Surf. Sci. 2018, 452, 223–231. [Google Scholar] [CrossRef]
- Reich, S.; Thomsen, C. Raman spectroscopy of graphite. Philos. Trans. R. Soc. A 2004, 362, 2271–2288. [Google Scholar] [CrossRef]
- Prawer, S.; Nugent, K.W.; Lifshitz, Y.; Lempert, G.D.; Grossman, E.; Kulik, J.; Avigal, I.; Kalish, R. Systematic variations of DLC films as a function of sp2:sp3 composition. Diam. Relat. Mater. 1996, 5, 433–438. [Google Scholar] [CrossRef]
- Ager, J.W.; Anders, S.; Anders, A.; Brown, I.G. Effect of intrinsic growth stress on the Raman spectra of vacuum-arc-deposited amorphous carbon films. Appl. Phys. Lett. 1995, 66, 3444–3446. [Google Scholar] [CrossRef]
- Shin, J.K.; Lee, C.S.; Lee, K.-R.; Eun, K.Y. Effect of the residual stress on the Raman-spectrum analysis of tetrahedral amorphous carbon films. Appl. Phys. Lett. 2001, 78, 631–633. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Kleinsorge, B.; Morrison, N.A.; Hart, A.; Stolojan, V.; Robertson, J. Stress reduction and bond stability during thermal annealing of tetrahedral amorphous carbon. J. Appl. Phys. 1999, 85, 7191–7197. [Google Scholar] [CrossRef]
- Tuinstra, F.; Koenig, J.L. Raman spectrum of graphite. J. Chem. Phys. 1970, 53, 1126–1130. [Google Scholar] [CrossRef]
- Knights, D.S.; White, W.B. Characterization of diamond films by Raman spectroscopy. J. Mater. Res. 1989, 4, 385–393. [Google Scholar] [CrossRef]
- Mallet-Ladeira, P.; Puech, P.; Toulouse, C.; Cazayous, M.; Ratel-Ramond, N.; Weisbecker, P.; Vignoles, G.L.; Monthioux, M. A Raman study to obtain crystallite size of carbon materials: A better alternative to the Tuinstra–Koenig law. Carbon 2014, 80, 629–639. [Google Scholar] [CrossRef]
- Cuesta, A.; Dhamelincourt, P.; Laureyns, J.; Martinez-Alonso, A.; Tascon, J.M.D. Comparative performance of X-ray diffraction and Raman microprobe techniques for the study of carbon materials. J. Mater. Chem. 1998, 8, 2875–2879. [Google Scholar] [CrossRef]
- Park, Y.S.; Cho, H.J.; Hong, B. Characteristics of conductive amorphous carbon (DLC) films prepared by using the magnetron sputtering method. J. Korean Phys. Soc. 2007, 51, 1119–1123. [Google Scholar] [CrossRef]
- Cho, N.H.; Krishnan, K.M.; Veirs, D.K.; Rubin, M.D.; Hopper, C.B.; Bhushan, B.; Bogy, D.B. Chemical structure and physical properties of diamond-like amorphous carbon films prepared by magnetron sputtering. J. Mater. Res. 1990, 5, 2543–2554. [Google Scholar] [CrossRef]
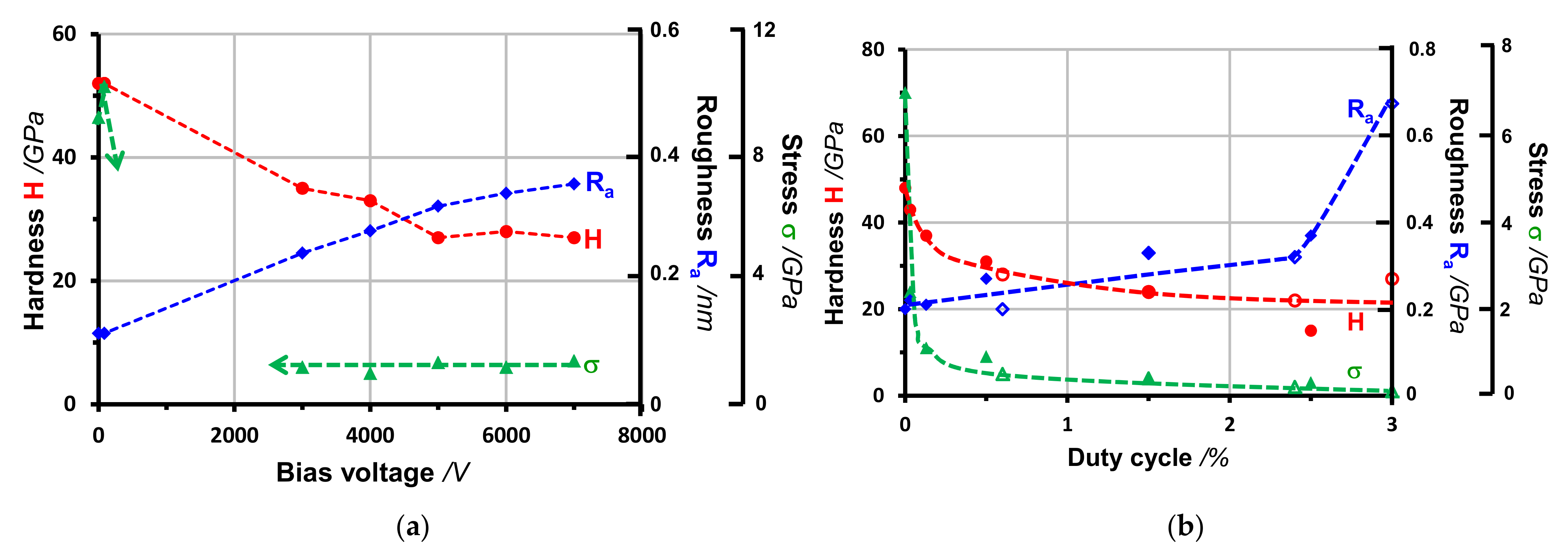
- Wang, Y.J.; Li, H.X.; Ji, L.; Zhao, F.; Liu, X.H.; Kong, Q.H.; Wang, Y.X.; Quan, W.L.; Zhou, H.D.; Chen, J.M. The effect of duty cycle on the microstructure and properties of graphite-like amorphous carbon films prepared by unbalanced magnetron sputtering. J. Phys. D 2010, 43, 505401. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Critical review of analysis and interpretation of nanoindentation test data. Surf. Coat. Technol. 2006, 200, 4153–4165. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Schneider, D.; Schwarz, T.; Schultrich, B. Determination of elastic modulus and thickness of surface layers by ultrasonic surface waves. Thin Solid Films 1992, 219, 92–102. [Google Scholar] [CrossRef]
- Schneider, D.; Schultrich, B. Elastic modulus: A suitable quantity for characterization of thin films. Surf. Coat. Technol. 1998, 98, 962–970. [Google Scholar] [CrossRef]
- Schneider, D. Laser induced surface acoustic waves for material testing. In Handbook of Advanced Nondestructive Evaluation; Ida, N., Meyendorf, N., Eds.; Springer: Cham, Switzerland, 2019; pp. 1–63. [Google Scholar]
- Kaulfuss, F.; Weihnacht, V.; Zawischa, M.; Lorenz, L.; Makowski, S.; Hofmann, F.; Leson, A. Effect of energy and temperature on tetrahedral amorphous carbon coatings deposited by filtered Laser-Arc. Materials 2021, 14, 2176. [Google Scholar] [CrossRef] [PubMed]
- Lau, W.M.; Bello, I.; Feng, X.; Huang, L.J.; Fuguang, Q.; Zhenyu, Y.; Zhizhang, R.; Lee, S.-T. Direct ion beam deposition of carbon films on silicon in the ion energy range of 15–500 eV. J. Appl. Phys. 1991, 70, 5623–5628. [Google Scholar] [CrossRef]
- Harkovirta, M.; Salo, J.; Lappalainen, R.; Anttila, A. Correlation of carbon ion energy with sp²/sp³ ratio in amorphous diamond films produced with a mass-separated ion beam. Phys. Lett. A 1995, 205, 287–289. [Google Scholar] [CrossRef]
- Lifshitz, Y.; Lempert, G.D.; Grossmann, E.; Avigal, I.; Uzan-Saguay, C.; Kalish, R.; Kulik, J.; Marton, D.; Rabalais, J.W. Growth mechanisms of DLC films from C+: Experimental studies. Diam. Relat. Mater. 1995, 4, 318–323. [Google Scholar] [CrossRef]
- Yamamoto, K.; Watanabe, T.; Wazumi, K.; Kokai, F.; Koga, Y.; Fujiwara, S. The sp3 bond fraction in carbon films prepared by mass-separated ion beam deposition. Diam. Relat. Mater. 2001, 10, 895–899. [Google Scholar] [CrossRef]
- Grossmann, E.; Lempert, G.D.; Kulik, J.; Marton, D.; Rabalais, J.W.; Lifshitz, Y. Role of ion energy in determination on the sp3 fraction of ion beam deposited carbon films. Appl. Phys. Lett. 1996, 68, 1214–1216. [Google Scholar] [CrossRef]
- Teo, E.H.T.; Kulik, J.; Kauffmann, Y.; Kalish, R.; Lifshitz, Y. Nanostructured carbon films with oriented graphitic planes. Appl. Phys. Lett. 2011, 98, 123104. [Google Scholar] [CrossRef]
- Yamamoto, K.; Wazumi, K.; Watanabe, T.; Koga, Y.; Iijima, S. Tribological properties of diamond-like carbon films prepared by mass-separated ion beam deposition. Diam. Relat. Mater. 2002, 11, 1130–1134. [Google Scholar] [CrossRef]
- Lifshitz, Y.; Lempert, G.D.; Grossman, E. Substantiation of subplantation model for diamondlike film growth by atomic force microscopy. Phys. Rev. Lett. 1994, 72, 2753–2757. [Google Scholar] [CrossRef]
- Yamamoto, K.; Watanabe, T.; Wazumi, K.; Koga, Y.; Iijima, S. Effect of substrate temperature on the structure. and chemical bonds of carbon films deposited with a mass-separated carbon ion beam. Diam. Relat. Mater. 2003, 12, 2088–2092. [Google Scholar] [CrossRef]
- Kulik, J.; Lempert, G.D.; Grossman, E.; Lifshitz, Y. Oriented graphitic carbon film grown by mass-selected ion beam deposition at elevated temperatures. In Amorphous and Nanostructured Carbon; Sullivan, J.P., Robertson, J., Zhou, G., Allen, T.B., Coll, B.F., Eds.; MRS Symposia Proceedings; MRS: Pittsburgh, PA, USA, 2000; Volume 593, pp. 305–310. [Google Scholar]
- Peng, H.Y.; Wang, N.; Zheng, Y.F.; Lifshitz, Y.; Kulik, J.; Zhang, C.S.; Lee, S.T. Smallest diameter carbon nanotubes. Appl. Phys. Lett. 2000, 77, 2831–2833. [Google Scholar] [CrossRef]
- Lifshitz, Y. Growth of a-C films using energetic species: Amorphous, nanotubes, and crystalline. In Dekker Encyclopedia of Nanoscience and Nanotechnology; Schwarz, J.A., Contescu, C.I., Putyera, K., Eds.; Dekker: New York, NY, USA, 2004; Volume 1, pp. 415–424. [Google Scholar]
- Schneider, D.; Meyer, C.F.; Mai, H.; Schöneich, B.; Ziegele, H.; Scheibe, H.J.; Lifshitz, Y. Non-destructive characterization of mechanical and structural properties of amorphous diamond-like carbon. Diam. Relat. Mater. 1998, 7, 973–980. [Google Scholar] [CrossRef]
- Anders, A.; Yushkov, G.Y. Ion flux from vacuum arc cathode spots in the absence and presence of a magnetic field. J. Appl. Phys. 2002, 91, 4824–4832. [Google Scholar] [CrossRef]
- Anders, A.; Yushkov, G.Y. The kinetic energy of carbon ions in vacuum arc plasmas: A comparison of measuring techniques. J. Appl. Phys. 2004, 96, 970–974. [Google Scholar] [CrossRef]
- Shi, X.; Tay, B.K.; Flynn, D.I.; Ye, Q.; Sun, Z. Characterization of filtered cathodic vacuum arc system. Surf. Coat. Technol. 1997, 94–95, 195–200. [Google Scholar] [CrossRef]
- Anders, A.; Pasaja, N.; Lim, S.H.N.; Petersen, T.C.; Keast, V.J. Plasma biasing to control the growth conditions of diamond-like carbon. Surf. Coat. Technol. 2007, 201, 4628–4632. [Google Scholar] [CrossRef][Green Version]
- Fallon, P.J.; Veerasamy, V.S.; Davis, C.A.; Robertson, J.; Amaratunga, G.A.J.; Milne, W.I.; Koskinen, J. Properties of filtered-ion-beam-deposited diamondlike carbon as a function of ion energy. Phys. Rev. B 1993, 48, 4777–4782, Erratum in Phys. Rev. B 1994, 49, 2287. [Google Scholar] [CrossRef]
- Anders, A. Energetics of vacuum arc cathode spots. Appl. Phys. Lett. 2001, 78, 2837–2839. [Google Scholar] [CrossRef]
- Tiainen, V.-M.; Alakoski, E.; Kiuru, M.; Soininen, A.; Anttila, A. Energies and charge-state fractions of carbon plasma ions measured with Doppler-shifts in the pulsed arc-discharge system. Eur. Phys. J. Appl. Phys. 2003, 22, 111–114. [Google Scholar] [CrossRef]
- Alakoski, E.; Tiainen, V.-M. Energy dependence of the carbon plasma beam on the arc voltage and the anode-cathode distance in the pulsed arc discharge method. Diam. Relat. Mater. 2005, 14, 1451–1454. [Google Scholar] [CrossRef]
- Drescher, D. Grundprozesse beim LASER-ARC-Beschichtungsverfahren und ihr Einfluß auf Struktur und Eigenschaften diamantähnlicher Kohlenstoffschichten. (= Basic Processes of the LASER-ARC Deposition Method and Their Influence on Structure And Properties of Diamondlike Carbon Films). Ph.D. Thesis, University Chemnitz-Zwickau, Chemnitz, Germany, 1996. [Google Scholar]
- Schulz, H. Amorphe Kohlenstoffschichten hergestellt mittels Laser-Arc Verfahren unter besonderer Berücksichtigung der Oberflächentopographie zur Herstellung superhydrophober Oberflächen. (= Amorphous Carbon Films Prepared by Means of Laser-Arc Method with Particular Consideration of the Surface Topography for the Preparation of Superhydrophobe Surfaces.); Fraunhofer IWS: Dresden, Germany, 2005; Unpublished work. [Google Scholar]
- Ziegele, H. Mechanische Eigenschaften von Schichtsystemen aus Amorphem Kohlenstoff. (= Mechanical properties of films Systems of Amorphous Carbon). Ph.D. Thesis, University Braunschweig, Braunschweig, Germany, 2001. Fraunhofer IRB Verlag, Stuttgart. [Google Scholar]
- Davis, W.D.; Miller, H.C. Analysis of the electrode products emitted by dc arcs in a vacuum ambient. J. Appl. Phys. 1969, 40, 2212–2221. [Google Scholar] [CrossRef]
- Kutzner, J.; Miller, H.C. Integrated ion flux emitted from the cathode spot region of a diffuse vacuum arc. J. Phys. D Appl. Phys. 1992, 25, 686–693. [Google Scholar] [CrossRef]
- Chhowalla, M.; Robertson, J.; Chen, C.W.; Silva, S.R.P.; Davis, C.A.; Amaratunga, G.A.J.; Milne, W.I. Influence of ion energy and substrate temperature on the optical and electronic properties of tetrahedral amorphous carbon (ta-C) films. J. Appl. Phys. 1997, 81, 139–145. [Google Scholar] [CrossRef]
- Schultrich, B. Modeling of ta-C growth: Influence of the technological parameters. Diam. Relat. Mater. 2011, 20, 785–792. [Google Scholar] [CrossRef]
- Koskinen, J.; Hirvonen, J.-P.; Keränen, J. Effect of deposition temperature and growth rate on the bond structure of hydrogen free carbon films. J. Appl. Phys. 1998, 84, 648–650. [Google Scholar] [CrossRef]
- Lau, D.W.M.; Moafi, A.; Taylor, M.B.; Partridge, J.G.; McCulloch, D.G.; Powles, R.C.; McKenzie, D.R. The structural phases of non-crystalline carbon prepared by physical vapour deposition. Carbon 2009, 47, 3263–3270. [Google Scholar] [CrossRef]
- Gerstner, E.G.; Lukins, P.; McKenzie, D.R.; McCulloch, D. Substrate bias effects on the structural and electronic properties of tetrahedral amorphous carbon. Phys. Rev. B 1996, 54, 14504–14510. [Google Scholar] [CrossRef]
- Silva, S.R.P.; Shi, X.; Tay, B.K.; Tan, H.S.; Milne, W.I. Nanocrystallites in tetrahedral amorphous carbon films. Appl. Phys. Lett. 1996, 69, 491–493. [Google Scholar] [CrossRef]
- Pharr, G.; Callahan, D.; McAdams, S.; Tsui, T.; Anders, S.; Anders, A.; Ager, J.; Brown, I.; Bhatia, C.; Silva, S.; et al. Hardness, elastic modulus, and structure of very hard carbon films produced by cathodic-arc deposition with substrate pulse biasing. Appl. Phys. Lett. 1996, 68, 779–781. [Google Scholar] [CrossRef]
- Englberger, G. Entwicklung einer Neuartigen Plasmafiltertechnik für die Abscheidung Defektarmer Superharter Kohlenstoffschichten (= Development of a New Plasma Filtering Technique for the Deposition of Low Defect Superhard Carbon Films). Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2018. [Google Scholar]
- Davis, C.A. A simple model for the formation of compressive stress in thin films by ion bombardment. Thin Solid Films 1993, 226, 30–34. [Google Scholar] [CrossRef]
- Robertson, J. Deposition mechanisms for promoting sp³ bonding in diamond-like carbon. Diam. Relat. Mater. 1993, 2, 984–989. [Google Scholar] [CrossRef]
- Sheeja, D.; Tay, B.K.; Lau, S.P.; Shi, X. Tribological properties and adhesive strength of DLC coatings prepared under different substrate bias voltages. Wear 2001, 249, 433–439. [Google Scholar] [CrossRef]
- Sheeja, D.; Tay, B.K.; Yu, L.J.; Lau, S.P.; Sze, J.Y.; Cheong, C.K. Effect of frequency and pulse width on the properties of ta:C films prepared by FCVA together with substrate pulse biasing. Thin Solid Films 2002, 420, 62–69. [Google Scholar] [CrossRef]
- Sze, J.Y.; Tay, B.K.; Sheeja, D.; Lau, S.P.; Chua, D.H.C.; Fu, Y.Q.; Milne, W.I. Optical and electrical properties of amorphous carbon films deposited using filtered cathodic vacuum arc with pulse biasing. Thin Solid Films 2004, 447–448, 148–152. [Google Scholar] [CrossRef]
- Lau, D.W.M.; McCulloch, D.G.; Taylor, M.B.; Partridge, J.G.; Marks, N.A.; McKenzie, D.R.; Teo, E.H.T.; Tay, B.K. Abrupt stress induced transformation in amorphous carbon films with a highly conductive transition phase. Phys. Rev. Lett. 2008, 100, 176101. [Google Scholar] [CrossRef]
- Veerasamy, V.S.; Amaratunga, G.A.J.; Milne, W.I.; Robertson, J.; Fallon, P.J. Influence of carbon ion energy on properties of highly tetrahedral diamond-like carbon. J. Non-Cryst. Solids 1993, 164–166, 1111–1114. [Google Scholar] [CrossRef]
- Shi, X.; Tay, B.K.; Tan, H.S.; Zhong, L.; Tu, Y.Q.; Silva, S.R.P.; Milne, W.I. Properties of carbon ion deposited tetrahedral amorphous carbon films as a function of ion energy. J. Appl. Phys. 1996, 79, 7234–7240. [Google Scholar]
- Polo, M.C.; Andujar, J.-L.; Hart, A.; Robertson, J.; Milne, W.I. Preparation of tetrahedral amorphous carbon films by filtered cathodic vacuum arc deposition. Diam. Relat. Mater. 2000, 9, 663–667. [Google Scholar] [CrossRef]
- Chhowalla, M.; Ferrari, A.C.; Robertson, J.; Amaratunga, G.A.J. Evolution of sp2 bonding with deposition temperature in tetrahedral amorphous carbon (ta-C) studied by Raman spectroscopy. Appl. Phys. Lett. 2000, 76, 1419–1421. [Google Scholar] [CrossRef]
- Tay, B.K.; Shi, X.; Tan, H.S.; Chua, D.H.C. Investigation of tetrahedral amorphous carbon films using X-ray photoelectron and Raman spectroscopy. Surf. Interface Anal. 1999, 28, 231–234. [Google Scholar] [CrossRef]
- Gago, R.; Vinnichenko, M.; Jäger, H.U.; Belov, A.Y.; Jiménez, I.; Huang, N.; Sun, H.; Maitz, M.F. Evolution of sp² networks with substrate temperature in amorphous carbon films: Experiment and theory. Phys. Rev. B 2005, 72, 014120. [Google Scholar] [CrossRef]
- Tay, B.K.; Shi, X.; Liu, E.J.; Tan, H.S.; Cheah, L.K. Effects of substrate temperature on the properties of tetrahedral amorphous carbon films. Thin Solid Films 1999, 346, 155–161. [Google Scholar] [CrossRef]
- Schultrich, B.; Scheibe, H.-J.; Drescher, D.; Ziegele, H. Deposition of superhard amorphous carbon films by pulsed vacuum arc deposition. Surf. Coat. Technol. 1998, 98, 1097–1101. [Google Scholar] [CrossRef]
- McKenzie, D.R. Generation and applications of compressive stress induced by low energy ion beam bombardment. J. Vac. Sci. Technol. B 1993, 11, 1928–1935. [Google Scholar] [CrossRef]
- Yin, Y.; Zhou, J.; McKenzie, D.R. Preferred orientation in carbon films induced by energetic condensation. Nucl. Instrum. Methods Phys. Res. B 1996, 119, 587–590. [Google Scholar] [CrossRef]
- Davis, C.A.; Amaratunga, G.A.J.; Knowles, K.M. Growth mechanism and cross-sectional structure of tetrahedral amorphous carbon thin films. Phys. Rev. Lett. 1998, 80, 3280–3283. [Google Scholar] [CrossRef]
- Kracica, M.; Kocer, C.; Lau, D.W.M.; Partridge, J.G.; Bradby, J.E.; Haberl, B.; McKenzie, D.R.; McCulloch, D.G. The mechanical properties of energetically deposited non-crystalline carbon thin films. Carbon 2016, 98, 391–396. [Google Scholar] [CrossRef]
- Tan, C.W.; Maziar, S.; Teo, E.H.T.; Tay, B.K. Microstructure and through-film electrical characteristics of vertically aligned amorphous carbon films. Diam. Relat. Mater. 2011, 20, 290–293. [Google Scholar] [CrossRef]
- Tucker, M.D.; Czigany, Z.; Broitman, E.; Näslund, L.-A.; Hultman, L.; Rosen, J. Filtered pulsed cathodic arc deposition of fullerene-like carbon and carbon nitride films. J. Appl. Phys. 2014, 115, 144312. [Google Scholar] [CrossRef]
- Lux, H.; Siemroth, P.; Sgarlata, A.; Prosposito, P.; Schubert, M.A.; Casalboni, M.; Schrader, S. Synthesis of graphene-like transparent conductive films on dielectric substrates using a modified filtered vacuum arc system. J. Appl. Phys. 2015, 117, 195304. [Google Scholar] [CrossRef]
- Piedade, A.P.; Cangueiro, L. Influence of carbyne content on the mechanical performance of nanothick amorphous carbon coatings. Nanomaterials 2020, 10, 780. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Z.; Shen, H.; Chen, J.; Li, J.; Zhang, S. Growth of ideal amorphous carbon films at low temperature by e-beam evaporation. RSC Adv. 2016, 6, 42353–42360. [Google Scholar] [CrossRef]
- Mounier, E.; Bertin, F.; Adamik, M.; Pauleau, Y.; Barna, P.B. Effect of the substrate temperature on the physical characteristics of amorphous carbon films deposited by d.c. magnetron sputtering. Diam. Relat. Mater. 1996, 5, 1509–1515. [Google Scholar] [CrossRef]
- Abrasonis, G.; Gago, R.; Vinnichenko, M.; Kreissig, U.; Kolitsch, A.; Möller, W. Sixfold ring clustering in sp²-dominated carbon and carbon nitride thin films: A Raman spectroscopy study. Phys. Rev. B 2006, 73, 125427. [Google Scholar] [CrossRef]
- Onoprienko, A.A.; Artamonov, V.V.; Yanchuk, I.B. Effect of magnetron discharge power on the resistivity and microstructure of carbon films. Surf. Coat. Technol. 2003, 172, 189–193. [Google Scholar] [CrossRef]






| Type | Bonds | Structure |
|---|---|---|
| graphitic | sp2 | extended stacks of graphene lamellae, possibly with preferential orientation, possibly with nano-/microporosity |
| nanostructured | sp2 + <20% sp3 | amorphous sp2 + graphitic hexagons (+sp3), possibly with nanoporosity |
| amorphous | sp3 + sp2 | amorphous sp3 + sp2 + (graphitic hexagons) |
| Method | Deposition | Growth |
|---|---|---|
| evaporation, ion beam sputtering | C atoms | surface condensation |
| ion beam assisted deposition (IBAD) | C atoms + energetic noble gas ions | surface condensation + atomic peening |
| pulsed laser deposition (PLD) | C1 + C2 + C3 atoms + C1+ + C2+ + C3+ ions | surface condensation + atomic peening + subplantation |
| vacuum arc | C+ (+ C++) ions | subplantation |
| ion beam deposition | C+ ions | subplantation |
| Characteristic | Method | Applicability |
|---|---|---|
| sp3 fraction s | EELS (high energy) | thin films, detached from the Si substrate |
| local density ρ | EELS (plasmon peak) | thin films, detached from the Si substrate |
| global density ρ | surface waves | real substrates, also thick films, also rough films |
| Raman peak ratio ID/IG G peak position νG | Raman spectroscopy | also rough films |
| Young’s modulus E | surface waves | also rough films |
| Young’s modulus E | indentation | smooth films |
| Hardness H | indentation | smooth films |
| Temperature | Process | Density | Bond | Structure |
|---|---|---|---|---|
| low | subplantation | ≈ ρth(s) | sp2, sp3 | disordered sp2/sp3 mixture |
| enhanced | subplantation + partial bond relaxation | < ρth(s) | sp2, sp3 | disordered sp2/sp3 mixture + sp2 cluster, nanoporosity |
| high | complete bond relaxation | < ρg | ≈ sp2 | disordered sp2 + graphitic cluster, nanoporosity |
| very high | crystalline ordering | ≈ ρg | sp2 | distorted graphitic structures |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schultrich, B. Structure and Characterization of Vacuum Arc Deposited Carbon Films—A Critical Overview. Coatings 2022, 12, 109. https://doi.org/10.3390/coatings12020109
Schultrich B. Structure and Characterization of Vacuum Arc Deposited Carbon Films—A Critical Overview. Coatings. 2022; 12(2):109. https://doi.org/10.3390/coatings12020109
Chicago/Turabian StyleSchultrich, Bernd. 2022. "Structure and Characterization of Vacuum Arc Deposited Carbon Films—A Critical Overview" Coatings 12, no. 2: 109. https://doi.org/10.3390/coatings12020109
APA StyleSchultrich, B. (2022). Structure and Characterization of Vacuum Arc Deposited Carbon Films—A Critical Overview. Coatings, 12(2), 109. https://doi.org/10.3390/coatings12020109






