Fatigue Property and Residual Stress Relaxation Behavior of High-Energy Shot Peened Pure Zr
Abstract
:1. Introduction
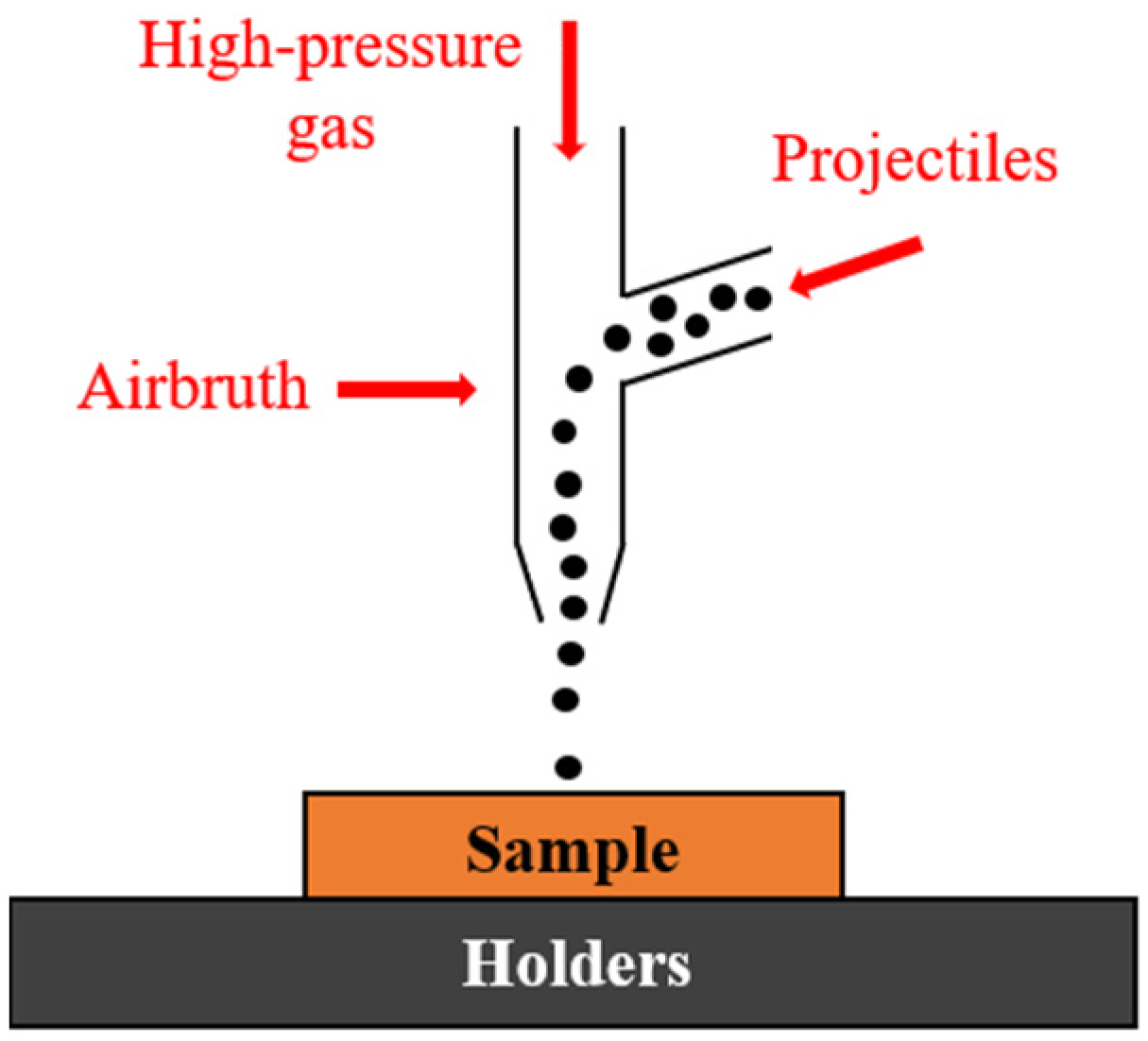
2. Materials and Methods
3. Results and Discussion
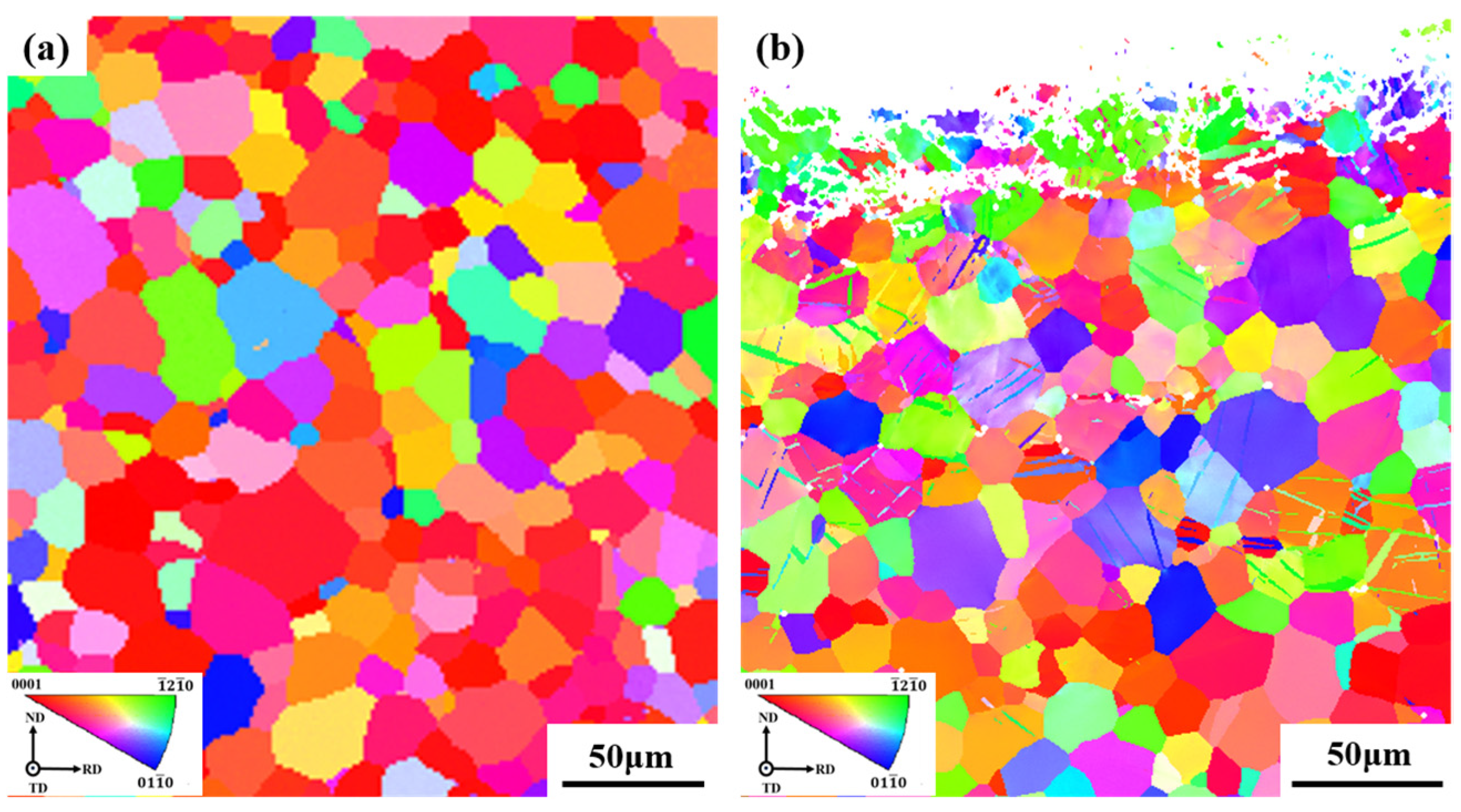
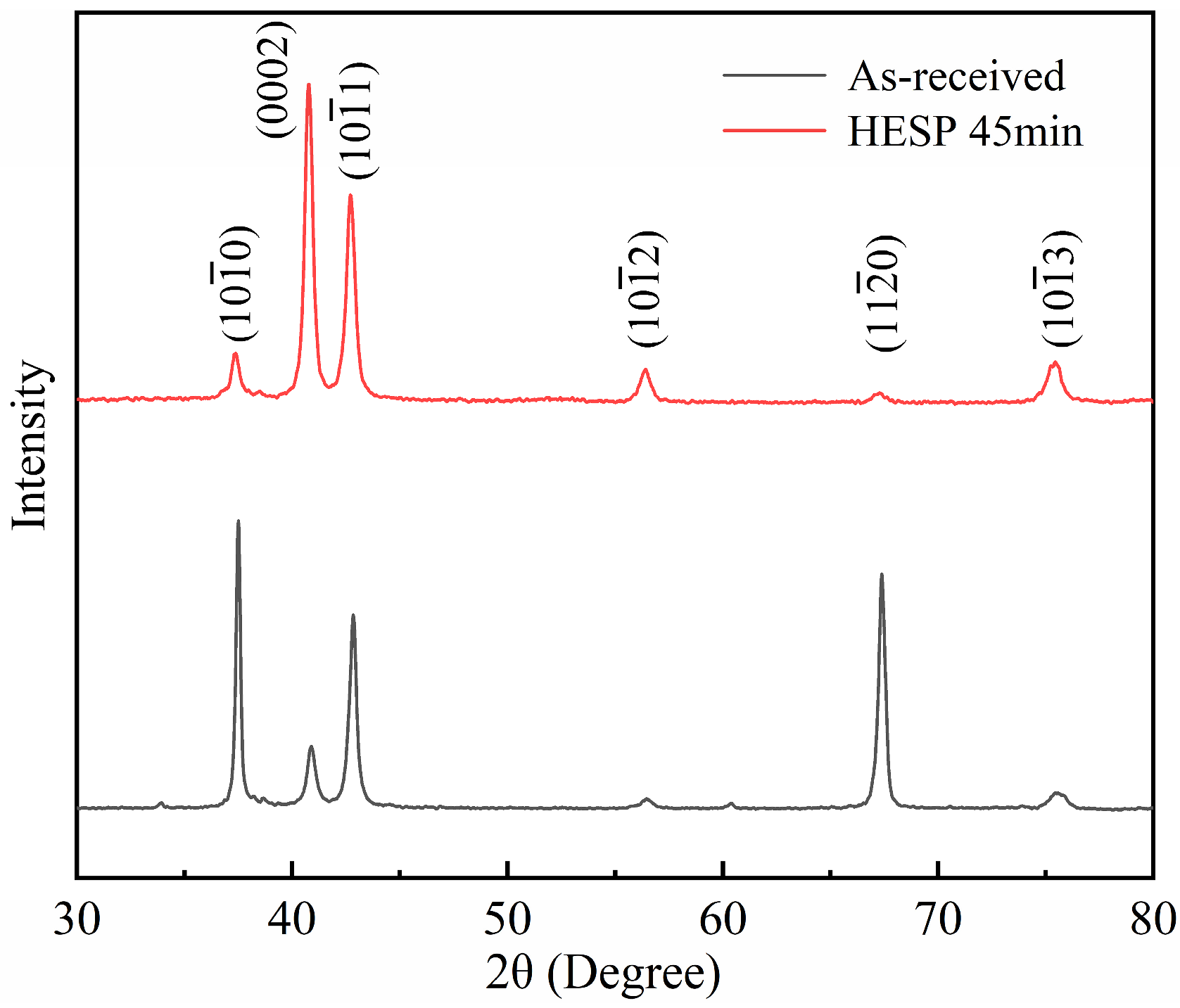
3.1. Microstructure and Residual Stress
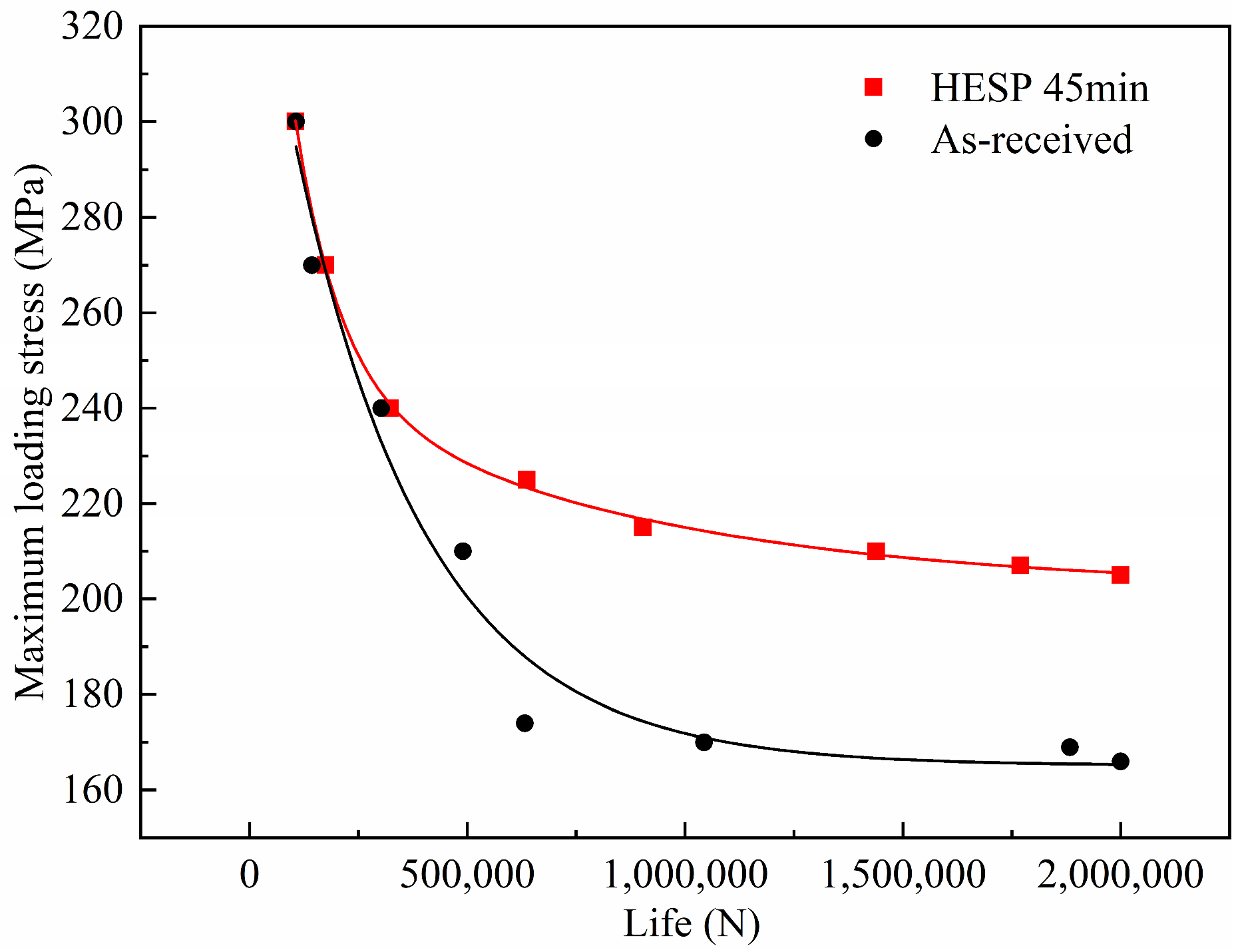
3.2. Fatigue Property
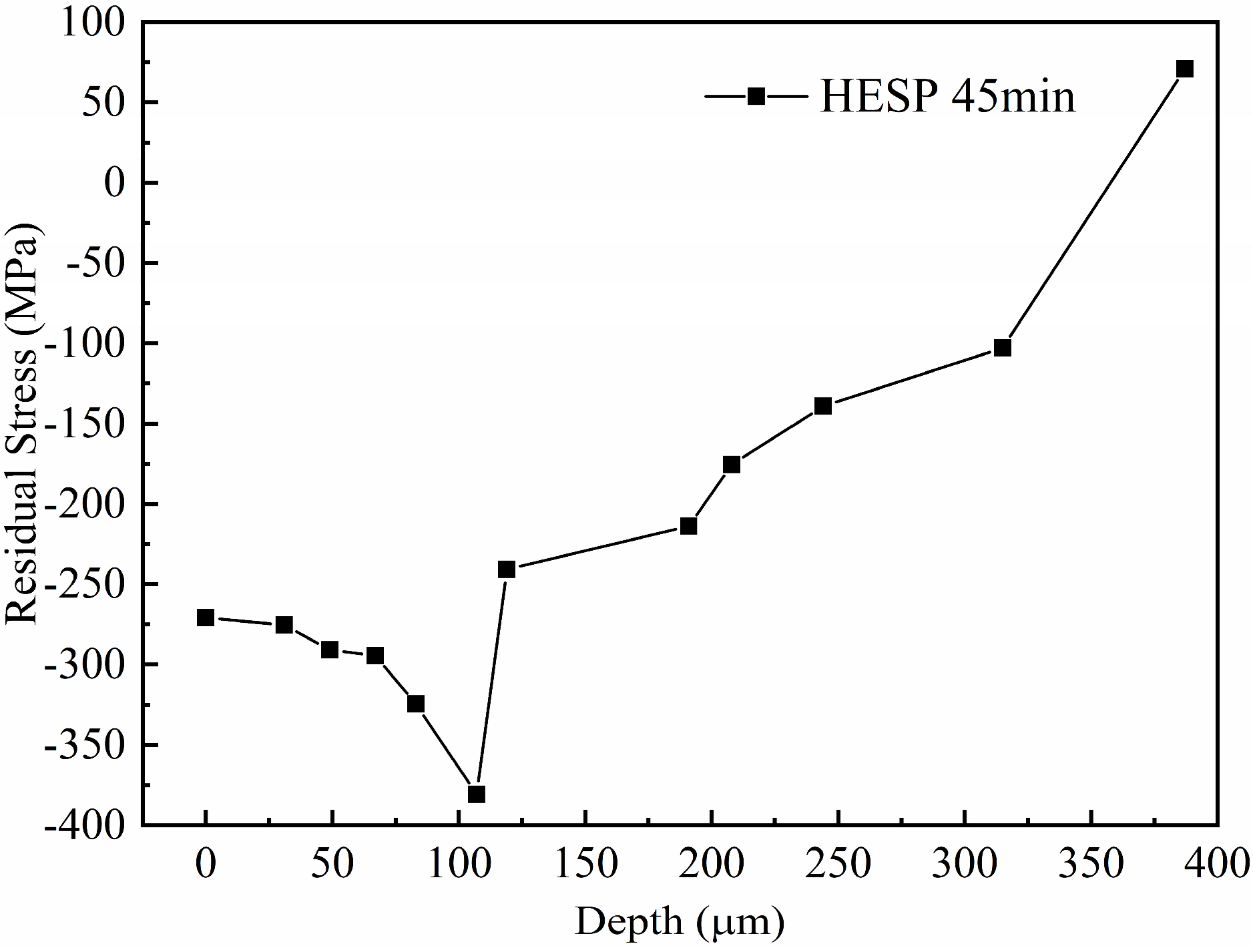
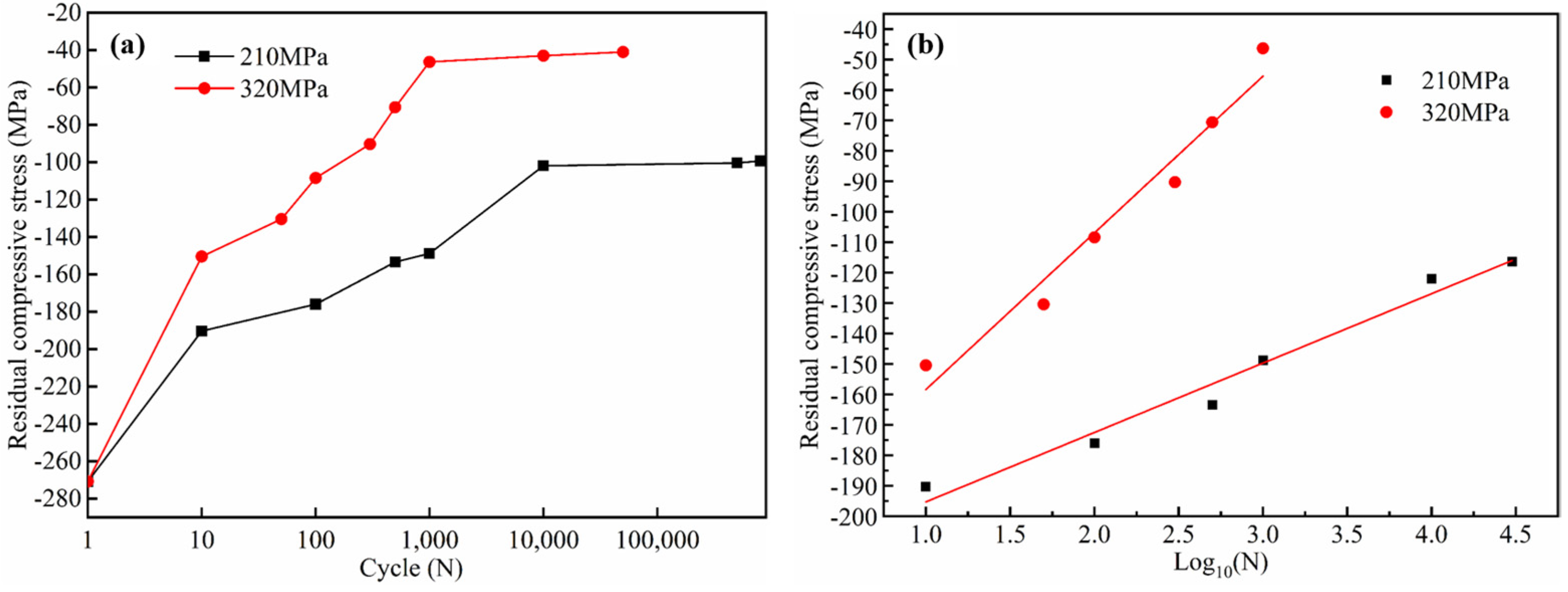
3.3. Residual Stress Relaxation during Fatigue Loading
3.4. Microstructure Evolution during Residual Stress Relaxation
4. Conclusions
- (1)
- HESP treatment can significantly improve the fatigue strength of pure Zr. The fatigue limit of the HESPed is 205 MPa, which is 23% higher than that of the as-received. The crack origin of the HESPed is transferred to the subsurface layer.
- (2)
- Most of the relaxation of residual stress occurs during the first 100 cycles. The greater the applied stress amplitude, the faster the residual stress is released. A linear correlation between the logarithm of the cycle numbers Log10(N) and the σsrs is established.
- (3)
- The surface nanocrystals coarsen and the dislocation density decreases during cyclic loading. The greater applied stress amplitudes, the faster the residual stress relaxation, and the more obvious nanocrystal coarsening and dislocation density reduction. Local plastic deformation causes grain coarsening and dislocation density reduction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, E.; Zhang, X.; Chen, J.; Luan, B.; Liu, Q.; Li, Z.; Zhou, J. Study on the texture of Zr-Nb and Zr-Sn-Nb alloys. Rare Metal Mat. Eng. 2012, 41, 226–229. [Google Scholar]
- Zhang, C.; Yang, J.; Song, G.; Ren, H. Effect of ultrasonic shot peening on tensile-tensile fatigue properties of commercially pure zirconium. Rare Metal Mat. Eng. 2019, 48, 1954–1960. [Google Scholar]
- Wang, L.; Zhang, X.; Xue, X.; Wen, H.; Li, Z. Study on the microstructure and texture of zirconium alloy tube. Rare Metal Mat. Eng. 2013, 42, 153–157. [Google Scholar]
- Duan, Z.; Yang, H.; Satoh, Y.; Murakami, K.; Kano, S.; Zhao, Z.; Shen, J.; Abe, H. Current status of materials development of nuclear fuel cladding tubes for light water reactors. Nucl. Eng. Des. 2017, 316, 131–150. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Y.; Ye, L.; Liu, Q.; Li, C.; Qiu, S.; Li, Z. Transmission electron microscopy observations on surface nanocrystallization of zircaloy-4. Rare Metal Mat. Eng. 2009, 38, 506–509. [Google Scholar]
- Unal, O.; Varol, R. Almen intensity effect on microstructure and mechanical properties of low carbon steel subjected to severe shot peening. Appl. Surf. Sci. 2014, 290, 40–47. [Google Scholar] [CrossRef]
- Wang, R.; Ru, J. Overall evaluation of the effect of residual stress induced by shot peening in the improvement of fatigue fracture resistance for metallic materials. Chin. J. Mech. Eng. 2015, 28, 416–421. [Google Scholar] [CrossRef]
- Tang, C.; Stueber, M.; Seifert, H.J.; Steinbrueck, M. Protective coatings on zirconium-based alloys as accident-tolerant fuel (ATF) claddings. Corros Rev. 2017, 35, 141–165. [Google Scholar] [CrossRef]
- Chai, L.; Chen, B.; Wang, S.; Zhang, Z.; Murty, K.L. Microstructural, textural and hardness evolution of commercially pure Zr surface-treated by high current pulsed electron beam. Appl. Surf. Sci. 2016, 390, 430–434. [Google Scholar] [CrossRef]
- Zhang, D.; Bai, X.; Chen, B.; Liu, F.; Wu, Z. Microarc oxidation of Zircalloy-4. Rare Metal Mat. Eng. 2003, 32, 658–661. [Google Scholar]
- Bagherifard, S.; Ghelichi, R.; Guagliano, M. A numerical model of severe shot peening to predict the generation of a nanostructured surface layer of material. Surf. Coat. Tech. 2010, 204, 4081–4090. [Google Scholar] [CrossRef]
- Yang, X. Effect of Nanocrystallization in Surface Layer on Fatigue Strength TC4 Titanium Alloy by High Energy Shot Peening. Master’s Thesis, Dalian Jiaotong University, Dalian, China, 2009. (In Chinese). [Google Scholar]
- Liu, C.; Liu, D.; Zhang, X.; Liu, D.; Ma, A.; Ao, N.; Xu, X. Improving fatigue performance of Ti-6Al-4V alloy via ultrasonic surface rolling process. J. Mater. Sci. Technol. 2019, 35, 1555–1562. [Google Scholar] [CrossRef]
- Webster, G.; Ezeilo, A. Residual stress distributions and their influence on fatigue lifetimes. Int. J. Fatigue 2001, 23, 375–383. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, K.; Zheng, M.; Zhu, W.; Song, G. Effect of surface nanocrystallization on fatigue properties of Ti-6Al-4V alloys with bimodal and lamellar structure. Mater. Sci. Eng. A 2021, 813, 141142. [Google Scholar] [CrossRef]
- Saalfeld, S.; Oevermann, T.; Niendorf, T.; Scholtes, B. Consequences of deep rolling on the fatigue behavior of steel SAE 1045 at high loading amplitudes. Int. J. Fatigue 2019, 118, 192–201. [Google Scholar] [CrossRef]
- Xie, L.; Wen, Y.; Zhan, K.; Wang, L.; Jiang, C.; Ji, V. Characterization on surface mechanical properties of Ti-6Al-4V after shot peening. J. Alloys Compd. 2016, 666, 65–70. [Google Scholar] [CrossRef]
- Kim, J.; Cheong, S.; Noguchi, H. Residual stress relaxation and low-and high-cycle fatigue behavior of shot-peened medium-carbon steel. Int. J. Fatigue 2013, 56, 114–122. [Google Scholar] [CrossRef]
- Maleki, E.; Farrahi, G.; Kashyzadeh, K.; Unal, O.; Gugaliano, M.; Bagherifard, S. Effects of conventional and severe shot peening on residual stress and fatigue strength of steel AISI 1060 and residual stress relaxation due to fatigue loading: Experimental and numerical simulation. Met. Mater. Int. 2021, 27, 2575–2591. [Google Scholar] [CrossRef]
- Williamson, G.; Hall, W. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Williamson, G.; Smallman, R. Dislocation densities in some annealed and cold-worked metals from measurements on the X-ray debye-scherrer spectrum. Philos Mag. 1956, 1, 34–46. [Google Scholar] [CrossRef]
- Dini, G.; Ueji, R.; Najafizadeh, A.; Monir-Vaghefi, M. Flow stress analysis of TWIP steel via the XRD measurement of dislocation density. Mater. Sci. Eng. A 2010, 527, 2759–2763. [Google Scholar] [CrossRef]
- Ni, S.; Wang, Y.; Liao, X.; Alhajeri, S.; Li, X.; Zhao, Y.; Lavernia, E.; Ringer, S.; Langdon, T.; Zhu, Y. Grain growth and dislocation density evolution in a nanocrystalline Ni-Fe alloy induced by high-pressure torsion. Scr. Mater. 2011, 64, 327–330. [Google Scholar] [CrossRef]
- Keijser, T.; Langford, J.; Mittemeijer, E.; Vogels, A. Use of the Voigt function in a single-line method for the analysis of X-ray diffraction line broadening. J. Appl. Crystallogr. 1982, 15, 308–314. [Google Scholar] [CrossRef]
- Wawszczak, R.; Baczmański, A.; Marciszko, M.; Wróbel, M.; Czeppe, T.; Sztwiertnia, K.; Braham, C.; Berent, K. Evolution of microstructure and residual stress during annealing of austenitic and ferritic steels. Mater. Charact. 2016, 112, 238–251. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Liu, D.; Tan, H.; Wang, X. Effect of TiN/Ti composite coating and shot peening on fretting fatigue behavior of TC17 alloy at 350 °C. Surf. Coat. Tech. 2009, 203, 2315–2321. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Ghasemi, A.; Farrahi, G.; Sherafatnia, K. A comprehensive experimental and numerical study on redistribution of residual stresses by shot peening. Mater Design. 2016, 90, 478–487. [Google Scholar] [CrossRef]
- Gao, Y. Residual compressive stress field in TC18 ultra-high strength titanium alloy by shot peening. Rare Metal Mat. Eng. 2004, 33, 1209–1212. [Google Scholar]
- Meng, X.; Zhou, J.; Su, C.; Huang, S.; Luo, K.; Sheng, J.; Tan, W. Residual stress relaxation and its effects on the fatigue properties of Ti6Al4V alloy strengthened by warm laser peening. Mater. Sci. Eng. A 2017, 680, 297–304. [Google Scholar] [CrossRef]
- Wick, A.; Schulze, V.; Vöhringer, O. Effects of warm peening on fatigue life and relaxation behavior of residual stresses in AISI 4140 steel. Mater. Sci. Eng. A 2000, 293, 191–197. [Google Scholar] [CrossRef]
- Ma, Q.; Huang, C. Fracture surface analysis of high-cycle fatigue for Ti-55531 alloy. Chin. J. Nonferrous Met. 2018, 28, 2467–2475. [Google Scholar]
- Wang, Y.; Yuan, L.; Zhang, S.; Sun, C.; Wang, W.; Yang, G.; Li, Q.; Wei, Y. The influence of combined gradient structure with residual stress on crack-growth behavior in medium carbon steel. Eng. Fract. Mech. 2019, 209, 369–381. [Google Scholar] [CrossRef] [Green Version]
- Meirom, R.; Alsem, D.; Romasco, A.; Clark, T.; Polcawich, R.; Pulskamp, J.; Dubey, M.; Ritchie, R.; Muhlstein, C. Fatigue-induced grain coarsening in nanocrystalline platinum films. Acta Mater. 2011, 59, 1141–1149. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Pan, Q.; Tao, N.; Lu, L. Abnormal grain coarsening in cyclically deformed gradient nanograined Cu. Scr. Mater. 2018, 145, 99–103. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, Y.; Huang, J.; Fu, Y.; Zhang, X.; Xin, Y.; Tu, S.; Mao, M.; Yang, F. Fatigue-induced evolution of nanograins and residual stress in the nanostructured surface layer of Ti-6Al-4V. Mater. Sci. Eng. A 2019, 764, 138205. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Wang, Y.; Li, F.; Xiao, G. Effects of cyclic loading on residual stress field in TC4 after USSP treatment. Rare Metal Mat. Eng. 2016, 45, 2642–2646. [Google Scholar]



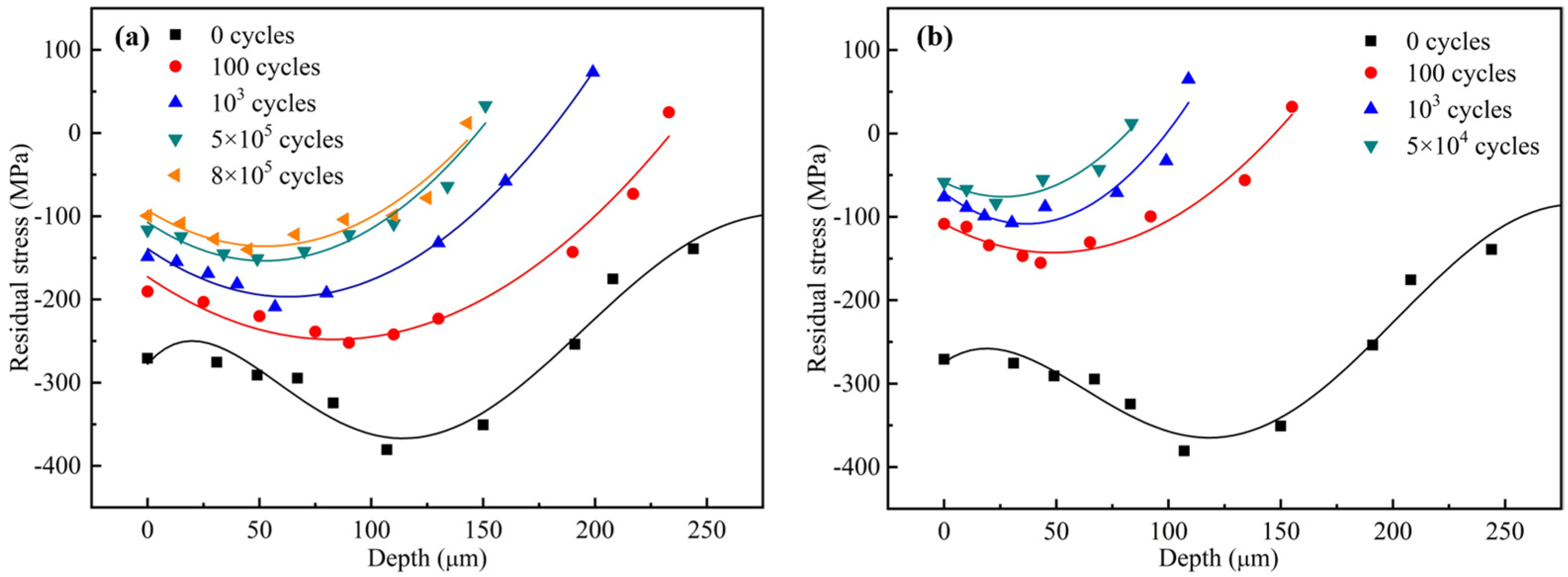



| Stress, MPa | Cycle | σsrs, MPa | σmrs, MPa | Zm, μm | Z0, μm |
|---|---|---|---|---|---|
| 210 | 0 | −270.8 | −375.6 | 112 | 330 |
| 100 | −190.3 | −257.8 | 80 | 235 | |
| 103 | −148.8 | −199.0 | 65 | 175 | |
| 5 × 105 | −100.4 | −139.8 | 55 | 148 | |
| 8 × 105 | −99.3 | −123.6 | 49 | 130 | |
| 320 | 0 | −270.8 | −375.6 | 112 | 330 |
| 100 | −108.4 | −115.0 | 65 | 149 | |
| 103 | −46.2 | −107.1 | 48 | 99 | |
| 5 × 104 | −41.4 | −85.3 | 35 | 49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, G.; Zhang, X.; Zhang, C.; Liu, Y.; Zhu, W. Fatigue Property and Residual Stress Relaxation Behavior of High-Energy Shot Peened Pure Zr. Coatings 2022, 12, 131. https://doi.org/10.3390/coatings12020131
Xiao G, Zhang X, Zhang C, Liu Y, Zhu W. Fatigue Property and Residual Stress Relaxation Behavior of High-Energy Shot Peened Pure Zr. Coatings. 2022; 12(2):131. https://doi.org/10.3390/coatings12020131
Chicago/Turabian StyleXiao, Guizhi, Xin Zhang, Conghui Zhang, Ying Liu, and Wenguang Zhu. 2022. "Fatigue Property and Residual Stress Relaxation Behavior of High-Energy Shot Peened Pure Zr" Coatings 12, no. 2: 131. https://doi.org/10.3390/coatings12020131






