Study on Phonon Localization in Silicon Film by Molecular Dynamics
Abstract
:1. Introduction
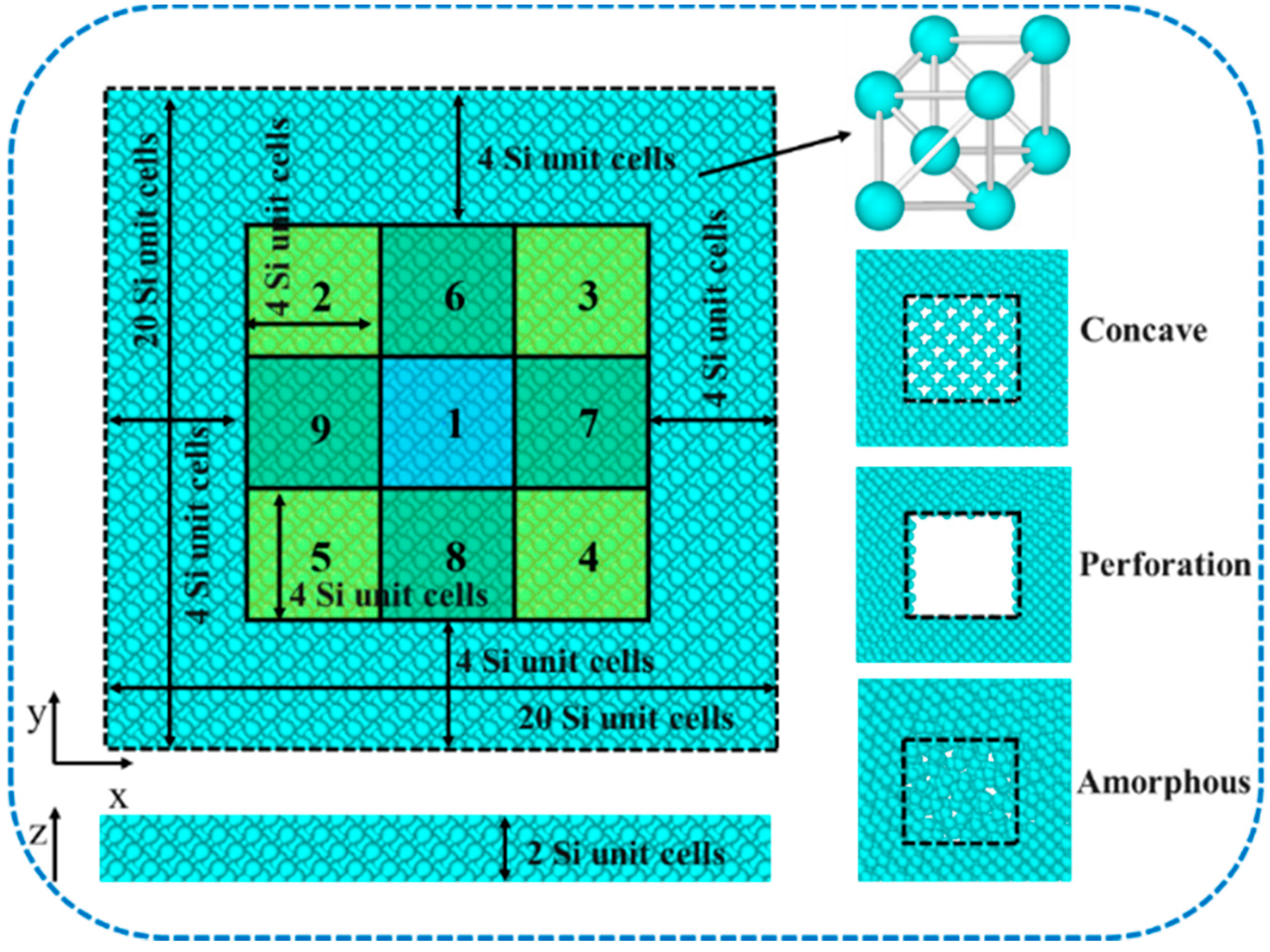
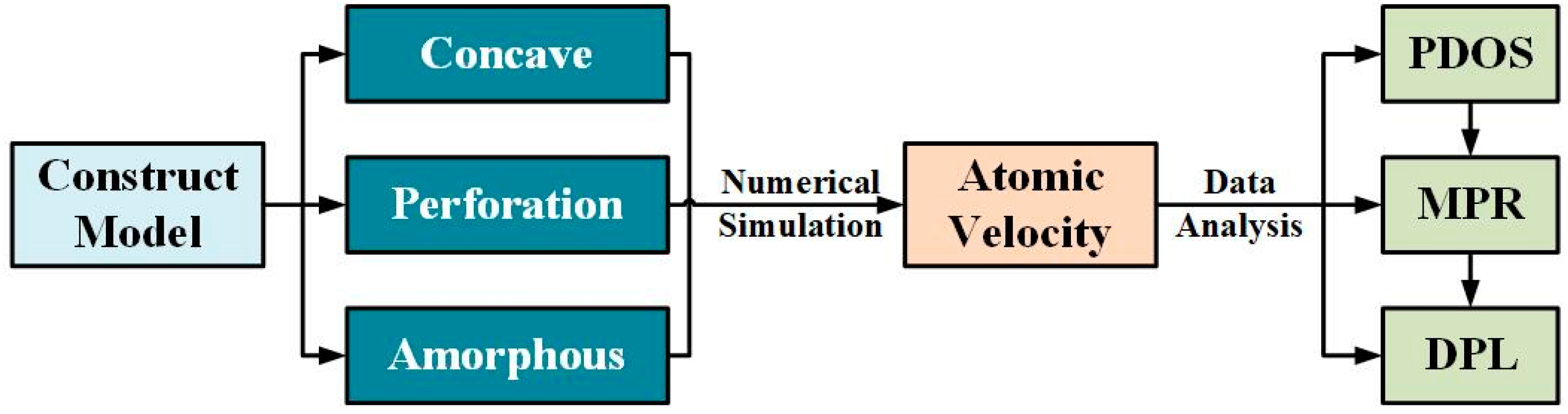
2. Theory and Methods
3. Results and Discussions
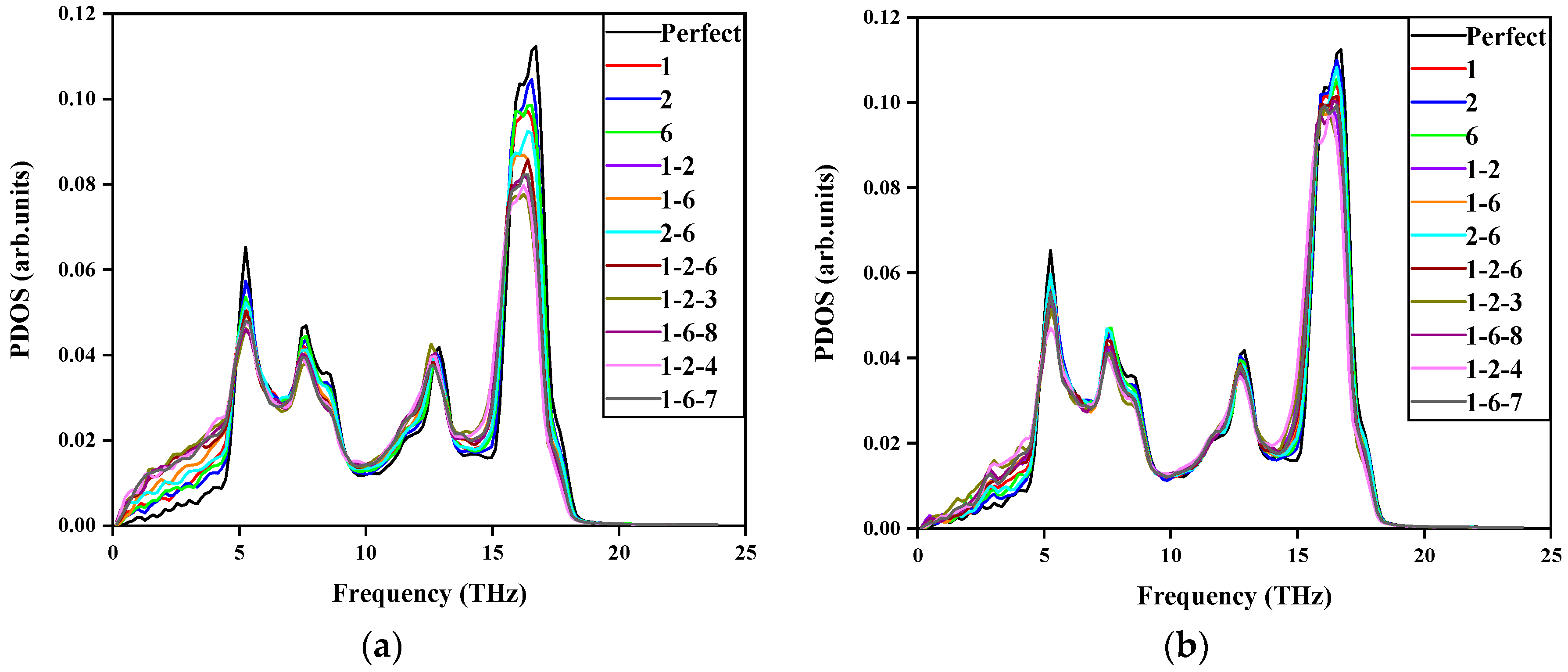
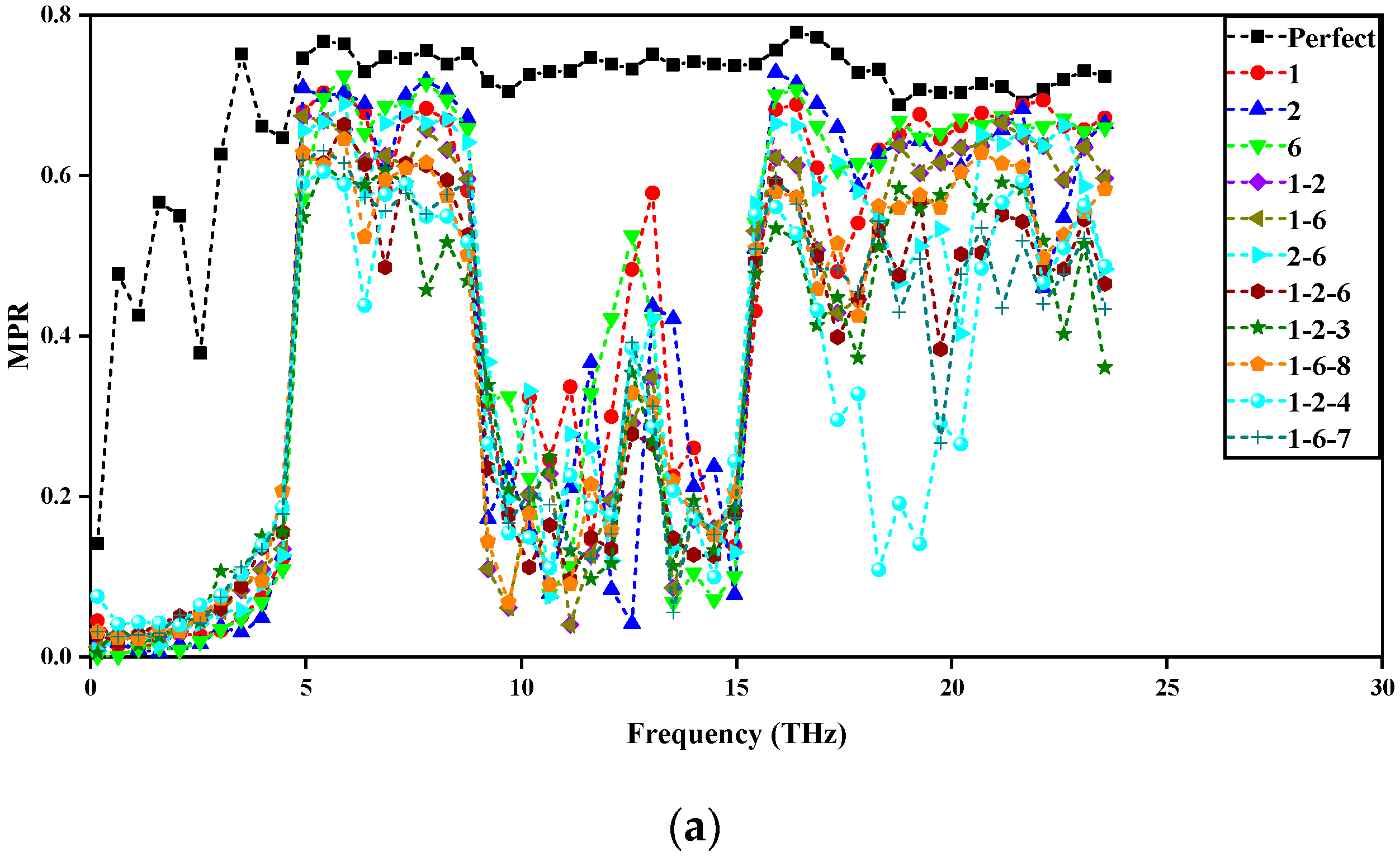
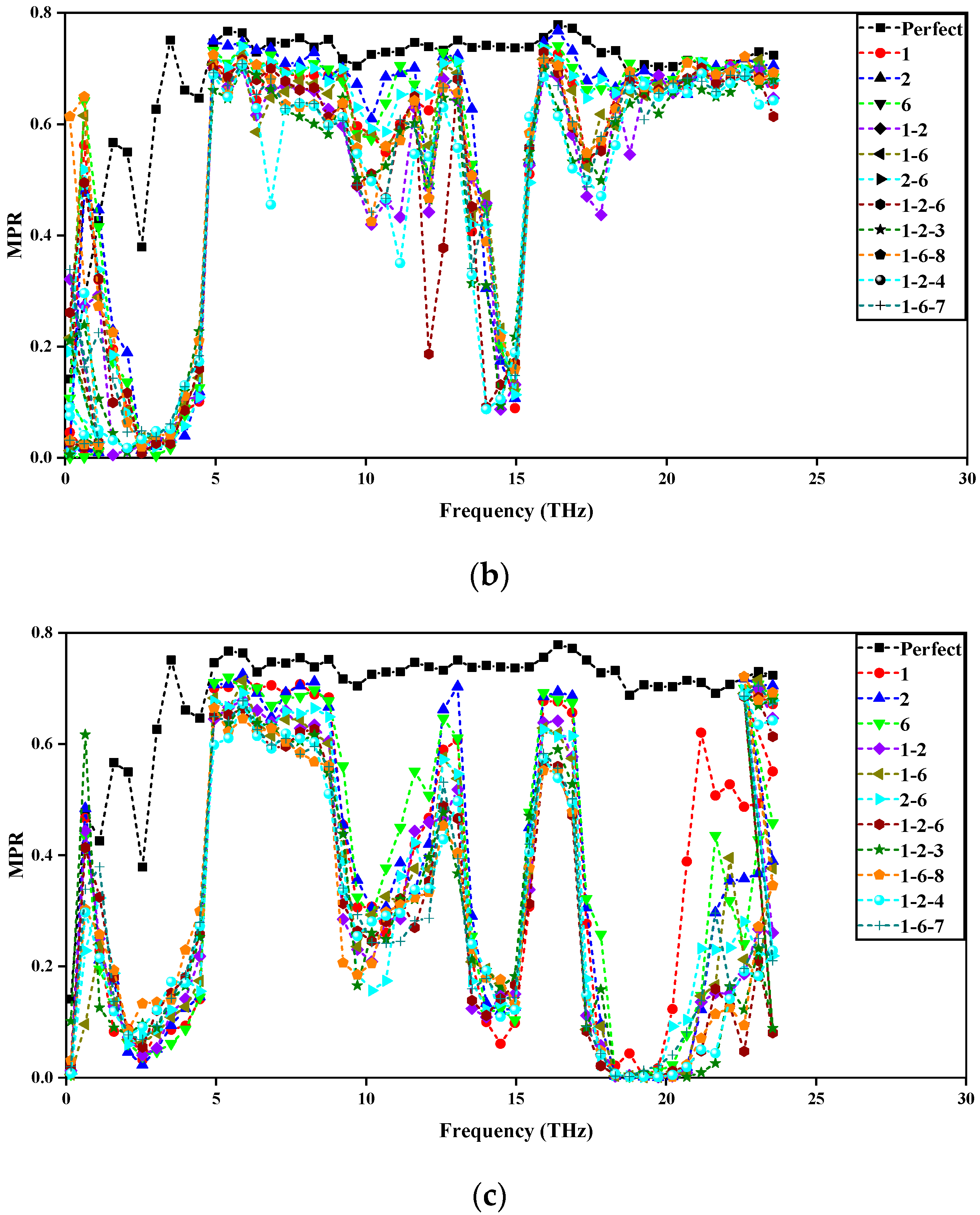
3.1. Central Region Impact
3.2. Edge Region Impact
3.3. Central/Edge Region Impact
3.4. Guidance for the Construction of Thermal Cloaks
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, C.Z.; Gao, Y.; Huang, J.P. Shaped graded materials with an apparent negative thermal conductivity. Appl. Phys. Lett. 2008, 92, 251907. [Google Scholar] [CrossRef]
- Nguyen, D.M.; Xu, H.G.; Zhang, Y.M.; Zhang, B.L. Active thermal cloak. Appl. Phys. Lett. 2015, 107, 121901. [Google Scholar] [CrossRef]
- Han, T.C.; Bai, X.; Gao, D.L.; Thong, J.T.L.; Li, B.W.; Qiu, C.W. Experimental Demonstration of a Bilayer Thermal Cloak. Phys. Rev. Lett. 2014, 112, 054302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, T.C.; Zhao, J.J.; Yuan, T.; Lei, D.Y.; Li, B.W.; Qiu, C.W. Theoretical realization of an ultra-efficient thermal-energy harvesting cell made of natural materials. Energy Environ. Sci. 2013, 6, 3537–3541. [Google Scholar] [CrossRef] [Green Version]
- Shen, X.Y.; Li, Y.; Jiang, C.R.; Ni, Y.S.; Huang, J.P. Thermal cloak-concentrator. Appl. Phys. Lett. 2016, 109, 031907. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.Y.; Shi, X.H.; Gao, F.; Sun, H.D.; Zhang, B.L. Ultrathin three-dimensional thermal cloak. Phys. Rev. Lett. 2014, 112, 054301. [Google Scholar] [CrossRef]
- Yang, T.Z.; Bai, X.; Gao, D.L.; Wu, L.Z.; Li, B.W.; Thong, J.T.L.; Qiu, C.W. Invisible Sensors: Simultaneous Sensing and Camouflaging in Multiphysical Fields. Adv. Mater. 2015, 27, 7752–7758. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.L.; Huang, S.Y.; Wang, M.; Hu, R.; Luo, X.B. While rotating while cloaking. Phys. Lett. A 2019, 383, 759–763. [Google Scholar] [CrossRef]
- Zhu, Z.; Ren, X.C.; Sha, W.; Xiao, M.; Hu, R.; Luo, X.B. Inverse design of rotating metadevice for adaptive thermal cloaking. Int. J. Heat Mass Transf. 2021, 176, 121417. [Google Scholar] [CrossRef]
- Guenneau, S.; Amra, C. Anisotropic conductivity rotates heat fluxes in transient regimes. Opt. Express 2013, 21, 6578–6583. [Google Scholar] [CrossRef]
- Hu, R.; Wei, X.L.; Hu, J.Y.; Luo, X.B. Local heating realization by reverse thermal cloak. Sci. Rep. 2014, 4, 3600. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.B.; Tian, B.Y.; Xu, L.J.; Huang, J.P. Experimental demonstration of thermal chameleonlike rotators with transformation-invariant metamaterials. Phys. Rev. Appl. 2020, 14, 054024. [Google Scholar] [CrossRef]
- Han, T.C.; Bai, X.; Thong, J.T.L.; Li, B.W.; Qiu, C.W. Full Control and Manipulation of Heat Signatures: Cloaking, Camouflage and Thermal Metamaterials. Adv. Mater. 2014, 26, 1731–1734. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Bai, X.; Yang, T.Z.; Luo, H.L.; Qiu, C.W. Structured thermal surface for radiative camouflage. Nat. Commun. 2018, 9, 273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Y.D.; Song, J.L.; Zhao, W.X.; Ren, X.C.; Cheng, Q.; Luo, X.B.; Fang, N.X.; Hu, R. Dynamic thermal camouflage via a liquid-crystal-based radiative metasurface. Nanophotonics 2020, 9, 855–863. [Google Scholar] [CrossRef] [Green Version]
- Qu, Y.R.; Li, Q.; Cai, L.; Pan, M.Y.; Ghosh, P.; Du, K.K.; Qiu, M. Thermal camouflage based on the phase-changing mate-rial GST. Light Sci. Appl. 2018, 7, 26. [Google Scholar] [CrossRef]
- Wang, J.; Bi, Y.Q.; Hou, Q.W. Three-dimensional illusion thermal device for location camouflage. Sci. Rep. 2017, 7, 7541. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.J.; Wang, R.Z.; Huang, J.P. Camouflage thermotics: A cavity without disturbing heat signatures outside. J. Appl. Phys. 2018, 123, 245111. [Google Scholar] [CrossRef]
- Yang, T.Z.; Su, Y.S.; Xu, W.K.; Yang, X.D. Transient thermal camouflage and heat signature control. Appl. Phys. Lett. 2016, 109, 121905. [Google Scholar] [CrossRef]
- Song, J.L.; Huang, S.Y.; Ma, Y.P.; Cheng, Q.; Hu, R.; Luo, X.B. Radiative metasurface for thermal camouflage, illusion and messaging. Opt. Express 2020, 28, 875–885. [Google Scholar] [CrossRef]
- Hu, R.; Wang, X.; Liu, Y.D.; Song, J.L.; Luo, X.B.; Wu, J.Q.; Qiu, C.W. Thermal camouflaging metamaterials. Mater. Today 2021, 45, 120–141. [Google Scholar] [CrossRef]
- Alwakil, A.; Zerrad, M.; Bellieud, M.; Amra, C. Inverse heat mimicking of given objects. Sci. Rep. 2017, 7, 43288. [Google Scholar] [CrossRef] [PubMed]
- Hu, R.; Zhou, S.L.; Li, Y.; Lei, D.Y.; Luo, X.B.; Qiu, C.W. Illusion Thermotics. Adv. Mater. 2018, 30, 1707237. [Google Scholar] [CrossRef]
- Zhou, S.L.; Hu, R.; Luo, X.B. Thermal illusion with twinborn-like heat signatures. Int. J. Heat Mass Transf. 2018, 127, 607–613. [Google Scholar] [CrossRef]
- Zhu, N.Q.; Shen, X.Y.; Huang, J.P. Converting the patterns of local heat flux via thermal illusion device. AIP Adv. 2015, 5, 053401. [Google Scholar] [CrossRef]
- Hu, R.; Huang, S.Y.; Wang, M.; Luo, X.B.; Shiomi, J.; Qiu, C.W. Encrypted Thermal Printing with Regionalization Transformation. Adv. Mater. 2019, 31, 1807849. [Google Scholar] [CrossRef]
- Hu, J.N.; Ruan, X.L.; Chen, Y.P. Molecular Dynamics Study of Thermal Rectification in Graphene Nanoribbons. Int. J. Thermophys. 2012, 33, 986–991. [Google Scholar] [CrossRef]
- Li, Y.; Shen, X.Y.; Wu, Z.H.; Huang, J.Y.; Chen, Y.X.; Ni, Y.S.; Huang, J.P. Temperature-dependent transformation thermotics: From switchable thermal cloaks to macroscopic thermal diodes. Phys. Rev. Lett. 2015, 115, 195503. [Google Scholar] [CrossRef]
- Tian, H.; Xie, D.; Yang, Y.; Ren, T.L.; Zhang, G.; Wang, Y.F.; Zhou, C.J.; Peng, P.G.; Wang, L.G.; Liu, L.T. A Novel Solid-State Thermal Rectifier Based on Reduced Graphene Oxide. Sci. Rep. 2012, 2, 523. [Google Scholar] [CrossRef]
- Wang, S.; Cottrill, A.L.; Kunai, Y.; Toland, A.R.; Liu, P.W.; Wang, W.J.; Strano, M.S. Microscale solid-state thermal diodes enabling ambient temperature thermal circuits for energy applications. Phys. Chem. Chem. Phys. 2017, 19, 13172–13181. [Google Scholar] [CrossRef]
- Qin, T.; Zhou, J.H.; Shi, J.R. Berry curvature and the phonon Hall effect. Phys. Rev. B 2012, 86, 104305. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Vallabhaneni, A.; Hu, J.N.; Qiu, B.; Chen, Y.P.; Ruan, X.L. Phonon Lateral Confinement Enables Thermal Rectification in Asymmetric Single-Material Nanostructures. Nano Lett. 2014, 14, 592–596. [Google Scholar] [CrossRef] [Green Version]
- Ye, Z.Q.; Cao, B.Y. Nanoscale thermal cloaking in graphene via chemical functionalization. Phys. Chem. Chem. Phys. 2016, 18, 32952–32961. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.D.; Cheng, Y.H.; Hu, R.; Luo, X.B. Nanoscale thermal cloaking by in-situ annealing silicon membrane. Phys. Lett. A 2019, 383, 2296–2301. [Google Scholar] [CrossRef]
- Choe, H.S.; Prabhakar, R.; Wehmeyer, G.; Allen, F.; Lee, W.; Jin, L.; Li, Y.; Yang, P.D.; Qiu, C.W.; Dames, C.; et al. Ion Write Microthermotics: Programing Thermal Metamaterials at the Microscale. Nano Lett. 2019, 19, 3830–3837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, J.; Zhang, H.C.; Li, Y.Y.; Zhang, D.; Wang, H.M. Numerical analysis on nanoscale thermal cloak in three-dimensional silicon film with circular cavities. Numer. Heat TR A-Appl. 2022, 81, 1–14. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.C.; Wang, H.M.; Xu, C.Z.; Wang, Q. Performance prediction of nanoscale thermal cloak by molecular dynamics. Appl. Phys. A-Mater. 2021, 127, 790. [Google Scholar] [CrossRef]
- Loh, G.C.; Teo, E.H.T.; Tay, B.K. Phononic and structural response to strain in wurtzite-gallium nitride nanowires. J. Appl. Phys. 2012, 111, 103506. [Google Scholar] [CrossRef]
- Jiang, P.F.; Hu, S.Q.; Ouyang, Y.L.; Ren, W.J.; Ren, C.Q.; Zhang, Z.W.; Chen, J. Remarkable thermal rectification in pristine and symmetric monolayer graphene enabled by asymmetric thermal contact. J. Appl. Phys. 2020, 127, 235101. [Google Scholar] [CrossRef]
- Lu, S.; Ouyang, Y.L.; Yu, C.Q.; Jiang, P.F.; He, J.; Chen, J. Tunable phononic thermal transport in two-dimensional C6CaC6 via guest atom intercalation. J. Appl. Phys. 2021, 129, 225106. [Google Scholar] [CrossRef]
- Liang, T.; Zhou, M.; Zhang, P.; Yuan, P.; Yang, D.G. Multilayer in-plane graphene/hexagonal boron nitride heterostructures: Insights into the interfacial thermal transport properties. Int. J. Heat Mass Transf. 2020, 151, 119395. [Google Scholar] [CrossRef]
- Wu, X.; Han, Q. Thermal transport in pristine and defective two-dimensional polyaniline (C3N). Int. J. Heat Mass Transf. 2021, 173, 121235. [Google Scholar] [CrossRef]
- Zhou, M.; Liang, T.; Wu, B.Y.; Liu, J.J.; Zhang, P. Phonon transport in antisite-substituted hexagonal boron nitride nanosheets: A molecular dynamics study. J. Appl. Phys. 2020, 128, 234304. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B. 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.N.; Latour, B.; Minnich, A.J. Phonon transmission at crystalline-amorphous interfaces studied using mode-resolved atomistic Green’s functions. Phys. Rev. B. 2018, 97, 205306. [Google Scholar] [CrossRef] [Green Version]
- Li, H.P.; Zhang, R.Q. Anomalous effect of hydrogenation on phonon thermal conductivity in thin silicon nanowires. EPL 2014, 105, 56003. [Google Scholar] [CrossRef]
- Ma, D.K.; Ding, H.R.; Meng, H.; Feng, L.; Wu, Y.; Shiomi, J.; Yang, N. Nano-cross-junction effect on phonon transport in silicon nanowire cages. Phys. Rev. B 2016, 94, 165434. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, D.; Vizuete, O.; Ranjan, H.; Pal, S.; Zhang, Z.B. The control of thermal conductivity through coherent and incoherent phonon scattering in 2-dimensional phononic crystals by incorporating elements of self-similarity. Appl. Phys. Lett. 2019, 115, 213903. [Google Scholar] [CrossRef]





| Calculation Region | DPL | |||||
|---|---|---|---|---|---|---|
| Concave | Perforation | Amorphous | Concave | Perforation | Amorphous | |
| 0 | - | 0.702 | 0.272 | - | 0.984 | 0.497 |
| 1 | 0.435 | 0.533 | 0.364 | 0.691 | 0.786 | 0.626 |
| 1-2 | 0.386 | 0.494 | 0.293 | 0.639 | 0.728 | 0.561 |
| 1-6 | 0.386 | 0.533 | 0.299 | 0.639 | 0.775 | 0.566 |
| 2-6 | 0.404 | 0.547 | 0.311 | 0.651 | 0.807 | 0.570 |
| 1-2-6 | 0.343 | 0.501 | 0.277 | 0.576 | 0.743 | 0.542 |
| 1-2-3 | 0.352 | 0.486 | 0.296 | 0.573 | 0.713 | 0.565 |
| 1-2-4 | 0.322 | 0.470 | 0.278 | 0.550 | 0.699 | 0.541 |
| 1-6-7 | 0.344 | 0.504 | 0.286 | 0.567 | 0.732 | 0.538 |
| 1-6-8 | 0.369 | 0.530 | 0.283 | 0.603 | 0.764 | 0.538 |
| Calculation Region | DPL | |||||
|---|---|---|---|---|---|---|
| Concave | Perforation | Amorphous | Concave | Perforation | Amorphous | |
| 2 | 0.419 | 0.561 | 0.354 | 0.688 | 0.831 | 0.613 |
| 6 | 0.429 | 0.554 | 0.389 | 0.704 | 0.817 | 0.624 |
| 2-6 | 0.404 | 0.547 | 0.306 | 0.651 | 0.807 | 0.583 |
| 2-7 | 0.385 | 0.519 | 0.294 | 0.634 | 0.759 | 0.562 |
| 2-3 | 0.412 | 0.539 | 0.328 | 0.654 | 0.786 | 0.581 |
| 2-4 | 0.412 | 0.542 | 0.316 | 0.654 | 0.789 | 0.570 |
| 2-3-6 | 0.371 | 0.553 | 0.297 | 0.606 | 0.811 | 0.558 |
| 2-6-7 | 0.370 | 0.470 | 0.275 | 0.603 | 0.696 | 0.544 |
| 2-6-4 | 0.370 | 0.530 | 0.283 | 0.602 | 0.766 | 0.555 |
| 2-3-7 | 0.365 | 0.510 | 0.290 | 0.592 | 0.744 | 0.539 |
| 2-3-4 | 0.287 | 0.501 | 0.270 | 0.542 | 0.718 | 0.543 |
| 2-7-8 | 0.352 | 0.495 | 0.282 | 0.568 | 0.715 | 0.539 |
| 2-8-5 | 0.359 | 0.523 | 0.288 | 0.589 | 0.755 | 0.550 |
| Number of Blocks | Concave | Perforation | Amorphous | |||
|---|---|---|---|---|---|---|
| Center | Edge | Center | Edge | Center | Edge | |
| 1 | 0.691 | 0.696 | 0.786 | 0.824 | 0.626 | 0.619 |
| 2 | 0.643 | 0.648 | 0.770 | 0.785 | 0.566 | 0.574 |
| 3 | 0.574 | 0.586 | 0.730 | 0.744 | 0.545 | 0.547 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhang, H.; Wang, Q.; Sun, W.; Zhang, D. Study on Phonon Localization in Silicon Film by Molecular Dynamics. Coatings 2022, 12, 422. https://doi.org/10.3390/coatings12040422
Zhang J, Zhang H, Wang Q, Sun W, Zhang D. Study on Phonon Localization in Silicon Film by Molecular Dynamics. Coatings. 2022; 12(4):422. https://doi.org/10.3390/coatings12040422
Chicago/Turabian StyleZhang, Jian, Haochun Zhang, Qi Wang, Wenbo Sun, and Dong Zhang. 2022. "Study on Phonon Localization in Silicon Film by Molecular Dynamics" Coatings 12, no. 4: 422. https://doi.org/10.3390/coatings12040422
APA StyleZhang, J., Zhang, H., Wang, Q., Sun, W., & Zhang, D. (2022). Study on Phonon Localization in Silicon Film by Molecular Dynamics. Coatings, 12(4), 422. https://doi.org/10.3390/coatings12040422







