Mesoscale Simulation and Evaluation of the Mechanical Properties of Ceramic Seal Coatings
Abstract
:1. Introduction
2. Model Construction and Analysis
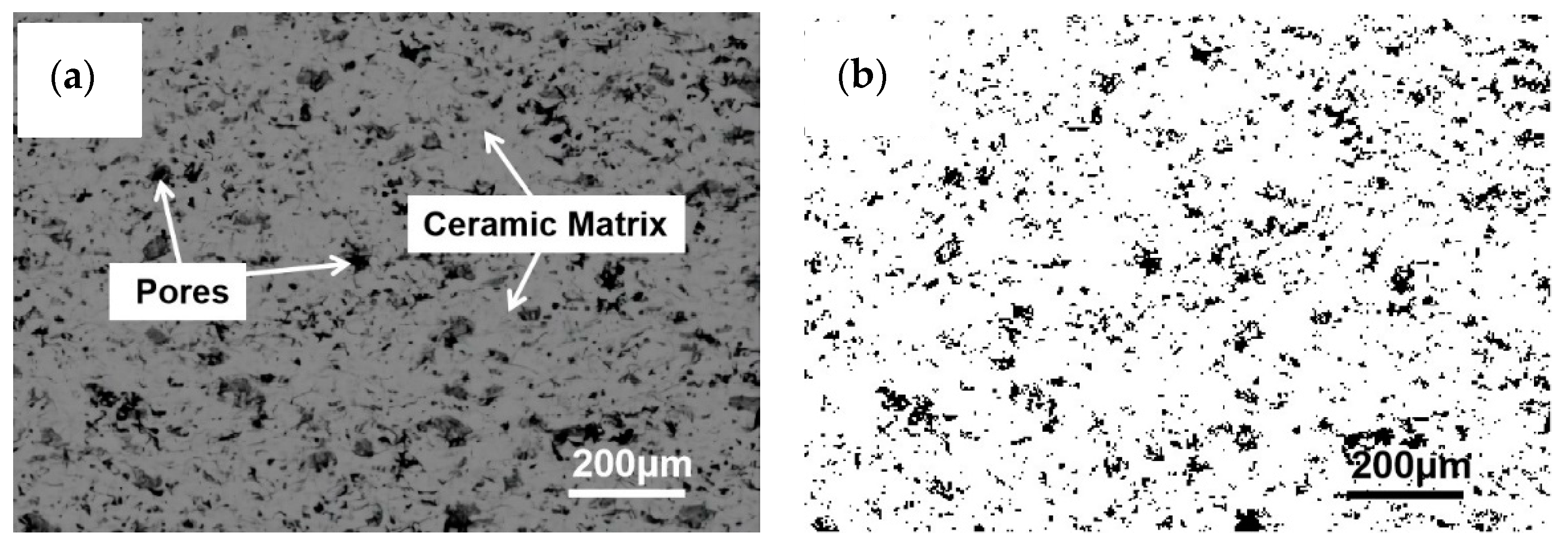
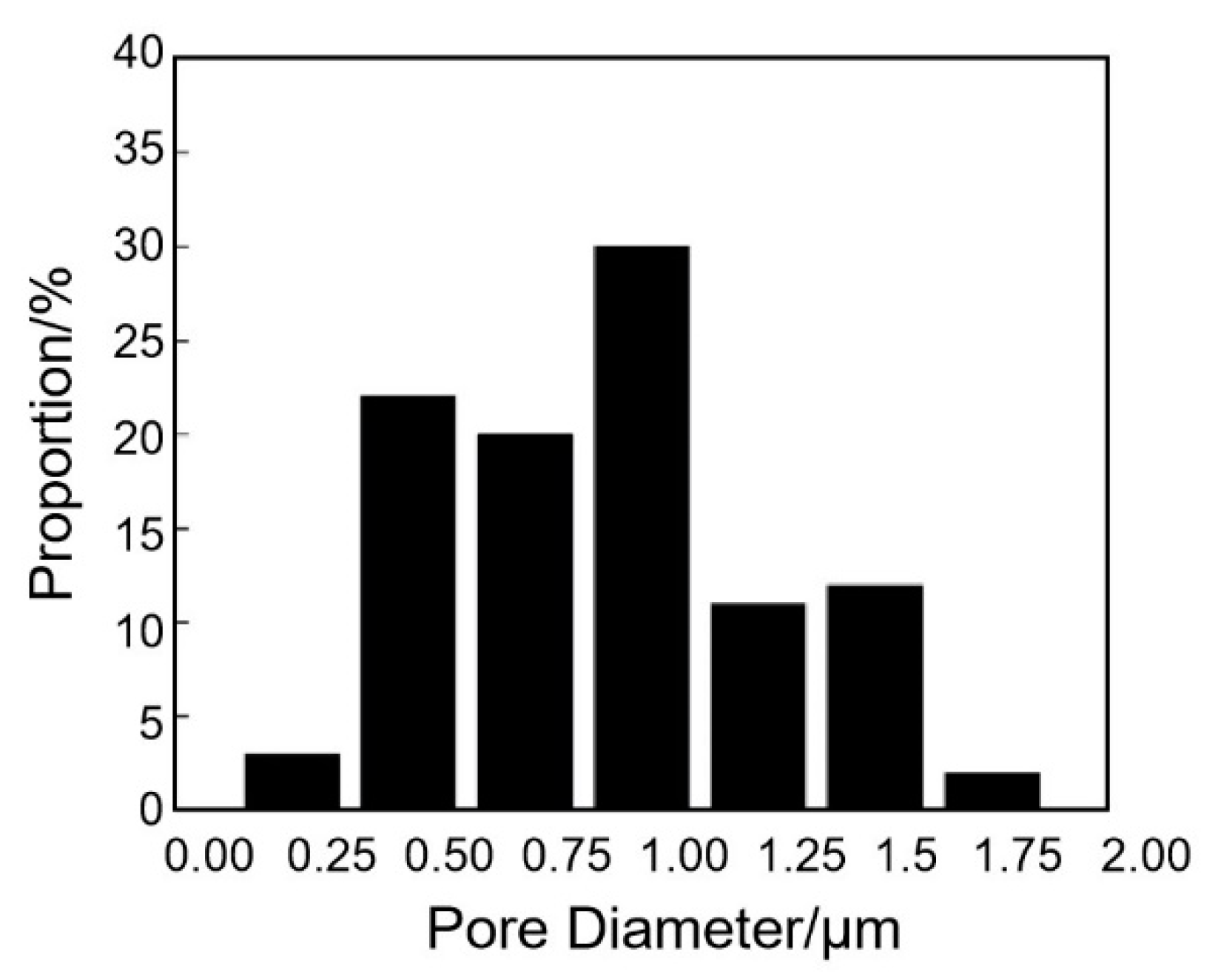
2.1. Pore Characteristic Parameter Acquisition
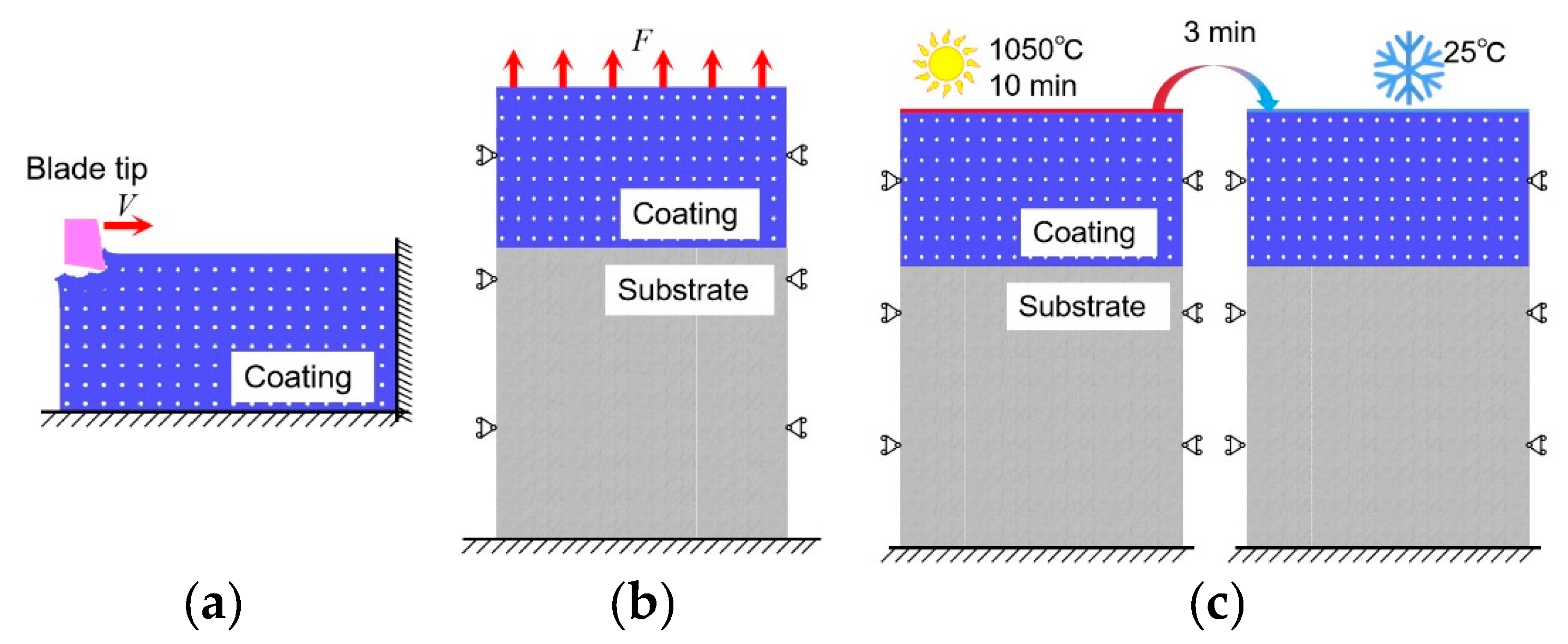
2.2. Finite Element Method-Based Numerical Model Building
2.3. Simulation Model Validation
3. Numerical Results and Discussion
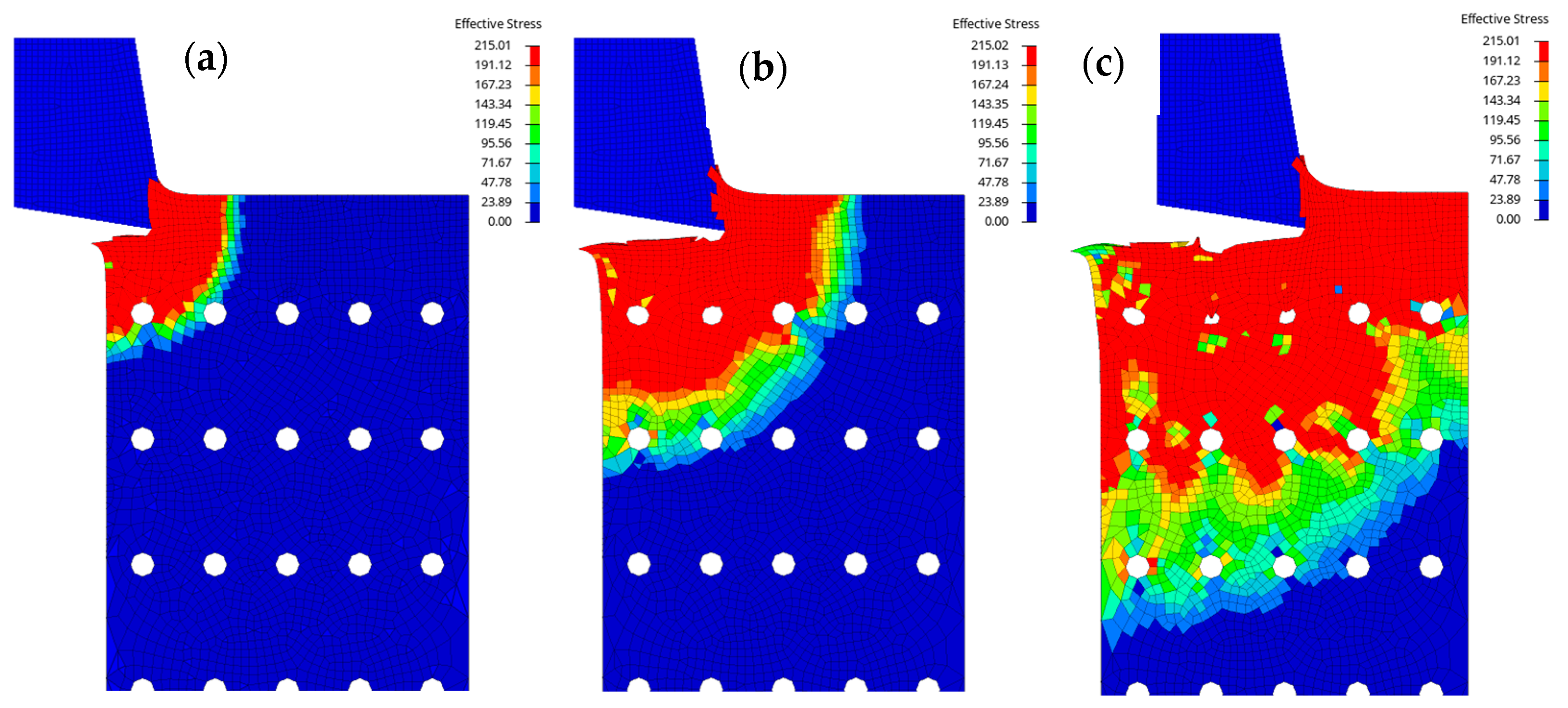
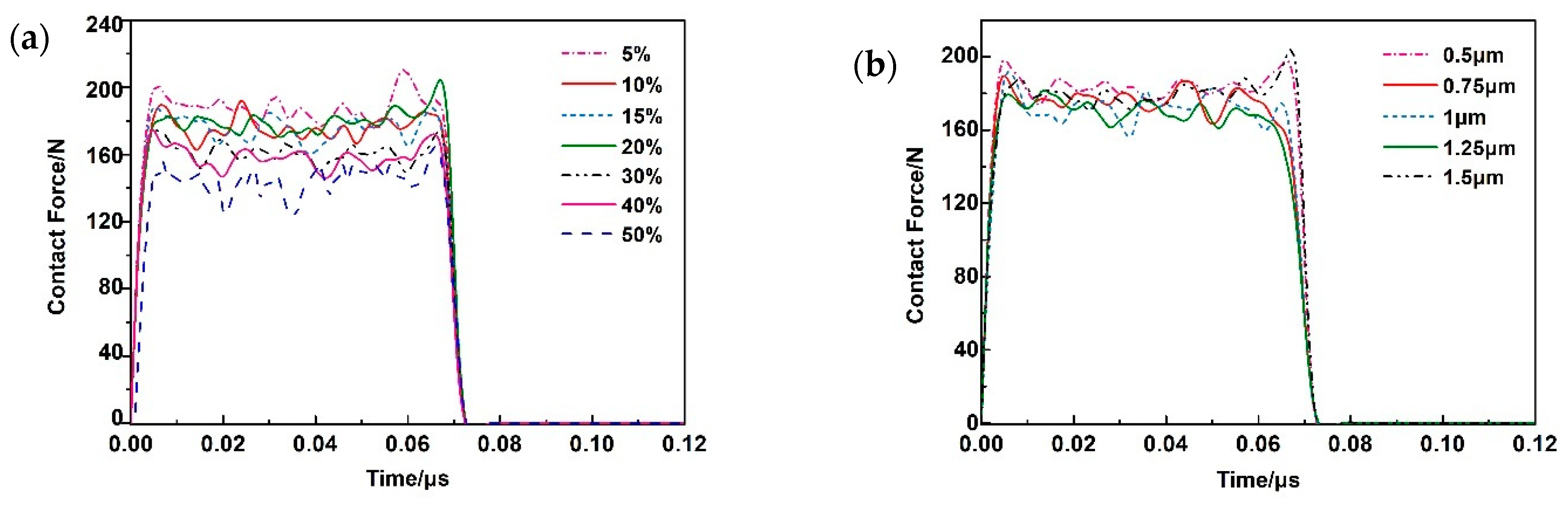
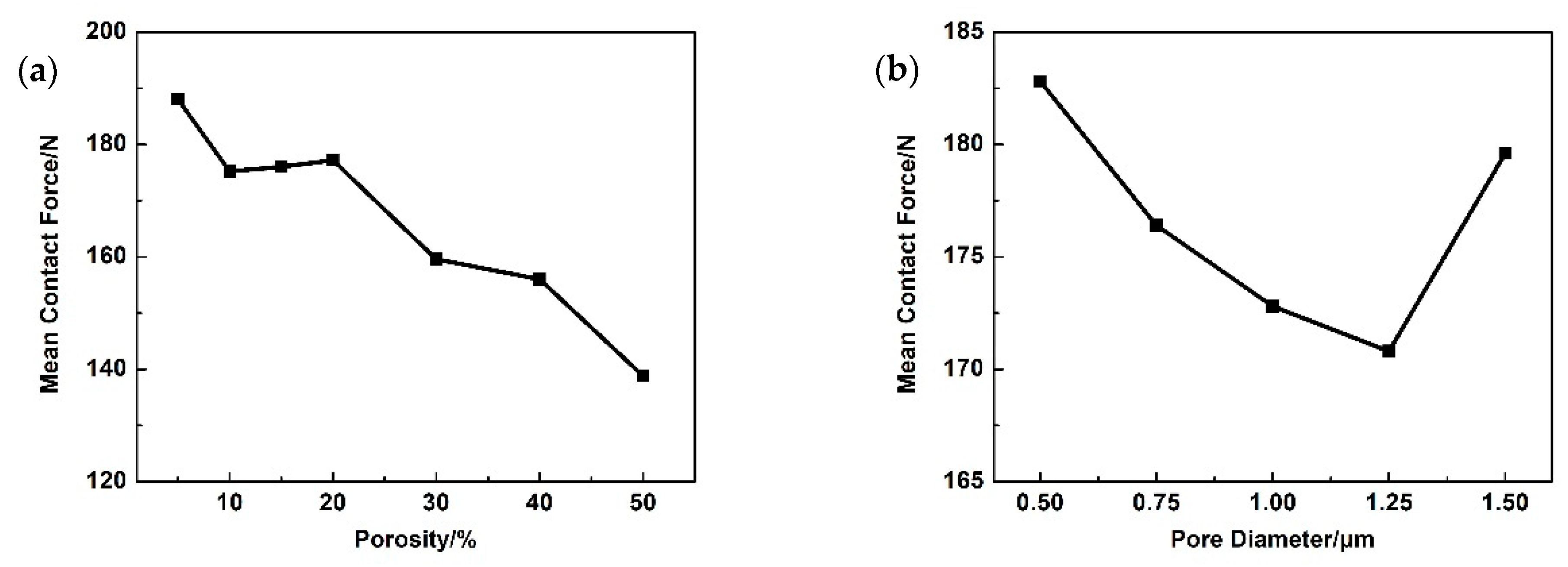
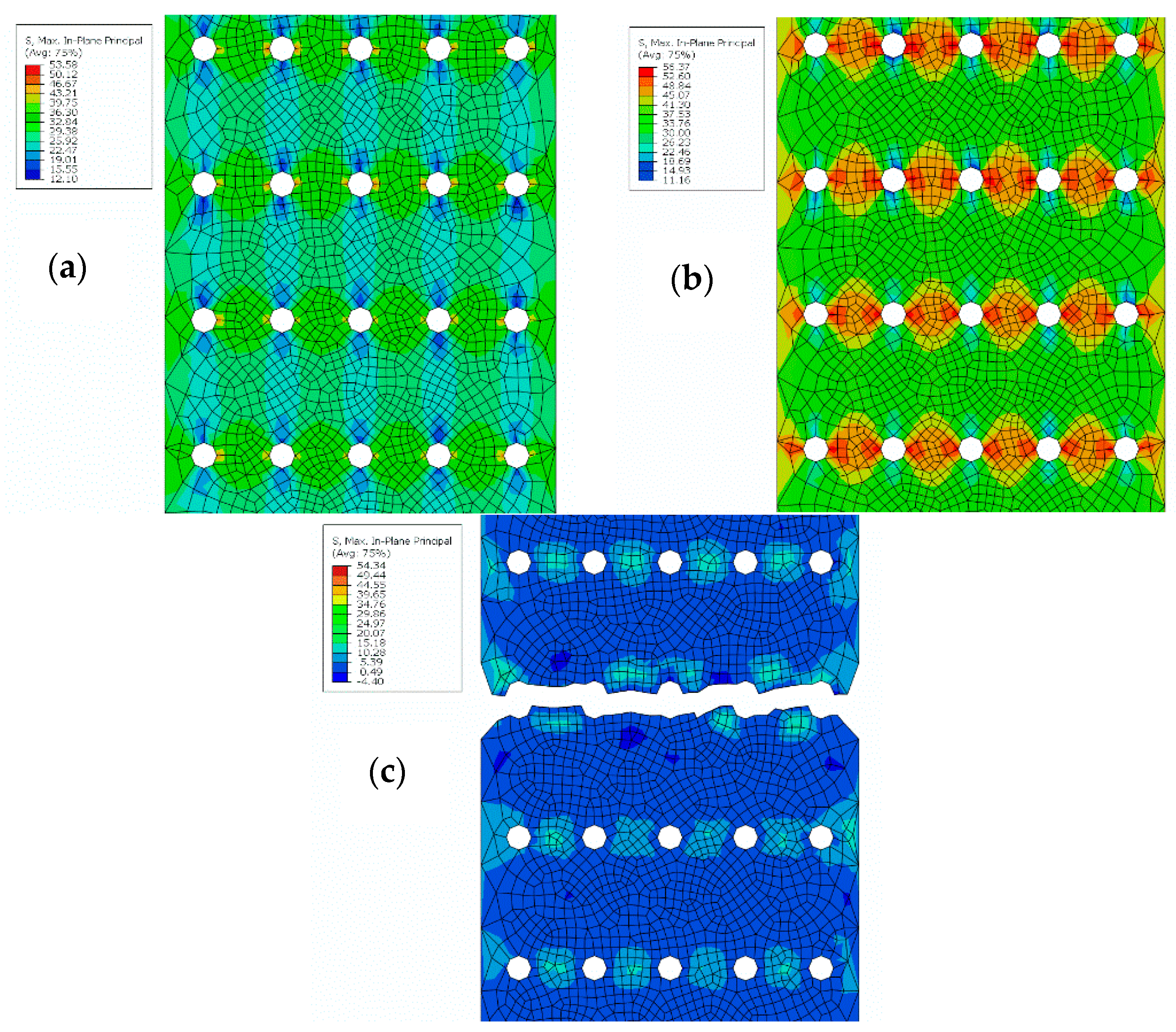
3.1. Abradability and Scraping Process Simulation
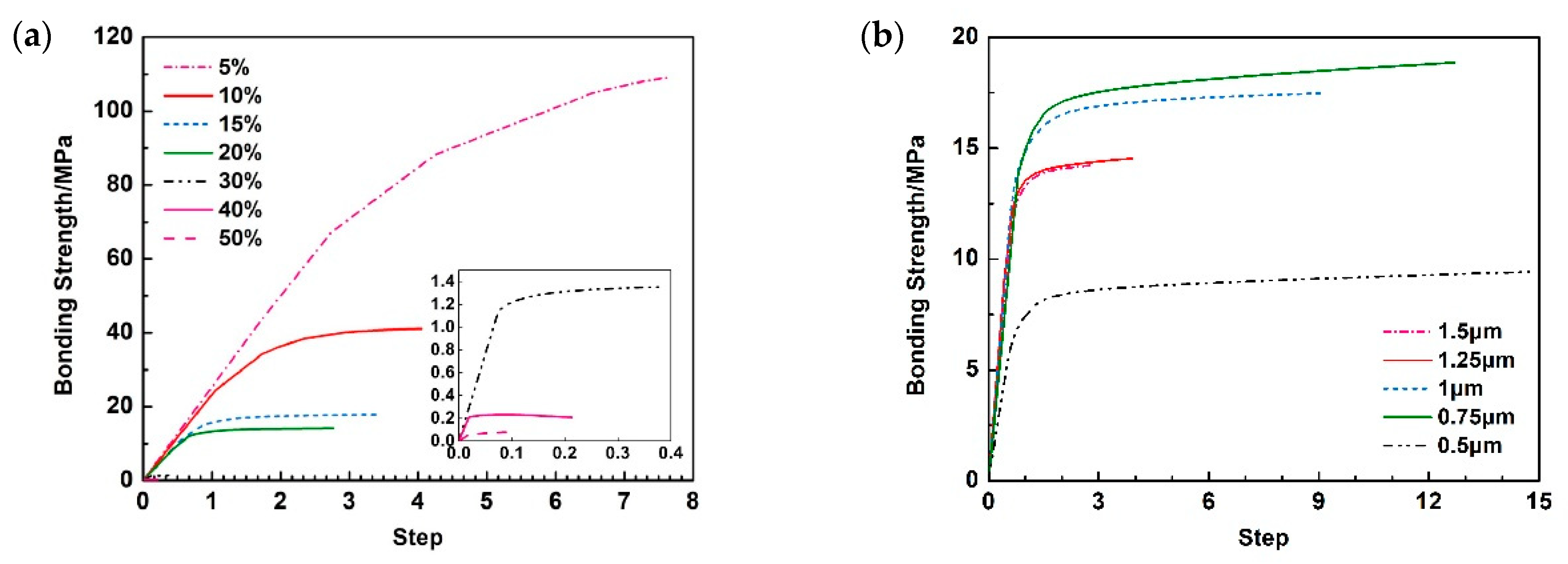
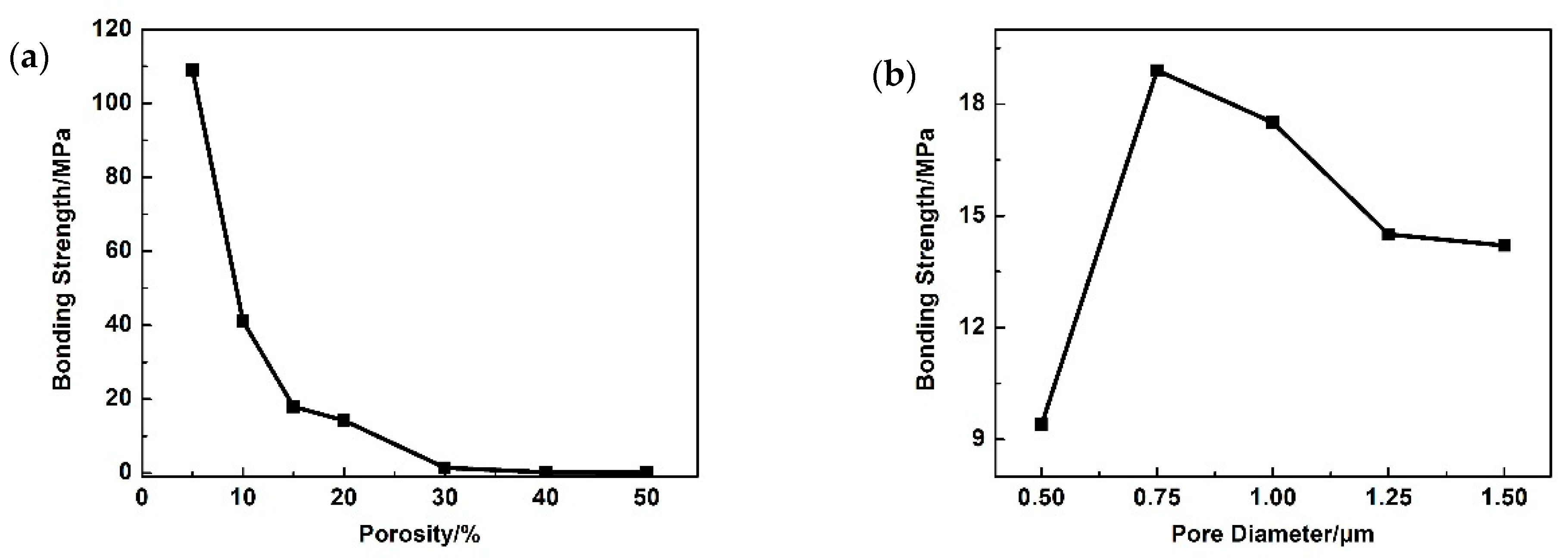
3.2. Bonding Strength and Tensile Test Simulation
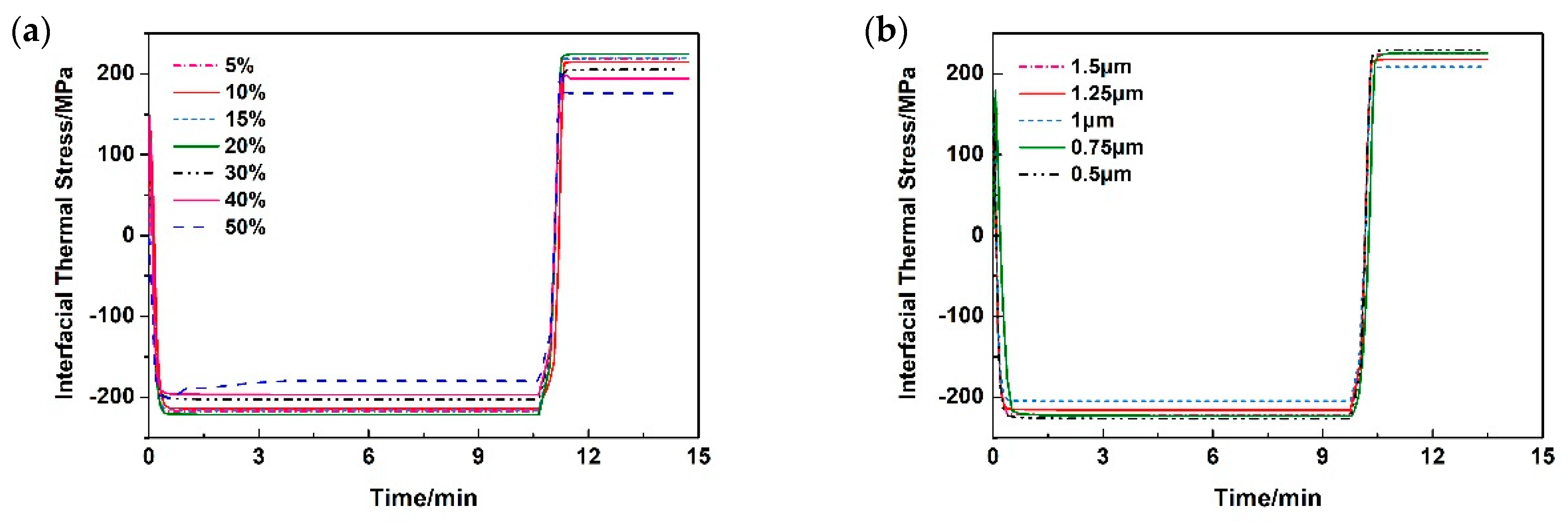
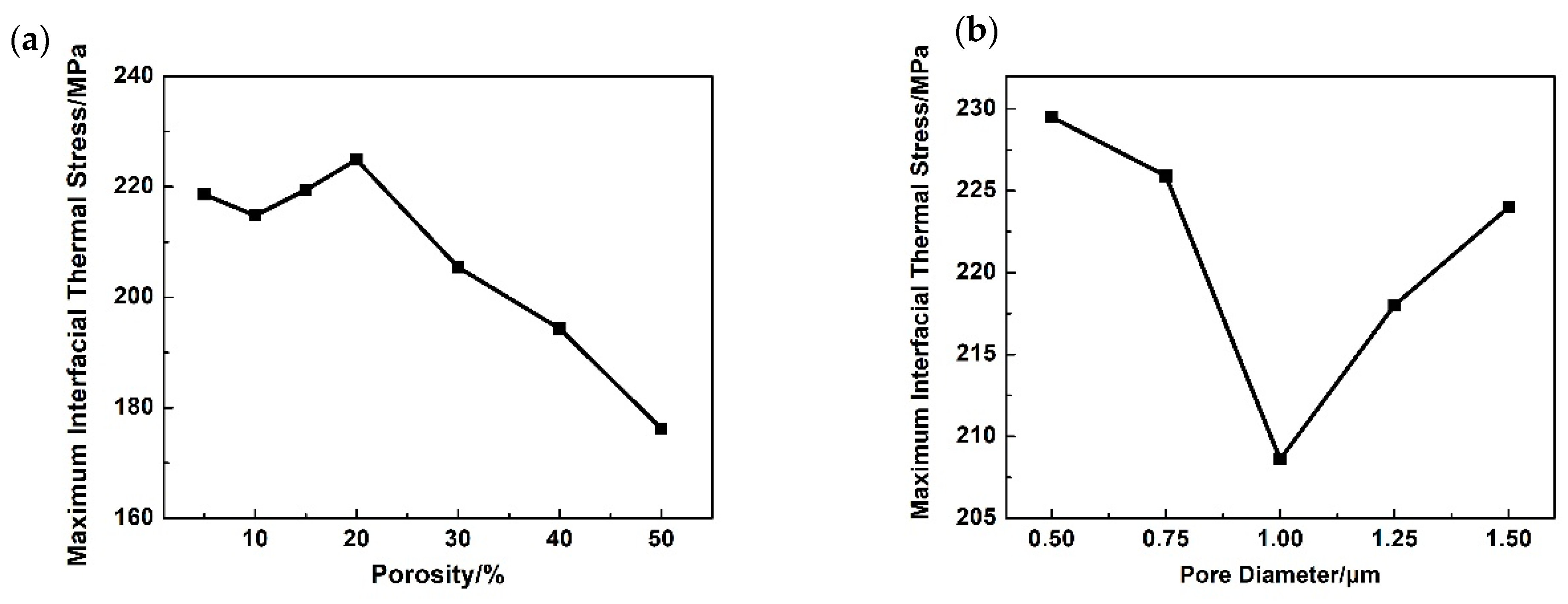
3.3. Thermal Shock Resistance and Thermal Cycling Process Simulation
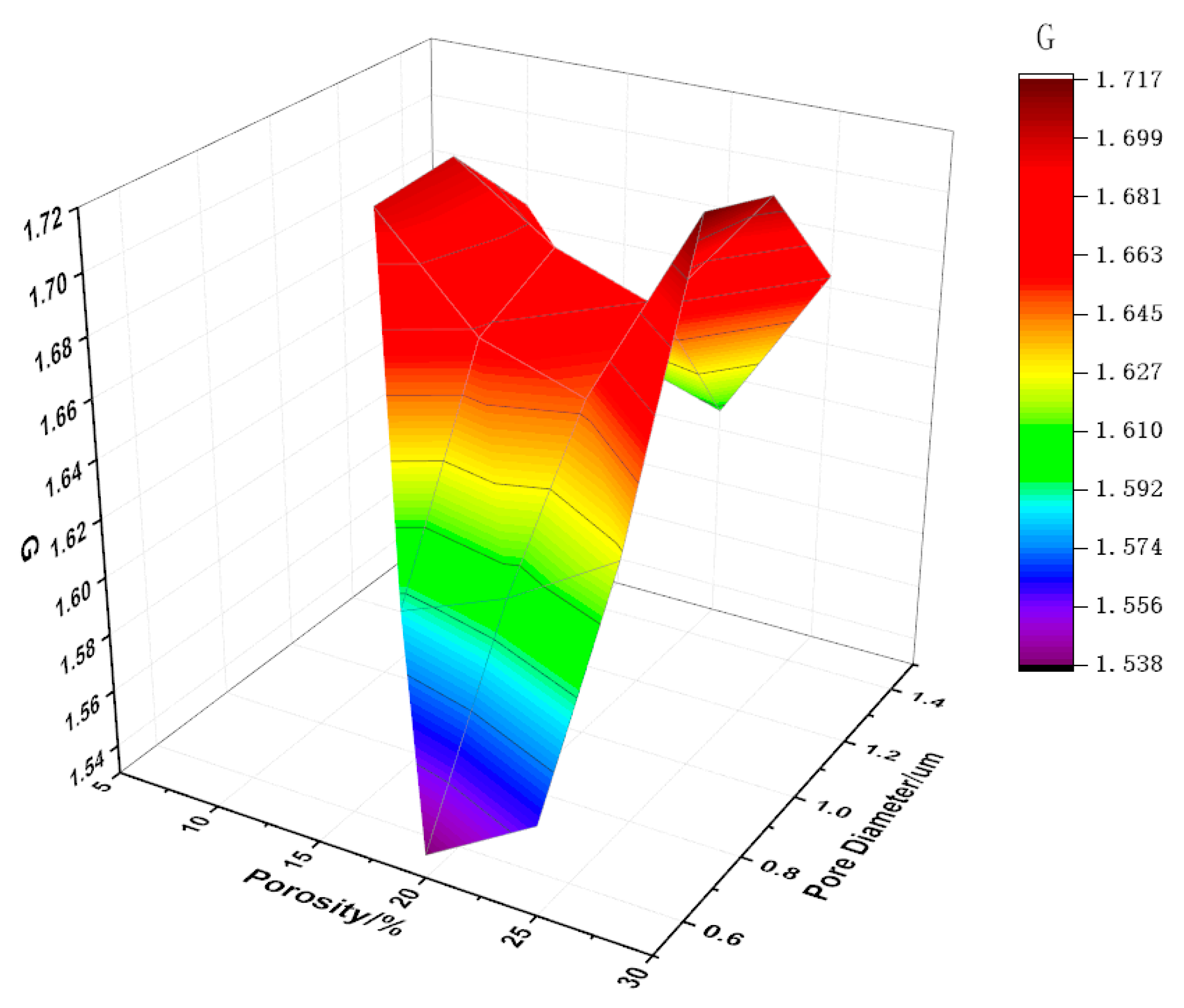
3.4. Comprehensive Performance Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ye, X.; Tan, J.; Song, H.; Zhang, Q. Study Advances of Blade Tip Coatings for Aero-Engine. Mater. Prot. 2018, 2, 87–94. [Google Scholar] [CrossRef]
- Rajendran, R. Gas Turbine Coatings—An Overview. Eng. Fail. Anal. 2012, 26, 355–369. [Google Scholar] [CrossRef]
- Sporer, D.; Wilson, S.; Giovannetti, I.; Refke, A.; Giannozzi, M. On the potential of metal and ceramic based abradables in turbine seal applications. In Proceedings of the 36th Turbomachinery Symposium, Colorado Springs, CO, USA, 22–26 August 2007; pp. 79–86. Available online: https://www.researchgate.net/publication/284088243_On_the_potential_of_metal_and_ceramic_based_abradables_in_turbine_seal_applications (accessed on 27 February 2022).
- Bartsch, M.; Baufeld, B.; Dalkiliç, S.; Mircea, I. Testing and Characterization of Ceramic Thermal Barrier Coatings. Mater. Sci. Forum. 2005, 492–493, 3–8. [Google Scholar] [CrossRef]
- Sporer, D.; Wilson, S.; Dorfman, M. Ceramics for Abradable Shroud Seal Applications. In Advanced Ceramic Coatings and Interfaces IV; Zhu, D., Lin, H.T., Singh, D., Salem, J., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2009; pp. 39–54. [Google Scholar]
- Zhao, M.; Zhang, L.X.; Pan, W. Properties of Yttria-Stabilized-Zirconia Based Ceramic Composite Abradable Coatings. Key Eng. Mater. 2012, 512–515, 1551–1554. [Google Scholar] [CrossRef]
- Carpio, P.; Salvador, M.D.; Benavente, R.; Miranda, M.; Borrell, A.; Sánchez, E. Impact of feedstock nature on thermal conductivity of YSZ thermal barrier coatings obtained by plasma spraying. J. Ceram. Sci. Technol. 2016, 7, 307–312. [Google Scholar] [CrossRef]
- Aussavy, D.; Bolot, R.; Montavon, G.; Peyraut, F.; Szyndelman, G.; Gurt-Santanach, J.; Selezneff, S. YSZ-Polyester Abradable Coatings Manufactured by APS. J. Therm. Spray Technol. 2016, 25, 252–263. [Google Scholar] [CrossRef]
- Bardi, U.; Giolli, C.; Scrivani, A.; Rizzi, G.; Borgioli, F.; Fossati, A.; Partes, K.; Seefeld, T.; Sporer, D.; Refke, A. Development and investigation on new composite and ceramic coatings as possible abradable seals. J. Therm. Spray Technol. 2008, 17, 805–811. [Google Scholar] [CrossRef]
- Sporer, D.; Dorfman, M.; Xie, L.; Refke, A.; Giovannetti, I.; Giannozzi, M. Processing and Properties of Advanced Ceramic Abradable Coatings. In Proceedings of the International Thermal Spray Conference and Exposition, Beijing, China, 14–16 May 2007; pp. 143–148. [Google Scholar]
- Ren, X.; Guo, S.; Zhao, M.; Pan, W.; Ren, X.; Guo, S.; Zhao, M.; Pan, W. Thermal conductivity and mechanical properties of YSZ/LaPO4 composites. J. Mater. Sci. 2014, 49, 2243–2251. [Google Scholar] [CrossRef]
- Kim, S.H.; Sekino, T.; Kusunose, T.; Hirvonen, A.T. Thermal properties and microstructure of zirconia/monazite-type LaPO4 composites for powder preparation methods. Mater. Sci. Forum 2007, 544–545, 909–912. [Google Scholar] [CrossRef]
- Scrivani, A.; Rizzi, G.; Berndt, C.C. Enhanced Thick Thermal Barrier Coatings that Exhibit Varying Porosity. Mater. Sci. Eng. A 2008, 476, 1–7. [Google Scholar] [CrossRef]
- Scrivani, A.; Rizzi, G.; Bardi, U.; Giolli, C.; Miranda, M.M.; Ciattini, S.; Fossati, A.; Borgioli, F. Thermal Fatigue Behavior of Thick and Porous Thermal Barrier Coatings Systems. J. Therm. Spray Technol. 2007, 16, 816–821. [Google Scholar] [CrossRef]
- MForoushani, M.H.; Shamanian, M.; Salehi, M.; Davar, F. Porosity analysis and oxidation behavior of plasma sprayed YSZ and YSZ/LaPO4 abradable thermal barrier coatings. Ceram. Int. 2016, 42, 15868–15875. [Google Scholar] [CrossRef]
- Kavaliauskas, Z.; Kėželis, R.; Milieška, M.; Marcinauskas, L.; Valinčius, V.; Aikas, M.; Uscila, R.; Baltušnikas, A.; Žunda, A. Influence of different plasma spraying methods on the physical properties of YSZ coatings. Surf. Interfaces 2021, 24, 101120. [Google Scholar] [CrossRef]
- Wang, J.; Bai, L.; Ma, F.; Wan, S.; Yi, G.; Sun, J.; Tian, X.; Yang, Z. Evaluation of microstructure evolution of thermal barrier YSZ coating after thermal exposure. Ceram. Int. 2022, 48, 6681–6690. [Google Scholar] [CrossRef]
- Batailly, A.; Legrand, M.; Millecamps, A.; Garcin, F. Numerical-experimental comparison in the simulation of rotor/stator interaction through blade-tip/abradable coating contact. J. Eng. Gas Turbines Power 2012, 134, 082504-1-11. [Google Scholar] [CrossRef]
- Berthoul, B.; Batailly, A.; Stainier, L.; Legrand, M.; Cartraud, P. Phenomenological modeling of abradable wear in turbomachines. Mech. Syst. Signal Process. 2018, 98, 770–785. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.W.; Ren, Z.W.; Chen, W.Z.; Zou, Z.F. Simulation research on wear of optimum design coated carbide turning tools. Mach. Tool Hydraul. 2021, 49, 141–145. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, W.; Zhang, L. Microstructure-based model of fracture of particulate reinforced metal matrix composites. Compos. Part B 2019, 163, 384–392. [Google Scholar] [CrossRef]
- Li, B.; Zhao, M.Y.; Wan, X.P. Influence of irregular-void on transverse tensile mechanical properties of composites. Acta Mater. Compos. Sin. 2019, 36, 356–361. [Google Scholar] [CrossRef]
- Limarga, A.M.; Vaßen, R.; Clarke, D.R. Stress Distributions in Plasma-Sprayed Thermal Barrier Coatings Under Thermal Cycling in a Temperature Gradient. J. Appl. Mech. 2011, 78, 011003-1-9. [Google Scholar] [CrossRef]
- Torkashvand, K.; Poursaeidi, E.; Ghazanfarian, J. Experimental and Numerical Study of Thermal Conductivity of Plasma-Sprayed Thermal Barrier Coatings with Random Distributions of Pores. Appl. Therm. Eng. 2018, 137, 494–503. [Google Scholar] [CrossRef]
- Liu, J.; Yu, Y.; Liu, T.; Cheng, X.; Shen, J.; Li, C. The Influence of Composition and Microstructure on the Abradability of Aluminum-Based Abradable Coatings. J. Therm. Spray Technol. 2017, 26, 1095–1103. [Google Scholar]
- Lu, Q.Y.; Shen, J.; Yu, Y.G.; Ren, X.J.; Xuan, H.J.; Liu, T. Progress on Facilities and Methodology to Evaluate Abradable Seal Coatings. Adv. Mater. Res. 2013, 690–693, 1992–1998. [Google Scholar] [CrossRef]
- Cheng, X.; Yu, Y.; Zhang, D.; Liu, T.; Liu, J.; Shen, J. Preparation and Performance of an Abradable NiCrFeAlBN-YSZ-NiCrAl Layered Seal Coating for Aircraft Engines. J. Therm. Spray Technol. 2020, 29, 1804–1814. [Google Scholar] [CrossRef]
- Gao, P.; Zeng, S.; Jin, C.; Zhang, B.; Chen, B.; Yang, Z.; Guo, Y.; Liang, M.; Li, J.; Wang, W.; et al. Mechanical Properties of Multi-Sized Porous Thermal Barrier Coatings at Micro and Nano Scales after Long-Term Service at High Temperature. Coatings 2022, 12, 165. [Google Scholar] [CrossRef]
- Brinkiene, K.; Kezelis, R.; Brinkiene, K.; Kezelis, R. Correlations between processing parameters and microstructure for YSZ films produced by plasma spray technique. J. Eur. Ceram. Soc. 2004, 24, 1095–1099. [Google Scholar] [CrossRef]
- Khor, K.; Gu, Y.; Dong, Z.; Khor, K.; Gu, Y.; Dong, Z. Mechanical behavior of plasma sprayed functionally graded YSZ/NiCoCrAlY composite coatings. Surf. Coat. Technol. 2001, 139, 200–206. [Google Scholar] [CrossRef]
- Steffens, H.D.; Babiak, Z.; Gramlich, M. Some Aspects of Thick Thermal Barrier Coating Lifetime Prolongation. J. Therm. Spray Technol. 1999, 8, 517–522. [Google Scholar] [CrossRef]
- Gao, P.-H.; Zeng, S.-C.; Jin, C.; Zhang, B.; Chen, B.-Y.; Yang, Z.; Guo, Y.-C.; Liang, M.-X.; Li, J.-P.; Li, Q.-P.; et al. Thermal Conductivity of Multi-Sized Porous Thermal Barrier Coatings at Micro and Nano Scales after Long-Term Service at High Temperatures. Coatings 2021, 11, 1183. [Google Scholar] [CrossRef]



| Coating | Technology | Argon Flow Rate/slpm | Hydrogen Flow Rate/slpm | Powder Feed Rate/g/min | Power/kw | Spray Distance/mm | Vacuum/mbar |
|---|---|---|---|---|---|---|---|
| MCrAlY | Low-pressure plasma spraying | 100~105 | 10~12 | 100 | 70~75 | 380~420 | 15~35 |
| YSZ | High energy plasma spraying | 50~55 | 12~16 | 200 | 50~60 | 110~130 | / |
| Porosity | 5% | 10% | 15% | 20% | 30% | 40% | 50% | |
|---|---|---|---|---|---|---|---|---|
| Pore Diameter | ||||||||
| 0.5 μm | / | / | / | ● | / | / | / | |
| 0.75 μm | / | / | / | ● | / | / | / | |
| 1 μm | / | / | / | ● | / | / | / | |
| 1.25 μm | / | / | / | ● | / | / | / | |
| 1.5 μm | ● | ● | ● | ● | ● | ● | ● | |
| Simulation Type | Software | Geometry Size | Boundary Conditions | Calculation Terminating Criteria |
|---|---|---|---|---|
| Abradability | LS-DYNA (ANSYS) | 25 μm × 10 μm | The bottom and the side faces were immobilized; the blade-tip penetrated the coating surface (depth: 0.3 μm) to scrape the coating surface at a velocity of 350 m/s. | Blade displacement > 25 μm |
| Bonding strength | ABAQUS | Coating: 30 μm × 1.5 mm Substrate: 30 μm × 3 mm | The substrate bottom was immobilized and a tensile load is applied to the coating surface. Moreover, the initial load was set at 0 N and then gradually increased until tensile failure occurred in the model. | σmax > σb, σb = 215 MPa (in Table 4) |
| Thermal shock resistance | The model experienced heat preservation for 10 min at an external environment temperature of 1050 °C and then cooled down to 25 °C within 3 min. The thermal load was applied to the surface of the coating. | t > 15 min |
| Material | T (°C) | E (GPa) | ν | σb (MPa) | Ρ (kg/m3) | α (ppm/°C) | λ (W/m·K) | C (J/kg·K) |
|---|---|---|---|---|---|---|---|---|
| IN-738 | 26 | 202 | 0.3 | 953 | 8500 | 11.44 | 8.72 | 428 |
| 650 | 165 | 817 | 14.44 | 19.66 | 594 | |||
| 800 | 156 | 789 | 15.16 | 22.28 | 636 | |||
| 900 | 150 | 555 | 15.64 | 24.03 | 675 | |||
| 1000 | 144 | 344 | 16.12 | 25.78 | 727 | |||
| YSZ | 25 | 50 | 0.25 | 215 | 5100 | 10.00 | 0.70 | 479 |
| 500 | 9.64 | 445 | ||||||
| 1000 | 10.34 | 445 |
| Type | Index | Experimental Data | Simulation Data | Error |
|---|---|---|---|---|
| Abradability | The contact force of the blade-scraping coating | 164.8 N | 176 N | 6.3% |
| Bonding strength | Tensile fracture strength | 13.8 MPa | 14.2 MPa | 3.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, X.; Yu, Y.; Liu, J.; Guo, D.; Lu, X.; Zhang, D.; Zhao, X.; Dai, S. Mesoscale Simulation and Evaluation of the Mechanical Properties of Ceramic Seal Coatings. Coatings 2022, 12, 438. https://doi.org/10.3390/coatings12040438
Cheng X, Yu Y, Liu J, Guo D, Lu X, Zhang D, Zhao X, Dai S. Mesoscale Simulation and Evaluation of the Mechanical Properties of Ceramic Seal Coatings. Coatings. 2022; 12(4):438. https://doi.org/10.3390/coatings12040438
Chicago/Turabian StyleCheng, Xuying, Yueguang Yu, Jianming Liu, Dan Guo, Xiaoliang Lu, Deming Zhang, Xuhe Zhao, and Sihang Dai. 2022. "Mesoscale Simulation and Evaluation of the Mechanical Properties of Ceramic Seal Coatings" Coatings 12, no. 4: 438. https://doi.org/10.3390/coatings12040438
APA StyleCheng, X., Yu, Y., Liu, J., Guo, D., Lu, X., Zhang, D., Zhao, X., & Dai, S. (2022). Mesoscale Simulation and Evaluation of the Mechanical Properties of Ceramic Seal Coatings. Coatings, 12(4), 438. https://doi.org/10.3390/coatings12040438





