Modeling Technology of Bonded Particle Model for Gold Ore and Its Validation Based on Drop Weight Test
Abstract
:1. Introduction
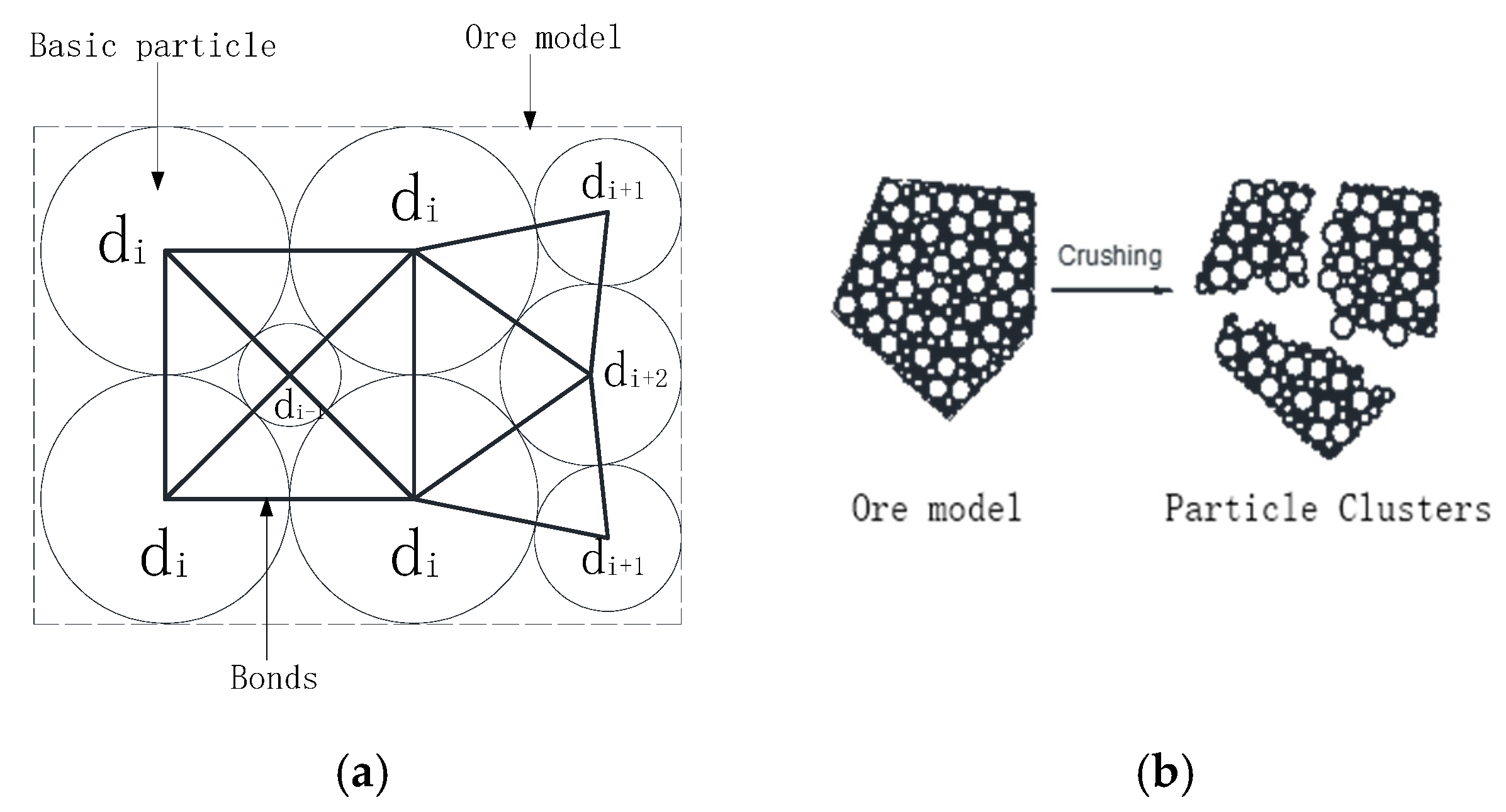
2. Bonded Particle Model
3. Mineral Crushing Methods
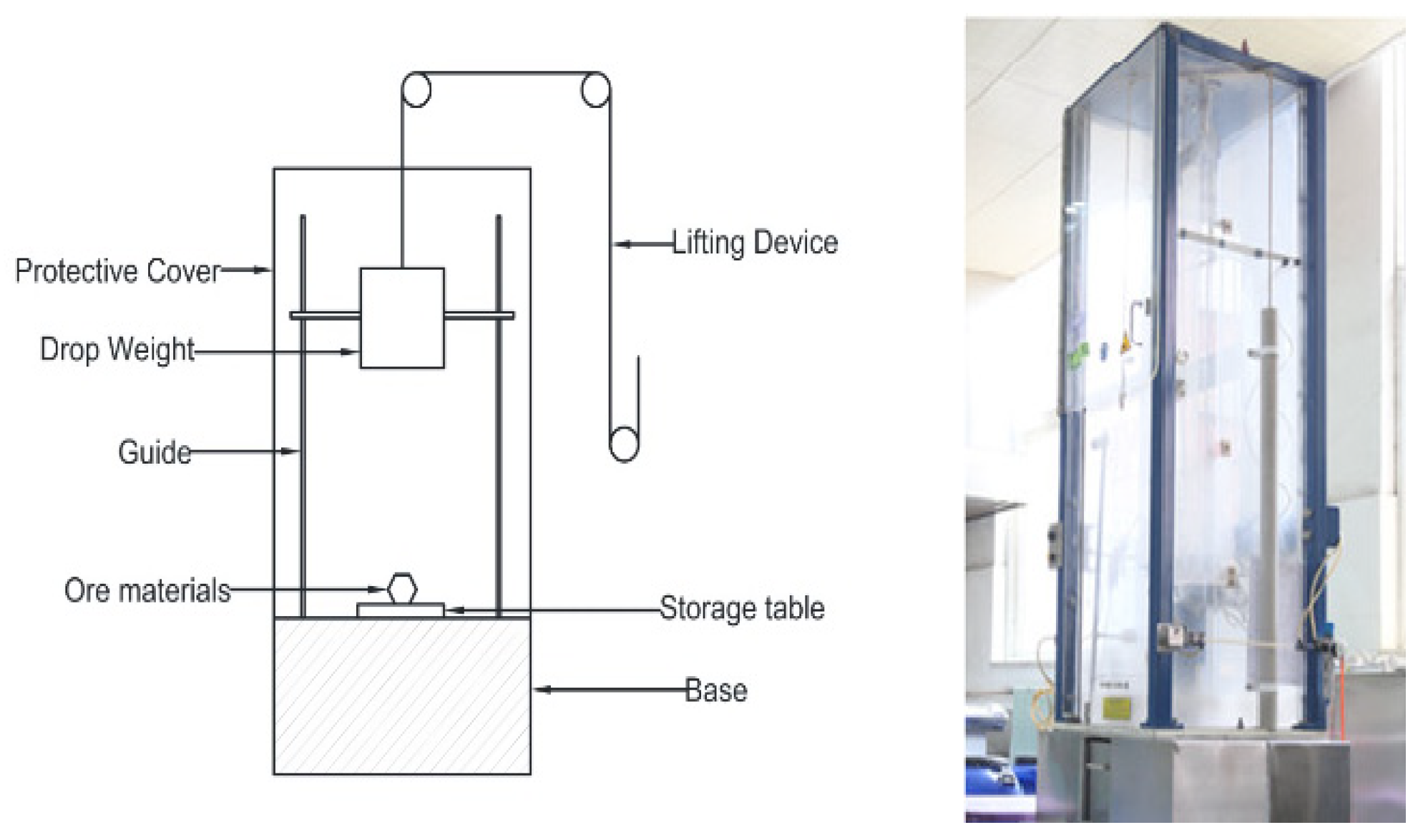
3.1. Drop Weight Test Method
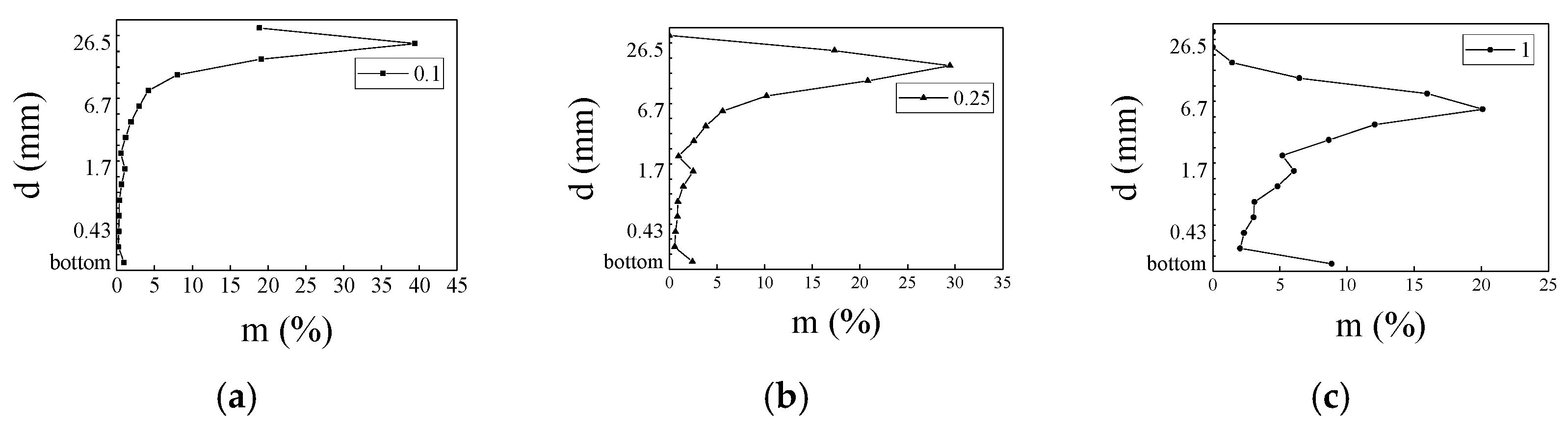
3.2. Mineral Crushing Size Distribution
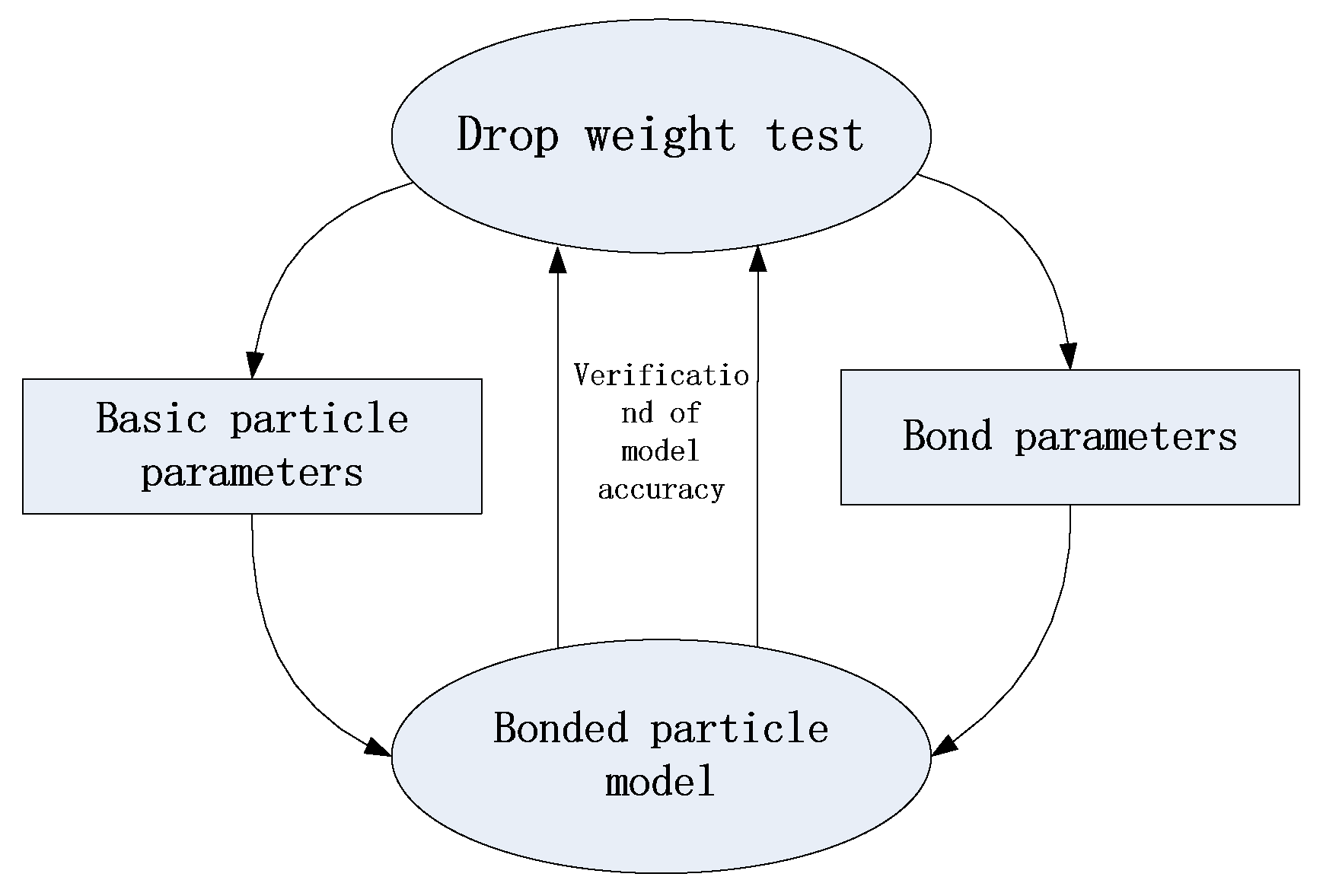
4. Determination of Model Parameters
4.1. The Diameter of the Basic Particle
4.1.1. The Method Adopted for the Determination of the Basic Particle’s Diameter
4.1.2. Determination of Basic Particle Diameters Based on the Drop Weight Test
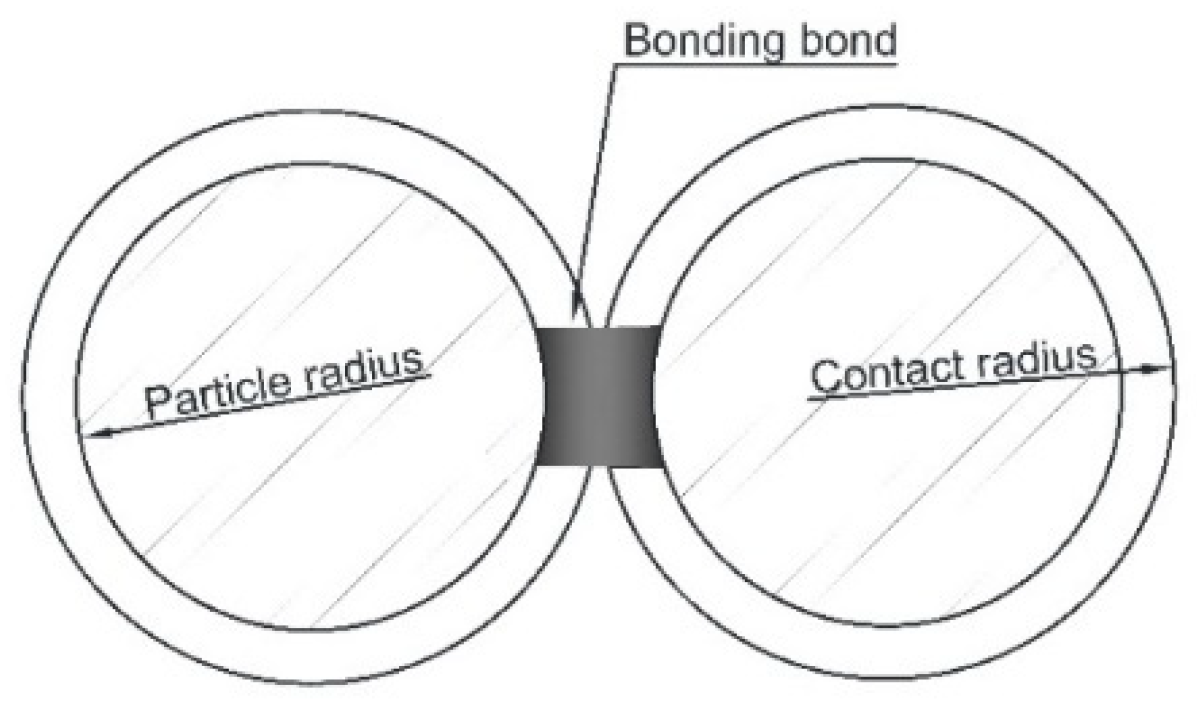
4.2. Bond Parameters between Particles
4.2.1. Determination Method of Bond Parameters
4.2.2. Determination of Bond Parameters in the Model
5. Simulation and Analysis of the Impact Crushing Process
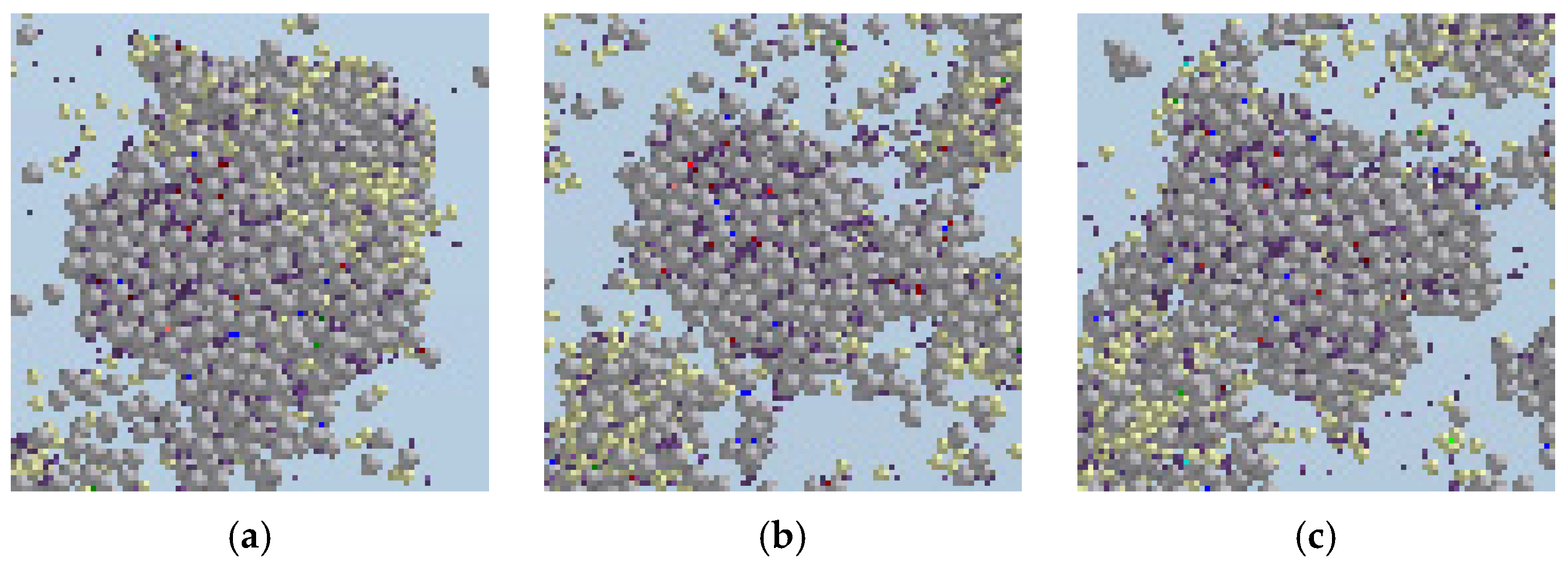
5.1. Modeling of the Crushing of Cohesive Multi-Particle Minerals
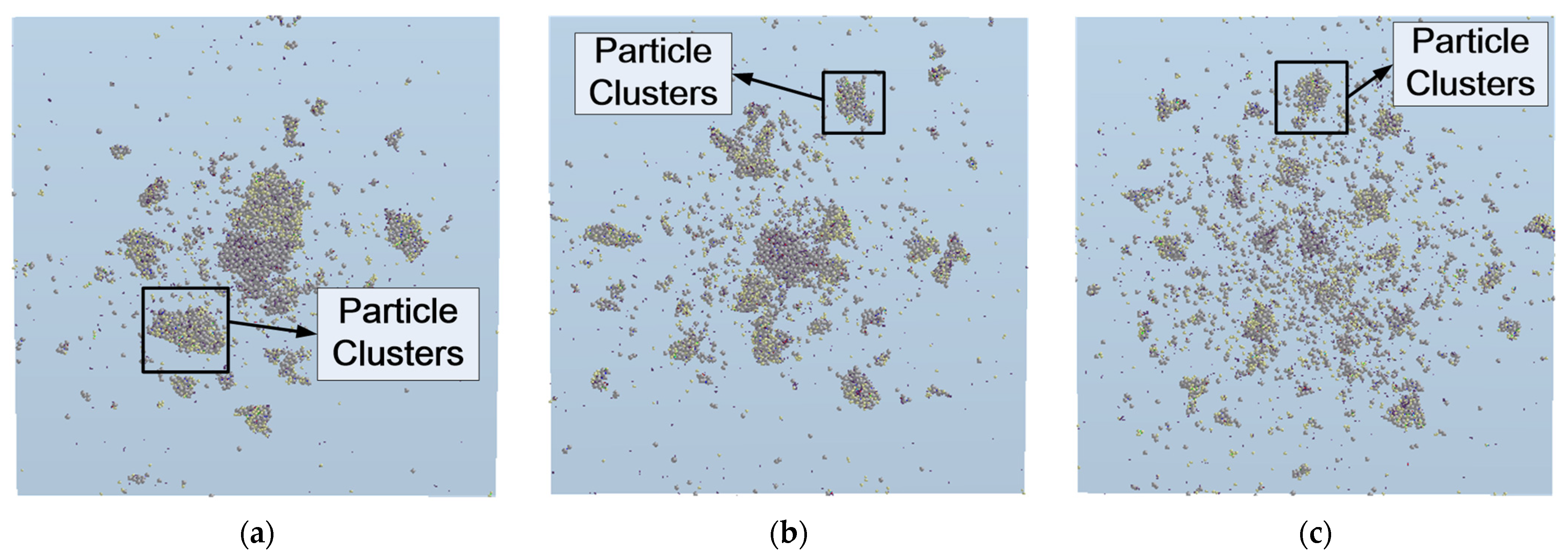
5.2. Discrete Element Simulation of the Mineral Crushing Process
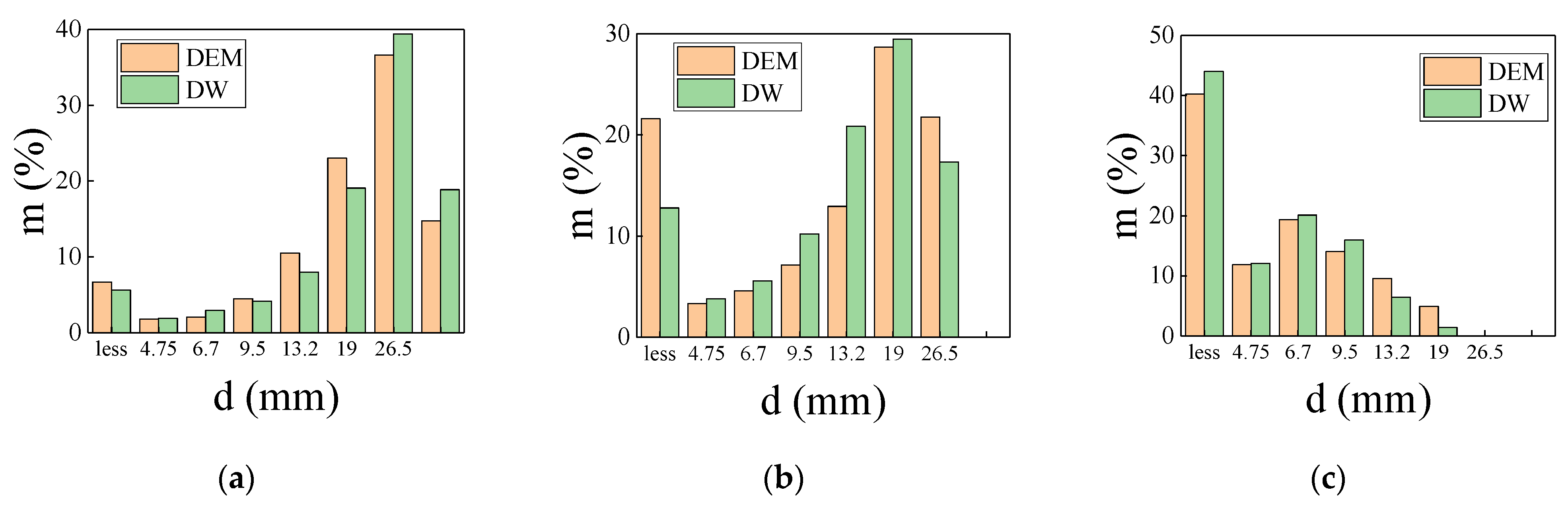
5.3. Comparison of Simulation and Test Results
6. Conclusions
- (1)
- A method of determining the basic particle type and the sizes of particles based on the sieve size distribution in the drop weight test was realized. When modeling ore 45–37.5 mm in size, a high-precision model can be obtained that considers the particle sizes of three kinds of basic particles to be 1, 2, and 3 mm.
- (2)
- The parameter setting and bond verification method was created. The bond parameters are set as per the actual ore strength parameters in the drop weight test. By comparing the broken particle size distribution obtained by simulation and drop weight test, the accuracy of the model was verified. The maximum mass distribution error of the model was no more than 3.31%.
- (3)
- Based on the proposed methodologies of the selection of particle size and bond parameters in mineral crushing processes in this paper, the discrete element method (DEM) can be used for mineral crushing simulation with accurate results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rasoul, P.; Kianoush, B. The effect of ball size distribution on power draw, charge motion and breakage mechanism of tumbling ball mill by discrete element method (DEM) simulation. Physicochem. Probl. Miner. Process. 2018, 54, 258–269. [Google Scholar]
- Nagata, Y.; Minagawa, M.; Hisatomi, S.; Tsunazawa, Y.; Okuyama, K.; Iwamoto, M.; Sekine, Y.; Tokoro, C. Investigation of optimum design for nanoparticle dispersion in centrifugal bead mill using DEM-CFD simulation. Adv. Powder Technol. 2019, 30, 1034–1042. [Google Scholar] [CrossRef]
- Jia, L.; Erich, B.; Wei, W. A combined method to model grain crushing with DEM. Geosci. Front. 2020, 11, 451–459. [Google Scholar]
- Kinaci, M.; Lichtenegger, T.; Schneiderbauer, S. A CFD-DEM model for the simulation of direct reduction of iron-ore in fluidized beds. Chem. Eng. Sci. 2020, 227, 115858. [Google Scholar] [CrossRef]
- Wentao, Z.; Yuexin, H.; Yanjun, L.; Jinlin, Y.; Shaojian, M.; Yongsheng, S. Research on prediction model of ore grinding particle size distribution. J. Dispers. Sci. Technol. 2019, 41, 537–546. [Google Scholar] [CrossRef]
- Cheng, Y.; Wong, L.N.Y. A study on mechanical properties and fracturing behavior of Carrera marble with the flat-jointed model. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 803–822. [Google Scholar] [CrossRef]
- Castro, F.U.; Alejano, L.R.; Ivars, D.M. Particle flow code simulation of intact and fissured granitic rock samples. J. Rock Mech. Geotech. Eng. 2020, 12, 960–974. [Google Scholar] [CrossRef]
- Xie, C.; Zhao, Y.; Song, T.; Zhao, Y. Investigation of the effect of filling level on the wear and vibration of a SAG mill by DEM. Particuology 2021, 63, 24–34. [Google Scholar] [CrossRef]
- Abid, S.R.; Abdul-Hussein, M.L.; Ayoob, N.S.; Ali, S.H.; Kadhum, A.L. Repeated drop-weight impact tests on self-compacting concrete reinforced with micro-steel fiber. Heliyon 2020, 6, e03198. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Han, Y.; Li, Y.; Sun, Y.; Yang, J.; Ma, S. Establishment and prediction of impact crushing particle size distribution model. Chin. J. Nonferrous Met. 2019, 29, 1316–1323. [Google Scholar] [CrossRef]
- Zhou, W.; Han, Y.; Li, Y.; Sun, Y.; Yang, J.; Ma, S. Multi-scale impact crushing characteristics of polymetal licsulphide ores. Trans. Nonferrous Met. Soc. China 2019, 29, 1929–1938. [Google Scholar] [CrossRef]
- Vu, G.; Iskhakov, T.; Timothy, J.J.; Schulte-Schrepping, C.; Breitenbücher, R.; Meschke, G. Cementitious Composites with High Compaction Potential: Modeling and Calibration. Materials 2020, 13, 4989. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Aragón, C.; Ordieres-Meré, J.; Alba-Elías, F.; González-Marcos, A. Numerical Modeling for Simulation of Compaction of Refractory Materials for Secondary Steelmaking. Materials 2020, 13, 224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jargalsaikhan, B.; Bor, A.; Lee, J.; Choi, H. Effect of Different Raw Material Property for the Fabrication on Al/CNT Nanocomposite Using a Ball Mill with a Discrete Element Method (DEM) Simulation. Materials 2019, 12, 3291. [Google Scholar] [CrossRef] [Green Version]
- Horabik, J.; Wiącek, J.; Parafiniuk, P.; Stasiak, M.; Bańda, M.; Kobyłka, R.; Molenda, M. Discrete Element Method Modelling of the Diametral Compression of Starch Agglomerates. Materials 2020, 13, 932. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi-Chahardeh, A.; Mollaabbasi, R.; Picard, D.; Taghavi, S.; Alamdari, H. Discrete Element Method Modeling for the Failure Analysis of Dry Mono-Size Coke Aggregates. Materials 2021, 14, 2174. [Google Scholar] [CrossRef]
- Chen, J.; Furuichi, M.; Nishiura, D. Discrete Element Simulation and Validation of a Mixing Process of Granular Materials. Materials 2020, 13, 1208. [Google Scholar] [CrossRef] [Green Version]
- Rojek, J.; Madan, N.; Nosewicz, S. Micro–Macro Relationships in the Simulation of Wave Propagation Phenomenon Using the Discrete Element Method. Materials 2019, 12, 4241. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Wu, C.; Yin, H. Virtual Experiments of Particle Mixing Process with the SPH-DEM Model. Materials 2021, 14, 2199. [Google Scholar] [CrossRef]
- Ferretti, E. DECM: A Discrete Element for Multiscale Modeling of Composite Materials Using the Cell Method. Materials 2020, 13, 880. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Pan, L.; Wang, F.; Zhang, Z.; Cui, J.; Liu, H.; Duan, Z.; Ji, X. Three-Dimensional Discrete Element Analysis on Tunnel Face Instability in Cobbles Using Ellipsoidal Particles. Materials 2019, 12, 3347. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, H.; Huang, Y.; Liu, Z.; Liu, W.; Zheng, Z. Applications of Discrete Element Method in the Research of Agricultural Machinery: A Review. Agriculture 2021, 11, 425. [Google Scholar] [CrossRef]
- Yao, Z.; Wu, W.; Lin, F.; Li, Y. Study on Impact Crushing Energy of Coal Body Based on Impact Crushing Experiment. Coal Technol. 2019, 38, 73–75. [Google Scholar] [CrossRef]
- Hong, J.; Li, J.; Shen, Y.; Wang, X. Particle Fracture Model Based on the Discrete Element Method. J. Tianjin Univ. Sci. Technol. 2018, 51, 1253–1259. [Google Scholar] [CrossRef]
- Raisianzadeh, J.; Mohammadi, S.; Mirghasemi, A. Micromechanical study of particle breakage in 2D angular rock fill media using combined DEM and XFEM. Granul. Matter 2019, 21, 48. [Google Scholar] [CrossRef]
- Huang, X.; Qi, S.; Zheng, B.; Guo, S.; Liang, N.; Zhan, Z. Progressive Failure Characteristics of Brittle Rock under High-Strain-Rate Compression Using the Bonded Particle Model. Materials 2020, 13, 3943. [Google Scholar] [CrossRef]
- Sun, Y.; Nimbalkar, S.; Chen, C. Particle breakage of granular materials during sample preparation. J. Rock Mech. Geotech. Eng. 2019, 11, 203–208. [Google Scholar] [CrossRef]
- Xu, K.; Huang, W.; Wang, J.; Zhang, T.; Chen, G. Progress in numerical simulation study of rock particle crushing. Sci. Technol. Eng. 2019, 19, 8–14. [Google Scholar] [CrossRef]
- Mao, H. Experimental and Numerical Studies on the Direct Shear Behavior of Sand–RCA (Recycled Concrete Aggregates) Mixtures with Different Contents of RCA. Materials 2021, 14, 2909. [Google Scholar] [CrossRef]
- Qian, J.; Yao, Y.; Li, J.; Xiao, H.; Luo, S. Resilient Properties of Soil-Rock Mixture Materials: Preliminary Investigation of the Effect of Composition and Structure. Materials 2020, 13, 1658. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.A.; Potyondy, D.O. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Tavares, L.M.; Chagas, A. A stochastic particle replacement strategy for simulating breakage in DEM. Powder Technol. 2020, 377, 222–232. [Google Scholar] [CrossRef]
- Potyondy, D.O. A flat-jointed bonded-particle material for hard rock. In Proceedings of the 46th U.S. Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24–27 June 2012; American Rock Mechanics Association (ARMA): Alexandria, VA, USA, 2012. [Google Scholar]
- Potyondy, D.O. The bonded-particle model as a tool for rock mechanics research and application: Current trends and future directions. Geosystem Eng. 2015, 18, 1–28. [Google Scholar] [CrossRef]
- Potyondy, D.O. A flat-jointed bonded-particle model for rock. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018; American Rock Mechanics Association (ARMA): Alexandria, VA, USA, 2018. [Google Scholar]
- Mao, Y.; Sun, Y.; Ji, S.; Shan, J.; Jin, X. Nipped Configuration of Unconfined Particle Beds under Falling Ball Impact Test. China Mech. Eng. 2016, 27, 168–172. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, X.P.; Ji, P.Q.; Zhang, H.; Wu, Z. Study of interaction mechanisms between multiple parallel weak planes and hydraulic fracture using the bonded-particle model based on moment tensors. J. Nat. Gas Sci. Eng. 2020, 76, 103176. [Google Scholar] [CrossRef]


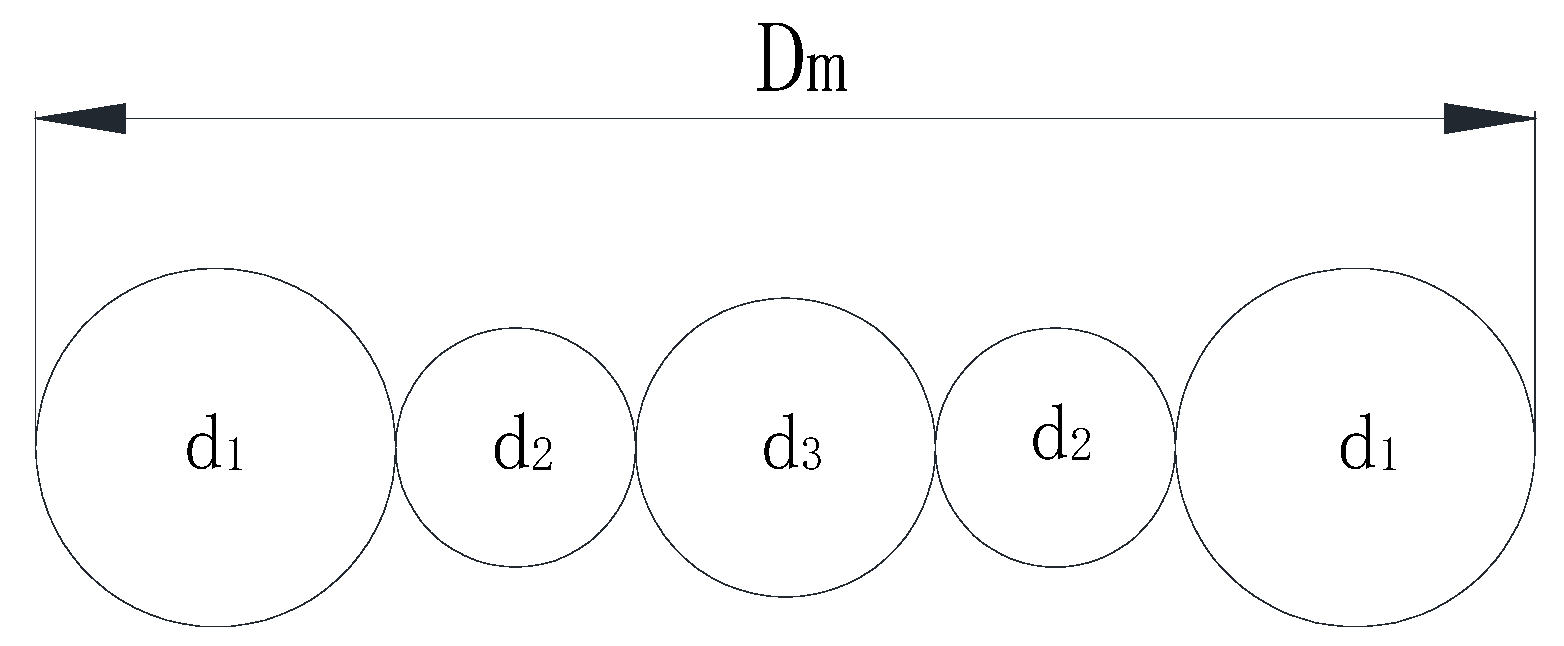

| Ore Size (mm) | 45–37.5 | ||
|---|---|---|---|
| Impact energy E (kWh/t) | 0.1 | 0.25 | 1 |
| Drop weight m (kg) | 4.76 | 14.95 | 49.91 |
| Drop height H (cm) | 99.69 | 79.25 | 94.14 |
| Group Number | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| Impact Energy E (kwh/t) | 0.10 | 0.25 | 1 | |||
| Sieving Size (mm) | Mass (g) | Percentage (%) | Mass (g) | Percentage (%) | Mass (g) | Percentage (%) |
| 37.50 | 355.30 | 18.87 | 0.00 | 0.00 | 0.00 | 0.00 |
| 26.50 | 742.20 | 39.41 | 325.30 | 17.33 | 0.00 | 0.00 |
| 19.00 | 359.70 | 19.10 | 553.00 | 29.46 | 26.90 | 1.43 |
| 13.20 | 150.60 | 8.00 | 391.00 | 20.83 | 121.30 | 6.44 |
| 9.50 | 78.60 | 4.17 | 191.50 | 10.20 | 300.60 | 15.97 |
| 6.70 | 55.50 | 2.95 | 104.90 | 5.59 | 378.30 | 20.10 |
| 4.75 | 35.60 | 1.89 | 71.80 | 3.82 | 227.10 | 12.06 |
| 3.35 | 22.10 | 1.17 | 48.10 | 2.56 | 162.50 | 8.63 |
| 2.36 | 10.10 | 0.54 | 17.90 | 0.95 | 97.50 | 5.18 |
| 1.70 | 20.60 | 1.09 | 46.70 | 2.49 | 113.70 | 6.04 |
| 1.18 | 12.00 | 0.64 | 27.20 | 1.45 | 90.70 | 4.82 |
| 0.85 | 6.90 | 0.37 | 16.50 | 0.88 | 58.30 | 3.10 |
| 0.60 | 6.30 | 0.33 | 15.70 | 0.84 | 57.10 | 3.03 |
| 0.43 | 5.20 | 0.28 | 12.10 | 0.64 | 43.70 | 2.32 |
| 0.30 | 4.40 | 0.23 | 10.30 | 0.55 | 38.10 | 2.02 |
| Sieve Bottom | 18.20 | 0.97 | 45.20 | 2.41 | 166.70 | 8.86 |
| Total | 1883.30 | 100.00 | 1877.20 | 100.00 | 1882.50 | 100.00 |
| Adjacent Particle Diameterd (mm) | Normal Stiffness per Unit Area Kn (N/m2) | Shear Stiffness per Unit Area Kt (N/m2) | Critical Normal Stress σ (Pa) | Critical Shear Stress τ (Pa) | Bonded Disk Radius r0 (mm) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 | Group 2 | Group 3 | Group 1 | Group 2 | Group 3 | |||||
| 1 | 1 | 8 × 107 | 8 × 107 | 8 × 107 | 5 × 107 | 5 × 107 | 5 × 107 | 30,000 | 30,000 | 0.6 |
| 2 | 2 | 7 × 107 | 7 × 107 | 7 × 107 | 4 × 107 | 4 × 107 | 4 × 107 | 31,000 | 31,000 | 1.1 |
| 3 | 3 | 6 × 107 | 5 × 107 | 4 × 107 | 3 × 107 | 2 × 107 | 2 × 107 | 32,000 | 32,000 | 1.6 |
| 1 | 2 | 5.5 × 107 | 5.5 × 107 | 5.5 × 107 | 2.5 × 107 | 2.5 × 107 | 2.5 × 107 | 33,000 | 33,000 | 0.6 |
| 2 | 3 | 5 × 107 | 4.5 × 107 | 3.5 × 107 | 2 × 107 | 1.5 × 107 | 1.5 × 107 | 34,000 | 34,000 | 1.1 |
| 1 | 3 | 4.5 × 107 | 4 × 107 | 2 × 107 | 1.5 × 107 | 1 × 107 | 7 × 106 | 35,000 | 35,000 | 0.6 |
| Bond Parameters Group | Group 1 | Group 2 | Group 3 |
|---|---|---|---|
| Maximum Size (mm) | 40.15 | 30.78 | 44.75 |
| Size d (mm) | 1 | 2 | 3 |
|---|---|---|---|
| Number n | 2500 | 1500 | 2000 |
| Sieving Size (mm) | Mass Percentage m (%) | ||
|---|---|---|---|
| E = 0.10 kwh/t | E = 0.25 kwh/t | E = 1 kwh/t | |
| 37.50 | 14.75 | 0.00 | 0.00 |
| 26.50 | 36.65 | 21.77 | 0.00 |
| 19.00 | 23.05 | 28.68 | 4.93 |
| 13.20 | 10.50 | 12.94 | 9.60 |
| 9.50 | 4.50 | 7.12 | 14.07 |
| 6.70 | 2.08 | 4.59 | 19.34 |
| 4.75 | 1.78 | 3.32 | 11.85 |
| Less than 4.75 | 6.69 | 21.58 | 40.22 |
| Total | 100 | 100 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Ma, X.; Zhang, M.; Huang, Y.; Guan, Z.; Li, J. Modeling Technology of Bonded Particle Model for Gold Ore and Its Validation Based on Drop Weight Test. Coatings 2022, 12, 731. https://doi.org/10.3390/coatings12060731
Wang X, Ma X, Zhang M, Huang Y, Guan Z, Li J. Modeling Technology of Bonded Particle Model for Gold Ore and Its Validation Based on Drop Weight Test. Coatings. 2022; 12(6):731. https://doi.org/10.3390/coatings12060731
Chicago/Turabian StyleWang, Xiao, Xiqiang Ma, Mian Zhang, Yuanyuan Huang, Zhiqiang Guan, and Jishun Li. 2022. "Modeling Technology of Bonded Particle Model for Gold Ore and Its Validation Based on Drop Weight Test" Coatings 12, no. 6: 731. https://doi.org/10.3390/coatings12060731
APA StyleWang, X., Ma, X., Zhang, M., Huang, Y., Guan, Z., & Li, J. (2022). Modeling Technology of Bonded Particle Model for Gold Ore and Its Validation Based on Drop Weight Test. Coatings, 12(6), 731. https://doi.org/10.3390/coatings12060731






