A Dual-Frequency Terahertz Metasurface Capable of Distinguishing the Handedness of Circularly Polarized Light
Abstract
:1. Introduction
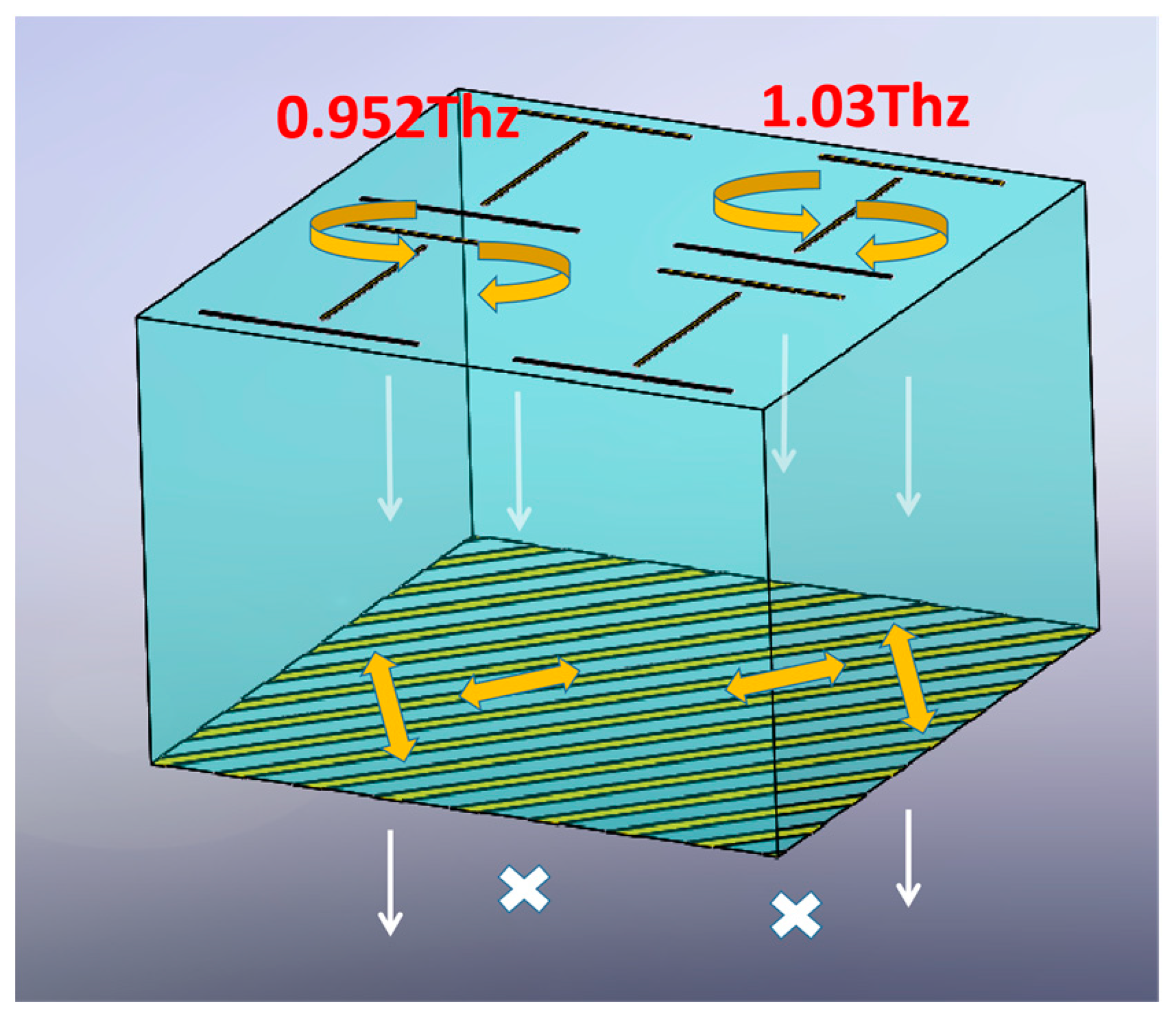
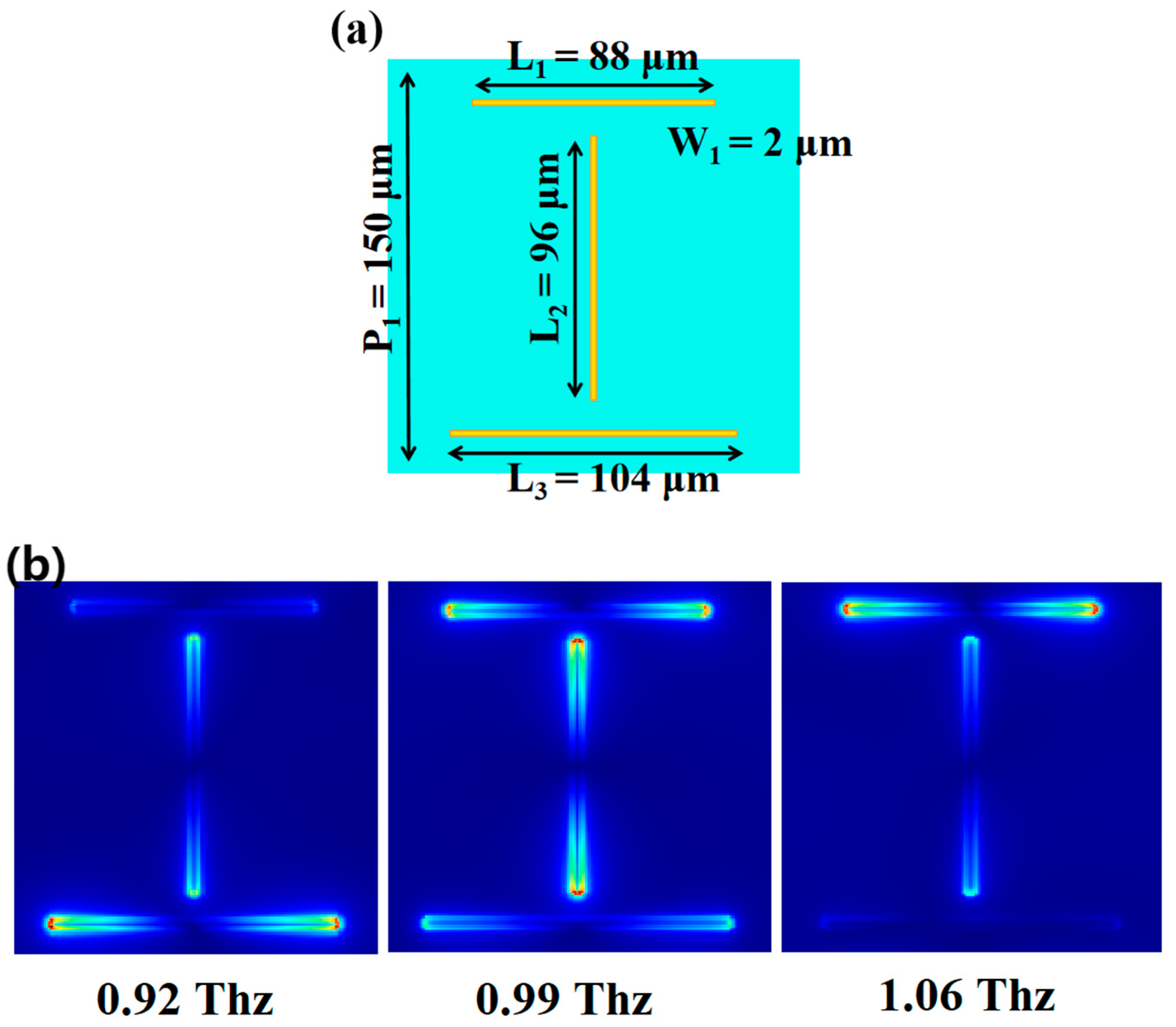
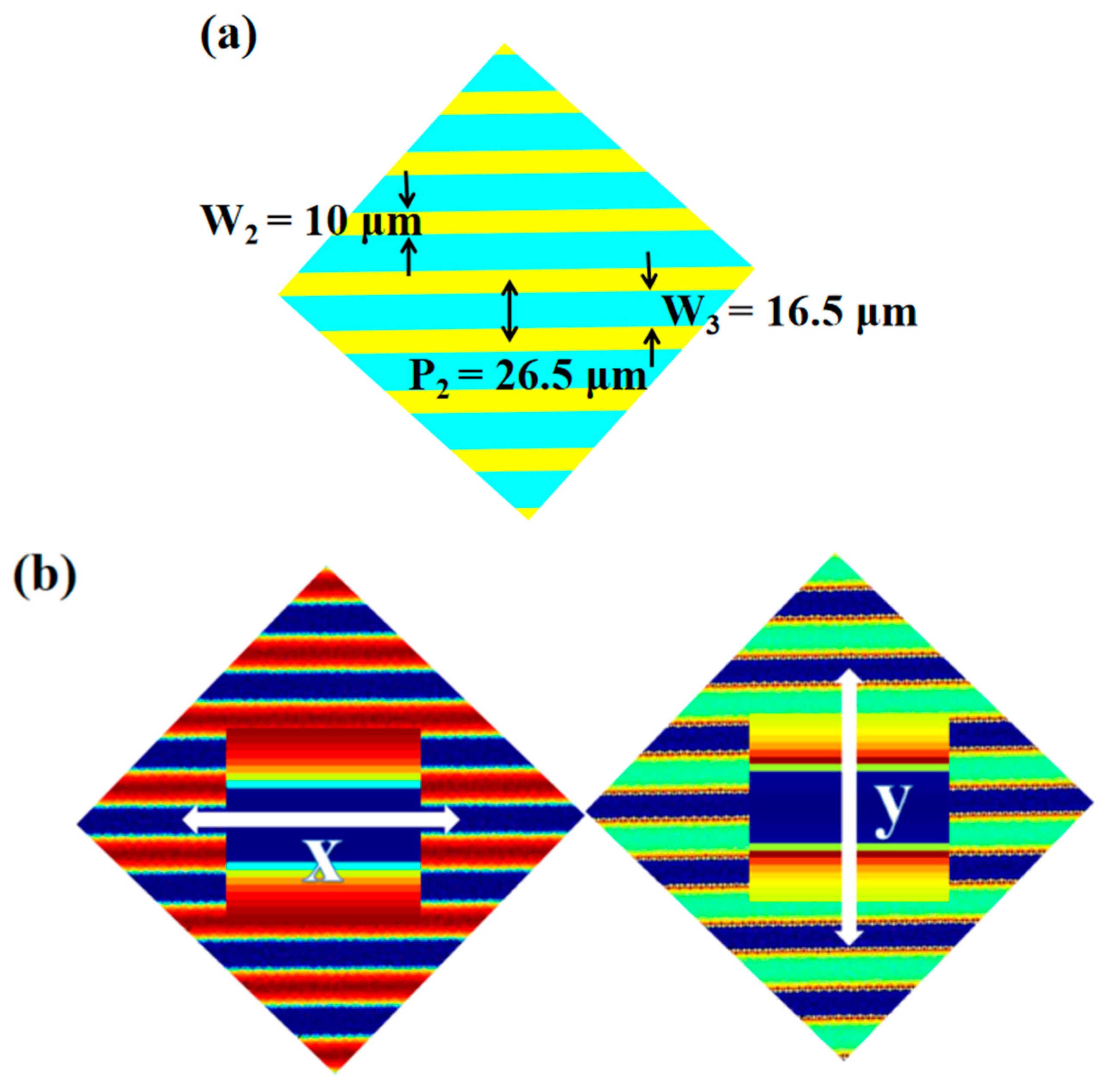
2. Structure Design and Theoretical Analysis
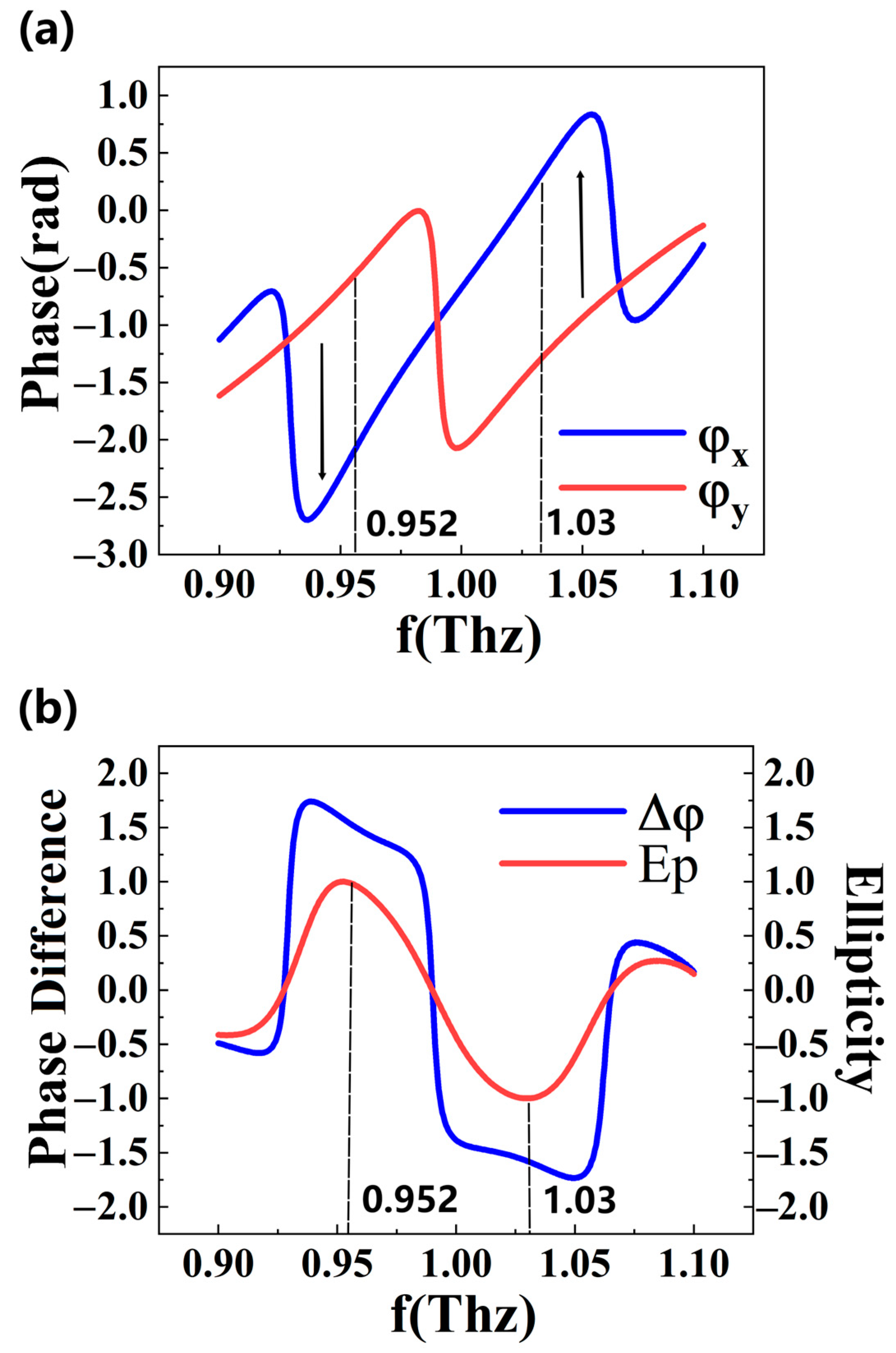
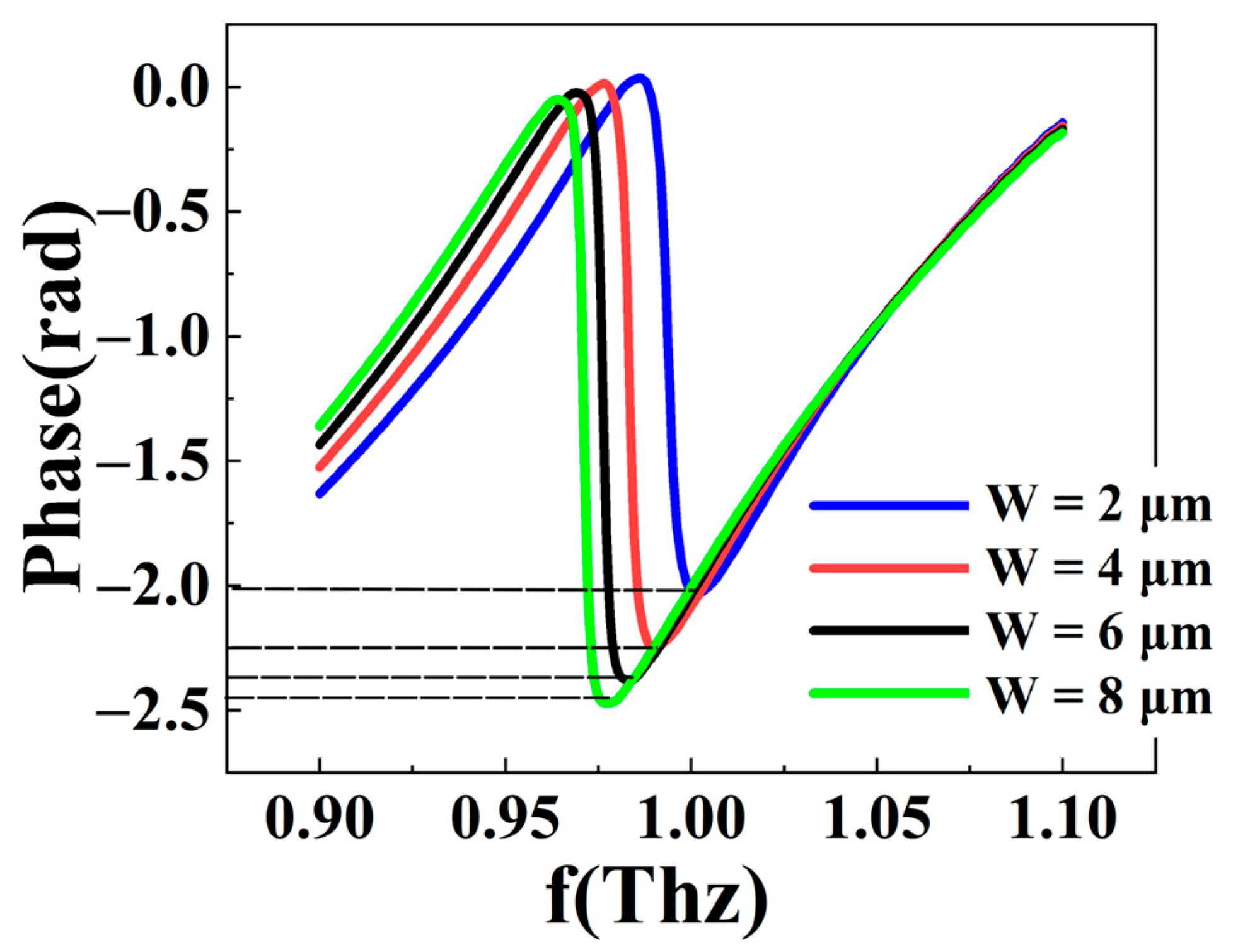
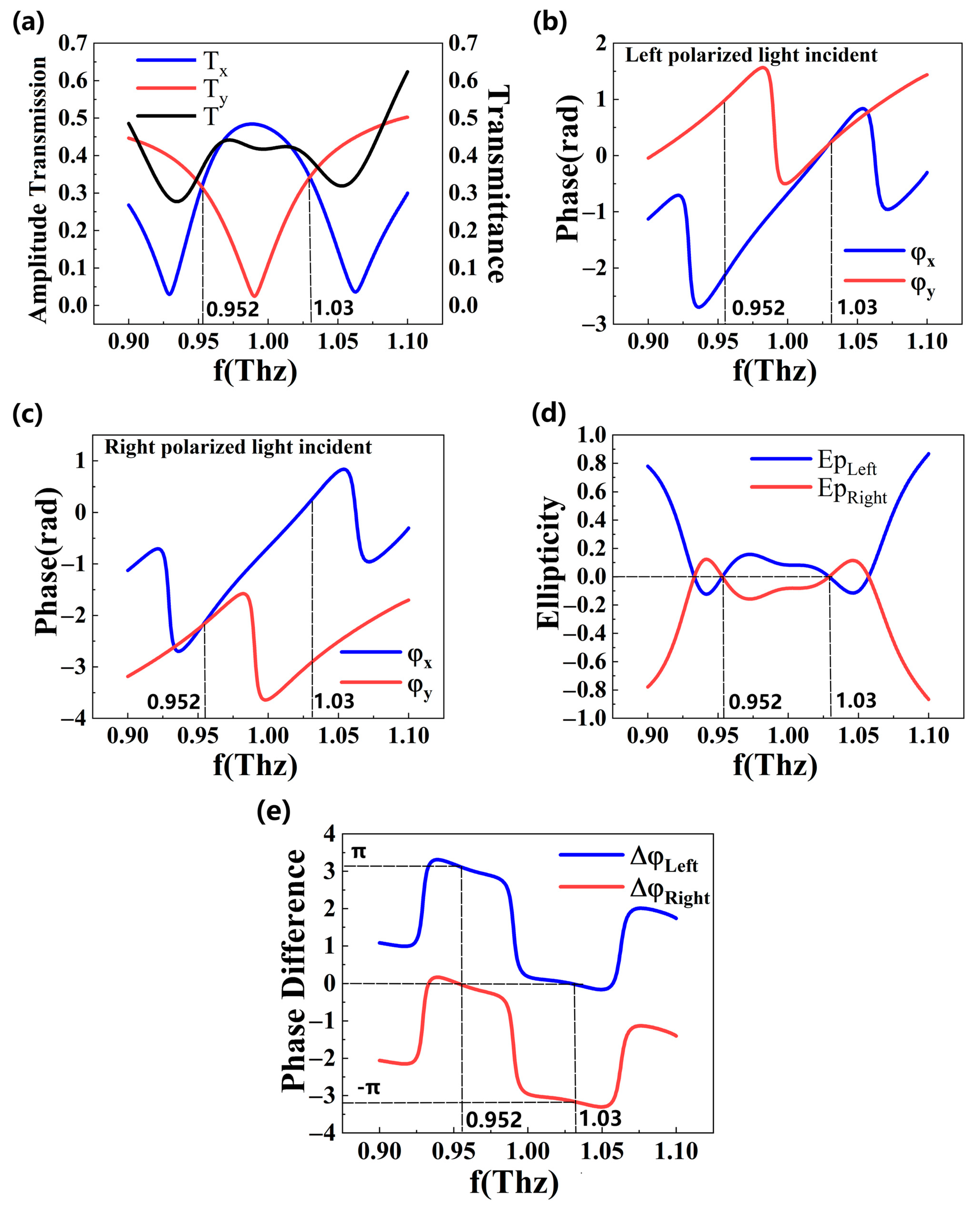
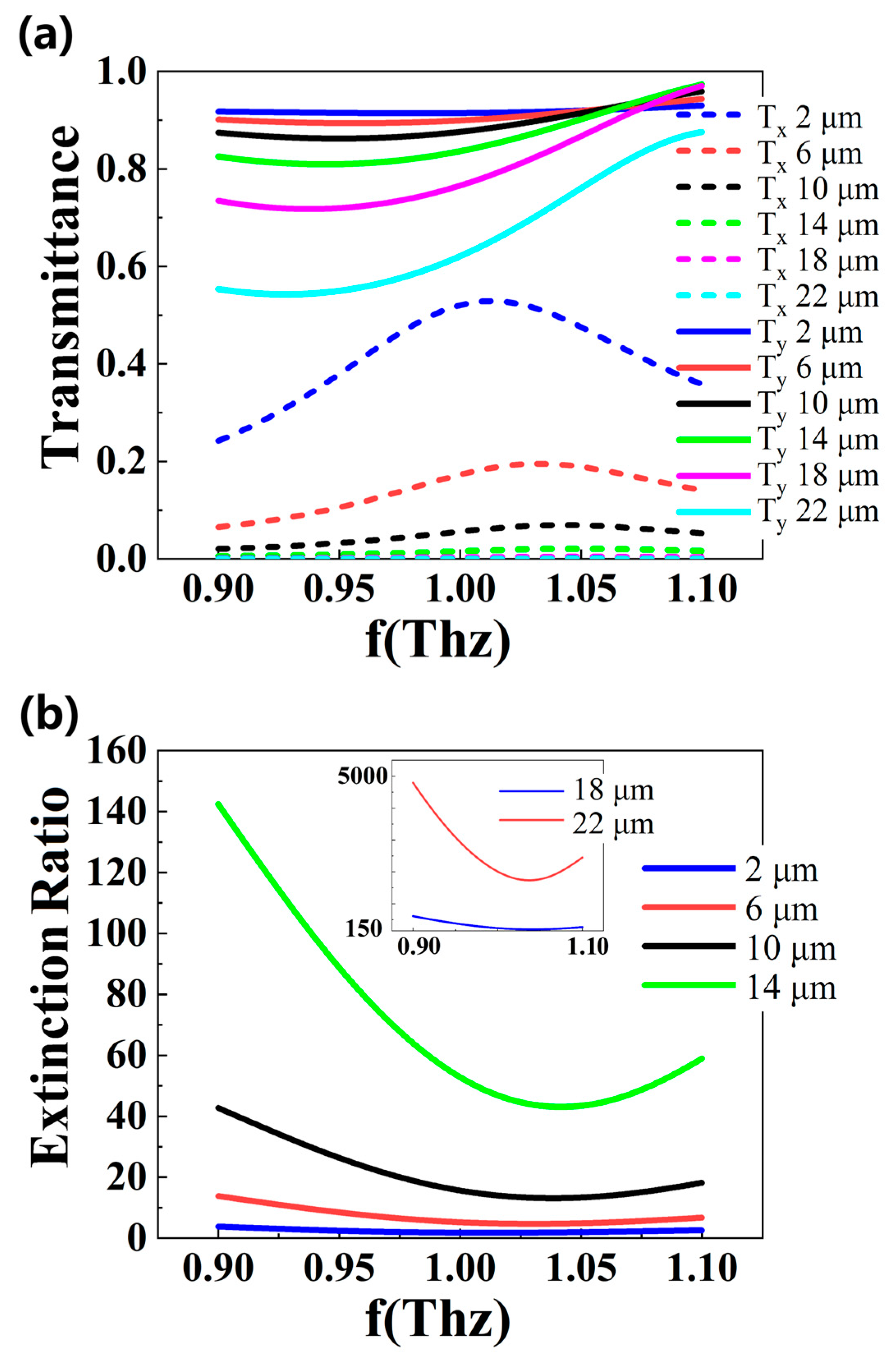
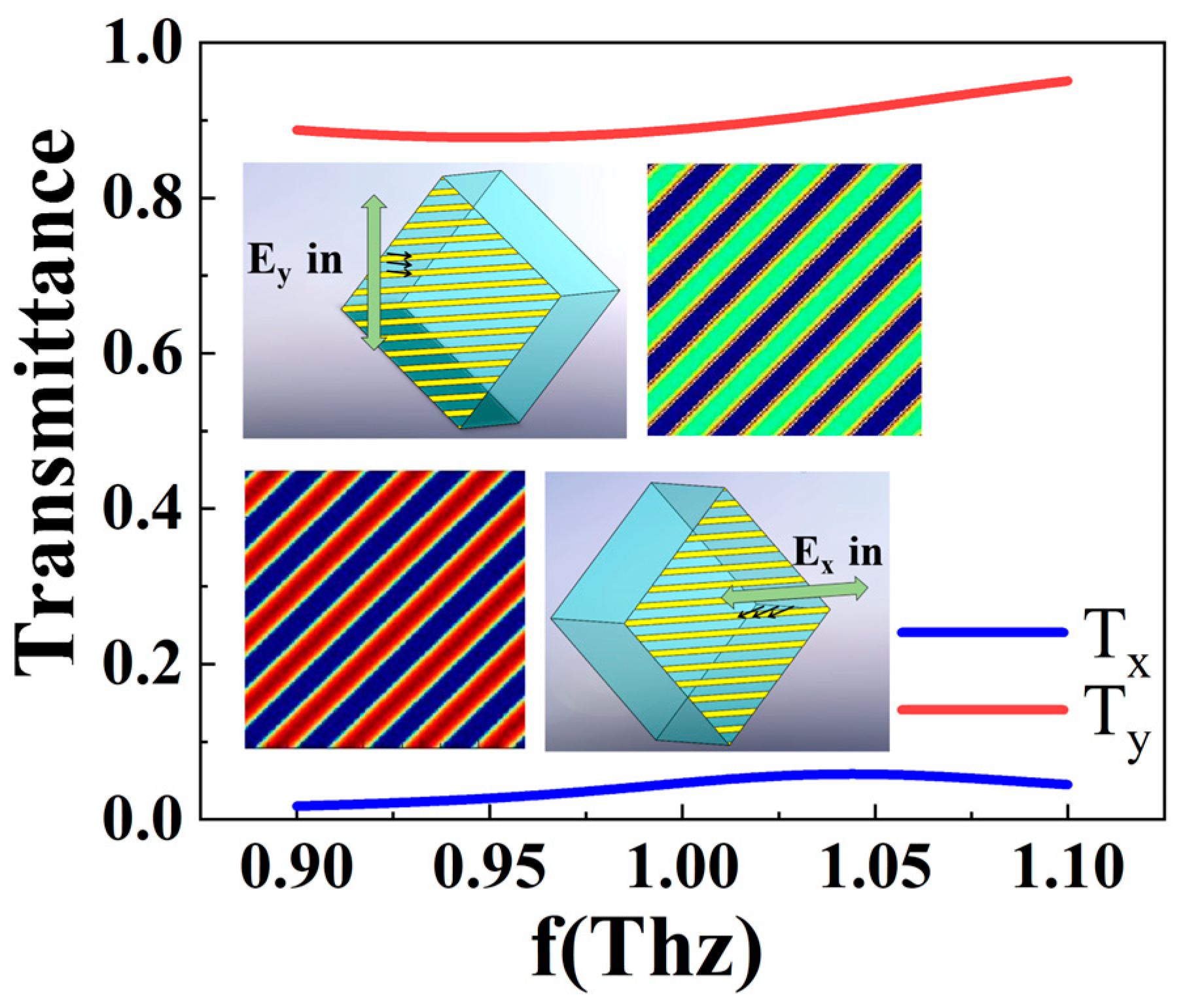
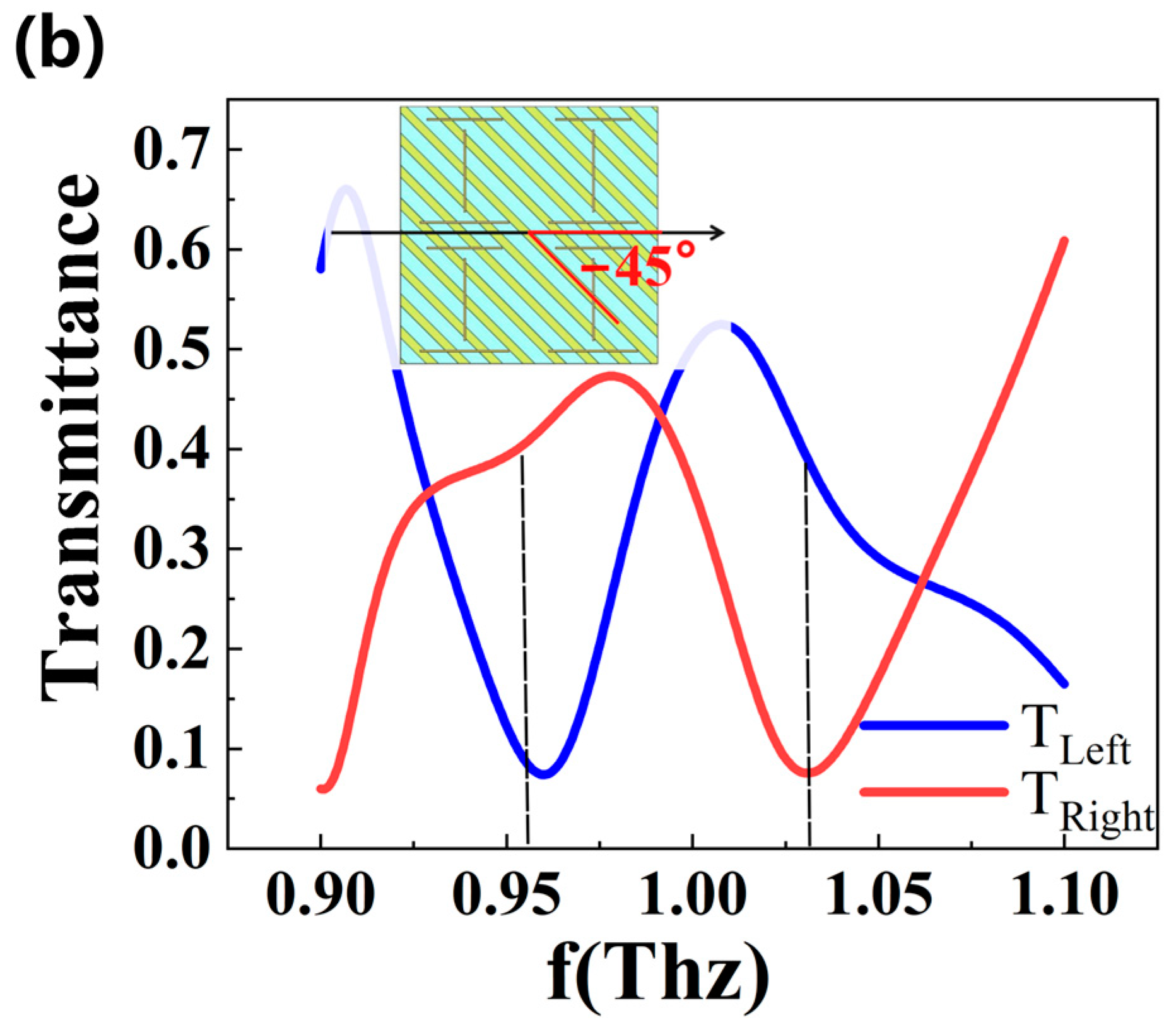
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, P.C.; Chen, J.W.; Yin, C.W.; Lai, Y.C.; Chung, T.L.; Liao, C.Y.; Chen, B.H.; Lee, K.W.; Chuang, C.J.; Wang, C.M.; et al. Visible metasurfaces for on-chip polarimetry. ACS Photonics 2017, 5, 2568–2573. [Google Scholar] [CrossRef]
- Hao, J.; Yuan, Y.; Ran, L.; Jiang, T.; Kong, J.A.; Chan, C.T.; Zhou, L. Manipulating electromagnetic wave polarizations by anisotropic metamaterials. Phys. Rev. Lett. 2007, 99, 063908. [Google Scholar] [CrossRef] [Green Version]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiao, S.; Liang, S.; Wu, Z.; Yang, Z.; Feng, Z.; Sun, H.; Zhou, Y.; Sun, L.; Chen, Z.; et al. Gbps terahertz external modulator based on a composite metamaterial with a double-channel heterostructure. Nano Lett. 2015, 15, 3501–3506. [Google Scholar] [CrossRef]
- Sabban, A. Wearable Circular Polarized Antennas for Health Care, 5G, Energy Harvesting, and IoT Systems. Electronics 2022, 11, 427. [Google Scholar] [CrossRef]
- Ranjbar, B.; Gill, P. Circular dichroism techniques: Biomolecular and nanostructural analyses-a review. Chem. Biol. Drug Des. 2009, 74, 101–120. [Google Scholar] [CrossRef]
- Choi, W.J.; Cheng, G.; Huang, Z.; Zhang, S.; Norris, T.B.; Kotov, N.A. Terahertz circular dichroism spectroscopy of biomaterials enabled by kirigami polarization modulators. Nat. Mater. 2019, 18, 820–826. [Google Scholar] [CrossRef]
- Giakos, G.C. Multifusion, multispectral, optical polarimetric imaging sensing principles. IEEE Trans. Instrum. Meas. 2006, 55, 1628–1633. [Google Scholar] [CrossRef]
- Zhang, Z.; Fan, F.; Shi, W.; Zhang, T.; Chang, S. Terahertz circular polarization sensing for protein denaturation based on a twisted dual-layer metasurface. Biomed. Opt. Express 2022, 13, 209–221. [Google Scholar] [CrossRef]
- Kim, M.; Rho, J. Metamaterials and imaging. Nano Converg. 2015, 2, 22. [Google Scholar] [CrossRef] [Green Version]
- Vedel, M.; Breugnot, S.; Lechocinski, N. Spatial calibration of full stokes polarization imaging camera[C]//Polarization: Measurement, Analysis, and Remote Sensing XI. Int. Soc. Opt. Photonics 2014, 9099, 90990I. [Google Scholar]
- McNichols, R.J.; Cote, G.L. Optical glucose sensing in biological fluids: An overview. J. Biomed. Opt. 2000, 5, 5–16. [Google Scholar] [CrossRef]
- Min, H.; Sekar, G.; Hilty, C. Polarization transfer from ligands hyperpolarized by dissolution dynamic nuclear polarization for screening in drug discovery. Chem. Med. Chem. 2015, 10, 1559–1563. [Google Scholar] [CrossRef]
- Saïdi, F.; Taulelle, F.; Martineau, C. Quantitative 13C solid-state NMR spectra by multiple-contact cross-polarization for drug delivery: From active principles to excipients and drug carriers. J. Pharm. Sci. 2016, 105, 2397–2401. [Google Scholar] [CrossRef]
- Aslan, K.; Lakowicz, J.R.; Geddes, C.D. Angular-dependent polarization-based plasmon light scattering for bioaffinity sensing. Appl. Phys. Lett. 2005, 87, 234108. [Google Scholar] [CrossRef]
- Zhang, M.; Hao, D.; Wang, S.; Li, R.; Wang, S.; Ma, Y.; Moro, R.; Ma, L. Chiral biosensing using terahertz twisted chiral metamaterial. Opt. Express 2022, 30, 14651–14660. [Google Scholar] [CrossRef]
- Pors, A.; Nielsen, M.G.; Bozhevolnyi, S.I. Plasmonic metagratings for simultaneous determination of Stokes parameters. Optica 2015, 2, 716–723. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Fu, Y.; Ma, C.; Yang, B.; Zhao, Y. Research on Fabrication Techniques and Focusing Characteristics of Metalens. Coatings 2022, 12, 359. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Crozier, K.B. Silicon nanofin grating as a miniature chirality-distinguishing beam-splitter. Nat. Commun. 2014, 5, 5386. [Google Scholar] [CrossRef] [Green Version]
- Shaltout, A.; Liu, J.; Kildishev, A.; Shalaev, V. Photonic spin Hall effect in gap–plasmon metasurfaces for on-chip chiroptical spectroscopy. Optica 2015, 2, 860–863. [Google Scholar] [CrossRef]
- Wen, D.; Yue, F.; Kumar, S.; Ma, Y.; Chen, M.; Ren, X.; Kremer, P.E.; Gerardot, B.D.; Taghizadeh, M.R.; Buller, G.S.; et al. Metasurface for characterization of the polarization state of light. Opt. Express 2015, 23, 10272–10281. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Rousso, D.; Capasso, F. Multispectral chiral imaging with a metalens. Nano Lett. 2016, 16, 4595–4600. [Google Scholar] [CrossRef]
- Arbabi, E.; Kamali, S.M.; Arbabi, A.; Faraon, A. Full-Stokes imaging polarimetry using dielectric metasurfaces. ACS Photonics 2018, 5, 3132–3140. [Google Scholar] [CrossRef] [Green Version]
- Politano, G.G.; Versace, C. Variable-Angle Spectroscopic Ellipsometry of Graphene-Based Films. Coatings 2021, 11, 462. [Google Scholar] [CrossRef]
- Dmitriev, V.; Nascimento, C.; Lima, R.; Prosvirnin, S.L. Controllable frequency and polarization TH z filter based on graphene fish-scale metamaterial. Microw. Opt. Technol. Lett. 2017, 59, 3115–3118. [Google Scholar] [CrossRef]
- Barkabian, M.; Sharifi, N.; Granpayeh, N. Multi-functional high-efficiency reflective polarization converter based on an ultra-thin graphene metasurface in the THz band. Opt. Express 2021, 29, 20160–20174. [Google Scholar] [CrossRef]
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 2012, 487, 345–348. [Google Scholar] [CrossRef]
- He, H.; Shang, X.; Xu, L.; Zhao, J.; Cai, W.; Wang, J.; Zhao, C.; Wang, L. Thermally switchable bifunctional plasmonic metasurface for perfect absorption and polarization conversion based on VO2. Opt. Express 2020, 28, 4563–4570. [Google Scholar] [CrossRef]
- Yu, F.; Zhu, J.; Shen, X. Tunable and reflective polarization converter based on single-layer vanadium dioxide-integrated metasurface in terahertz region. Opt. Mater. 2022, 123, 111745. [Google Scholar] [CrossRef]
- Basiri, A.; Chen, X.; Bai, J.; Amrollahi, P.; Carpenter, J.; Holman, Z.; Wang, C.; Yao, Y. Nature-inspired chiral metasurfaces for circular polarization detection and full-Stokes polarimetric measurements. Light: Sci. Appl. 2019, 8, 78. [Google Scholar] [CrossRef]
- Xu, M.; Cao, Y.; Sun, X.; Miao, Y.; Dong, X.; Zhang, Y.; Gao, X. Circular polarization detection metasurface inspired by the polarized vision of mantis shrimp. Opt. Commun. 2022, 507, 127599. [Google Scholar] [CrossRef]
- Han, Z.; Ohno, S.; Tokizane, Y.; Nawata, K.; Notake, T.; Takida, Y.; Minamide, H. Off-resonance and in-resonance metamaterial design for a high-transmission terahertz-wave quarter-wave plate. Opt. Lett. 2018, 43, 2977–2980. [Google Scholar] [CrossRef] [PubMed]
- Cong, L.; Xu, N.; Gu, J.; Singh, R.; Han, J.; Zhang, W. Highly flexible broadband terahertz metamaterial quarter-wave plate. Laser Photonics Rev. 2014, 8, 626–632. [Google Scholar] [CrossRef]
- Brand, G.F. The strip grating as a circular polarizer. Am. J. Phys. 2003, 71, 452–456. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Ouyang, M.; Ren, H.; Ma, C.; Zhao, Y.; Zhang, Y.; Fu, Y. A Dual-Frequency Terahertz Metasurface Capable of Distinguishing the Handedness of Circularly Polarized Light. Coatings 2022, 12, 736. https://doi.org/10.3390/coatings12060736
Yang B, Ouyang M, Ren H, Ma C, Zhao Y, Zhang Y, Fu Y. A Dual-Frequency Terahertz Metasurface Capable of Distinguishing the Handedness of Circularly Polarized Light. Coatings. 2022; 12(6):736. https://doi.org/10.3390/coatings12060736
Chicago/Turabian StyleYang, Bowei, Mingzhao Ouyang, Hang Ren, Chenhao Ma, Yu Zhao, Yuhui Zhang, and Yuegang Fu. 2022. "A Dual-Frequency Terahertz Metasurface Capable of Distinguishing the Handedness of Circularly Polarized Light" Coatings 12, no. 6: 736. https://doi.org/10.3390/coatings12060736
APA StyleYang, B., Ouyang, M., Ren, H., Ma, C., Zhao, Y., Zhang, Y., & Fu, Y. (2022). A Dual-Frequency Terahertz Metasurface Capable of Distinguishing the Handedness of Circularly Polarized Light. Coatings, 12(6), 736. https://doi.org/10.3390/coatings12060736





