Mathematical Model of Surface Topography of Corroded Steel Foundation in Submarine Soil Environment
Abstract
:1. Introduction
2. Electrolytic Accelerated Corrosion Experiment
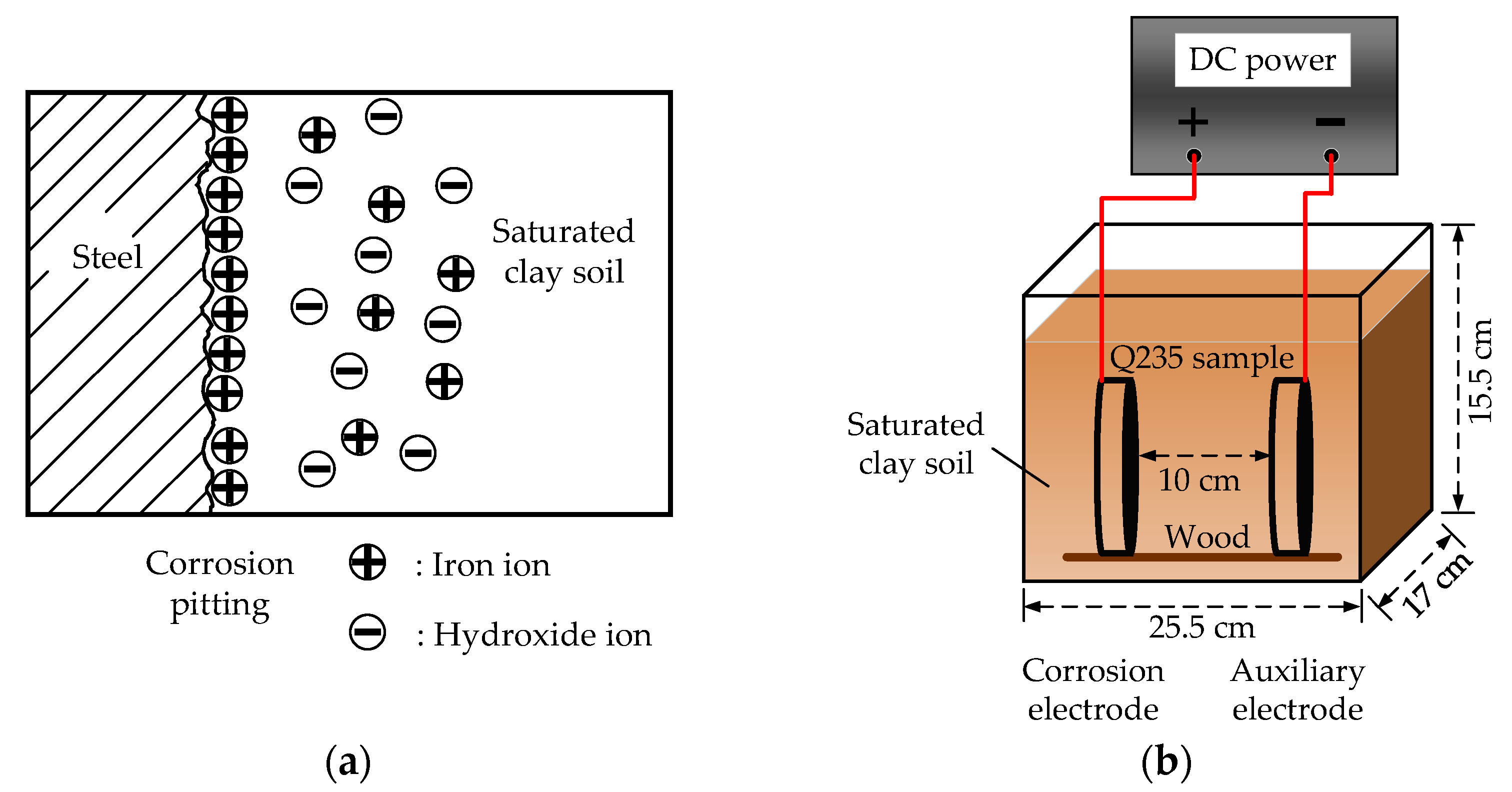
2.1. Experimental Principle
2.2. Experimental Process
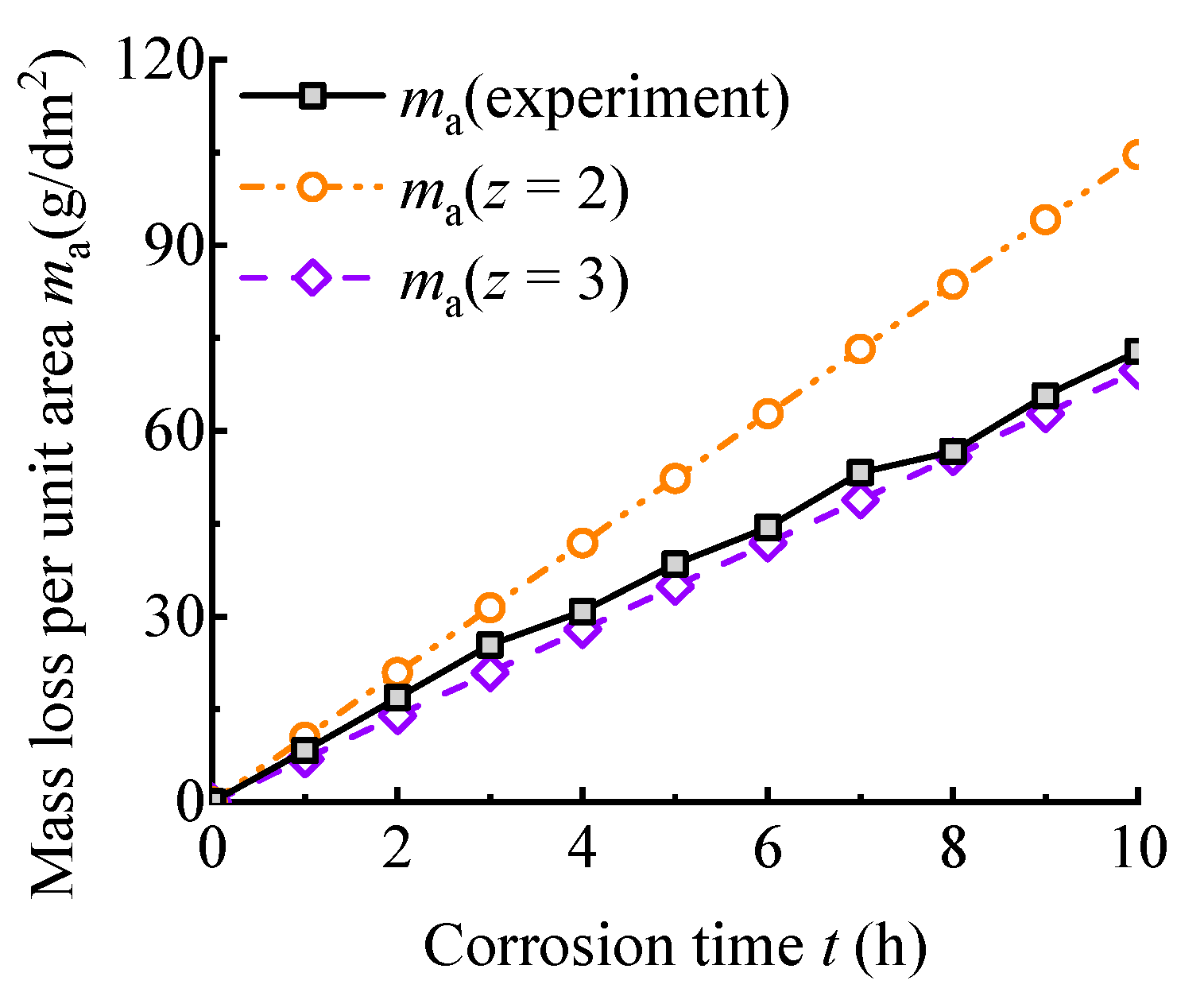
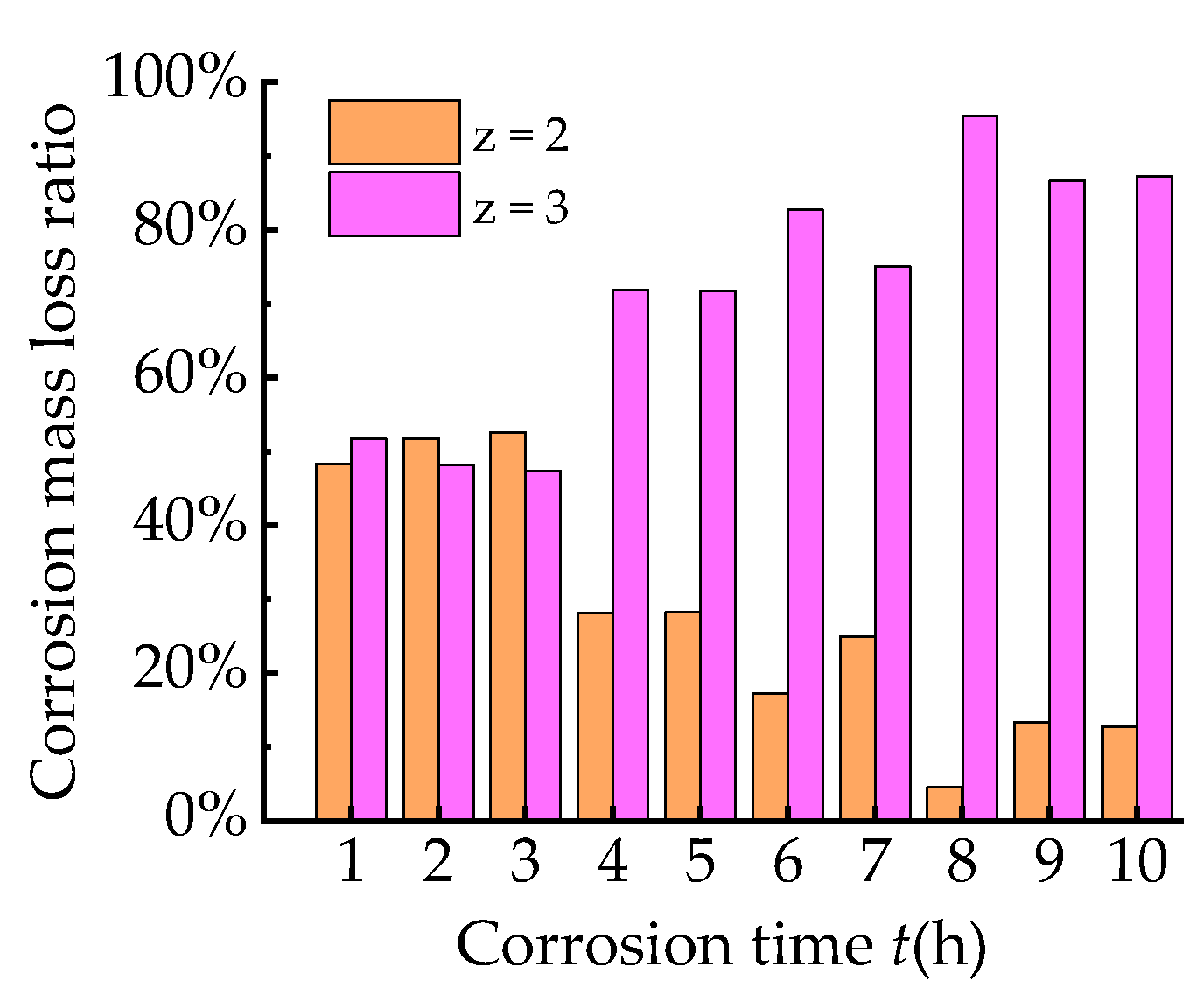
2.3. Mass Loss per Unit Area
3. Mathematical Model of Corroded Steel Surface
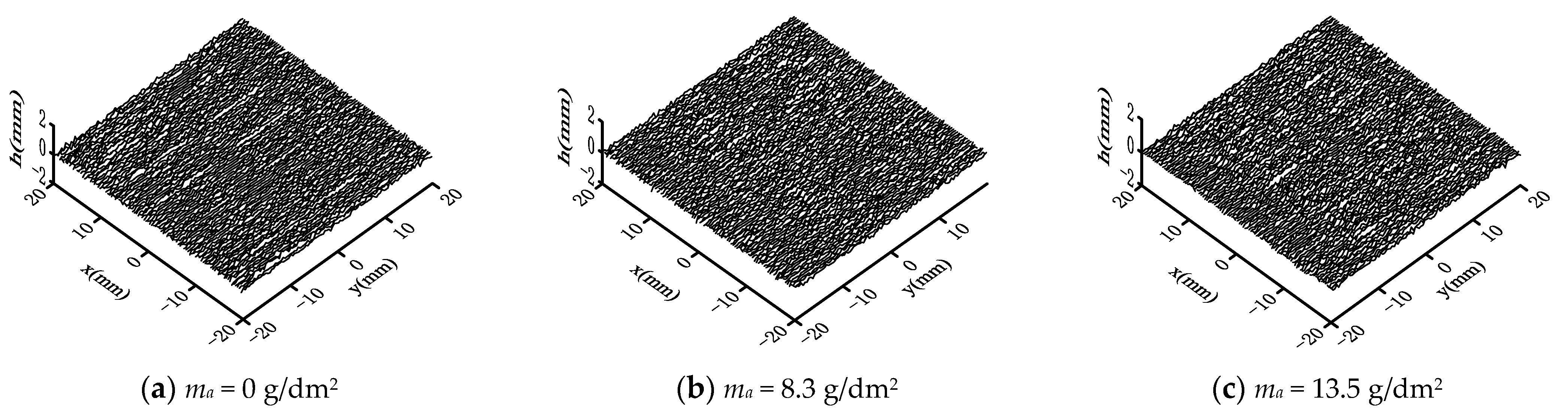
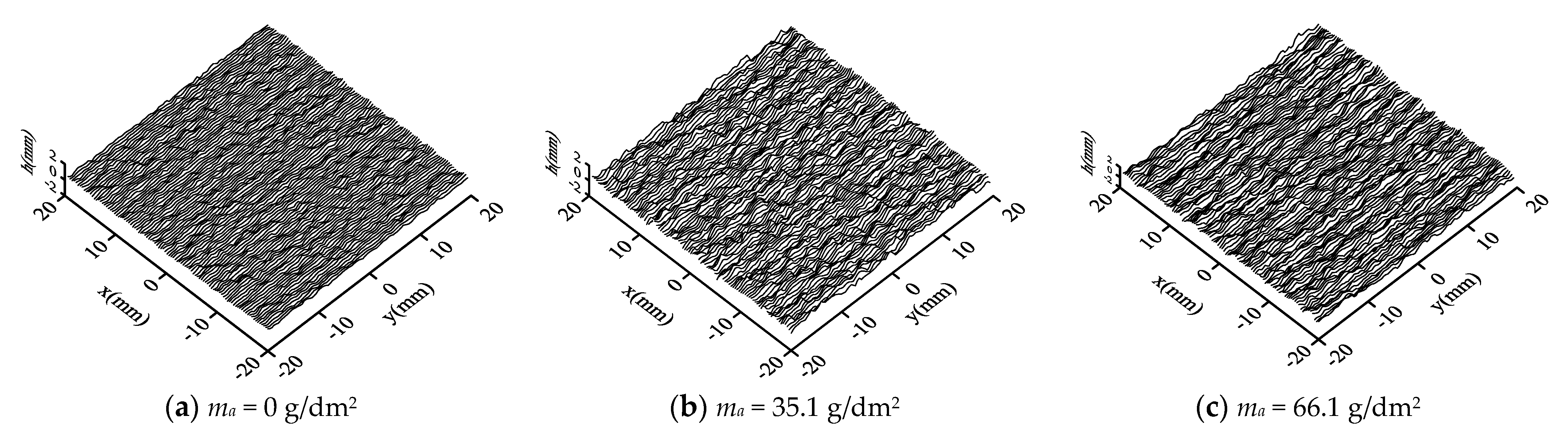
3.1. Surface Topography
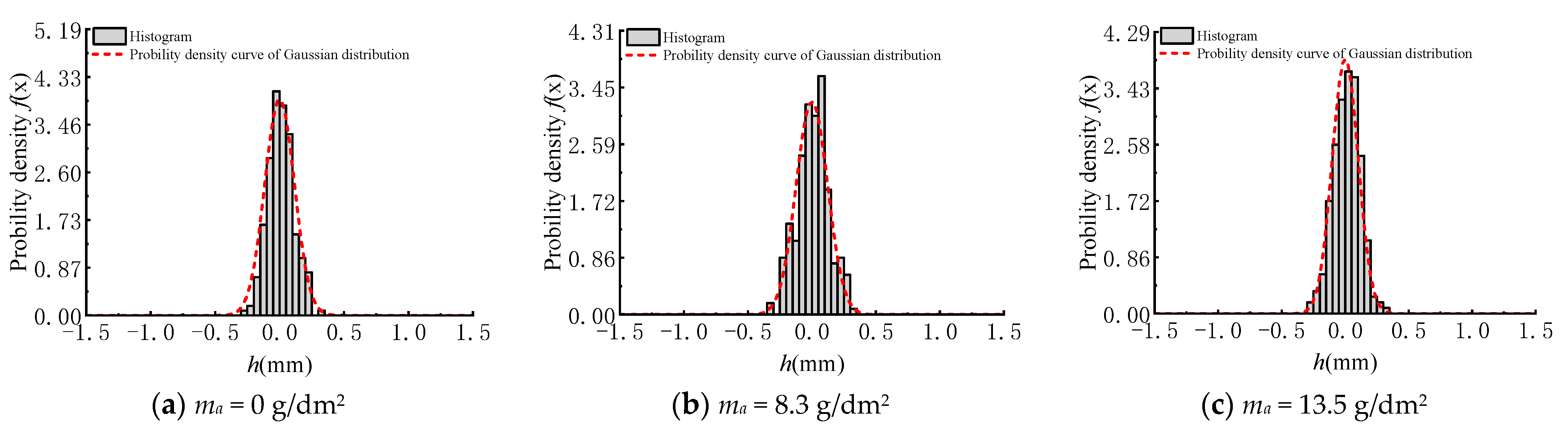
3.2. Surface Height Distribution
3.3. Development of Mathematical Model
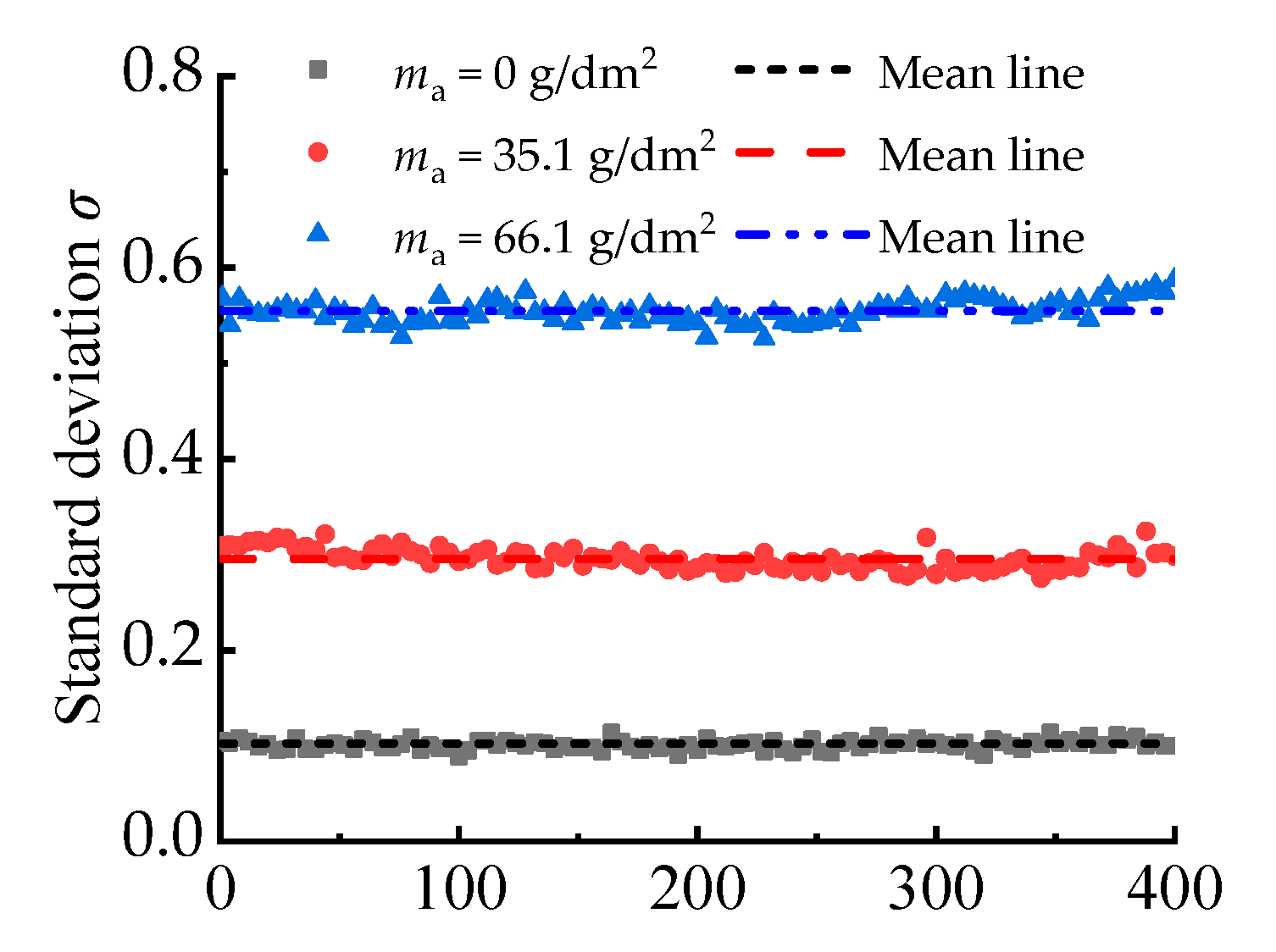
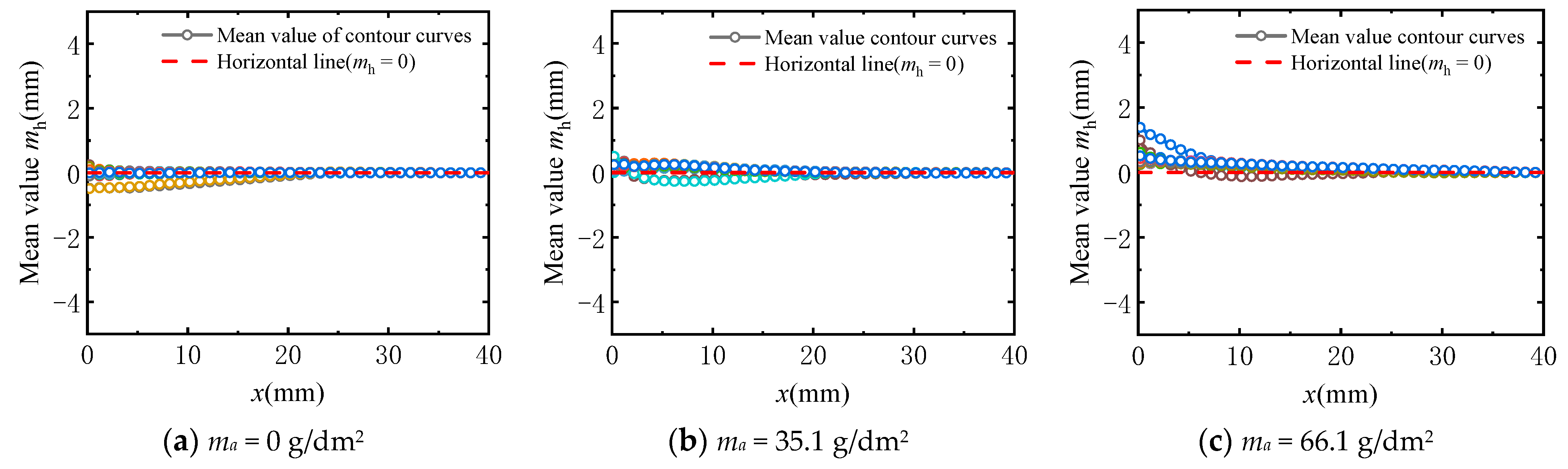
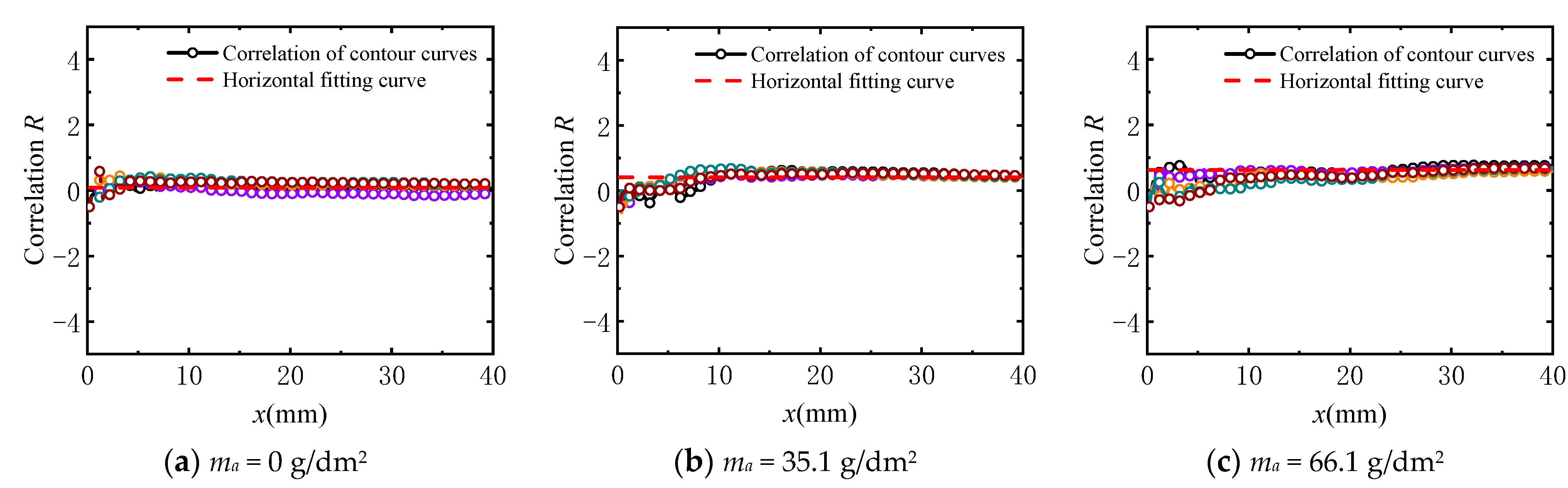
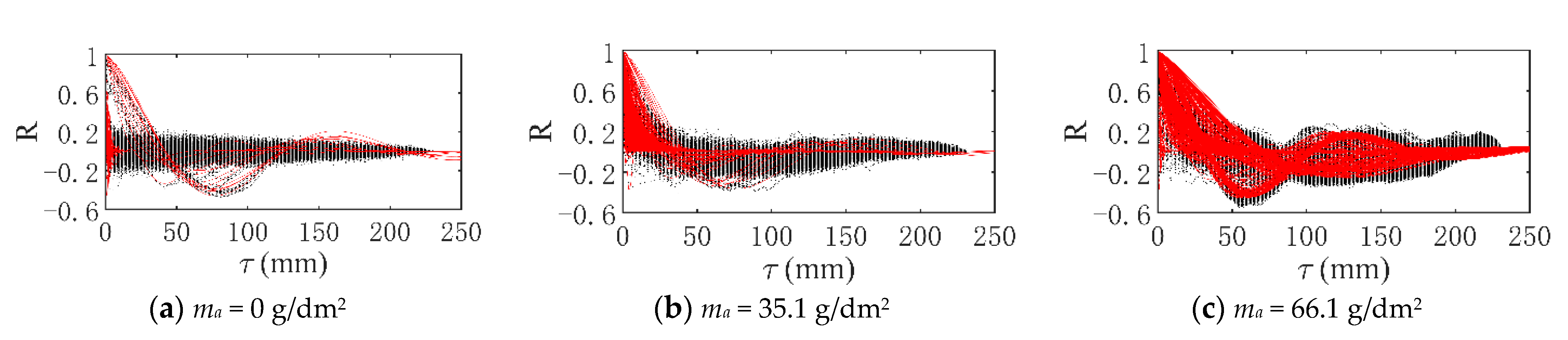
3.3.1. Verification of Stationarity
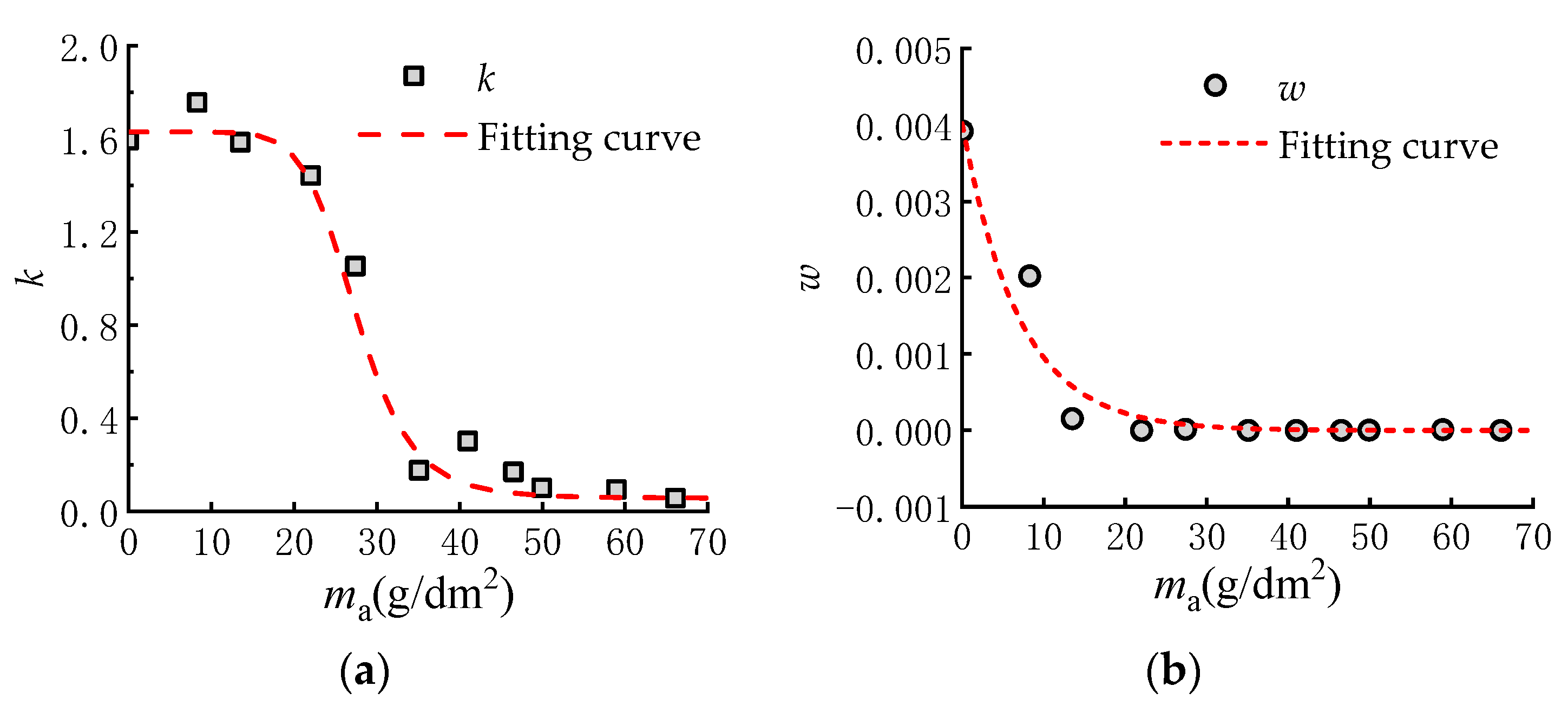
3.3.2. Mathematical Model
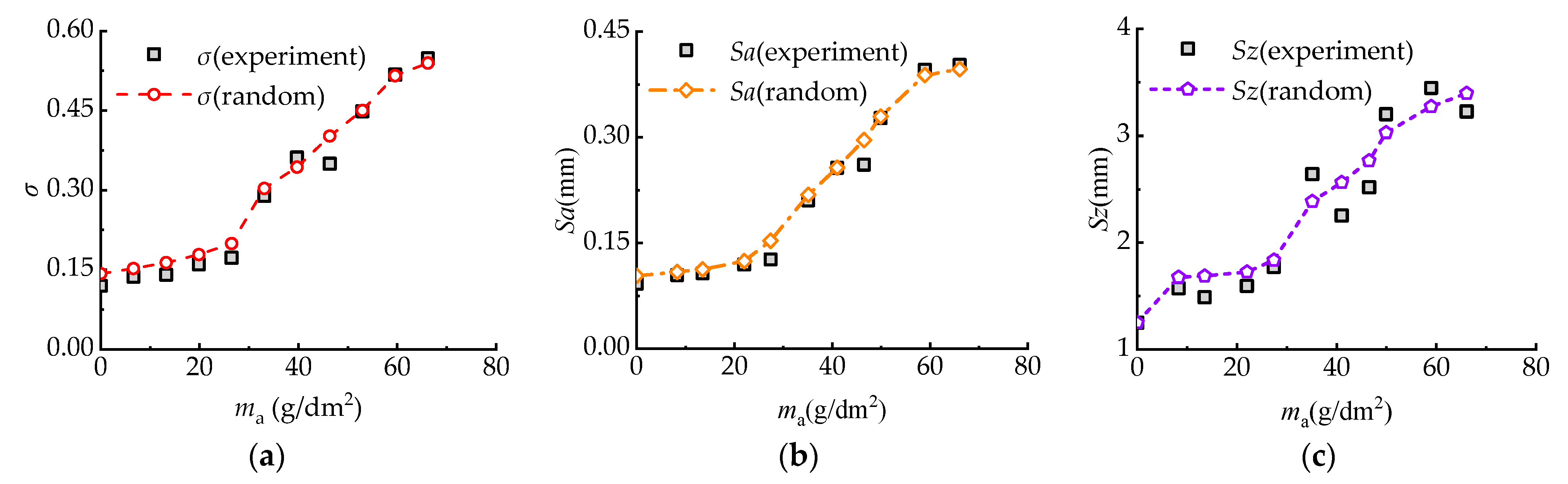
3.4. Stochastic Result Validation
4. Discussion
5. Conclusions
- (1)
- The mass loss per unit area increases linearly with the corrosion time. Based on Faraday’s law, the experimental value and theoretical value of mass loss are compared. The result indicates that when the corrosion time is less than 3 h, the mass loss rates of two electrochemical reaction processes during which the corrosion product is divalent iron and trivalent iron, respectively, are similar. With the increasing corrosion time, the corrosion products of experiments are mainly trivalent iron.
- (2)
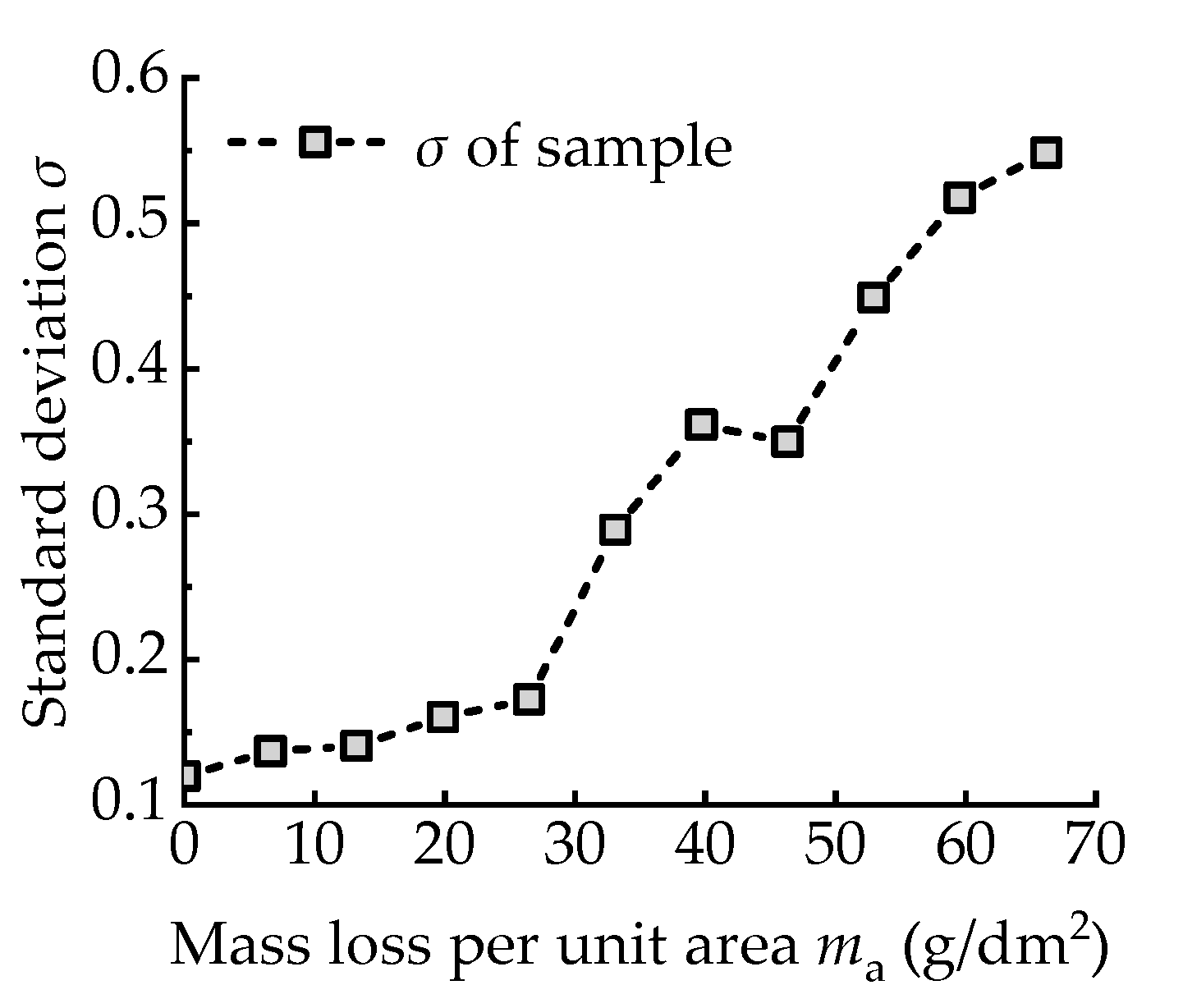
- With the increasing corrosion degree, the corroded steel surface becomes rougher, and the number and size of corrosion pits increase. The height of surface two-dimensional contour curves under different corrosion degrees obeys the Gaussian distribution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sathish, T.; Mohanavel, V.; Arunkumar, T.; Raja, T.; Rashedi, A.; Alarifi, I.M.; Badruddin, I.A.; Algahtani, A.; Afzal, A. Investigation of Mechanical Properties and Salt Spray Corrosion Test Parameters Optimization for AA8079 with Reinforcement of TiN + ZrO2. Materials 2021, 14, 5260. [Google Scholar] [CrossRef] [PubMed]
- Momber, A. Corrosion and corrosion protection of support structures for offshore wind energy devices (OWEA). Mater. Corros. 2010, 62, 391–404. [Google Scholar] [CrossRef]
- Kirchgeorg, T.; Weinberg, I.; Hörnig, M.; Baier, R.; Schmid, M.; Brockmeyer, B. Emissions from corrosion protection systems of offshore wind farms: Evaluation of the potential impact on the marine environment. Mar. Pollut. Bull. 2018, 136, 257–268. [Google Scholar] [CrossRef] [PubMed]
- Kovendhan, M.; Kang, H.; Jeong, S.; Youn, J.-S.; Oh, I.; Park, Y.-K.; Jeon, K.-J. Study of stainless steel electrodes after electrochemical analysis in sea water condition. Environ. Res. 2019, 173, 549–555. [Google Scholar] [CrossRef]
- James, M.; Hattingh, D. Case studies in marine concentrated corrosion. Eng. Fail. Anal. 2015, 47, 1–15. [Google Scholar] [CrossRef]
- Lv, K.; Xu, S.; Liu, L.; Wang, X.; Li, C.; Wu, T.; Yin, F. Comparative Study on the Corrosion Behaviours of High-Silicon Chromium Iron and Q235 Steel in a Soil Solution. Int. J. Electrochem. Sci. 2020, 5193–5207. [Google Scholar] [CrossRef]
- Wei, B.; Qin, Q.; Bai, Y.; Yu, C.; Xu, J.; Sun, C.; Ke, W. Short-period corrosion of X80 pipeline steel induced by AC current in acidic red soil. Eng. Fail. Anal. 2019, 105, 156–175. [Google Scholar] [CrossRef]
- Karagah, H.; Shi, C.; Dawood, M.; Belarbi, A. Experimental investigation of short steel columns with localized corrosion. Thin-Walled Struct. 2015, 87, 191–199. [Google Scholar] [CrossRef]
- Liu, X.; Nanni, A.; Silva, P.F. Rehabilitation of Compression Steel Members Using FRP Pipes Filled with Non-Expansive and Expansive Light-Weight Concrete. Adv. Struct. Eng. 2005, 8, 129–142. [Google Scholar] [CrossRef]
- Wang, K.; Zhao, M.-J. Mathematical Model of Homogeneous Corrosion of Steel Pipe Pile Foundation for Offshore Wind Turbines and Corrosive Action. Adv. Mater. Sci. Eng. 2016, 2016, 9014317. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Li, Z.; Zhao, M. Mechanism of Localized Corrosion of Steel Pipe Pile Foundation for Offshore Wind Turbines and Corrosive Action. Open Civ. Eng. J. 2016, 10, 685–694. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, N.; Ikegami, K. A Study on the Degradation of Coating and Corrosion of Ship’s Hull Based on the Probabilistic Approach. J. Offshore Mech. Arct. Eng. 1998, 120, 121–128. [Google Scholar] [CrossRef]
- Akpan, U.O.; Koko, T.; Ayyub, B.; Dunbar, T. Risk assessment of aging ship hull structures in the presence of corrosion and fatigue. Mar. Struct. 2002, 15, 211–231. [Google Scholar] [CrossRef]
- Guo, J.; Wang, G.; Ivanov, L.; Perakis, A.N. Time-varying ultimate strength of aging tanker deck plate considering corrosion effect. Mar. Struct. 2008, 21, 402–419. [Google Scholar] [CrossRef]
- Jiang, X.; Soares, C.G. Ultimate capacity of rectangular plates with partial depth pits under uniaxial loads. Mar. Struct. 2012, 26, 27–41. [Google Scholar] [CrossRef]
- Ahmmad, M.; Sumi, Y. Strength and deformability of corroded steel plates under quasi-static tensile load. J. Mar. Sci. Technol. 2009, 15, 1–15. [Google Scholar] [CrossRef]
- Nakai, T.; Matsushita, H.; Yamamoto, N. Effect of pitting corrosion on local strength of hold frames of bulk carriers (2nd Report)—Lateral-distortional buckling and local face buckling. Mar. Struct. 2004, 17, 612–641. [Google Scholar] [CrossRef]
- Nakai, T.; Matsushita, H.; Yamamoto, N. Effect of pitting corrosion on the ultimate strength of steel plates subjected to in-plane compression and bending. J. Mar. Sci. Technol. 2006, 11, 52–64. [Google Scholar] [CrossRef]
- Chen, J.; Fu, C.; Ye, H.; Jin, X. Corrosion of steel embedded in mortar and concrete under different electrolytic accelerated corrosion methods. Constr. Build. Mater. 2020, 241, 117971. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Zhang, R.H.; Liu, Q.; Wang, X.H.; Chen, Y.C. Effects of Stray AC Interference on Corrosion Behavior of X70 Pipeline Steel in a Simulated Marine Soil Solution. Int. J. Electrochem. Sci. 2017, 1829–1845. [Google Scholar] [CrossRef]
- Xu, Z.; Du, Y.; Qin, R.; Zhang, H. Study of Corrosion Behavior of X80 Steel in Clay Soil with Different Water Contents under HVDC Interference. Int. J. Electrochem. Sci. 2020, 3935–3954. [Google Scholar] [CrossRef]
- Wang, X.; Song, X.; Chen, Y.; Wang, Z.; Zhang, L. Corrosion Behavior of X70 and X80 Pipeline Steels in Simulated Soil Solution. Int. J. Electrochem. Sci. 2018, 13, 6436–6450. [Google Scholar] [CrossRef]
- Su, X.; Yin, Z.; Cheng, Y.F. Corrosion of 16Mn Line Pipe Steel in a Simulated Soil Solution and the Implication on Its Long-Term Corrosion Behavior. J. Mater. Eng. Perform. 2012, 22, 498–504. [Google Scholar] [CrossRef]
- Shinozuka, M.; Deodatis, G. Simulation of Multi-Dimensional Gaussian Stochastic Fields by Spectral Representation. Appl. Mech. Rev. 1996, 49, 29–53. [Google Scholar] [CrossRef]
- Shinozuka, M.; Deodatis, G. Simulation of Stochastic Processes by Spectral Representation. Appl. Mech. Rev. 1991, 44, 191–204. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, W.; Peng, Y. Random function based spectral representation of stationary and non-stationary stochastic processes. Probabilistic Eng. Mech. 2016, 45, 115–126. [Google Scholar] [CrossRef]
- Hu, Y.; Tonder, K. Simulation of 3-D random rough surface by 2-D digital filter and fourier analysis. Int. J. Mach. Tools Manuf. 1992, 32, 83–90. [Google Scholar] [CrossRef]
- Hu, B.; Schiehlen, W. On the simulation of stochastic processes by spectral representation. Probabilistic Eng. Mech. 1997, 12, 105–113. [Google Scholar] [CrossRef]
- Uzielli, M.; Vannucchi, G.; Phoon, K.K. Random field characterisation of stress-nomalised cone penetration testing parameters. Geotechnique 2005, 55, 3–20. [Google Scholar] [CrossRef]
- Phoon, K.-K.; Quek, S.T.; An, P. Identification of Statistically Homogeneous Soil Layers Using Modified Bartlett Statistics. J. Geotech. Geoenvironmental Eng. 2003, 129, 649–659. [Google Scholar] [CrossRef]
- Manesh, K.; Ramamoorthy, B.; Singaperumal, M. Numerical generation of anisotropic 3D non-Gaussian engineering surfaces with specified 3D surface roughness parameters. Wear 2010, 268, 1371–1379. [Google Scholar] [CrossRef]
- Gathimba, N.; Kitane, Y.; Yoshida, T.; Itoh, Y. Surface roughness characteristics of corroded steel pipe piles exposed to marine environment. Constr. Build. Mater. 2019, 203, 267–281. [Google Scholar] [CrossRef]
- Xia, M.; Wang, Y.; Xu, S. Study on surface characteristics and stochastic model of corroded steel in neutral salt spray environment. Constr. Build. Mater. 2020, 272, 121915. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, Y.; Huang, J.; Luo, L. Mathematical Model of Surface Topography of Corroded Steel Foundation in Submarine Soil Environment. Coatings 2022, 12, 1078. https://doi.org/10.3390/coatings12081078
Wang W, Wang Y, Huang J, Luo L. Mathematical Model of Surface Topography of Corroded Steel Foundation in Submarine Soil Environment. Coatings. 2022; 12(8):1078. https://doi.org/10.3390/coatings12081078
Chicago/Turabian StyleWang, Wei, Yuan Wang, Jingqi Huang, and Lunbo Luo. 2022. "Mathematical Model of Surface Topography of Corroded Steel Foundation in Submarine Soil Environment" Coatings 12, no. 8: 1078. https://doi.org/10.3390/coatings12081078
APA StyleWang, W., Wang, Y., Huang, J., & Luo, L. (2022). Mathematical Model of Surface Topography of Corroded Steel Foundation in Submarine Soil Environment. Coatings, 12(8), 1078. https://doi.org/10.3390/coatings12081078





