A Dynamic Wear Prediction Model for Studying the Interactions between Surface Wear and Dynamic Response of Spur Gears
Abstract
:1. Introduction
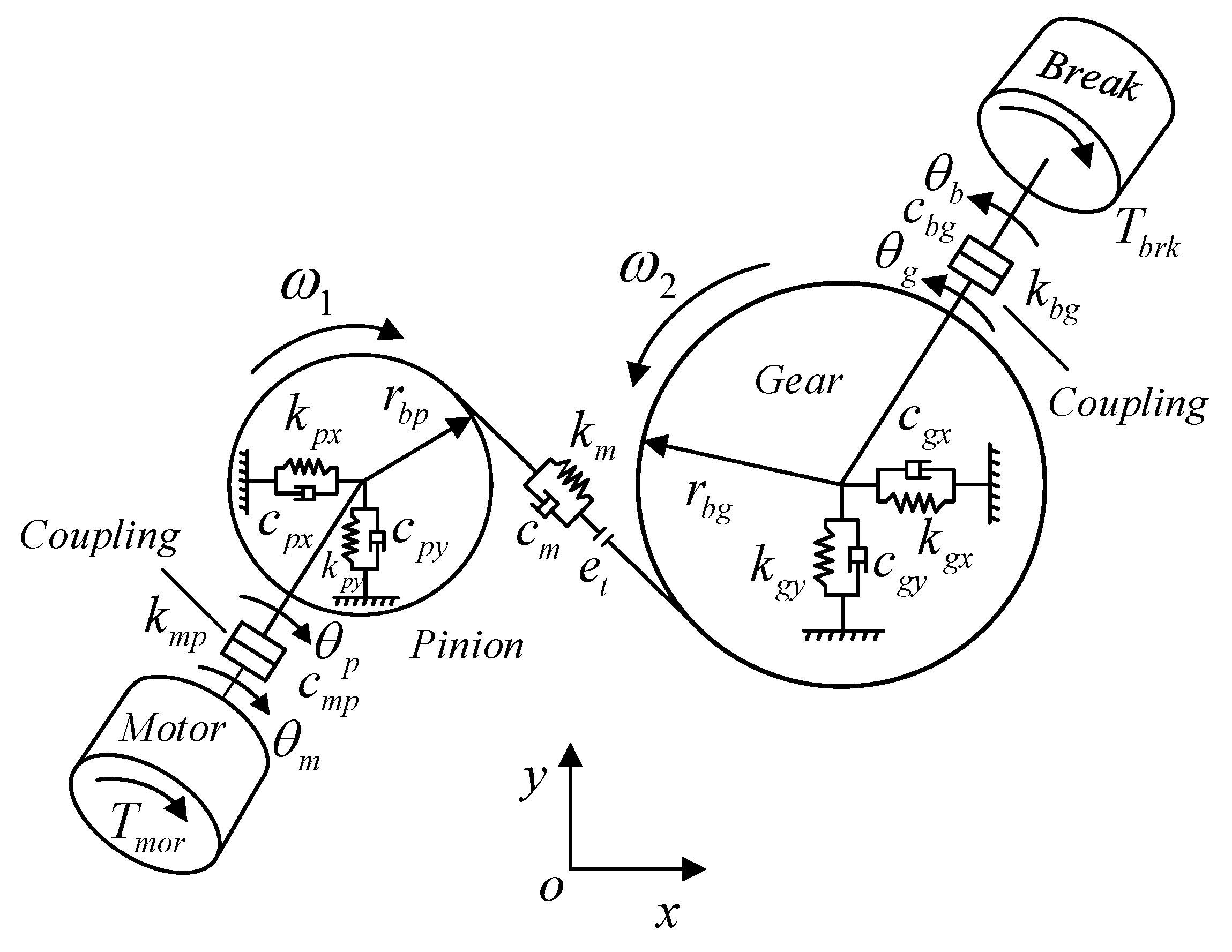
2. Dynamic Model Development
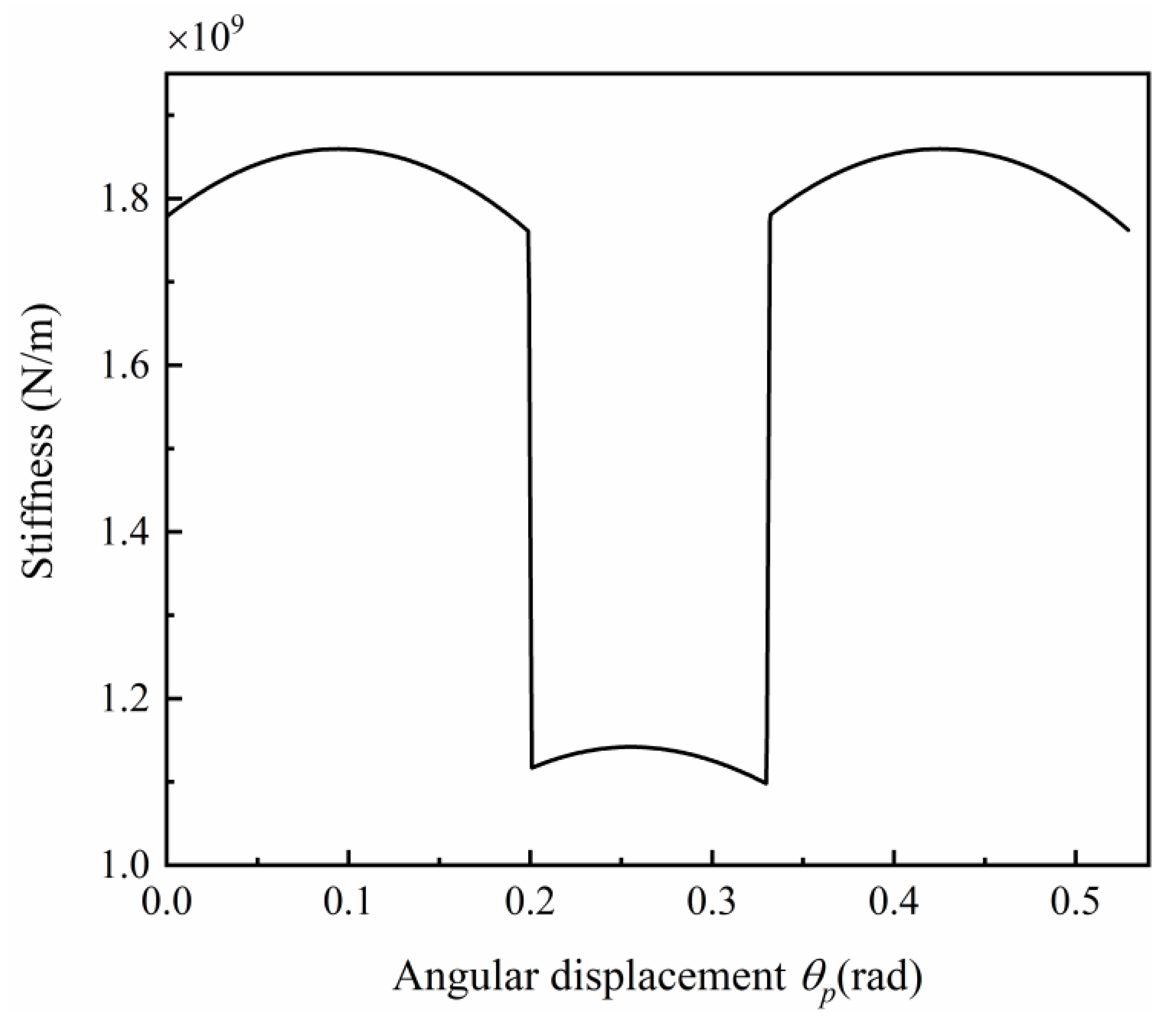
3. Dynamic Wear Prediction Model
4. Numerical Results and Discussion
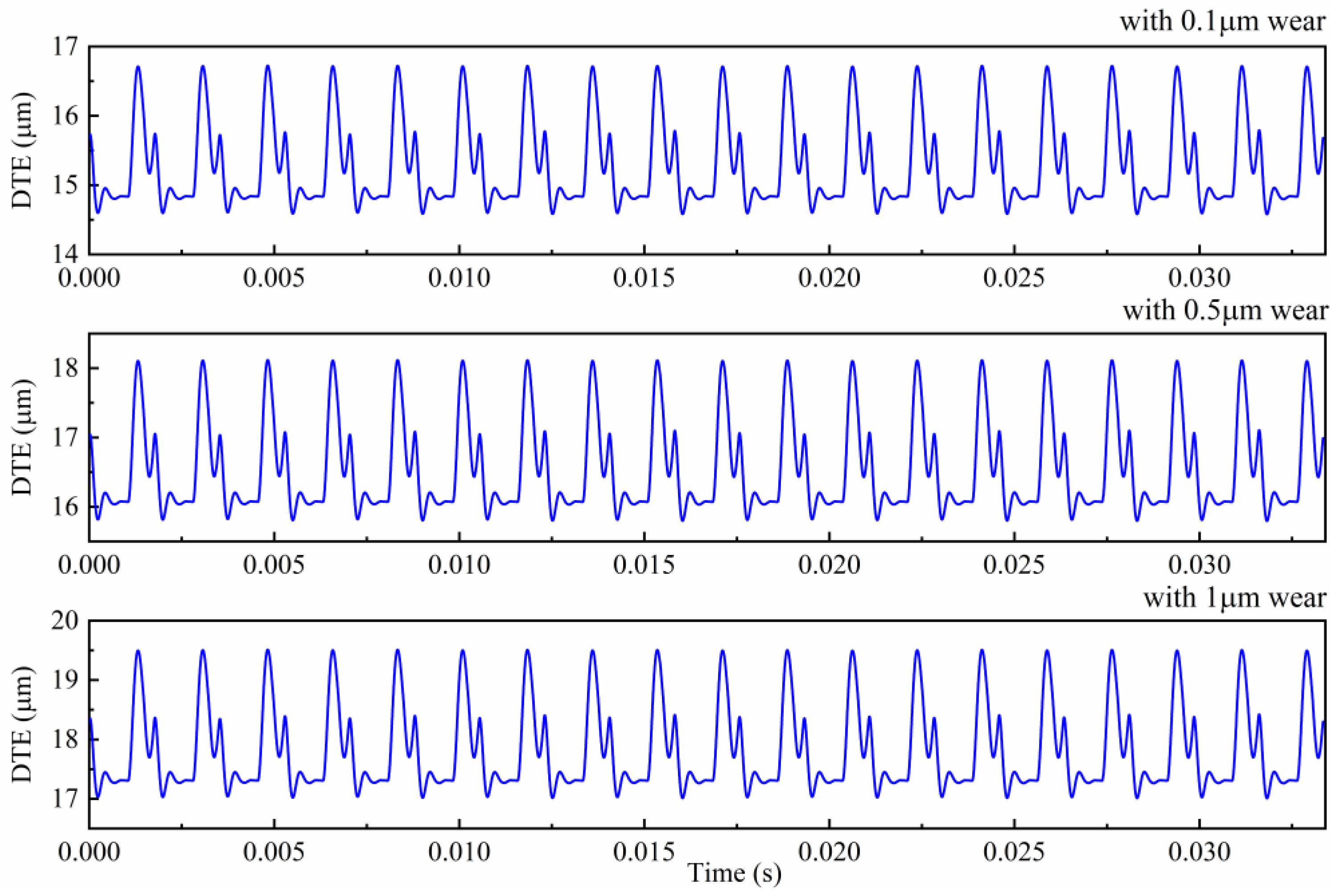
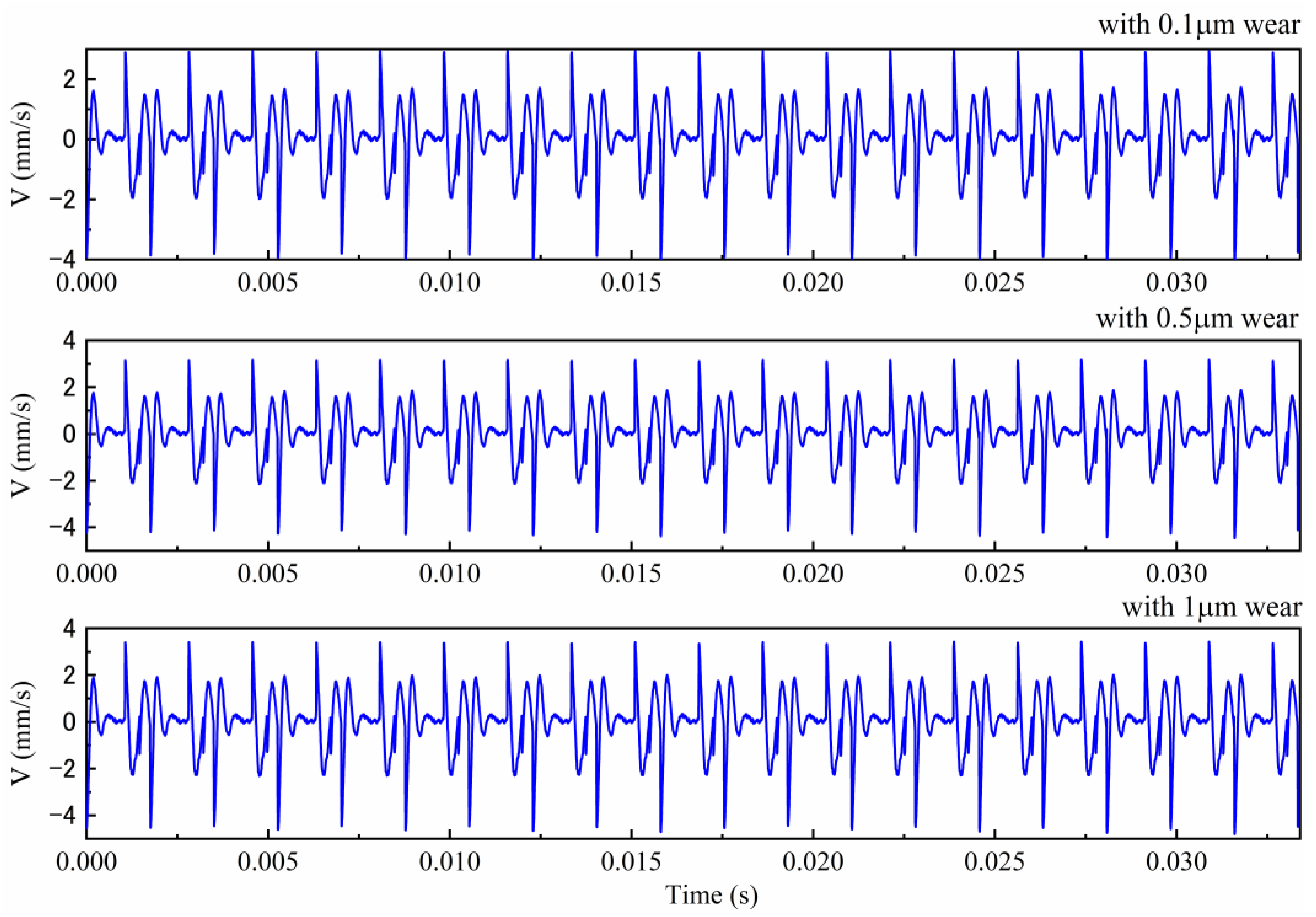
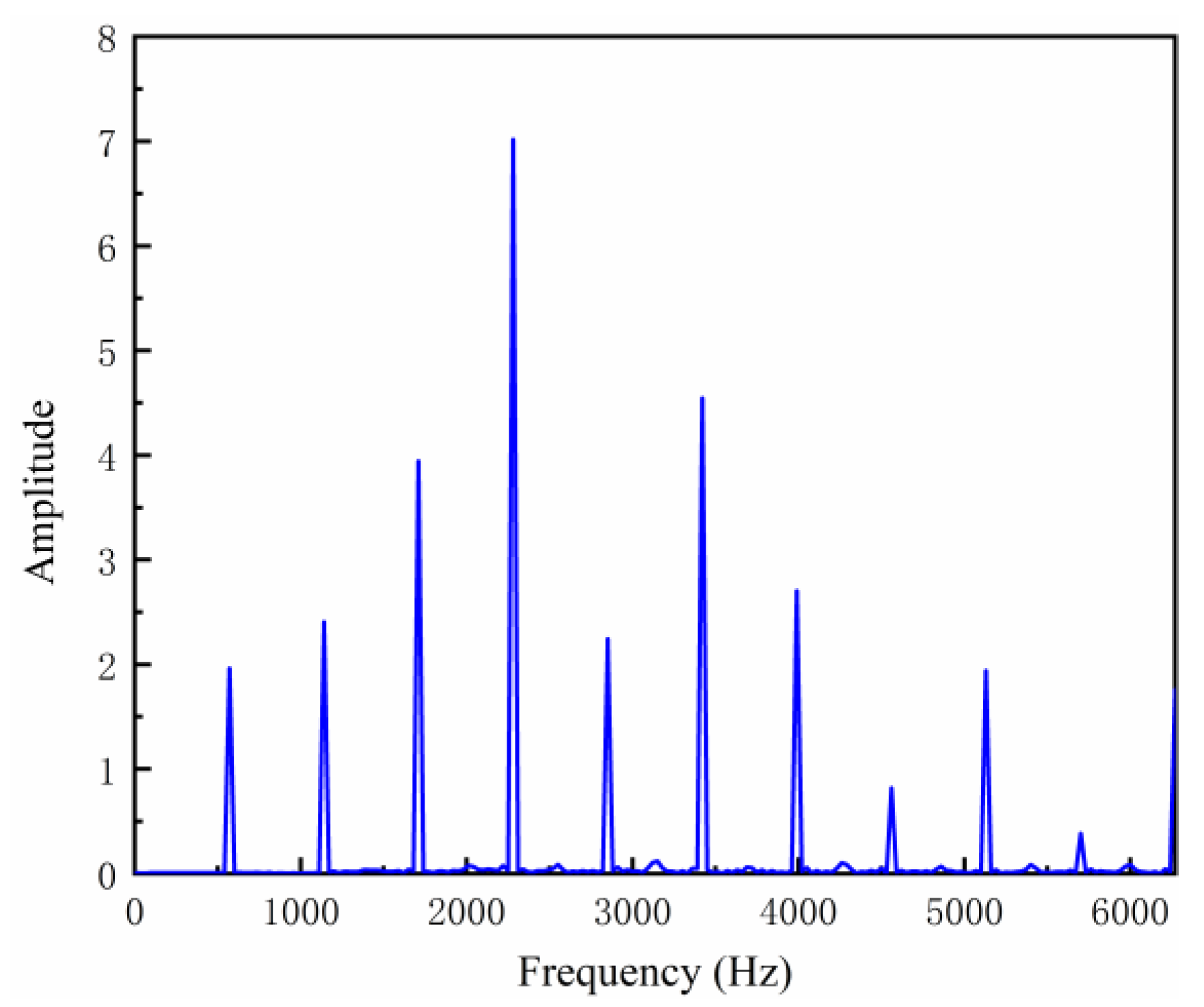
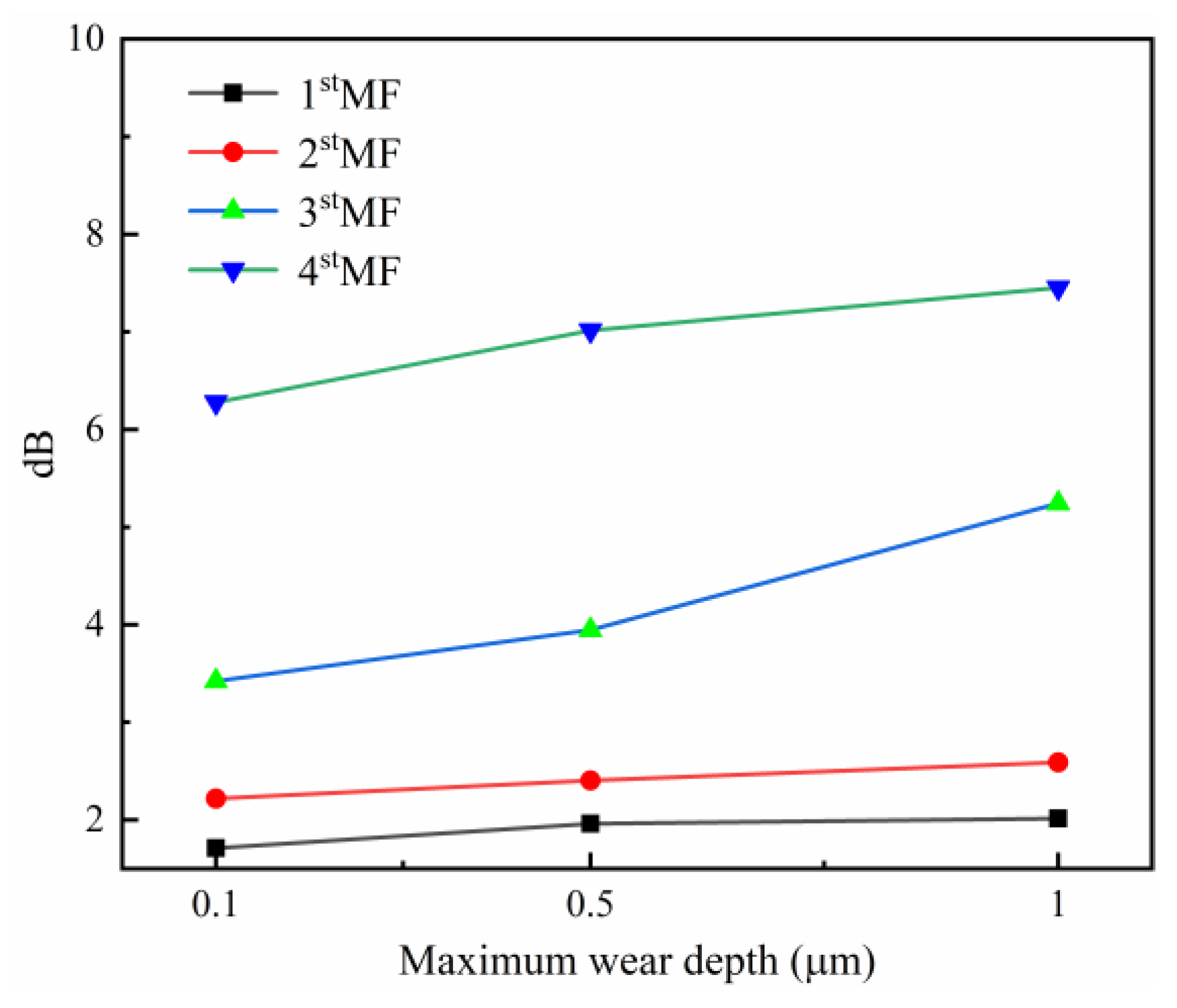
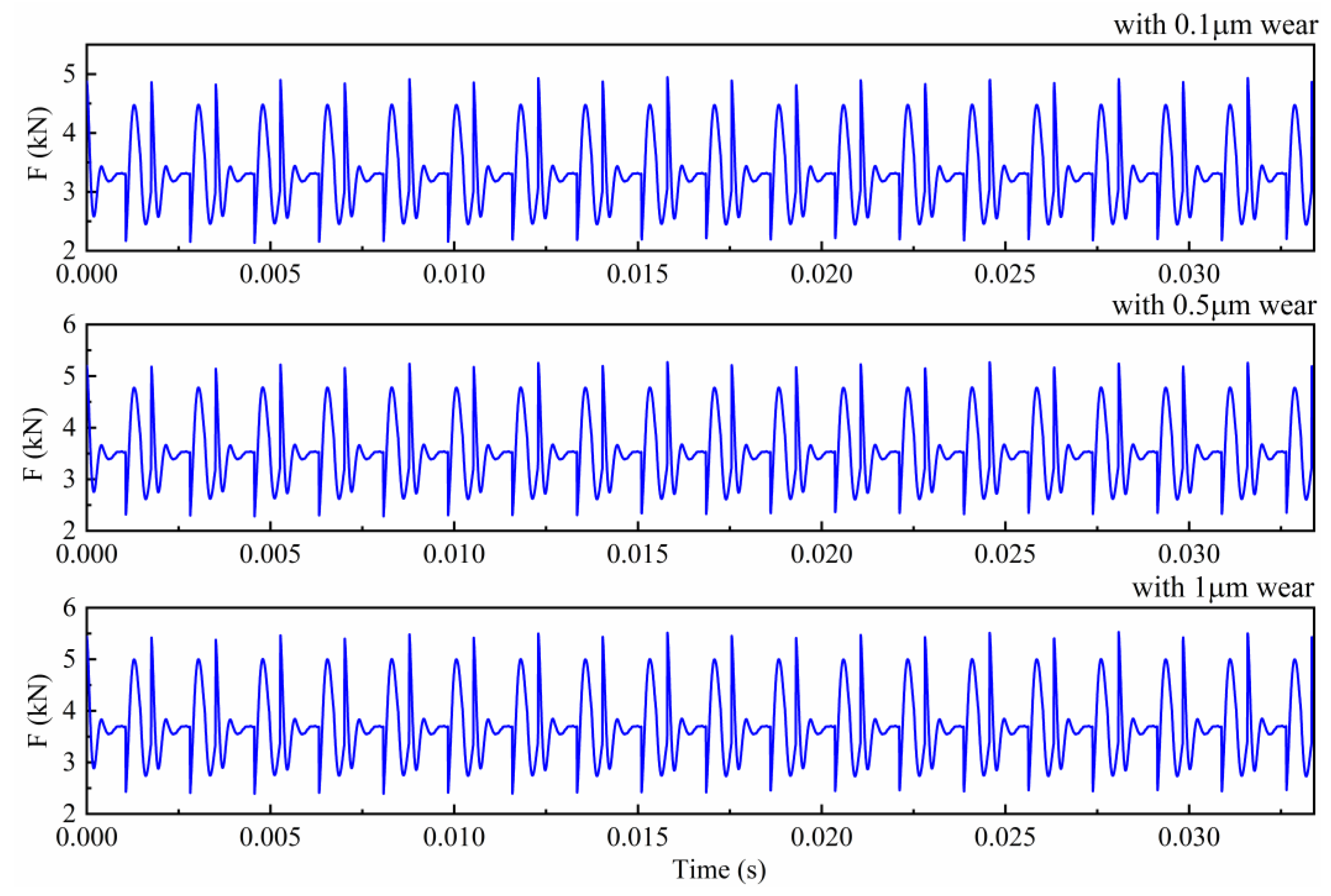
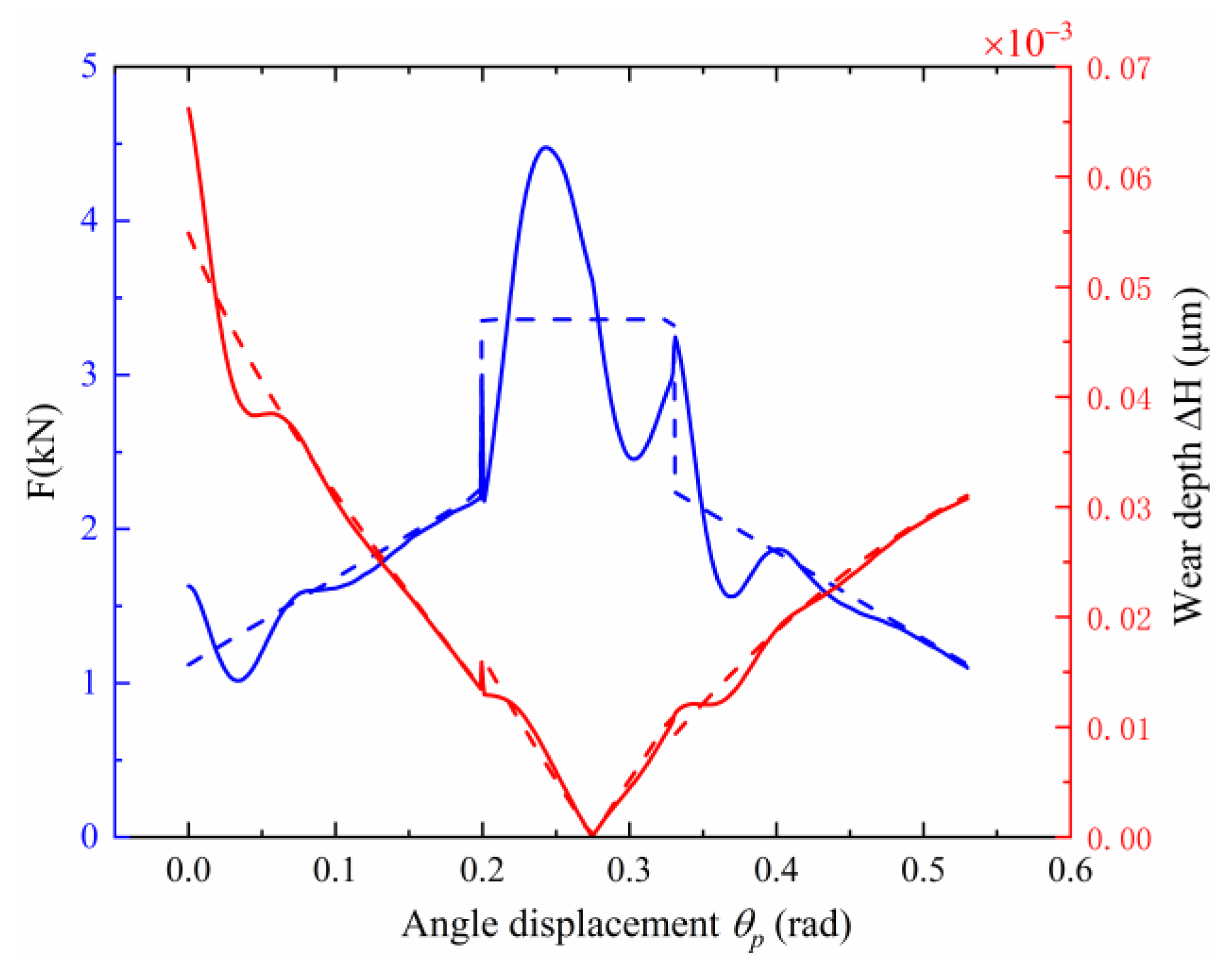
4.1. Effects of Gear Surface Wear on the Dynamic Response
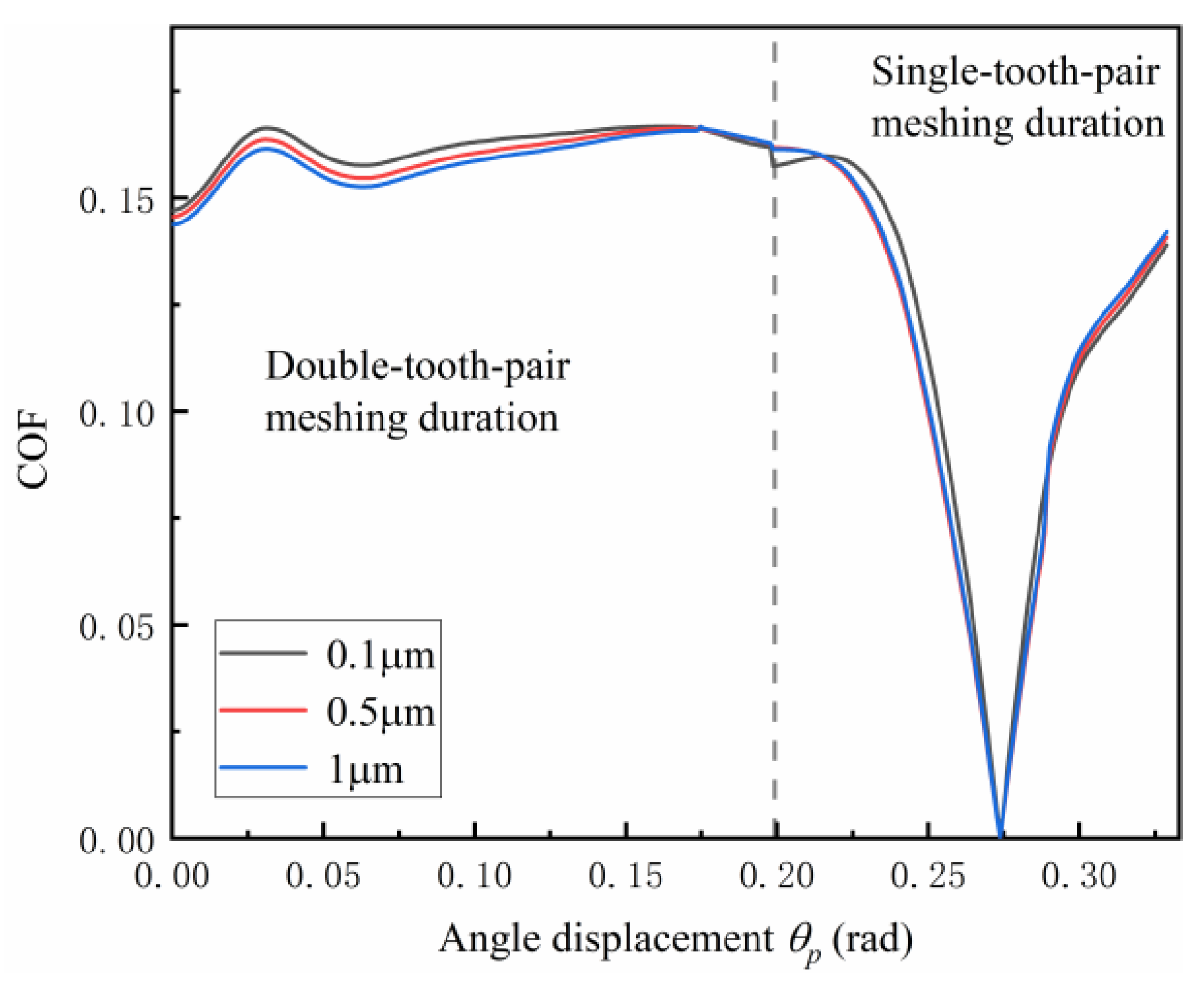
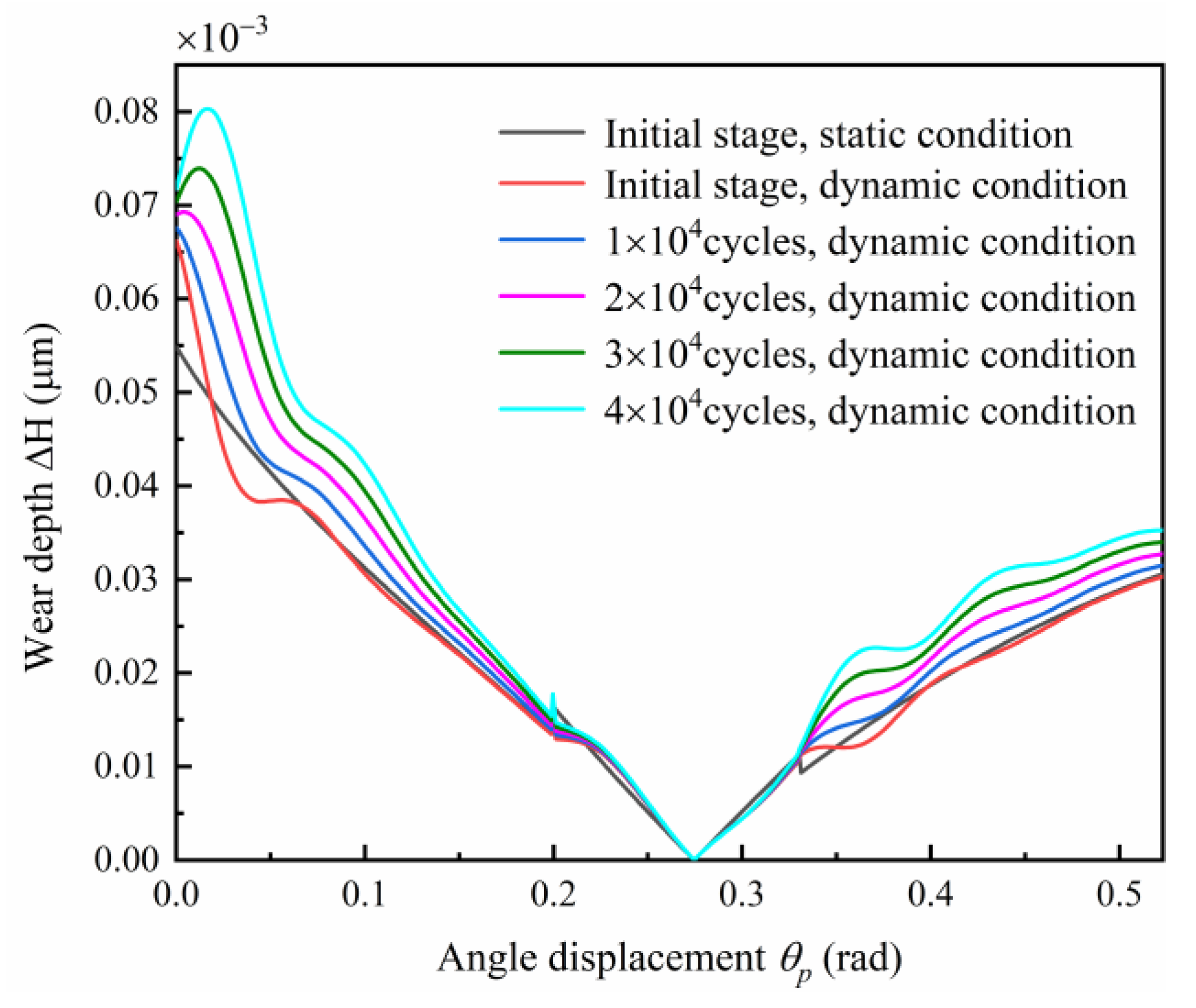
4.2. Effects of the Dynamic Response on Gear Surface Wear
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fernandes, P.; McDuling, C. Surface contact fatigue failures in gears. Eng. Fail. Anal. 1997, 4, 99–107. [Google Scholar] [CrossRef]
- Wojnarowski, J.; Onishchenko, V. Tooth wear effects on spur gear dynamics. Mech. Mach. Theory 2003, 38, 161–178. [Google Scholar] [CrossRef]
- Osman, T.; Velex, P. Static and dynamic simulations of mild abrasive wear in wide-Faced solid spur and helical gears. Mech. Mach. Theory 2010, 45, 911–924. [Google Scholar] [CrossRef]
- Jamari, J.; Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; van der Heide, E. In Silico Contact Pressure of Metal-On-Metal Total Hip Implant with Different Materials Subjected to Gait Loading. Metals 2022, 12, 1241. [Google Scholar] [CrossRef]
- Choy, F.; Polyshchuk, V.; Zakrajsek, J.; Handschuh, R.; Townsend, D. Analysis of the effects of surface pitting and wear on the vibration of a gear transmission system. Tribol. Int. 1996, 29, 77–83. [Google Scholar] [CrossRef]
- Kuang, J.H.; Lin, A.D. The effect of tooth wear on the vibration spectrum of a spur gear pair. J. Vib. Acoust. 2001, 123, 311–317. [Google Scholar] [CrossRef]
- Yesilyurt, I.; Gu, F.; Ball, A.D. Gear tooth stiffness reduction measurement using modal analysis and its use in wear fault severity assessment of spur gears. NDT E Int. 2003, 36, 357–372. [Google Scholar] [CrossRef]
- Yuksel, C.; Kahraman, A. Dynamic tooth loads of planetary gear sets having tooth profile wear. Mech. Mach. Theory 2004, 39, 695–715. [Google Scholar] [CrossRef]
- Ding, H.; Kahraman, A. Interactions between nonlinear spur gear dynamics and surface wear. J. Sound Vib. 2007, 307, 662–679. [Google Scholar] [CrossRef]
- Kahraman, A.; Ding, H. A Methodology to Predict Surface Wear of Planetary Gears Under Dynamic Conditions. Mech. Based Des. Struct. Mach. 2010, 38, 493–515. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Zhang, J. Investigation on coupling effects between surface wear and dynamics in a spur gear system. Tribol. Int. 2016, 101, 383–394. [Google Scholar] [CrossRef]
- Flodin, A.; Andersson, S. Simulation of mild wear in spur gears. Wear 1997, 207, 16–23. [Google Scholar] [CrossRef]
- Bajpai, P.; Kahraman, A.; Anderson, N.E. A Surface Wear Prediction Methodology for Parallel-Axis Gear Pairs. J. Tribol. 2004, 126, 597–605. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M. On the prediction of steady-State wear rate in spur gears. Wear 2015, 342, 234–243. [Google Scholar] [CrossRef]
- Feng, K.; Borghesani, P.; Smith, W.A.; Randall, R.B.; Chin, Z.Y.; Ren, J.; Peng, Z. Vibration-Based updating of wear prediction for spur gears. Wear 2019, 426, 1410–1415. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.; Ni, Q.; Beer, M. A review of vibration-Based gear wear monitoring and prediction techniques. Mech. Syst. Signal Process. 2023, 182, 109605. [Google Scholar] [CrossRef]
- Mark, W.D. Performance-Based Gear Metrology: Kinematic-Transmission-Error Computation and Diagnosis; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Jamari, J.; Ammarullah, M.; Afif, I.; Ismail, R.; Tauviqirrahman, M.; Bayuseno, A. Running-In Analysis of Transmission Gear. Tribol. Ind. 2021, 43, 434–441. [Google Scholar] [CrossRef]
- He, S.; Gunda, R.; Singh, R. Effect of sliding friction on the dynamics of spur gear pair with realistic time-Varying stiffness. J. Sound Vib. 2007, 301, 927–949. [Google Scholar] [CrossRef]
- Chen, S.; Tang, J.; Luo, C.; Wang, Q. Nonlinear dynamic characteristics of geared rotor bearing systems with dynamic backlash and friction. Mech. Mach. Theory 2011, 46, 466–478. [Google Scholar] [CrossRef]
- Jiang, H.; Shao, Y.; Mechefske, C.K. Dynamic characteristics of helical gears under sliding friction with spalling defect. Eng. Fail. Anal. 2014, 39, 92–107. [Google Scholar] [CrossRef]
- Luo, Y.; Baddour, N.; Liang, M. Dynamical modeling and experimental validation for tooth pitting and spalling in spur gears. Mech. Syst. Signal Process. 2018, 119, 155–181. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, L.; Gou, X.; Shi, J.; Jin, G. Modeling and analyzing of nonlinear dynamics for spur gear pair with pitch deviation under multi-State meshing. Mech. Mach. Theory 2021, 163, 104378. [Google Scholar] [CrossRef]
- Pedrero, J.I.; Pleguezuelos, M.; Artés, M.; Antona, J.A. Load distribution model along the line of contact for involute external gears. Mech. Mach. Theory 2010, 45, 780–794. [Google Scholar] [CrossRef]
- Xu, H.; Kahraman, A.; Anderson, N.E.; Maddock, D.G. Prediction of Mechanical Efficiency of Parallel-Axis Gear Pairs. J. Mech. Des. 2006, 129, 58–68. [Google Scholar] [CrossRef]
- Liang, X.; Zuo, M.J.; Pandey, M. Analytically evaluating the influence of crack on the mesh stiffness of a planetary gear set. Mech. Mach. Theory 2014, 76, 20–38. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Lin, J.Y. Hertzian Damping, Tooth Friction and Bending Elasticity in Gear Impact Dynamics. J. Mech. Transm. Autom. Des. 1987, 109, 189–196. [Google Scholar] [CrossRef]
- Yang, D.C.H.; Sun, Z.S. A Rotary Model for Spur Gear Dynamics. J. Mech. Transm. Autom. Des. 1985, 107, 529–535. [Google Scholar] [CrossRef]
- Yu, W. Dynamic Modelling of Gear Transmission Systems with and without Localized Tooth Defects. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2017. [Google Scholar]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Brauer, J.; Andersson, S. Simulation of wear in gears with flank interference—A mixed FE and analytical approach. Wear 2003, 254, 1216–1232. [Google Scholar] [CrossRef]
- Jamari, J.; Ammarullah, M.; Saad, A.; Syahrom, A.; Uddin, M.; van der Heide, E.; Basri, H. The Effect of Bottom Profile Dimples on the Femoral Head on Wear in Metal-On-Metal Total Hip Arthroplasty. J. Funct. Biomater. 2021, 12, 38. [Google Scholar] [CrossRef]
- Feng, K.; Smith, W.A.; Peng, Z. Use of an improved vibration-Based updating methodology for gear wear prediction. Eng. Fail. Anal. 2020, 120, 105066. [Google Scholar] [CrossRef]



| Parameters | Pinion | Gear |
|---|---|---|
| Gear type | Standard involute, full teeth | |
| Material | S45 C | |
| Modulus of elasticity, | 205 | |
| Poisson’s ratio, | 0.3 | |
| Face width, | 20 | |
| Module, | 2 mm | |
| Pressure angle | ||
| Addendum | 1.00 | |
| Dedendum | 1.25 | |
| Number of teeth | 19 | 31 |
| Pitch radius, | 19 | 31 |
| Parameters | Values |
|---|---|
| Mass of the pinion, | 0.7 kg |
| Mass of the gear, | 1.822 kg |
| Mass moment inertia of the pinion, | |
| Mass moment inertia of the gear, | |
| Mass moment inertia of the motor, | |
| Mass moment inertia of break, | |
| Damping coefficient of bearing, | |
| Stiffness of bearing, | |
| Damping of coupling, | |
| Coupling stiffness, |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Yuan, H. A Dynamic Wear Prediction Model for Studying the Interactions between Surface Wear and Dynamic Response of Spur Gears. Coatings 2022, 12, 1250. https://doi.org/10.3390/coatings12091250
Ren J, Yuan H. A Dynamic Wear Prediction Model for Studying the Interactions between Surface Wear and Dynamic Response of Spur Gears. Coatings. 2022; 12(9):1250. https://doi.org/10.3390/coatings12091250
Chicago/Turabian StyleRen, Jinzhao, and Huiqun Yuan. 2022. "A Dynamic Wear Prediction Model for Studying the Interactions between Surface Wear and Dynamic Response of Spur Gears" Coatings 12, no. 9: 1250. https://doi.org/10.3390/coatings12091250
APA StyleRen, J., & Yuan, H. (2022). A Dynamic Wear Prediction Model for Studying the Interactions between Surface Wear and Dynamic Response of Spur Gears. Coatings, 12(9), 1250. https://doi.org/10.3390/coatings12091250






