Modelling of Lead Corrosion in Contact with an Anaerobic HCl Solution, Influence of the Corrosion Product Presence
Abstract
:1. Introduction
2. Mathematical Model
2.1. Model
- -
- The Tertiary Current Distribution, Nernst–Planck module describes the current and potential distribution in an electrochemical cell, taking into account the individual transport of charged species (ions) and uncharged species in the electrolyte due to diffusion, migration, and convection using the Nernst–Planck equations. The physics interface supports different descriptions of the coupled charge and mass transport in the electrolyte. The electrode kinetics for the charge transfer reactions can be described by using arbitrary expressions or by using the predefined Butler–Volmer and Tafel expressions.
- -
- PDE interfaces for equation-based modeling, distinguished by the equation formulation used for entering the equations, which allows encoding of the variation over time of the porosity.
- -
- The Deformed Geometry interface is used to study how physics changes when the geometry, here represented by the mesh, changes due to an externally imposed geometric change.
- -
- The multiphysics coupling features are simulated by the Multiphysics module that is a quick entry point for common multiphysics applications.
2.2. Governing Equation for the Electrolyte
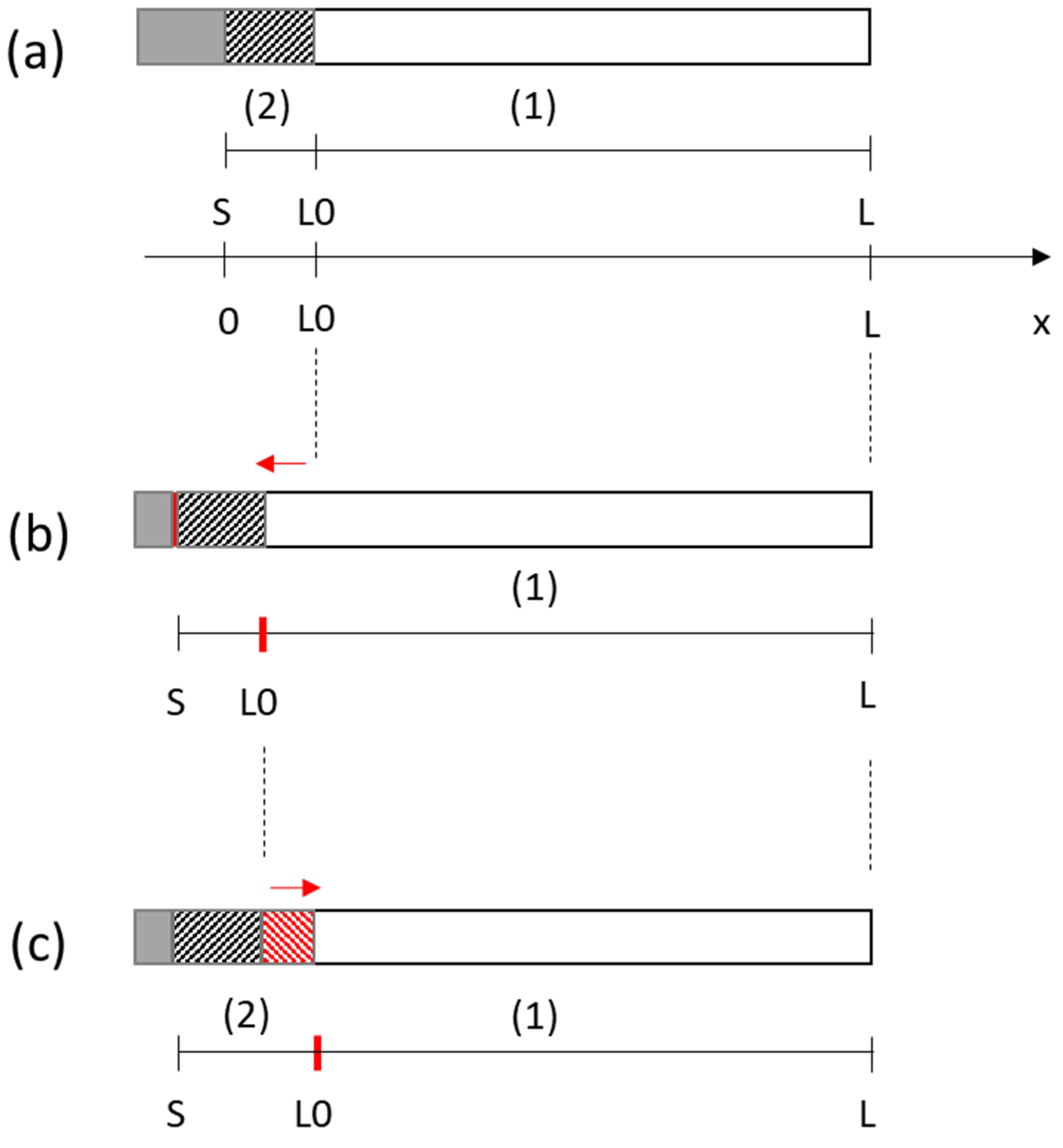
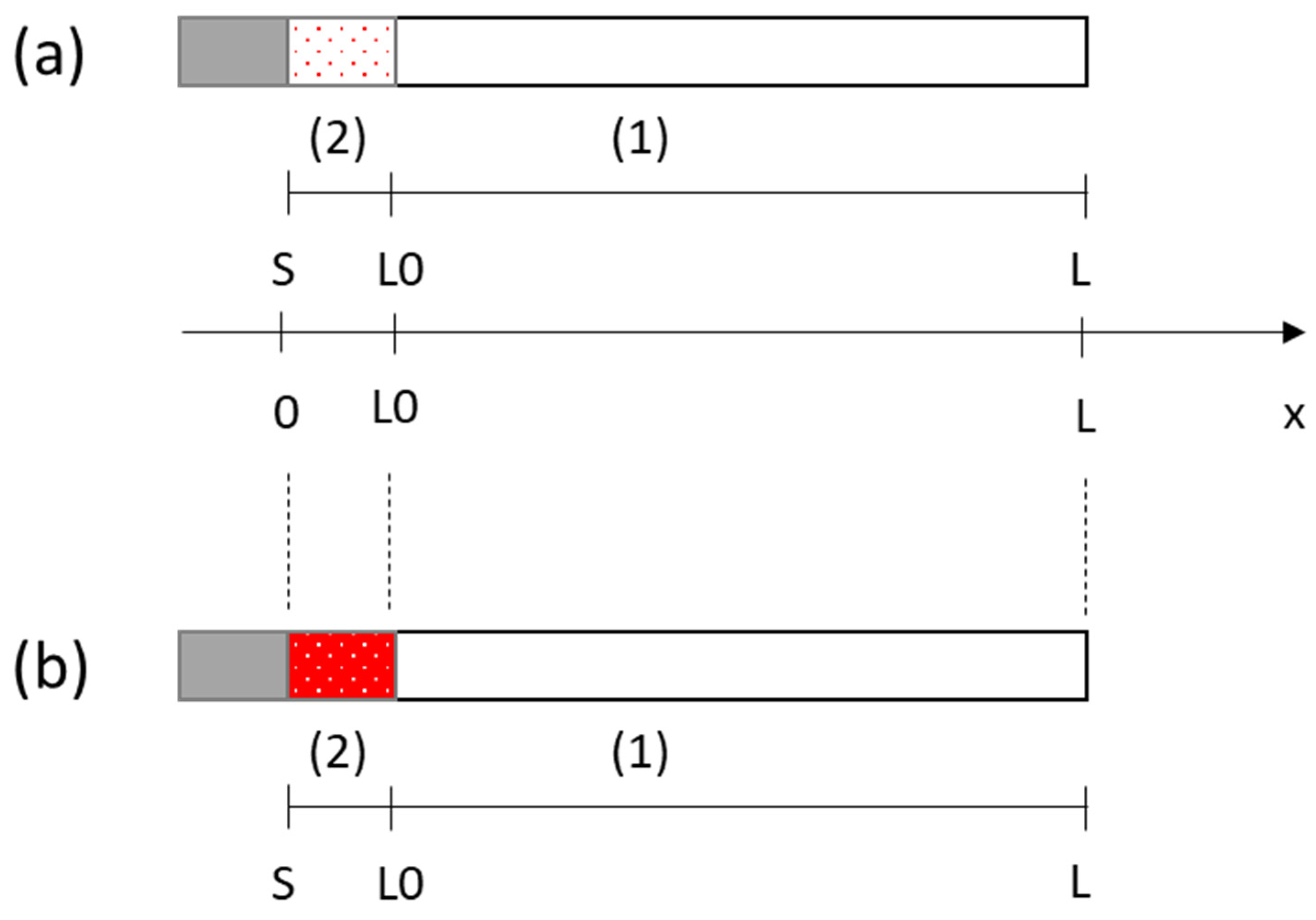
2.3. Boundary Conditions
2.4. Governing Equation for the CPL
2.5. Parameter
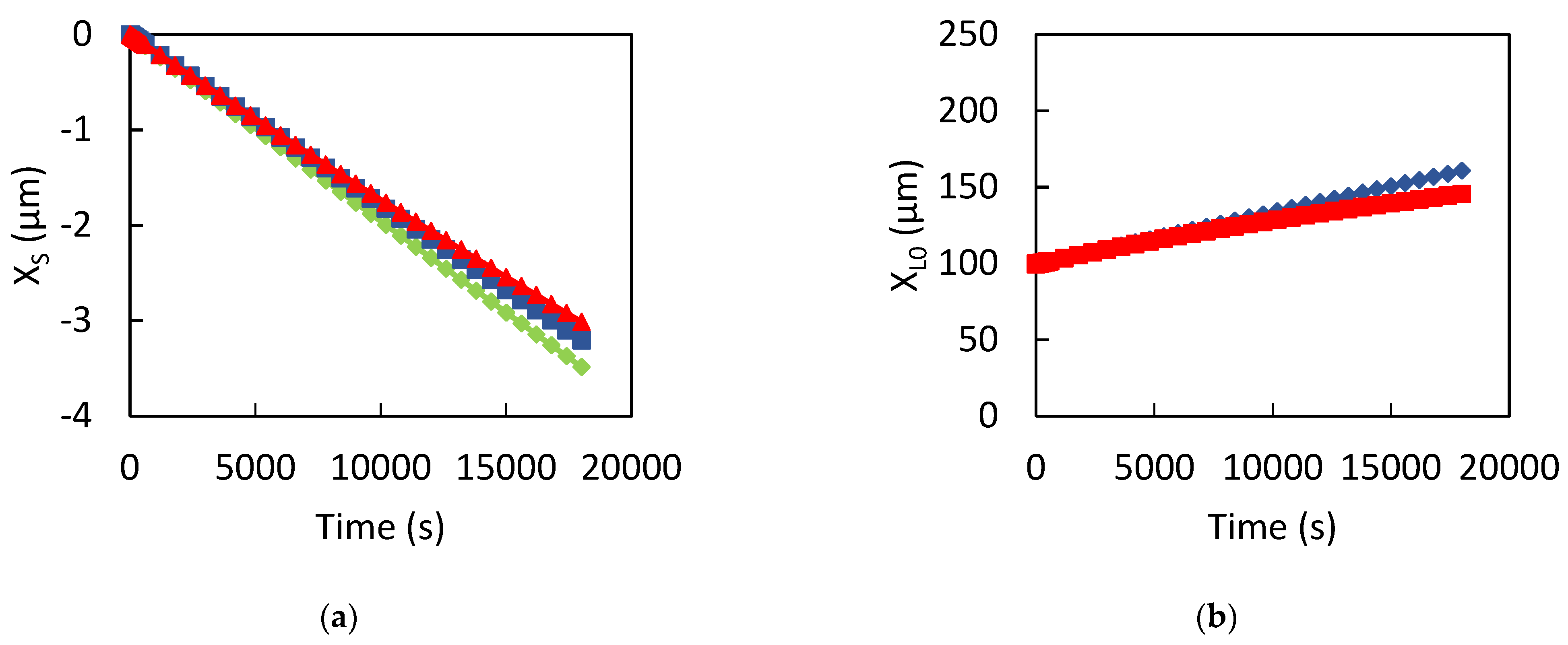
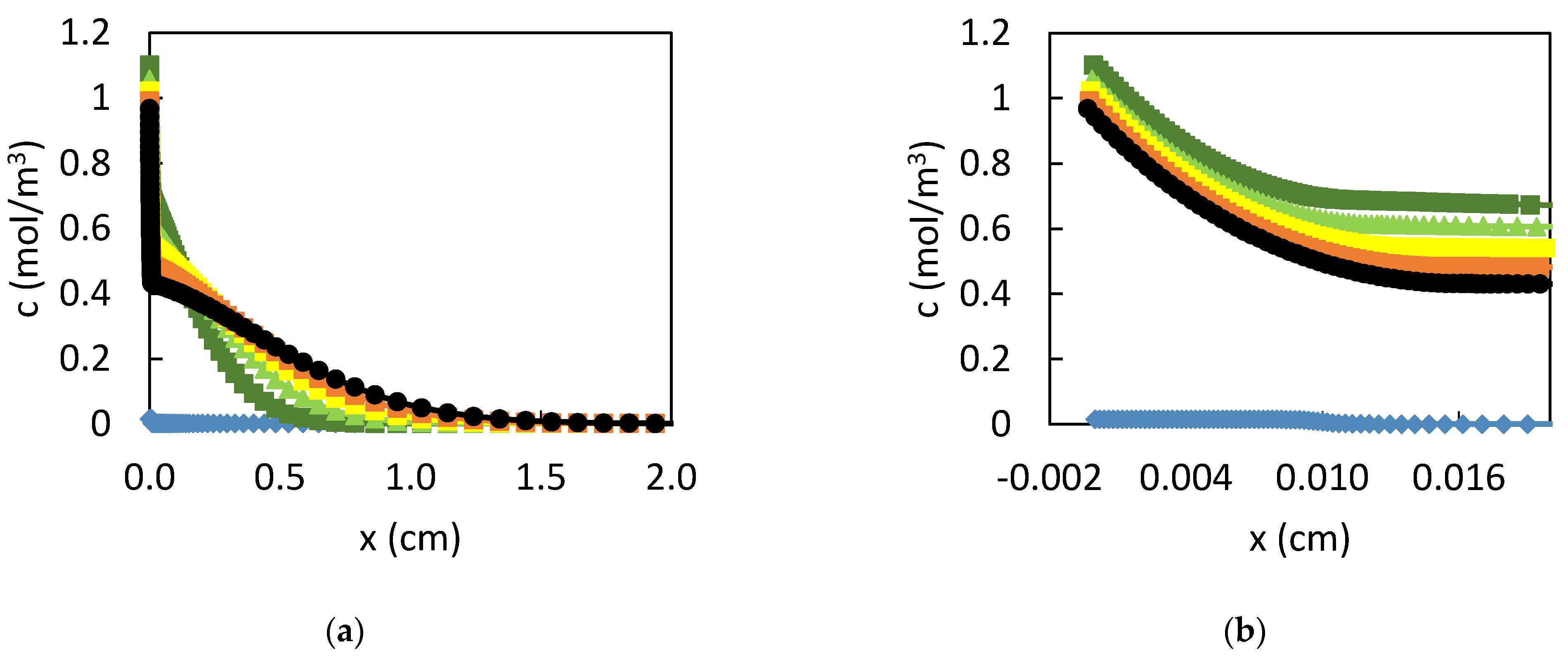
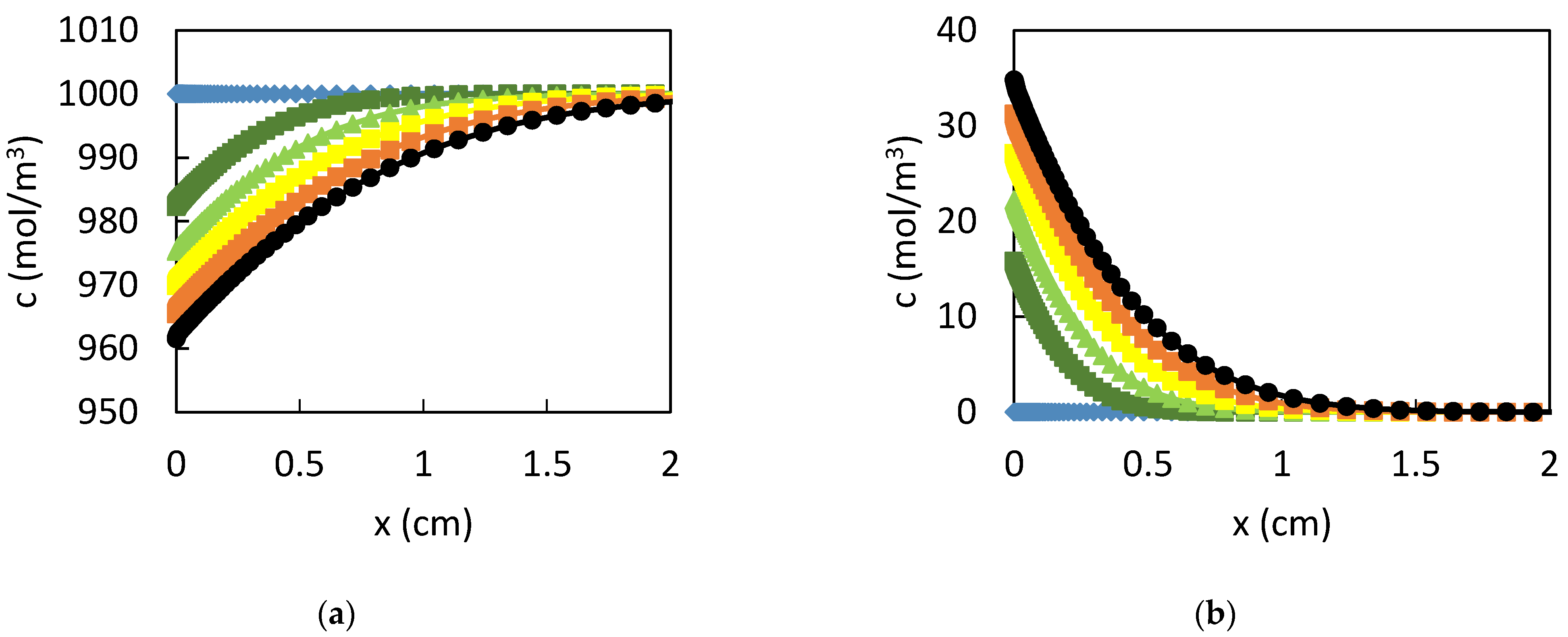
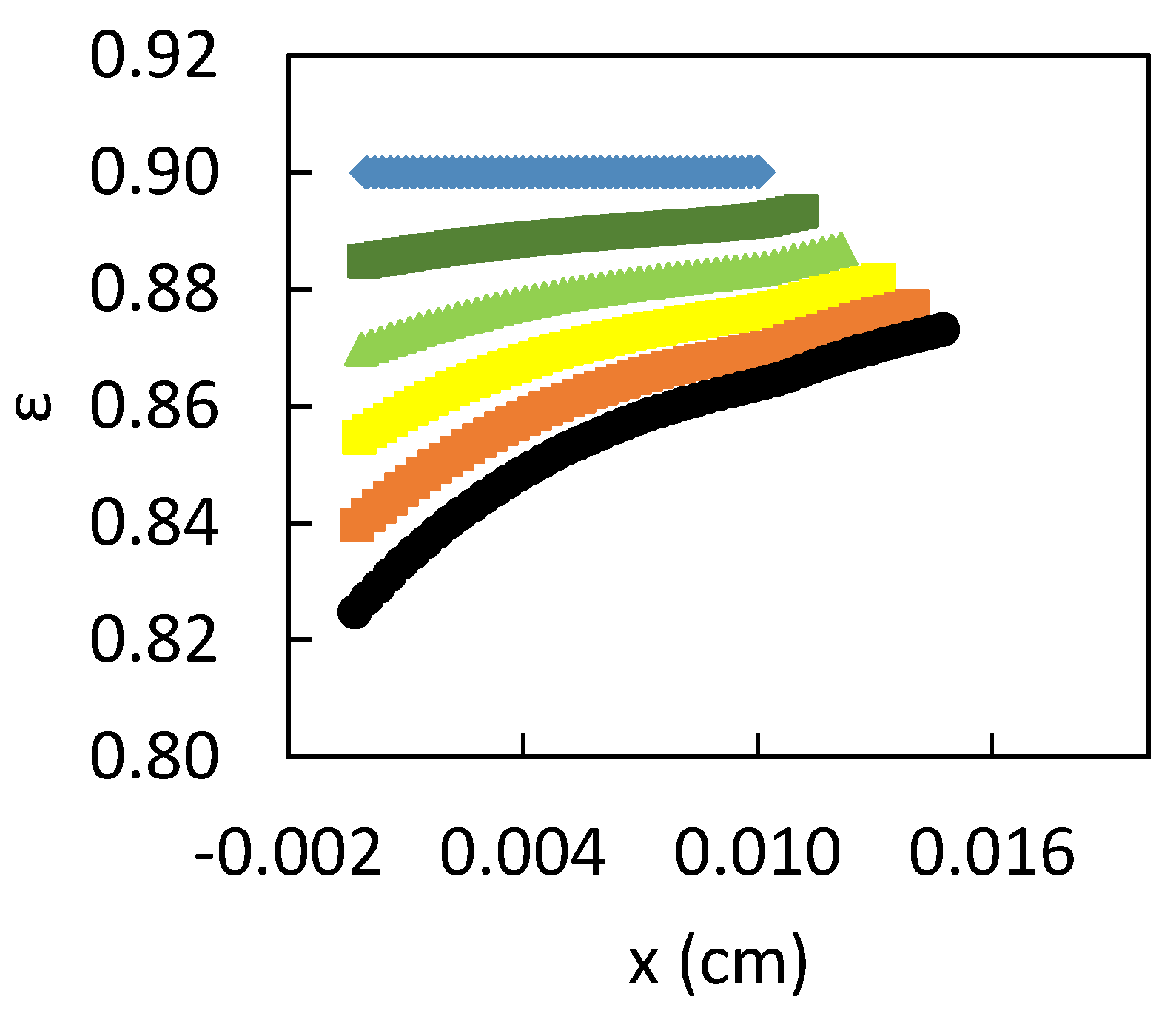
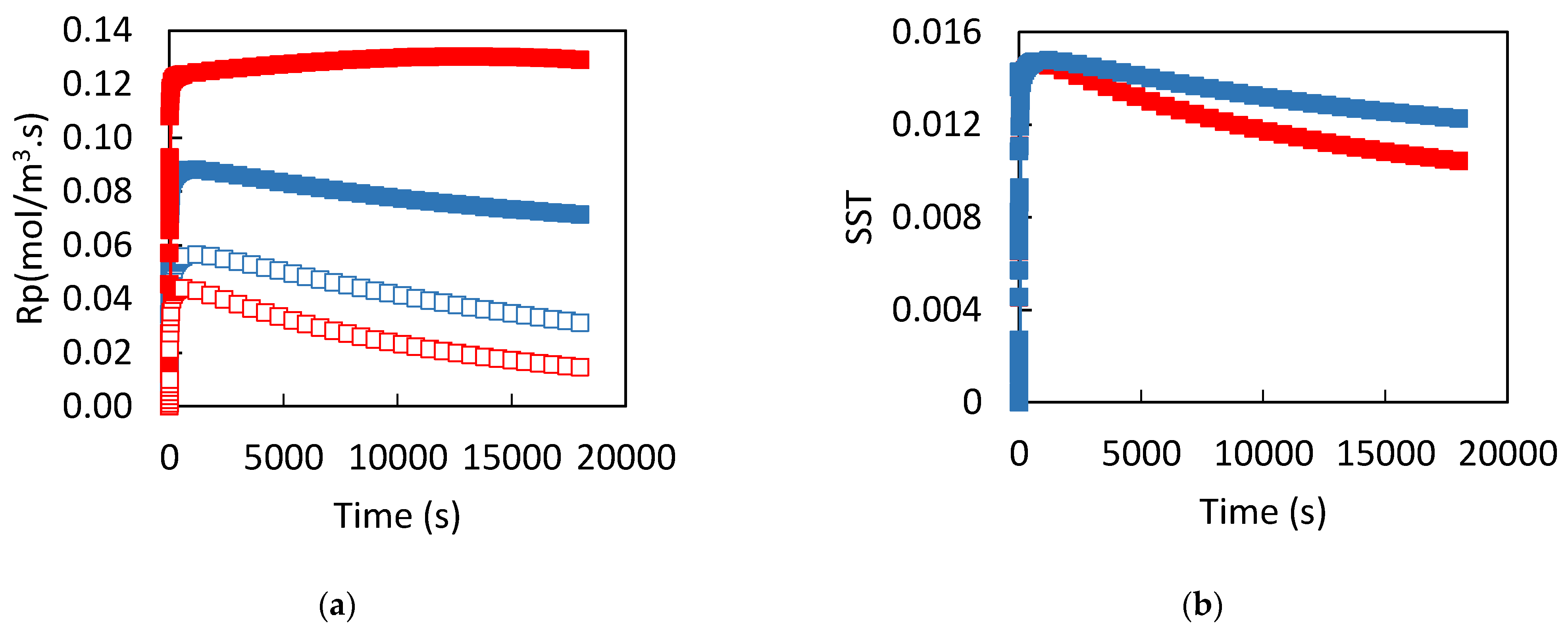
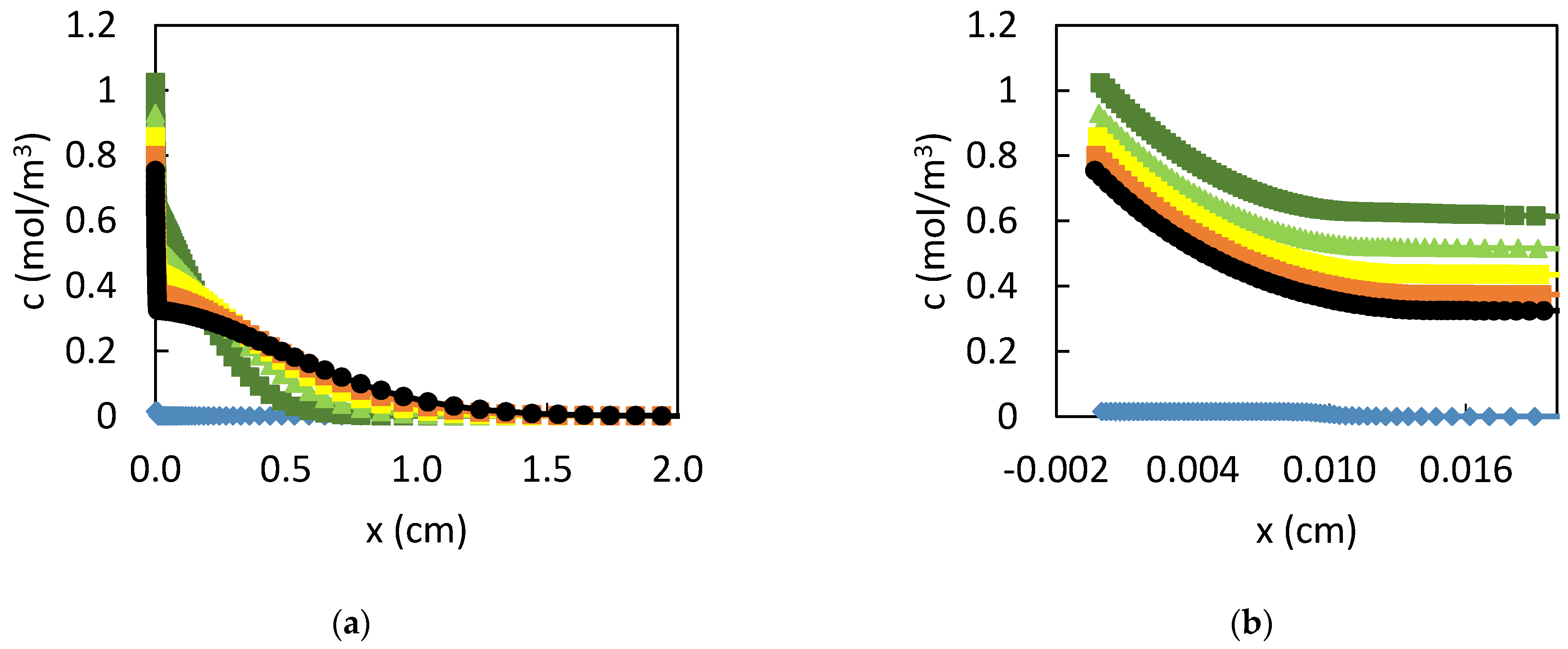
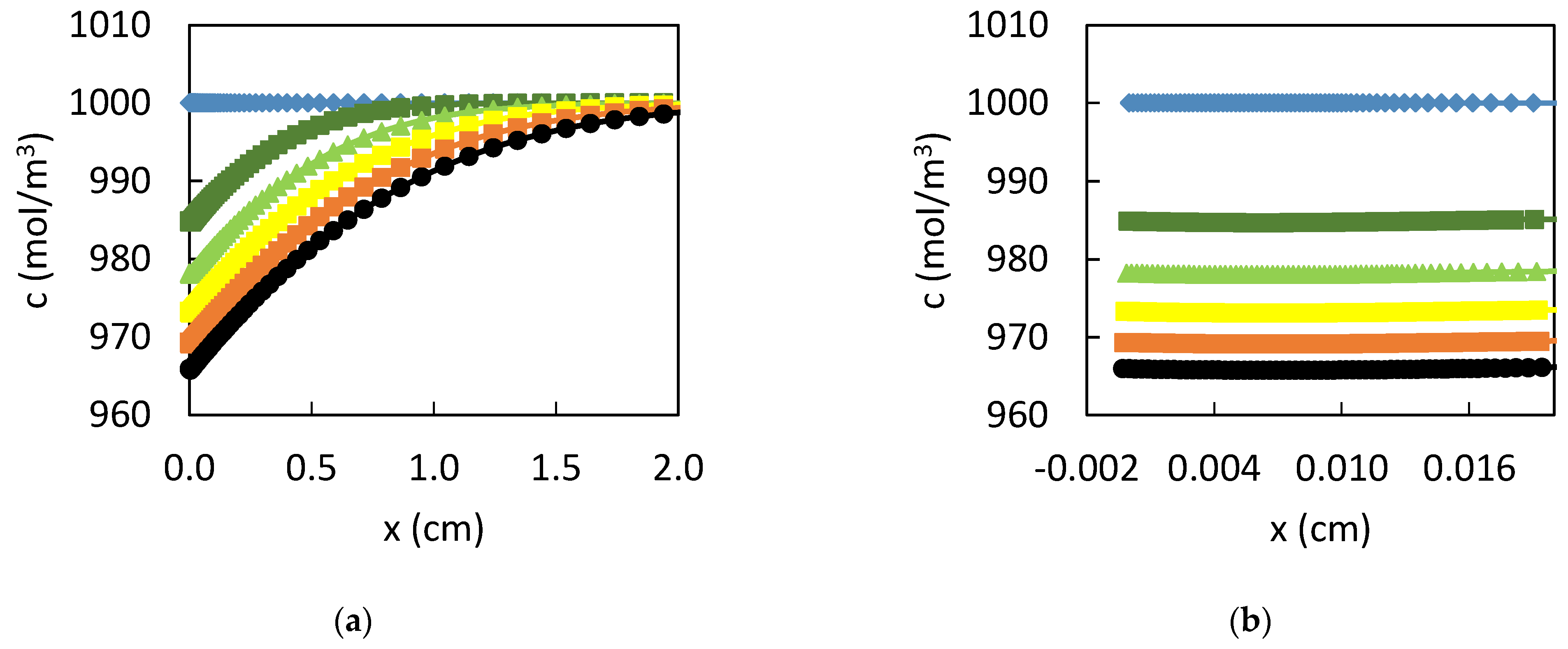
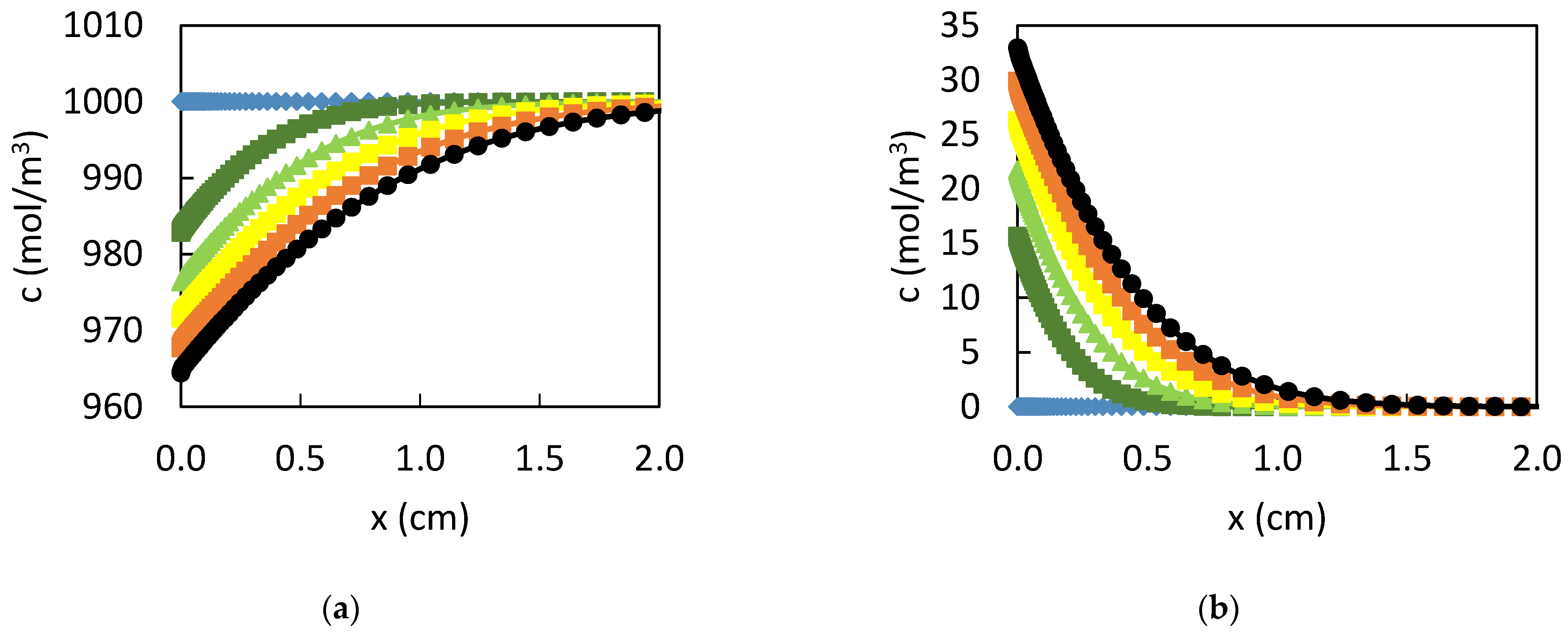
3. Results
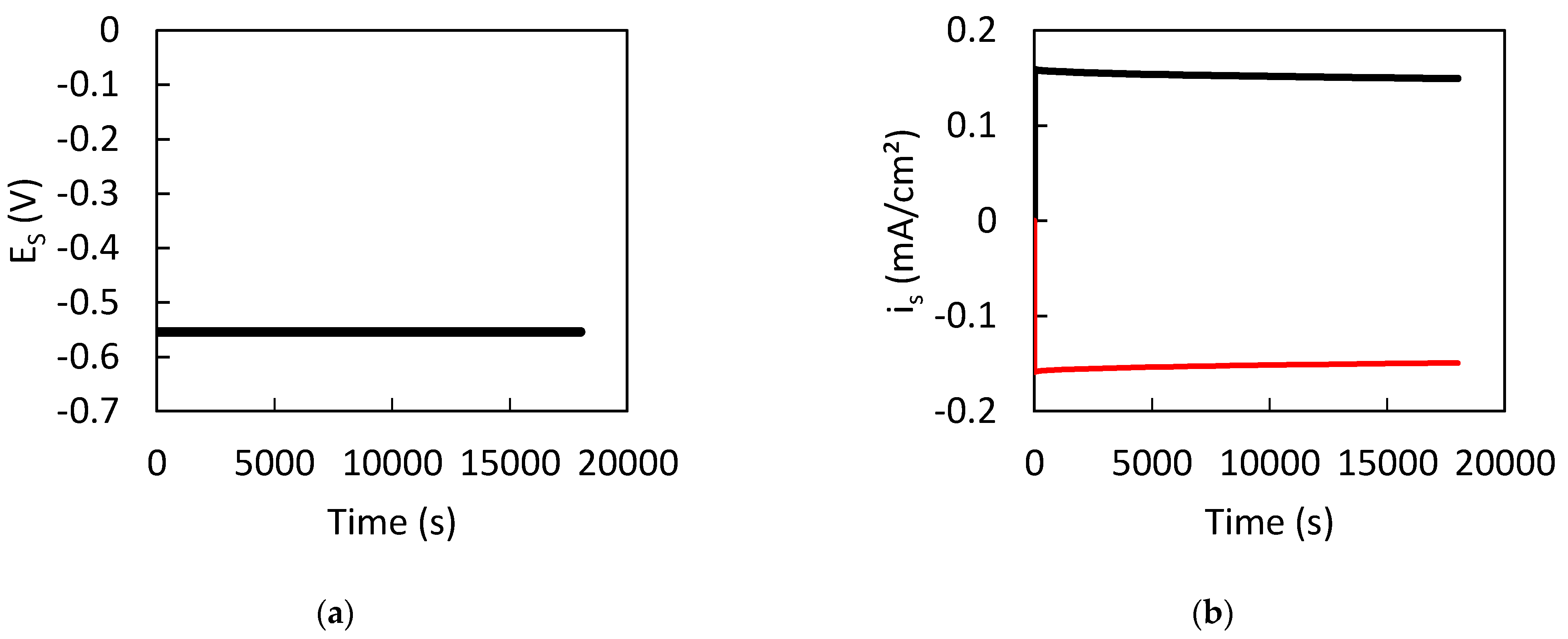
3.1. Dissolution of Lead
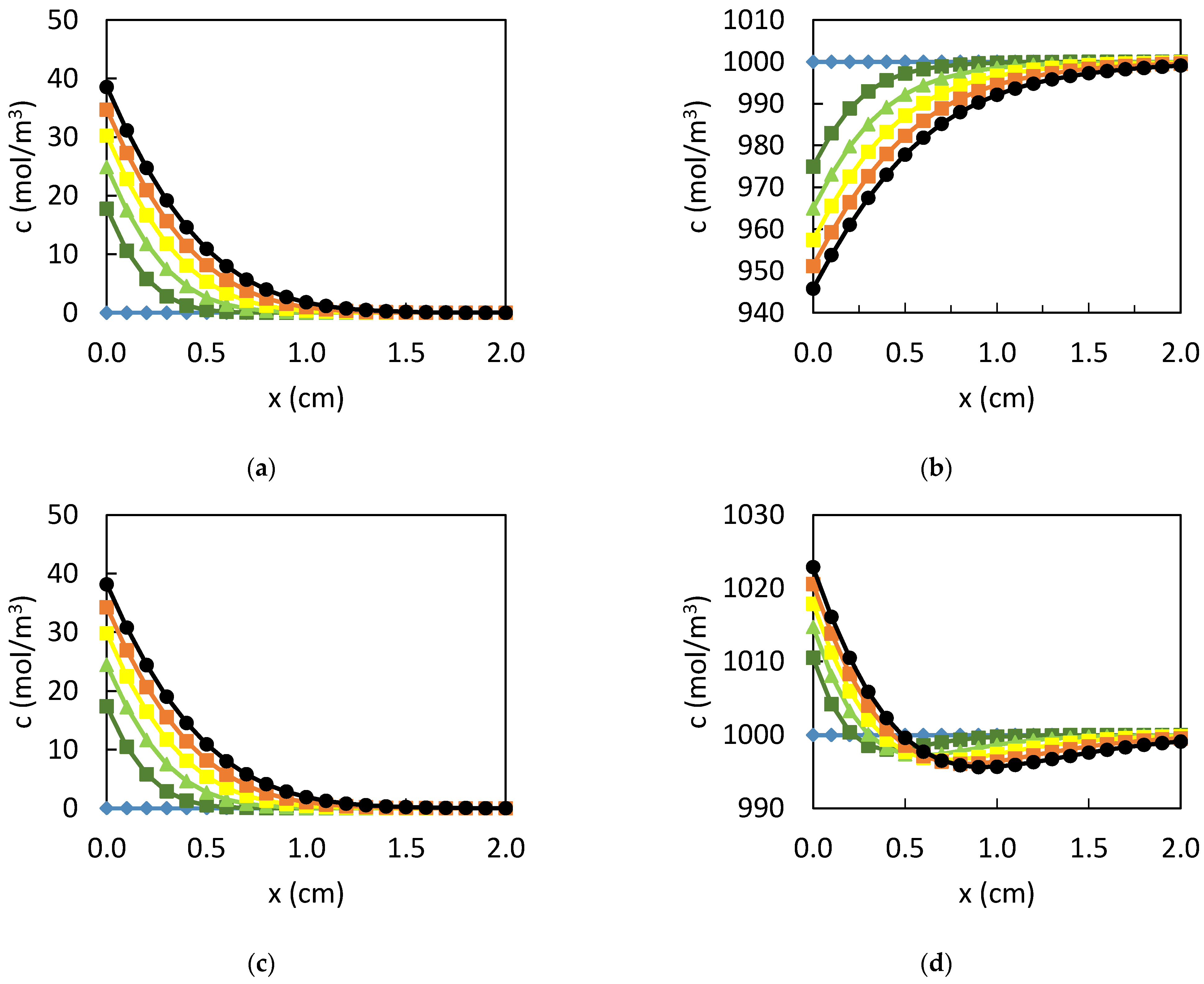
3.2. Influence of the CPL
4. Discussion
5. Conclusions
- When lead is immersed in HCl, it dissolves. This dissolution leads to saturation of the electrolyte with the consequent precipitation of corrosion product;
- The PbCl2 corrosion product layer has an impact on the dissolution kinetics. Its development takes place by growth in space but also by densification, with an evolution of epsilon;
- The PbCl2 layer is more compact near the surface of the electrode in accordance with the place of creation of the ions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Austin, S.; Glowacki, A. Hydrochloric Acid. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Lecloux, A. Chemical, biological and physical constrains in catalytic reduction processes for purification of drinking water. Catal. Today 1999, 53, 23–34. [Google Scholar] [CrossRef]
- Bagchi, P.; Karpinski, P.H.; McIntire, G.L. Microprecipitation of Nanoparticulate Pharmaceutical Agents. U.S. Patent US5560932A, 1 October 1996. [Google Scholar]
- Karlsson, A.; Ejlertsson, J. Addition of HCl as a means to improve biogas production from protein-rich food industry waste. Biochem. Eng. J. 2012, 61, 43–48. [Google Scholar] [CrossRef]
- Kim, J.; McVittie, J.; Saraswat, K.; Nishi, Y.; Liu, S.; Tan, S. Germanium Surface Cleaning with Hydrochloric Acid. ECS Trans. 2006, 3, 1191–1196. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Z.; Sun, S.; Pianetta, P. The effectiveness of HCl and HF cleaning of Si0.85Ge0.15 surface. J. Vac. Sci. Technol. A Vac. Surf. Film. 2008, 26, 1248–1250. [Google Scholar] [CrossRef]
- Tomaszewska, M.; Gryta, M.; Morawski, A.W. Recovery of hydrochloric acid from metal pickling solutions by membrane distillation. Sep. Purif. Technol. 2001, 22-23, 591–600. [Google Scholar] [CrossRef]
- Li, L.-F.; Caenen, P.; Celis, J.-P. Effect of hydrochloric acid on pickling of hot-rolled 304 stainless steel in iron chloride-based electrolytes. Corros. Sci. 2008, 50, 804–810. [Google Scholar] [CrossRef]
- Lin, H.-W.; Cejudo-Marín, R.; Jeremiasse, A.W.; Rabaey, K.; Yuan, Z.; Pikaar, I. Direct anodic hydrochloric acid and cathodic caustic production during water electrolysis. Sci. Rep. 2016, 6, 20494. [Google Scholar] [CrossRef]
- Subramanian, K. Lead-Free Electronic Solders: A Special Issue of the Journal of Materials Science: Materials in Electronics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Lim, S.-R.; Schoenung, J.M. Human health and ecological toxicity potentials due to heavy metal content in waste electronic devices with flat panel displays. J. Hazard. Mater. 2010, 177, 251–259. [Google Scholar] [CrossRef]
- World Health Organization. Toolkit for Establishing Laws to Eliminate Lead in Paint; World Health Organization: Geneva, Switzerland, 2021. [Google Scholar]
- Baba, A.A.; Adekola, F.; Ghosh, M.K.; Salubi, Y.A.; Oyedotun, M.O.; Rout, P.O.; Sheik, A.R.; Pradhan, S.R. Leaching of Lead from Spent Motorcycle Battery in Hydrochloric Acid. Part I: Dissolution kinetics. Acta Metall. Slovaca 2010, 16, 194–204. [Google Scholar]
- El Wanees, S.A.; El Aal, E.A. N-Phenylcinnamimide and some of its derivatives as inhibitors for corrosion of lead in HCl solutions. Corros. Sci. 2010, 52, 338–344. [Google Scholar] [CrossRef]
- El Rehim, S.A.; El-Halim, A.A.; Foad, E. Potentiodynamic and cyclic voltammetric behaviour of the lead electrode in HCl solutions. Surf. Technol. 1983, 18, 313–325. [Google Scholar] [CrossRef]
- Aaal, E.E.A.E.; El Wanees, S.A. Kinetics of anodic behaviour of Pb in HCl solutions. Corros. Sci. 2009, 51, 458–462. [Google Scholar] [CrossRef]
- Barradas, R.G.; Belinko, K.; Ghibaudi, E. Rotating Ring-disc Electrode Studies of Lead in HCl and NaCl Solutions. Can. J. Chem. 1975, 53, 407–413. [Google Scholar] [CrossRef]
- Barradas, R.; Fletcher, S.; Porte, J. The anodic behaviour of lead amalgam electrodes in HCl solution. J. Electroanal. Chem. Interfacial Electrochem. 1977, 80, 295–304. [Google Scholar] [CrossRef]
- Barradas, R.; Belinko, K.; Shoesmith, W. Study of surface effects in the formation of lead chloride on lead electrodes in aqueous HCl by electrochemical methods and scanning electron microscopy. Electrochim. Acta 1976, 21, 357–365. [Google Scholar] [CrossRef]
- Ambrose, J.; Barradas, R.; Belinko, K.; Shoesmith, D. Reactions at the lead electrode/hydrochloric acid interface. J. Colloid Interface Sci. 1974, 47, 441–454. [Google Scholar] [CrossRef]
- Azizi, A.; Ghasemi, S.M.S. A comparative analysis of the dissolution kinetics of lead from low grade oxide ores in HCl, H2SO4, HNO3 and citric acid solutions. Met. Res. Technol. 2017, 114, 406. [Google Scholar] [CrossRef]
- Baba, A.; Sheik, A.R.; Olawale, K.I.; Young, T.; Ghosh, M.K.; Folahan, A.A. Kinetic analysis of total Lead from spent Car battery by hydrochloric acid leaching. J. Iran. Chem. Res. 2011, 4, 291–300. [Google Scholar]
- Barradas, R.; Fletcher, S. Temperature effects in the electrochemical behaviour of cycled lead electrodes in HCl solutions. Electrochim. Acta 1977, 22, 237–242. [Google Scholar] [CrossRef]
- Van Herck, P.; Van der Bruggen, B.; Vogels, G.; Vandecasteele, C. Application of computer modelling to predict the leaching behaviour of heavy metals from MSWI fly ash and comparison with a sequential extraction method. Waste Manag. 2000, 20, 203–210. [Google Scholar] [CrossRef]
- Rooney, C.P.; McLaren, R.G.; Condron, L.M. Control of lead solubility in soil contaminated with lead shot: Effect of soil pH. Environ. Pollut. 2007, 149, 149–157. [Google Scholar] [CrossRef] [PubMed]
- Inamuddin, A.M.I.; Luqman, M.; Altalhi, T. Sustainable Corrosion Inhibitors; Materials Research Forum: Millersville, PA, USA, 2021; Volume 107. [Google Scholar]
- Liu, C.; Kelly, R.G. A Review of the Application of Finite Element Method (FEM) to Localized Corrosion Modeling. Corrosion 2019, 75, 1285–1299. [Google Scholar] [CrossRef] [Green Version]
- Simillion, H.; Dolgikh, O.; Terryn, H.; Deconinck, J. Atmospheric corrosion modeling. Corros. Rev. 2014, 32, 73–100. [Google Scholar] [CrossRef]
- Tricoit, S. Modeling and Numerical Simulation of the Propagation of Pitting Corrosion of Iron in Chlorinated Medium: Contribution to the Evaluation of the Durability of Carbon Steels in Geological Storage Conditions. Ph.D. Thesis, Université de Bourgogne, UFR Sciences et Techniques, Laboratoire Interdisciplinaire Carnot de Bourgogne-LICB (France), Dijon, France, 2012. [Google Scholar]
- Radouani, R.; Echcharqy, Y.; Essahli, M. Numerical Simulation of Galvanic Corrosion between Carbon Steel and Low Alloy Steel in a Bolted Joint. Int. J. Corros. 2017, 2017, 6174904. [Google Scholar] [CrossRef]
- Trinh, D.; Ducharme, P.D.; Tefashe, U.M.; Kish, J.R.; Mauzeroll, J. Influence of Edge Effects on Local Corrosion Rate of Magnesium Alloy/Mild Steel Galvanic Couple. Anal. Chem. 2012, 84, 9899–9906. [Google Scholar] [CrossRef]
- Landolt, D. Corrosion et Chimie de Surfaces des Métaux; Traité des Matériaux, Collection; Romandes, P.P.E.U., Ed.; EPFL Press: Lousanne, Switzerland, 1997. [Google Scholar]
- Mohamed-Saïd, M. Modélisation du Rôle des Produits de Corrosion sur L’évolution de la Vitesse de Corrosion des Aciers au Carbone en Milieu Désaéré et Carbonaté: Modelling of the Role of Corrosion Products on the Evolution of the Corrosion Rate of Carbon Steel in Deaerated and Carbonated Media. Ph.D. Thesis, University de Bourgogne Franche-Comté, Dijon, France, 2018. [Google Scholar]
- Mohamed-Said, M.; Vuillemin, B.; Oltra, R.; Marion, A.; Trenty, L.; Crusset, D. Predictive modelling of the corrosion rate of carbon steel focusing on the effect of the precipitation of corrosion products. Corros. Eng. Sci. Technol. 2017, 52, 178–185. [Google Scholar] [CrossRef]
- Mohamed-Said, M.; Vuillemin, B.; Oltra, R.; Trenty, L.; Crusset, D. One-Dimensional Porous Electrode Model for Predicting the Corrosion Rate under a Conductive Corrosion Product Layer. J. Electrochem. Soc. 2017, 164, E3372. [Google Scholar] [CrossRef]
- El-Lateef, H.M.A.; El-Sayed, A.-R.; Mohran, H.S.; Shilkamy, H.A.S. Corrosion inhibition and adsorption behavior of phytic acid on Pb and Pb–In alloy surfaces in acidic chloride solution. Int. J. Ind. Chem. 2019, 10, 31–47. [Google Scholar] [CrossRef]
- Sato, H.; Yui, M.; Yoshikawa, H. Ionic Diffusion Coefficients of Cs+, Pb2+, Sm3+, Ni2+, SeO2−4 and TcO−4 in Free Water Determined from Conductivity Measurements. J. Nucl. Sci. Technol. 1996, 33, 950–955. [Google Scholar] [CrossRef]
- Lothenbach, B.; Ochs, M.; Wanner, H.; Yui, M. Thermodynamic Data for the Speciation and Solubility of Pd, Pb, Sn, Sb, Nb and Bi in Aqueous Solution; Japan Nuclear Cycle Development Institute: Tokai, Japan, 1999. [Google Scholar]
- Poorqasemi, E.; Abootalebi, O.; Peikari, M.; Haqdar, F. Investigating accuracy of the Tafel extrapolation method in HCl solutions. Corros. Sci. 2009, 51, 1043–1054. [Google Scholar] [CrossRef]
- Lequien, F.; Moine, G. Corrosion of a 75Sn/25Pb coating on a low carbon steel in a gaseous environment polluted with HCl: Mechanism. Mater. Corros. 2018, 69, 1422–1430. [Google Scholar] [CrossRef]
- Lequien, F.; Moine, G.; Lequien, A.; Neff, D. The corrosion mechanism initiation of a 75Sn–25Pb coating on a low-carbon steel sample in HCl environments. Mater. Corros. 2021, 72, 1488–1505. [Google Scholar] [CrossRef]
- Barradas, R.G.; Belinko, K.; Ambrose, J. Electrochemical Behavior of the Lead Electrode in HCl and NaCl Aqueous Electrolytes. Can. J. Chem. 1975, 53, 389–406. [Google Scholar] [CrossRef]
- Poupelloz, E. Etude des Processus de Germination-Croissance de L’ettringite, Seule ou dans un Système Aluminate Tricalcique/Sulfate de Calcium. Ph.D. Thesis, Université Bourgogne Franche Comté, Dijon, France, 2019. [Google Scholar]
- Cormier, L. La Théorie Classique de la Nucléation; Université Pierre et Marie Curie: Paris, France, 2013. [Google Scholar]
- De Yoreo, J.J.; Vekilov, P.G. Principles of Crystal Nucleation and Growth. Rev. Mineral. Geochem. 2003, 54, 57–94. [Google Scholar] [CrossRef]
- Acevedo Reyes, D. Evolution de L’état de Précipitation au Cours de L’austénitisation D’aciers Microalliés au Vanadium et au Niobium. Ph.D. Thesis, INSA de Lyon, Lyon, France, 2007. [Google Scholar]
- Wei, L.-Y.; Yang, Y.-W.; Lee, J.-F. Lead speciation in 0.1 N HCl-extracted residue of analog of Pb-contaminated soil. J. Electron Spectrosc. Relat. Phenom. 2005, 144, 299–301. [Google Scholar] [CrossRef]
- Mohammadi, M.; Alfantazi, A. Anodic behavior and corrosion resistance of the Pb-MnO2 composite anodes for metal electrowinning. J. Electrochem. Soc. 2013, 160, C253. [Google Scholar] [CrossRef]




| Parameters | Description | Value/Unit | Ref. |
|---|---|---|---|
| Ecor | Corrosion potential | −0.554 V | [36] |
| Eeq_Pb | Reference potential for Pb2+/Pb | −0.688 V | [14] |
| Eeq_H | Reference potential for H+/H2 | −0.248 V | |
| i0_Pb | Apparent exchange current density of Pb2+ | 1.05 × 10−4 mA/cm² | [36] |
| i0_H | Apparent exchange current density of H+ | 11.82 × 10−4 mA/cm² | [36] |
| ba | Anodic Tafel parameter | 0.041 V/dec | [36] |
| bc | Cathodic Tafel parameter | −0.138 V/dec | [36] |
| α | Transfer charge coefficient | 0.4 | |
| DPb2+ | Diffusion coefficient of Pb2+ | 9.39 × 10−10 m²/s | [37] |
| DH+ | Diffusion coefficient of H+ | 9.30 × 10−9 m²/s | [33] |
| DH2 | Diffusion coefficient of H2 | 1.00 × 10−9 m²/s | [33] |
| DCl- | Diffusion coefficient of Cl− | 2.03 × 10−9 m²/s | [33] |
| c0 | Initial concentration | 1000 mol/m3 | |
| cH2_0 | Initial concentration | 10−6 mol/m3 | |
| cCl_0 | Initial concentration | 1000 mol/m3 | [36] |
| cH_0 | Initial concentration | 1000 mol/m3 | [36] |
| Ksp | Solubility product | 10−4.81 | [38] |
| kp | Precipitation kinetic constant of PbCl2 | 10−4 mol/(m²·s) | |
| ρPbCl2 | PbCl2 density | 5.85 g/m3 | |
| MPbCl2 | Molar PbCl2 weight | 278.10 g/mol | |
| ρPb | Pb density | 11.35 g/m3 | |
| MPb | Molar Pb weight | 207.20 g/mol | |
| Rp | Size of a crystal and is fixed | 10−7 m | [33]. |
| Scheme | Slope (µm/s) | Corrosion Rate (µm/yr) |
|---|---|---|
| Dissolution | 1.944 × 10−4 | 6130.6 |
| Fixe epsilon | 1.785 × 10−4 | 5629.2 |
| Variable epsilon | 1.696 × 10−4 | 5348.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menut, M.; Lequien, F. Modelling of Lead Corrosion in Contact with an Anaerobic HCl Solution, Influence of the Corrosion Product Presence. Coatings 2022, 12, 1291. https://doi.org/10.3390/coatings12091291
Menut M, Lequien F. Modelling of Lead Corrosion in Contact with an Anaerobic HCl Solution, Influence of the Corrosion Product Presence. Coatings. 2022; 12(9):1291. https://doi.org/10.3390/coatings12091291
Chicago/Turabian StyleMenut, Martin, and Florence Lequien. 2022. "Modelling of Lead Corrosion in Contact with an Anaerobic HCl Solution, Influence of the Corrosion Product Presence" Coatings 12, no. 9: 1291. https://doi.org/10.3390/coatings12091291
APA StyleMenut, M., & Lequien, F. (2022). Modelling of Lead Corrosion in Contact with an Anaerobic HCl Solution, Influence of the Corrosion Product Presence. Coatings, 12(9), 1291. https://doi.org/10.3390/coatings12091291






