Effect of the Injection Structure on Gas Velocity Distribution in a 3D Vertical Oven
Abstract
:1. Introduction
2. Numerical Model
2.1. Pyshical Model
2.2. Mathematical Model
2.3. Simulation Setup
2.4. Indicated Parameters
3. Results and Discussion
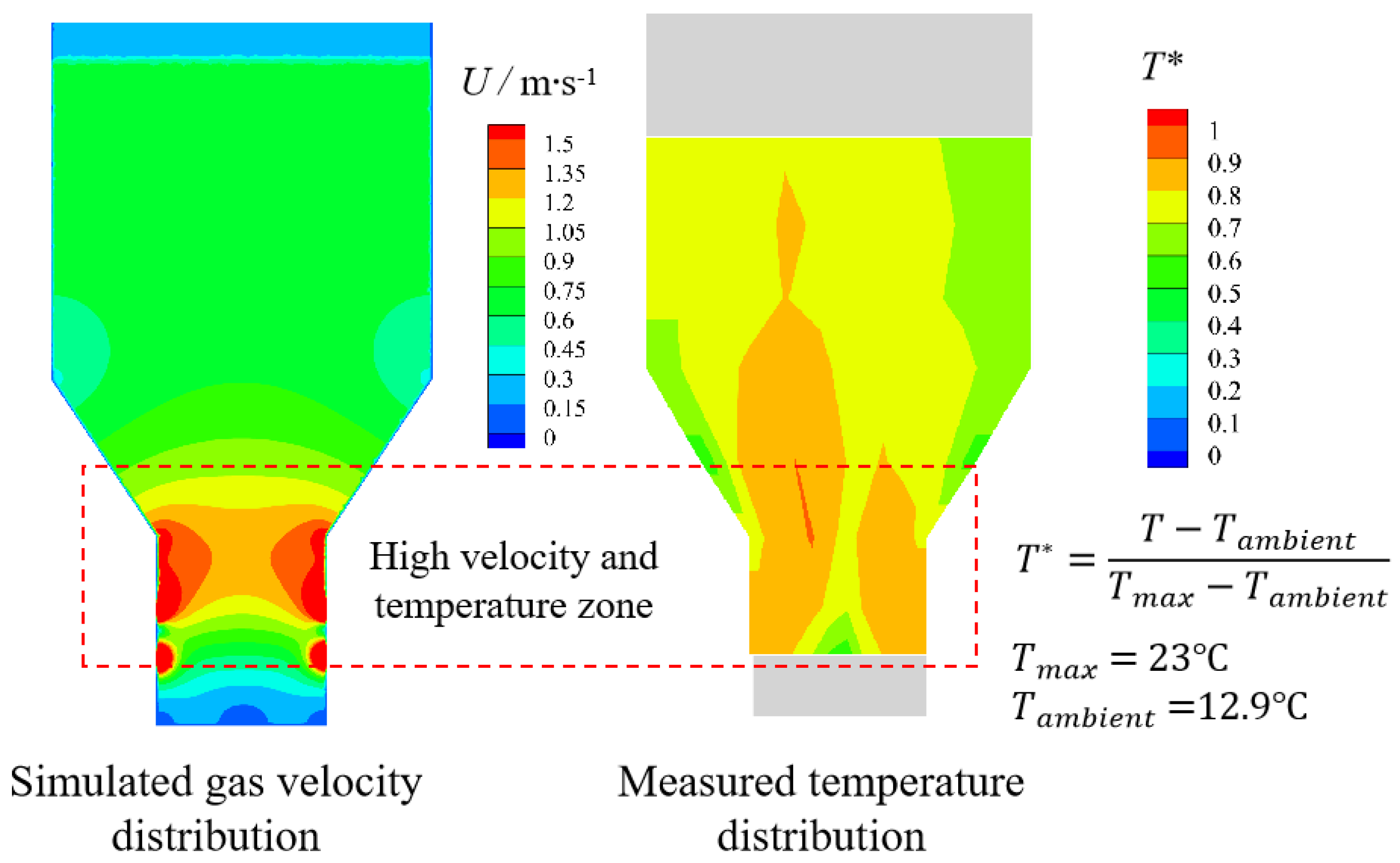
3.1. Wall Temperature Distribution
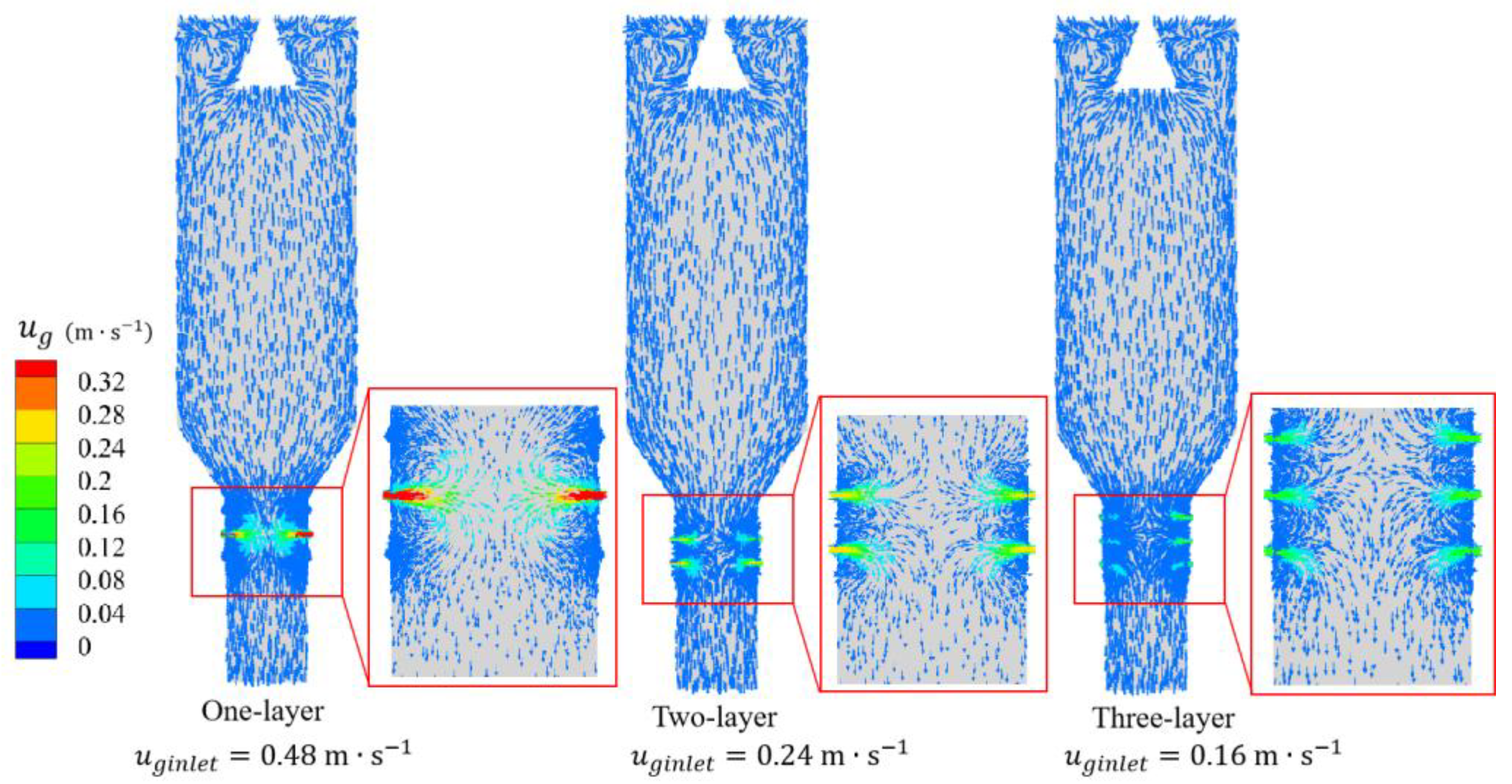
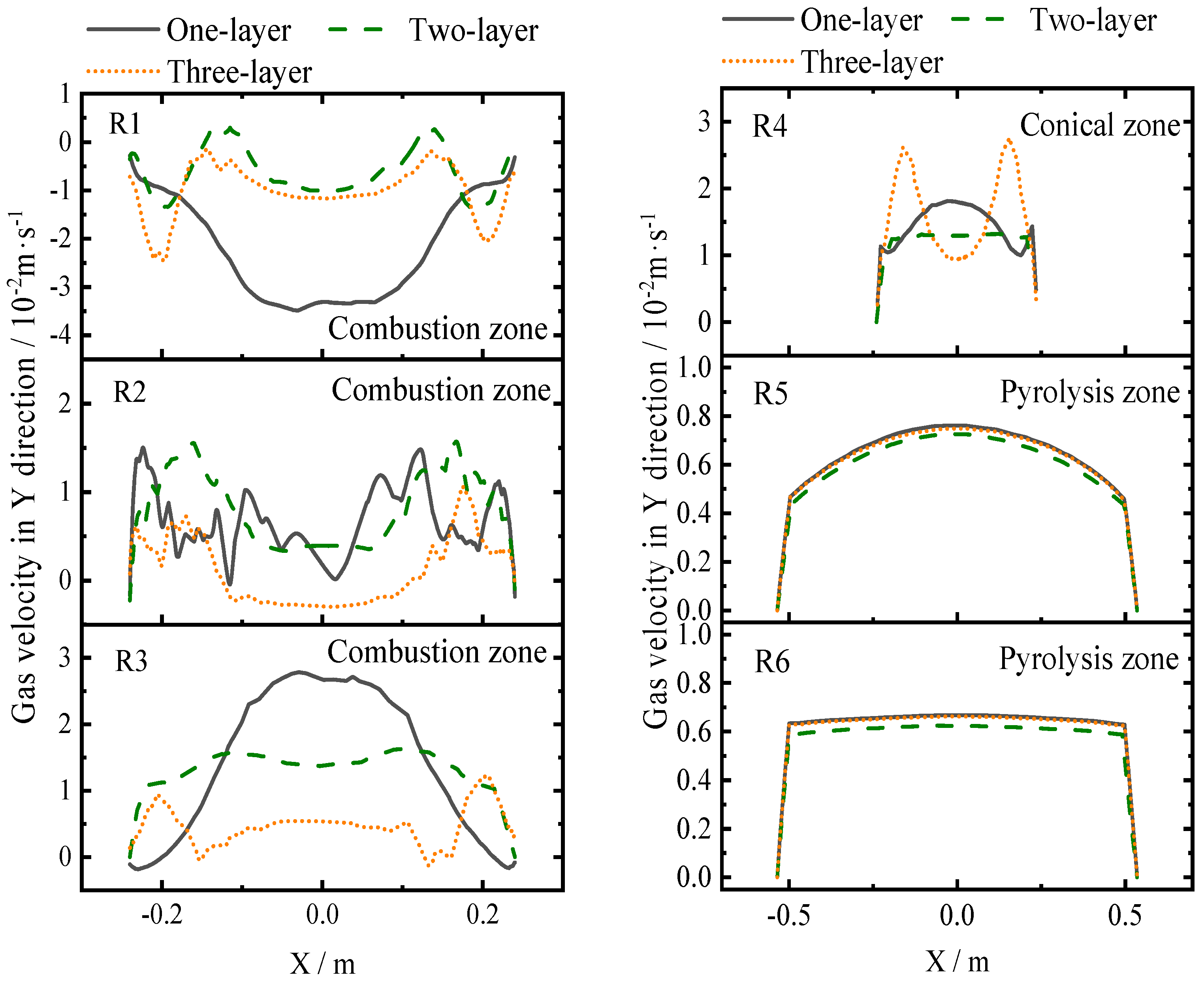
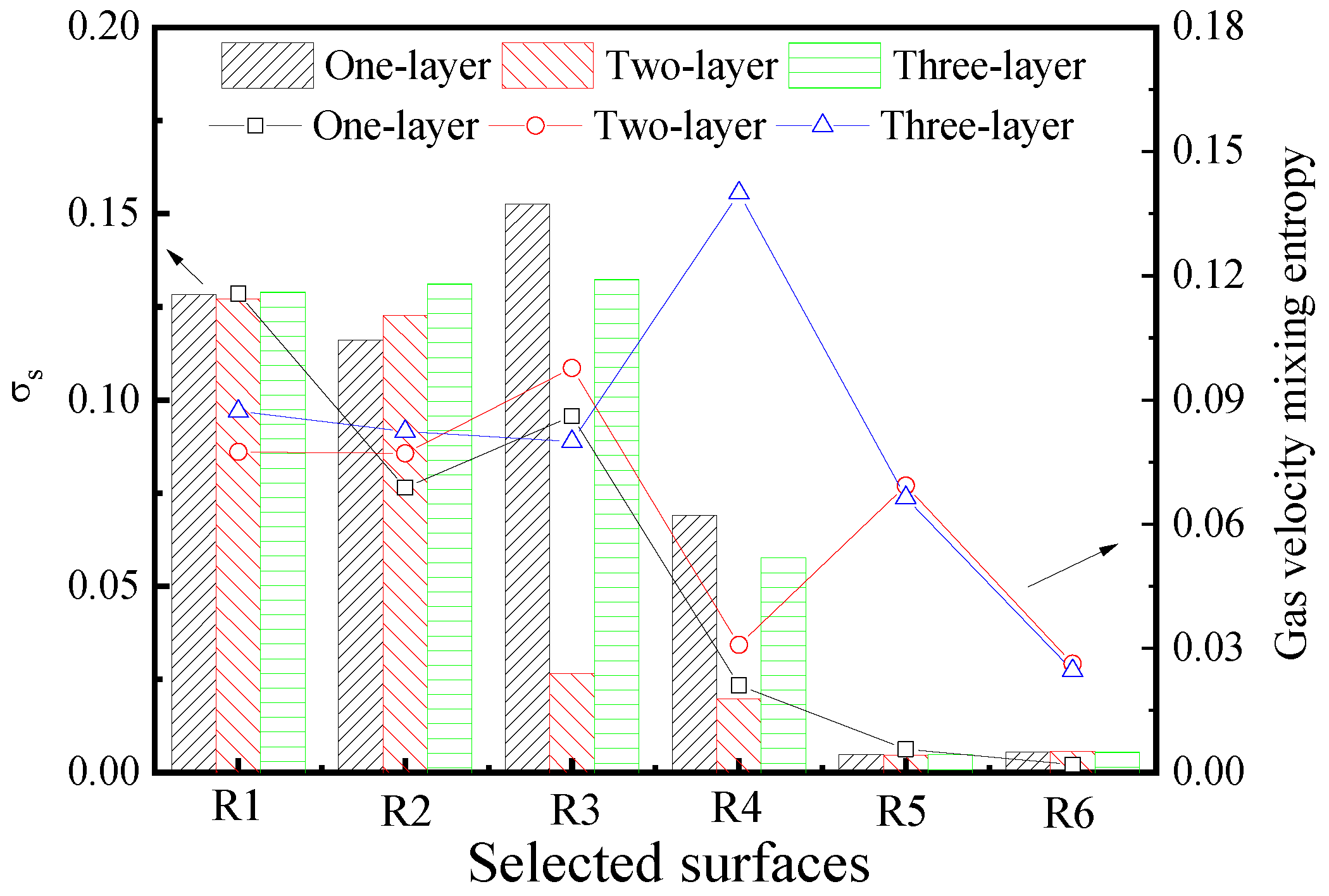
3.2. Effect of Gas-Feeding Layers
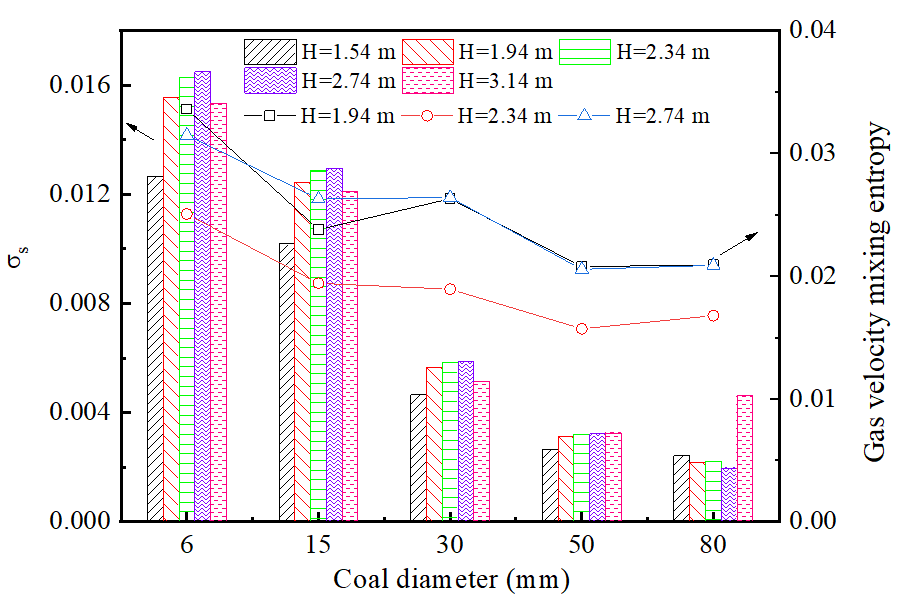
3.3. Effect of the Particle Size
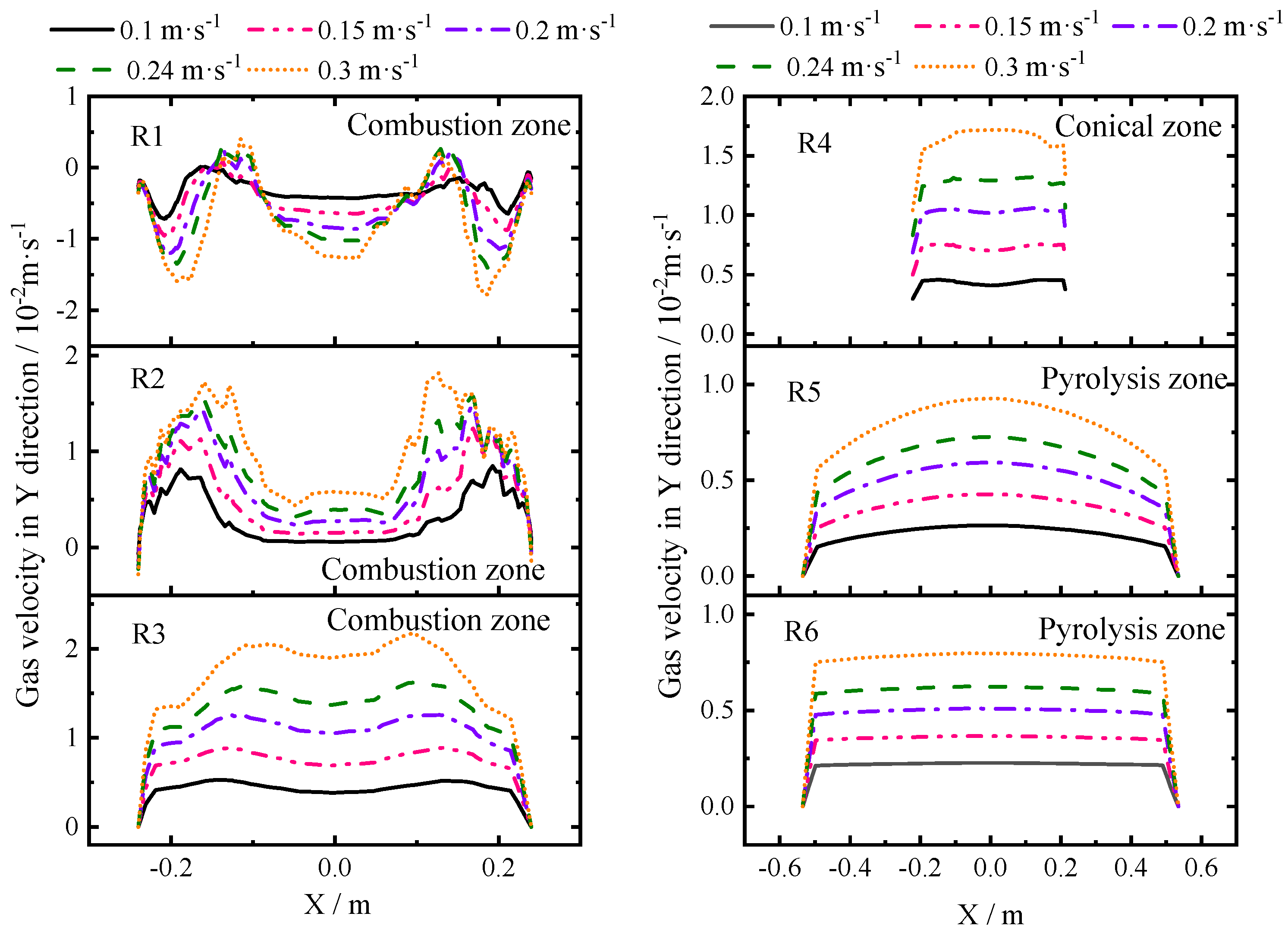
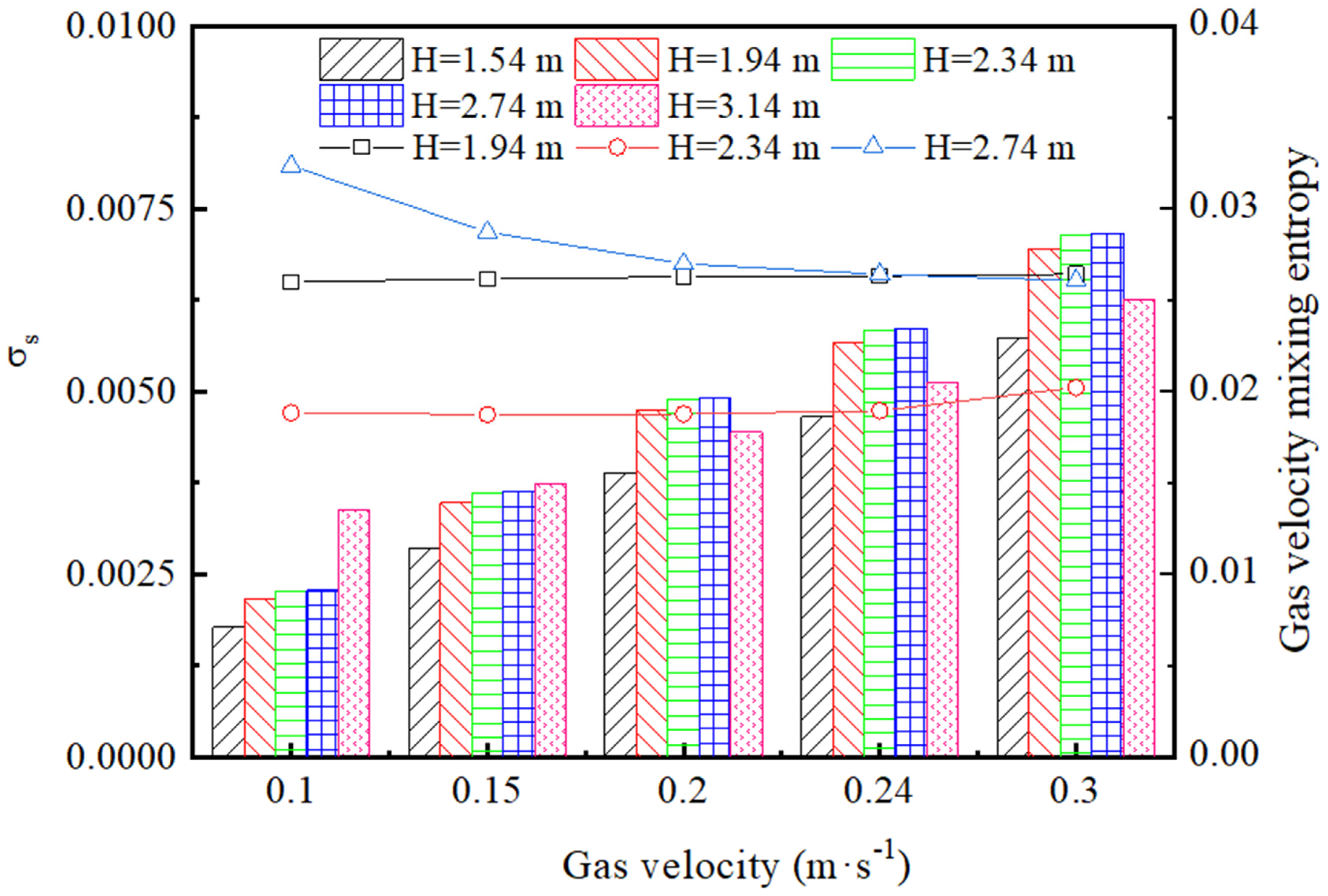
3.4. Effect of Gas Feeding Velocity
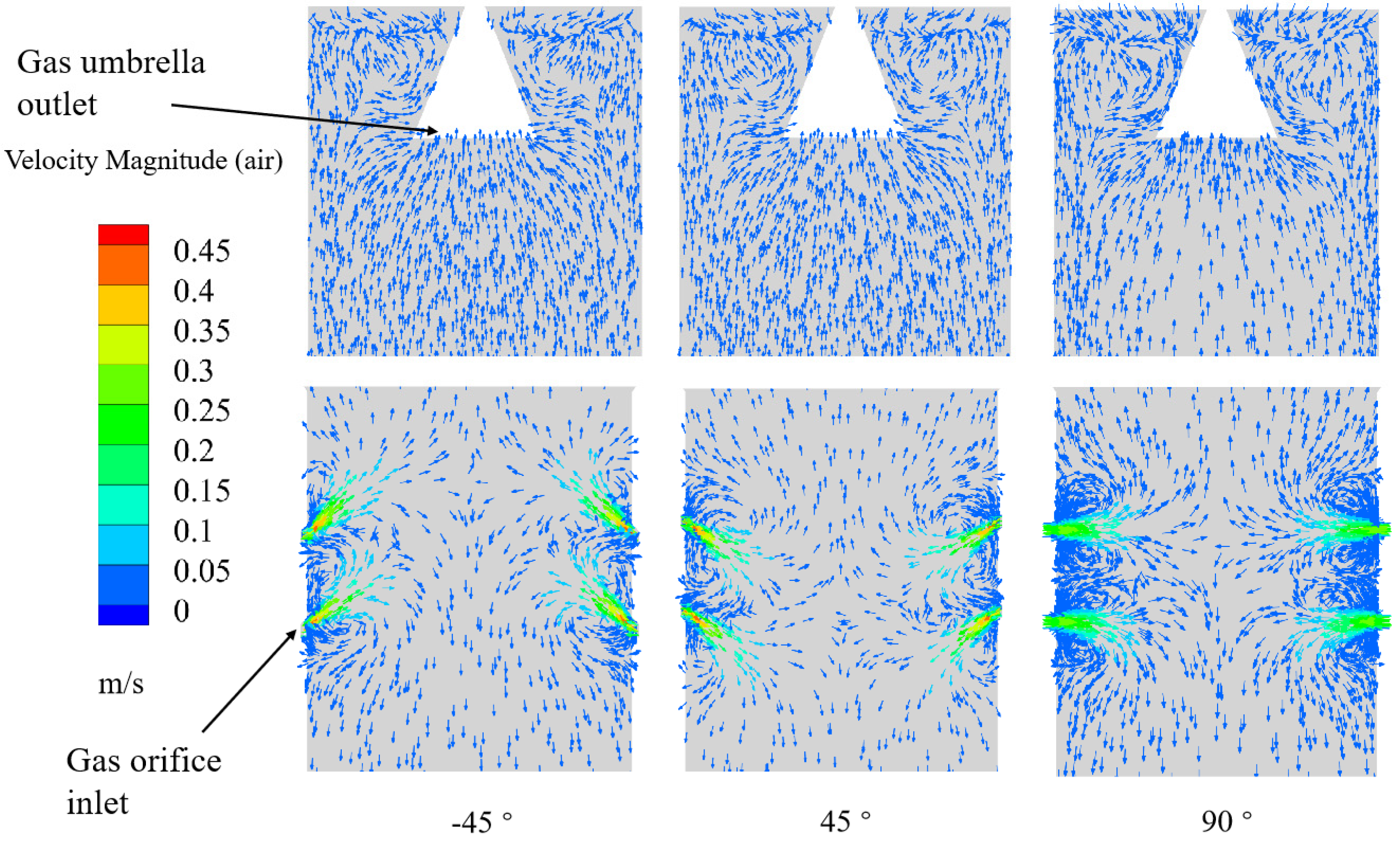
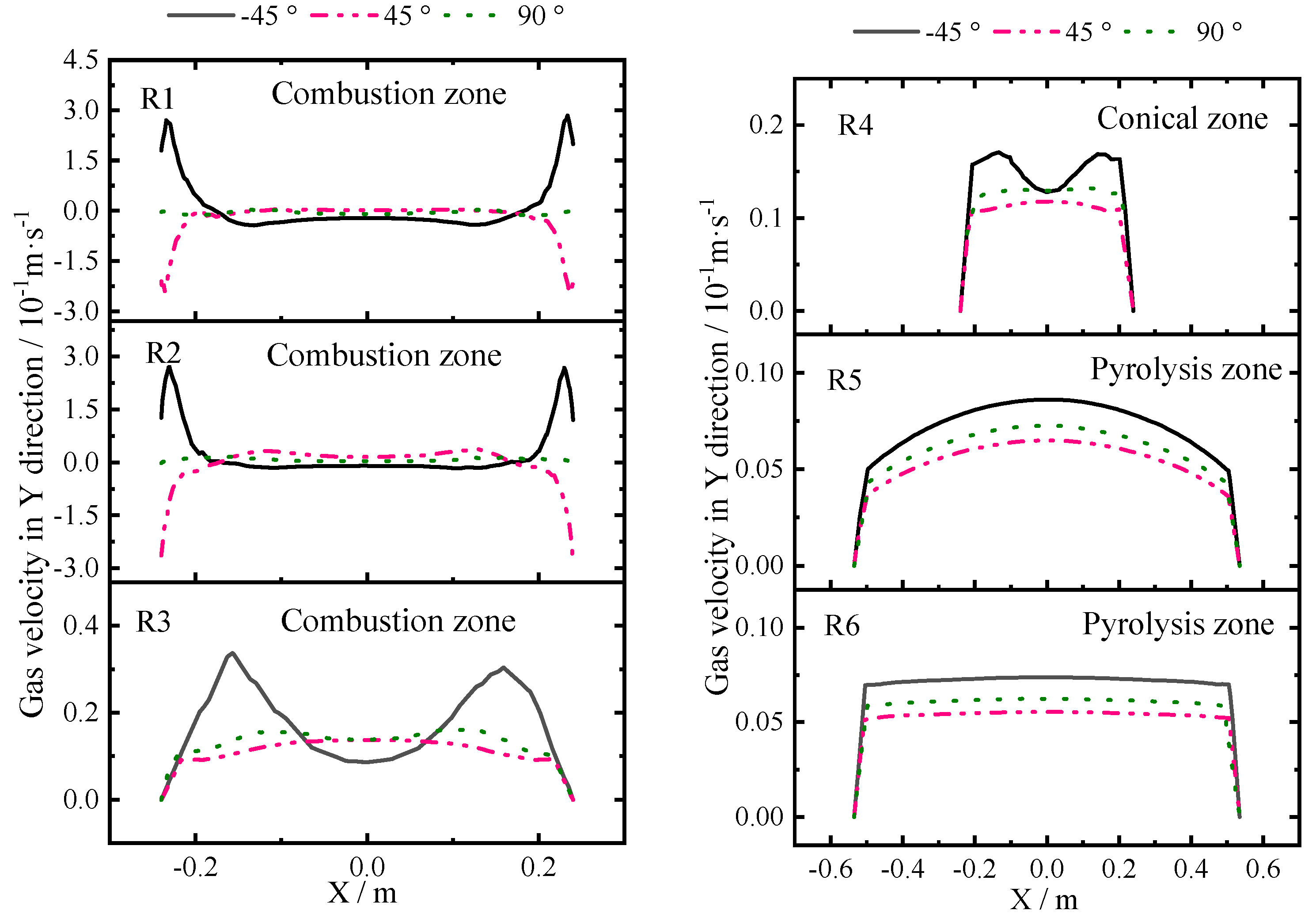
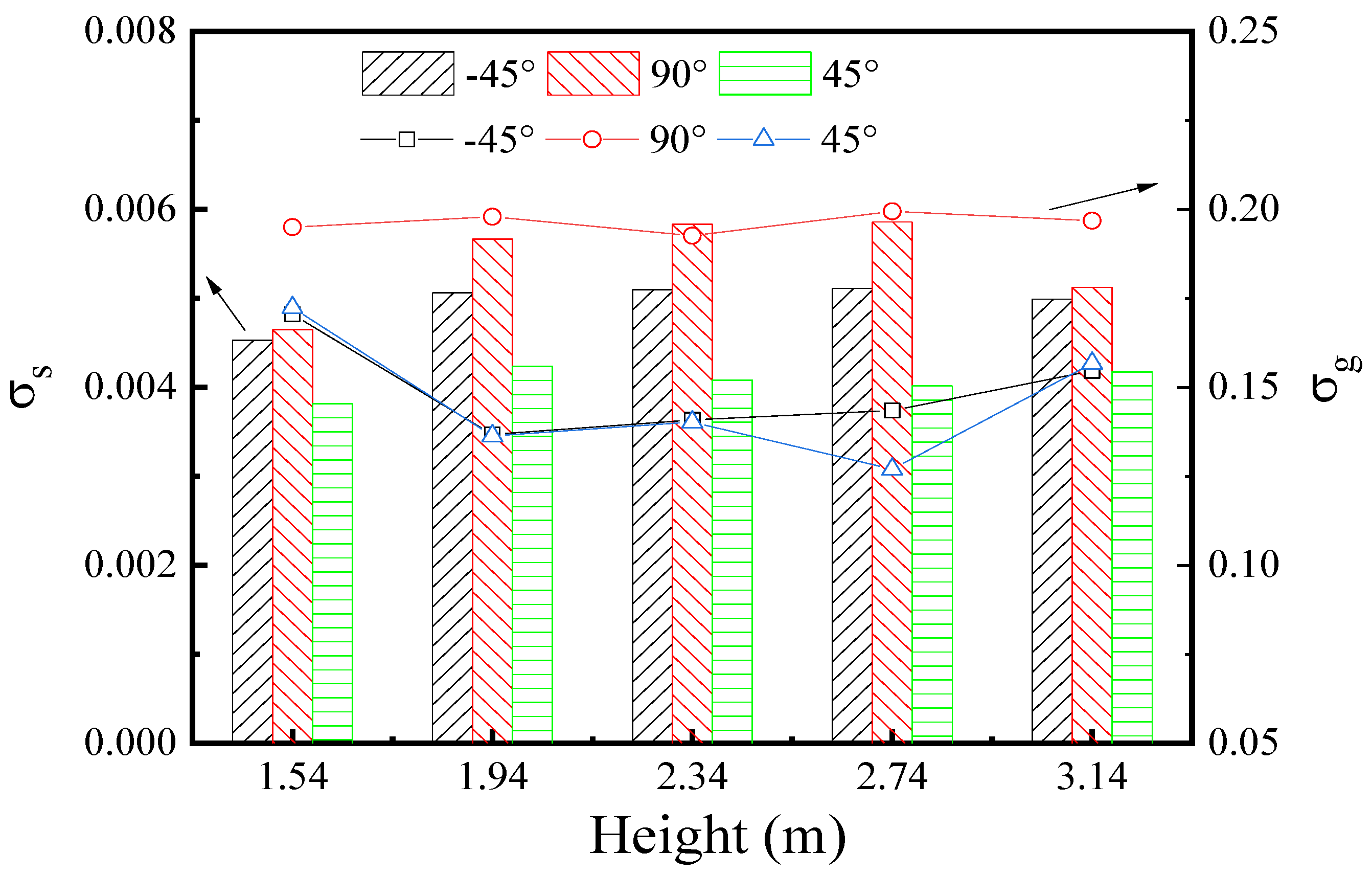
3.5. Effect of Gas Feeding Angle
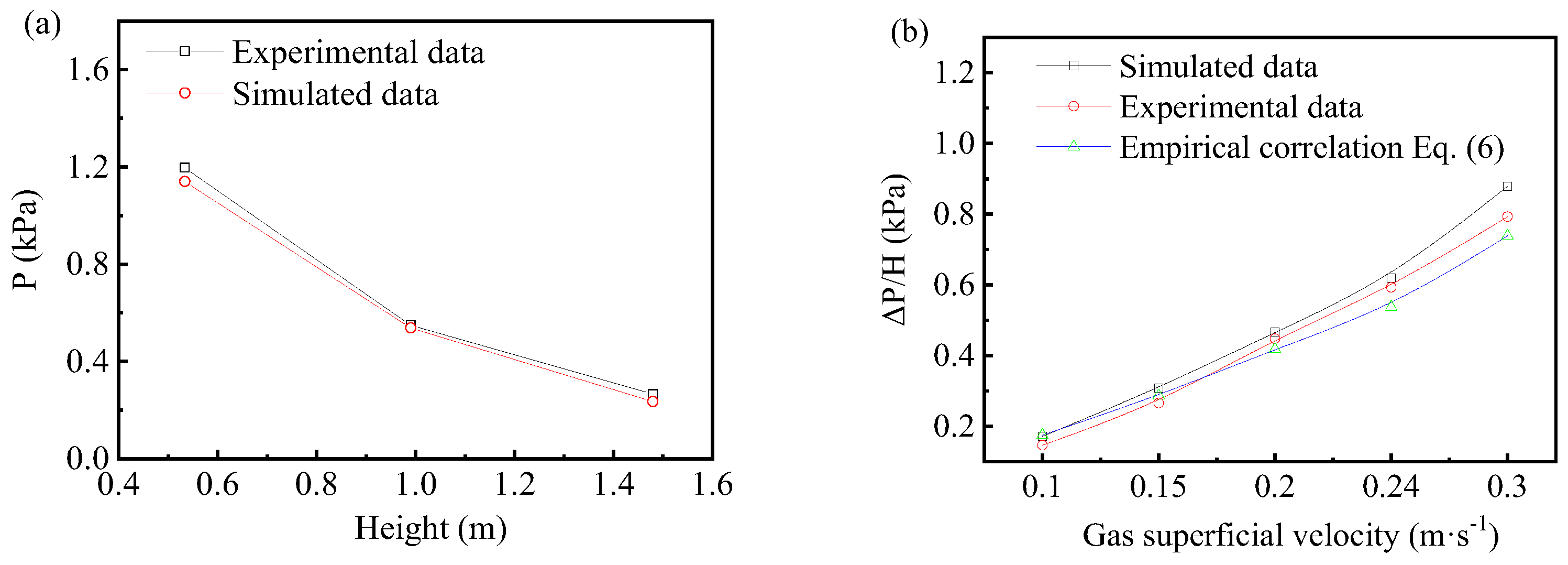
4. Model Validation
5. Preliminary Economic Analysis
5.1. Cost Breakdown
- ✧
- Raw coal washing and screening;
- ✧
- Vertical oven and auxiliary equipment;
- ✧
- Gas purification and air system;
- ✧
- Tar recovery equipment;
- ✧
- Power distribution and control system;
- ✧
- Waste gas and wastewater treatment.
5.2. Potential Income
6. Conclusions
- The number of gas injection layers had a significant effect on the gas velocity distribution in the lower zone but a small impact on the upper zone. In the upper zone, the velocity profile closely resembled the contour of an open–upward parabola with a large range. Compared with one or three injection layers, the distribution of coal particles was more uniform when two injection layers were used.
- The decrease in the particle size led to an increase in the bed resistance, which in turn led to a decrease in the gas velocity in the Y direction in the upper zone. Small particle sizes of 6–15 mm increased the bed resistance and solid fraction standard deviation and made the gas fraction distribution uneven.
- The increased inlet gas velocity could increase the velocity values in the Y direction. The reduction of the gas velocity had no significant effect on the gas distribution uniformity. The simulation results suggested using an angle of 45°, instead of the present angle of 90°, could improve the gas distribution.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Pressure (Pa) | |
| Gas velocity mixing entropy | |
| Velocity (m s−1) | |
| Phase fraction | |
| Density (kg m−3) | |
| Viscosity (Pa s) | |
| Standard deviation | |
| Subscripts | |
| cell | Cell |
| g | Gas phase |
| m | Mean diameter |
| s | Solid phase |
| Particle shape factor |
References
- Feng, Y.; Xu, S. Blue-coke production technology and the current state-of-the-art in China. Carbon Resour. Convers. 2020, 3, 82–94. [Google Scholar] [CrossRef]
- Li, K.; Zhu, W.; Peng, J.; Sun, X.T.; Liu, G. Semi-coke producers in Shenfu area today and suggestions on improvement. Sino-Glob. Energy 2016, 21, 21–30. (In Chinese) [Google Scholar]
- Zhou, Q.; Wei, L.; Shen, L.; Ma, B. Development characteristics and suggestions of blue-coke industry in China. Coal Process. Comprehesive Util. 2022, 69–72. [Google Scholar] [CrossRef]
- Xue, F.; Li, D.; Guo, Y.; Liu, X.; Zhang, X.; Zhou, Q.; Ma, B. Technical progress and the prospect of low-rank coal pyrolysis in China. Energy Technol. 2017, 5, 1897–1907. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, X.F.; Gao, W.J.; Xue, X.P.; Shi, J.P. Low-tempe-rature carbonization of Shenfu coal through the vertical internal heating re-tort furnace. Anhui Chem. Ind. 2010, 36–38. (In Chinese) [Google Scholar]
- Gao, W.J.; Xue, X.P.; Shi, J.P.; Zhang, J.Q. Research, development and design of SH2007 internally heated vertical oven. Gas Heat 2010, 30, 14–17+25. (In Chinese) [Google Scholar]
- Wang, L.; Li, N. Technical characteristics and application of RNZL vertical oven 10. Coal Process. Compr. Util. 2015, 185, 48–49+80. (In Chinese) [Google Scholar]
- Song, J.T.; Zhang, L. Discussion on technical renovation of small grained coal. vertical internally heated retort furnace (in Chinese). Coal Chem. Ind. 2017, 45, 27–29. Available online: http://qikan.cqvip.com/Qikan/Article/Detail?id=673029358 (accessed on 10 June 2022).
- Gao, Y.; Yan, L.; Li, J.; Fan, X.; Sun, Y.-Y. Influence of Inlet Diameter on Temperature and Pressure in SJ Low Temperature Dry Distillation Furnace. Liaoning Chem. Ind. 2018, 47, 647–648. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, R.; Hu, E.; Liu, S.; Xu, G. Coal Pyrolysis for High-Quality Tar and Gas in 100 kg Fixed Bed Enhanced with Internals. Energy Fuels 2014, 28, 7294–7302. [Google Scholar] [CrossRef]
- Xu, S.; Lai, D.; Zeng, X.; Zhang, L.; Han, Z.; Cheng, J.; Wu, R.; Mašek, O.; Xu, G. Pyrolysis characteristics of waste tire particles in fixed-bed reactor with internals. Carbon Resour. Convers. 2018, 1, 228–237. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, X.; Wang, Y.; Qu, S.-j.; Zhang, Y.; Bai, X.-y.; Pei, X.-f. Pyrolysis behavior of coal in a moving bed with baffled internals under different residence times. J. Fuel Chem. Technol. 2021, 49, 703–711. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Hsieh, H.-T.; Siegel, N. Computational Fluid Dynamics Modeling of Gas-Particle Flow Within a Solid-Particle Solar Receiver. J. Sol. Energy Eng. 2006, 129, 160–170. [Google Scholar] [CrossRef]
- Mathiesen, V.; Solberg, T.; Arastoopour, H.; Hjertager, B.H. Experimental and computational study of multiphase gas/particle flow in a CFB riser. Aiche J. 1999, 45, 2503–2518. [Google Scholar] [CrossRef]
- Roussel, N.; Geiker, M.R.; Dufour, F.; Thrane, L.N.; Szabo, P. Computational modeling of concrete flow: General overview. Cem. Concr. Res. 2007, 37, 1298–1307. [Google Scholar] [CrossRef]
- Baldelli, A.; Esmeryan, K.D.; Popovicheva, O. Turning a negative into a positive: Trends, guidelines and challenges of developing multifunctional non-wettable coatings based on industrial soot wastes. Fuel J. Fuel Sci. 2021, 301, 121068. [Google Scholar] [CrossRef]
- Yousefian, P.; Pimputkar, S. Computational fluid dynamics modeling of a new high-pressure chemical vapor deposition reactor design. J. Cryst. Growth 2021, 566–567, 126155. [Google Scholar] [CrossRef]
- Gao, G.; Zhang, X.; Xu, M.; Han, Y.; Ao, J.; Cai, Y.; Wang, J. Structural Optimized Design of a Powder Mixer for Multi-Material Directed Energy Deposition Based on CFD-DPM. Coatings 2023, 13, 773. [Google Scholar] [CrossRef]
- Wei, L.; Gu, Y.; Wang, Y.; Lu, Y. Multi-fluid Eulerian simulation of fluidization characteristics of mildly-cohesive particles: Cohesive parameter determination and granular flow kinetic model evaluation. Powder Technol. 2020, 364, 264–275. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, Imperial College London (University of London), London, UK, 2003. [Google Scholar]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of Circulating Fluidized Beds: Kinetic Theory Approach; Department of Chemical Engineering, Illinois Institute of Technology: Chicago, IL, USA, 1991. [Google Scholar]
- Gidaspow, D. 2—ONE-DIMENSIONAL STEADY GAS–SOLID FLOW. In Multiphase Flow and Fluidization; Gidaspow, D., Ed.; Academic Press: San Diego, CA, USA, 1994; pp. 31–60. [Google Scholar]
- Wei, L.; Lu, Y. Numerical investigation of binary particle mixing in gas-solid fluidized bed with a bubble-based drag EMMS model. Adv. Powder Technol. 2020, 31, 1529–1542. [Google Scholar] [CrossRef]
- Li, T.; Pougatch, K.; Salcudean, M.; Grecov, D. Mixing of secondary gas injection in a bubbling fluidized bed. Chem. Eng. Res. Des. 2009, 87, 1451–1465. [Google Scholar] [CrossRef]
- Hu, X. Simulation Research on the Combustion of Re-turned Gas in the Low-Temperature Distillation Furnace. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2012. [Google Scholar]
- Wu, C.; Zhuo, Y.; Xu, X.; Farajzadeh, E.; Dou, J.; Yu, J.; Shen, Y.; Zhang, Z. A combined experimental and numerical study of coal briquettes pyrolysis using recycled gas in an industrial scale pyrolyser. Powder Technol. 2022, 404, 117477. [Google Scholar] [CrossRef]
- Yin, R.; Liu, R.; Wu, J.; Wu, X.; Sun, C.; Wu, C. Influence of particle size on performance of a pilot-scale fixed-bed gasification system. Bioresour. Technol. 2012, 119, 15–21. [Google Scholar] [CrossRef]
- Patel, V.R.; Upadhyay, D.S.; Patel, R.N. Gasification of lignite in a fixed bed reactor: Influence of particle size on performance of downdraft gasifier. Energy 2014, 78, 323–332. [Google Scholar] [CrossRef]
- Martínez, L.V.; Rubiano, J.E.; Figueredo, M.; Gómez, M.F. Experimental study on the performance of gasification of corncobs in a downdraft fixed bed gasifier at various conditions. Renew. Energy 2020, 148, 1216–1226. [Google Scholar] [CrossRef]
- Mi, W. Study on Temperature Field and Pressure Field of SJ Low-temperature Drying Furnace. Master’s Thesis, Northwest University, Kirkland, WA, USA, 2018. [Google Scholar]
- Wei, L.; Lu, Y.; Wei, J. Hydrogen production by supercritical water gasification of biomass: Particle and residence time distribution in fluidized bed reactor. Int. J. Hydrog. Energy 2013, 38, 13117–13124. [Google Scholar] [CrossRef]
- Rau, G.C.; Andersen, M.S.; McCallum, A.M.; Roshan, H.; Acworth, R.I. Heat as a tracer to quantify water flow in near-surface sediments. Earth-Sci. Rev. 2014, 129, 40–58. [Google Scholar] [CrossRef]
- Shaanxi Coal and Chemical Industry Group Co., Ltd.; Beijing Guodian Futong Technology Development Co., Ltd. Industrial Technology (SM-GF) of Coal Gas Heat Carrier Segment Multilayer Low Rank Coal Pyrolysis. Shaanxi Coal and Chemical Industry Group Co., Ltd.: Xi’an, China, 2018. [Google Scholar]
- Zhang, X.-H.; Qin, F.-F.; Miao, W.-H.; Wu, P.; Chen, Z.-G. Experimental study on bed resistance of moving bed in pyrolysis of coal. Chem. Eng. 2018, 46, 35–39. [Google Scholar]
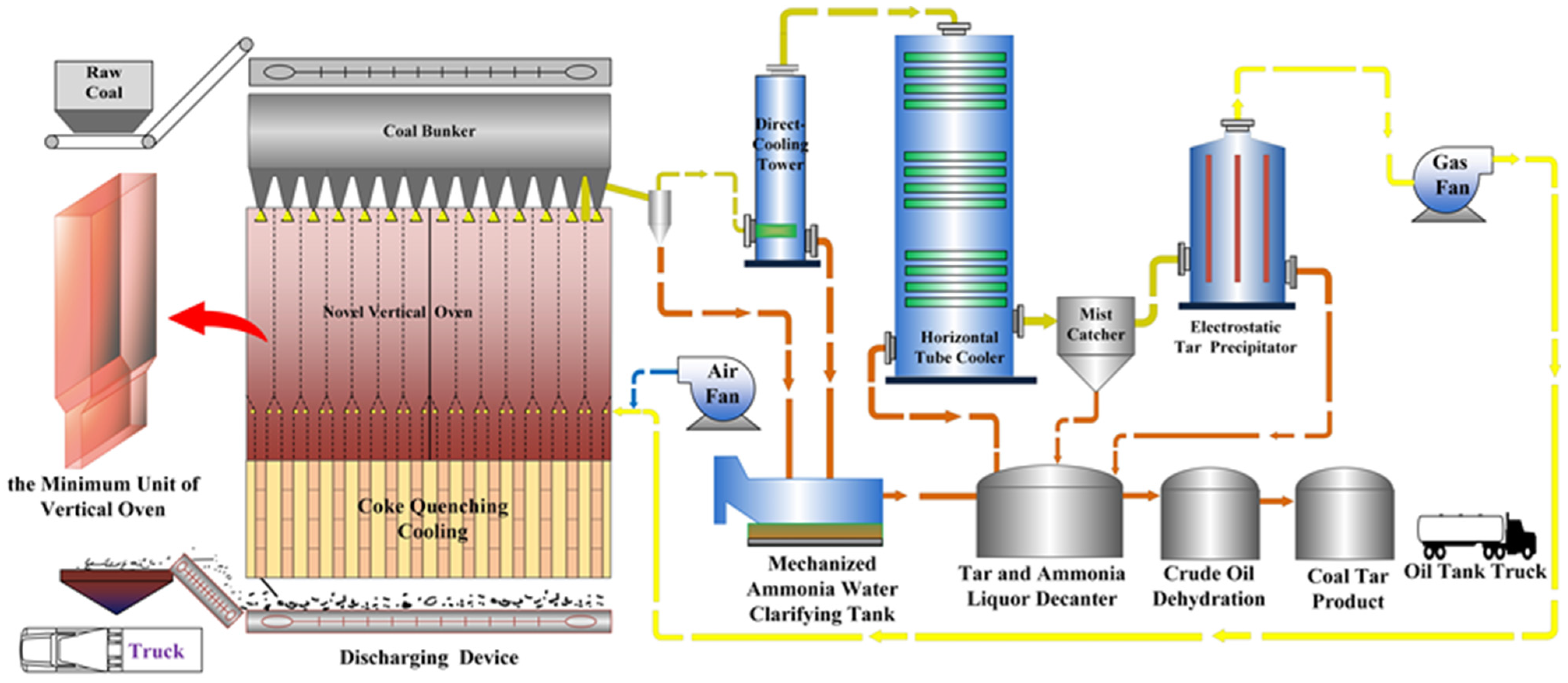


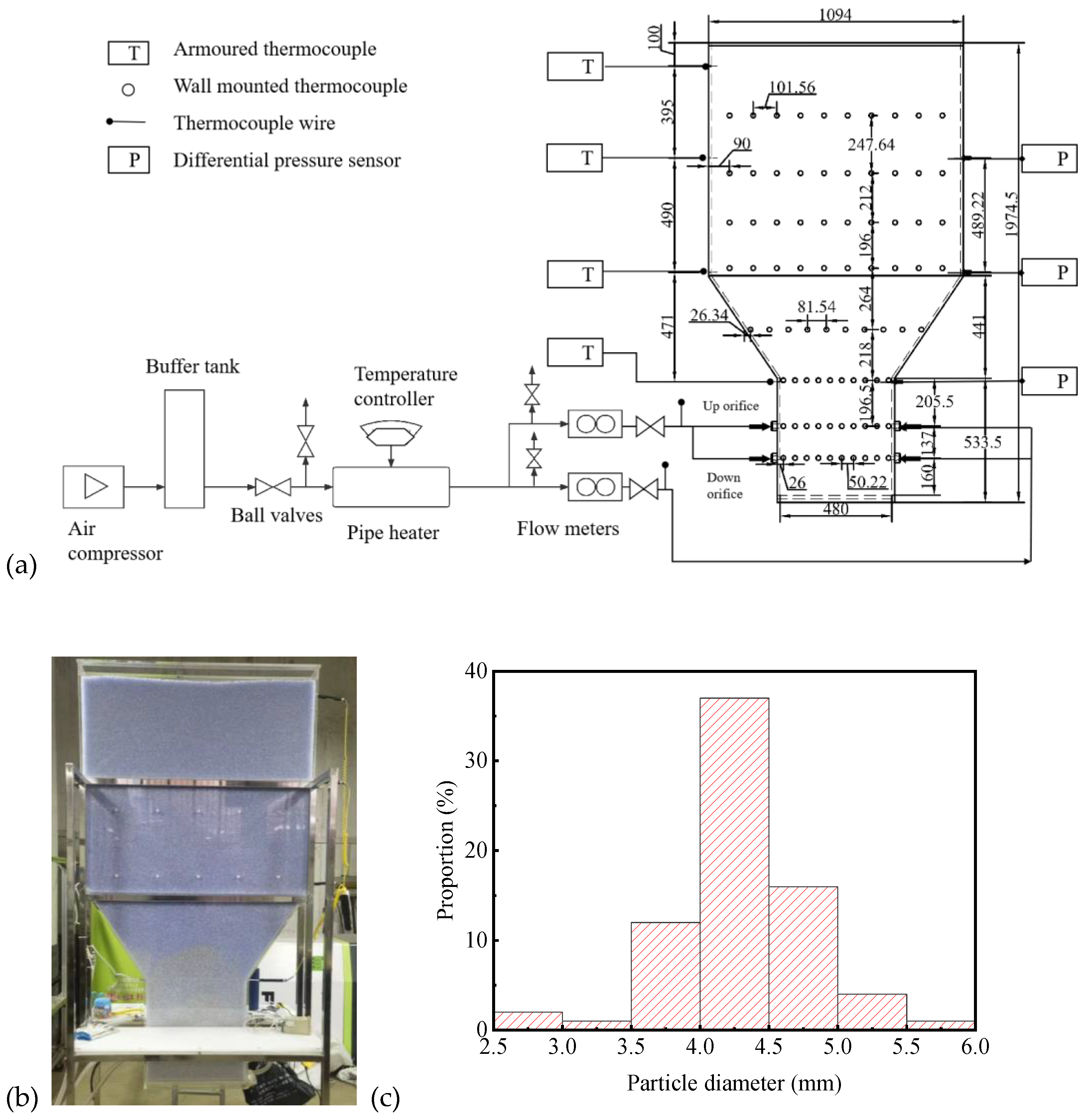
| Items | Unit | Value |
|---|---|---|
| Oven size (length × width × height) | mm | 15,580 mm × 3600 mm × 8200 mm |
| Oven combustion chamber number | / | 14 |
| Oven section area | m2 | 56.088 m2 |
| Amount of raw coal treated | t/a | 30 × 104 |
| Coal diameter | mm | 0–30 |
| Residence time | h | 9~11 |
| Oven air feeding volume | m3/t | 330 |
| Oven coal gas feeding volume | m3/t | 550 |
| Pyrolysis temperature | °C | 600~750 |
| Raw gas outlet temperature | °C | 60~80 |
| Blue-coke outlet temperature | °C | <90 |
| Raw gas outlet pressure | pa | −100~150 |
| Furnace pressure in middle position | pa | 1200~1800 |
| Tar yield | wt% | 6.5 |
| Number of Grids | Solid Volume Fraction Mixing Entropy |
|---|---|
| 515,000 | 0.15723 |
| 825,000 | 0.15766 |
| 1,425,000 | 0.15794 |
| 2,193,000 | 0.15793 |
| 3,046,000 | 0.15802 |
| Central Line | Distance from the Bottom H (m) |
|---|---|
| R1 | 0.75 |
| R2 | 0.89 |
| R3 | 1.02 |
| R4 | 1.09 |
| R5 | 1.54 |
| R6 | 1.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Yang, Z.; Zheng, C.; Wei, L.; Li, D.; Fan, X. Effect of the Injection Structure on Gas Velocity Distribution in a 3D Vertical Oven. Coatings 2023, 13, 1707. https://doi.org/10.3390/coatings13101707
Zhou Q, Yang Z, Zheng C, Wei L, Li D, Fan X. Effect of the Injection Structure on Gas Velocity Distribution in a 3D Vertical Oven. Coatings. 2023; 13(10):1707. https://doi.org/10.3390/coatings13101707
Chicago/Turabian StyleZhou, Qiucheng, Zhanyu Yang, Changsong Zheng, Liping Wei, Dong Li, and Xiaoyong Fan. 2023. "Effect of the Injection Structure on Gas Velocity Distribution in a 3D Vertical Oven" Coatings 13, no. 10: 1707. https://doi.org/10.3390/coatings13101707
APA StyleZhou, Q., Yang, Z., Zheng, C., Wei, L., Li, D., & Fan, X. (2023). Effect of the Injection Structure on Gas Velocity Distribution in a 3D Vertical Oven. Coatings, 13(10), 1707. https://doi.org/10.3390/coatings13101707






