Prediction of Surface Residual Stresses after Laser Shock Processing on TC4 Titanium Alloy Using Different Neural Network Agent Models
Abstract
:1. Introduction
2. Establishment of Simulation Model
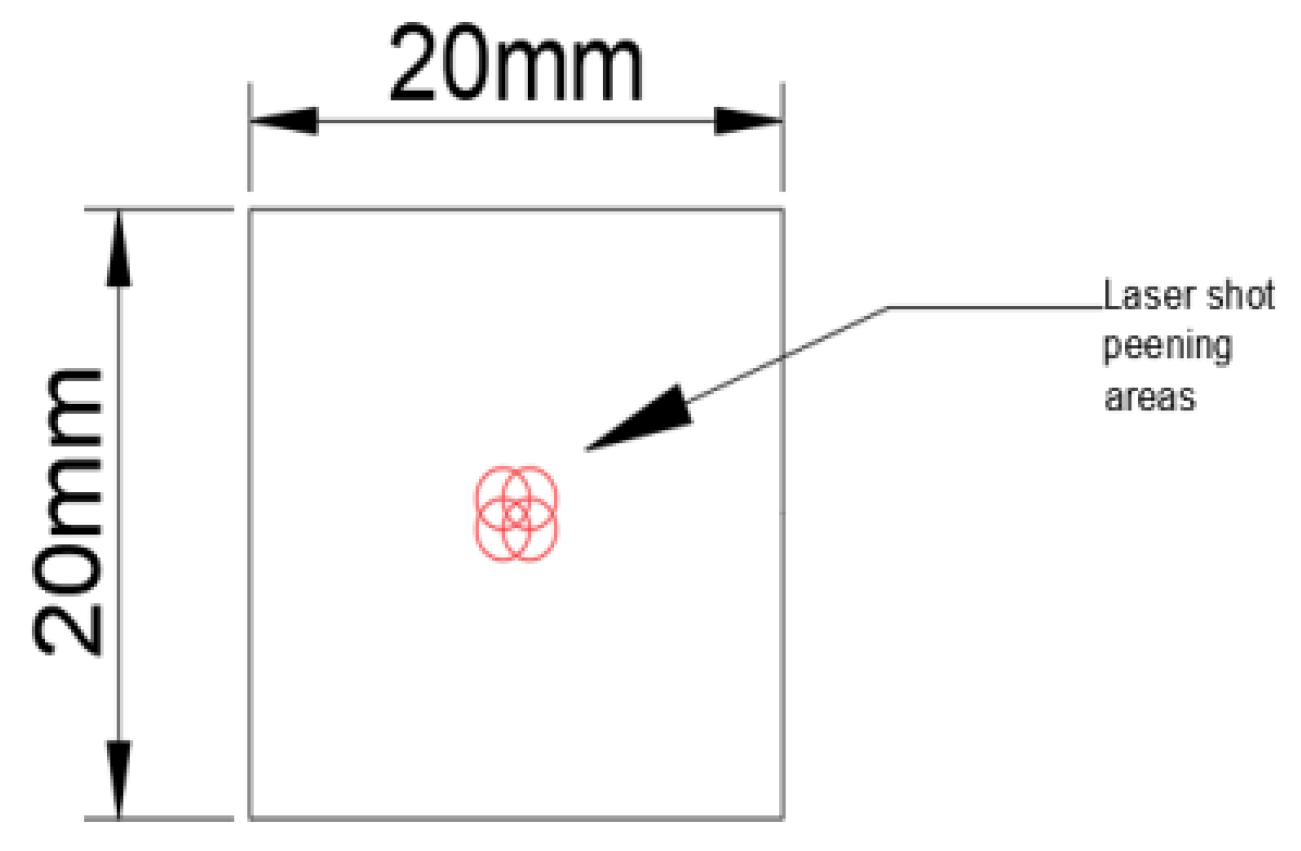
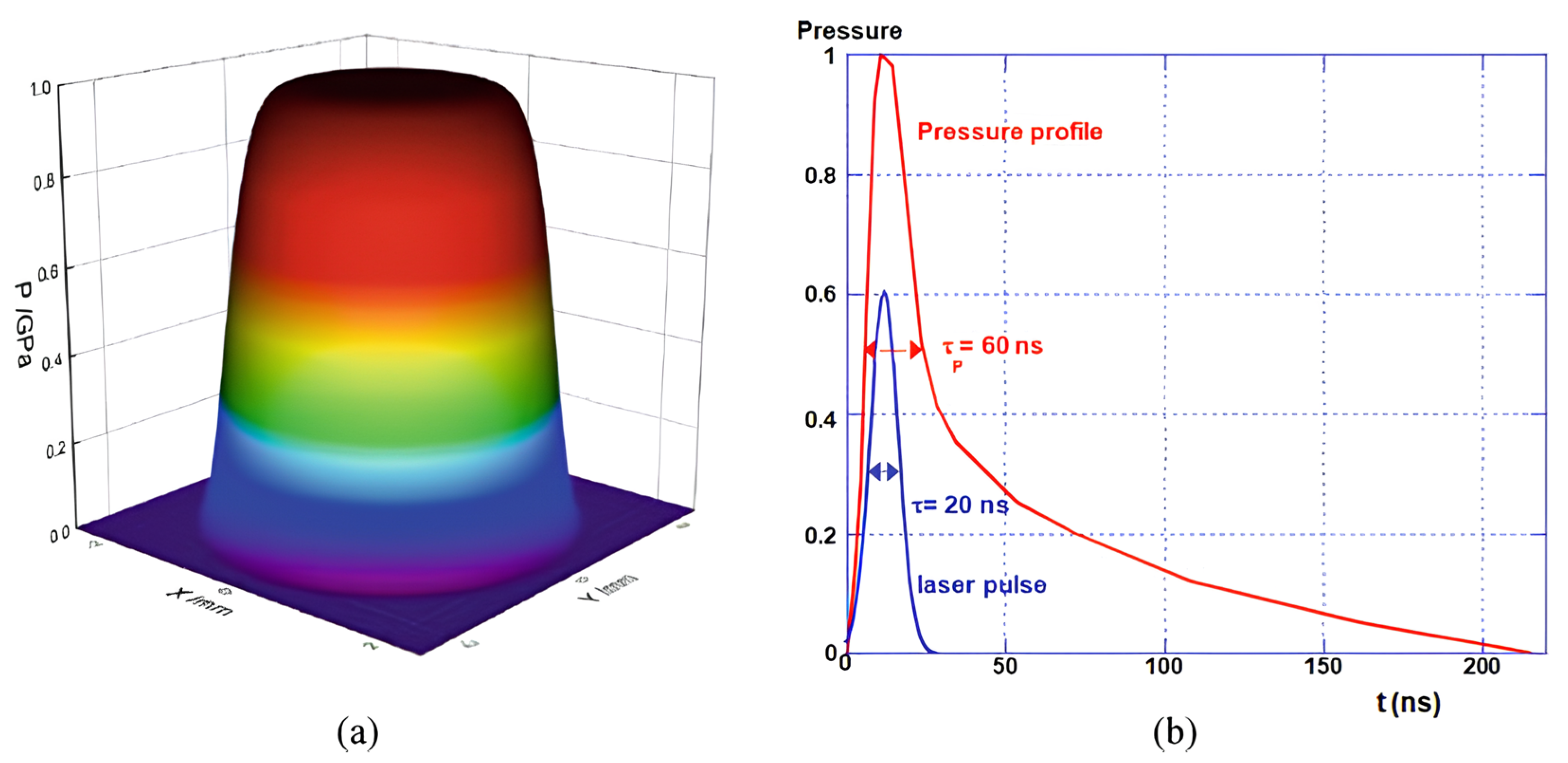
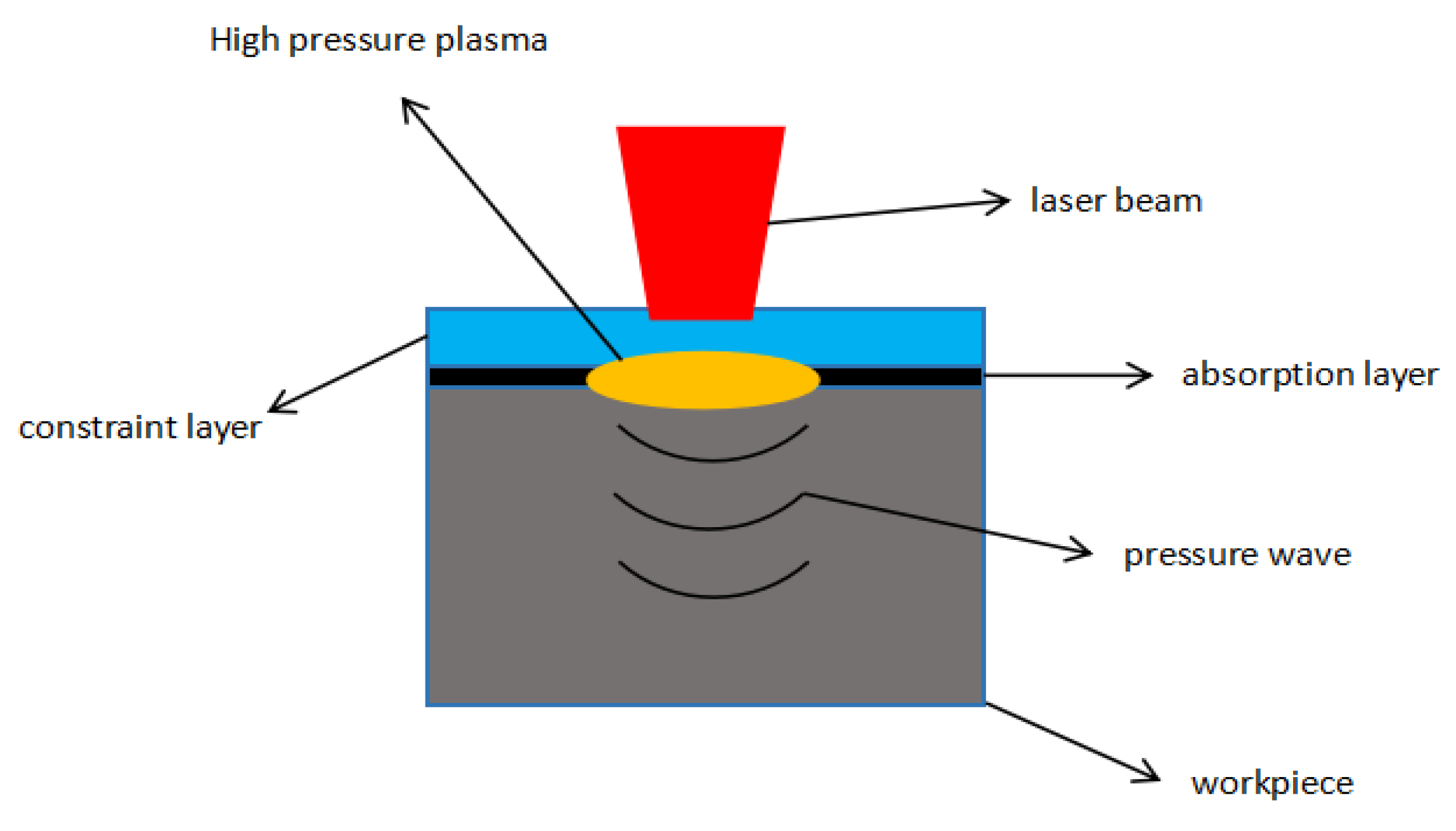
2.1. Model Parameters
Simulation of Laser Shock Processing
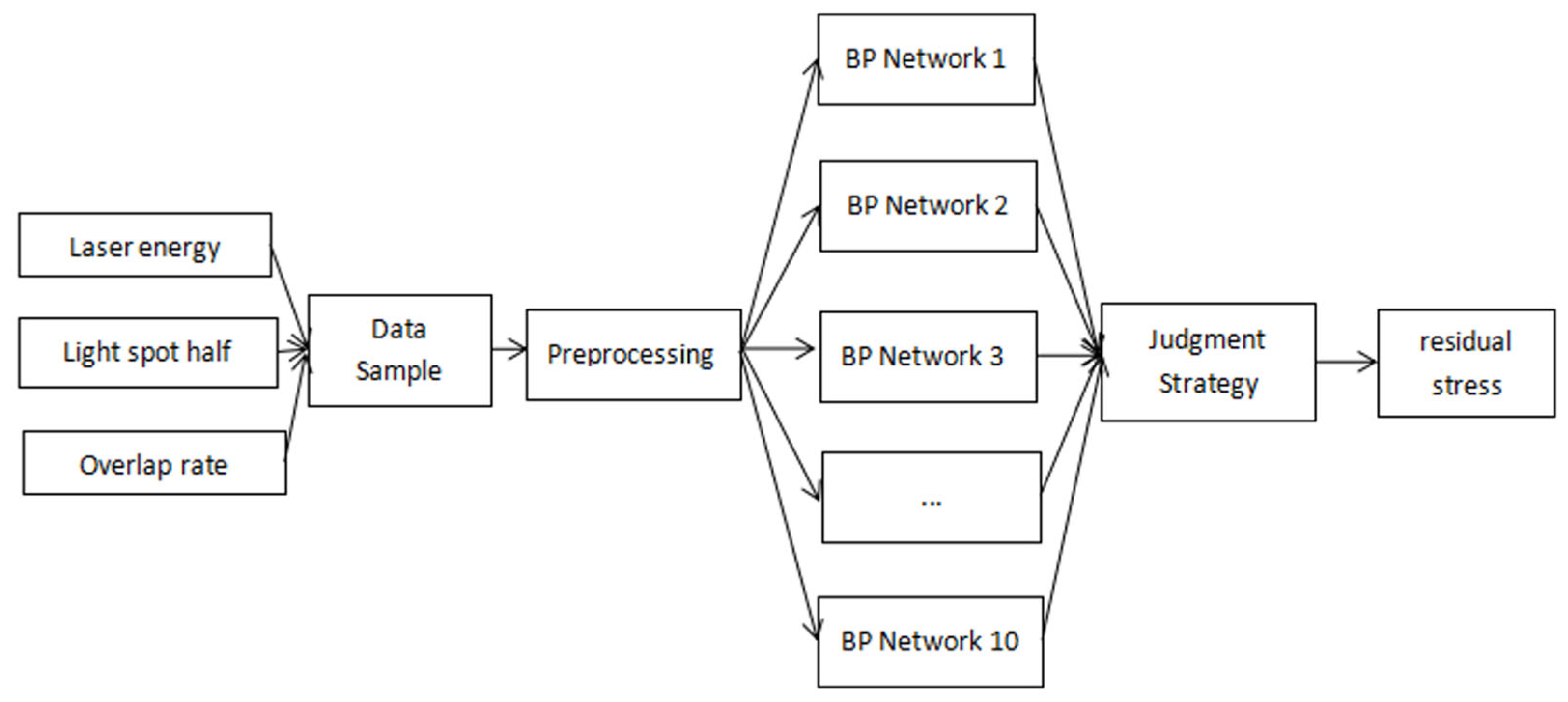
2.2. Modeling Neural Network Agents
2.2.1. Genetic Algorithm Used to Optimize BP Networks
2.2.2. Strong Classifier Design Based on BP_Adaboost
2.2.3. Extreme Learning Machine Optimization Method
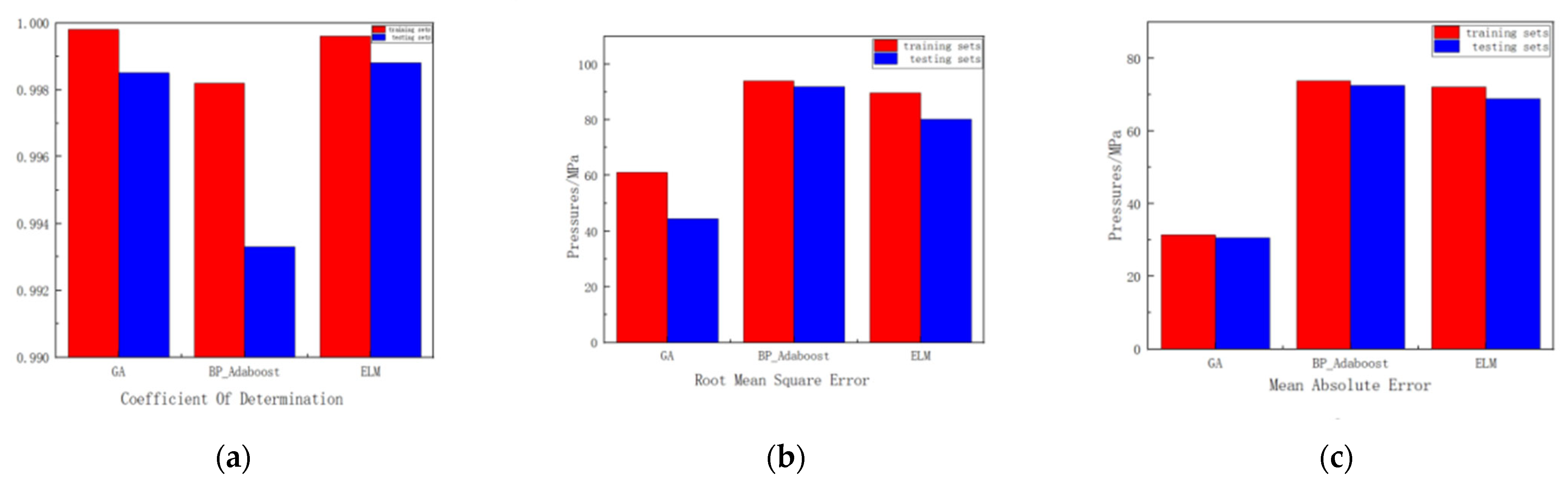
2.3. Model Comparison
3. Conclusions
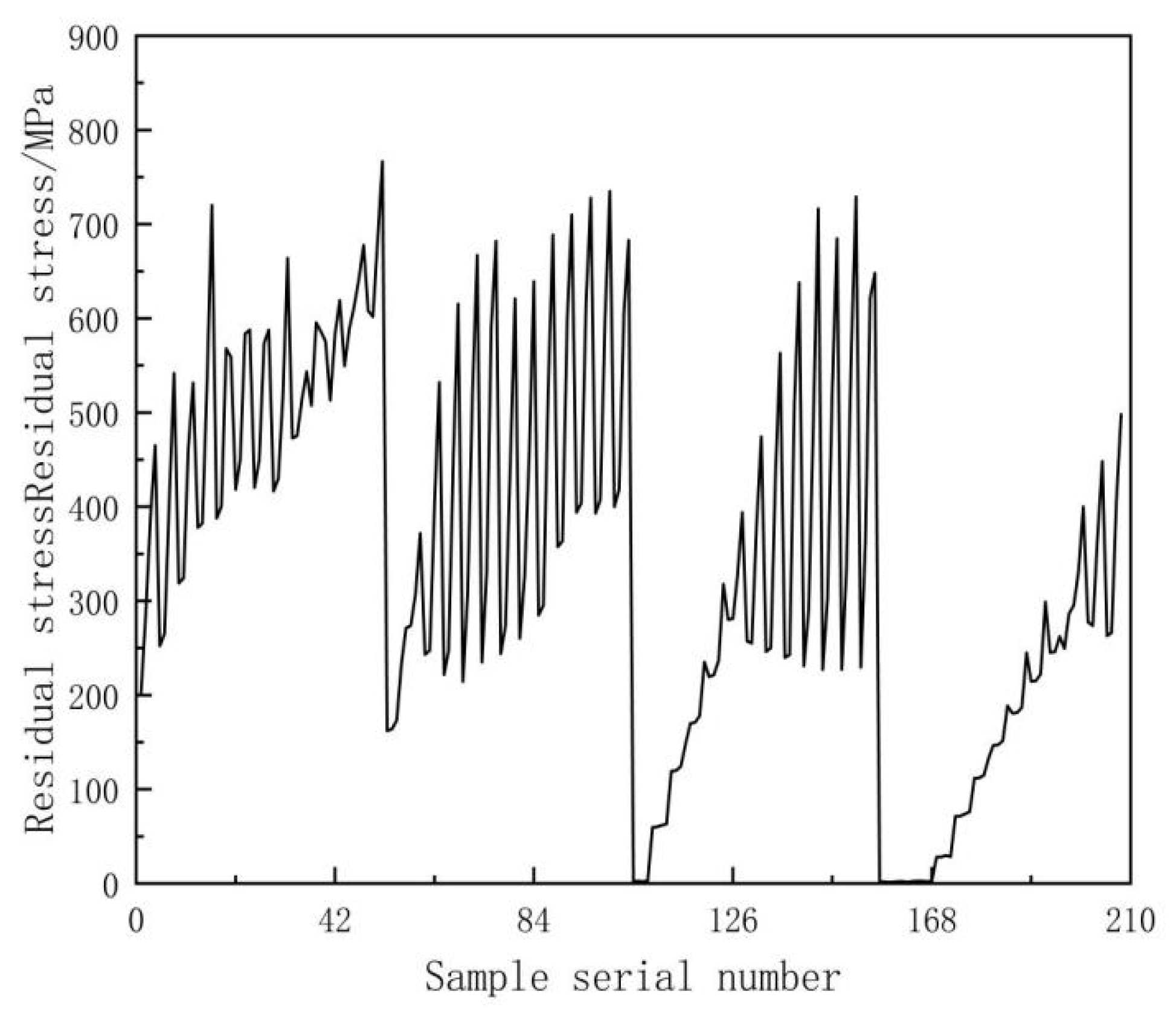
- In the simulation experiment undertaken to simulate the TC4 titanium alloy laser shock experiment, the surface residual stress reached under a laser energy of 2 J, a radius of 2.5 mm, and a lap rate of 0% a minimum value of 1.71 MPa. The surface residual stress under a laser energy of 8 J, radius of 1 mm, and lap rate of 70% reached a maximum value of 7.67 × 102 MPa;
- The residual stresses on the surfaces of laser-impacted TC4 titanium alloy plates increased with the increase in laser energy, decreased with the increase in spot radius, and increased with the increase in overlap rate, while all other laser parameters remained constant;
- The agent model built by optimizing a BP network with the genetic algorithm achieved the best performance in predicting the residual stresses of laser-shocked TC4 plates with the performance metrics of R2, RMSE, and MAE of 0.9985, 44.4518, and 30.6285, respectively, in the testing sets;
- In cases with limited experimental data provided through the establishment of a neural network agent model, the limited data were used learned and used to predict the unknown data. Compared with the limited element simulation neural network agent model, this model was more convenient and faster, and the prediction results were similar to those of the actual results. In cases with limited data, the establishment of a genetic algorithm-optimized BP network as a proxy model to predict the residual stress on the surface of TC4 titanium alloy strengthened by laser shocking is effective.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gan, L.P. Fatigue Life Prediction and Reliability Analysis Method for Key Rotating Parts of Aero-Engine. Ph.D. Thesis, University of Electronic Science and Technology, Chengdu, China, 2014. [Google Scholar]
- Wang, M. Simulation of Surface Integrity and Deformation of Shot Peening Titanium Alloy Blades. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2022. [Google Scholar] [CrossRef]
- Wang, R.; Liu, P.T.; Liu, D.Y.; Zhao, X. Effect of surface ultrasonic rolling process parameters on the surface properties of EA4T axles. Therm. Process. Technol. 2021, 50, 88–92. [Google Scholar] [CrossRef]
- Zhao, X.J.; Ma, Y.X.; Zhang, Z.; Zhang, X.; Liu, Z.; Yang, W. Current status of research and application of laser impact peening technology. Appl. Lasers 2022, 42, 111–119. [Google Scholar] [CrossRef]
- He, Z.; Shen, Y.; Zhou, J.; Liu, W.; Sun, R. Advances in microstructure evolution and properties of laser impact strengthening. Aerosp. Manuf. Technol. 2021, 64, 48–58. [Google Scholar] [CrossRef]
- Savkovic, B.; Kovac, P.; Rodic, D.; Strbac, B.; Klancnik, S. Comparison of artificial neural network, fuzzy logic and genetic algorithm for cutting temperature and surface roughness prediction during the face milling process. Adv. Prod. Eng. Manag. 2020, 15, 137–150. [Google Scholar] [CrossRef]
- Savkovic, B.; Kovac, P.; Dudic, B.; Gregus, M.; Rodic, D.; Strbac, B.; Ducic, N. Comparative characteristics of ductile iron and austempered ductile iron modeled by Neural Network. Materials 2019, 12, 2864. [Google Scholar] [CrossRef] [PubMed]
- Jovicic, G.; Milosevic, A.; Kanovic, Z.; Sokac, M.; Simunovic, G.; Savkovic, B.; Vukelic, D. Optimization of Dry Turning of Inconel 601 Alloy Based on Surface Roughness, Tool Wear, and Material Removal Rate. Metals 2023, 13, 1068. [Google Scholar] [CrossRef]
- Zheng, L.; Pan, W.L.; Cheng, N. Artificial intelligence technology application and its development trend. Technol. Innov. 2022, 209, 164–166+169. [Google Scholar] [CrossRef]
- Chess, L.B. Theoretical development and application status of machine learning. China New Commun. 2019, 21, 60–62. [Google Scholar]
- Dai, F.; Zhou, J.; Lu, J.; Luo, X. A technique to decrease surface roughness in overlapping laser shock peening. Appl. Surf. Sci. 2016, 370, 501–507. [Google Scholar] [CrossRef]
- Troiani, Z. The effect of laser peening without coating on the fatigue of a 6082-t6 aluminum alloy with a curved notch. Metals 2019, 9, 728. [Google Scholar] [CrossRef]
- Kay, G. Failure Modeling of Titanium-6Al-4V and 2024-T3 Aluminum with the Johnson-Cook Material Model; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2002. [Google Scholar]
- Wang, X.; Shi, F.; Yu, L.; Li, Y. Neural Networks Matlab 43 Case Studies; Beijing University of Aeronautics and Astronautics: Beijing, China, 2011; pp. 11–256. [Google Scholar]
- Wu, J.-J.; Zheng, H.; Qiao, H.-C.; Wei, B.-X.; Zhao, Y.-J.; Li, J.-F.; Zhao, J.-B. Prediction about residual stress and microhardness of material subjected to multiple overlap laser shock processing using artificial neural network. J. Cent. South Univ. 2022, 29, 3346–3360. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Z.; Qiao, H.; Zhao, Y.; Lie, J.; Zhao, J. Artificial neural network approach for mechanical properties prediction of TC4 titanium alloy treated by laser shock processing. Opt. Laser Technol. 2021, 143, 107385. [Google Scholar] [CrossRef]
- Qiao, H.; Zhao, J.; Yu, Y. Parameters and performance analysis of laser impact strengthening of TC4 titanium alloy. Adv. Laser Optoelectron. 2013, 50, 142–147. [Google Scholar]
- Liu, Y.; Shi, Z.; Zhao, Y. Effect of laser impact and shot peening composite peening on the DFRcutoff of fatigue rated strength of TC4 titanium alloy details. China Laser 2020, 47, 371–378. [Google Scholar]







| Alloy Elements | Al | V | O | C | N | Ti |
|---|---|---|---|---|---|---|
| Content (%) | 5.5–6.8 | 3.5–4.5 | 0.20 | 0.10 | 0.05 | Residuals |
| Density (g/cm3) | Poisson’s Ratio μ | Modulus of Elasticity (GPa) |
|---|---|---|
| 4.44 | 0.334 | 109 |
| A (MPa) | B (MPa) | C | n | ε | T0 | Tm | m |
|---|---|---|---|---|---|---|---|
| 1098 | 1092 | 1.1 | 0.93 | 1 | 298 | 1680 | 1.1 |
| Sample Number | Laser Energy (J) | Optical Shift Radius (mm) | Overlap Rate (%) | Residual Stress (Mpa) |
|---|---|---|---|---|
| 1 | 2 | 1 | 0 | 2.00 × 102 |
| 2 | 2 | 1 | 20 | 2.85 × 102 |
| 3 | 2 | 1 | 50 | 3.88 × 102 |
| 4 | 2 | 1 | 70 | 4.65 × 102 |
| 5 | 2.5 | 1 | 0 | 2.52 × 102 |
| 6 | 2.5 | 1 | 20 | 2.65 × 102 |
| … | ||||
| 207 | 8 | 2.5 | 50 | 4.06 × 102 |
| 208 | 8 | 2.5 | 70 | 4.98 × 102 |
| Sample | Neural Network Types | ||
|---|---|---|---|
| GA | BP_Adaboost | ELM | |
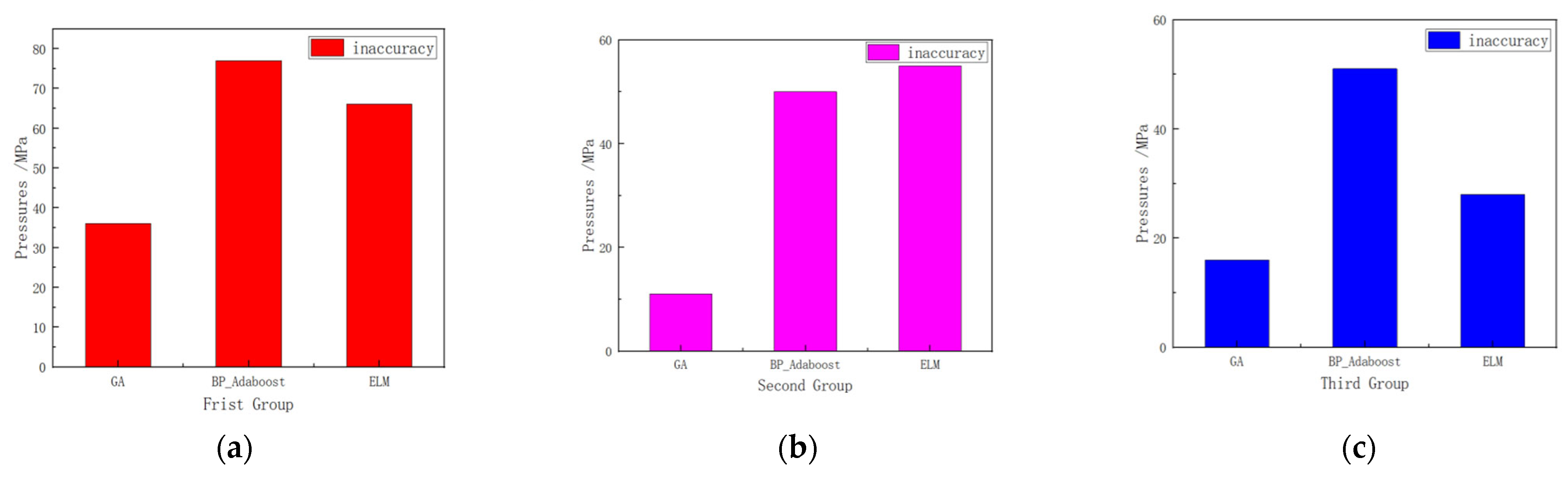
| First set of errors (MPa) | 56 | 77 | 66 |
| Second set of errors (MPa) | 11 | 50 | 55 |
| Third set of errors (MPa) | 16 | 51 | 28 |
| Energies (J) | Radius (mm) | Overlap Ratio (%) | Actual Result (MPa) | Projected Results (MPa) | Error Ratio (%) |
|---|---|---|---|---|---|
| 3 | 1.5 | 10 | 223 | 227 | 1.7 |
| 7 | 1.5 | 50 | 634 | 614 | 3.2 |
| 2.7 | 0.6 | 50 | 573 | 535 | 6.6 |
| 6 | 1.5 | 40 | 327 | 377 | 15.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Li, H.; Jiang, Z.; Zhang, J.; Ma, S.; Zhong, J.; Wang, S.; Wang, C. Prediction of Surface Residual Stresses after Laser Shock Processing on TC4 Titanium Alloy Using Different Neural Network Agent Models. Coatings 2023, 13, 1889. https://doi.org/10.3390/coatings13111889
Ding X, Li H, Jiang Z, Zhang J, Ma S, Zhong J, Wang S, Wang C. Prediction of Surface Residual Stresses after Laser Shock Processing on TC4 Titanium Alloy Using Different Neural Network Agent Models. Coatings. 2023; 13(11):1889. https://doi.org/10.3390/coatings13111889
Chicago/Turabian StyleDing, Xiangyu, Hongliang Li, Zonghong Jiang, Junlong Zhang, Sijie Ma, Jida Zhong, Shengchao Wang, and Cheng Wang. 2023. "Prediction of Surface Residual Stresses after Laser Shock Processing on TC4 Titanium Alloy Using Different Neural Network Agent Models" Coatings 13, no. 11: 1889. https://doi.org/10.3390/coatings13111889





