General Curve Model for Evaluating Mechanical Properties of Concrete at Different Ages

Abstract

During the process of pouring and solidification of concrete, the compressive strength and elastic modulus of concrete exhibit dynamic growth patterns. The mechanical properties of concrete usually remain stable in the later stage (28 days after pouring). Studying appropriate curve models to accurately evaluate the changes in early mechanical properties of concrete has always been an important topic in the field of concrete materials. This work proposes a new dual parameter curve model for accurately evaluating the growth pattern of early compressive strength and elastic modulus of concrete. A comparative study was conducted between the proposed new curve model and existing curve models using 18 sets of experimental data from 10 literature sources. The research results indicate that the fitting average error and standard deviation of this new curve model are significantly smaller than the existing curve models. For some examples, the fitting error and standard deviation of the new model are only about 20%–30% of those of the existing models. The main advantages of this new curve model lie in two aspects. The first advantage is that this new curve model only contains two unknown parameters, so only a small amount of experimental data is required for data fitting and does not require complex mathematical operations. The second advantage is that this new curve model has a wide range of applications, which include compressive strength evaluation and elastic modulus evaluation and can also be extended to the evaluation of the mechanical properties of other materials similar to concrete.

1. Introduction

Concrete is a widely used building material for residential buildings, factories, and bridges. The mechanical properties of concrete, such as compressive strength and elastic modulus, exhibit dynamic growth patterns after pouring and remain stable until 28 days later. Evaluating the early mechanical properties of concrete can effectively guide the early construction and design of concrete engineering [1,2,3,4], such as prestressed tensioning or formwork removal. For example, in the production of large-volume concrete for bridge box girders, steel reinforcement prestressing should be applied as early as possible to prevent concrete cracks. Therefore, it is necessary to accurately evaluate the compressive strength and elastic modulus of concrete at an early stage to determine the time for steel reinforcement tensioning [5]. In high-rise buildings and other projects that use a large amount of concrete, the cost of formwork engineering is very high. If the formwork can be removed as early as possible, it can accelerate the turnover of formwork and thus save construction costs. Thus, accurately evaluating the strength of concrete at early ages is also very important for determining the time of formwork removal [6]. At present, there are two main methods for evaluating the early mechanical properties of concrete, namely machine learning-based evaluation methods and mathematical curve-based evaluation methods. Machine learning-based evaluation methods typically utilize large amounts of experimental data to train artificial neural network (ANN) models. The trained ANN models can then be used to evaluate the mechanical properties of concrete at various ages. Jaf et al. [7] used machine learning technology to evaluate the effects of silicon dioxide and calcium oxide in fly ash on the compressive strength of green concrete. Ahmed et al. [8] employed innovative machine learning techniques to predict the compressive strength of geopolymer concrete modified with nanoparticles. Trtnik et al. [9] analyzed the relationship between ultrasonic pulse velocity, static and dynamic Young’s modulus, and shear modulus. Based on the experimental results, they demonstrated that the model constructed via artificial neural networks can estimate the compressive strength of concrete using only ultrasonic pulse velocity values and some mix ratio parameters of concrete. Yousif and Abdullah [10] found that water–cement ratio is the most important factor affecting the output of neural network models, and neural networks have strong potential as a tool for predicting concrete compressive strength. Duan et al. [11] constructed, trained, and tested a neural network model for predicting the compressive strength of recycled aggregate concrete using 146 sets of available data obtained from 16 different published literature sources. Nikoo et al. [12] used an artificial neural network model to calculate the compressive strength of concrete and optimized it using genetic algorithms. Khashman and Akpinar [13] designed an artificial neural network model for predicting the compressive strength of different concrete mixtures. Deng et al. [14] proposed a prediction model based on deep learning theory, which learns the deep features of concrete components via convolutional neural networks. The research results indicate that the prediction model based on deep learning has the advantages of high accuracy, high efficiency, and strong generalization ability and can be used as a new method for calculating the strength of recycled concrete. Feng et al. [15] proposed an intelligent prediction method for concrete compressive strength based on machine learning technology. Use adaptive boosting algorithm to predict the compressive strength of concrete. Muliauwan et al. [16] used three artificial intelligence methods: ANN, support vector machines (SVM), and linear regression (LR) to predict the compressive strength of concrete. Asteris and Mokos [17] studied the application of artificial neural networks in predicting the compressive strength of concrete in existing structures. Bka et al. [18] constructed three different neural network models using the Levenberg Marquardt (LM) algorithm to predict the compressive strength of recycled aggregate concrete. The results indicate that the prediction model for compressive strength of recycled aggregate concrete based on artificial neural networks has high accuracy and can be further used for mix ratio optimization design. Cui et al. [19] used seven machine learning algorithms to apply machine learning to predict the compressive strength of concrete. The experimental results indicate that the model has high prediction accuracy when the compressive strength is greater than 40 MPa. Kumar et al. [20] used machine learning algorithms such as Gaussian progressive regression (GPR), support vector machine regression (SVMR), ensemble learning (EL), and optimized GPR, SVMR, and EL to predict the compressive strength of lightweight concrete (LWC). Pakzad et al. [21] used machine learning (ML) and deep learning (DL) algorithms to predict the compressive strength (CS) of steel fiber-reinforced concrete (SFRC) containing hooked industrial steel fibers (ISF). Cünyt et al. [22] studied the performance of adaptive neural fuzzy inference system (ANFIS) in predicting the elastic modulus of ordinary concrete and high-strength concrete. The results indicate that their proposed ANFIS outperforms other models in terms of predictive ability. Demir [23] used collected data to establish, train, and test artificial neural network models and compared the predicted elastic modulus results with building codes and practical experience results. The results indicate that artificial neural networks have strong potential in predicting the elastic modulus of high-strength concrete and ordinary concrete. Ahmadi [24] further validated the method for predicting elastic modulus based on the ANFIS model. The experimental comparison shows that the ANFIS model is superior to the other three nonlinear regression models. Han et al. [25] proposed a comprehensive machine learning (ML) model for predicting the elastic modulus of concrete prepared from recycled concrete aggregates. They compared the predictive performance of the integrated ML model with five commonly used ML models. The results indicate that compared to independent models, integrated ML models always produce more accurate predictions. Hasanzadeh et al. [26] utilized machine learning to predict the mechanical properties of basalt fiber-reinforced high-performance concrete by simulating the compressive strength and elastic modulus of concrete.

The second method is to evaluate the relationship between the mechanical properties of concrete and its age based on a certain function curve. The basic principle of this method is to obtain the functional equation between concrete mechanical parameters and age via data fitting based on early experimental data, and then calculate the concrete mechanical parameters at any time. The main advantage of this method is that it can be carried out with only a small amount of experimental data. At present, the commonly used concrete compressive strength–age curve models are the exponential model [27,28,29], the logarithmic model [30,31], the hyperbolic model [32,33], and the polynomial model [33,34]. Yang et al. [27] tested the compressive strength and elastic modulus of high-strength concrete within 28 days via experiments and proposed an exponential model for data fitting. Zhao et al. [28] measured the compressive strength and elastic modulus of C50 concrete at 1, 2, 3, 5, 7, 11, 14, 28, and 40 days and fitted the exponential curves of compressive strength and elastic modulus with these data. Yang et al. [29] combined regression fitting methods with exponential models to establish a prediction model for the relationship between the compressive strength and age of C60 concrete. Liu [30] analyzed the changes in compressive strength and elastic modulus of C50 concrete over time via experiments. Zhao [31] measured the compressive strength of concrete at 3, 7, 28, and 60 days via experiments and fitted the corresponding logarithmic function formula via data regression. Carino [32] and Viviani [33] fitted the changes in compressive strength of concrete over time using hyperbolic models, thereby establishing a prediction of compressive strength over age of concrete. Jin [34] used a polynomial model to fit the test data of early-age compressive strength and elastic modulus of high-strength concrete. Ling [35] identified the components that have an impact on the compressive strength of concrete by analyzing the composition of the concrete and built a prediction model for the compressive strength of mechanical sand concrete using a third-order nonlinear function. Jia et al. [36] obtained the compressive strength of ordinary Portland concrete at 1 to 28 days via concrete compressive strength experiments and fitted the obtained data using a cubic polynomial model to obtain a fitting curve of concrete compressive strength over time. Yeh [37] proposed a parametric trend regression and a four-parameter optimization method for predicting the compressive strength of concrete. Elaty [38] analyzed experimental data and revealed that a model can be constructed using two constants to predict the compressive strength of concrete at any age. Guo et al. [39] developed a time-dependent relationship model between concrete compressive strength and elastic modulus by referring to the existing curve models. Wang and Yue [40] analyzed the existing time-varying models of compressive strength, summarized the advantages and disadvantages of these models, and proposed further research directions.

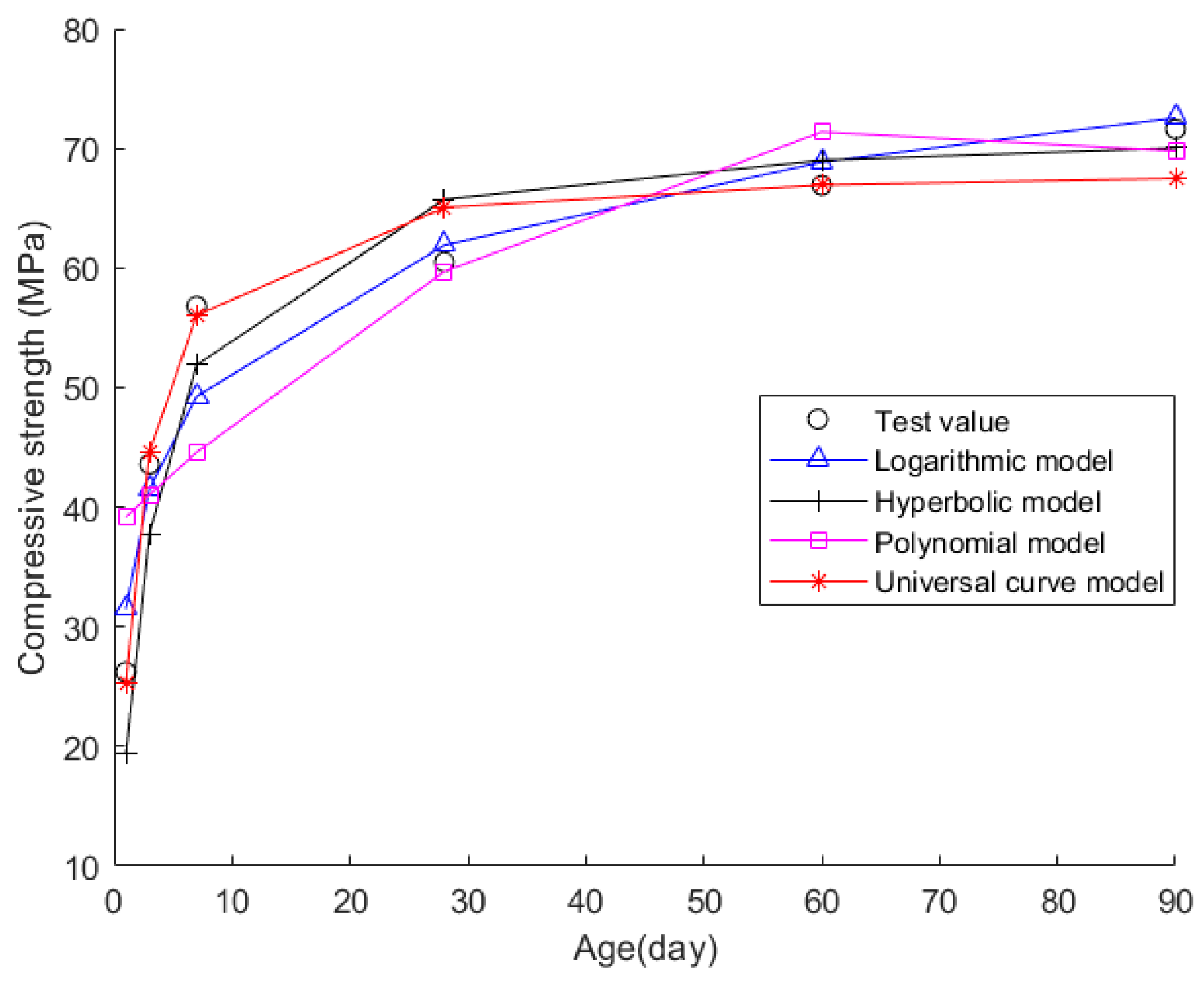
Generally, although existing prediction models can predict the mechanical properties of concrete to a certain extent, they also have certain shortcomings in some aspects. The limitations of the ANN-based evaluation models lie in two aspects. Firstly, the accuracy of the ANN model is greatly affected by the number of neurons. However, there is currently no rigorous mathematical basis for determining the optimal number of neurons in the ANN model. Secondly, the ANN model can only be used for evaluation after being trained and matured. Usually, the training of the ANN model requires a lot of experimental data, which increases the cost of the experiment. The limitations of current curve regression models mainly lie in their low fitting accuracy and weak universality. For example, polynomial models are inaccurate in predicting the mechanical properties of concrete in the later stage. Although logarithmic and exponential models can converge to a certain extent in the later stage, they cannot predict the mechanical properties of concrete well in the later stage. These types of prediction models do not perform well with data with high dispersion, resulting in low fitting accuracy. The three-parameter model has one more unknown fitting parameter than the two-parameter model, so more experimental data is needed to perform curve fitting accordingly. When there is little experimental data, the fitting accuracy of the three-parameter model may not be as good as that of the two-parameter model. In addition, the three-parameter model is more complex to calculate than the two-parameter model. In order to improve evaluation accuracy, it is necessary to overcome the shortcomings of existing curves and integrate the advantages of existing curves to study a new mathematical curve model for predicting the mechanical properties of concrete. The goal of this work is to develop a new dual parameter curve model that can more accurately evaluate the compressive strength and elastic modulus changes of concrete at early age compared to the existing curve models. Based on the evaluation results of the proposed model, it can more reliably guide the construction or mechanical calculation of concrete components at early age. To this end, this work first analyzes the advantages and disadvantages of the existing logarithmic model, exponential model, hyperbolic model, and polynomial model. Subsequently, this work develops a new curve model that overcomes the shortcomings of existing curve models, which can be used for the evaluation of concrete compressive strength at early ages as well as for the evaluation of elastic modulus at early ages. The improvements provided by the new model mainly lie in three aspects. The first is that the mathematical formula of the new model is concise, including only two unknown parameters, which is very convenient for engineering applications. The second is that the curves used by the new model are more in line with the changes in mechanical properties of concrete at early age, so the fitting accuracy of the new model is higher than that of existing models. Thirdly, the new model has better universality, can be applied to more types of concrete, and may also be applicable to other cementitious materials. This work focuses on the performance of the proposed new model in evaluating the compressive strength and elastic modulus of concrete at early age. Using 18 sets of experimental data from existing literature, a comparative study was conducted on the computational accuracy of the new model and existing models to illustrate the superiority of the proposed new model.

2. Mathematical Models for Predicting the Mechanical Properties of Concrete

As mentioned earlier, the prediction method of concrete mechanical properties based on some assumed mathematical curve is a simple and feasible method in engineering practice, because it only needs a few early test data for concrete. Figure 1 shows the operational process of this type of method in practice.

Obviously, the suitable mathematical curve is an important factor in accurately predicting the mechanical properties of concrete. The commonly used curve models can be divided into two-parameter models and three-parameter models based on the number of unknown parameters that need to be fitted in the curve equations. In this section, the common two-parameter and three-parameter models are reviewed, and the advantages and disadvantages of each model are briefly analyzed. Finally, a new universal two-parameter model is proposed to predict the mechanical properties of concrete at different ages. Without losing generality, in the following mathematical equations of curve models, $t$ represents the time (age) after concrete pouring, and $z(t)$ represents the mechanical parameters (compressive strength or elastic modulus) of the concrete at time $t$.

2.1. Two-Parameter Curve Model

The commonly used two-parameter curve models include exponential model, logarithmic model, and hyperbolic model. The curve equation of exponential model is expressed by

$$z(t)=a\cdot e^{-b/t}$$

(1)

in which $a$ and $b$ represent two unknown non-negative parameters that need to be determined based on experimental data. As can be seen from Equation (1), the advantage of exponential model is that the exponential function increases monotonically, so with the increase of $t$, the value of $z(t)$ function will increase. This is consistent with the fact that the mechanical properties of concrete will increase with time in engineering practice. When $t\to \infty$, $z(t)\to \mathrm{a}$, it is also consistent with the law that the mechanical properties of concrete will remain basically unchanged after a period of growth. However, the exponential model also has some shortcomings. The first drawback of this model is the lack of $t$ = 0 point in the definition domain because $t$ is the denominator of $\frac{b}{t}$ in Equation (1). In practical application, when $t$ = 0, the mechanical property of concrete is 0. Therefore, it is important to note that the exponential model cannot include this point. In addition, because the equation of exponential model contains only two fitting parameters, the fitting accuracy may be low for experimental data with large dispersion, and it can easily produce large errors.

The curve equation of logarithmic model is expressed as:

$$z(t)=a+b\cdot \ln (t)$$

(2)

In Equation (2), $a$ and $b$ represent the two fitting parameters, which are obtained by combining partial experimental data with curve fitting. Comparing Equations (1) and (2), it can be seen that the logarithmic model can be seen as a modified equation obtained by taking the logarithms of both sides of the exponential model equation. Therefore, the advantages and disadvantages of the logarithmic model and the exponential model are similar. The advantage of the logarithmic model is that the function is a monotonically increasing function, which is consistent with the law of concrete mechanical properties increasing over time in practical engineering. The disadvantage is that its definition domain also lacks the point $t$ = 0. Meanwhile, due to its monotonic increasing function, when $t\to \infty$, although the growth rate slows down, the results do not converge, which is inconsistent with the actual growth law of concrete mechanical properties. Since this equation only contains two fitting parameters, the fitting accuracy of this equation may be low for data with large dispersion.

The curve equation of hyperbolic model is expressed as:

$$z(t)=\frac{t}{a+b\cdot t}$$

(3)

In the above formula, $a$ and $b$ are two fitting parameters of the hyperbolic model. The advantage of hyperbolic model compared with other models is that the predicted mechanical properties of concrete will gradually approach a fixed number with the increase of time, which is consistent with the fact that the mechanical properties of concrete remain basically unchanged in the later stage. The disadvantage of hyperbolic model is that the fitting accuracy of the model is not very good when dealing with some very discrete data.

2.2. Three-Parameter Curve Model

The common three-parameter models include polynomial model and hybrid curve model. The curve equation of polynomial model is expressed as

$$z(t)=a+b\cdot t+c\cdot t^2$$

(4)

Equation (4) is a quadratic polynomial model, where $a$, $b$ and $c$ are the three fitting parameters of this model. Compared to the previous three prediction models, the advantage of the polynomial model is that its definition domain includes point $t$ = 0, and the fitted function is also a monotonically increasing function, which is in line with the development laws of concrete mechanical properties in practical engineering. Meanwhile, due to the fact that the prediction model has three fitting parameters, its fitting accuracy is correspondingly more accurate than the logarithmic model, the exponential model, and the hyperbolic model with only two fitting parameters. The disadvantage of the polynomial model is that at $t\to \infty$, the growth rate of $z(t)$ will be too fast, which is different from the law in engineering practice that the mechanical properties of concrete will increase slowly or even remain basically unchanged in the later stage. The reason for the faster growth rate in the later stage of the polynomial model is the square term of time (i.e., $c\cdot t^2$) in the model. The longer the time, the faster the square term of time increases. Therefore, this prediction model is not suitable for predicting the later mechanical properties of concrete.

The curve equation of the hybrid curve model is expressed as

$$z(t)=at\ln (1+\frac{1}{b+ct})$$

(5)

Equation (5) is a mixed curve model, which includes a logarithmic model and a hyperbolic model. $a$, $b$ and $c$ are the three fitting parameters of this equation. The advantages of this model are that its definition domain includes point $t$ = 0, the fitting function is also a monotonically increasing function, and the prediction model will eventually converge to a value, which is more in line with the development law of concrete mechanical properties in practical engineering. Meanwhile, due to the fact that the prediction model has three fitting parameters, its fitting accuracy is correspondingly higher than those of the logarithmic model and the hyperbolic model. However, although the three-parameter model has higher fitting accuracy than the two-parameter model, it is less convenient to use in practical engineering applications due to the need for an additional parameter for data fitting.

2.3. A Universal Two-Parameter Model

Based on the above analysis, a new mathematical model is proposed to accurately describe the changes in mechanical properties of concrete over time in practical engineering. The mathematical expression for the new dual parameter curve model is given as:

$$z(t)=\frac{a\cdot t}{t+1}+b\cdot \arctan (\frac{t}{t+1})$$

(6)

In Equation (6), $t$ and $z(t)$ represent the time and the corresponding mechanical parameters at time $t$, which are consistent with the previous definitions. The two unknown parameters $a$ and $b$ represent the fitting coefficients that need to be determined based on experimental data. The new model can be seen as a combination of hyperbolic function and arctangent function, and the accuracy of function fitting can be further improved by adding an item of arctangent function. The new model also inherits the advantage that its definition domain contains a point $t$ = 0. At the same time, when $t$ approaches infinity, $z(t)$ tends toward a certain value, which is in line with the fact that the mechanical properties of concrete in the later stage remain basically unchanged in practical engineering. This compensates for the defect of polynomial models that cannot converge when $t$ approaches infinity, so this model can be used to predict the mechanical properties of concrete in the later stage. In addition, the prediction model only needs to fit two parameters, which is more convenient to use in practical engineering than the above three-parameter model. The physical meanings of parameters $a$ and $b$ are the weights of the hyperbolic function and the arctangent function in the sum function shown in Equation (6), respectively. From Equation (6), one obtains:

$$\underset{t\to \infty }{\lim }z(t)=a+b\cdot \frac{\pi }{4}$$

(7)

Therefore, the physical meaning of $a+b\cdot \frac{\pi }{4}$ is the stable mechanical parameter of concrete in the later stage, such as compressive strength or elastic modulus. Note that this new model only has two fitting parameters, $a$ and $b$, that need to be determined via data fitting. When the new model is compared with the existing two-parameter models, it can be found that the new model is a combination of two types of curves (hyperbolic and arctangent curves), while the existing two-parameter models are all based on a single curve. The reason why the new model yields fewer errors compared to the existing models is that it introduces a new curve of the arctangent function, which is more in line with the growth law of mechanical properties of concrete at early age.

In summary,

Table 1. The advantages/disadvantages of various curve models.

Model	Number of Fitting Parameters	Definition Domain	$\mathbf{Convergence}\mathbf{of}\mathit{z}(\mathit{t})$$\mathbf{When}\mathit{t}\to \mathit{\infty }$
Exponential model	2	Missing point with $t$ = 0	Yes
Logarithmic model	2	Missing point with $t$ = 0	No convergence
Hyperbolic model	2	Including point with $t$ = 0	Yes
Polynomial model	3	Including point with $t$ = 0	No convergence
Hybrid model	3	Including point with $t$ = 0	Yes
New dual parameter model	2	Including point with $t$ = 0	Yes

presents the advantages/disadvantages of the above curve models for clarity. The improvement in fitting accuracy of the new model can be seen in the calculation results of multiple sets of experimental data in the next section.

The next section describes the fitting parameter calculation method for the mathematical model described above. Firstly, a linear equation system of mechanical properties and age is established based on the measured data obtained from experiments, and then the corresponding fitting parameters are further calculated. Using $n$ sets of experimental data, the linear system corresponding Equation (6) can be expressed as:

$$y=C\cdot x$$

(8)

$$y=\left\{\begin{array}{c}\mathrm{z}(t_1)\\ ⋮\\ \mathrm{z}(t_n)\end{array}\right\},$$

(9)

$$x=\left\{\begin{array}{c}a\\ b\end{array}\right\}$$

(10)

$$C=\left[\begin{array}{cc}\frac{t_1}{t_1+1}& \arctan (\frac{t_1}{t_1+1})\\ ⋮& ⋮\\ \frac{t_n}{t_n+1}& \arctan (\frac{t_n}{t_n+1})\end{array}\right]$$

(11)

where $z(t_n)$ represents the mechanical parameter (elastic modulus or compressive strength) measured at time $t_n$. Clearly, the vector $y$ and coefficient matrix $C$ in Equation (8) can be obtained from the experimental data. Thus, the unknown fitting parameter vector $x$ can be further calculated using the least square method. For this purpose, Equation (8) can be rewritten as

$$C^{T}y=(C^{T}C)\cdot x$$

(12)

From Equation (11), the solution of $x$ is expressed as:

$$\widehat{x}={(C^{T}C)}^{-1}{C}^{T}y$$

(13)

The calculated $\widehat{x}$ refers to the least squares estimate of $x$.

The fitted parameters obtained from the calculation can be used to obtain the specific curve equation of the prediction model, and the accuracy of the model prediction can be verified by comparing the difference between the predicted value and the experimental value. The difference between the predicted value and the experimental value is defined as:

$$\left\{\delta \right\}=\left|C\cdot \widehat{x}-y\right|$$

(14)

where $\left\{\delta \right\}={({\delta }_1,\cdots ,{\delta }_n)}^T$ is called as the residual vector. Specifically, ${\delta }_i$ is the residual error between the $i$th experimental data and the predicted value. Average and standard deviation of the residual errors can be calculated by:

$$\overline{\delta }=\frac{{\delta }_1+\cdots +{\delta }_n}{n}$$

(15)

$$\sigma =\sqrt{\frac{{\displaystyle \sum _{i=1}^n{({\delta }_i-\overline{\delta })}^2}}{n}}$$

(16)

where $\overline{\delta }$ is the average of the residual errors, $\sigma$ is the corresponding standard deviation. The smaller the value of $\overline{\delta }$ and $\sigma$, the higher the fitting accuracy of the curve model.

3. Model Verification and Comparison via Concrete Experiment Data

The newly proposed evaluation model was validated using experimental data from references [28,30,34,36,39,41,42,43,44,45] (referred to as cases 1 to 11). The results were compared with the fitting results of existing logarithmic, hyperbolic and polynomial models to demonstrate the superiority of the model.

3.1. Evaluation of Compressive Strength

Case 1. In reference [36], 32 groups of concrete specimens with a water–cement ratio of 0.56 and 50 mm × 50 mm × 150 mm were cured under standard curing conditions. The components of concrete materials are listed in

Table 2. The components of concrete materials in case 1 (kg/m³).

Ordinary Portland Cement	Standard Sand	Water	Water–Cement Ratio
460	800	180	0.56

. The experimental data for the compressive strength are shown in

Table 3. Compressive strength of concrete blocks in case 1 (MPa).

Age (Unit: day)	Compressive Strength	Age (Unit: day)	Compressive Strength
1	4.26	15	70.56
2	23.83	16	71.31
3	36.42	17	68.29
4	43.28	18	66.04
5	45.85	19	73.79
6	44.91	20	70.81
7	54.21	21	76.95
8	57.99	22	76.65
9	58.75	23	68.26
10	62.26	24	78.46
11	60.33	25	75.66
12	65.72	26	79.92
13	68.72	27	79.73
14	68.90	28	85.39

. The logarithmic, hyperbolic, polynomial, and new models are used to fit the experimental data, and the fitting curves are shown in Figure 2. The fitting average error and standard deviation of these models are shown in

Table 4. The fitting mean errors and standard deviations from the four models in case 1.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	1.4240	1.6451	4.3428	0.4712
Fitted standard deviation $\sigma$	0.2581	0.2895	0.8066	0.0669

. The specific fitting equations for the four models are as follows:

$$z(t)=10.2190+21.3746\ln (t)$$

(17)

$$z(t)=\frac{t}{0.0822+0.0093\cdot t}$$

(18)

$$z(t)=17.6264+5.1571\cdot t-0.1102\cdot t^2$$

(19)

$$z(t)=519.5090\cdot (\frac{t}{t+1})-554.0748\cdot \arctan (\frac{t}{t+1})$$

(20)

According to the average error and standard deviation of the four models in Table 4, it can be seen that the average error and standard deviation of the new model are significantly smaller than those of the hyperbolic, polynomial, and logarithmic models. Figure 2 shows that compared to the logarithmic, polynomial, and hyperbolic models, the prediction curve of the new model is closer to the experimental test data. The results indicate that the new model has better data fitting ability than the logarithmic, polynomial, and hyperbolic models and is more accurate and reliable in evaluating the compressive strength of concrete.

Case 2. In reference [41], 14 groups of concrete specimens with 150 mm × 150 mm × 300 mm were manufactured and cured under standard and natural conditions. The components of concrete materials are listed in

Table 5. The components of concrete materials in case 2 (kg/m³).

Cement	Fine Aggregate	Coarse Aggregate	Water	Water Reducer	Admixture
357	712	1115	123	8.82	63

. The experimental data of compressive strength are shown in

Table 6. Compressive strength of concrete blocks in case 2 (MPa).

Age (Unit: hour)	Natural Conservation Condition	Standard Maintenance Condition
12	4.9	2.7
16	14.5	10.7
20	19.0	16.0
24	22.9	19.1
28	24.9	22.4
32	27.2	25.3
36	28.7	26.1
40	29.6	27.6
44	30.3	30.0
48	30.7	30.4
52	31.2	30.6
56	32.9	31.6
60	33.7	33.2
64	34.0	32.3

. Figure 3 and Figure 4 illustrate the fitting curves for the four models. The fitting average errors and standard deviations for these models are shown in

Table 7. The fitting mean errors and standard deviations of the four models for natural conservation condition in case 2.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	1.0084	1.0436	0.8495	0.2083
Fitted standard deviation $\sigma$	0.2524	0.2214	0.2087	0.0497

and

Table 8. The fitting mean errors and standard deviations of the four models for standard maintenance condition in case 2.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	1.2761	1.5086	1.0147	0.2415
Fitted standard deviation $\sigma$	0.3257	0.2926	0.2571	0.0578

. The specific fitting equations for the four models are as follows:

Natural conservation conditions:

$$z(t)=-29.0860+15.6257\ln (t)$$

(21)

$$z(t)=\frac{t}{1.1927+0.0073\cdot t}$$

(22)

$$z(t)=-6.5801+1.4516\cdot t-0.0132\cdot t^2$$

(23)

$$z(t)=1283.1235\cdot (\frac{t}{t+1})-1581.0830\cdot \arctan (\frac{t}{t+1})$$

(24)

Standard maintenance conditions:

$$z(t)=-36.8725+17.2964\ln (t)$$

(25)

$$z(t)=\frac{t}{2.1067-0.0101\cdot t}$$

(26)

$$z(t)=-11.2280+1.5518\cdot t-0.0138\cdot t^2$$

(27)

$$z(t)=1411.1477\cdot (\frac{t}{t+1})-1744.6763\cdot \arctan (\frac{t}{t+1})$$

(28)

Table 7 and Table 8 show that the new model outperforms the hyperbolic, logarithmic, and polynomial models regarding fitting mean error and standard deviation. Figure 3 and Figure 4 visually demonstrate that the fitting curve of the new model aligns more closely with the experimental data. These findings indicate that the new model is a better fit for the test data than the logarithmic, hyperbolic, and polynomial models.

Case 3. In reference [28], 30 sets of concrete specimens were manufactured using C50 grade concrete and cured under standard curing conditions. The components of the concrete are listed in

Table 9. The components of concrete materials in case 3 (kg/m³).

Cement	Fine Aggregate	Coarse Aggregate	Water	Water Reducer	Admixture
400	382	1166	170	4.3	115

. The tested compressive strength is shown in

Table 10. Compressive strength of concrete specimens in case 3 (MPa).

Age (Unit: day)	Compressive Strength
1	24.0
2	32.1
3	39.6
5	45.7
7	46.8
11	47.6
14	49.9
28	56.8
40	58.4

. The four fitting curves are presented in Figure 5 using these experimental data. The fitting average errors and standard deviations are shown in

Table 11. The fitting mean errors and standard deviations of case 3.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	0.1907	0.2214	0.3991	0.1231
Fitted standard deviation $\sigma$	0.0410	0.0492	0.0984	0.0163

. The specific fitting equations for the four models are as follows:

$$z(t)=27.2818+8.9263\ln (t)$$

(29)

$$z(t)=\frac{t}{0.0332+0.0165\cdot t}$$

(30)

$$z(t)=30.1059+2.0246\cdot t-0.0340\cdot t^2$$

(31)

$$z(t)=122.6500\cdot (\frac{t}{t+1})-82.8490\cdot \arctan (\frac{t}{t+1})$$

(32)

Table 11 indicates that the new model has a smaller fitting mean error and standard deviation compared to the other models. The new model’s average fitting error is approximately 35% lower than that of the logarithmic model, about 44% lower than that of the hyperbolic model, and about 35% lower than that of the polynomial model. The fitting standard error of the new model is roughly 40% for the logarithmic model, about 33% for the hyperbolic model, and about 16% for the polynomial model.

Case 4. In reference [42], 36 sets of 100 mm × 100 mm × 100 mm high-strength concrete specimens were manufactured and cured under standard curing conditions. The components of concrete materials are listed in

Table 12. The components of concrete materials in case 4 (kg/m³).

Powder	Steel Fiber	Water
2130	160	196

. The experimental data of compressive strength are shown in

Table 13. Compressive strength of concrete cubes in case 4 (Mpa).

Age (Unit: day)	Compressive Strength
0.5	43.303
1	71.012
2	99.915
3	108.909
4	114.274
5	114.300
6	118.566
7	119.790
8	121.774
9	122.116
10	122.919

, and the fitting curves are shown in Figure 6. The fitting average errors and standard deviations are shown in

Table 14. The fitting mean errors and standard deviations of case 4.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	0.3023	0.1885	0.4164	0.1564
Fitted standard deviation $\sigma$	0.0703	0.0495	0.1001	0.0388

. The specific fitting equations for the four models are as follows:

$$z(t)=71.7838+25.4840\ln (t)$$

(33)

$$z(t)=\frac{t}{0.0061+0.0075\cdot t}$$

(34)

$$z(t)=48.6435+21.4047\cdot t-1.4696\cdot t^2$$

(35)

$$z(t)=81.4696\cdot (\frac{t}{t+1})+68.7367\cdot \arctan (\frac{t}{t+1})$$

(36)

Table 14 shows that the fitting mean error and standard deviation of the new model are significantly smaller than those of the hyperbolic, logarithmic, and polynomial models. This again indicates that the new model can more accurately evaluate the compressive strength of concrete.

Case 5. In reference [30], some concrete specimens with 150 mm × 150 mm × 300 mm were manufactured, and the experimental data of compressive strength are shown in

Table 15. Compressive strength (MPa) of case 5.

Age (Unit: day)	Compressive Strength
1	25.63
2	40.71
3	48.50
5	52.30
7	53.20
10	55.00
20	62.30
28	64.00
50	65.00

. The fitting curves for the four models are shown in Figure 7, and the fitting average errors and standard deviations are shown in

Table 16. The fitting mean errors and standard deviations of case 5.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	0.3389	0.1337	0.5670	0.1332
Fitted standard deviation of error $\sigma$	0.0937	0.0309	0.1621	0.0276

. The specific fitting equations for the four models are as follows:

$$z(t)=33.3919+9.2854\ln (t)$$

(37)

$$z(t)=\frac{t}{0.0229+0.0149\cdot t}$$

(38)

$$z(t)=37.3494+1.8490\cdot t-0.0265\cdot t^2$$

(39)

$$z(t)=123.1825\cdot (\frac{t}{t+1})-72.9417\cdot \arctan (\frac{t}{t+1})$$

(40)

From Table 16, it can be seen that the fitting accuracy of the new model is the highest. This indicates that the new model can more accurately evaluate the compressive strength of concrete.

3.2. Evaluation of Elastic Modulus

Case 6. In reference [30], Case 5 was followed as the experimental design scheme.

Table 17. Elastic modulus (GPa) of case 6.

Age (Unit: day)	Elastic Modulus
1	26.90
2	32.10
3	35.30
5	37.10
7	37.32
10	37.54
20	40.39
28	41.65
50	42.10

presents the experimental data of elastic modulus. The fitting curve, depicted in Figure 8, was obtained using four models. The average fitting error and standard deviation of the four models are stated in

Table 18. The fitting mean errors and standard deviations for elastic modulus of case 6.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	0.1278	0.1701	0.2164	0.0787
Fitted standard deviation $\sigma$	0.0325	0.0425	0.0549	0.0158

. The specific fitting equations for the four models are as follows:

$$z(t)=29.5469+3.6042\ln (t)$$

(41)

$$z(t)=\frac{t}{0.0196+0.0234\cdot t}$$

(42)

$$z(t)=31.1455+0.6973\cdot t-0.0098\cdot t^2$$

(43)

$$z(t)=-16.9105\cdot (\frac{t}{t+1})+74.1154\cdot \arctan (\frac{t}{t+1})$$

(44)

According to the fitting average error and standard deviation of the four models in Table 18, it can be seen that the fitting average error and fitting standard error of the new model are smaller than those of the hyperbolic model, the logarithmic model, and the polynomial model. The average fitting error of the new model is about 61% of the logarithmic model, 46% of the hyperbolic model, and 36% of the polynomial model. Regarding fitting standard deviation, that of the new model is about 48% of that of the logarithmic model, about 37% of that of the hyperbolic model, and 28% of that of the polynomial model. The results indicate that the proposed new evaluation model is more accurate than the other three models in evaluating the elastic modulus of concrete.

Case 7. In reference [34], some concrete cube test blocks were manufactured with a design strength of 90 MPa. The mix proportions of concrete materials are listed in

Table 19. The mix proportions of concrete materials in case 7.

Cement	Slag	Silica Fume	Water	Sand	Stone
0.5	0.4	0.1	0.23	1.2	1.8

. The experimental data of elastic modulus are shown in

Table 20. Elastic modulus of concrete cube in case 7 (GPa).

Age (Unit: hour)	Elastic Modulus
18	10.53
24	18.88
48	22.39
72	28.24
168	30.02

, and the fitting curves are shown in Figure 9. The average fitting error and standard deviation of the models are shown in

Table 21. The fitting mean errors and standard deviations of case 7.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	0.3788	0.3428	0.3174	0.1944
Fitted standard deviation $\sigma$	0.1194	0.1170	0.1182	0.0495

. The specific fitting equations for the four models are as follows:

$$z(t)=-9.6390+8.1827\ln (t)$$

(45)

$$z(t)=\frac{t}{0.8203+0.0278\cdot t}$$

(46)

$$z(t)=5.9162+0.4396\cdot t-0.0018\cdot t^2$$

(47)

$$z(t)=1085.9326\cdot (\frac{t}{t+1})-1341.0266\cdot \arctan (\frac{t}{t+1})$$

(48)

According to Table 21, the new model’s fitting average error and standard deviation are smaller than those of the other models. It has been shown that the new model can more accurately evaluate the elastic modulus of concrete.

Case 8. The components of concrete materials are listed in

Table 22. The components of concrete materials in case 8 (kg/m³).

Cement	Fine Aggregate (Machine Made Sand)	Coarse Aggregate	Water	Water Reducer	Admixture
465.9	478.8	1069.9	125.8	8.2	54.8

. The experimental data of elastic modulus in reference [39] are shown in

Table 23. Elastic modulus of concrete cube in case 8 (GPa).

Age (Unit: day)	Elastic Modulus
2	13.25
3	21.86
4	27.76
5	29.90
6	38.29
7	41.33
14	46.93
28	48.02

. The fitting curves of the four models are shown in Figure 10, and the corresponding fitting errors are shown in

Table 24. The fitting mean errors and standard deviations in case 8.

Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
Fitting mean error $\overline{\delta }$	0.4490	0.4344	0.4345	0.1667
Fitted standard deviation $\sigma$	0.1143	0.1177	0.1210	0.0293

. The specific fitting equations for the four models are as follows:

$$z(t)=8.6594+13.6630\ln (t)$$

(49)

$$z(t)=\frac{t}{0.0749+0.0175\cdot t}$$

(50)

$$z(t)=9.1545+4.8177\cdot t-0.1236\cdot t^2$$

(51)

$$z(t)=344.8215\cdot (\frac{t}{t+1})-367.0881\cdot \arctan (\frac{t}{t+1})$$

(52)

Table 24 shows that the new model’s average error and standard deviation are smaller than those of the hyperbolic, polynomial, and logarithmic models. This again indicates that the new model can better evaluate the elastic modulus of concrete than the existing models. Using Equation (7), the predicted long-term elastic modulus values in cases 6–8 are 41.30 MPa, 32.69 MPa, and 56.51 MPa, respectively. The coarse and fine aggregates in Cases 6 and 7 are both natural sand and gravel, while the fine aggregates in Case 8 are machine-made sand and the coarse aggregates are crushed stone. It can be observed that the type of aggregate has a significant impact on the elastic modulus of concrete, and the mechanism sand used in Case 8 may increase the elastic modulus. The research results of references [46,47] also show that the use of machine-made sand can improve the elastic modulus of concrete to a certain extent. Further research is needed in the future on the impact of aggregate types on elastic modulus of concrete.

3.3. High Strength Concrete and Lightweight Concrete

More types of concrete are further used to validate the new model to show its wider applicability and its practical implications. Cases 9 and 10 are high-strength concrete and Case 11 is lightweight concrete.

Case 9. In reference [43], a concrete mix design was developed by carefully combining different particle sizes of aggregates, setting the adjustment factor of cementitious materials, and determining parameters such as sand ratio, water–cement ratio, and dosage of admixtures. The relevant concrete material components for the three match ratios are listed in

Table 25. The components of concrete materials in case 9 (kg/m³).

Match Ratio	Adjustment Coefficient	Cement	Mineral Admixtures	Microsphere	Silica Fume	Spall	Artificial-Sand	Admixture	Water
1	1.0	182	26	26	17	1203	985	6.2	55
2	1.2	218	31	31	20	1169	956	7.4	66
3	1.5	273	39	39	26	1117	914	9.3	83

. The experimental data of compressive strength are shown in

Table 26. Compressive strength of concrete blocks in case 9 (MPa).

Age (Unit: day)	Compressive Strength
	Match Ratio 1	Match Ratio 2	Match Ratio 3
1	11.5	17.8	26.2
3	23.8	31.5	43.6
7	28.8	40.0	56.8
28	33.3	46.2	60.5
60	37.8	50.3	66.9
90	42.3	57.5	71.6

. Figure 11, Figure 12 and Figure 13 present the fitting curves of the logarithmic, hyperbolic, polynomial, and new models for the three match ratios, respectively. In the Appendix A, Case 9 is also used as an example to elaborate in detail on the fitting process of the new model. The average fitting errors and standard deviations of these models are shown in

Table 27. The fitting mean errors and standard deviations from the four models in case 9.

Match Ratio	Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
1	Fitting mean error $\overline{\delta }$	0.3013	0.3971	0.7499	0.1568
	Fitted standard deviation $\sigma$	0.0894	0.1024	0.2597	0.0380
2	Fitting mean error $\overline{\delta }$	0.2174	0.4132	0.6019	0.1561
	Fitted standard deviation $\sigma$	0.0579	0.1105	0.1989	0.0343
3	Fitting mean error $\overline{\delta }$	0.2500	0.3215	0.5478	0.1036
	Fitted standard deviation $\sigma$	0.0761	0.0879	0.1858	0.0281

. The specific fitting equations for the four models are as follows:

For the first match ratio, one obtains

$$z(t)=14.4787+6.0536\ln (t)$$

(53)

$$z(t)=\frac{t}{0.0964+0.0235\cdot t}$$

(54)

$$z(t)=19.0340+0.5839\cdot t-0.0038\cdot t^2$$

(55)

$$z(t)=131.9067\cdot (\frac{t}{t+1})-118.1620\cdot \arctan (\frac{t}{t+1})$$

(56)

For the second match ratio, one obtains

$$z(t)=20.9103+7.8711\ln (t)$$

(57)

$$z(t)=\frac{t}{0.0667+0.0174\cdot t}$$

(58)

$$z(t)=26.8811+0.7510\cdot t-0.0048\cdot t^2$$

(59)

$$z(t)=164.1922\cdot (\frac{t}{t+1})-141.7374\cdot \arctan (\frac{t}{t+1})$$

(60)

For the third match ratio, one obtains

$$z(t)=31.5073+9.1214\ln (t)$$

(61)

$$z(t)=\frac{t}{0.0379+0.0139\cdot t}$$

(62)

$$z(t)=38.2221+0.9551\cdot t-0.0067\cdot t^2$$

(63)

$$z(t)=167.9351\cdot (\frac{t}{t+1})-126.4422\cdot \arctan (\frac{t}{t+1})$$

(64)

To quantify the improved accuracy over existing models,

Table 28. The relative ratios of fitting error and standard deviation in case 9 (based on polynomial model).

Match Ratio	Relative Ratios	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
1	Fitting mean error	0.4018	0.5295	1.0000	0.2091
	Fitted standard deviation	0.3442	0.3943	1.0000	0.1463
2	Fitting mean error	0.3612	0.6865	1.0000	0.2593
	Fitted standard deviation	0.2911	0.5556	1.0000	0.1724
3	Fitting mean error	0.4564	0.5869	1.0000	0.1891
	Fitted standard deviation	0.4096	0.4731	1.0000	0.1512

shows the relative ratios of fitting error and standard deviation for each model, when the error and standard deviation of the polynomial model are set to 1.

From Table 28, it can be seen that the relative values of the fitting error and standard deviation of the new model are the smallest, which are approximately 20% of the values of the polynomial model. These results indicate that the new model has significantly improved fitting accuracy compared to existing models. The practical implications of these results mainly lie in the precise correspondence between compressive strength and time can be obtained via the fitting equation of the new model. For example, when using concrete to manufacture large-volume box beams, the prestressing force of the steel bars should be applied as early as possible in order to prevent concrete cracks. In engineering practice, it is generally required that the compressive strength of concrete reach at least 25 MPa before prestressing can be applied, which requires accurate estimation of the corresponding time when the compressive strength reaches 25 MPa. This goal can be achieved via the specific fitting equation obtained from the new model. For concrete with the first match ratio, the time $t$ corresponding to $z(t)$ = 25 MPa obtained from the fitting Equation (56) of the new model is $t$ = 3.70 d. For concrete with the second match ratio, the time $t$ corresponding to $z(t)$ = 25 MPa obtained from the fitting Equation (60) of the new model is $t$ = 1.85 d. For concrete with the third match ratio, the time $t$ corresponding to $z(t)$ = 25 MPa obtained from the fitting Equation (64) of the new model is $t$ = 0.98 d. These results can be used to guide prestressed construction in bridge engineering.

Case 10. In reference [44], two types of high-strength concrete test blocks were designed: natural aggregate concrete and self-compacting aggregate concrete. These test blocks contained three different design strengths. The 100 mm × 100 mm × 100 mm concrete specimens were manufactured and tested. The mix proportions of concrete materials are listed in

Table 29. Mix proportions of concrete in case 10 (kg/m³).

Number	Water	Cement	Fly Ash	Sand	Natural Aggregate	Water Reducer (%)	Water–cement Ratio (%)
NA-C-30	189.0	420	0	680.0	1110.0	0.07	45
NA-C-40	171.0	450	0	640.0	1138.0	0.33	38
NA-C-50	189.0	450	0	670.0	1090.0	0.10	42
NA-SCC-30	192.0	336	144	839.0	839.0	1.00	57
NA-SCC-40	176.8	364	156	826.6	826.0	1.20	49
NA-SCC-50	180.0	350	150	835.0	835.0	1.20	51

. The experimental data of their compressive strength are shown in

Table 30. Compressive strength of concrete blocks in case 10 (MPa).

Age (Unit: day)	Compressive Strength
	NA-C-30	NA-C-40	NA-C-50	NA-SCC-30	NA-SCC-40	NA-SCC-50
7	21.67	29.43	29.75	19.37	24.87	30.73
28	44.17	50.71	53.40	35.33	49.40	53.20
56	45.70	52.75	55.47	40.53	55.60	55.75
90	47.22	53.86	54.72	40.57	57.91	57.13

. Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 show the fitting curves of the four models, and

Table 31. The fitting mean errors and standard deviations from the four models in case 10.

Number	Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
NA-C-30	Fitting mean error $\overline{\delta }$	0.1895	0.1700	0.1715	0.0517
	Fitted standard deviation $\sigma$	0.0583	0.0690	0.0395	0.0131
NA-C-40	Fitting mean error $\overline{\delta }$	0.1445	0.1201	0.1281	0.0362
	Fitted standard deviation $\sigma$	0.0409	0.0489	0.0296	0.0100
NA-C-50	Fitting mean error $\overline{\delta }$	0.1780	0.1970	0.1322	0.0627
	Fitted standard deviation $\sigma$	0.0423	0.0776	0.0301	0.0185
NA-SCC-30	Fitting mean error $\overline{\delta }$	0.1238	0.0899	0.0858	0.0343
	Fitted standard deviation $\sigma$	0.0153	0.0320	0.0205	0.0095
NA-SCC-40	Fitting mean error $\overline{\delta }$	0.1279	0.0811	0.1219	0.0195
	Fitted standard deviation $\sigma$	0.0303	0.0301	0.0291	0.0055
NA-SCC-50	Fitting mean error $\overline{\delta }$	0.1398	0.1091	0.1260	0.0295
	Fitted standard deviation $\sigma$	0.0394	0.0444	0.0293	0.0081

presents the fitting average errors and standard deviations. The specific fitting equations for the four models are as follows:

For natural aggregate concrete with a design strength of 30 MPa (NA-C-30), one obtains

$$z(t)=4.3947+10.2281\ln (t)$$

(65)

$$z(t)=\frac{t}{0.1451+0.0194\cdot t}$$

(66)

$$z(t)=17.1393+1.0002\cdot t-0.0075\cdot t^2$$

(67)

$$z(t)=607.0926\cdot (\frac{t}{t+1})-708.3099\cdot \arctan (\frac{t}{t+1})$$

(68)

For natural aggregate concrete with a design strength of 40 MPa (NA-C-40), one obtains

$$z(t)=12.7301+9.8404\ln (t)$$

(69)

$$z(t)=\frac{t}{0.0924+0.0174\cdot t}$$

(70)

$$z(t)=24.9121+0.9669\cdot t-0.0073\cdot t^2$$

(71)

$$z(t)=564.4074\cdot (\frac{t}{t+1})-645.6422\cdot \arctan (\frac{t}{t+1})$$

(72)

For natural aggregate concrete with a design strength of 50 MPa (NA-C-50), one obtains

$$z(t)=12.8294+10.2890\ln (t)$$

(73)

$$z(t)=\frac{t}{0.0787+0.0171\cdot t}$$

(74)

$$z(t)=24.4671+1.1061\cdot t-0.0087\cdot t^2$$

(75)

$$z(t)=603.5390\cdot (\frac{t}{t+1})-692.4944\cdot \arctan (\frac{t}{t+1})$$

(76)

For self-compacting aggregate concrete with a design strength of 30 MPa (NA-SCC-30), one obtains

$$z(t)=3.7122+8.7625\ln (t)$$

(77)

$$z(t)=\frac{t}{0.1778+0.0223\cdot t}$$

(78)

$$z(t)=14.7409+0.8316\cdot t-0.0061\cdot t^2$$

(79)

$$z(t)=503.7077\cdot (\frac{t}{t+1})-586.3501\cdot \arctan (\frac{t}{t+1})$$

(80)

For self-compacting aggregate concrete with a design strength of 40 MPa (NA-SCC-40), one obtains

$$z(t)=0.9832+13.3191\ln (t)$$

(81)

$$z(t)=\frac{t}{0.1544+0.0154\cdot t}$$

(82)

$$z(t)=18.6628+1.1919\cdot t-0.0085\cdot t^2$$

(83)

$$z(t)=772.2900\cdot (\frac{t}{t+1})-905.7117\cdot \arctan (\frac{t}{t+1})$$

(84)

For self-compacting aggregate concrete with a design strength of 50 MPa (NA-SCC-50), one obtains

$$z(t)=12.5453+10.6228\ln (t)$$

(85)

$$z(t)=\frac{t}{0.0926+0.0164\cdot t}$$

(86)

$$z(t)=25.8732+1.0270\cdot t-0.0077\cdot t^2$$

(87)

$$z(t)=608.5387\cdot (\frac{t}{t+1})-697.6181\cdot \arctan (\frac{t}{t+1})$$

(88)

To quantify improved accuracy over existing models,

Table 32. The relative ratios of fitting error and standard deviation in case 10 (based on hyperbolic model).

Number	Relative Ratios	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
NA-C-30	Fitting mean error	1.1147	1.0000	1.0088	0.3041
	Fitted standard deviation	0.8449	1.0000	0.5725	0.1899
NA-C-40	Fitting mean error	1.2032	1.0000	1.0666	0.3014
	Fitted standard deviation	0.8364	1.0000	0.6053	0.2045
NA-C-50	Fitting mean error	0.9036	1.0000	0.6711	0.3183
	Fitted standard deviation	0.5451	1.0000	0.3879	0.2384
NA-SCC-30	Fitting mean error	1.3771	1.0000	0.9544	0.3815
	Fitted standard deviation	0.4781	1.0000	0.6406	0.2969
NA-SCC-40	Fitting mean error	1.5771	1.0000	1.5031	0.2404
	Fitted standard deviation	1.0066	1.0000	0.9668	0.1827
NA-SCC-50	Fitting mean error	1.2814	1.0000	1.1549	0.2704
	Fitted standard deviation	0.8874	1.0000	0.6599	0.1824

shows the relative ratios of fitting error and standard deviation for each model, when the error and standard deviation of the hyperbolic model are set to 1.

From Table 32, one can observe that the relative values of the fitting error and standard deviation of the new model are the smallest, approximately 20%–30% of the values of the hyperbolic model. These results again indicate that the new model has significantly improved fitting accuracy compared to existing models. These results can also be used to accurately evaluate the corresponding time when the compressive strength of concrete will reach 25 MPa, in order to guide prestressed construction in practical engineering. Without loss of generality, for NA-C-50, the time $t$ corresponding to $z(t)$ = 25 MPa obtained from the fitting Equation (76) of the new model is $t$ = 5.63 d. For NA-SCC-50, the time $t$ corresponding to $z(t)$ = 25 MPa obtained from the fitting Equation (88) of the new model is $t$ = 5.50 d.

In order to explore the relationship between the fitting parameters ($a$ and $b$) of the new model and the water–cement ratio (w/c) of concrete, Figure 20 shows the variation curves of parameters $a$, $b$, and $a+b\cdot \frac{\pi }{4}$ with the water–cement ratio. From Figure 20, it can be seen that the variation patterns of the absolute values of parameters $a$ and $b$ are basically consistent. When the water–cement ratio is about 50%, the long-term strength (i.e., $a+b\cdot \frac{\pi }{4}$) of concrete is relatively great, up to 60 MPa.

Case 11. In reference [45], some lightweight concrete specimens with dimensions of 100 mm × 100 mm × 100 mm were manufactured using CL30 grade concrete, cured under standard curing conditions. The composition of the concrete can be found in

Table 33. Mix proportions of concrete in case 11 (kg/m³).

Cement	Water	Sand	Coarse Aggregate
386	244	705	591

. The test results of the compressive strength for the three batches are shown in

Table 34. Compressive strength of concrete blocks in case 11 (MPa).

Age (Unit: day)	Compressive Strength
	Batch 1	Batch 2	Batch 3
3	22.1	18.8	16.8
7	32.0	28.5	27.7
14	35.2	35.7	34.0
21	38.3	36.8	38.0
28	39.7	37.3	38.7

. Figure 21, Figure 22 and Figure 23 show the fitted curves of the four models based on experimental data. The fitting average error and standard deviation are listed in

Table 35. The fitting mean errors and standard deviations of the four models in case 11.

Batch	Index	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
1	Fitting mean error $\overline{\delta }$	0.0908	0.0448	0.1215	0.0390
	Fitted standard deviation $\sigma$	0.0317	0.0153	0.0342	0.0121
2	Fitting mean error $\overline{\delta }$	0.1182	0.0798	0.956	0.0398
	Fitted standard deviation $\sigma$	0.0288	0.0261	0.0210	0.0116
3	Fitting mean error $\overline{\delta }$	0.0946	0.0523	0.1164	0.0441
	Fitted standard deviation $\sigma$	0.0204	0.0148	0.0347	0.0076

. The fitting equations for the four models are as follows:

For batch 1, one obtains

$$z(t)=15.0016+7.6525\ln (t)$$

(89)

$$z(t)=\frac{t}{0.0660+0.0230\cdot t}$$

(90)

$$z(t)=18.9782+1.7046\cdot t-0.0352\cdot t^2$$

(91)

$$z(t)=180.1339\cdot (\frac{t}{t+1})-175.5051\cdot \arctan (\frac{t}{t+1})$$

(92)

For batch 2, one obtains

$$z(t)=10.7864+8.5543\ln (t)$$

(93)

$$z(t)=\frac{t}{0.0789+0.0236\cdot t}$$

(94)

$$z(t)=13.5875+2.2685\cdot t-0.0517\cdot t^2$$

(95)

$$z(t)=220.5330\cdot (\frac{t}{t+1})-227.9646\cdot \arctan (\frac{t}{t+1})$$

(96)

For batch 3, one obtains

$$z(t)=6.9371+9.9926\ln (t)$$

(97)

$$z(t)=\frac{t}{0.1061+0.0218\cdot t}$$

(98)

$$z(t)=11.5844+2.3295\cdot t-0.0492\cdot t^2$$

(99)

$$z(t)=268.1057\cdot (\frac{t}{t+1})-286.9670\cdot \arctan (\frac{t}{t+1})$$

(100)

To quantify the improved accuracy over existing models,

Table 36. The relative ratios of fitting error and standard deviation in case 11 (based on logarithmic model).

Batch	Relative Ratios	Logarithmic Model	Hyperbolic Model	Polynomial Model	Universal Curve Model
1	Fitting mean error	1.0000	0.4934	1.3381	0.4295
	Fitted standard deviation	1.0000	0.4826	1.0789	0.3817
2	Fitting mean error	1.0000	0.6751	8.0880	0.3367
	Fitted standard deviation	1.0000	0.9063	0.7292	0.4028
3	Fitting mean error	1.0000	0.5529	1.2304	0.4662
	Fitted standard deviation	1.0000	0.7255	1.7010	0.3725

shows the relative ratios of fitting error and standard deviation for each model, when the error and standard deviation of the logarithmic model are set to 1.

From Table 36, one can observe that the relative values of the fitting error and standard deviation of the new model are the smallest, approximately 30%–40% of the values of the logarithmic model. These results indicate that the fitting equation obtained from the new model can more accurately evaluate the correspondence between compressive strength and time. The fitting equation of the new model can be used not only to guide prestressed construction, as in Cases 9 and 10, but also to guide the time for template removal. For example, if the template can be removed when the compressive strength reaches 15 MPa, the removal time for the first batch of concrete can be calculated from the fitting Equation (92) of the new model as $t$ = 1.73 d. The removal time for the second batch of concrete can be calculated from the fitting Equation (96) as $t$ = 2.31 d. The removal time for the third batch of concrete can be calculated from the fitting Equation (100) as $t$ = 2.74 d.

4. Conclusions

This article proposes a new curve model for evaluating the mechanical properties of concrete. This model can evaluate the mechanical properties of concrete at different ages by fitting a small amount of experimental data. The model was validated using multiple sets of experimental data. Based on the calculation results, the following main conclusions can be drawn:

• Logarithmic models and exponential models have similar advantages and disadvantages. Both models are incremental functions, which align with the law of mechanical properties of concrete increasing with time in engineering practice, and both lack a point of $t$ = 0. The hyperbolic model can gradually approach a fixed value as time increases, which is consistent with the fact that the mechanical properties of concrete remain unchanged in the later stage. However, when dealing with some very discrete data, the fitting accuracy of the logarithmic, exponential, and hyperbolic models is not very good. The advantage of the polynomial model is that its domain of definition includes the point $t$ = 0. However, its fitting function is a monotonically increasing function. It cannot be used for the prediction of the mechanical properties of concrete in the later stage.
• The new model proposed in this article can be seen as a combination of the hyperbolic and arctangent functions. This model makes up for the deficiencies of the existing models and includes the point t = 0. While it tends toward infinity, the function of this new model can approach a specific value, which is in line with the fact that the mechanical properties of concrete remain unchanged in the later stages. In addition, the new model only needs to fit two parameters, making it easier to use in practical engineering than the three-parameter model.
• Based on the case studies of multiple sets of experimental data, the results show that the new model proposed in this article can evaluate concrete’s compressive strength and elastic modulus. This model can evaluate the mechanical properties of concrete under different curing environments and concrete strength levels and has a broader range of applications in practical engineering.

It should be noted that this article mainly discusses the law of changes in the mechanical properties of concrete over time, and other factors that affect the mechanical properties of concrete are not fully considered. The proposed model cannot simultaneously establish the relationship between multiple factors and the mechanical properties of concrete like machine learning. However, the proposed model only requires a small amount of experimental data to establish the mathematical equation for evaluation. In the case of insufficient experimental data, the proposed model can be combined with ANNs to simulate and generate more data for the training of ANNs, thereby improving the generalization ability of the ANN model. Further research is needed in the future to verify the fitting and evaluation capabilities of this new model under more complex conditions. This new model may also be applicable to other cementitious materials besides concrete. In subsequent studies, relevant experiments on other cementitious materials can be conducted to verify the feasibility of this dual parameter curve model.